Directional Multi-Resonant Micro-Electromechanical System Acoustic Sensor for Low Frequency Detection
Abstract
:1. Introduction
1.1. Subwavelength-Sized Directional Sensors
1.2. Resonant MEMS Sensors
1.3. Multi-Resonant MEMS Sensors
1.4. Environmental Sensing
2. Design and Modeling
2.1. Design Requirements
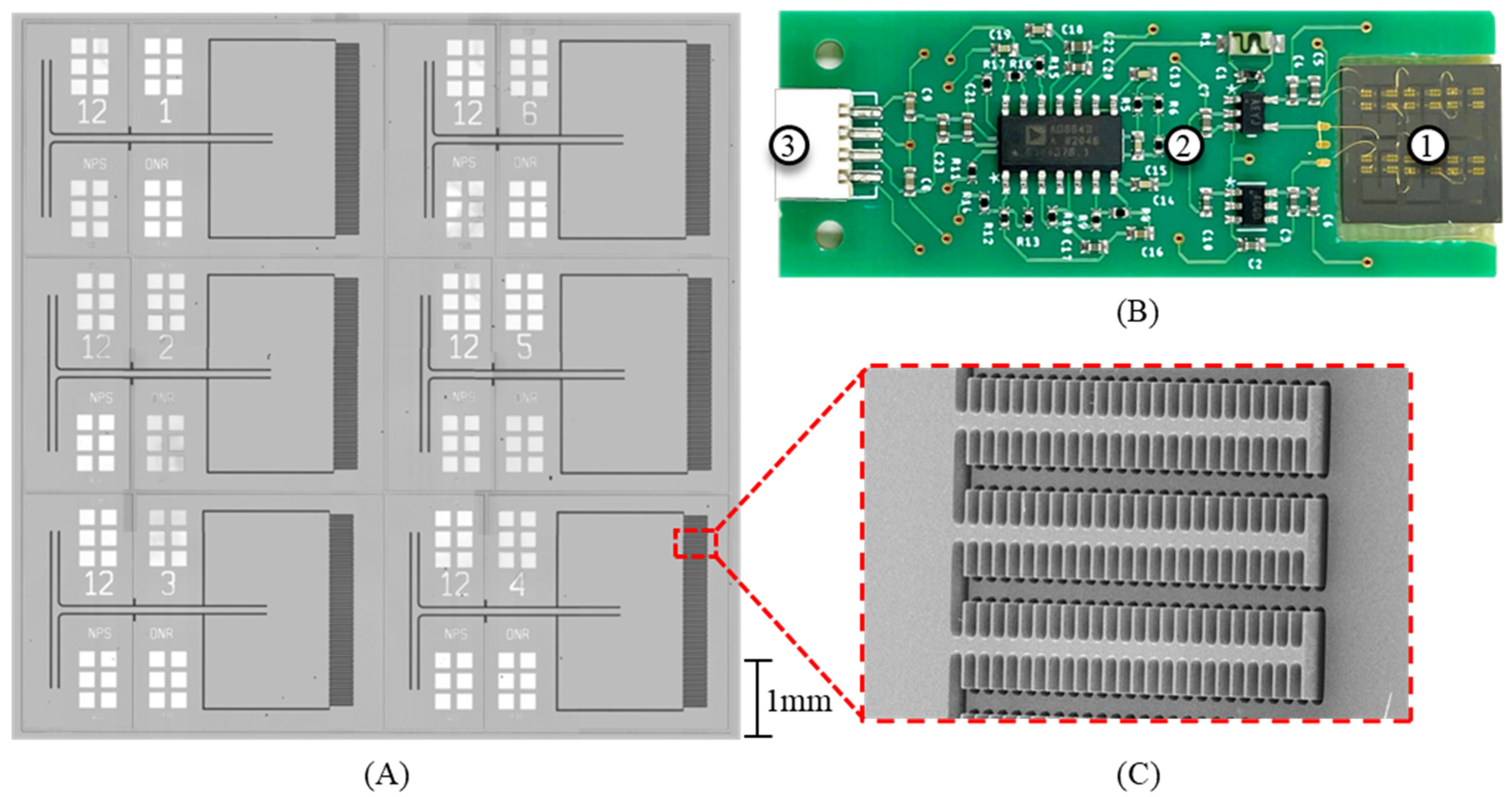
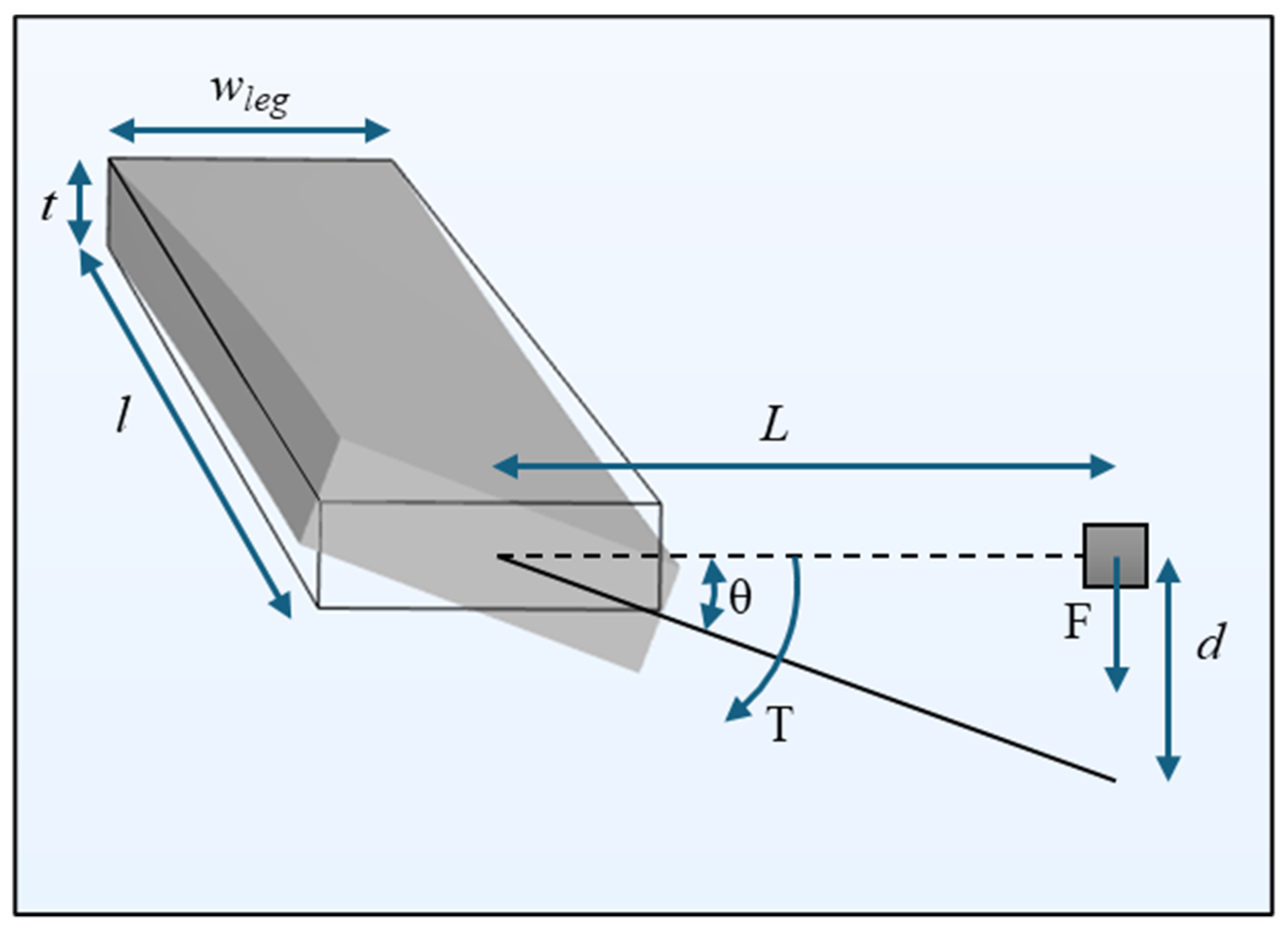
2.2. Design Parameters
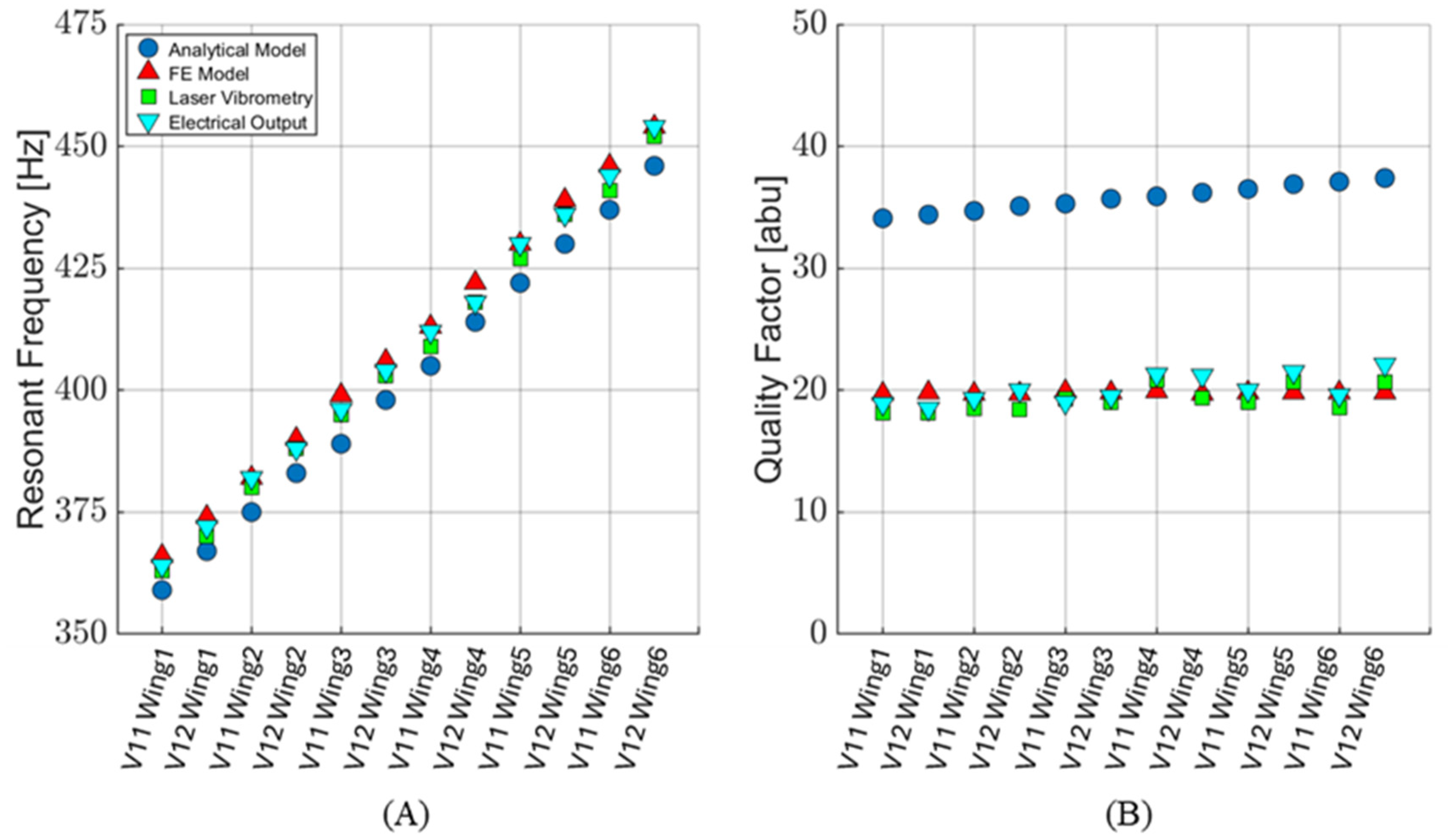
2.3. Analytical Modeling
2.4. Finite Element Modeling
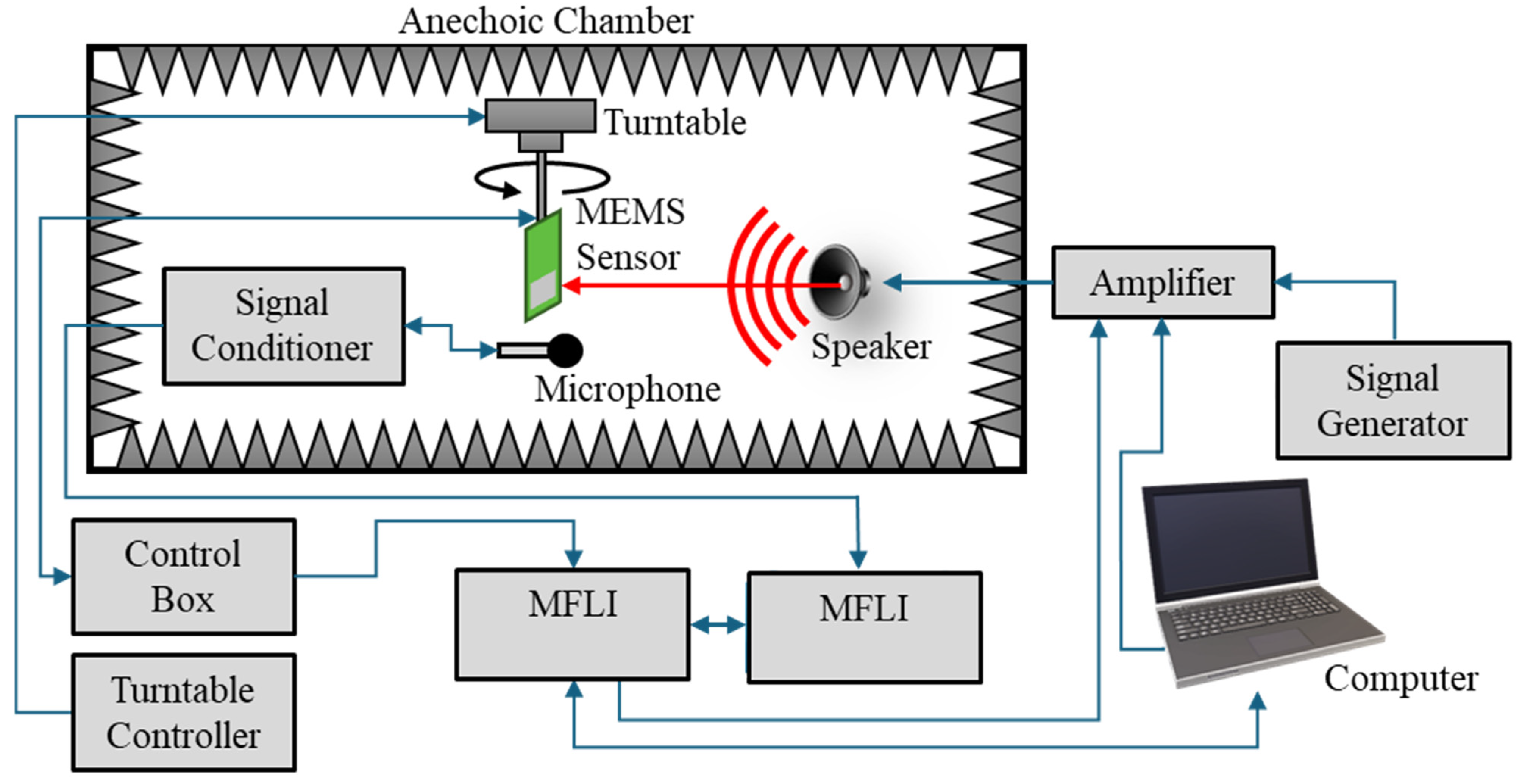
3. Experimental Methods
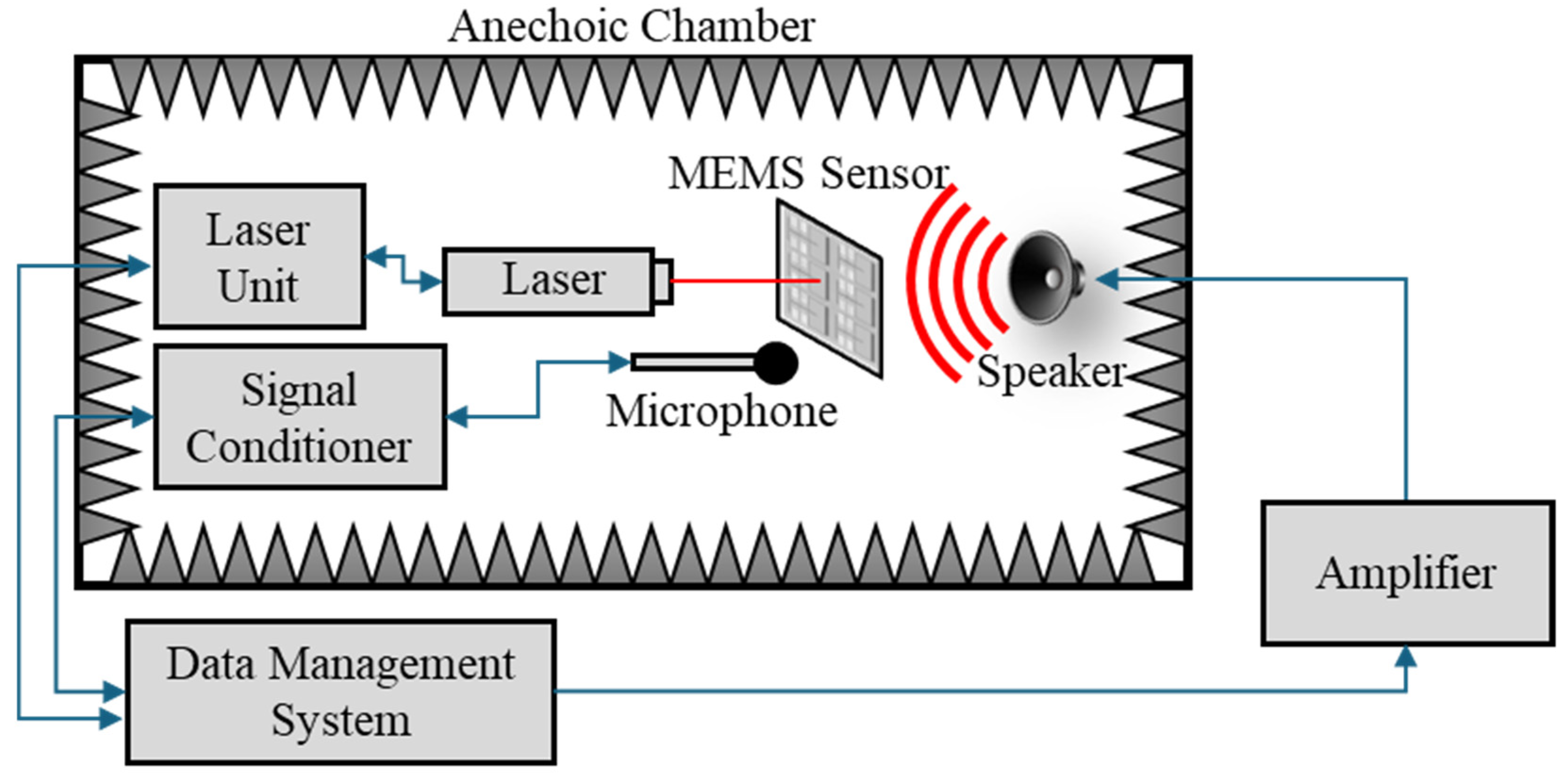
3.1. Mechanical Sensitivity
3.2. Electrical Characterization in Air
3.3. Underwater Electrical Characterization
4. Experimental Results
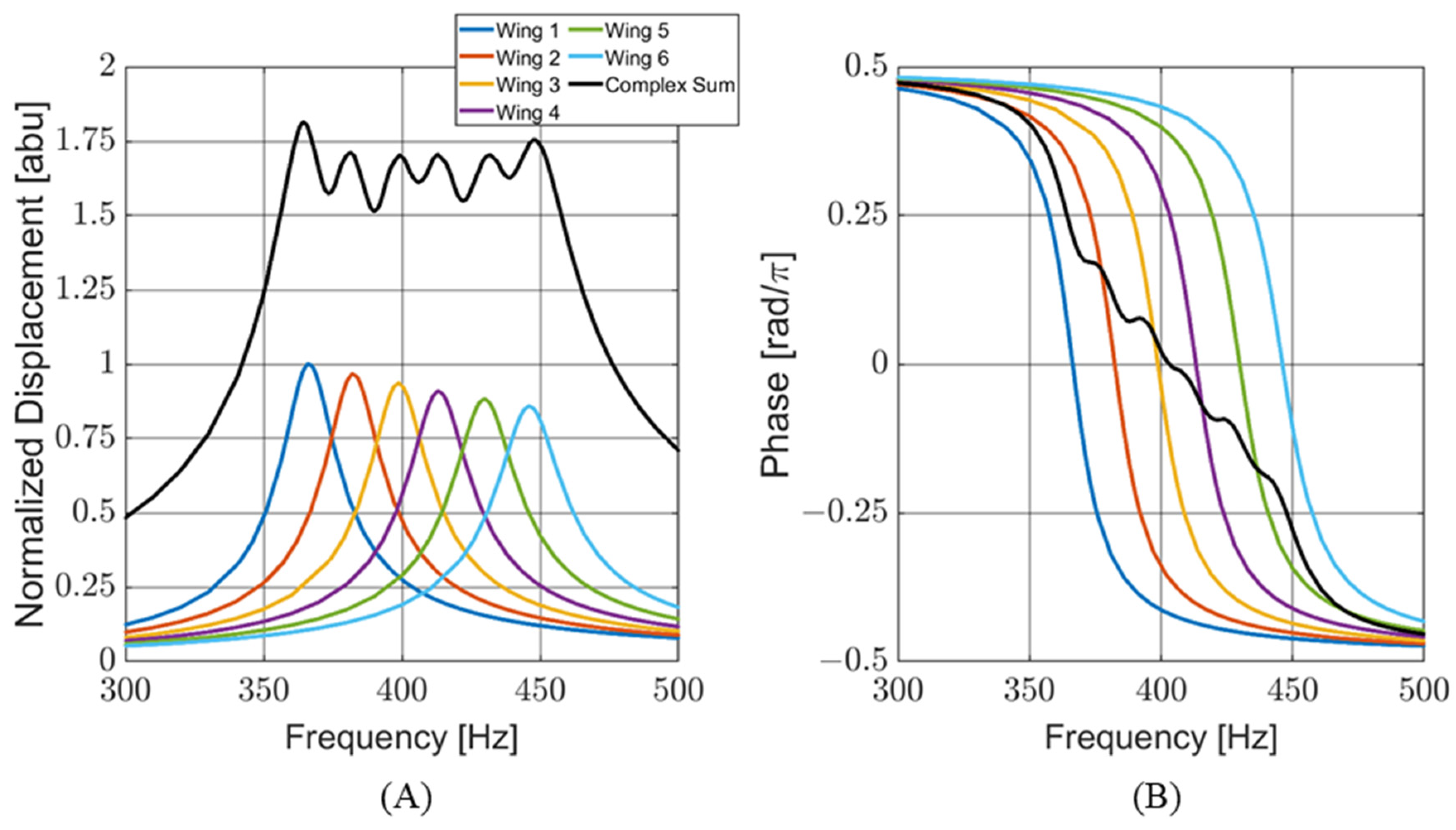
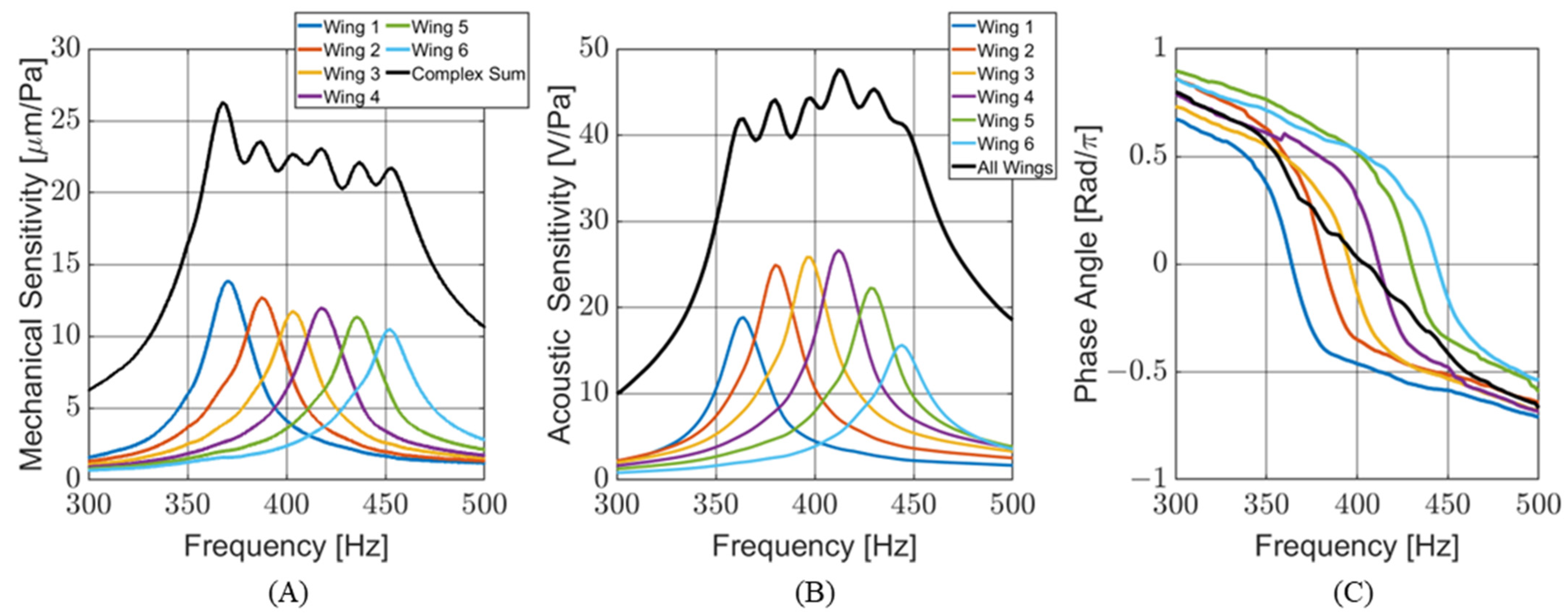
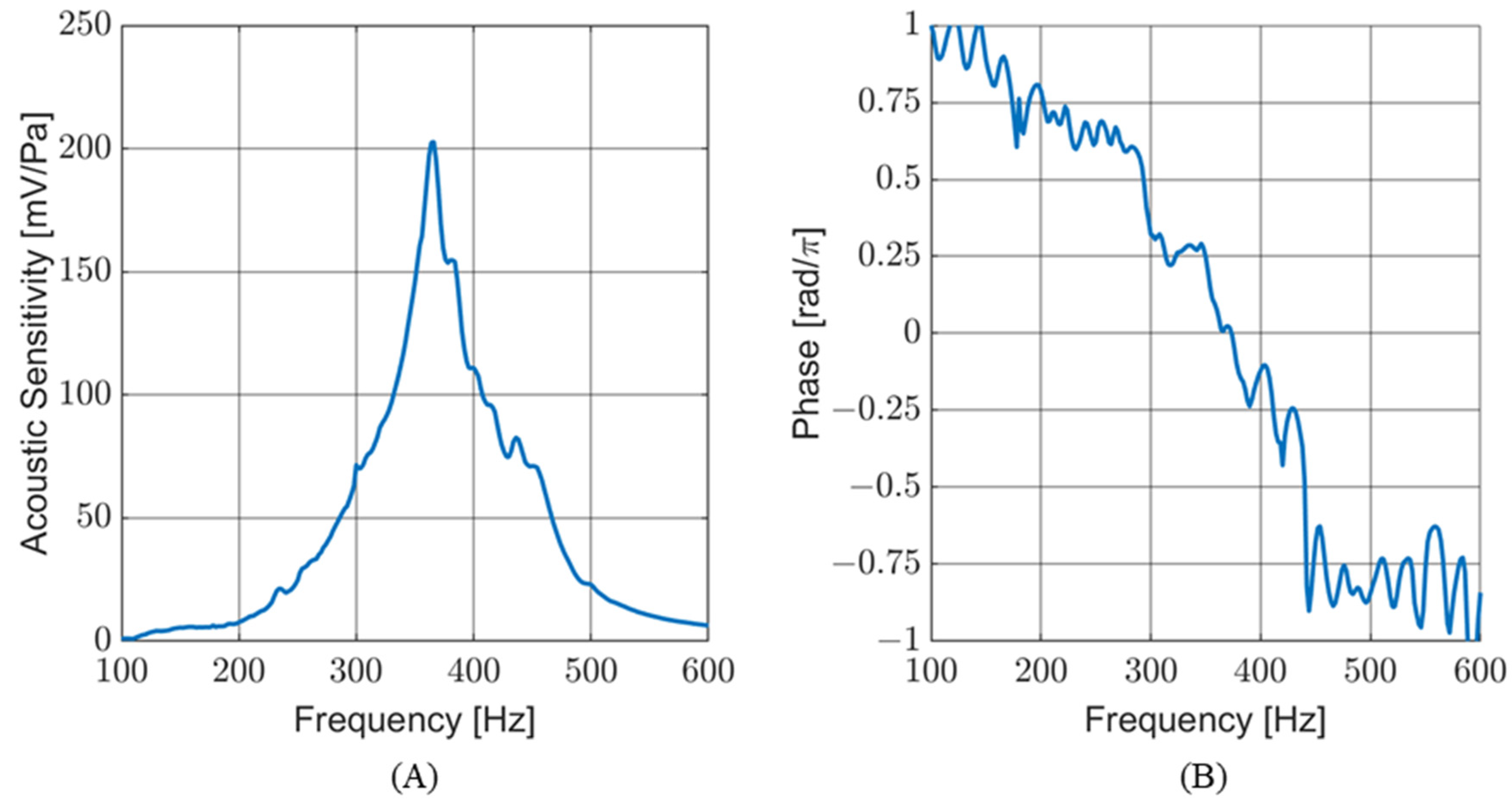
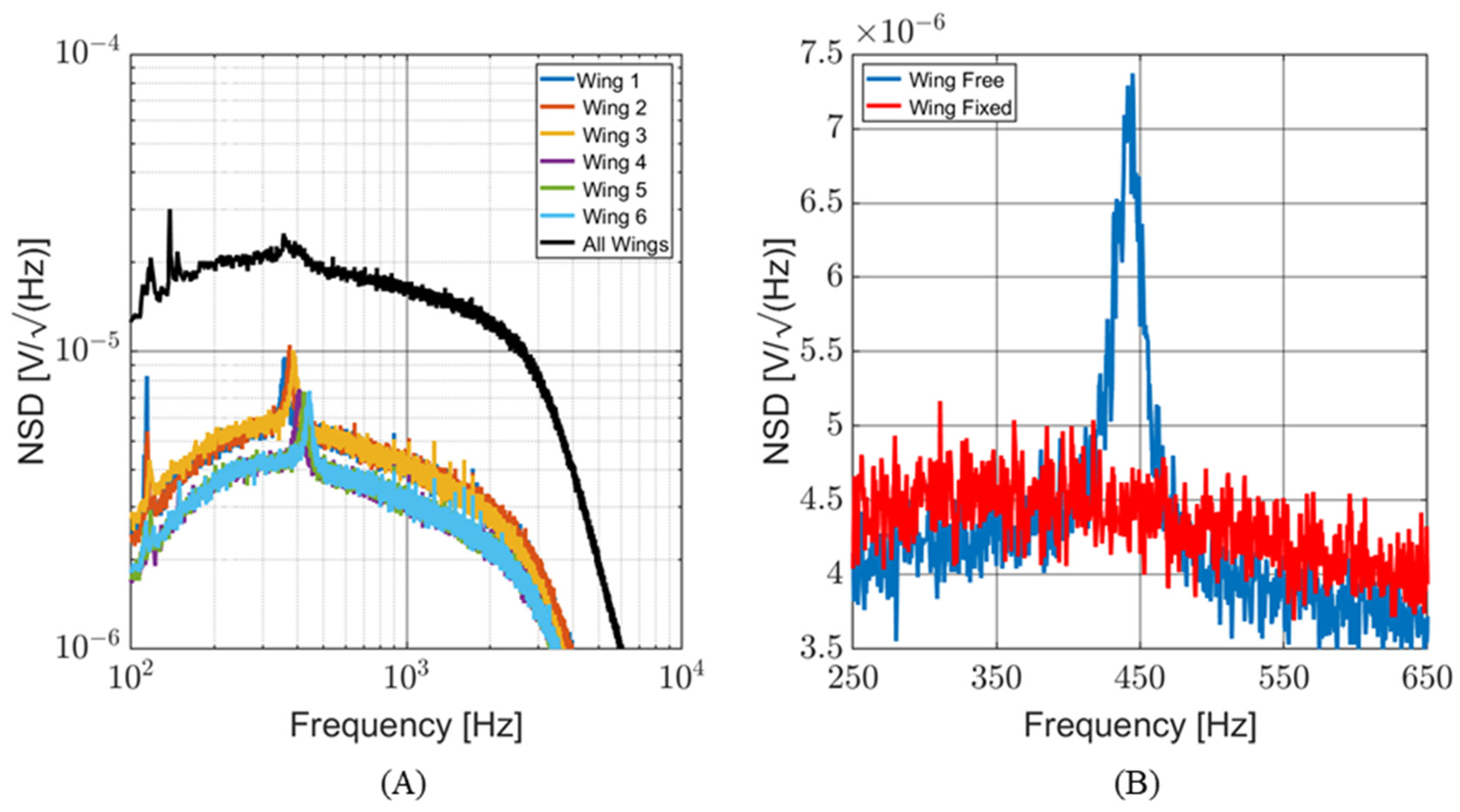
4.1. Frequency Response
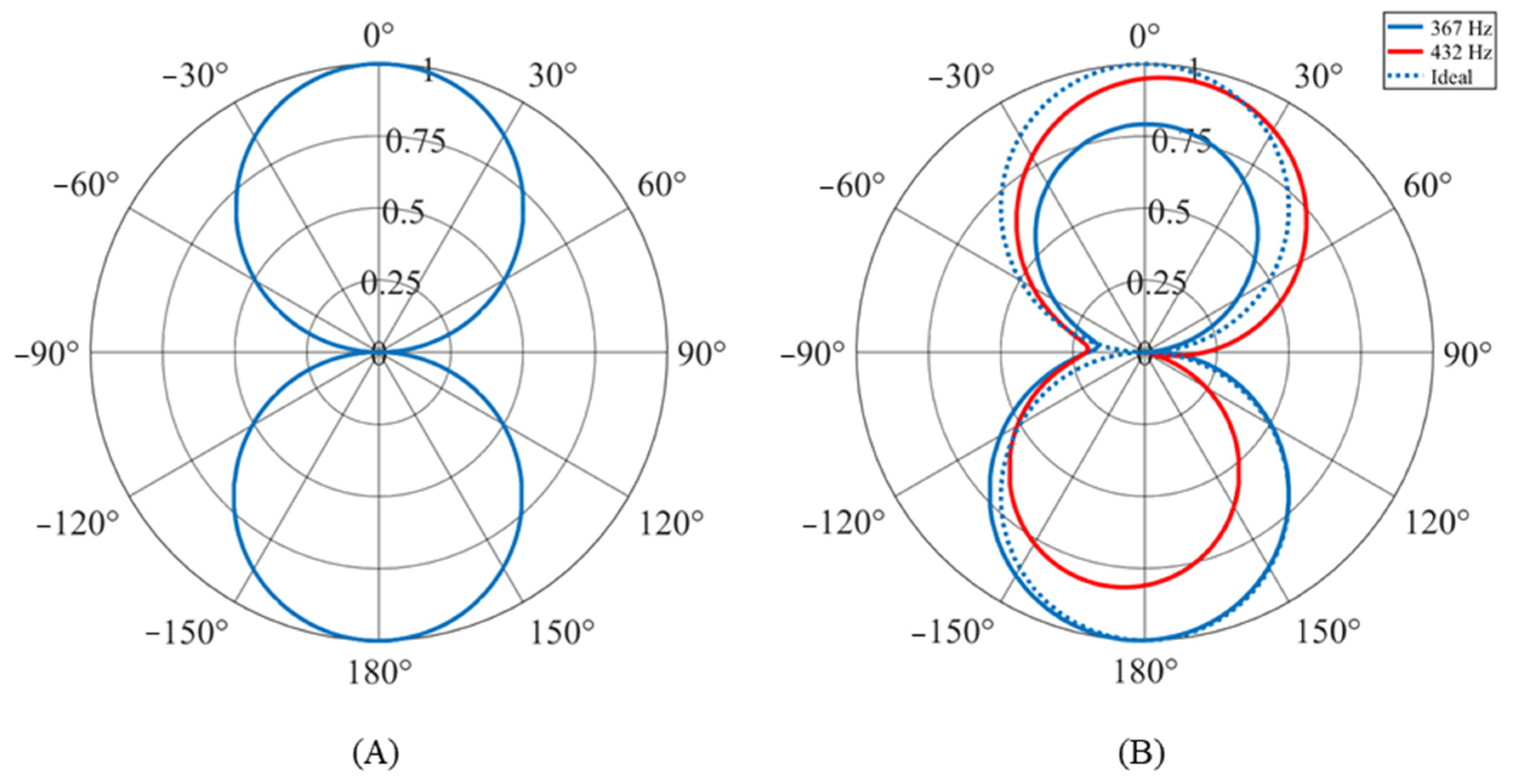
4.2. Directionality
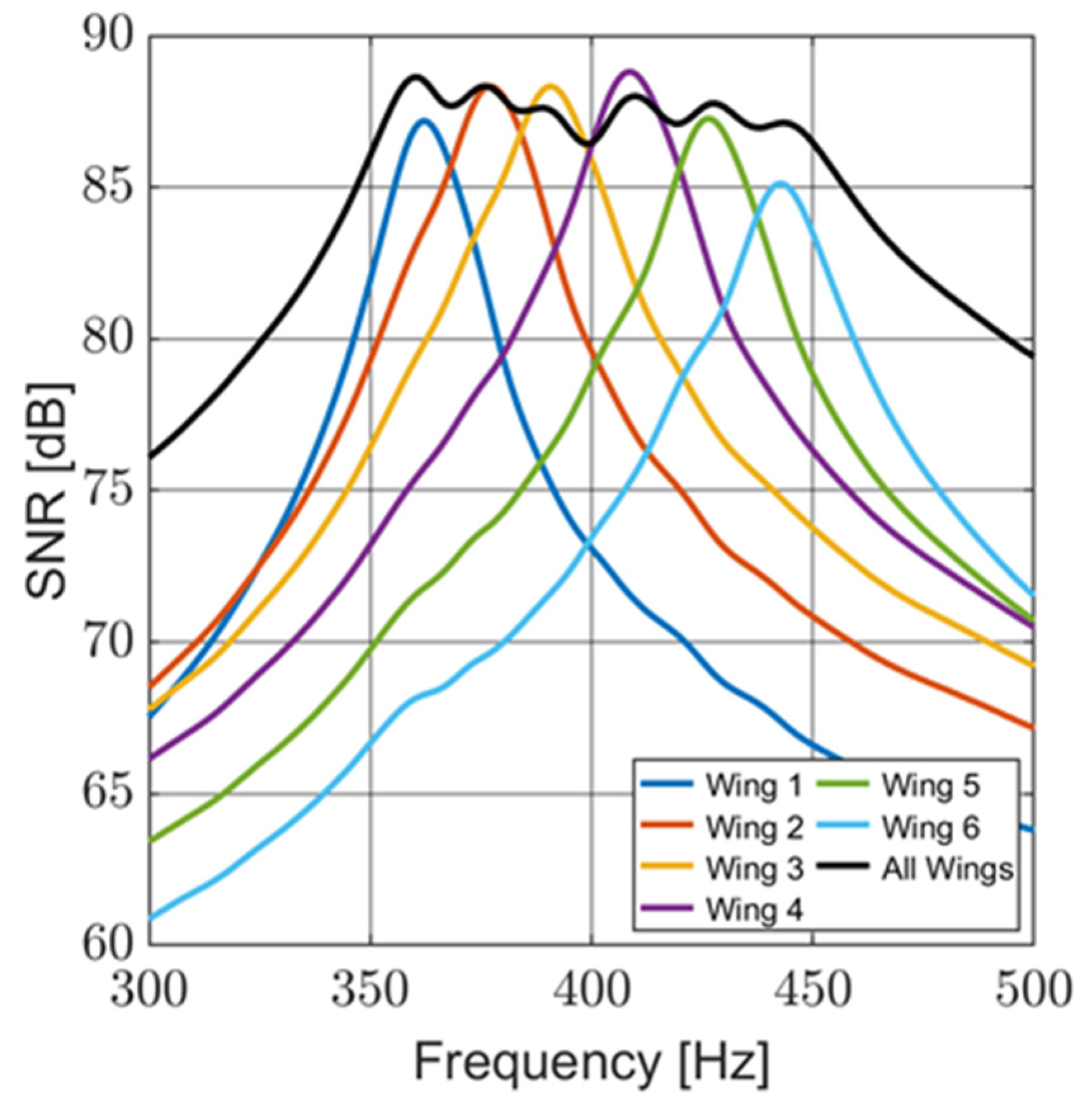
4.3. Signal-to-Noise Ratio
5. Discussion and Conclusions
5.1. Sensor Characterization
5.2. Comparison with Similar Sensors
5.3. Improving Sensor Designs
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schoess, J.N.; Zook, J.D. Test results of a resonant integrated microbeam sensor (RIMS) for acoustic emission monitoring. J. Intell. Mater. Syst. Struct. 1998, 9, 947–951. [Google Scholar] [CrossRef]
- Rahaman, A.; Kim, B. Microscale Devices for Biomimetic Sound Source Localization: A Review. J. Microelectromech. Syst. 2022, 31, 9–18. [Google Scholar] [CrossRef]
- Zhou, J.; Miles, R.N. Directional Sound Detection by Sensing Acoustic Flow. IEEE Sens. Lett. 2018, 2, 1501204. [Google Scholar] [CrossRef]
- Lee, T.; Nomura, T.; Su, X.; Iizuka, H. Fano-Like Acoustic Resonance for Subwavelength Directional Sensing: 0–360 Degree Measurement. Adv. Sci. 2020, 7, 1903101. [Google Scholar] [CrossRef]
- Chen, T.; Jiao, J.; Yu, D. Strongly coupled phononic crystals resonator with high energy density for acoustic enhancement and directional sensing. J. Sound Vib. 2022, 529, 116911. [Google Scholar] [CrossRef]
- Chen, T.; Wang, C.; Yu, D. Pressure amplification and directional acoustic sensing based on a gradient metamaterial coupled with space-coiling structure. Mech. Syst. Signal Process. 2022, 181, 109499. [Google Scholar] [CrossRef]
- Rayburn, R. Eargle’s The Microphone Book: From Mono to Stereo to Surround—A Guide to Microphone Design and Application, 3rd ed.; Routledge: New York, NY, USA, 2011; ISBN 978-0-240-82078-1. [Google Scholar]
- Rahaman, A.; Kim, B. Fly-Inspired MEMS Directional Acoustic Sensor for Sound Source Direction. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 905–908. [Google Scholar] [CrossRef]
- Rahaman, A.; Kim, B. Sound source localization by Ormia ochracea inspired low–noise piezoelectric MEMS directional microphone. Sci. Rep. 2020, 10, 9545. [Google Scholar] [CrossRef] [PubMed]
- Rahaman, A.; Kim, B. AI speaker: A scope of utilizing sub–wavelength directional sensing of bio–inspired MEMS directional microphone. In Proceedings of the 2020 IEEE SENSORS, Rotterdam, The Netherlands, 25–28 October 2020; pp. 1–4. [Google Scholar]
- Espinoza, A.; Alves, F.; Rabelo, R.; Da Re, G.; Karunasiri, G. Fabrication of MEMS Directional Acoustic Sensors for Underwater Operation. Sensors 2020, 20, 1245. [Google Scholar] [CrossRef] [PubMed]
- Rabelo, R.C.; Alves, F.D.; Karunasiri, G. Electronic phase shift measurement for the determination of acoustic wave DOA using single MEMS biomimetic sensor. Sci. Rep. 2020, 10, 12714. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Omori, T.; Watabe, K.; Toshiyoshi, H. Improved Piezoelectric MEMS Acoustic Emission Sensors. In Proceedings of the 2021 21st International Conference on Solid-State Sensors, Actuators and Microsystems (Transducers), Orlando, FL, USA, 20–24 June 2021; pp. 238–241. [Google Scholar]
- Li, Y.; Omori, T.; Watabe, K.; Toshiyoshi, H. Bandwidth and Sensitivity Enhancement of Piezoelectric MEMS Acoustic Emission Sensor Using Multi-Cantilevers. In Proceedings of the 2022 IEEE 35th International Conference on Micro Electro Mechanical Systems Conference (MEMS), Tokyo, Japan, 9–13 January 2022; pp. 868–871. [Google Scholar] [CrossRef]
- Rahaman, A.; Kim, B. An mm-sized biomimetic directional microphone array for sound source localization in three dimensions. Microsyst. Nanoeng. 2022, 8, 66. [Google Scholar] [CrossRef] [PubMed]
- Ivancic, J.; Karunasiri, G.; Alves, F. Directional Resonant MEMS Acoustic Sensor and Associated Acoustic Vector Sensor. Sensors 2023, 23, 8217. [Google Scholar] [CrossRef] [PubMed]
- Baumgartel, L.; Vafanejad, A.; Chen, S.-J.; Kim, E.S. Resonance-Enhanced Piezoelectric Microphone Array for Broadband or Prefiltered Acoustic Sensing. J. Microelectromech. Syst. 2013, 22, 107–114. [Google Scholar] [CrossRef]
- Shkel, A.A.; Baumgartel, L.; Kim, E.S. A resonant piezoelectric microphone array for detection of acoustic signatures in noisy environments. In Proceedings of the 2015 28th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 917–920. [Google Scholar] [CrossRef]
- Liu, H.; Liu, S.; Shkel, A.A.; Kim, E.S. Active Noise Cancellation With MEMS Resonant Microphone Array. J. Microelectromech. Syst. 2020, 29, 839–845. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.; Hong, H.-K.; Rhee, C.-H.; Yoon, Y.; Kim, C.-H. Directional Sound Sensor With Consistent Directivity and Sensitivity in the Audible Range. J. Microelectromech. Syst. 2021, 30, 471–479. [Google Scholar] [CrossRef]
- Alves, F.; Rabelo, R.; Karunasiri, G. Dual Band MEMS Directional Acoustic Sensor for Near Resonance Operation. Sensors 2022, 22, 5635. [Google Scholar] [CrossRef] [PubMed]
- MEMSCAP|SOIMUMPs and MEMS Multi Project Wafer Service. Available online: http://www.memscap.com/products/mumps/soimumps/ (accessed on 24 January 2023).
- Touse, M.; Sinibaldi, J.; Simsek, K.; Catterlin, J.; Harrison, S.; Karunasiri, G. Fabrication of a microelectromechanical directional sound sensor with electronic readout using comb fingers. Appl. Phys. Lett. 2010, 96, 173701. [Google Scholar] [CrossRef]
- Garrett, S.L. Understanding Acoustics: An Experimentalist’s View of Sound and Vibration; Springer Nature: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-44787-8. [Google Scholar]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zou, H.-X.; Wei, K.-X.; Zhou, S.-X.; Meng, G.; Zhang, W.-M. Mechanical Intelligent Energy Harvesting: From Methodology to Applications. Adv. Energy Mater. 2023, 13, 2300557. [Google Scholar] [CrossRef]
- Zhao, L.-C.; Zhou, T.; Chang, S.-D.; Zou, H.-X.; Gao, Q.-H.; Wu, Z.-Y.; Yan, G.; Wei, K.-X.; Yeatman, E.M.; Meng, G.; et al. A disposable cup inspired smart floor for trajectory recognition and human-interactive sensing. Appl. Energy 2024, 357, 122524. [Google Scholar] [CrossRef]




| Wing Width | Wing Length | Wing Thickness |
|---|---|---|
| 2500 μm | 1600 μm | 25 μm |
| Design Freq (V11 Wing 1) | Bridge Length (V11 Wing 1) | Torsional Leg Length |
| 366 Hz | 2900 μm | 1000 μm |
| Version V11 Resonant Frequency [Hz]/Quality Factor | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Data Source | Wing 1 | Wing 2 | Wing 3 | Wing 4 | Wing 5 | Wing 6 | ||||||
| Analytical Model | 359 | 34.1 | 375 | 34.7 | 389 | 35.3 | 405 | 35.9 | 422 | 36.5 | 437 | 37.1 |
| Finite Element Model | 366 | 19.7 | 382 | 19.7 | 399 | 19.9 | 413 | 19.9 | 430 | 19.8 | 446 | 19.8 |
| Laser Vibrometry | 363 | 18.1 | 380 | 18.5 | 395 | 19.3 | 409 | 20.8 | 427 | 19.0 | 441 | 18.6 |
| Electrical Output | 364 | 18.9 | 382 | 19.3 | 396 | 19.0 | 412 | 21.3 | 430 | 20.0 | 444 | 19.6 |
| Version V12 Resonant Frequency [Hz]/Quality Factor | ||||||||||||
| Data Source | Wing 1 | Wing 2 | Wing 3 | Wing 4 | Wing 5 | Wing 6 | ||||||
| Analytical Model | 367 | 34.4 | 383 | 35.1 | 398 | 35.7 | 414 | 36.2 | 430 | 36.9 | 446 | 37.4 |
| Finite Element Model | 374 | 19.8 | 390 | 19.7 | 406 | 19.8 | 422 | 19.7 | 439 | 19.8 | 454 | 19.8 |
| Laser Vibrometry | 370 | 18.1 | 388 | 18.4 | 403 | 19.0 | 418 | 19.4 | 436 | 20.7 | 452 | 20.7 |
| Electrical Output | 372 | 18.5 | 388 | 20.0 | 404 | 19.5 | 418 | 21.2 | 436 | 21.5 | 454 | 22.1 |
| Sensor | Sensitivity | SNR [dB] | Bandwidth |
|---|---|---|---|
| Multi-Resonant | 48 V/Pa | 88.6 (97.4) 1 | 300 Hz–500 Hz |
| Double-Wing Design [16] | 59 V/Pa | 88 (102) 1 | 658 Hz–684 Hz |
| Dual-Band Design [21] | 13 V/Pa | 91 1 | 650 Hz–725 Hz 2 |
| Double-Wing [9] | 3.45 mV/Pa | 68.5 | Not Discussed |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivancic, J.; Alves, F. Directional Multi-Resonant Micro-Electromechanical System Acoustic Sensor for Low Frequency Detection. Sensors 2024, 24, 2908. https://doi.org/10.3390/s24092908
Ivancic J, Alves F. Directional Multi-Resonant Micro-Electromechanical System Acoustic Sensor for Low Frequency Detection. Sensors. 2024; 24(9):2908. https://doi.org/10.3390/s24092908
Chicago/Turabian StyleIvancic, Justin, and Fabio Alves. 2024. "Directional Multi-Resonant Micro-Electromechanical System Acoustic Sensor for Low Frequency Detection" Sensors 24, no. 9: 2908. https://doi.org/10.3390/s24092908
APA StyleIvancic, J., & Alves, F. (2024). Directional Multi-Resonant Micro-Electromechanical System Acoustic Sensor for Low Frequency Detection. Sensors, 24(9), 2908. https://doi.org/10.3390/s24092908






