Satellite Selection Strategy and Method for Signals of Opportunity Navigation and Positioning with LEO Communication Satellites
Abstract
1. Introduction
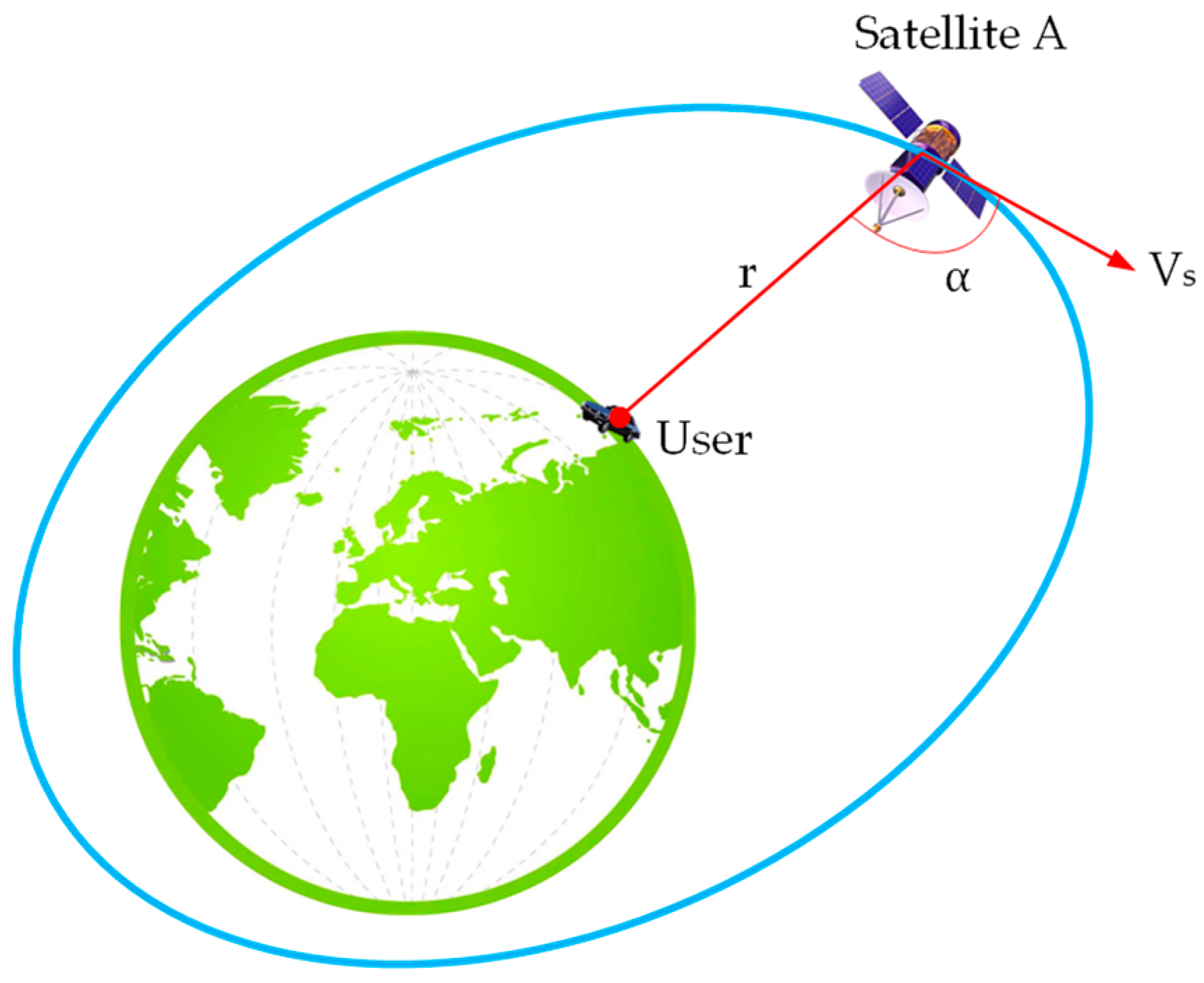
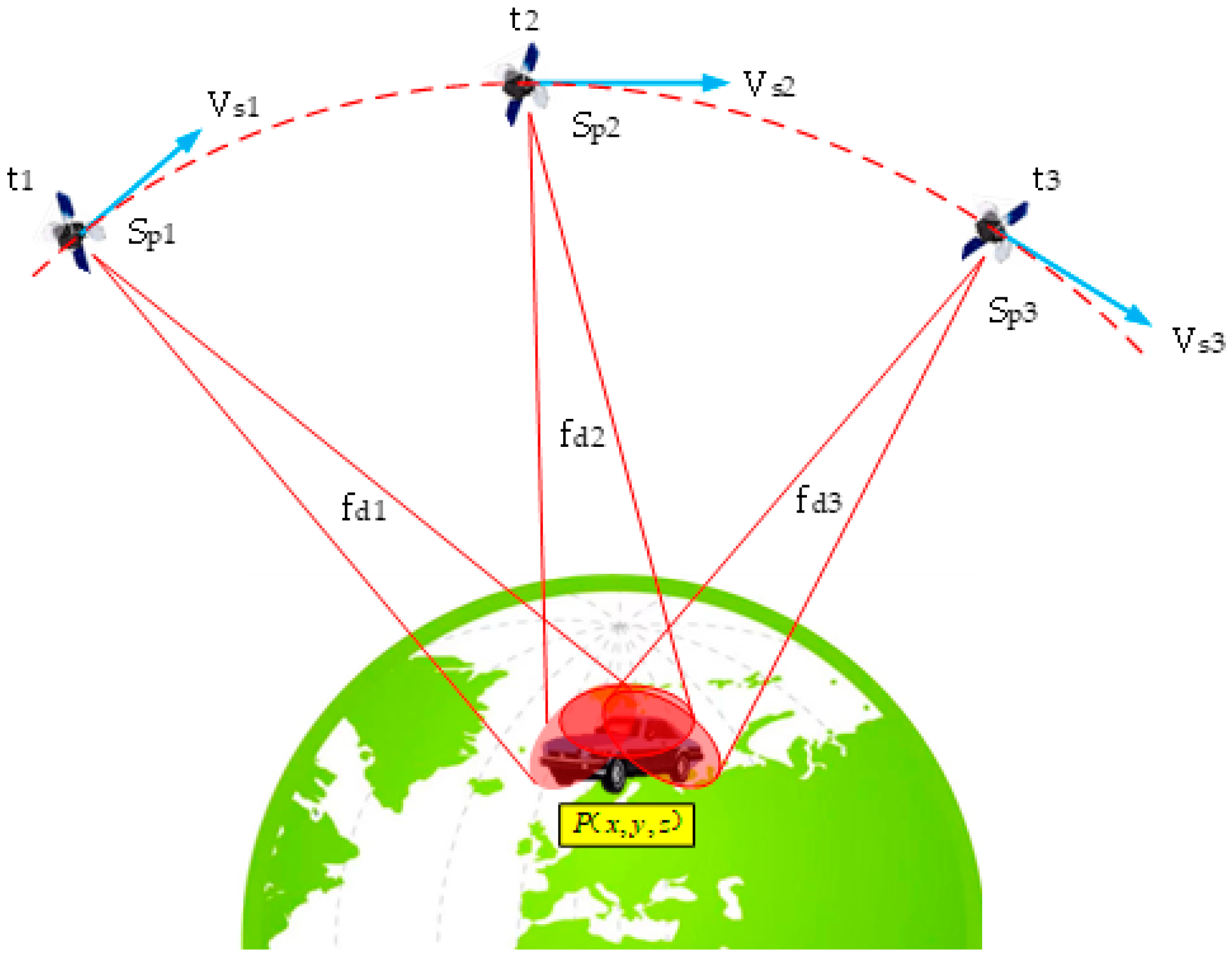
2. The Principle of DS Positioning with LEO Communication Satellites
2.1. DS Calculation of LEO Communication Satellite Signals
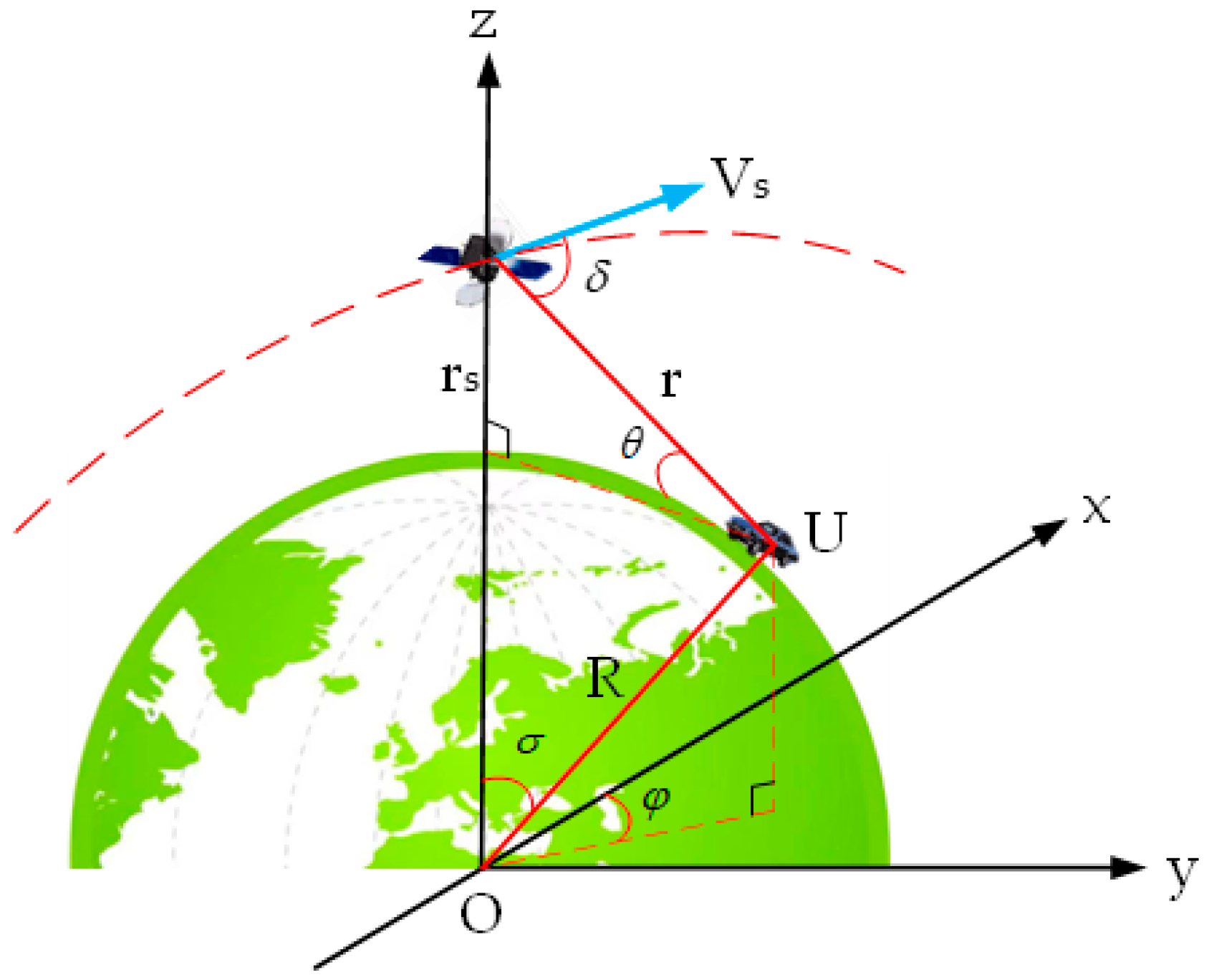
2.2. The Principle of DS Positioning
2.3. PDOP
3. The Influence of Satellite Elevation Angle on Positioning Accuracy
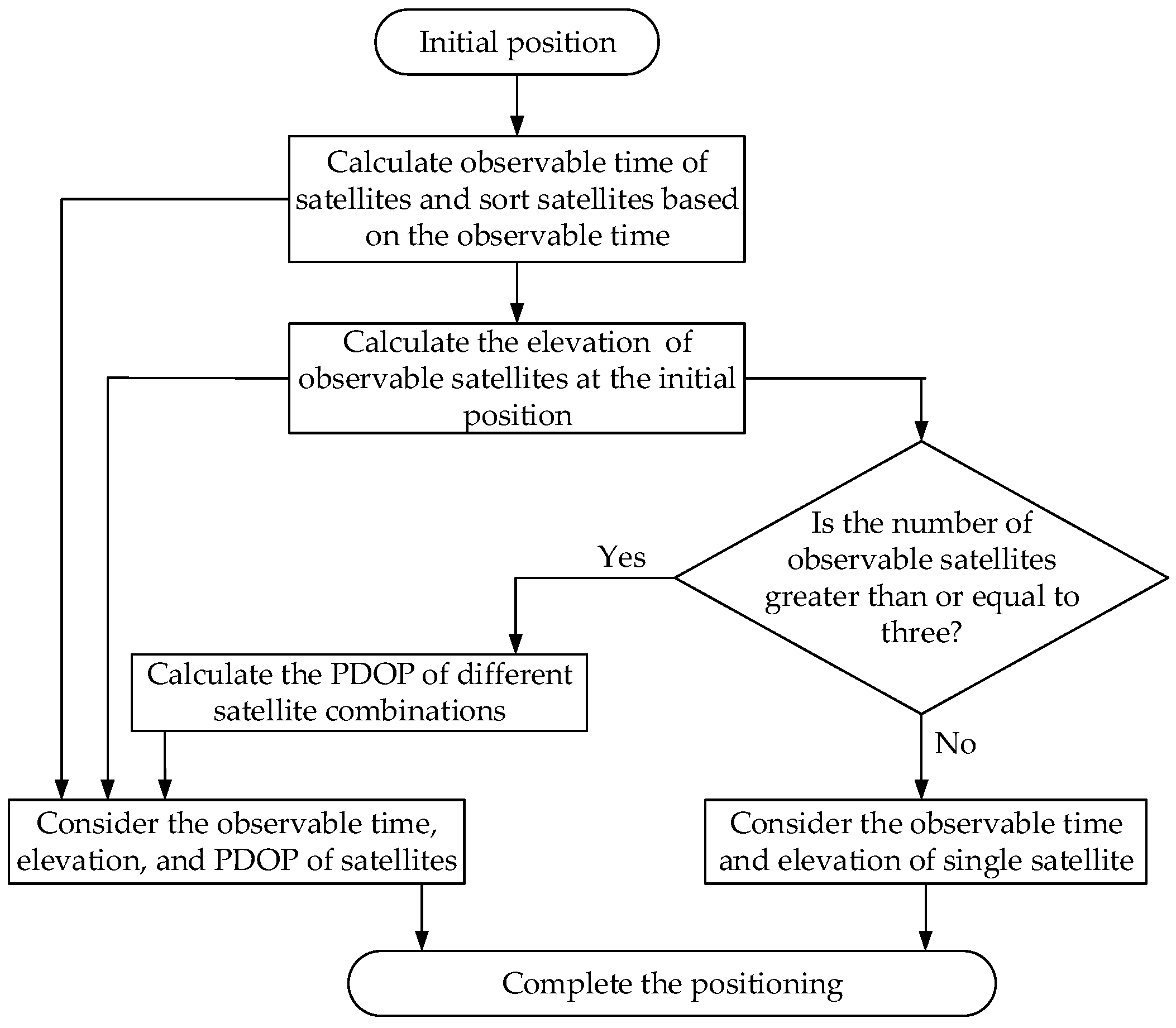
4. The Satellite Selection Strategy
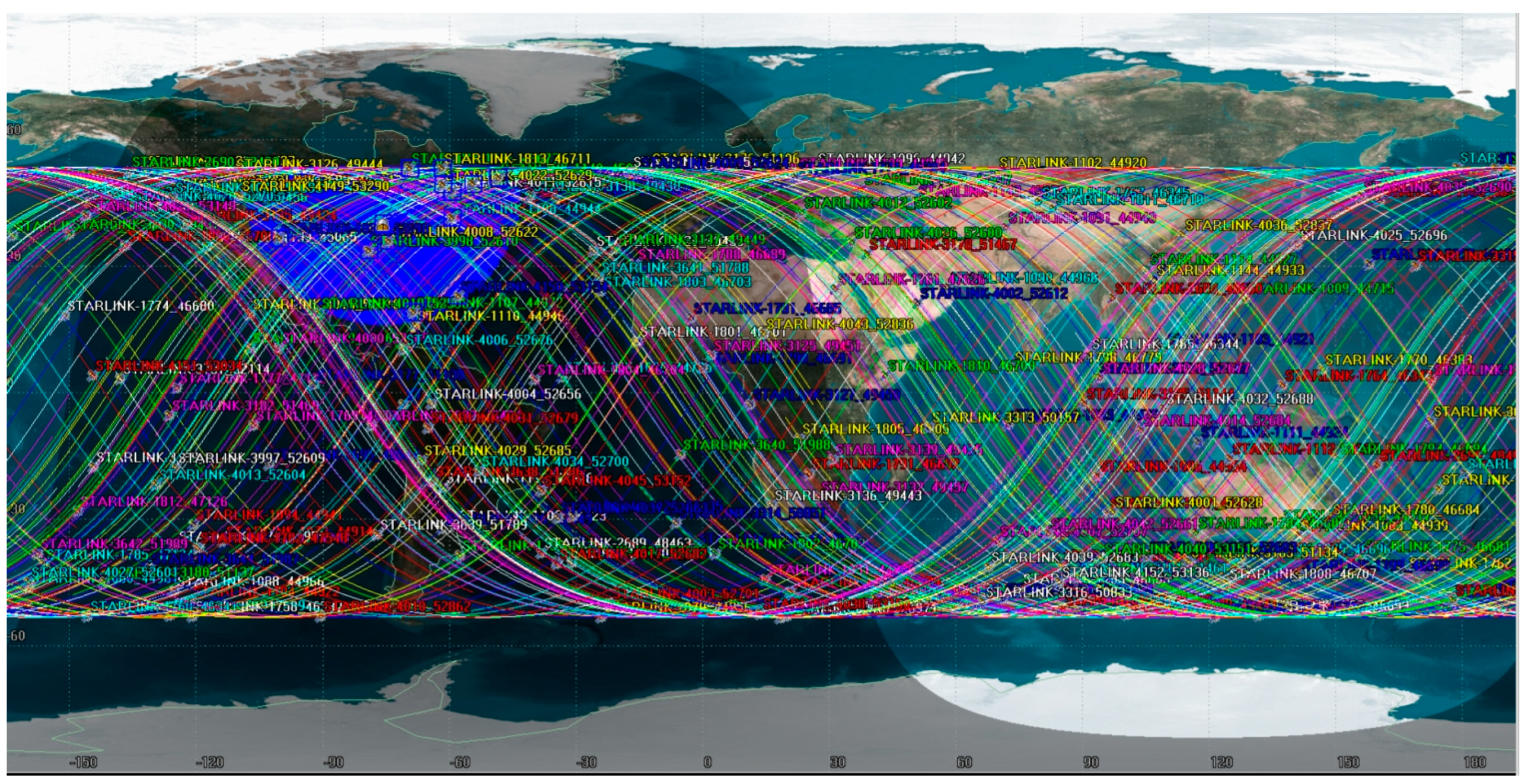
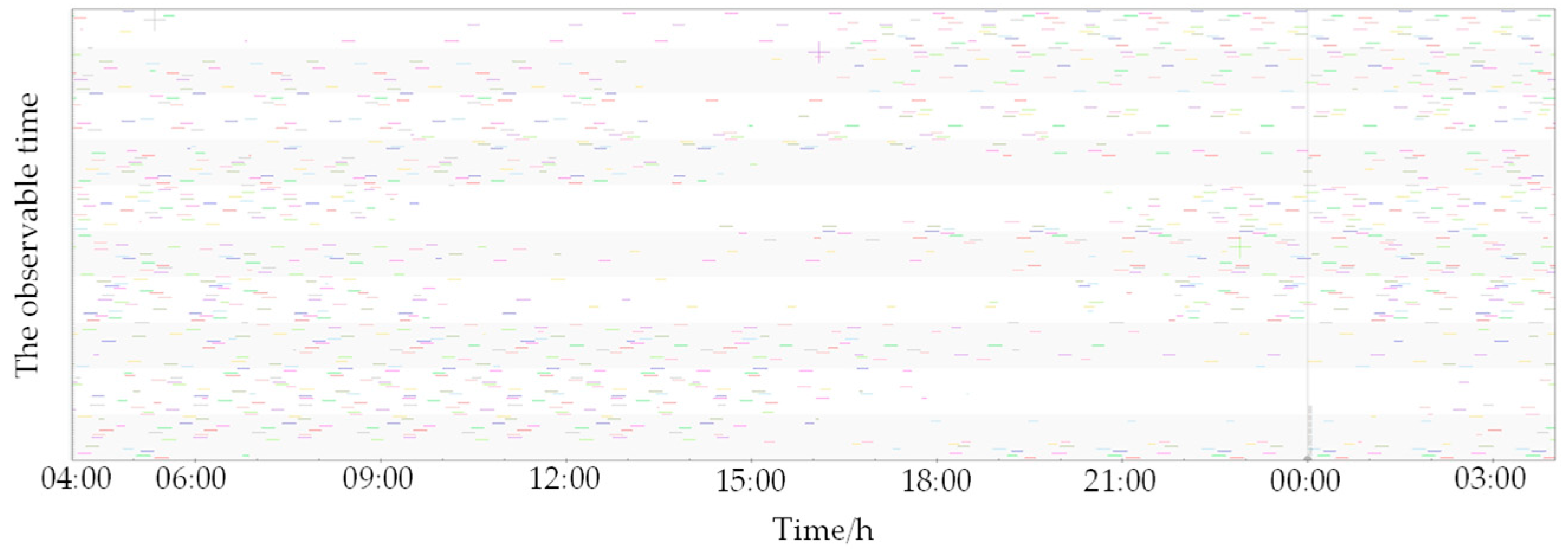
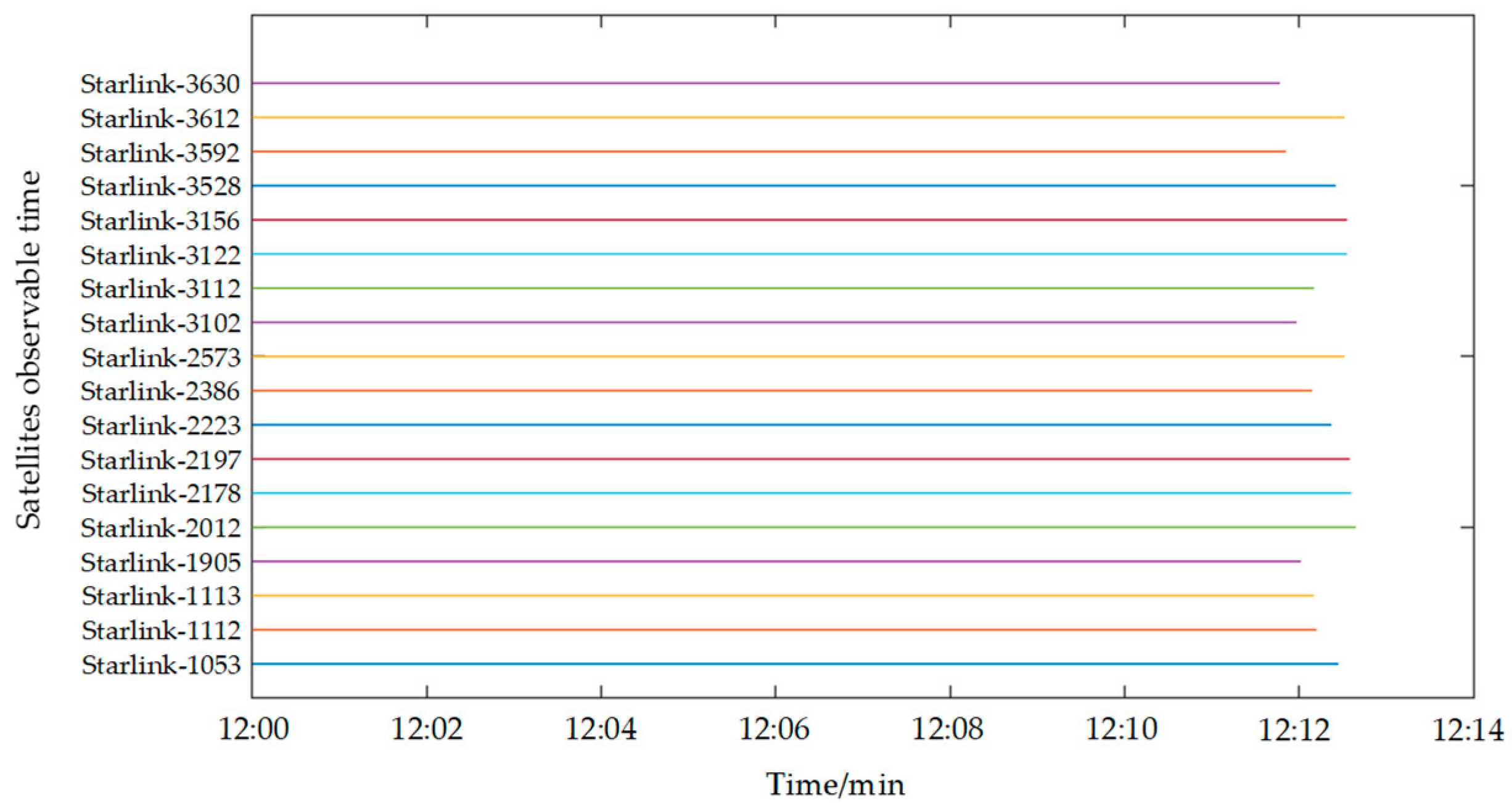
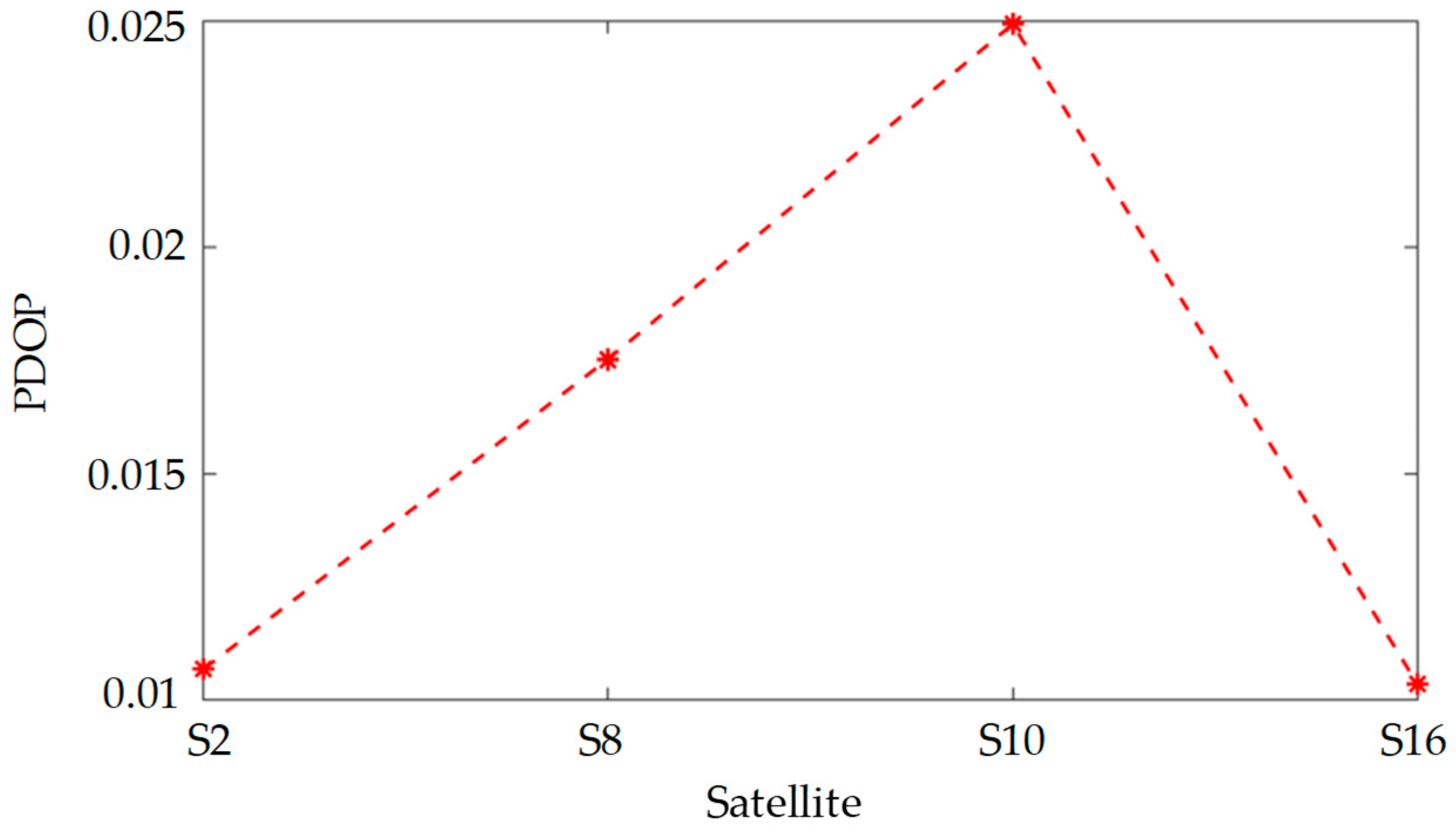
5. Results and Discussion
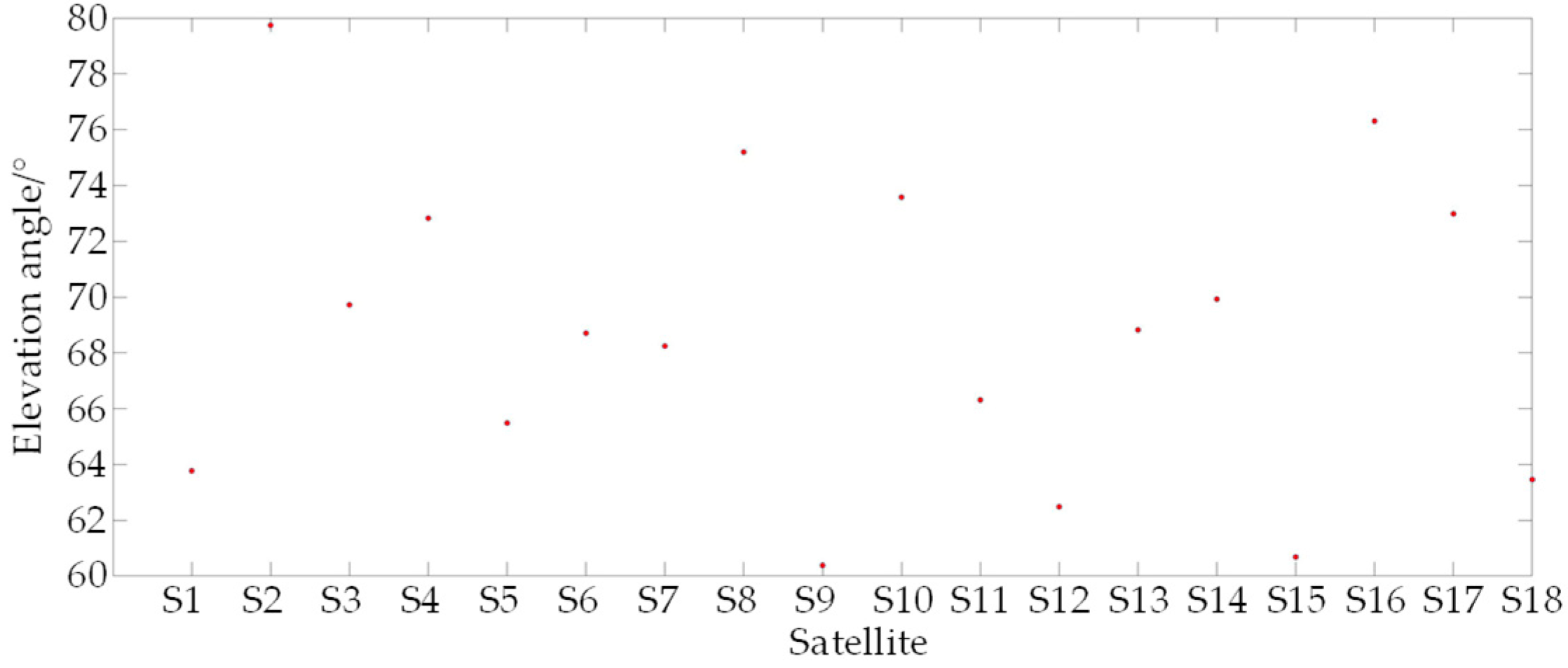
5.1. Satellite Observable Time
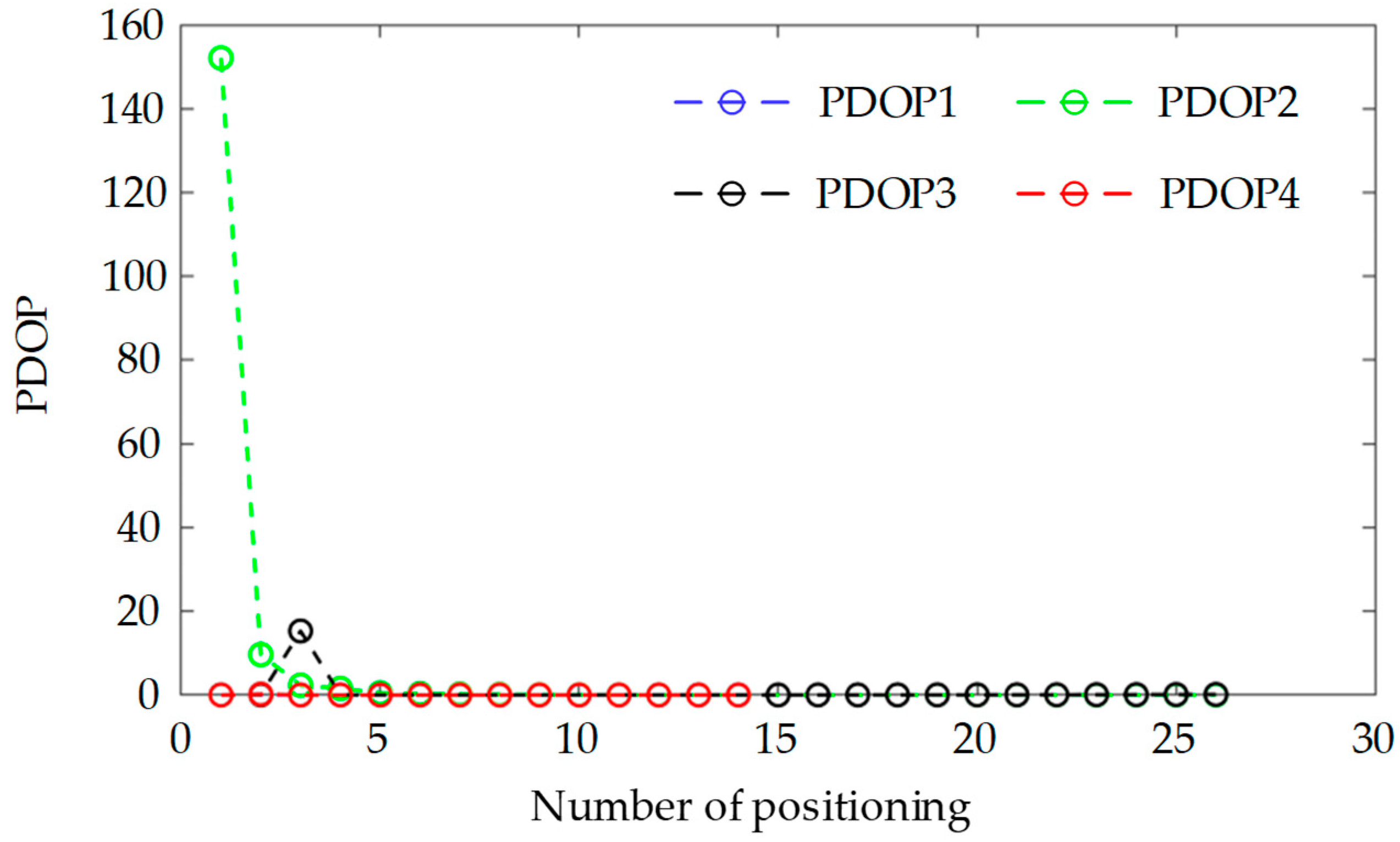
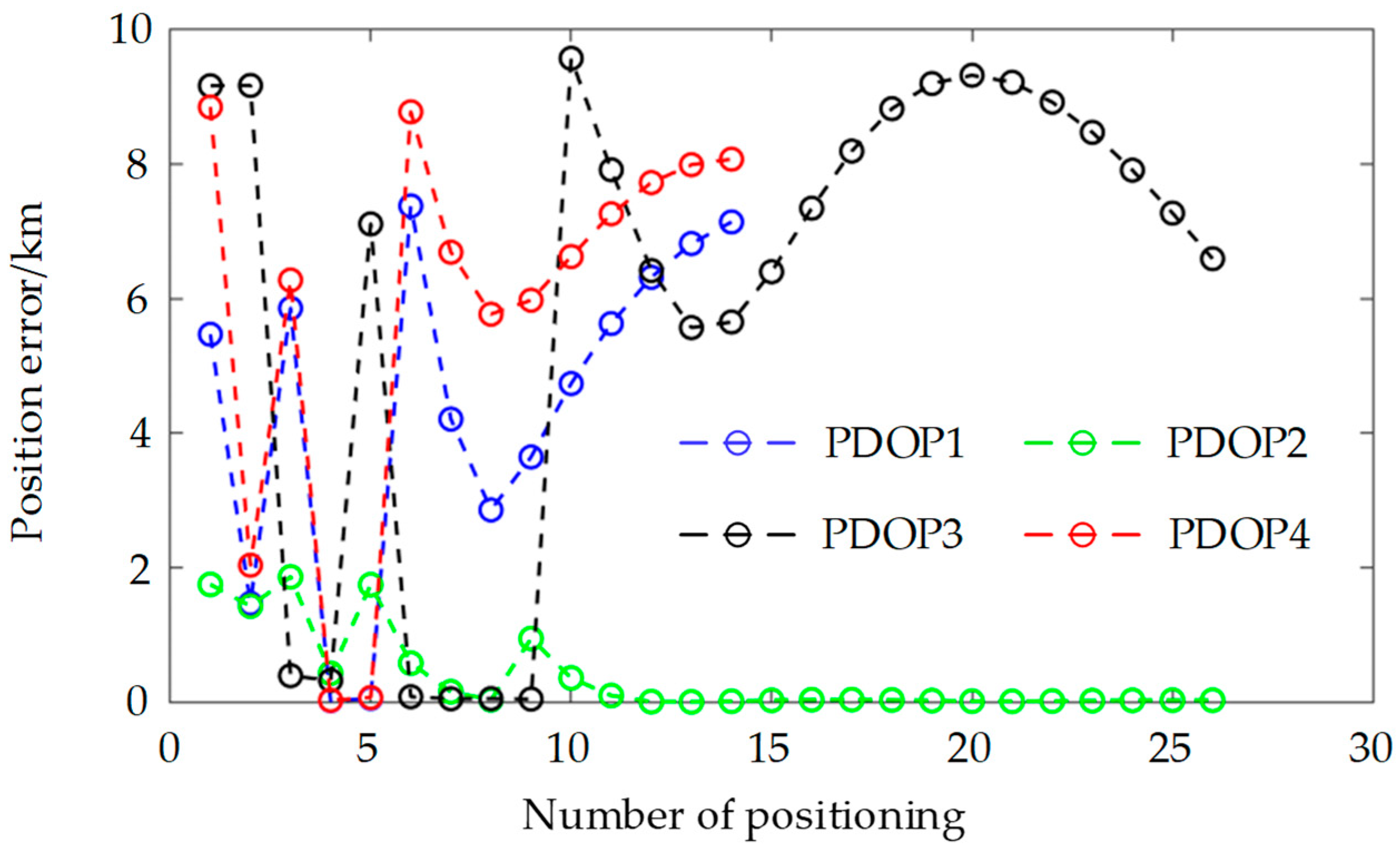
5.2. Position Error and PDOP of a Single Satellite
5.3. Position Error and PDOP of the Satellite Permutations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nikookar, H.; Oonincx, P. An introduction to radio locationing with signals of opportunity. J. Commun. Navig. Sens. Serv. (CONASENSE) 2016, 2016, 1–10. [Google Scholar]
- Ma, C.; Wu, B.; Poslad, S.; Selviah, D.R. Wi-Fi RTT ranging performance characterization and positioning system design. IEEE Trans. Mob. Comput. 2020, 21, 740–756. [Google Scholar] [CrossRef]
- Palmer, D.; Moore, T.; Hill, C.; Andreotti, M.; Park, D. Radio positioning using the digital audio broadcasting (DAB) signal. J. Navig. 2011, 64, 45–59. [Google Scholar] [CrossRef]
- Chen, R.; Li, Z.; Ye, F.; Guo, G.; Xu, S.; Qian, L.; Liu, Z.; Huang, L. Precise indoor positioning based on acoustic ranging in smartphone. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, H. A BA-RRT-Based Indoor Geomagnetic Positioning Algorithm. In Proceedings of the 4th International Seminar on Artificial Intelligence, Networking and Information Technology (AINIT), Nanjing, China, 16–18 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 511–514. [Google Scholar]
- Maheepala, M.; Kouzani, A.Z.; Joordens, M.A. Light-based indoor positioning systems: A review. IEEE Sens. J. 2020, 20, 3971–3995. [Google Scholar] [CrossRef]
- Li, B.; Zhao, K.; Shen, X. Dilution of precision in positioning systems using both angle of arrival and time of arrival measurements. IEEE Access 2020, 8, 192506–192516. [Google Scholar] [CrossRef]
- Müürsepp, I.; Kulmar, M.; Elgarhy, O.; Alam, M.M.; Chen, T.; Horsmanheimo, S.; Scholliers, J. Performance evaluation of 5g-nr positioning accuracy using time difference of arrival method. In Proceedings of the 2021 IEEE International Mediterranean Conference on Communications and Networking (MeditCom), Athens, Greece, 23 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 494–499. [Google Scholar]
- Li, C.; Zhen, J.; Chang, K.; Xu, A.; Zhu, H.; Wu, J. An indoor positioning and tracking algorithm based on angle-of-arrival using a dual-channel array antenna. Remote Sens. 2021, 13, 4301. [Google Scholar] [CrossRef]
- Plets, D.; Deprez, W.; Trogh, J.; Martens, L.; Joseph, W. Joint received signal strength, angle-of-arrival, and time-of-flight positioning. In Proceedings of the 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 31 March–5 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Halili, R.; BniLam, N.; Yusuf, M.; Tanghe, E.; Joseph, W.; Weyn, M.; Berkvens, R. Vehicle localization using Doppler shift and time of arrival measurements in a tunnel environment. Sensors 2022, 22, 847. [Google Scholar] [CrossRef] [PubMed]
- Iridium Announces Successful First Launch of Iridium Next Satellites. Available online: https://www.thalesgroup.com/en/worldwide/space/press-release/iridium-announces-successful-first-launch-iridium-next-satellites (accessed on 4 January 2025).
- McDowell, J.C. The low earth orbit satellite population and impacts of the SpaceX Starlink constellation. Astrophys. J. Lett. 2020, 892, L36. [Google Scholar] [CrossRef]
- Henri, Y. The OneWeb satellite system. In Handbook of Small Satellites: Technology, Design, Manufacture, Applications, Economics and Regulation; Springer International Publishing: Cham, Switzerland, 2020; pp. 1091–1100. [Google Scholar]
- Qin, H.L.; Tan, Z.Z.; Cong, L.; Zhao, C. Positioning technology based on IRIDIUM signals of opportunity. J. Beijing Univ. Aeronaut. Astronaut. 2019, 45, 1691–1699. [Google Scholar]
- Qin, H.L.; Tan, Z.Z.; Cong, L.; Zhao, C. Positioning technology based on ORBCOMM signals of opportunity. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 1999–2006. [Google Scholar]
- Qin, H.L.; Zhang, Y. Positioning technology based on Starlink signal of opportunity. J. Navig. Position. 2023, 11, 67–73. [Google Scholar]
- Orabi, M.; Khalife, J.; Kassas, Z.M. Opportunistic navigation with Doppler measurements from Iridium Next and Orbcomm LEO satellites. In Proceedings of the 2021 IEEE Aerospace Conference (50100), Big Sky, MT, USA, 6–13 March 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–9. [Google Scholar]
- Khalife, J.; Neinavaie, M.; Kassas, Z.M. The first carrier phase tracking and positioning results with Starlink LEO satellite signals. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 1487–1491. [Google Scholar] [CrossRef]
- Khalife, J.; Kassas, Z.M. Assessment of differential carrier phase measurements from Orbcomm LEO satellite signals for opportunistic navigation. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 4053–4063. [Google Scholar]
- Norouzi, Y.; Kashani, E.S.; Ajorloo, A. Angle of arrival-based target localization with low Earth orbit satellite observer. IET Radar Sonar Navig. 2016, 10, 1186–1190. [Google Scholar] [CrossRef]
- Thompson, S.; Martin, S.; Bevly, D. Single differenced doppler positioning with low Earth orbit signals of opportunity and angle of arrival estimation. In Proceedings of the 2021 International Technical Meeting of the Institute of Navigation, Online, 25–28 January 2021; pp. 497–509. [Google Scholar]
- Florio, A.; Bnilam, N.; Talarico, C.; Crosta, P.; Avitabile, G.; Coviello, G. LEO-Based Coarse Positioning Through Angle-of-Arrival Estimation of Signals of Opportunity. IEEE Access 2024, 12, 17446–17459. [Google Scholar] [CrossRef]
- Barry, C.; Weiss, M. Alternative Position, Navigation and Timing (A-PNT) Using Time Difference of Arrival (TDOA) of Low Earth Orbit (LEO) Signals of Opportunity (SOOP). In Proceedings of the International Telemetering Conference Proceedings, Glendale, AZ, USA, 24–27 October 2022; Volume 57. [Google Scholar]
- Kihara, M.; Okada, T. A satellite selection method and accuracy for the global positioning system. Navigation 1984, 31, 8–20. [Google Scholar] [CrossRef]
- Guo, J.; Wang, Y.; Xie, X.; Sun, C. A fast satellite selection algorithm for positioning in LEO constellation. Adv. Space Res. 2024, 73, 271–285. [Google Scholar] [CrossRef]
- Wang, D.Y.; Qin, H.L.; Wang, Y.L. Minimum error vector synthetic positioning algorithm using LEO satellites. J. Navig. Position. 2023, 11, 74–79. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, Y.; Guo, Y.; Wang, S.; Yu, C.; Zhu, Z. Satellite Selection Strategy and Method for Signals of Opportunity Navigation and Positioning with LEO Communication Satellites. Sensors 2025, 25, 267. https://doi.org/10.3390/s25010267
Tao Y, Guo Y, Wang S, Yu C, Zhu Z. Satellite Selection Strategy and Method for Signals of Opportunity Navigation and Positioning with LEO Communication Satellites. Sensors. 2025; 25(1):267. https://doi.org/10.3390/s25010267
Chicago/Turabian StyleTao, Yanhua, Yang Guo, Shaobo Wang, Chuanqiang Yu, and Zimo Zhu. 2025. "Satellite Selection Strategy and Method for Signals of Opportunity Navigation and Positioning with LEO Communication Satellites" Sensors 25, no. 1: 267. https://doi.org/10.3390/s25010267
APA StyleTao, Y., Guo, Y., Wang, S., Yu, C., & Zhu, Z. (2025). Satellite Selection Strategy and Method for Signals of Opportunity Navigation and Positioning with LEO Communication Satellites. Sensors, 25(1), 267. https://doi.org/10.3390/s25010267




