Monitoring a Railway Bridge with Distributed Fiber Optic Sensing Using Specially Installed Fibers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Principles of Distributed Fiber Optic Sensing
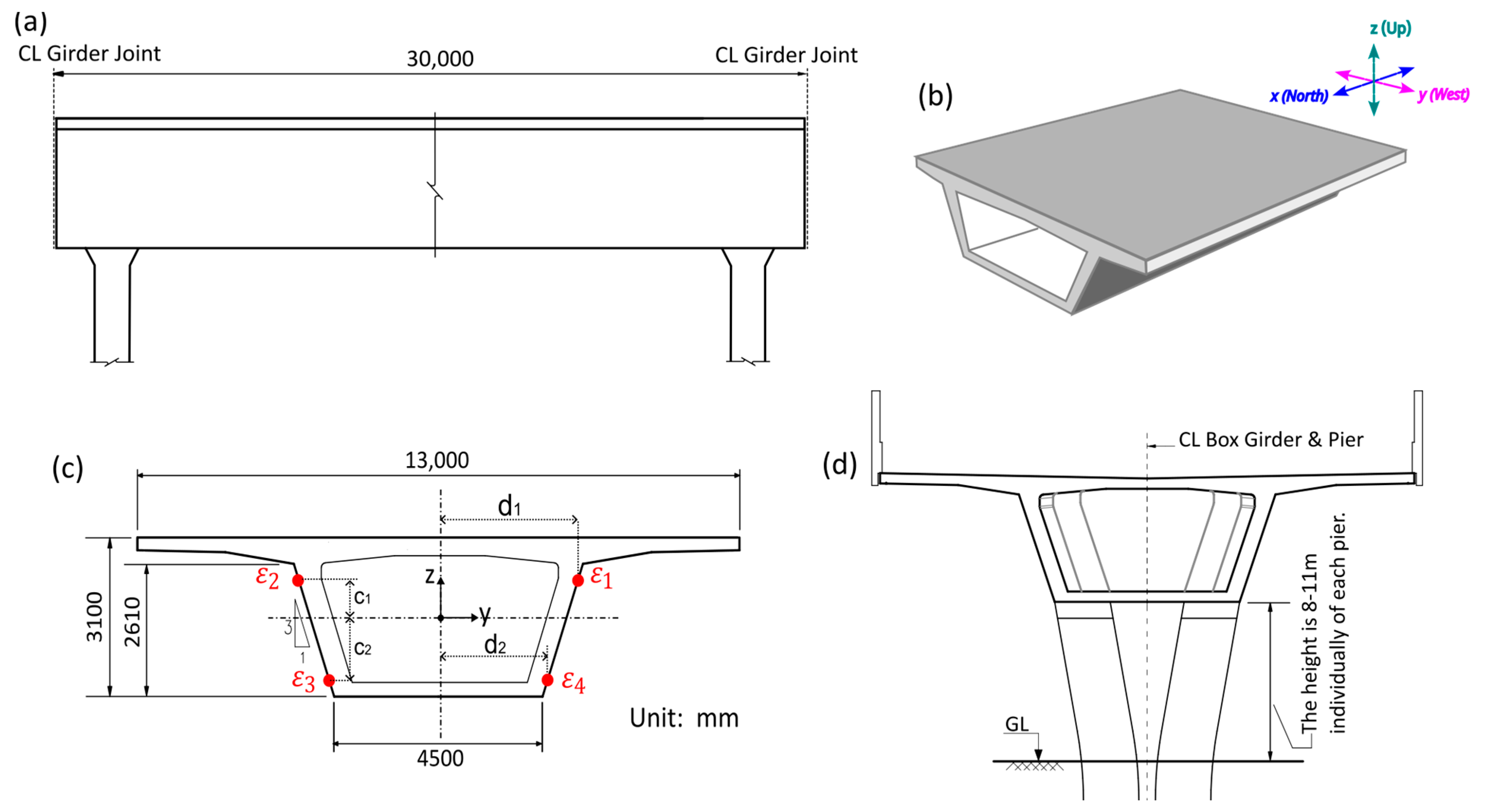
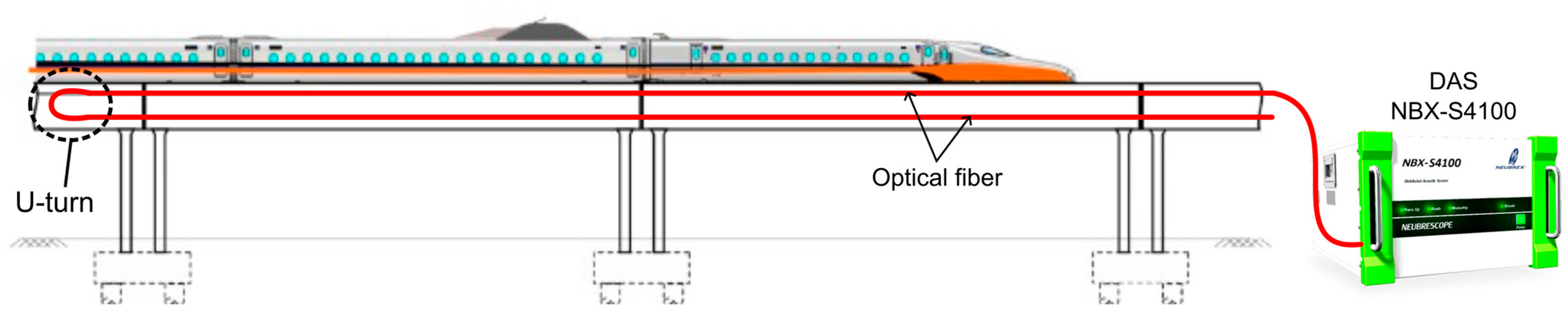
2.2. Installation of Sensing Fibers on the Railway Bridge
2.3. Temperature Compensation
2.4. Analytical Model for Bridge Deformation
3. Results and Discussion
3.1. Static Measurements with BOTDA
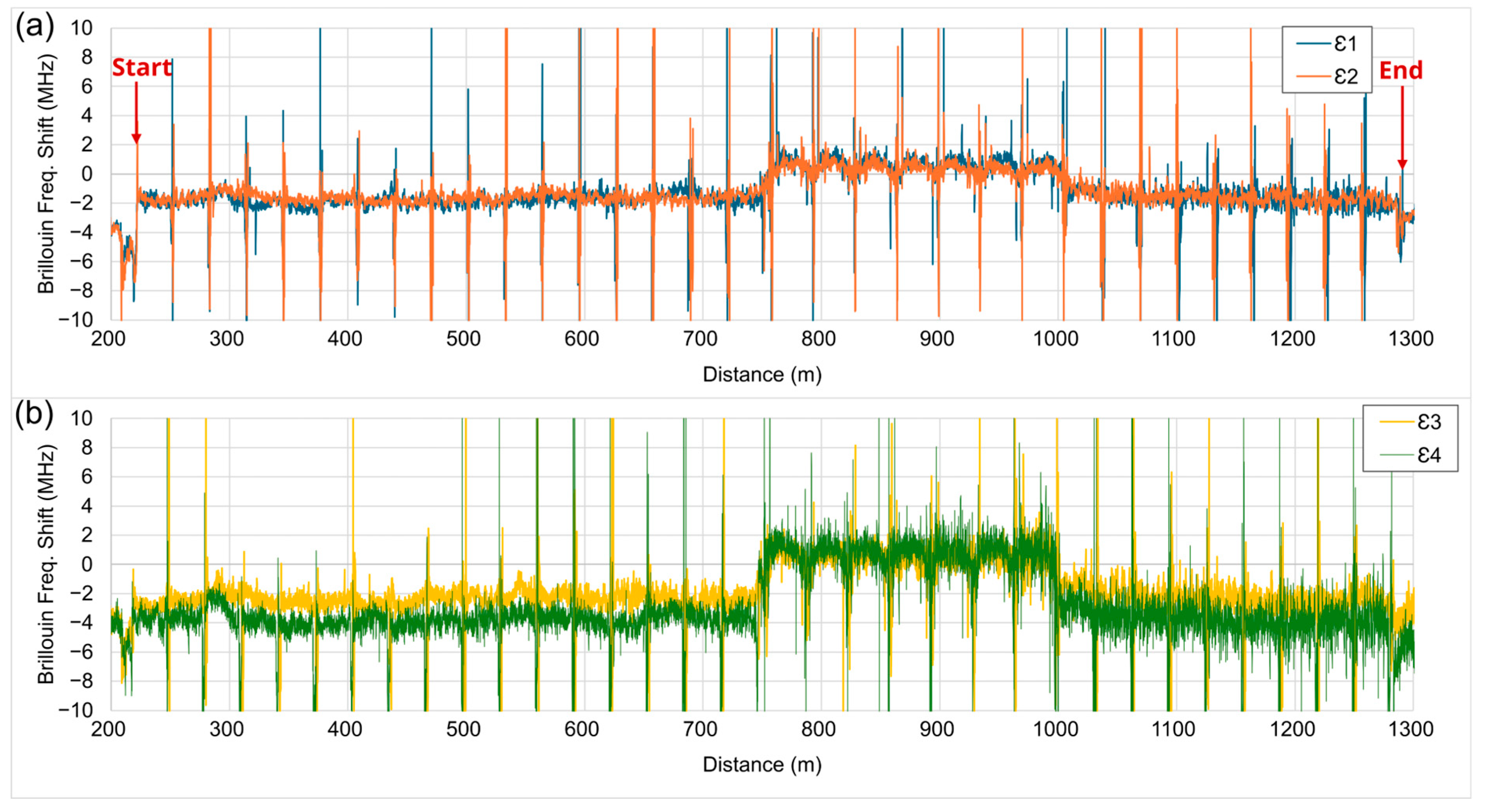
3.1.1. Brillouin Frequency Shift
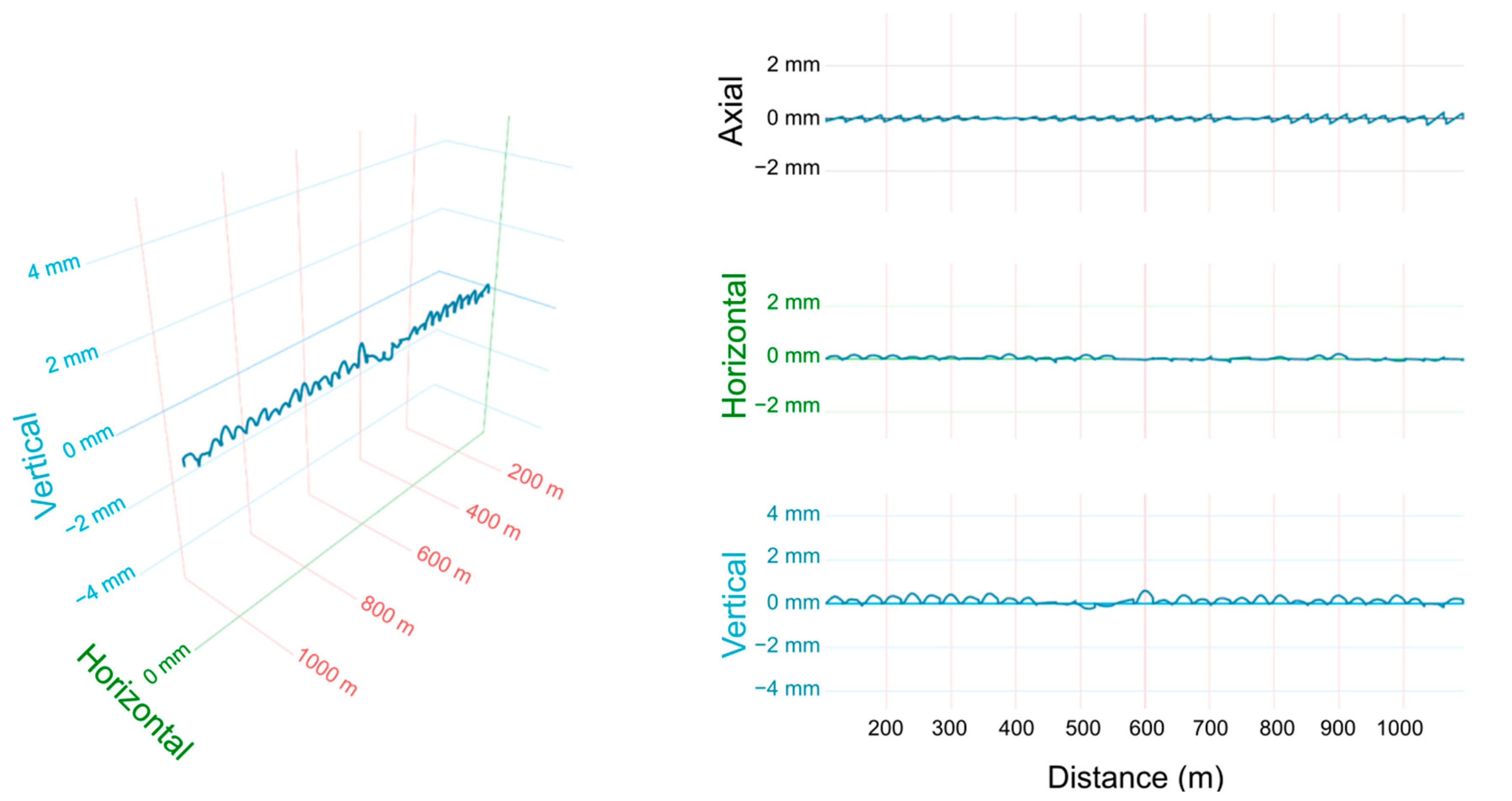
3.1.2. Bridge Displacement Results
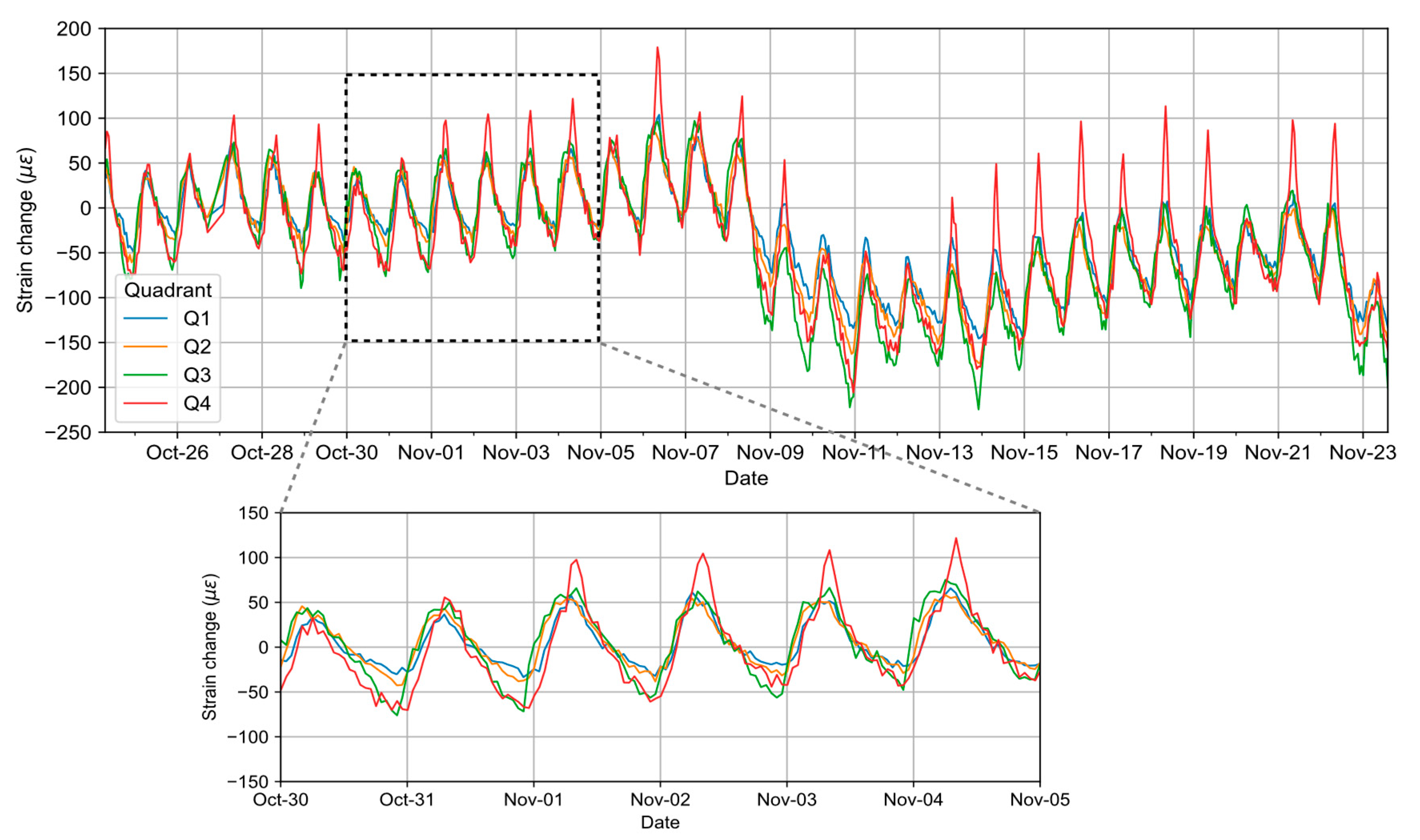
3.1.3. Long-Term Monitoring Results
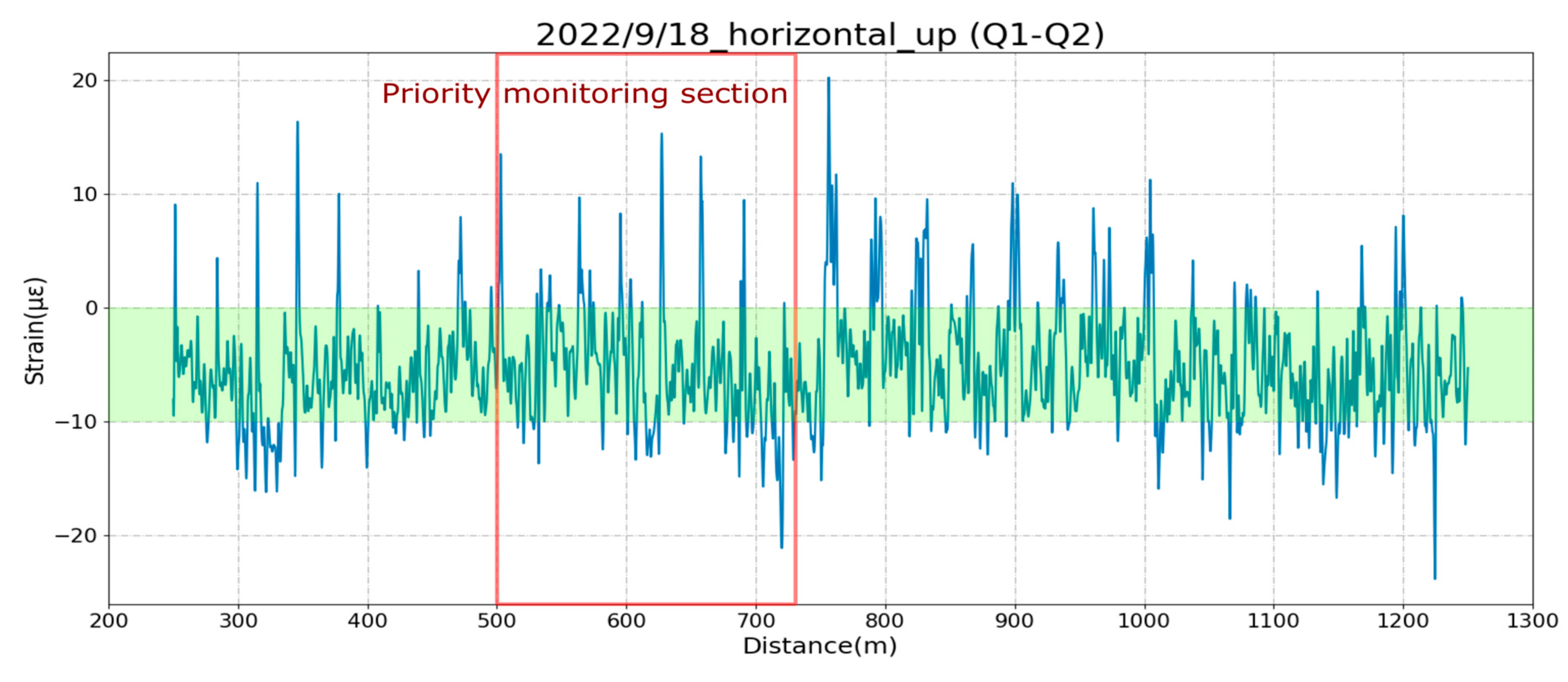
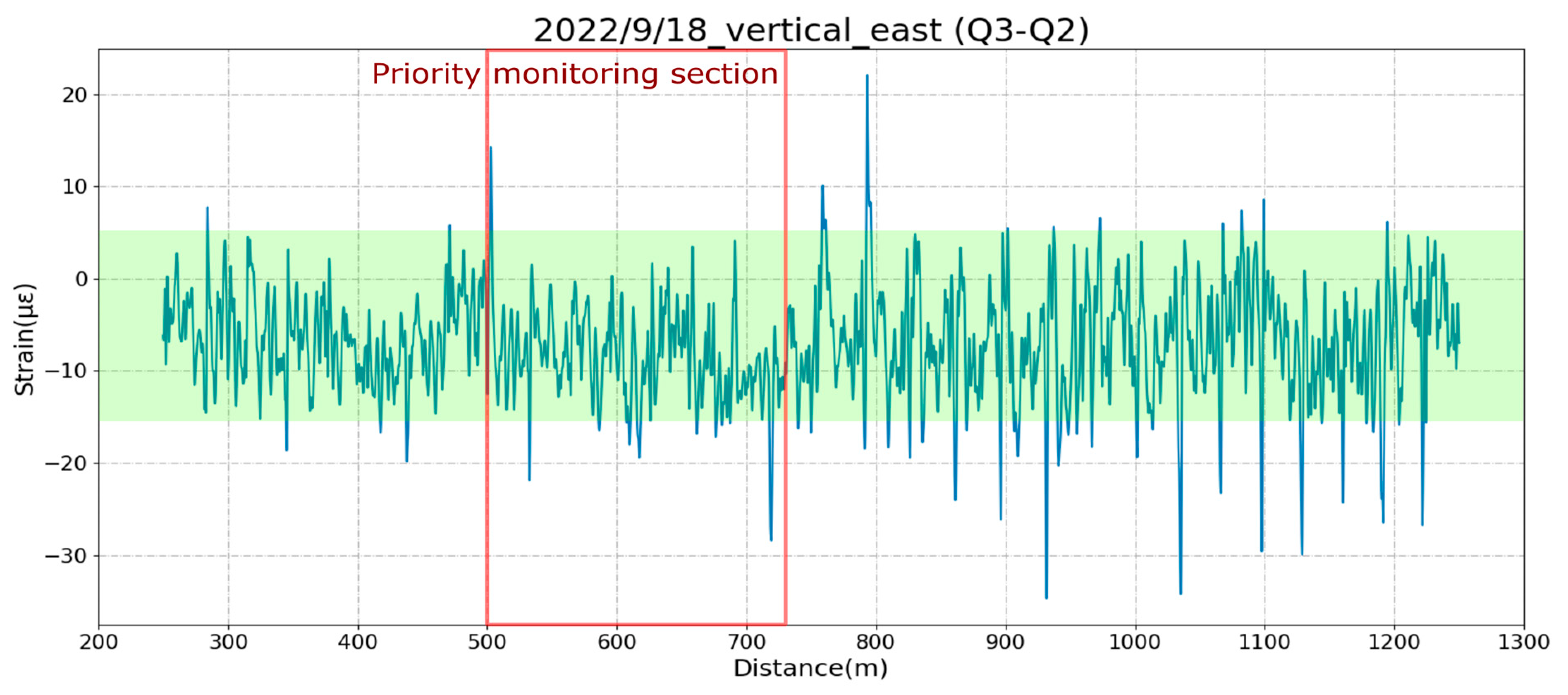
3.1.4. Confirmation of Safety of Bridge Structure After an Earthquake
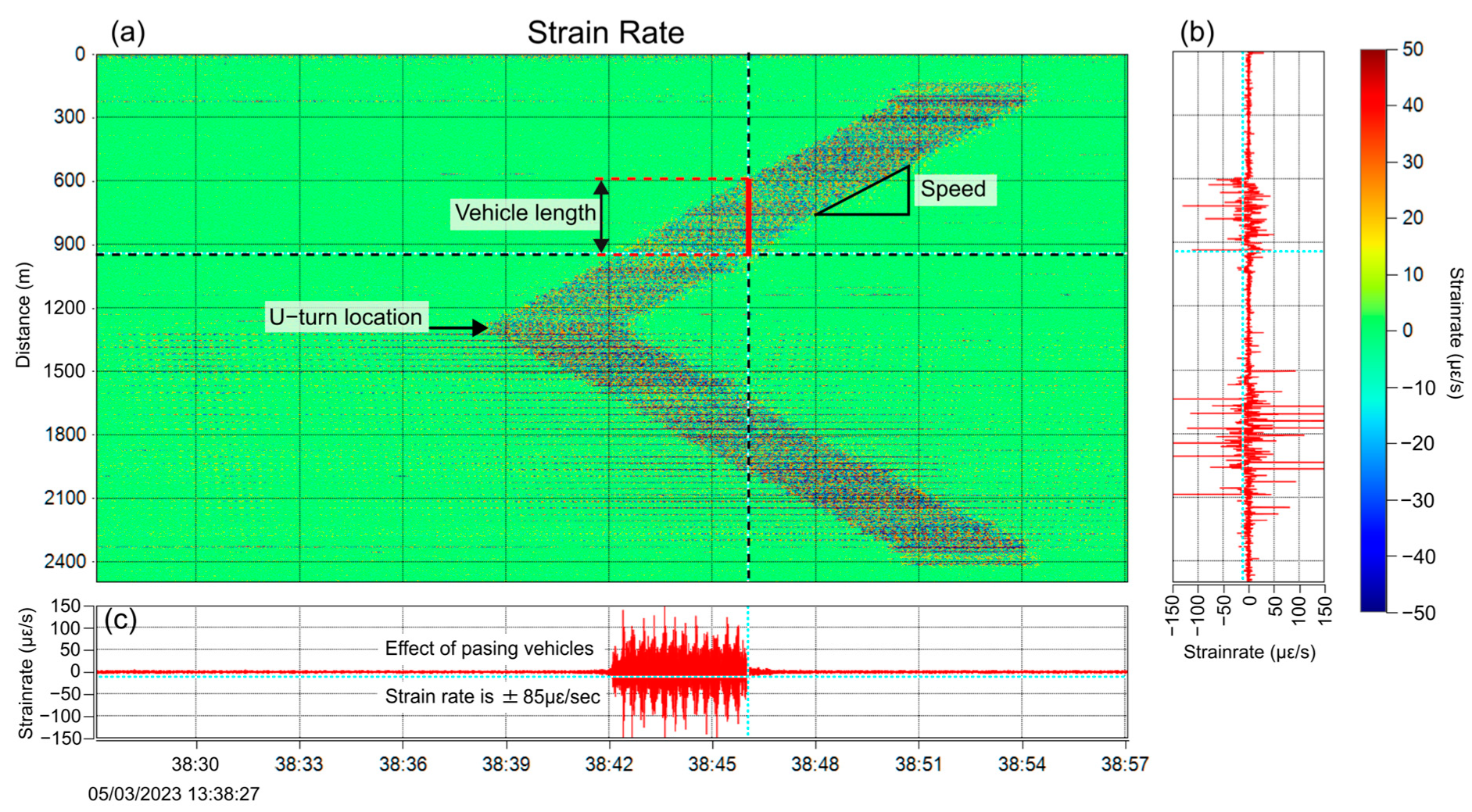
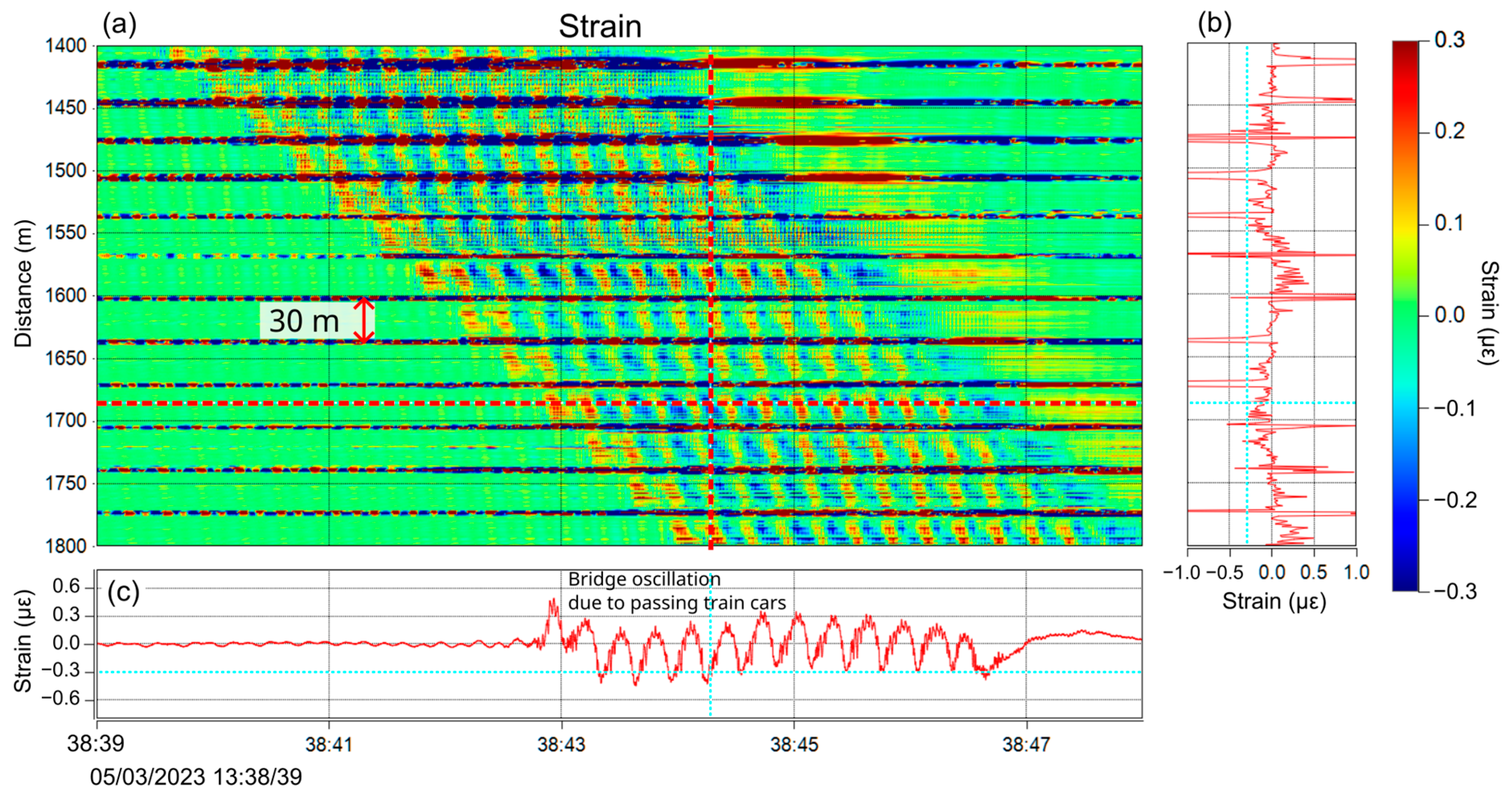
3.2. Dynamic Measurements with DAS
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed Optical Fiber Sensing: Review and Perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Kefal, A.; Yildiz, M. Modeling of Sensor Placement Strategy for Shape Sensing and Structural Health Monitoring of a Wing-Shaped Sandwich Panel Using Inverse Finite Element Method. Sensors 2017, 17, 2775. [Google Scholar] [CrossRef]
- Vagnoli, M.; Remenyte-Prescott, R.; Andrews, J. Railway Bridge Structural Health Monitoring and Fault Detection: State-of-the-Art Methods and Future Challenges. Struct. Health Monit. 2017, 17, 971–1007. [Google Scholar] [CrossRef]
- Hénault, J.-M.; Benzarti, K.; Quiertant, M.; Kishida, K.; Imai, M.; Kawabata, J.; Guzik, A. Distributed Optical Fiber Sensors for Monitoring of Civil Engineering Structures. Sensors 2022, 22, 4368. [Google Scholar] [CrossRef] [PubMed]
- López-Higuera, J.M.; Cobo, L.R.; Incera, A.Q.; Cobo, A. Fiber Optic Sensors in Structural Health Monitoring. J. Light. Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Fan, L.; Bao, Y. Review of Fiber Optic Sensors for Corrosion Monitoring in Reinforced Concrete. Cem. Concr. Compos. 2021, 120, 104029. [Google Scholar] [CrossRef]
- Sui, Y.; Cheng, X.; Wei, J. Distributed Fibre Optic Monitoring of Damaged Lining in Double-Arch Tunnel and Analysis of Its Deformation Mode. Tunn. Undergr. Space Technol. 2021, 110, 103812. [Google Scholar] [CrossRef]
- He, Z.; Li, W.; Salehi, H.; Zhang, H.; Zhou, H.; Jiao, P. Integrated Structural Health Monitoring in Bridge Engineering. Autom. Constr. 2022, 136, 104168. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ni, Y.Q.; Wang, S.M. Structural Health Monitoring of Railway Bridges Using Innovative Sensing Technologies and Machine Learning Algorithms: A Concise Review. Intell. Transp. Infrastruct. 2022, 1, liac009. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A Review of Recent Distributed Optical Fiber Sensors Applications for Civil Engineering Structural Health Monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.; Cigada, A.; Zappa, E.; Gilbert, M.; Lang, Z.Q. Dynamic Monitoring of a Masonry Arch Rail Bridge Using a Distributed Fiber Optic Sensing System. J. Civ. Struct. Health Monit. 2024, 14, 1075–1090. [Google Scholar] [CrossRef]
- Strasser, L.; Lienhart, W.; Winkler, M. Static and Dynamic Bridge Monitoring with Distributed Fiber Optic Sensing. Structural Health Monitoring 2023: Designing SHM for Sustainability, Maintainability, and Reliability. In Proceedings of the 14th International Workshop on Structural Health Monitoring, Standford, CA, USA, 12–14 September 2023; pp. 1745–1752. [Google Scholar] [CrossRef]
- Wu, R.; Biondi, A.; Cao, L.; Gandhi, H.; Abedin, S.; Cui, G.; Yu, T.; Wang, X. Composite Bridge Girders Structure Health Monitoring Based on the Distributed Fiber Sensing Textile. Sensors 2023, 23, 4856. [Google Scholar] [CrossRef]
- Barrias, A.; Rodriguez, G.; Casas, J.R.; Villalba, S. Application of Distributed Optical Fiber Sensors for the Health Monitoring of Two Real Structures in Barcelona. Struct. Infrastruct. Eng. 2018, 14, 967–985. [Google Scholar] [CrossRef]
- Webb, G.T.; Vardanega, P.J.; Hoult, N.A.; Fidler, P.R.A.; Bennett, P.J.; Middleton, C.R. Analysis of Fiber-Optic Strain-Monitoring Data from a Prestressed Concrete Bridge. J. Bridge Eng. 2017, 22, 05017002. [Google Scholar] [CrossRef]
- Wiesmeyr, C.; Litzenberger, M.; Waser, M.; Papp, A.; Garn, H.; Neunteufel, G.; Döller, H. Real-Time Train Tracking from Distributed Acoustic Sensing Data. Appl. Sci. 2020, 10, 448. [Google Scholar] [CrossRef]
- Mariscotti, A.; Lakuši´c, S.L.; Vraneši´c, K.V.; Wagner, A.; Nash, A.; Michelberger, F.; Grossberger, H.; Lancaster, G. The Effectiveness of Distributed Acoustic Sensing (DAS) for Broken Rail Detection. Energies 2023, 16, 522. [Google Scholar] [CrossRef]
- Rahman, M.A.; Taheri, H.; Dababneh, F.; Karganroudi, S.S.; Arhamnamazi, S. A Review of Distributed Acoustic Sensing Applications for Railroad Condition Monitoring. Mech. Syst. Signal Process 2024, 208, 110983. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Wang, M.; Chai, J.; Wu, Y.; Peng, F. An Anti-Noise ϕ-OTDR Based Distributed Acoustic Sensing System for High-Speed Railway Intrusion Detection. Laser Phys. 2020, 30, 085103. [Google Scholar] [CrossRef]
- Kishida, K.; Guzik, A.; Nishiguchi, K.; Li, C.H.; Azuma, D.; Liu, Q.; He, Z. Development of Real-Time Time Gated Digital (TGD) OFDR Method and Its Performance Verification. Sensors 2021, 21, 4865. [Google Scholar] [CrossRef] [PubMed]
- NEUBRESCOPE NBX-7031. Available online: https://www.neubrex.com/pdf/NBX_7031.pdf (accessed on 9 December 2024).



| Total Distance | 4 km (1 km × 4) |
| Spatial resolution | 20 cm |
| Sampling interval | 5 cm |
| Time interval | ≈1.5 min |
| Strain accuracy (σ) | 15 με |
| Temperature accuracy | 0.75 °C |
| Measurement mode | PPP-BOTDA |
| Spatial resolution | 1 m |
| Gauge length | 1 m |
| Spatial sampling interval | 1 m |
| Time sampling interval | 0.001 s |
| Interrogation rate | 1000 samples/s |
| Date of Earthquake | 17 September 2022 | 18 September 2022 |
|---|---|---|
| Richter scale | 6.4 | 6.8 |
| Time of earthquake | 21:41 | 14:44 |
| Pre-earthquake measurement time | 21:00 | 14:00 |
| Post-earthquake measurement time | 22:00 | 15:00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kishida, K.; Aung, T.L.; Lin, R. Monitoring a Railway Bridge with Distributed Fiber Optic Sensing Using Specially Installed Fibers. Sensors 2025, 25, 98. https://doi.org/10.3390/s25010098
Kishida K, Aung TL, Lin R. Monitoring a Railway Bridge with Distributed Fiber Optic Sensing Using Specially Installed Fibers. Sensors. 2025; 25(1):98. https://doi.org/10.3390/s25010098
Chicago/Turabian StyleKishida, Kinzo, Thein Lin Aung, and Ruiyuan Lin. 2025. "Monitoring a Railway Bridge with Distributed Fiber Optic Sensing Using Specially Installed Fibers" Sensors 25, no. 1: 98. https://doi.org/10.3390/s25010098
APA StyleKishida, K., Aung, T. L., & Lin, R. (2025). Monitoring a Railway Bridge with Distributed Fiber Optic Sensing Using Specially Installed Fibers. Sensors, 25(1), 98. https://doi.org/10.3390/s25010098






