A Metrological Near-Room-Temperature Photon-Number-Resolving Detector: A Design Study
Abstract
1. Introduction
2. Design and Performance
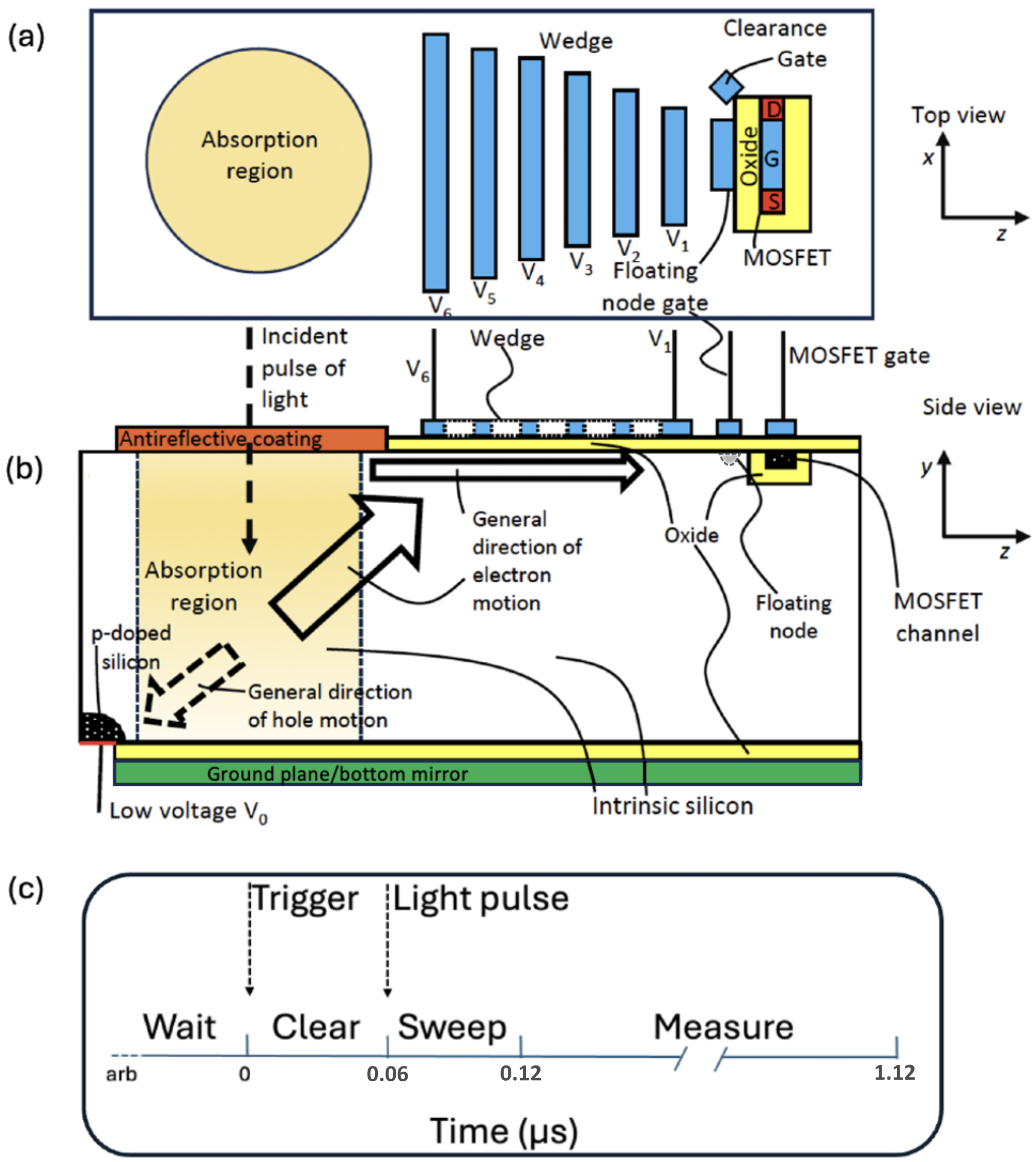
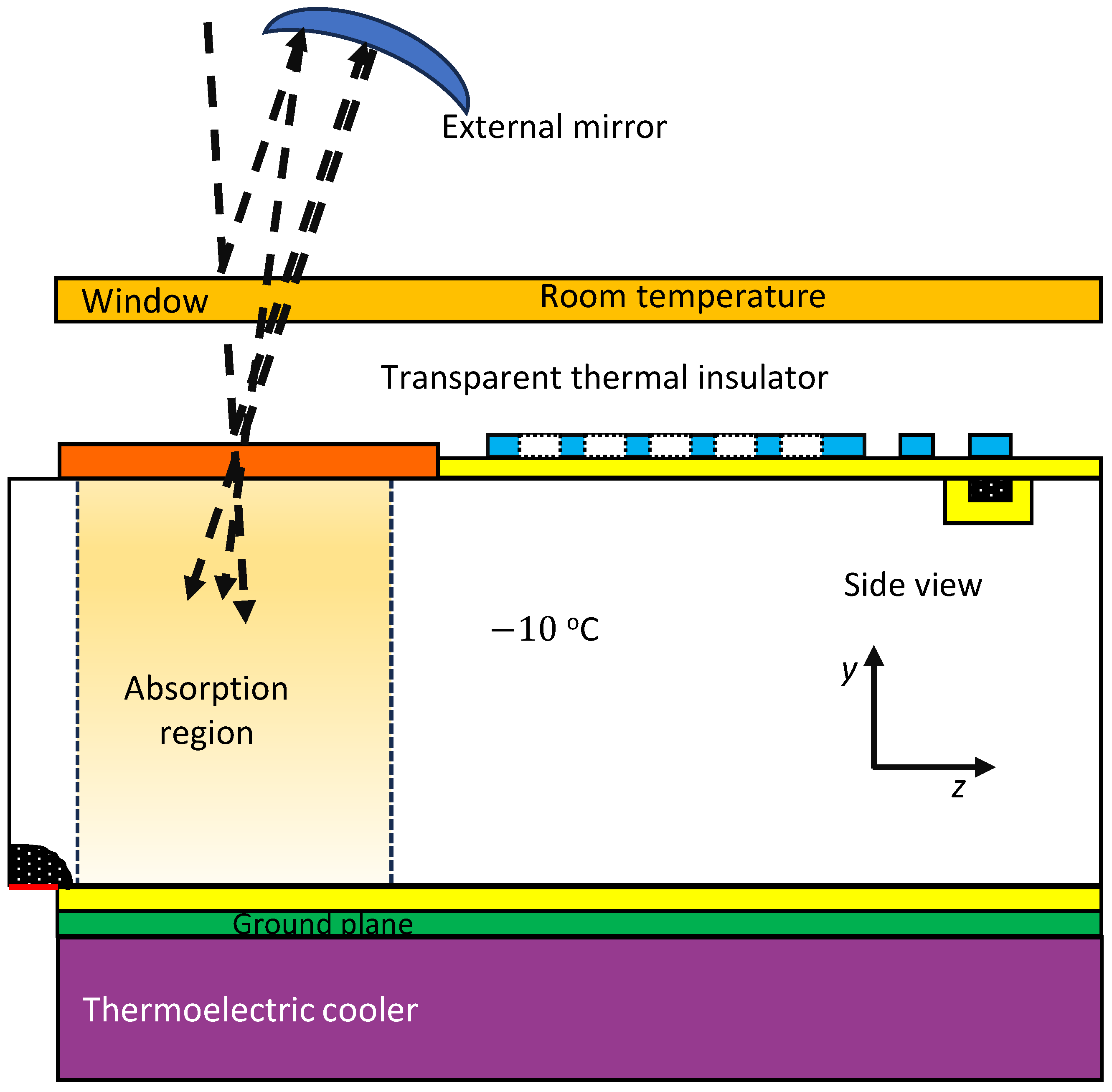
2.1. System Overview
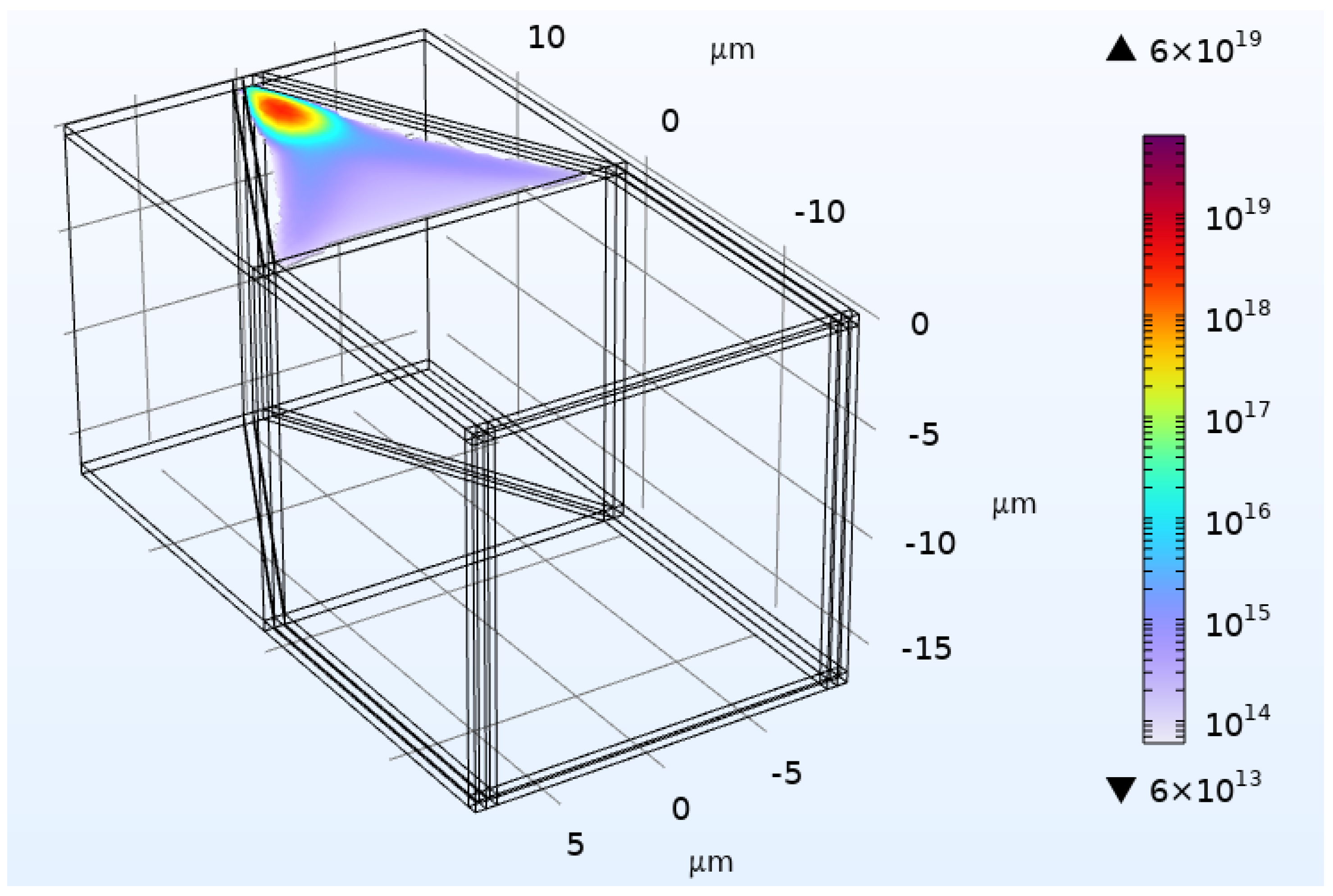
2.2. Photoabsorption Region
2.3. Electron Transport to Floating Node
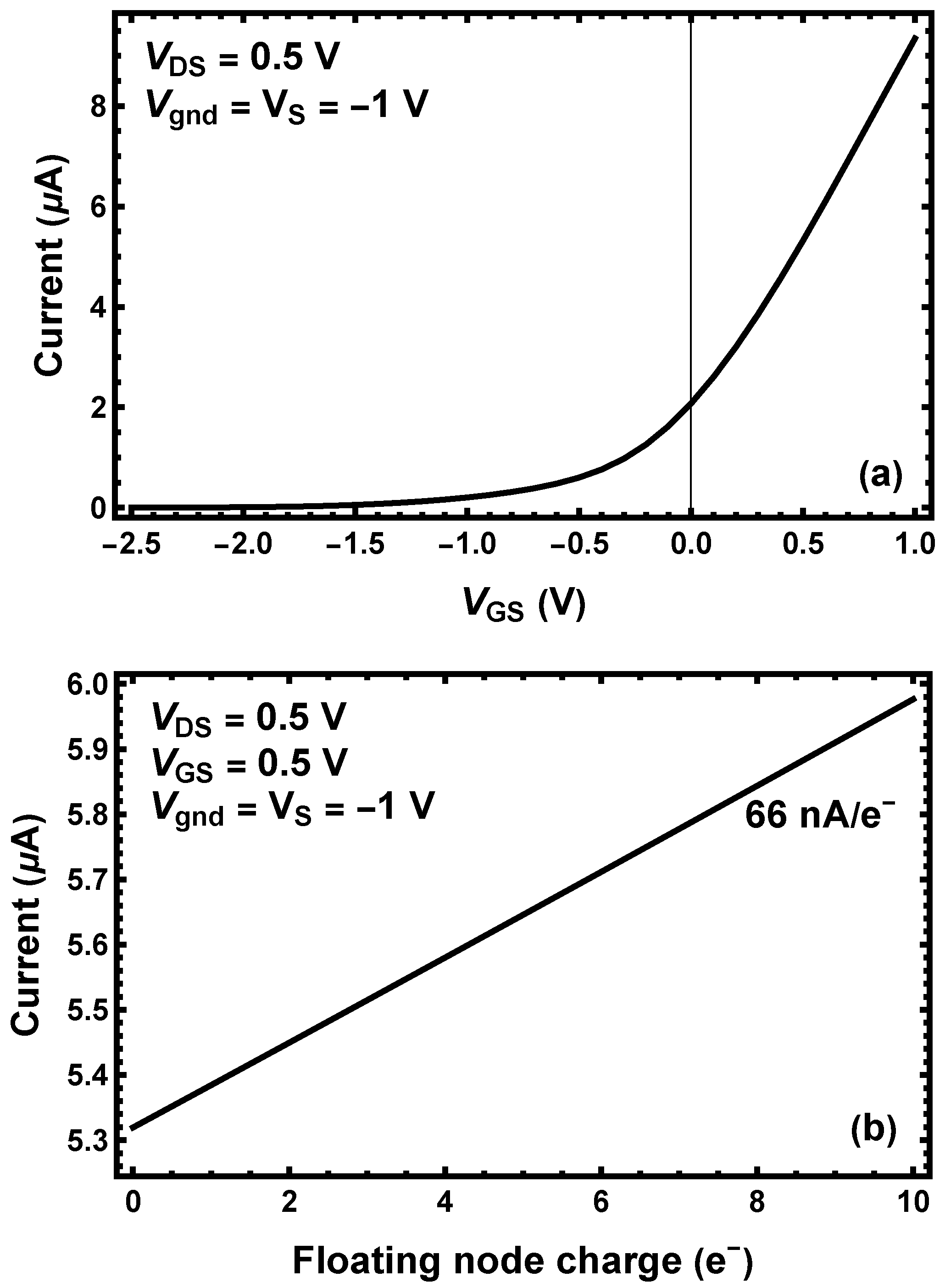
2.4. MOSFET and Floating Node
2.5. Device Reset
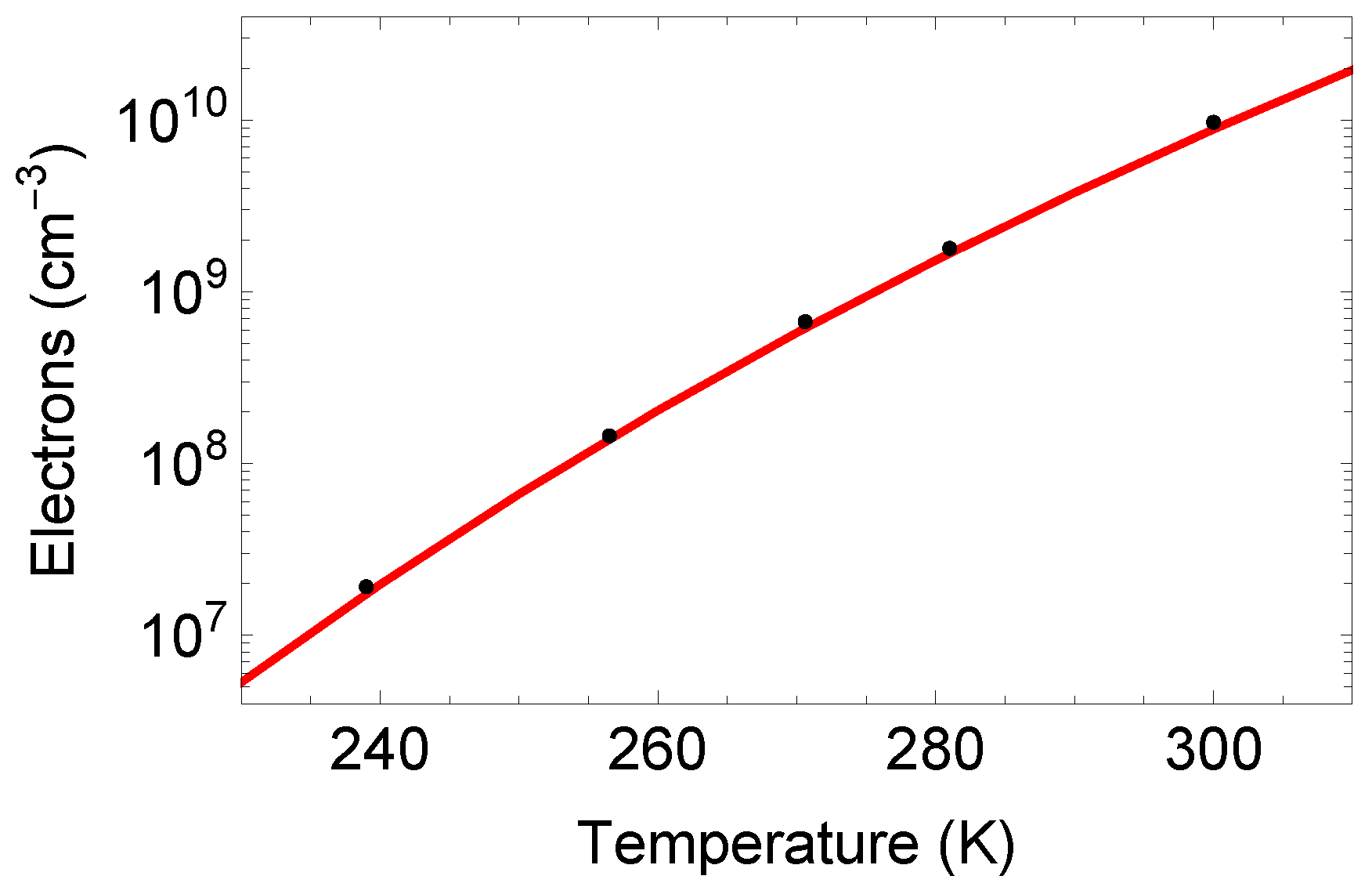
2.6. Carrier Lifetime Effects
2.7. Error Rate Estimate
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Terms Related to “Error Rate”
Appendix B. Poisson Distribution and Photon Uncertainty
Appendix C. Absorption with the Back Mirror
Appendix D. Least-Time Theorem
Appendix E. The Laplace Equation and Wire Spacing
Appendix F. Parallel-Plate Capacitance
References
- Matthews, J.C.F.; Zhou, X.Q.; Cable, H.; Shadbolt, P.J.; Saunders, D.J.; Durkin, G.A.; Pryde, G.J.; O’Brien, J.L. Towards practical quantum metrology with photon counting. NPJ Quantum Inf. 2016, 2, 16023. [Google Scholar] [CrossRef]
- Wu, J.Y.; Toda, N.; Hofmann, H.F. Quantum enhancement of sensitivity achieved by photon-number-resolving detection in the dark port of a two-path interferometer operating at high intensities. Phys. Rev. A 2019, 100, 013814. [Google Scholar] [CrossRef]
- Ralph, T.C.; Gilchrist, A.; Milburn, G.J.; Munro, W.J.; Glancy, S. Quantum computation with optical coherent states. Phys. Rev. A 2003, 68, 042319. [Google Scholar] [CrossRef]
- Pan, J.W.; Chen, Z.B.; Lu, C.Y.; Weinfurter, H.; Zeilinger, A.; Żukowski, M. Multiphoton entanglement and interferometry. Rev. Mod. Phys. 2012, 84, 777–838. [Google Scholar] [CrossRef]
- Hamilton, C.S.; Kruse, R.; Sansoni, L.; Barkhofen, S.; Silberhorn, C.; Jex, I. Gaussian boson sampling. Phys. Rev. Lett. 2017, 119, 170501. [Google Scholar] [CrossRef]
- Madsen, L.S.; Laudenbach, F.; Askarani, M.F.; Rortais, F.; Vincent, T.; Bulmer, J.F.; Miatto, F.M.; Neuhaus, L.; Helt, L.G.; Collins, M.J.; et al. Quantum computational advantage with a programmable photonic processor. Nature 2022, 606, 75–81. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Invited review article: Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef]
- Panuski, C.; Pant, M.; Heuck, M.; Hamerly, R.; Englund, D. Single photon detection by cavity-assisted all-optical gain. Phys. Rev. B 2019, 99, 205303. [Google Scholar] [CrossRef]
- Los, J.W.N.; Sidorova, M.; Lopez-Rodriguez, B.; Qualm, P.; Chang, J.; Steinhauer, S.; Zwiller, V.; Zadeh, I.E. High-performance photon number resolving detectors for 850–950 nm wavelength range. APL Photonics 2024, 9, 066101. [Google Scholar] [CrossRef]
- Migdall, A.; Polyakov, S.V.; Fan, J.; Bienfang, J.C. Single-Photon Generation and Detection: Physics and Applications; Academic Press: Cambridge, MA, USA, 2013; Volume 45. [Google Scholar]
- Bienfang, J.C.; Gerrits, T.; Kuo, P.; Migdall, A.; Polyakov, S.; Slattery, O.T. Single-Photon Sources and Detectors Dictionary; NIST Internal Report 8486; US Department of Commerce, National Institute of Standards and Technology: Gaithersburg, MD, USA, 2023.
- Jönsson, M.; Björk, G. Evaluating the performance of photon-number-resolving detectors. Phys. Rev. A 2019, 99, 043822. [Google Scholar] [CrossRef]
- Miller, A.J.; Nam, S.W.; Martinis, J.M.; Sergienko, A.V. Demonstration of a low-noise near-infrared photon counter with multiphoton discrimination. Appl. Phys. Lett. 2003, 83, 791–793. [Google Scholar] [CrossRef]
- Manenti, L.; Pepe, C.; Sarnoff, I.; Ibrayev, T.; Oikonomou, P.; Knyazev, A.; Monticone, E.; Garrone, H.; Alder, F.; Fawwaz, O.; et al. Dark counts in optical superconducting transition-edge sensors for rare-event searches. Phys. Rev. Appl. 2024, 22, 024051. [Google Scholar] [CrossRef]
- Fukuda, D.; Fujii, G.; Numata, T.; Amemiya, K.; Yoshizawa, A.; Tsuchida, H.; Fujino, H.; Ishii, H.; Itatani, T.; Inoue, S.; et al. Titanium-based transition-edge photon number resolving detector with 98% detection efficiency with index-matched small-gap fiber coupling. Opt. Express 2011, 19, 870–875. [Google Scholar] [CrossRef]
- Lolli, L.; Taralli, E.; Rajteri, M. Ti/Au TES to discriminate single photons. J. Low Temp. Phys. 2012, 167, 803–808. [Google Scholar] [CrossRef]
- Fujiwara, A.; Yamazaki, K.; Takahashi, Y. Detection of single charges and their generation-recombination dynamics in Si nanowires at room temperature. Appl. Phys. Lett. 2002, 80, 4567–4569. [Google Scholar] [CrossRef]
- Nishiguchi, K.; Ono, Y.; Fujiwara, A.; Yamaguchi, H.; Inokawa, H.; Takahashi, Y. Infrared detection with silicon nano-field-effect transistors. Appl. Phys. Lett. 2007, 90, 223108. [Google Scholar] [CrossRef]
- Du, W.; Inokawa, H.; Satoh, H.; Ono, A. SOI metal-oxide-semiconductor field-effect transistor photon detector based on single-hole counting. Opt. Lett. 2011, 36, 2800–2802. [Google Scholar] [CrossRef][Green Version]
- Ma, J.; Fossum, E.R. Quanta image sensor jot with sub 0.3 e-rms read noise and photon counting capability. IEEE Electron Device Lett. 2015, 36, 926–928. [Google Scholar] [CrossRef]
- Ma, J.; Fossum, E.R. A pump-gate jot device with high conversion gain for a quanta image sensor. IEEE J. Electron Devices Soc. 2015, 3, 73–77. [Google Scholar] [CrossRef]
- Ma, J.; Masoodian, S.; Starkey, D.A.; Fossum, E.R. Photon-number-resolving megapixel image sensor at room temperature without avalanche gain. Optica 2017, 4, 1474–1481. [Google Scholar] [CrossRef]
- Holland, S.E.; Groom, D.E.; Palaio, N.P.; Stover, R.J.; Wei, M. Fully depleted, back-illuminated charge-coupled devices fabricated on high-resistivity silicon. IEEE Trans. Electron Devices 2003, 50, 225–238. [Google Scholar] [CrossRef]
- Groom, D.; Haque, S.; Holland, S.; Kolbe, W. Quantum efficiency modeling for a thick back-illuminated astronomical CCD. J. Appl. Phys. 2017, 122, 055301. [Google Scholar] [CrossRef]
- Tilke, A.; Shum, D.P.C.; Pescini, L.; Kakoschke, R.; Strenz, K.R.; Stiftinger, M. Deep Trench Isolation Structures and Methods of Formation Thereof. U.S. Patent 7,679,130, 16 March 2010. [Google Scholar]
- Raut, H.K.; Ganesh, V.A.; Nair, A.S.; Ramakrishna, S. Anti-reflective coatings: A critical, in-depth review. Energy Environ. Sci. 2011, 4, 3779–3804. [Google Scholar] [CrossRef]
- Gerrits, T.; Migdall, A.; Bienfang, J.C.; Lehman, J.; Nam, S.W.; Splett, J.; Vayshenker, I.; Wang, J. Calibration of free-space and fiber-coupled single-photon detectors. Metrologia 2020, 57, 015002. [Google Scholar] [CrossRef]
- Pakik, E.D. (Ed.) Handbook of Optical Constants of Solids; Academic Press: New York, NY, USA, 1985; pp. 547–569. [Google Scholar]
- Hass, G. Reflectance and preparation of front-surface mirrors for use at various angles of incidence from the ultraviolet to the far infrared. J. Opt. Soc. Am. 1982, 72, 27–39. [Google Scholar] [CrossRef]
- Vavilov, V.S. On photo-ionization by fast electrons in germanium and silicon. J. Phys. Chem. Solids 1959, 8, 223–226. [Google Scholar] [CrossRef]
- Ablassmeier, U.; Kellner, W.; Herbst, H.; Kniepkamp, H. Three-phase GaAs Schottky-barrier CCD operated up to 100-MHz clock frequency. IEEE Trans. Electron Devices 1980, 27, 1181–1183. [Google Scholar] [CrossRef]
- Tiffenberg, J.; Sofo-Haro, M.; Drlica-Wagner, A.; Essig, R.; Guardincerri, Y.; Holland, S.; Volansky, T.; Yu, T.T. Single-electron and single-photon sensitivity with a silicon Skipper CCD. Phys. Rev. Lett. 2017, 119, 131802. [Google Scholar] [CrossRef]
- Ohmori, K.; Amakawa, S. Direct white noise characterization of short-channel MOSFETs. IEEE Trans. Electron Devices 2021, 68, 1478–1482. [Google Scholar] [CrossRef]
- Schroder, D.K. Carrier lifetimes in silicon. IEEE Trans. Electron Devices 1997, 44, 160–170. [Google Scholar] [CrossRef]
- Tanabe, T.; Taniyama, H.; Notomi, M. Carrier diffusion and recombination in photonic crystal nanocavity optical switches. J. Light. Technol. 2008, 26, 1396–1403. [Google Scholar] [CrossRef]
- Pang, S.; Rohatgi, A. Record high recombination lifetime in oxidized magnetic Czochralski silicon. Appl. Phys. Lett. 1991, 59, 195–197. [Google Scholar] [CrossRef]
- Wang, S.; MacDonald, D. Temperature dependence of Auger recombination in highly injected crystalline silicon. J. Appl. Phys. 2012, 112, 113708. [Google Scholar] [CrossRef]
- Sproul, A.; Green, M.A. Improved value for the silicon intrinsic carrier concentration from 275 to 375 K. J. Appl. Phys. 1991, 70, 846–854. [Google Scholar] [CrossRef]
- Misiakos, K.; Tsamakis, D. Accurate measurements of the silicon intrinsic carrier density from 78 to 340 K. J. Appl. Phys. 1993, 74, 3293–3297. [Google Scholar] [CrossRef]
- Singh, P. Intrinsic Carrier Concentration Calculator. Available online: https://www.omnicalculator.com/physics/intrinsic-carrier-concentration (accessed on 8 August 2025).
- Larionova, Y.; Mertens, V.; Harder, N.P.; Brendel, R. Surface passivation of n-type Czochralski silicon substrates by thermal-SiO2/plasma-enhanced chemical vapor deposition SiN stacks. Appl. Phys. Lett. 2010, 96, 032105. [Google Scholar] [CrossRef]
- Levine, Z.H.; Zimmerman, N.M.; Bienfang, J.C.; Migdall, A.L. Metrological Photon Counter and Metrologically Counting Photons at Room Temperature. U.S. Patent Application PCT/US25/12217, 17 January 2025. [Google Scholar]
| Temperature (K) | 300 | 263 |
|---|---|---|
| Mobility–bulk (cm2/(V·s)) | 1440 | 1800 |
| Mobility–near interface (cm2/(V·s)) | 500 | 600 |
| Drift velocity (m/s) | 5500 | 6600 |
| Drift time (ns) | 72 | 60 |
| Diffusion coefficient D (m2/s) | 0.0039 | 0.0046 |
| (V) | 0.69 | 0.60 |
| (V) | 0.99 | 0.86 |
| Electron lifetime–bulk (ms) | 5 | 4 |
| Electron lifetime–near interface (ms) | 2 | 2 |
| Intrinsic carrier concentration (1/cm3) | ||
| Carrier generation rate (1/(cm3· s)) |
| Floating Node Electrons | Gate Electrons |
|---|---|
| 10 |
| Issue | Sign of Effect | Uncertainty | Remark | |
|---|---|---|---|---|
| Discrete photon-number uncertainties | ||||
| Reflection from three front surfaces | − | 0.0002 | 0.002 | AR coating (99%) with recycling mirror (99.4%) |
| Reflection loss, bottom mirror | − | 0.0001 | 0.001 | nm, 0.33% to mirror, 3% absorbed |
| Transmission through absorption region | − | nm (worst in visible) | ||
| Beam-aperture interaction Equation (1) | − | 0.001 | 0.010 | m, m |
| Subtotal | 0.0013 | 0.013 | Added linearly | |
| Discrete electron number uncertainties | ||||
| Electrons generated in absorption region | + | 0.003 | 0.003 | Clearing before pulse, gate |
| Recombined electrons | − | 0.0005 | 0.005 | 1.06 s transport plus measurement time over 2 ms lifetime |
| Multiple photoelectron generation | + | negligible | nm | |
| Lagging electrons | − | negligible | 60 ns twice average transit time | |
| Electrons that never reach floating node | − | negligible | ||
| Subtotal | 0.0035 | 0.008 | Added linearly | |
| Continuous uncertainties | ||||
| Short-channel MOSFET noise | ± | negligible | 0.06 photon equivalent standard error | |
| Subtotal | negligible | Not likely to cause error after rounding | ||
| Total | 0.005 | 0.021 | Added linearly | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levine, Z.H.; Bienfang, J.C.; Migdall, A.L.; Zimmerman, N.M. A Metrological Near-Room-Temperature Photon-Number-Resolving Detector: A Design Study. Sensors 2025, 25, 5470. https://doi.org/10.3390/s25175470
Levine ZH, Bienfang JC, Migdall AL, Zimmerman NM. A Metrological Near-Room-Temperature Photon-Number-Resolving Detector: A Design Study. Sensors. 2025; 25(17):5470. https://doi.org/10.3390/s25175470
Chicago/Turabian StyleLevine, Zachary H., Joshua C. Bienfang, Alan L. Migdall, and Neil M. Zimmerman. 2025. "A Metrological Near-Room-Temperature Photon-Number-Resolving Detector: A Design Study" Sensors 25, no. 17: 5470. https://doi.org/10.3390/s25175470
APA StyleLevine, Z. H., Bienfang, J. C., Migdall, A. L., & Zimmerman, N. M. (2025). A Metrological Near-Room-Temperature Photon-Number-Resolving Detector: A Design Study. Sensors, 25(17), 5470. https://doi.org/10.3390/s25175470







