Preliminary Study on the Purity Analysis of Primary Certified Gas Mixtures Using Different Spectroscopic Techniques
Abstract
Highlights
- Different spectroscopic techniques were applied to purity analysis of pure gases.
- Impurities of CO2 and H2O in ultrapure gases used for CRM production were quantified.
- FTIR, NDIR and CRDS are useful spectroscopic techniques for purity determination.
- CRMs produced with tested pure gases can be applied for calibration of gas sensors.
Abstract
1. Introduction
2. Materials and Methods
2.1. CO2 Impurity Determination via FTIR
2.2. CO2 Impurity Determination via NDIR
2.3. H2O Impurity Determination via CRDS
3. Results
3.1. CO2 Impurities via FTIR

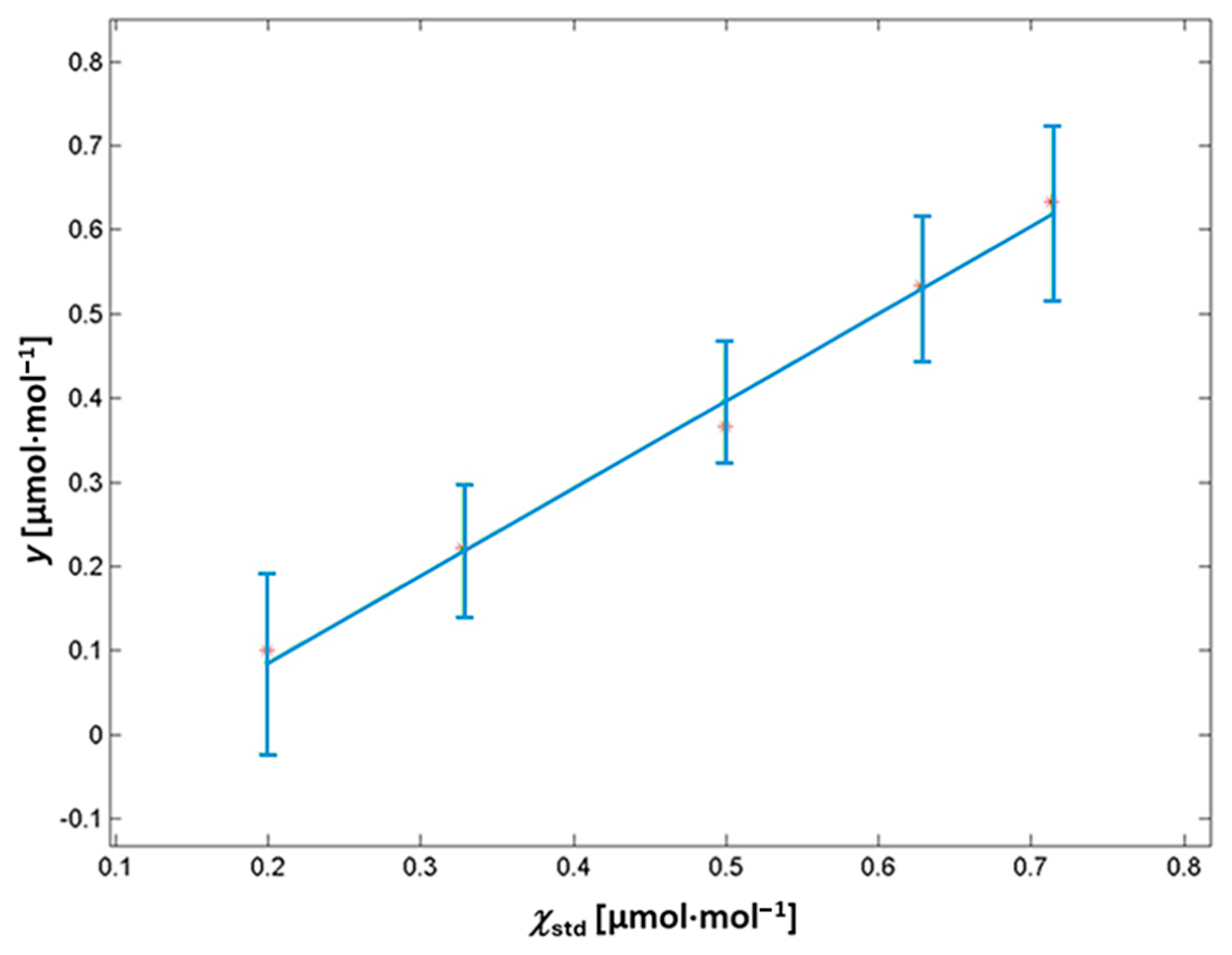
3.2. CO2 Impurities via NDIR
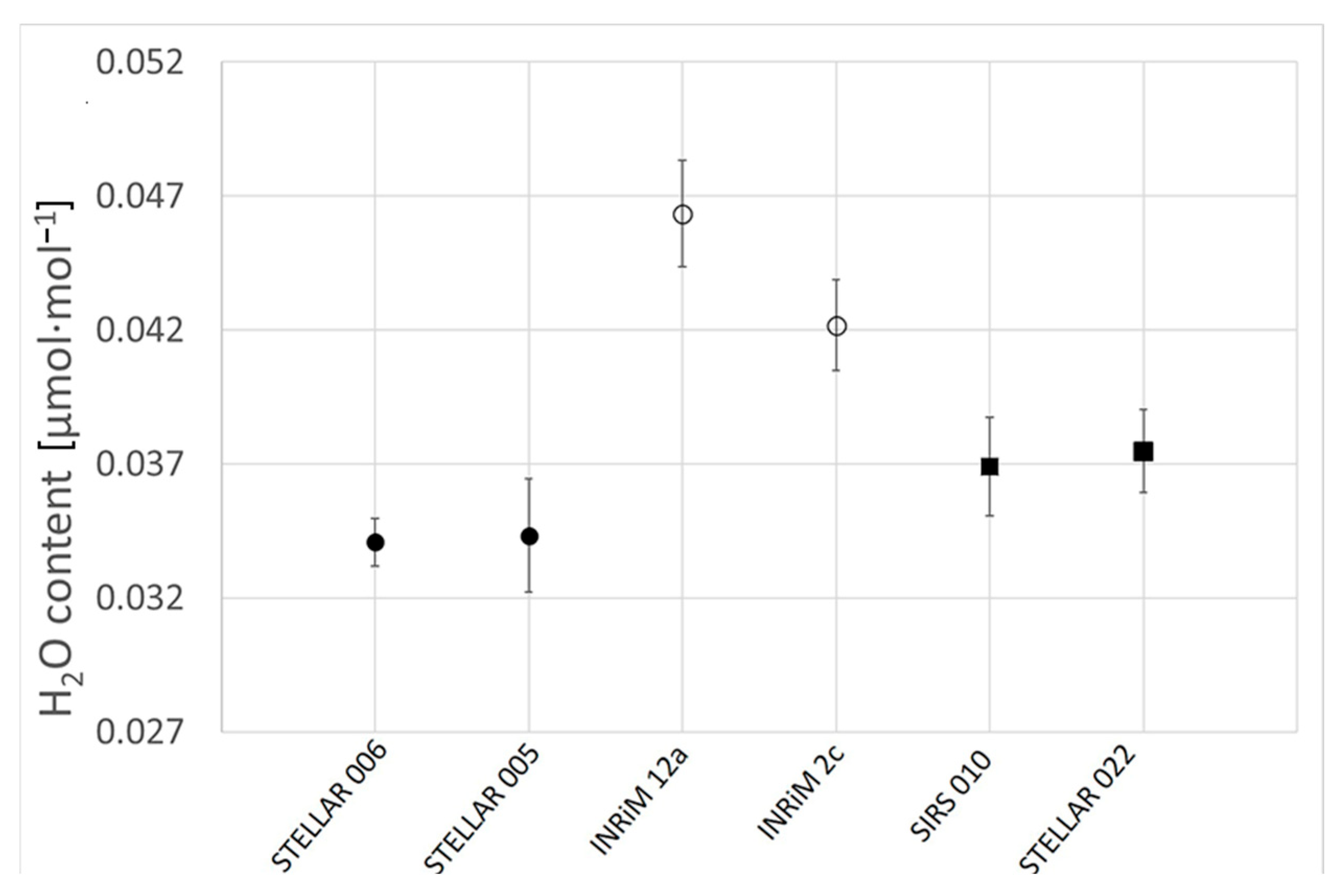
3.3. H2O Impurities via CRDS
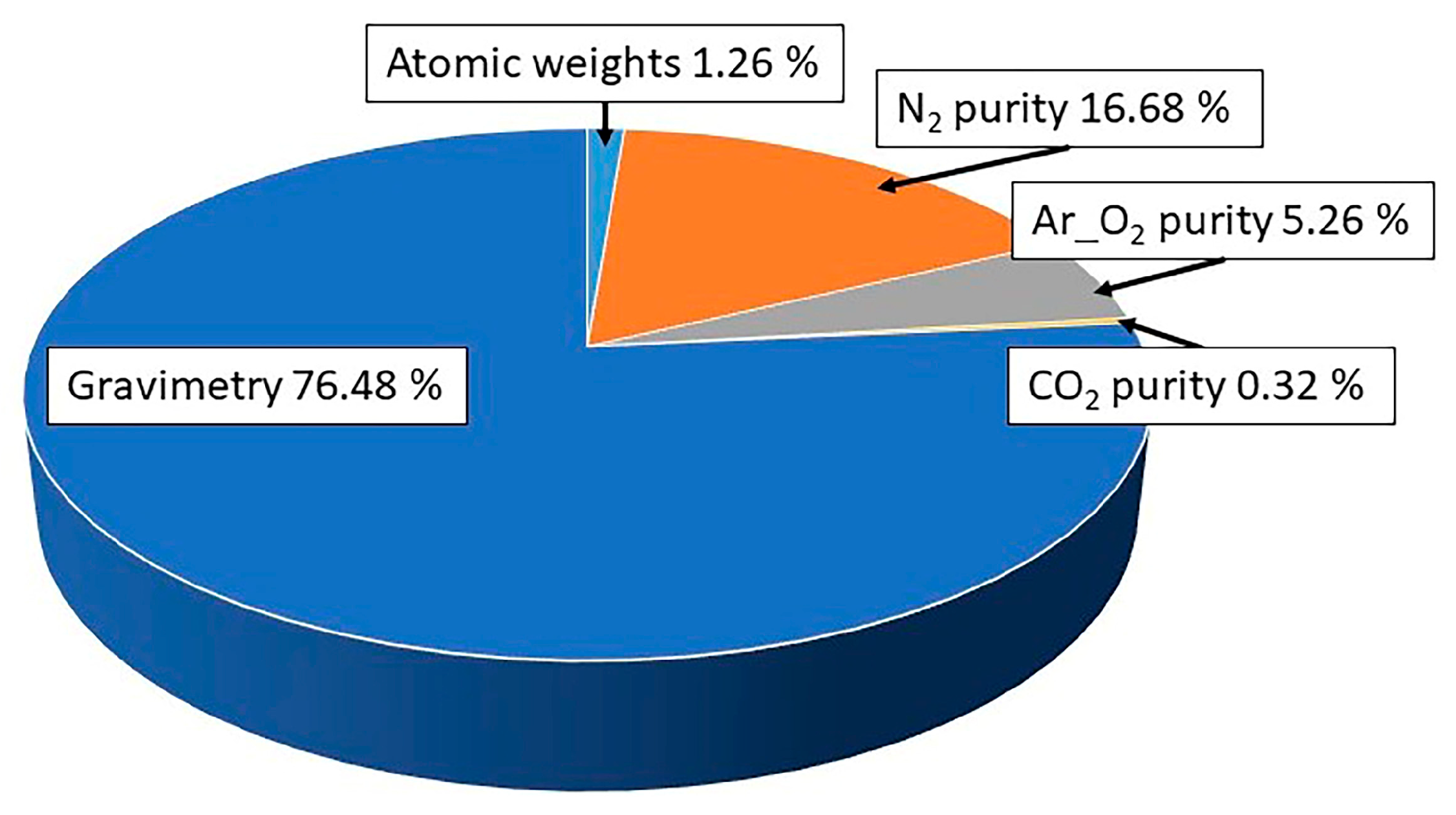
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ISO 19229; Gas Analysis—Purity Analysis and the Treatment of Purity Data, 2nd Edition. ISO: Geneva, Switzerland, 2019.
- Mulyana, M.R.; Budiman, H.; Zuas, O.; Hindayani, A. Trace impurities measurement in ultra-high purity gases and their uncertainties: Case study on permanent gas impurities in pure nitrogen. J. Phys. Conf. Ser. 2019, 1153, 012035. [Google Scholar] [CrossRef]
- Loianno, V.; Mensitieri, G.; Baldanza, A.; Scherillo, G.; Musto, P. Combining FTIR spectroscopy and pressure-decay techniques to analyze sorption isotherms and sorption kinetics of pure gases and their mixtures in polymers: The case of CO2 and CH4 sorption in polydimethylsiloxane. J. Membr. Sci. 2022, 652, 120445. [Google Scholar] [CrossRef]
- Frey, M.; Hase, F.; Blumenstock, T.; Groß, J.; Kiel, M.; Tsidu, G.M.; Schäfer, K.; Sha, M.K.; Orphal, J. Calibration and instrumental line shape characterization of a set of portable FTIR spectrometers for detecting greenhouse gas emissions. Atmos. Meas. Tech. 2015, 8, 3047–3057. [Google Scholar] [CrossRef]
- Ogawara, Y.; Bruneau, A.; Kimura, T. Determination of ppb-Level CO, CO2, CH4, and H2O in High-Purity Gases Using Matrix Isolation FT-IR with an Integrating Sphere. Anal. Chem. 1994, 66, 4354–4358. [Google Scholar] [CrossRef]
- Dinh, T.-V.; Choi, I.-Y.; Son, Y.-S.; Kim, J.-C. A review on non-dispersive infrared gas sensors: Improvement of sensor detection limit and interference correction. Sens. Actuat. B Chem. 2016, 231, 529–538. [Google Scholar] [CrossRef]
- Sun, Q.; Liu, T.; Yu, X.; Huang, M. Non-interference NDIR detection method for mixed gases based on differential elimination. Sens. Actuat. B Chem. 2023, 390, 133901. [Google Scholar] [CrossRef]
- Liu, H.; Chen, T.; Chen, D.; Chang, D.; Frost, R.L. The development of a new method for the determination of concentrations of carbonaceous gases using a non-dispersive infrared sensor. Fuel 2013, 104, 749–751. [Google Scholar] [CrossRef]
- Berden, G.; Peeters, R.; Meijer, G. Cavity ring-down spectroscopy: Experimental schemes and applications. Int. Rev. Phys. Chem. 2000, 19, 565–607. [Google Scholar] [CrossRef]
- Abe, H. Trace-moisture measurement using cavity ringdown spectroscopy at NMIJ. J. Phys. Conf. Ser. 2023, 2439, 012001. [Google Scholar] [CrossRef]
- Abe, H.; Hashiguchi, K.; Lisak, D.; Honda, S.; Miyake, T.; Shimizu, H. A miniaturized trace-moisture sensor based on cavity ring-down spectroscopy. Sens. Actuat. A 2021, 320, 112559. [Google Scholar] [CrossRef]
- Ma, J.; Fan, E.; Liu, H.; Zhang, Y.; Mai, C.; Li, X.; Jin, W.; Guan, B.-O. Microscale fiber photoacoustic spectroscopy for in situ and real-time trace gas sensing. Adv. Photonics 2024, 6, 066008. [Google Scholar] [CrossRef]
- Sun, J.; Wang, F.; Zhang, L.; Shao, J. A novel photoacoustic gas sensor for dual-component identification and concentration analysis. Infrared Phys. Technol. 2025, 145, 105711. [Google Scholar] [CrossRef]
- Rey, J.M.; Sigrist, M.W. Non-dispersive sensing scheme based on mid-infrared LED and differential mode excitation photoacoustic spectroscopy. Photoacoustics 2023, 29, 100455. [Google Scholar] [CrossRef]
- Sun, H.; Qiao, S.; He, Y.; Sun, X.; Ma, Y. Parts-per-quadrillion level gas molecule detection: CO-LITES sensing. Light Sci. Appl. 2025, 14, 180. [Google Scholar] [CrossRef]
- Yang, Q.-Y.; Tan, Y.; Qu, Z.-H.; Sun, Y.; Liu, A.-W.; Hu, S.-M. Multiple Gas Detection by Cavity-Enhanced Raman Spectroscopy with Sub-ppm Sensitivity. Anal. Chem. 2023, 95, 5652–5660. [Google Scholar] [CrossRef] [PubMed]
- Petrov, D.V.; Matrosov, I.I.; Kostenko, M.A. Multipass Raman gas analyzer for monitoring of atmospheric air composition. Opt. Laser Technol. 2022, 152, 108155. [Google Scholar] [CrossRef]
- Komal; Soni, D. A review on preparation methods and measurement techniques of reference gas mixtures. Microchem. J. 2024, 197, 109742. [Google Scholar] [CrossRef]
- Durbiano, F.; Pennecchi, F.R.; Rolle, F.; Pavarelli, S.; Sega, M. Stability study and uncertainty evaluation of CO2 certified reference materials for greenhouse gases monitoring. Measurement 2024, 232, 114653. [Google Scholar] [CrossRef]
- Dias, F.A.; Palma, C.; Costa, C.J. Preparation of multicomponent mixtures to support carbon metrology. Measurement 2025, 239, 115453. [Google Scholar] [CrossRef]
- ISO 6142-1; Gas analysis—Preparation of Calibration Gas Mixtures. Part 1: Gravimetric Method for Class I mixtures, 1st Edition. ISO: Geneva, Switzerland, 2015.
- Garg, G.; Kumari, P.; Soni, D.; Singh, K.; Aggarwal, S.G.; Deep, A. Impurity Analysis of 5.5 N Nitrogen Gas and Its Impact on the Preparation of Class I Type Calibration Gas Mixtures. ChemistrySelect 2023, 8, e202300557. [Google Scholar] [CrossRef]
- EURAMET. Available online: https://www.euramet.org/technical-committees/tc-projects/details/project/analysis-of-the-impurities-in-pure-and-balance-gases-used-to-prepare-primary-standard-gas-mixtures-b (accessed on 15 July 2025).
- Miñarro, M.D.; Brewer, P.J.; Brown, R.J.C.; Persijn, S.; van Wijk, J.; Nieuwenkamp, G.; Baldan, A.; Kaiser, C.; Sutour, C.; Macé, T.; et al. Zero gas reference standards. Anal. Methods 2016, 8, 3014–3022. [Google Scholar] [CrossRef]
- Andrade, J.M.; Terán-Baamonde, J.; Soto-Ferreiro, R.M.; Carlosena, A. Interpolation in the standard additions method. Anal. Chim. Acta 2013, 780, 13–19. [Google Scholar] [CrossRef]
- Radičević, I.; Hudoklin, D. Empirical enhancement factors for trace moisture in nitrogen and argon: Bridging measurement principles. Sens. Actuat. B Chem. 2025, 435, 137617. [Google Scholar] [CrossRef]
- Mondelain, D.; Aradj, A.; Kassi, S.; Campargue, A. The water vapour self-continuum by CRDS at room temperature in the 1.6 µm transparency window. J. Quant. Spectrosc. Radiat. Transf. 2013, 130, 381–391. [Google Scholar] [CrossRef]
- JCGM 100:2008(E); GUM 1995 with Minor Corrections, Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. Joint Committee for Guides in Metrology: Paris, France, 2008. [CrossRef]
- JCGM 101:2008; Evaluation of Measurement Data-Supplement 1 to the Guide to the Expression of Uncertainty in Measurement-Propagation of Distributions Using a Monte Carlo Method. Joint Committee for Guides in Metrology: Paris, France, 2008. [CrossRef]
- Sega, M.; Pennecchi, F.R.; Rinaldi, S.; Rolle, F. Uncertainty evaluation for the quantification of low masses of benzo[a]pyrene: Comparison between the Law of Propagation of Uncertainty and the Monte Carlo method. Anal. Chim. Acta 2016, 920, 10–17. [Google Scholar] [CrossRef] [PubMed]
- Oudwater, R.J.; van Wijk, J.I.T.; Persijn, S.; Wessel, R.M.; van der Veen, A.M.H.; Mace, T.; Sutour, C.; Couette, J.; Milton, M.; Harling, A.; et al. Final report on EURAMET.QM-S8: Analysis of impurities in pure and balance gases used to prepare primary standard gas mixtures by the gravimetric method. Metrologia 2013, 50, 08023. [Google Scholar] [CrossRef]

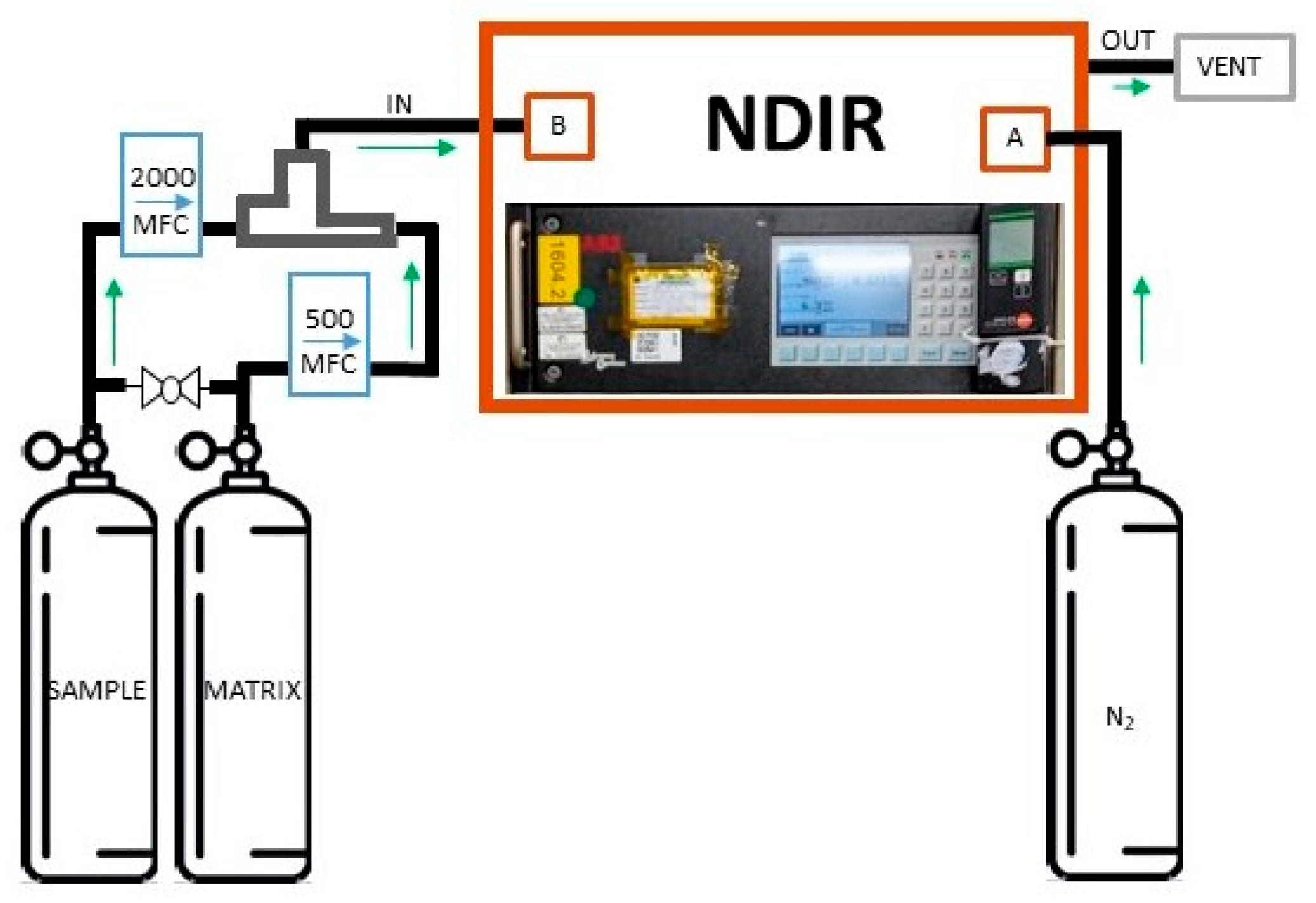


| Flow Q1 (CO2 in N2 Parent Mixture) | Flow Q2 (Pure N2 grade 6.0) | CO2 Amount Fraction χout | u(χout) |
|---|---|---|---|
| sccm | sccm | µmol mol−1 | µmol mol−1 |
| 8 | 1192 | 3.55 | 0.06 |
| 12 | 1188 | 5.27 | 0.06 |
| 18 | 1182 | 7.83 | 0.06 |
| 30 | 1170 | 12.90 | 0.06 |
| Flow Q1 (CO2 in SA Parent Mixture) | Flow Q2 (Synthetic Air Grade 5.7) | CO2 Amount Fraction χout | u (χout) |
|---|---|---|---|
| sccm | sccm | µmol mol−1 | µmol mol−1 |
| 7 | 1193 | 0.199 | 0.003 |
| 10 | 1190 | 0.328 | 0.005 |
| 14 | 1186 | 0.499 | 0.008 |
| 17 | 1183 | 0.628 | 0.010 |
| 19 | 1181 | 0.714 | 0.011 |
| Cylinder Code | Matrix Type | Preparation Date | CRDS CO2 Amount Fraction µmol mol−1 | CRDS H2O Amount Fraction µmol mol−1 |
|---|---|---|---|---|
| STELLAR 006 | Scrubbed natural air | 27 January 2022 | 406.72 | 0.0341 |
| STELLAR 005 | Scrubbed natural air | 27 January 2022 | 406.73 | 0.0343 |
| INRiM 12A | Synthetic air (with 1% Ar) | 9 August 2024 | 403.56 | 0.0463 |
| INRiM 2C | Synthetic air (with 1% Ar) | 26 July 2024 | 413.45 | 0.0422 |
| SIRS 010 | Synthetic air (with 1% Ar) | 13 January 2020 | 387.05 | 0.0369 |
| STELLAR 022 | Synthetic air (with 1% Ar) | 4 April 2022 | 402.09 | 0.0375 |
| Quantity | Quantity Value | Standard Uncertainty |
|---|---|---|
| Intercept of the calibration curve, a | 0.06 μmol·mol−1 | 0.15 μmol·mol−1 |
| Slope of the calibration curve, b | 0.954 | 0.016 |
| Covariance u(a, b) | ||
| −0.0023 |
| Quantity | Quantity Value | Standard Uncertainty |
|---|---|---|
| Intercept of the calibration curve, a | 0.121 μmol·mol−1 | 0.081 μmol·mol−1 |
| Slope of the calibration curve, b | 1.04 | 0.15 |
| Covariance u(a, b) | ||
| −0.012 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rolle, F.; Durbiano, F.; Pavarelli, S.; Russo, R.; Festevole, C.; Spazzini, P.G.; Pennecchi, F.R.; Sega, M. Preliminary Study on the Purity Analysis of Primary Certified Gas Mixtures Using Different Spectroscopic Techniques. Sensors 2025, 25, 6068. https://doi.org/10.3390/s25196068
Rolle F, Durbiano F, Pavarelli S, Russo R, Festevole C, Spazzini PG, Pennecchi FR, Sega M. Preliminary Study on the Purity Analysis of Primary Certified Gas Mixtures Using Different Spectroscopic Techniques. Sensors. 2025; 25(19):6068. https://doi.org/10.3390/s25196068
Chicago/Turabian StyleRolle, Francesca, Francesca Durbiano, Stefano Pavarelli, Ramona Russo, Chiara Festevole, Pier Giorgio Spazzini, Francesca Romana Pennecchi, and Michela Sega. 2025. "Preliminary Study on the Purity Analysis of Primary Certified Gas Mixtures Using Different Spectroscopic Techniques" Sensors 25, no. 19: 6068. https://doi.org/10.3390/s25196068
APA StyleRolle, F., Durbiano, F., Pavarelli, S., Russo, R., Festevole, C., Spazzini, P. G., Pennecchi, F. R., & Sega, M. (2025). Preliminary Study on the Purity Analysis of Primary Certified Gas Mixtures Using Different Spectroscopic Techniques. Sensors, 25(19), 6068. https://doi.org/10.3390/s25196068









