The Design and Validation of an Open-Palm Data Glove for Precision Finger and Wrist Tracking
Abstract
1. Introduction
2. Related Works
3. Materials
3.1. Glove Design
3.1.1. Inertial Measurement Units
3.1.2. Resistive Flex Sensors
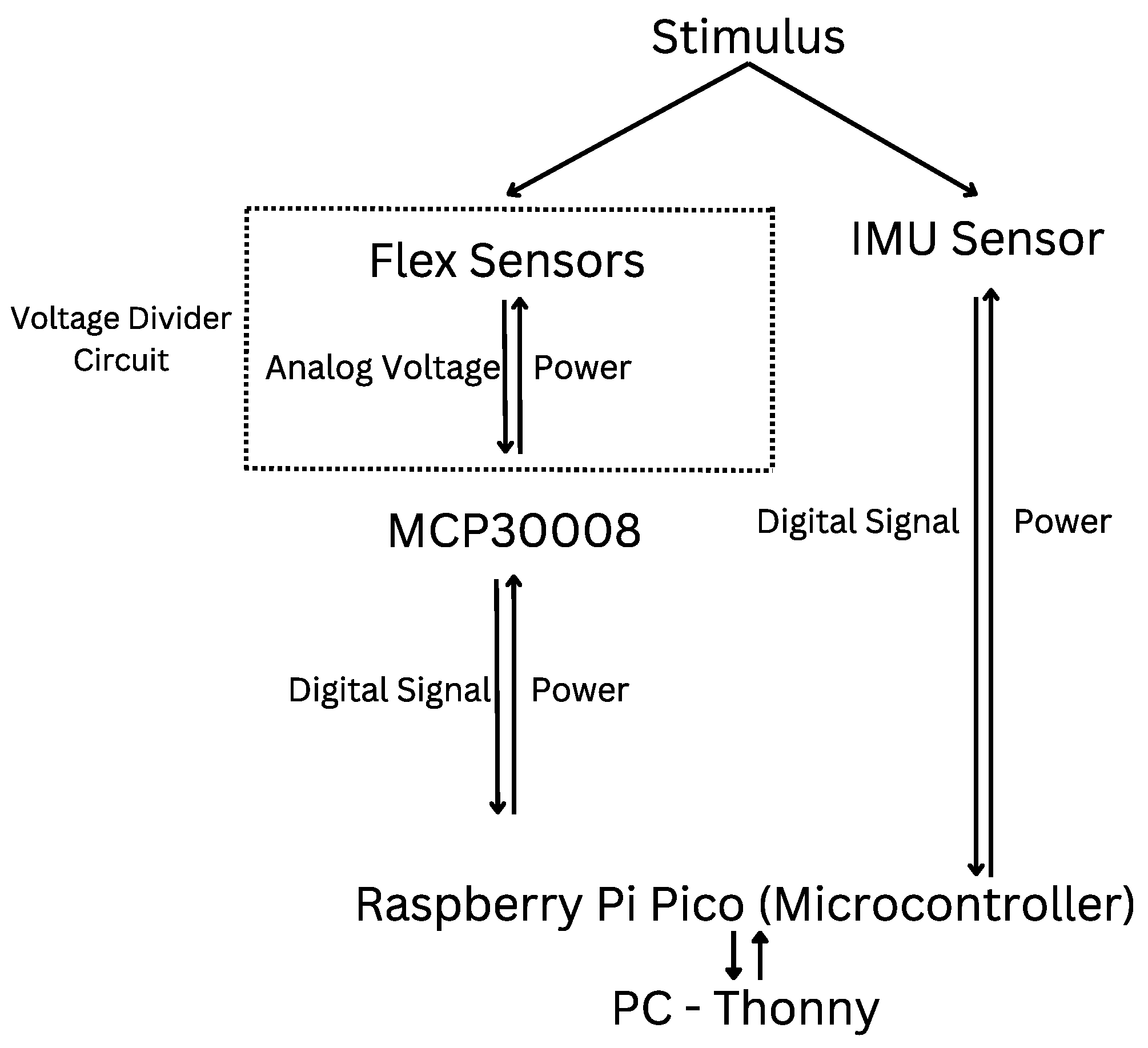
3.2. Data Aquisition
3.3. Glove Evaluation Setup
4. Methods
4.1. Sensor Testing
4.1.1. Drift and Delay
4.1.2. Linear Mapping of the RFSs
4.2. Glove Testing
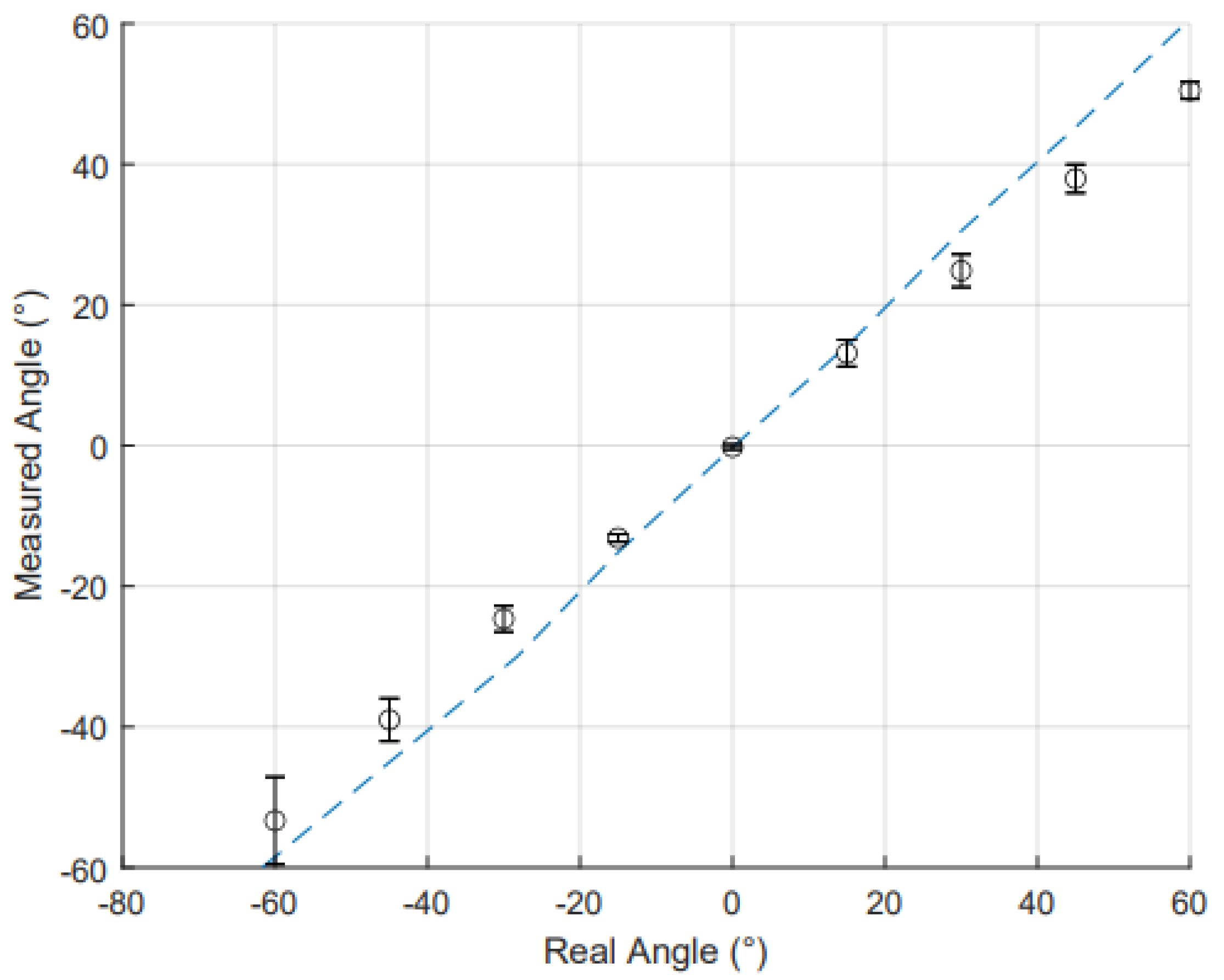
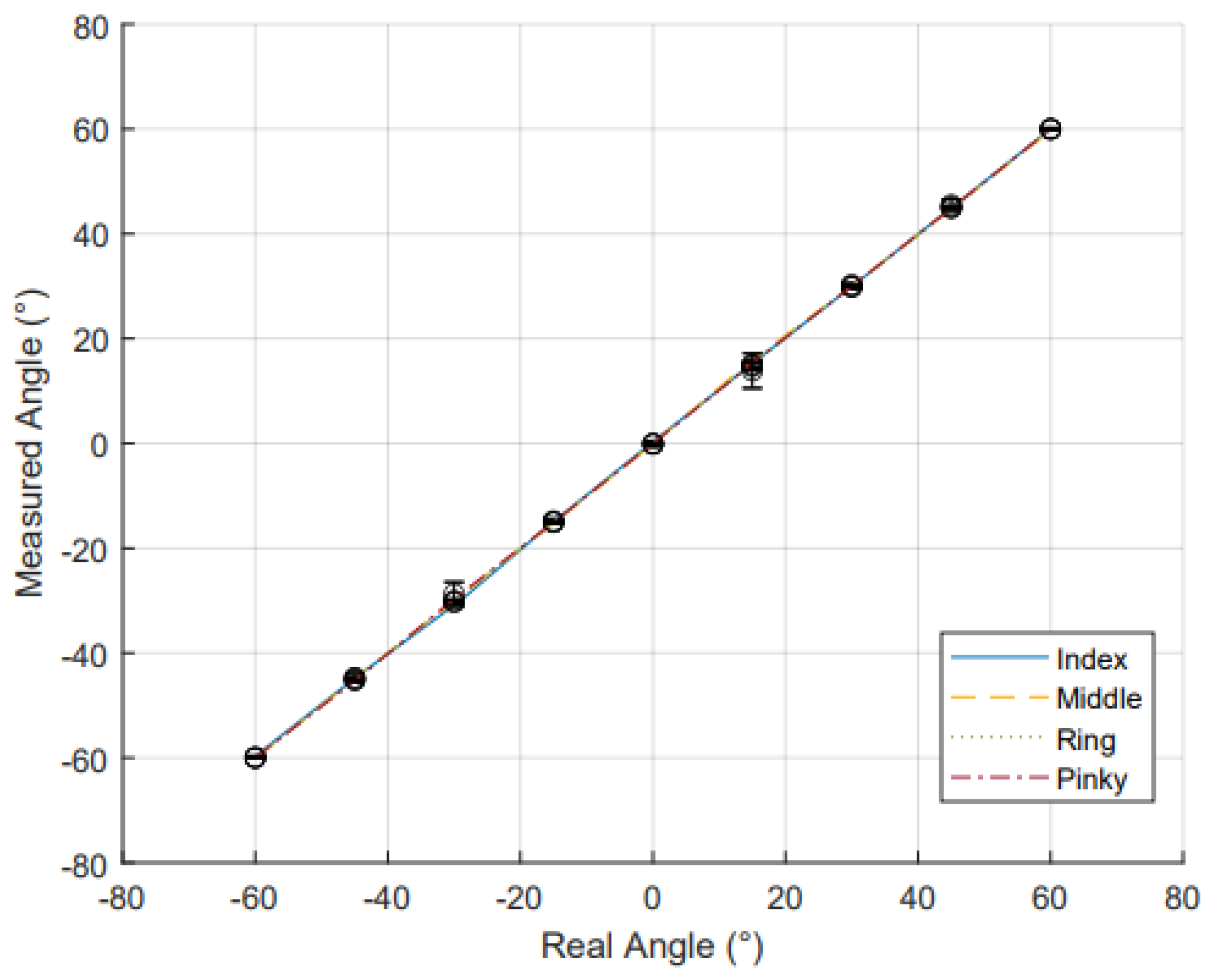
4.2.1. Static Measurements
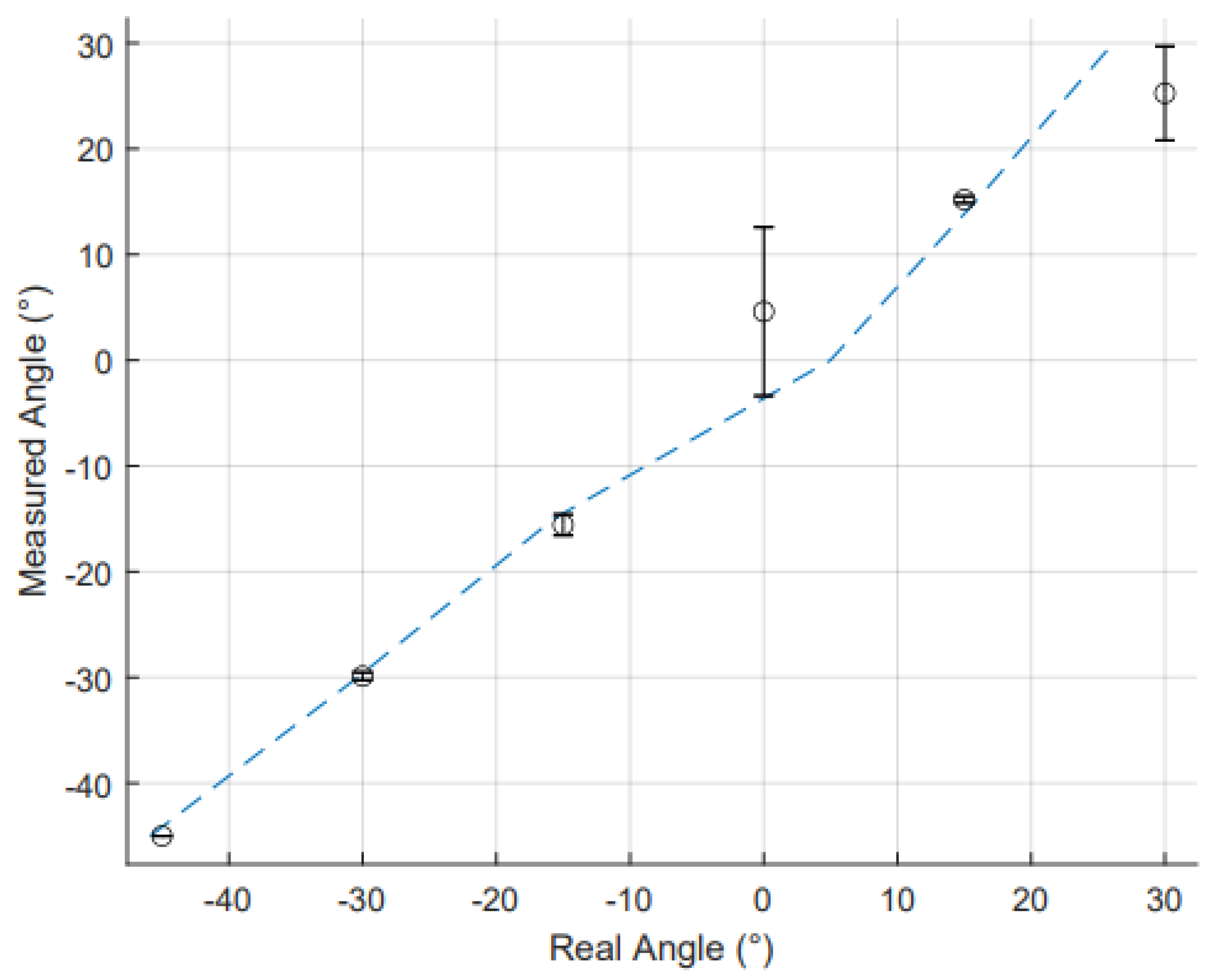
4.2.2. Dynamic Measurements
4.2.3. Data Analysis
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.; Chen, B.; Ren, B.; Tu, D.; Wang, Z.; Wang, C.; Zheng, Y.; Li, X.; Wang, D.; Ren, Z.; et al. Smart Mechanoluminescent Phosphors: A Review of Strontium-Aluminate-Based Materials, Properties, and Their Advanced Application Technologies. Adv. Sci. 2023, 10, 2204925. [Google Scholar] [CrossRef] [PubMed]
- Schröder, M.; Maycock, J.; Botsch, M. Reduced marker layouts for optical motion capture of hands. In Proceedings of the 8th ACM SIGGRAPH Conference on Motion in Games, MIG’15, Paris, France, 16–18 November 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 7–16. [Google Scholar] [CrossRef]
- Casile, A.; Fregna, G.; Boarini, V.; Paoluzzi, C.; Manfredini, F.; Lamberti, N.; Baroni, A.; Straudi, S. Quantitative Comparison of Hand Kinematics Measured with a Markerless Commercial Head-Mounted Display and a Marker-Based Motion Capture System in Stroke Survivors. Sensors 2023, 23, 7906. [Google Scholar] [CrossRef] [PubMed]
- Bank, P.J.; Marinus, J.; Meskers, C.G.; de Groot, J.H.; van Hilten, J.J. Optical Hand Tracking: A Novel Technique for the Assessment of Bradykinesia in Parkinson’s Disease. Mov. Disord. Clin. Pract. 2017, 4, 875–883. [Google Scholar] [CrossRef] [PubMed]
- Caeiro-Rodríguez, M.; Otero-González, I.; Mikic-Fonte, F.A.; Llamas-Nistal, M. A Systematic Review of Commercial Smart Gloves: Current Status and Applications. Sensors 2021, 21, 2667. [Google Scholar] [CrossRef] [PubMed]
- Moreira, A.H.; Queirós, S.; Fonseca, J.; Rodrigues, P.L.; Rodrigues, N.F.; Vilaca, J.L. Real-time hand tracking for rehabilitation and character animation. In Proceedings of the 2014 IEEE 3nd International Conference on Serious Games and Applications for Health (SeGAH), Rio de Janeiro, Brazil, 14–16 May 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Mohan, A.; Tharion, G.; Kumar, R.K.; Devasahayam, S.R. An instrumented glove for monitoring hand function. Rev. Sci. Instrum. 2018, 89, 105001. [Google Scholar] [CrossRef]
- Weber, P.; Rueckert, E.; Calandra, R.; Peters, J.; Beckerle, P. A low-cost sensor glove with vibrotactile feedback and multiple finger joint and hand motion sensing for human-robot interaction. In Proceedings of the 2016 25th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), New York, NY, USA, 26–31 August 2016; pp. 99–104. [Google Scholar] [CrossRef]
- Chander, H.; Burch, R.F.; Talegaonkar, P.; Saucier, D.; Luczak, T.; Ball, J.E.; Turner, A.; Kodithuwakku Arachchige, S.N.K.; Carroll, W.; Smith, B.K.; et al. Wearable Stretch Sensors for Human Movement Monitoring and Fall Detection in Ergonomics. Int. J. Environ. Res. Public Health 2020, 17, 3554. [Google Scholar] [CrossRef]
- Saggio, G.; Orengo, G.; Pallotti, A.; Errico, V.; Ricci, M. Evaluation of an integrated sensory glove at decreasing joint flexion degree. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Calado, A.; Lin, B.S.; Lee, I.J.; Saggio, G. Quasi-Static Measurement Performances of Flex-Sensor-Based and Inertial-Measurement-Unit-Based Sensory Gloves. IEEE Sens. J. 2024, 24, 2162–2171. [Google Scholar] [CrossRef]
- Surangsrirat, D.; Bualuangngam, T.; Sri-iesaranusorn, P.; Chaiyaroj, A.; Buekban, C.; Thanawattano, C.; Poopitaya, S. Comparison of the Wrist Range of Motion Measurement between Inertial Measurement Unit Glove, Smartphone Device and Standard Goniometer. Appl. Sci. 2022, 12, 3418. [Google Scholar] [CrossRef]
- Dipietro, L.; Sabatini, A.M.; Dario, P. Evaluation of an instrumented glove for hand-movement acquisition. J. Rehabil. Res. Dev. 2003, 40, 179–189. [Google Scholar] [CrossRef]
- Cavallo, P.; Saggio, G. Conversion of Sign Language to Spoken Sentences by Means of a Sensory Glove. J. Softw. 2014, 9, 2002–2009. [Google Scholar] [CrossRef][Green Version]
- Perret, J.; Vander Poorten, E. Touching Virtual Reality: A Review of Haptic Gloves. In Proceedings of the ACTUATOR 2018: 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; pp. 1–5. [Google Scholar]
- Sim, D.; Baek, Y.; Cho, M.; Park, S.; Sagar, A.S.M.S.; Kim, H.S. Low-Latency Haptic Open Glove for Immersive Virtual Reality Interaction. Sensors 2021, 21, 3682. [Google Scholar] [CrossRef] [PubMed]
- Connolly, J.; Condell, J.; Curran, K.; Gardiner, P. Improving Data Glove Accuracy and Usability Using a Neural Network When Measuring Finger Joint Range of Motion. Sensors 2022, 22, 2228. [Google Scholar] [CrossRef] [PubMed]
- Khamis, H.; Xia, B.; Redmond, S.J. Real-time Friction Estimation for Grip Force Control. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 1608–1614. [Google Scholar] [CrossRef]
- He, K.; Choosri, N. Commercial Data Glove Selection for VR-based hand Rehabilitation Gaming project. In Proceedings of the 2023 Joint International Conference on Digital Arts, Media and Technology with ECTI Northern Section Conference on Electrical, Electronics, Computer and Telecommunications Engineering (ECTI DAMT & NCON), Phuket, Thailand, 22–25 March 2023; pp. 177–182. [Google Scholar] [CrossRef]
- Rokoko. Smartgloves Product Page. Available online: https://www.rokoko.com/products/smartgloves (accessed on 19 December 2024).
- Manus Meta. Entertainment Solutions Overview. Available online: https://www.manus-meta.com/entertainment (accessed on 19 December 2024).
- StretchSense. MoCap Studio Product Page. Available online: https://stretchsense.com/mocap-studio/ (accessed on 19 December 2024).
- Lin, B.S.; Lee, I.J.; Chiang, P.Y.; Huang, S.Y.; Peng, C.W. A Modular Data Glove System for Finger and Hand Motion Capture Based on Inertial Sensors. J. Med. Biol. Eng. 2019, 39, 532–540. [Google Scholar] [CrossRef]
- Metcalf, C.D.; Robinson, R.; Malpass, A.J.; Bogle, T.P.; Dell, T.A.; Harris, C.; Demain, S.H. Markerless Motion Capture and Measurement of Hand Kinematics: Validation and Application to Home-Based Upper Limb Rehabilitation. IEEE Trans. Biomed. Eng. 2013, 60, 2184–2192. [Google Scholar] [CrossRef]
- Fang, B.; Sun, F.; Liu, H.; Guo, D. A novel data glove using inertial and magnetic sensors for motion capture and robotic arm-hand teleoperation. Ind. Robot. Int. J. 2017, 44, 155–165. [Google Scholar] [CrossRef]
- Siddiqui, N.; Chan, R.H.M. Multimodal hand gesture recognition using single IMU and acoustic measurements at wrist. PLoS ONE 2020, 15, e0227039. [Google Scholar] [CrossRef]
- He, C.; Kazanzides, P.; Sen, H.; Kim, S.; Liu, Y. An Inertial and Optical Sensor Fusion Approach for Six Degree-of-Freedom Pose Estimation. Sensors 2015, 15, 16448–16465. [Google Scholar] [CrossRef]
- Hu, C.; Meng, M.Q.H.; Mandal, M. A Linear Algorithm for Tracing Magnet Position and Orientation by Using Three-Axis Magnetic Sensors. IEEE Trans. Magn. 2007, 42, 4096–4101. [Google Scholar] [CrossRef]
- Lv, J.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. A method of low-cost IMU calibration and alignment. In Proceedings of the 2016 IEEE/SICE International Symposium on System Integration (SII), Sapporo, Japan, 13–15 December 2016; pp. 373–378. [Google Scholar] [CrossRef]
- Ahmad, N.; Ghazilla, R.A.R.; Khairi, N.M.; Kasi, V. Reviews on various inertial measurement unit (IMU) sensor applications. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Shi, J.; Chang, Q.; Zheng, Y.P. Feasibility of controlling prosthetic hand using sonomyography signal in real time: Preliminary study. J. Rehabil. Res. Dev. 2010, 47, 87–98. [Google Scholar] [CrossRef]
- Sbcrnini, L.; Pallotti, A.; Saggio, G. Evaluation of a Stretch Sensor for its Inedited Application in Tracking Hand Finger Movements. In Proceedings of the 2016 IEEE International Symposium on Medical Measurements and Applications (MEMEA), Benevento, Italy, 15–18 May 2016; pp. 626–631. [Google Scholar]
- Orengo, G.; Lagati, A.; Saggio, G. Modeling Wearable Bend Sensor Behavior for Human Motion Capture. IEEE Sens. J. 2014, 14, 2307–2316. [Google Scholar] [CrossRef]
- Saggio, G.; Bisegna, P.; Latessa, G.; Bocchetti, S. Mechanical modeling of bend sensors exploited to measure human joint movements. In Proceedings of the 2009 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks & Workshops, Kos, Greece, 15–19 June 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Universal Robots. Robot STEP File for UR5e (E-Series). Available online: https://www.universal-robots.com/download/mechanical-e-series/ur5e/robot-step-file-ur5e-e-series/ (accessed on 1 October 2024).
- Lee, K.S.; Jung, M.C. Flexion and Extension Angles of Resting Fingers and Wrist. Int. J. Occup. Saf. Ergon. 2014, 20, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Ompusunggu, A.P.; Bey-Temsamani, A. 2-Level error (drift) compensation for low-cost MEMS-based inertial measurement unit (IMU). Microsyst. Technol. 2016, 22, 1601–1612. [Google Scholar] [CrossRef]
- Saggio, G.; Orengo, G. Flex sensor characterization against shape and curvature changes. Sens. Actuators A Phys. 2018, 273, 221–231. [Google Scholar] [CrossRef]
- Connolly, J.; Condell, J.; O’Flynn, B.; Sanchez, J.T.; Gardiner, P. IMU Sensor-Based Electronic Goniometric Glove for Clinical Finger Movement Analysis. IEEE Sens. J. 2018, 18, 1273–1281. [Google Scholar] [CrossRef]
- Hazman, M.A.W.; Nordin, I.N.A.M.; Noh, F.H.M.; Khamis, N.; Razif, M.R.M.; Faudzi, A.A.; Hanif, A.S.M. IMU sensor-based data glove for finger joint measurement. Indones. J. Electr. Eng. Comput. Sci. 2020, 20, 82–88. [Google Scholar] [CrossRef]
- Gentner, R.; Classen, J. Development and evaluation of a low-cost sensor glove for assessment of human finger movements in neurophysiological settings. J. Neurosci. Methods 2009, 178, 138–147. [Google Scholar] [CrossRef]
- Simone, L.K.; Sundarrajan, N.; Luo, X.; Jia, Y.; Kamper, D.G. A low cost instrumented glove for extended monitoring and functional hand assessment. J. Neurosci. Methods 2007, 160, 335–348. [Google Scholar] [CrossRef]
- Saggio, G.; Calado, A.; Errico, V.; Lin, B.S.; Lee, I.J. Dynamic Measurement Assessments of Sensory Gloves Based on Resistive Flex Sensors and Inertial Measurement Units. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]







| Component | Unit Cost | Quantity Needed | Total Cost |
|---|---|---|---|
| Fabric | AUD 8 per metre | 250 mm × 250 mm | $2 |
| Elastic | AUD 6 per metre | 100 mm strip | AUD 0.6 |
| Velcro | AUD 12 per metre | 100 mm strip | AUD 1.2 |
| RFSs | AUD 19 each | 5 | AUD 95 |
| IMU | AUD 3.75 each | 1 | AUD 3.75 |
| Raspberry Pi Pico WH | AUD 11.5 each | 1 | AUD 11.5 |
| MCP30008 | AUD 8.7 each | 1 | AUD 8.7 |
| 380 resistor | AUD 0.1 each | 5 | AUD 0.5 |
| Breadboard with wire | AUD 6 each | 2 | AUD 12 |
| Total | AUD 135.25 |
| RFS Placement | Linear Fit | of the Fit |
|---|---|---|
| thumb | 12.87 x − 93.11 | 0.95 |
| index | 14.07 x − 109.30 | 0.94 |
| middle | 11.70 x − 105.90 | 0.98 |
| ring | 11.39 x − 123.4 | 0.97 |
| little | 11.82 x − 78.46 | 0.94 |
| Sensor Type | Joint | MAE [95% CI] (°) | |
|---|---|---|---|
| IMU | Wrist | 4.85 [4.78, 4.91] | 0.99 |
| RFS | Index | 0.28 [0.27, 0.29] | 0.98 |
| RFS | Middle | 0.19 [0.19, 0.20] | 0.97 |
| RFS | Ring | 0.13 [0.13, 0.14] | 0.99 |
| RFS | Little | 0.14 [0.14, 0.15] | 0.97 |
| RFS | Thumb | 1.71 [1.64, 1.77] | 0.90 |
| Values | ||||
|---|---|---|---|---|
| Sensor Type | Joint | Slow Speed | Medium Speed | Fast Speed |
| IMU | Wrist | 0.999 | 0.999 | 0.999 |
| RFS | Index | 0.978 | 0.979 | 0.982 |
| RFS | Middle | 0.959 | 0.966 | 0.972 |
| RFS | Ring | 0.980 | 0.989 | 0.964 |
| RFS | Little | 0.978 | 0.967 | 0.981 |
| RFS | Thumb | 0.959 | 0.903 | 0.972 |
| Mean Absolute Error Averages ° | ||||
| Sensor Type | Joint | Slow Speed | Medium Speed | Fast Speed |
| IMU | Wrist | 3.933 | 4.052 | 3.668 |
| RFS | Index | 5.273 | 4.134 | 4.787 |
| RFS | Middle | 5.006 | 4.450 | 4.143 |
| RFS | Ring | 4.632 | 3.762 | 4.862 |
| RFS | Little | 5.603 | 5.468 | 4.632 |
| RFS | Thumb | 5.409 | 5.955 | 4.067 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosie, O.; Isaksson, M.; McCormick, J.; Tirosh, O.; Hensman, C. The Design and Validation of an Open-Palm Data Glove for Precision Finger and Wrist Tracking. Sensors 2025, 25, 367. https://doi.org/10.3390/s25020367
Hosie O, Isaksson M, McCormick J, Tirosh O, Hensman C. The Design and Validation of an Open-Palm Data Glove for Precision Finger and Wrist Tracking. Sensors. 2025; 25(2):367. https://doi.org/10.3390/s25020367
Chicago/Turabian StyleHosie, Olivia, Mats Isaksson, John McCormick, Oren Tirosh, and Chrys Hensman. 2025. "The Design and Validation of an Open-Palm Data Glove for Precision Finger and Wrist Tracking" Sensors 25, no. 2: 367. https://doi.org/10.3390/s25020367
APA StyleHosie, O., Isaksson, M., McCormick, J., Tirosh, O., & Hensman, C. (2025). The Design and Validation of an Open-Palm Data Glove for Precision Finger and Wrist Tracking. Sensors, 25(2), 367. https://doi.org/10.3390/s25020367







