An Optimization Coverage Strategy for Wireless Sensor Network Nodes Based on Path Loss and False Alarm Probability
Abstract
1. Introduction
- Most of the research focuses on the improvement of optimization algorithms, but the basic model of network coverage is not studied and discussed much.
- The sensor based on the 0/1 perception model is often regarded as an independent detection unit, but in the actual WSN, the work of multiple sensors is not completely independent, and the joint perception function of multiple sensors should be considered.
- In the wider application scenarios of WSN, there is often a lot of interference, the sensor as a sensing instrument has the possibility of misjudgment or failure, and the existing model lacks response to such problems.
- By investigating the characteristics of wireless signal transmission and detection, we account for the multipath characteristics of non-line-of-sight transmission and the impact of false alarm and missed detection rates in signal detection. We construct a probabilistic perception model and analyze the influence of key parameters on this model.
- Recognizing that, in WSNs, the perception of any point typically results from the cooperative functioning of multiple sensors rather than a single sensor, we develop an evaluation function for network coverage based on the proposed model and multi-sensor joint perception relationships.
2. Research Background
2.1. The Types of WSN Node Coverage Problems
2.2. Sensor Node Perception Model
2.2.1. 0/1 Perception Model
2.2.2. Exponential Decay Model
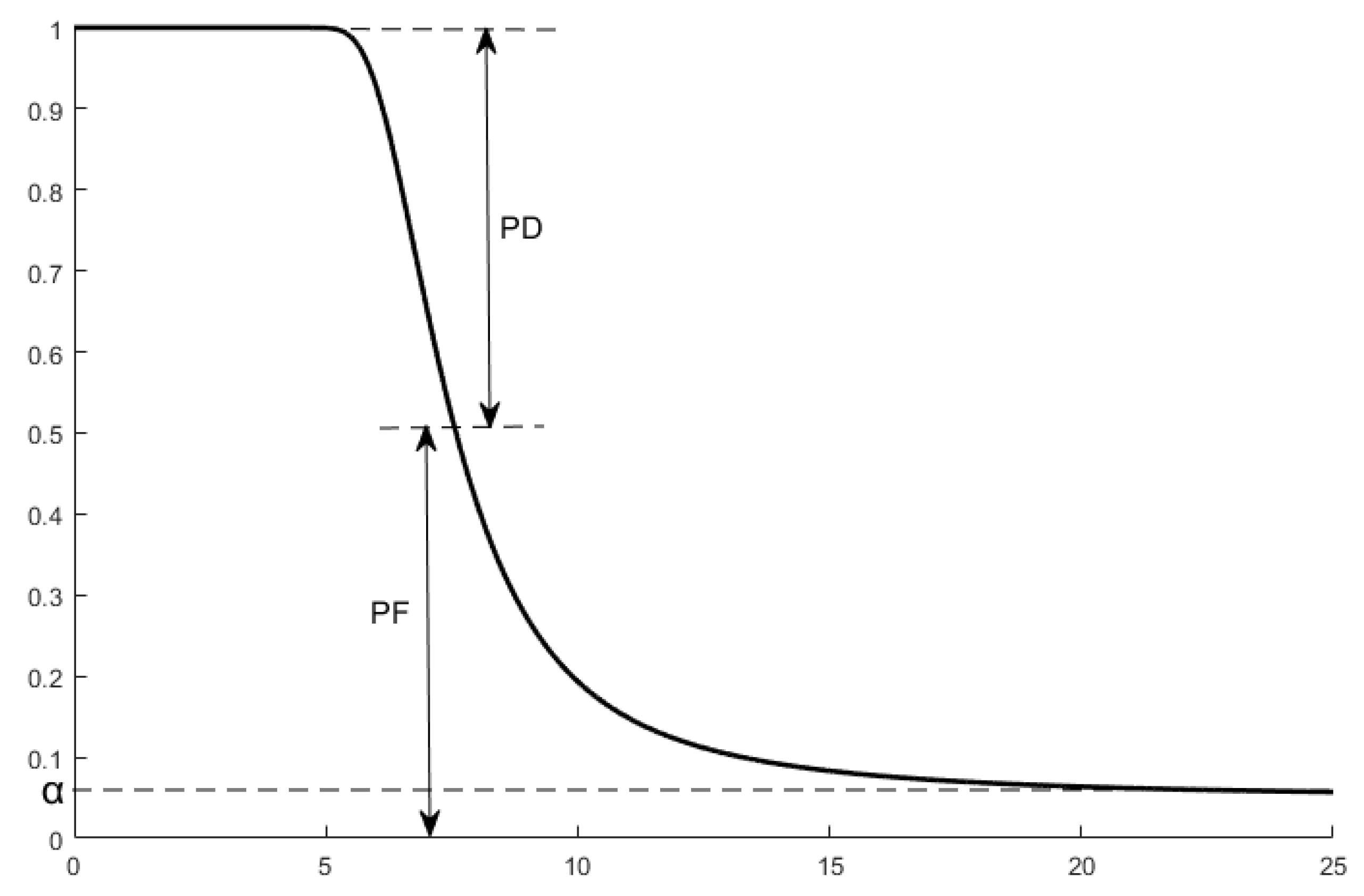
2.3. Classical Signal Detection Criteria
3. Perception Model Based on Path Loss and False Alarm Probability
3.1. Model Derivation
3.2. Maximum Sensing Radius
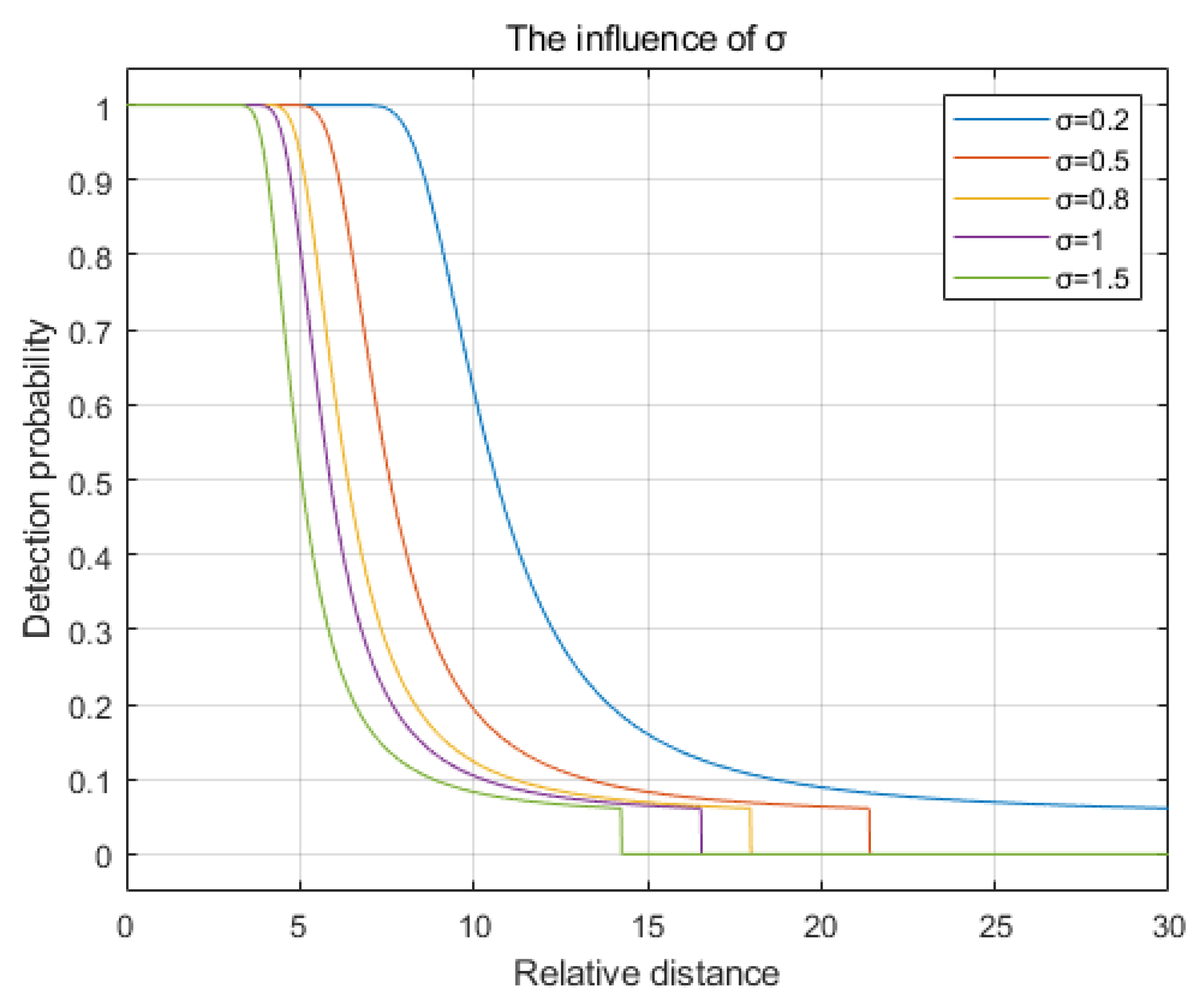
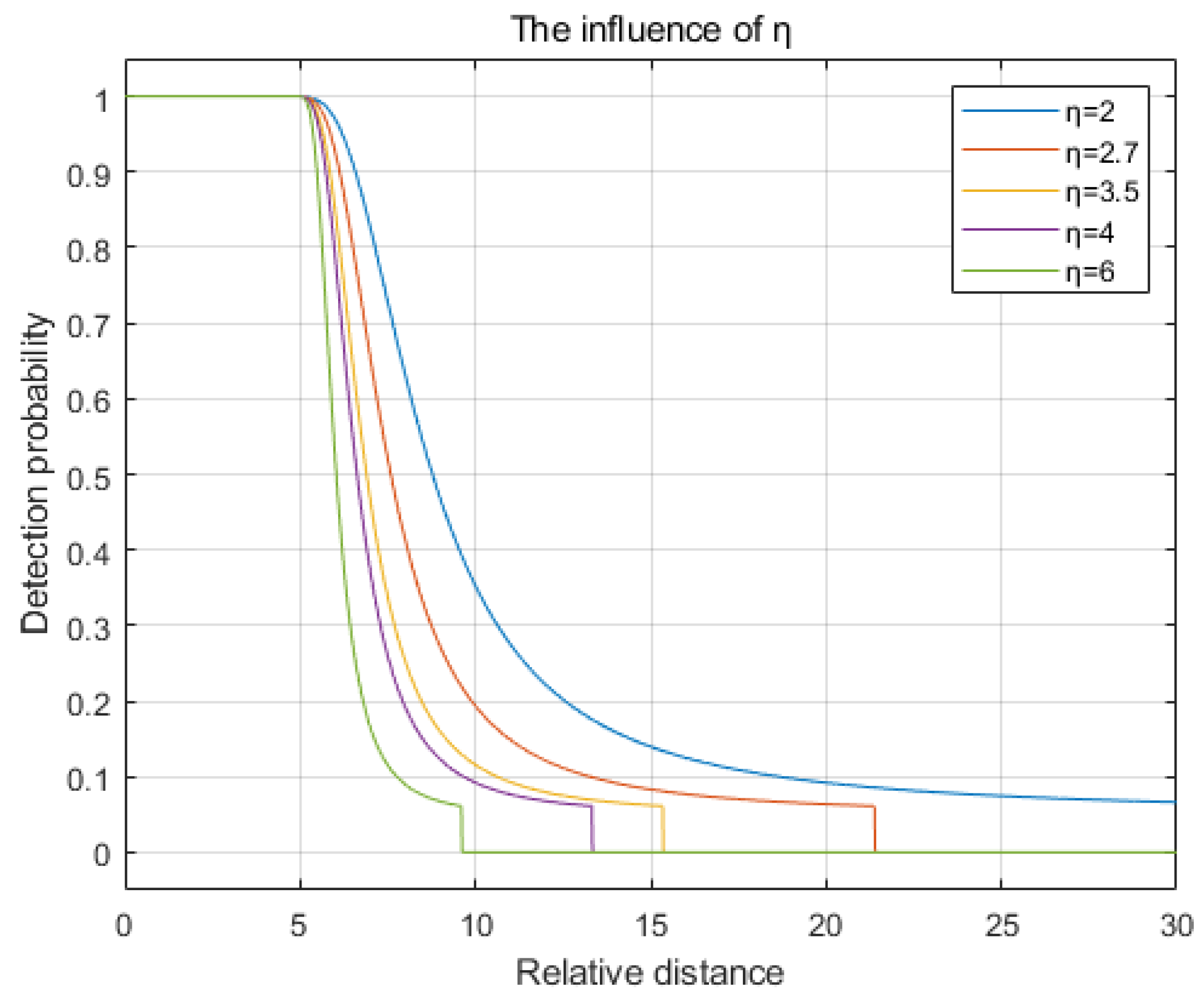
3.3. Parameter Influence
3.4. Differences Between Perception Models
4. Analysis of WSN Node Coverage Problem Based on the Probabilistic Model
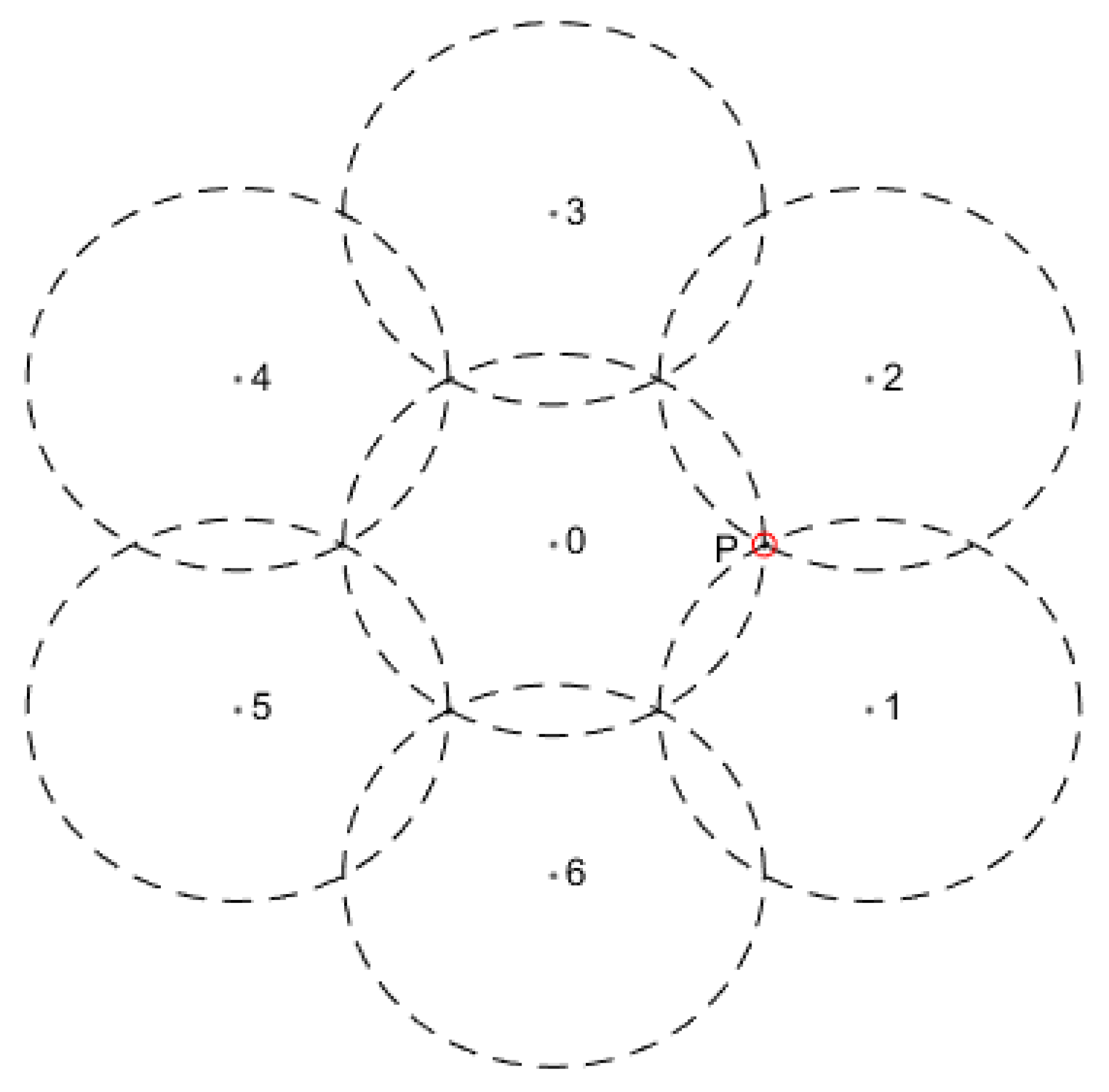
4.1. Coverage Rate Model Based on Joint Perception Probability
4.2. Computational Complexity
4.3. Full Coverage Analysis
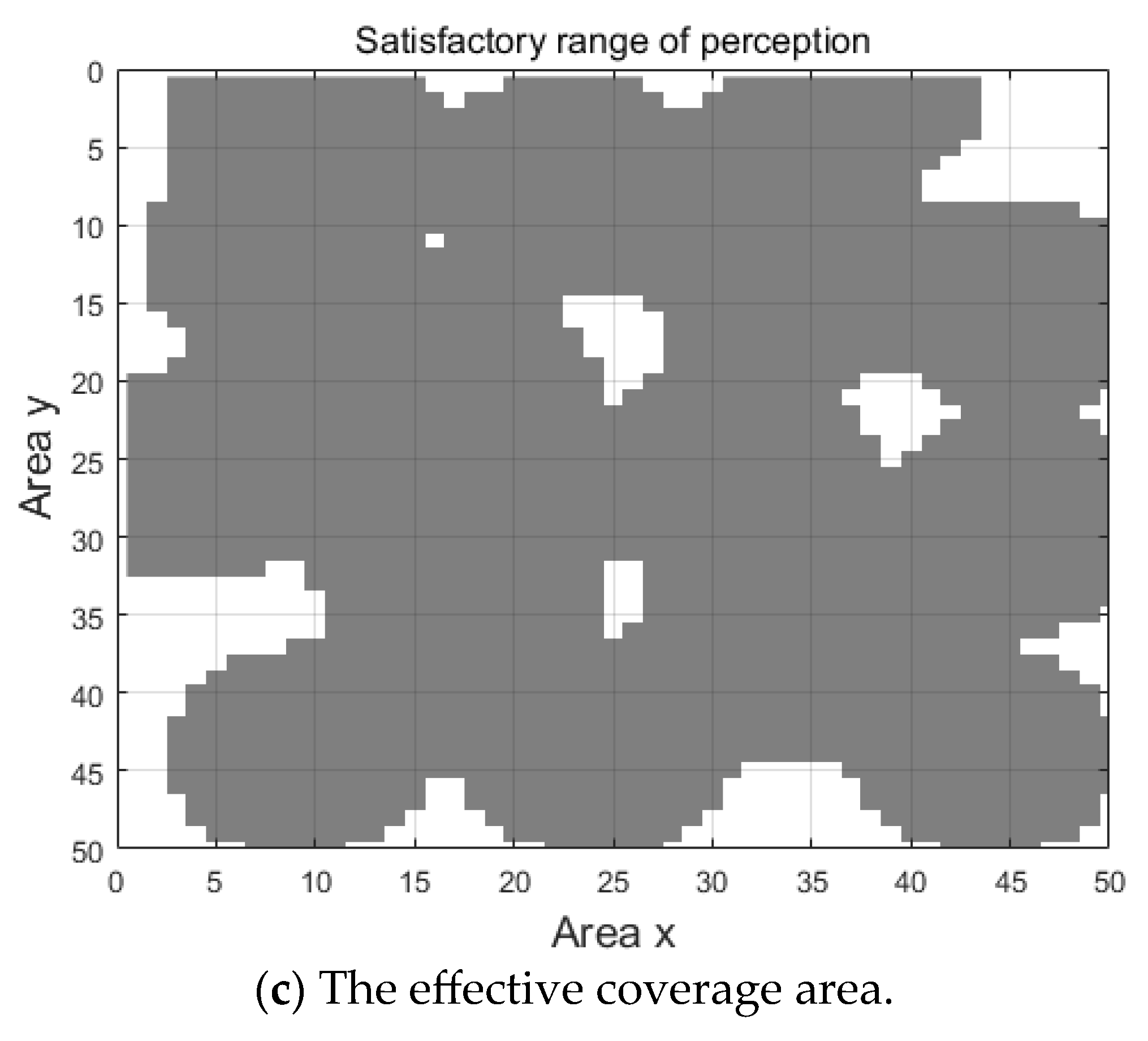
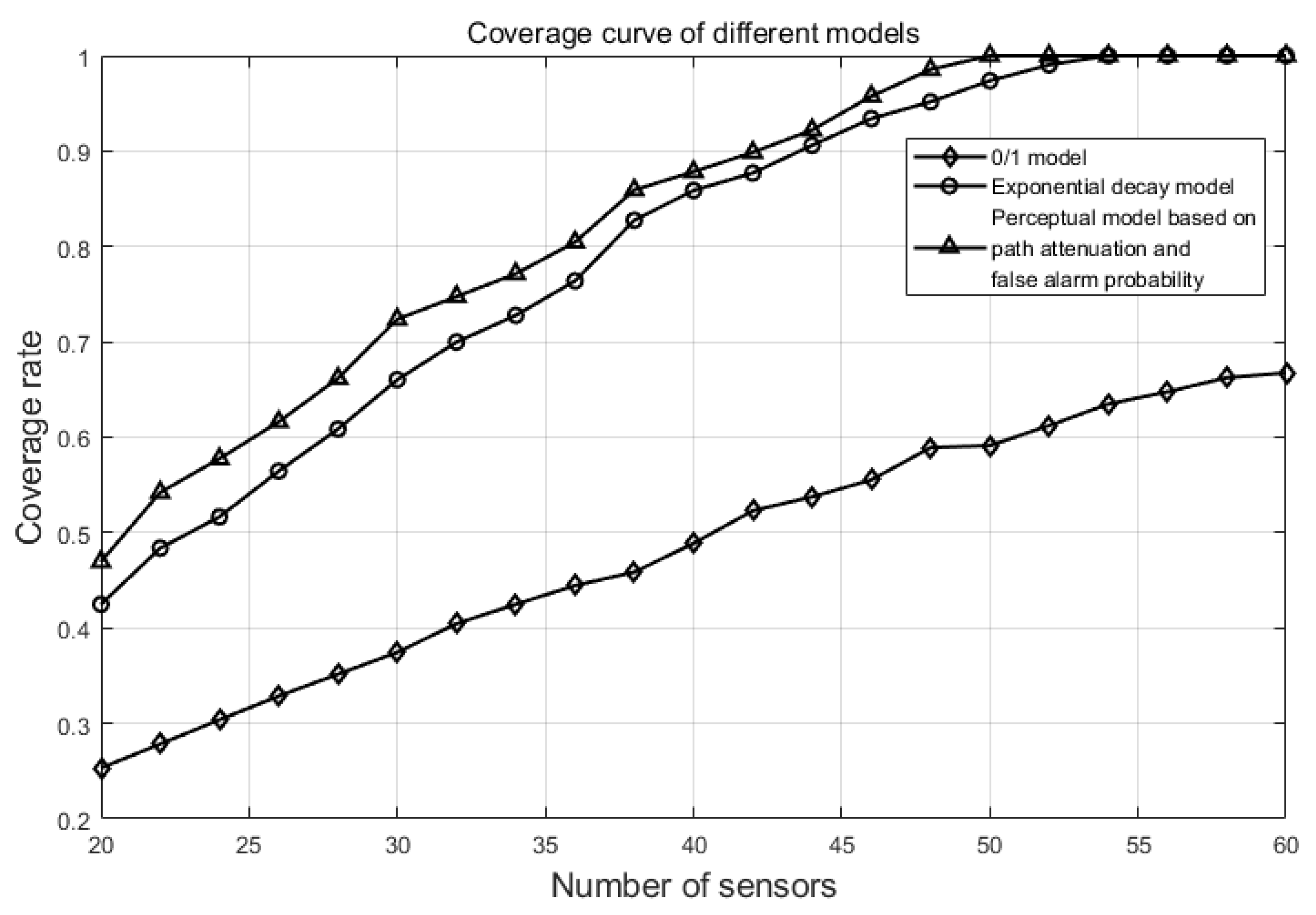
5. Simulation Testing
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nayyar, A.; Singh, R. IEEMARP—A novel energy efficient multipath routing protocol based on ant Colony optimization (ACO) for dynamic sensor networks. Multimed. Tools Appl. 2020, 79, 35221–35252. [Google Scholar] [CrossRef]
- Tao, M.; Wang, S.P.; Chen, H.; Wang, X.J. Information space of multi-sensor networks. Inf. Sci. 2021, 565, 128–145. [Google Scholar] [CrossRef]
- Tripathi, A.; Gupta, H.P.; Dutta, T.; Mishra, R.; Shukla, K.K.; Jit, S. Coverage and Connectivity in WSNs: A Survey, Research Issues and Challenges. IEEE Access 2018, 6, 26971–26992. [Google Scholar] [CrossRef]
- Zheng, K.C.; Luo, R.W.; Liu, X.Y.; Qiu, J.F.; Liu, J. Distributed DDPG-Based Resource Allocation for Age of Information Minimization in Mobile Wireless-Powered Internet of Things. IEEE Internet Things J. 2024, 11, 29102–29115. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Hu, Y.B.; Jiang, N.; Yetisen, A.K. Wearable artificial intelligence biosensor networks. Biosens. Bioelectron. 2023, 219, 114825. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.Y.; Du, J.; Ren, Y.; Han, Z. Distributed Artificial Intelligence Enabled Aerial-Ground Networks: Architecture, Technologies and Challenges. IEEE Access 2022, 10, 105447–105457. [Google Scholar] [CrossRef]
- Chen, Y.N.; Zhu, X.H.; Fang, K.; Chen, X.X.; Guo, T.; Li, C.; Ren, Q.S.; Zou, Z.Y. An improved method for sink node deployment in wireless sensor network to big data. Neural Comput. Appl. 2022, 34, 9499–9510. [Google Scholar] [CrossRef]
- He, Y.X.; Wang, D.W.; Huang, F.H.; Zhang, R.N.; Min, L.T. Aerial-Ground Integrated Vehicular Networks: A UAV-Vehicle Collaboration Perspective. IEEE Trans. Intell. Transp. Syst. 2024, 25, 5154–5169. [Google Scholar] [CrossRef]
- Gutierrez, E.A.; Mondragon, I.F.; Colorado, J.D.; Ch, D.M. Optimal Deployment of WSN Nodes for Crop Monitoring Based on Geostatistical Interpolations. Plants 2022, 11, 1636. [Google Scholar] [CrossRef]
- Ramya, R.; Brindha, T. A Comprehensive Review on Optimal Cluster Head Selection in WSN-IoT. Adv. Eng. Softw. 2022, 171, 103170. [Google Scholar] [CrossRef]
- Younus, H.A.; Koçak, C. Optimized Routing by Combining Grey Wolf and Dragonfly Optimization for Energy Efficiency in Wireless Sensor Networks. Appl. Sci. 2022, 12, 10948. [Google Scholar] [CrossRef]
- Jia, R.L.; Zhang, H.Y. Wireless Sensor Network (WSN) Model Targeting Energy Efficient Wireless Sensor Networks Node Coverage. IEEE Access 2024, 12, 27596–27610. [Google Scholar] [CrossRef]
- Li, Q.Y.; Liu, N.Z. Coverage optimization algorithm based on control nodes position in wireless sensor networks. Int. J. Commun. Syst. 2022, 35, e4599. [Google Scholar] [CrossRef]
- Egwuche, O.S.; Singh, A.; Ezugwu, A.E.; Greeff, J.; Olusanya, M.O.; Abualigah, L. Machine learning for coverage optimization in wireless sensor networks: A comprehensive review. Ann. Oper. Res. 2023, 1–67. [Google Scholar] [CrossRef]
- Pavithra, R.; Arivudainambi, D. Coverage-Aware Sensor Deployment and Scheduling in Target-Based Wireless Sensor Network. Wirel. Pers. Commun. 2023, 130, 421–448. [Google Scholar] [CrossRef]
- Dao, T.K.; Nguyen, T.T.; Ngo, T.G.; Nguyen, T.D. An Optimal WSN Coverage Based on Adapted Transit Search Algorithm. Int. J. Softw. Eng. Knowl. Eng. 2023, 33, 1489–1512. [Google Scholar] [CrossRef]
- Dande, B.; Chang, C.Y.; Liao, W.W.; Roy, D.S. MSQAC: Maximizing the Surveillance Quality of Area Coverage in Wireless Sensor Networks. IEEE Sens. J. 2022, 22, 6150–6163. [Google Scholar] [CrossRef]
- Zhang, M.J.; Wang, D.G.; Yang, M.; Tan, W.; Yang, J. HPSBA: A Modified Hybrid Framework with Convergence Analysis for Solving Wireless Sensor Network Coverage Optimization Problem. Axioms 2022, 11, 675. [Google Scholar] [CrossRef]
- Yi, J.W.; Qiao, G.H.; Yuan, F.; Tian, Y.; Wang, X.L. Sensor Deployment Strategies for Target Coverage Problems in Underwater Acoustic Sensor Networks. IEEE Commun. Lett. 2023, 27, 836–840. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y.B.; Chen, L.; Duan, Y.Z.; Li, J. WSN node coverage optimization algorithm based on global and neighborhood difference DE. China Commun. 2022, 19, 215–229. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, L.Q.; Wang, Y.F.; Wen, Q. Improved sand cat swarm optimization algorithm for enhancing coverage of wireless sensor networks. Measurement 2024, 233, 114649. [Google Scholar] [CrossRef]
- Jebi, R.C.; Baulkani, S. Mitigation of coverage and connectivity issues in wireless sensor network by multi-objective randomized grasshopper optimization based selective activation scheme. Sustain. Comput. Inform. Syst. 2022, 35, 100728. [Google Scholar] [CrossRef]
- Ali, N.H.; Ozdag, R. Coverage analysis and a new metaheuristic approach using the Elfes Probabilistic detection model in Wireless sensor networks. Measurement 2022, 20, 111627. [Google Scholar] [CrossRef]
- Yang, Y.R.; Kang, Q.Y.; She, R. The Effective Coverage of Homogeneous Teams with Radial Attenuation Models. Sensors 2023, 23, 350. [Google Scholar] [CrossRef]
- Jin, Z.K.; Geng, Y.X.; Zhu, C.L.; Xia, Y.Z.; Deng, X.J.; Yi, L.Z.; Wang, X.L. Deployment optimization for target perpetual coverage in energy harvesting wireless sensor network. Digit. Commun. Netw. 2024, 10, 498–508. [Google Scholar] [CrossRef]
- Van Quan, L.; Hanh, N.T.; Binh, H.T.T.; Toan, V.D.; Ngoc, D.T.; Lam, B.T. A bi-population Genetic algorithm based on multi-objective optimization for a relocation scheme with target coverage constraints in mobile wireless sensor networks. Expert Syst. Appl. 2023, 217, 119486. [Google Scholar] [CrossRef]
- Subramanian, K.; Shanmugavel, S. Intelligent Deployment Model for Target Coverage in Wireless Sensor Network. Intell. Autom. Soft Comput. 2023, 35, 739–754. [Google Scholar] [CrossRef]
- Chen, G.; Xiong, Y.H.; She, J.H. A k-Barrier Coverage Enhancing Scheme Based on Gaps Repairing in Visual Sensor Network. IEEE Sens. J. 2023, 23, 2865–2877. [Google Scholar] [CrossRef]
- Li, H.P.; Feng, D.Z.; Wang, X.H. Optimization method of linear barrier coverage deployment for multistatic radar. J. Syst. Eng. Electron. 2023, 34, 68–80. [Google Scholar] [CrossRef]
- Kumar, D.; Banerjee, A.; Majumder, K.; Kotecha, K.; Abraham, A. Coverage Area Maximization Using MOFAC-GA-PSO Hybrid Algorithm in Energy Efficient WSN Design. IEEE Access 2023, 11, 99901–99917. [Google Scholar] [CrossRef]
- Nematzadeh, S.; Torkamanian-Afshar, M.; Seyyedabbasi, A.; Kiani, F. Maximizing coverage and maintaining connectivity in WSN and decentralized IoT: An efficient metaheuristic-based method for environment-aware node deployment. Neural Comput. Appl. 2023, 35, 611–641. [Google Scholar] [CrossRef]
- Priyadarshi, R.; Gupta, B.; Anurag, A. Wireless Sensor Networks Deployment: A Result Oriented Analysis. Wirel. Pers. Commun. 2020, 113, 843–866. [Google Scholar] [CrossRef]
- Paulswamy, S.L.; Roobert, A.A.; Hariharan, K. A Novel Coverage Improved Deployment Strategy for Wireless Sensor Network. Wirel. Pers. Commun. 2022, 124, 867–891. [Google Scholar] [CrossRef]
- Xu, P.; Wu, J.G.; Chang, C.Y.; Shang, C.J.; Roy, D.S. MCDP: Maximizing Cooperative Detection Probability for Barrier Coverage in Rechargeable Wireless Sensor Networks. IEEE Sens. J. 2021, 21, 7080–7092. [Google Scholar] [CrossRef]
- Chauhan, N.; Chauhan, S. A Novel Area Coverage Technique for Maximizing the Wireless Sensor Network Lifetime. Arab. J. Sci. Eng. 2021, 46, 3329–3343. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Ge, B.; Zhang, T.; Zhu, Z.H. A Multi-Strategy Improved Sparrow Search Algorithm for Coverage Optimization in a WSN. Sensors 2023, 23, 4124. [Google Scholar] [CrossRef]
- Tripathi, R.N.; Gaurav, K.; Singh, Y.N. Configuration of the Communication Radius for Partial Coverage in WSN. Adv. Signal Process. Commun. Eng. 2022, 929, 37–45. [Google Scholar]
- Fan, H.S.; Li, M.M.; Sun, X.W.; Wan, P.J.; Zhao, Y.C. Barrier Coverage by Sensors with Adjustable Ranges. ACM Trans. Sens. Netw. 2014, 11, 14. [Google Scholar] [CrossRef]
- Elfouly, F.H.; Ramadan, R.A.; Khedr, A.Y.; Yadav, K.; Azar, A.T. Efficient Node Deployment of Large-Scale Heterogeneous Wireless Sensor Networks. Appl. Sci. 2021, 11, 10924. [Google Scholar] [CrossRef]
- Li, L.; Funan, P.; Weiru, C. Node Deployment of Wireless Sensor Networks Based on MOEA/P Algorithm. In Proceedings of the 2021 13th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 4–7 June 2021; Volume 5, p. 6. [Google Scholar]
- Lu, C.; Li, X.B.; Yu, W.J.; Zeng, Z.; Yan, M.M.; Li, X. Sensor network sensing coverage optimization with improved artificial bee colony algorithm using teaching strategy. Computing 2021, 103, 1439–1460. [Google Scholar] [CrossRef]
- Dao, T.K.; Chu, S.C.; Nguyen, T.T.; Nguyen, T.D.; Nguyen, V.T. An Optimal WSN Node Coverage Based on Enhanced Archimedes Optimization Algorithm. Entropy 2022, 24, 1018. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Dao, T.K.; Nguyen, T.D.; Nguyen, V.T. An Improved Honey Badger Algorithm for Coverage Optimization in Wireless Sensor Network. J. Internet Technol. 2023, 24, 363–377. [Google Scholar] [CrossRef]
- Hefeeda, M.; Ahmadi, H. Energy-Efficient Protocol for Deterministic and Probabilistic Coverage in Sensor Networks. IEEE Trans. Parallel Distrib. Syst. 2010, 21, 579–593. [Google Scholar] [CrossRef]
- Yang, Q.Q.; He, S.B.; Li, J.K.; Chen, J.M.; Sun, Y.X. Energy-Efficient Probabilistic Area Coverage in Wireless Sensor Networks. IEEE Trans. Veh. Technol. 2015, 64, 367–377. [Google Scholar] [CrossRef]
- Chen, Y.N.; Lin, W.H.; Chen, C.Y. An Effective Sensor Deployment Scheme that Ensures Multilevel Coverage of Wireless Sensor Networks with Uncertain Properties. Sensors 2020, 20, 1831. [Google Scholar] [CrossRef]





| Environment Type | Path Loss Exponent |
|---|---|
| Free Space | 2 |
| Urban Cellular | 2.7~3.5 |
| Urban Cellular with Shadowing | 3~5 |
| Indoor Short-Distance Line-of-Sight | 1.6~1.8 |
| Indoor Non-Line-of-Sight | 4~6 |
| Factory Non-Line-of-Sight | 2~3 |
| Parameter Name | Value |
|---|---|
| Transmit Power | |
| Transmit Gain | |
| Receive Gain | |
| Carrier Wavelength | |
| System Hardware Loss | |
| Reference Distance | |
| Minimum Detectable Power | |
| False Alarm Rate | (Default value) |
| Standard Deviation | (Default value) |
| Path Loss Coefficient | (Default value) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Sun, Y.; Liu, T.; Li, Y.; Fei, T. An Optimization Coverage Strategy for Wireless Sensor Network Nodes Based on Path Loss and False Alarm Probability. Sensors 2025, 25, 396. https://doi.org/10.3390/s25020396
Guo J, Sun Y, Liu T, Li Y, Fei T. An Optimization Coverage Strategy for Wireless Sensor Network Nodes Based on Path Loss and False Alarm Probability. Sensors. 2025; 25(2):396. https://doi.org/10.3390/s25020396
Chicago/Turabian StyleGuo, Jianing, Yunshan Sun, Ting Liu, Yanqin Li, and Teng Fei. 2025. "An Optimization Coverage Strategy for Wireless Sensor Network Nodes Based on Path Loss and False Alarm Probability" Sensors 25, no. 2: 396. https://doi.org/10.3390/s25020396
APA StyleGuo, J., Sun, Y., Liu, T., Li, Y., & Fei, T. (2025). An Optimization Coverage Strategy for Wireless Sensor Network Nodes Based on Path Loss and False Alarm Probability. Sensors, 25(2), 396. https://doi.org/10.3390/s25020396






