Squat Motion of a Humanoid Robot Using Three-Particle Model Predictive Control and Whole-Body Control
Abstract
:1. Introduction
1.1. Background
1.2. Motivation
1.3. Related Works
1.4. Contribution
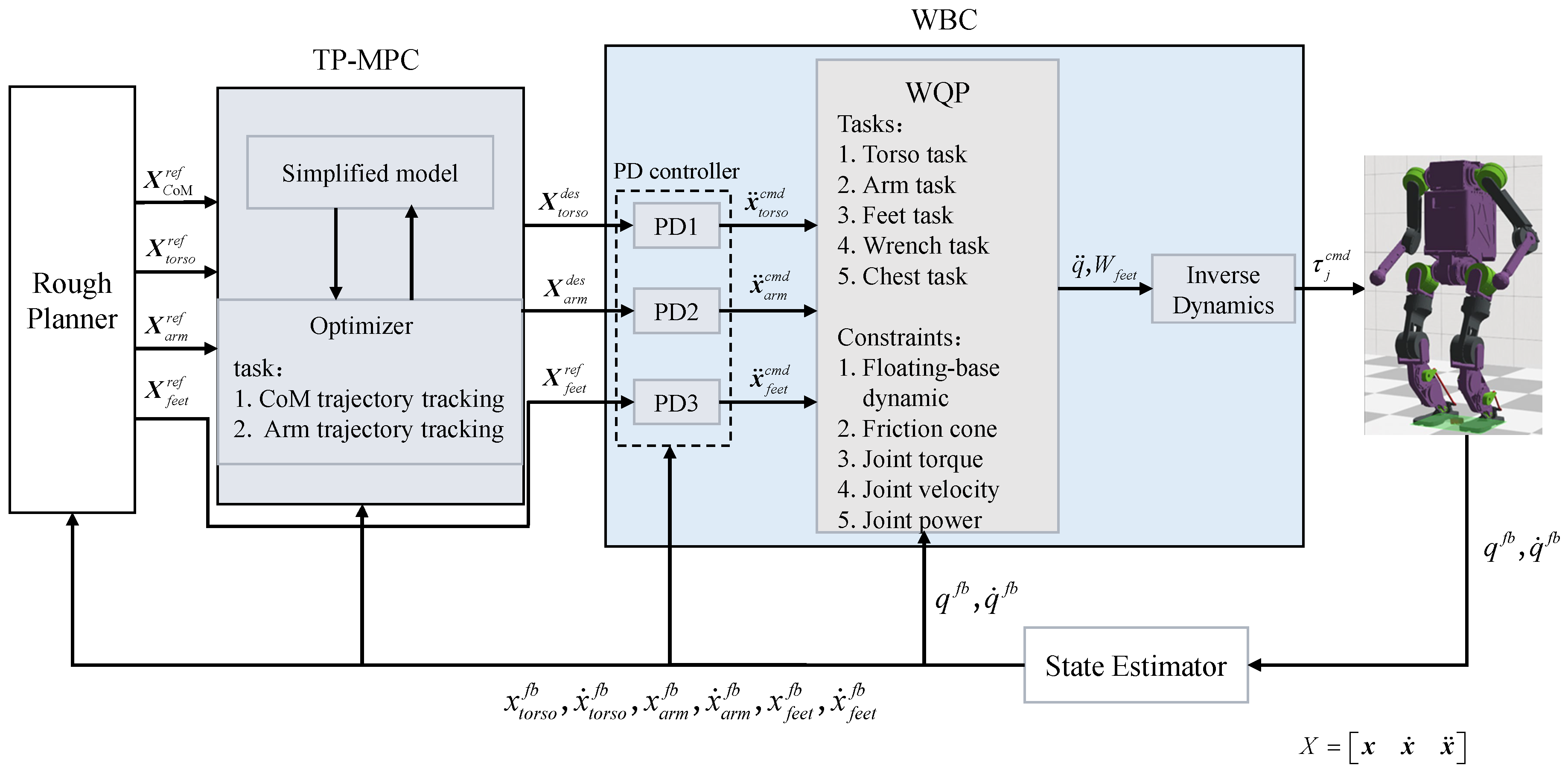
2. Methods
2.1. Three-Particle Model Predictive Control
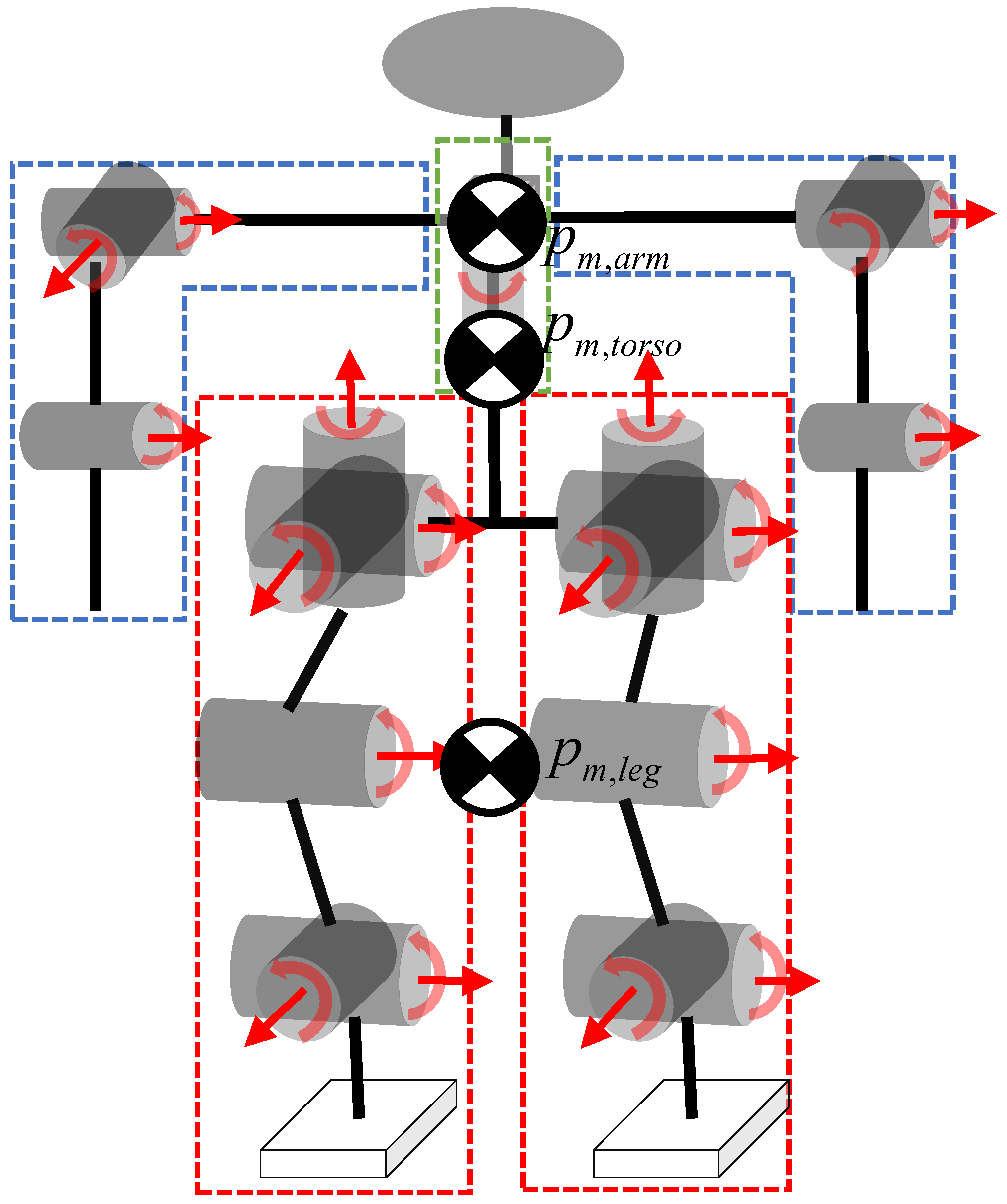
2.1.1. Modeling
2.1.2. Cost Function
2.2. Whole-Body Control
2.2.1. Modeling
2.2.2. Whole-Body Control Formulation
2.2.3. Tasks
Torso Trajectory Tracking Task
Arm Trajectory Tracking Task
Foot Trajectory Tracking Task
Chest Trajectory Tracking Task
Wrench Task
2.2.4. Constraints
Floating Base Dynamics Constraint
Contact Force Constraint
Joint Torque Constraint
Joint Velocity Constraint
Joint Power Constraint
2.3. Experimental Design for Simulation
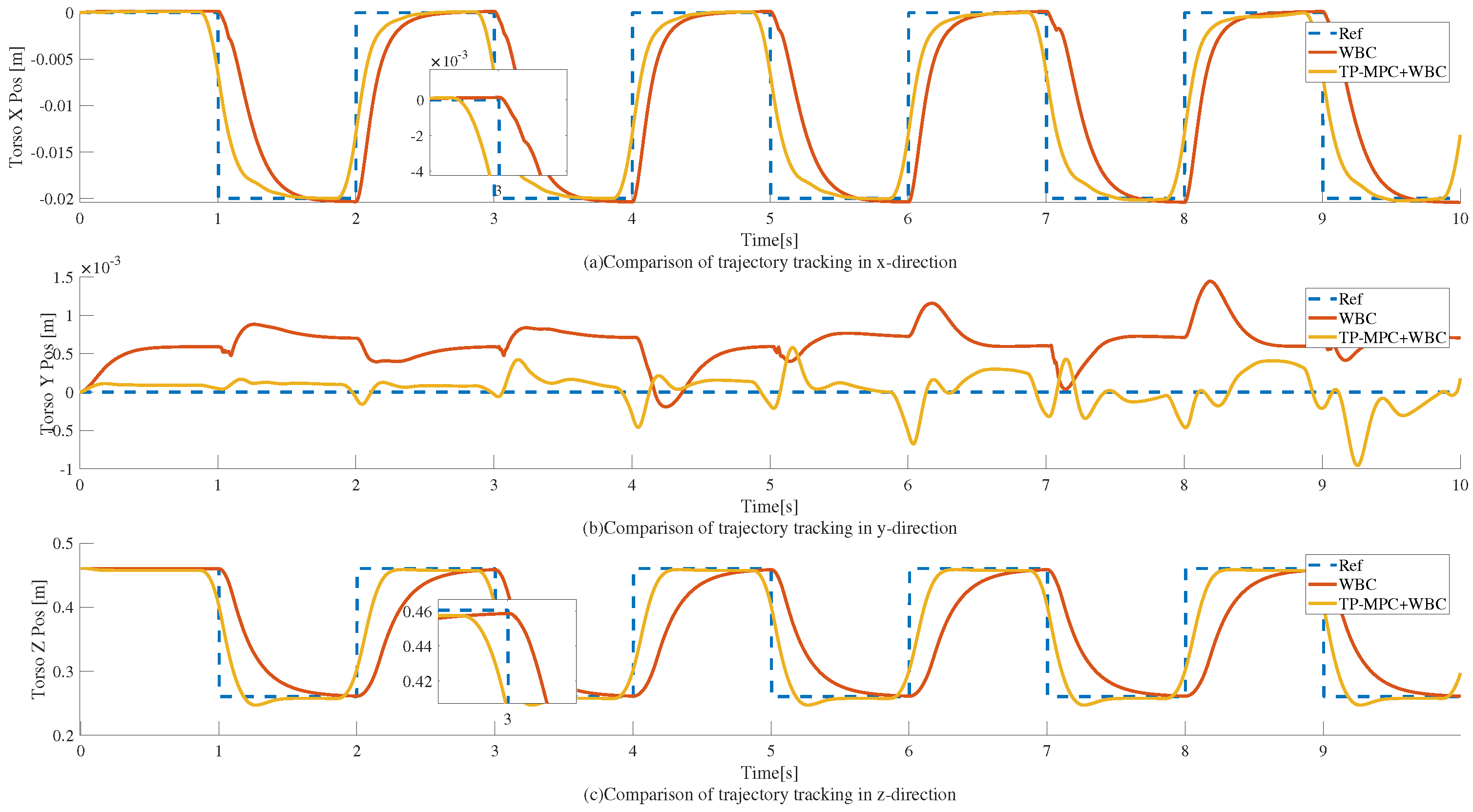
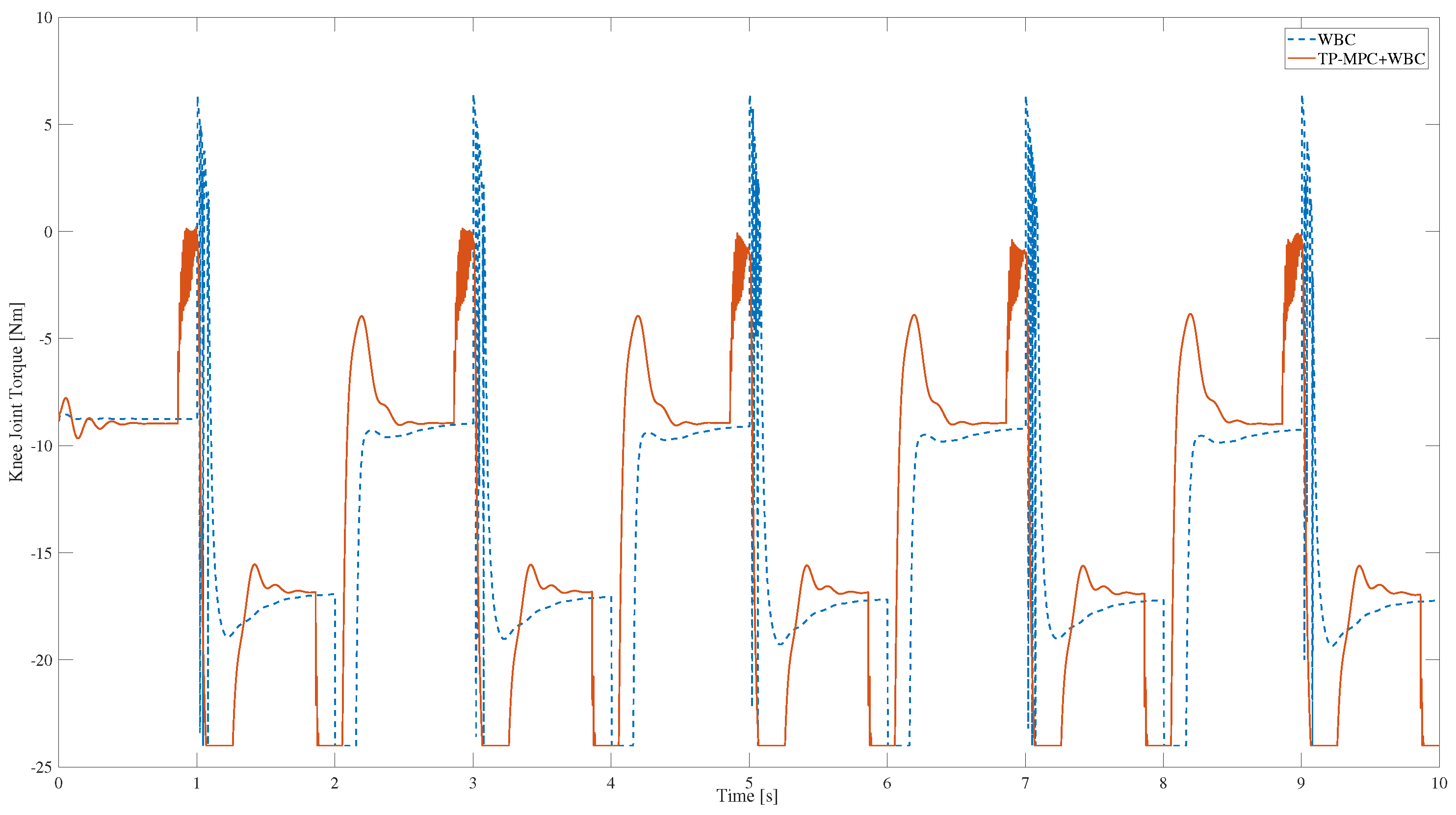
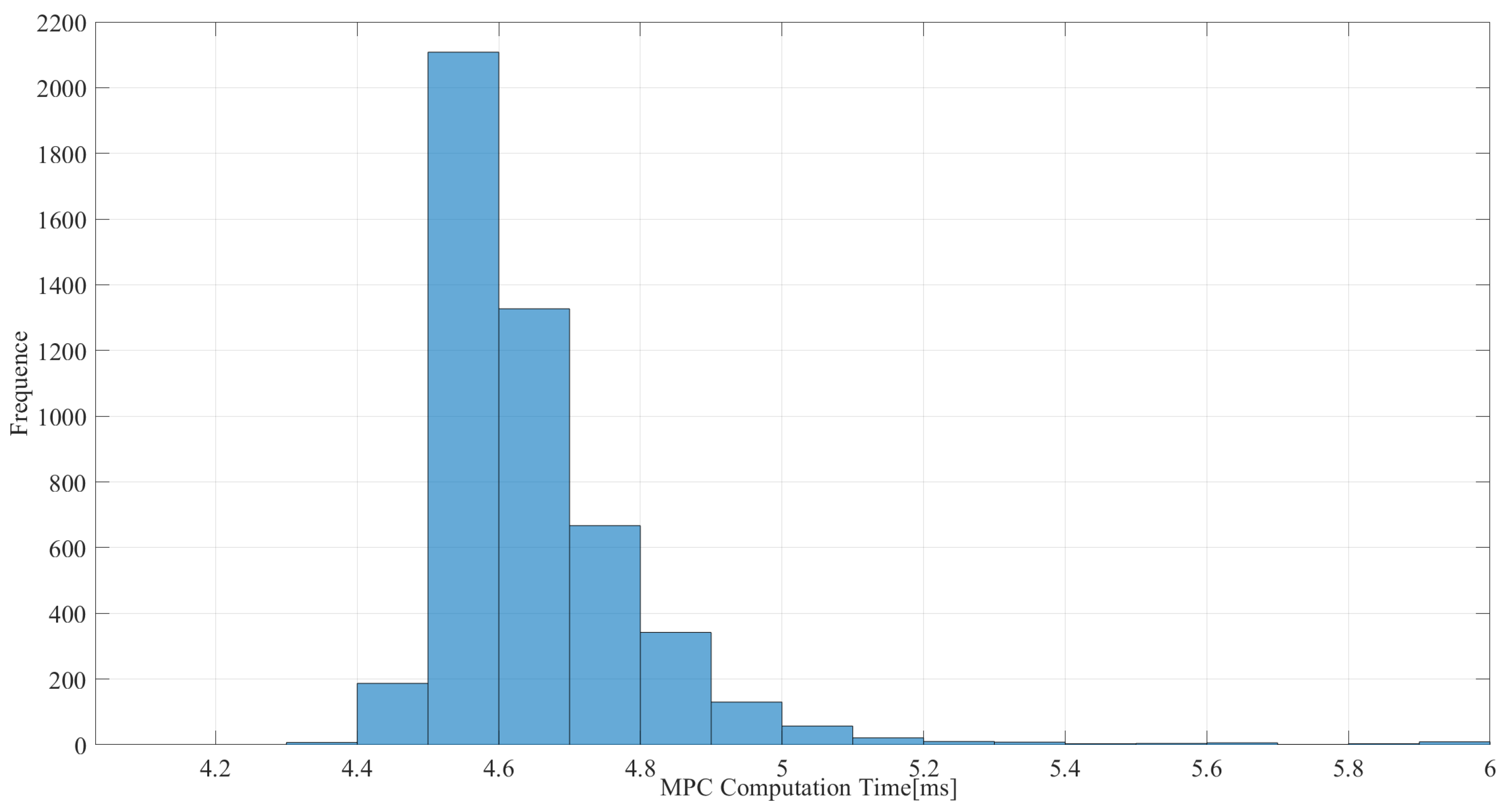
3. Results and Discussion
3.1. Square Wave
3.2. Triangle Wave
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| LIP | Linear inverted pendulum |
| SLIP | Spring-loaded inverted pendulum |
| HQP | Hierarchical quadratic programming |
| WQP | Weighted quadratic programming |
| WBC | Whole-body control |
| IK | Inverse kinematics |
| pid | Proportional integral derivative |
| RKP | Real-time kinematic programming |
| TP-MPC | Three-particle model predictive control |
| CoM | Center of mass |
| ZMP | Zero-moment point |
| DoF | Degrees of freedom |
| QP | Quadratic programming |
| LQR | Linear quadratic regulator |
| RL | Reinforcement learning |
References
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 1, pp. 1405–1411. [Google Scholar]
- Xiong, X.; Ames, A.D. Coupling Reduced Order Models via Feedback Control for 3D Underactuated Bipedal Robotic Walking. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018; Volume 11, pp. 1–9. [Google Scholar]
- Di Carlo, J.; Wensing, P.M.; Katz, B.; Bledt, G.; Kim, S. Dynamic Locomotion In The Mit Cheetah 3 Through Convex Model-Predictive Control. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; Volume 10, pp. 1–5. [Google Scholar]
- Kim, D.; Di Carlo, J.; Katz, B.; Bledt, G.; Kim, S. Highly Dynamic Quadruped Locomotion via Whole-Body Impulse Control and Model Predictive Control. arXiv 2019, arXiv:1909.06586. [Google Scholar]
- Yang, Y.; Shi, J.; Huang, S.; Ge, Y.; Cai, W.; Li, Q.; Chen, X.; Li, X.; Zhao, M. Balanced Standing on One Foot of Biped Robot Based on Three-Particle Model Predictive Control. Biomimetics 2022, 7, 244. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Nori, F.; Mombaur, K. Squat motion generation for the humanoid robot iCub with Series Elastic Actuators. In Proceedings of the 2016 6th IEEE International Conference on Biomedical Robotics and Biomechatronics (BioRob), Singapore, 26–29 June 2016; Volume 10, pp. 207–212. [Google Scholar]
- Grimes, D.B.; Chalodhorn, R.; Rao, R.P. Dynamic Imitation in a Humanoid Robot through Nonparametric Probabilistic Inference. In Robotics: Science and Systems; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Asano, Y.; Mizoguchi, H.; Kozuki, T.; Motegi, Y.; Urata, J.; Nakanishi, Y.; Okada, K.; Inaba, M. Achievement of twist squat by musculoskeletal humanoid with screw-home mechanism. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 4649–4654. [Google Scholar]
- Ariki, Y.; Hyon, S.H.; Morimoto, J. Extraction of primitive representation from captured human movements and measured ground reaction force to generate physically consistent imitated behaviors. Neural Netw. 2013, 40, 32–43. [Google Scholar] [CrossRef] [PubMed]
- Galdeano, D.; Chemori, A.; Krut, S.; Fraisse, P. Task-based whole-body control of humanoid robots with ZMP regulation, real-time application to a squat-like motion. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Signals & Devices (SSD14), Barcelona, Spain, 11–14 February 2014; Volume 10, pp. 1–6. [Google Scholar]
- Mason, S.; Righetti, L.; Schaal, S. Full dynamics LQR control of a humanoid robot: An experimental study on balancing and squatting. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014; Volume 10, pp. 374–379. [Google Scholar]
- Kajita, S.; Sakaguchi, T.; Nakaoka, S.I.; Morisawa, M.; Kaneko, K.; Kanehiro, F. Quick squatting motion generation of a humanoid robot for falling damage reduction. In Proceedings of the 2017 IEEE International Conference on Cyborg and Bionic Systems (CBS), Beijing, China, 17–19 October 2017; Volume 10, pp. 45–49. [Google Scholar]
- Penco, L.; Clément, B.; Modugno, V.; Hoffman, E.M.; Nava, G.; Pucci, D.; Tsagarakis, N.G.; Mouret, J.-B.; Ivaldi, S. Robust Real-Time Whole-Body Motion Retargeting from Human to Humanoid. In Proceedings of the 2018 IEEE-RAS 18th International Conference on Humanoid Robots (Humanoids), Beijing, China, 6–9 November 2018; Volume 10, pp. 425–432. [Google Scholar]
- Gams, A.; Petrič, T.; Babič, J.; Žlajpah, L.; Ude, A. Constraining Movement Imitation with Reflexive Behavior: Robot Squatting. In Proceedings of the 2011 11th IEEE-RAS International Conference on Humanoid Robots, Bled, Slovenia, 26–28 October 2011; pp. 294–299. [Google Scholar]
- Durán-Hernández, J.; Fuentes-Aguilar, R.Q.; Campos-Macías, L.; Carbajal-Espinosa, O. Control Implementation in a Low-cost Designed Biped Robot to Reproduce Squats. In Proceedings of the 2022 10th International Conference on Control, Mechatronics and Automation (ICCMA), Belval, Luxembourg, 9–12 November 2022; pp. 36–41. [Google Scholar]
- Hyon, S.H. A Motor Control Strategy with Virtual Musculoskeletal Systems for Compliant Anthropomorphic Robots. IEEE/ASME Trans. Mechatron. 2009, 14, 677–688. [Google Scholar] [CrossRef]
- Hyon, S.H.; Suewaka, D.; Torii, Y.; Oku, N. Design and Experimental Evaluation of a Fast Torque-Controlled Hydraulic Humanoid Robot. IEEE/ASME Trans. Mechatron. 2017, 22, 623–634. [Google Scholar] [CrossRef]
- Luo, D.; Deng, Y.; Han, X.; Hu, F.; Wu, X. Learning task transition from standing-up to walking for a squatted bipedal humanoid robot. In Proceedings of the 2016 IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016. [Google Scholar]
- Bonnet, V.; Mazza, C.; Fraisse, P.; Cappozzo, A. Real-time Estimate of Body Kinematics During a Planar Squat Task Using a Single Inertial Measurement Unit. IEEE Trans. Biomed. Eng. 2013, 60, 1920–1926. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.; Androwis, G.; Adamovich, S.; Su, H.; Nunez, E.; Zhou, X. Reinforcement Learning and Control of a Lower Extremity Exoskeleton for Squat Assistance. Front. Robot. AI 2021, 8, 702845. [Google Scholar] [CrossRef]
- Miyadaira, A.N.; Madrid, M.K.; Garcia, J.C.; Gualda, D.; Delai, A.L. Squat Vertical Jump of a 3DOF Robot Leg over an Inclined Plane: Analysis with Joint Torque Profile Approximation. IEEE Lat. Am. Trans. 2018, 16, 80–87. [Google Scholar] [CrossRef]
- Lee, I.F.; Lin, C.I.; Wu, H.C.; Wu, L.C.; Lin, P.C.; Chiang, M.H.; Shih, W.P. Squat and Standing Motion of a Single Robotic Leg Using Pneumatic Artificial Muscles. J. Appl. Sci. Eng. 2015, 18, 363–370. [Google Scholar]
- Zhang, L.; Cheng, Z.; Gan, Y.; Zhu, G.; Shen, P.; Song, J. Fast Human Whole Body Motion Imitation Algorithm For Humanoid Robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Biomimetics (ROBIO), Qingdao, China, 3–7 December 2016; Volume 10, pp. 1430–1435. [Google Scholar]
- Chen, J.; Wang, G.; Hu, X.; Shen, J. Lower-body control of humanoid robot NAO via Kinect. Multimed. Tools Appl. 2018, 77, 10883–10898. [Google Scholar] [CrossRef]
- Cai, W.; Li, Q.; Huang, S.; Zhu, H.; Yang, Y.; Zhao, M. Squat motion of a bipedal robot using real-time kinematic prediction and whole-body control. IET Cyber-Syst. Robot. 2022, 4, 298–312. [Google Scholar] [CrossRef]
- Lin, P. Trajectory Planning of a Humanoid One-legged Robot with Tendon Elastic Actuation during Squatting after Landing. In Proceedings of the 2023 9th International Conference on Control, Automation and Robotics (ICCAR), Beijing, China, 21–23 April 2023; pp. 121–129. [Google Scholar]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. Qpoases: A parametric active-set algorithm for quadratic programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- Felis, M.L. Rbdl: An efficient rigid-body dynamics library using recursive algorithms. Auton. Robot. 2017, 41, 495–511. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, J.; Dong, H.; Ren, X.; Huang, L.; Zhao, M. Dynamic Balancing of Humanoid Robot with Proprioceptive Actuation: Systematic Design of Algorithm, Software, and Hardware. Micromachines 2022, 13, 1458. [Google Scholar] [CrossRef]





| Weight Term | Weight Matrix |
|---|---|
| diag(, , ) | |
| diag(7.0, , 2.5) | |
| diag(, , , , , ) | |
| diag(1.0, , 2.5, 1.0, , 2.5) | |
| diag(, 1.0, , 1.0, 1.0, 1.0, 1.0, 1.0, 1.0) |
| Tasks | Constraints |
|---|---|
| Torso trajectory tracking task | Floating-base dynamic |
| Arm trajectory tracking task | Friction cone |
| Feet trajectory tracking task | Joint torque |
| Wrench task | Joint velocity |
| Chest joint immobilization task | Joint power |
| Weight Term | Weight Matrix |
|---|---|
| diag(1750, 450, 300, 70, 150, 50) | |
| diag( 300, 300, 300, 200, 200, 200) | |
| diag(900, 900, 900, 190, 140, 150) | |
| diag(1, 1, 1, 2, 2, 2) | |
| diag(70) |
| Item | TP-MPC + WBC | WBC |
|---|---|---|
| Torso X Pos ( · ) | 0.98 | 4.6 |
| Torso Y Pos ( · ) | 0.46 | 4.5 |
| Torso Z Pos ( · ) | 1.1 | 5.8 |
| Item | TP-MPC + WBC | WBC |
|---|---|---|
| Torso X Pos ( · ) | 1.1 | 3.7 |
| Torso Y Pos ( · ) | 0.1 | 6.2 |
| Torso Z Pos ( · ) | 1.2 | 3.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Zhang, X.; Zhao, M. Squat Motion of a Humanoid Robot Using Three-Particle Model Predictive Control and Whole-Body Control. Sensors 2025, 25, 435. https://doi.org/10.3390/s25020435
Chen H, Zhang X, Zhao M. Squat Motion of a Humanoid Robot Using Three-Particle Model Predictive Control and Whole-Body Control. Sensors. 2025; 25(2):435. https://doi.org/10.3390/s25020435
Chicago/Turabian StyleChen, Hongxiang, Xiuli Zhang, and Mingguo Zhao. 2025. "Squat Motion of a Humanoid Robot Using Three-Particle Model Predictive Control and Whole-Body Control" Sensors 25, no. 2: 435. https://doi.org/10.3390/s25020435
APA StyleChen, H., Zhang, X., & Zhao, M. (2025). Squat Motion of a Humanoid Robot Using Three-Particle Model Predictive Control and Whole-Body Control. Sensors, 25(2), 435. https://doi.org/10.3390/s25020435






