Finite Element Analysis of Electromagnetic Characteristics of a Single-Phase Permanent Magnet Linear Oscillation Actuator
Abstract
:1. Introduction
2. Motor Structure Analysis
3. Electromagnetic Field Equation and Finite Element Calculation
3.1. Electromagnetic Field Equation
- For the stator slot area containing the armature winding, assuming .
- The stator core is made of thin silicon steel sheets stacked together, and there is a certain air gap between the stacked sheets. Therefore, the eddy current loss in this area can be ignored, and the total current density and air gap area are the same .
- Due to the presence of a solid permanent magnet and a supporting iron core, the moving sub region has a certain degree of conductivity, resulting in a current density in this area .
- The boundary conditions for each solution domain are .
3.2. Finite Element Calculation
4. Electromagnetic Parameters
4.1. Inductance
4.2. Magnetic Flux
4.3. Induced Electromotive Force
4.4. Electromagnetic Force
5. Comparison of Simulation Results
5.1. Magnetic Field Distribution
5.2. No-Load Permanent Magnet Flux
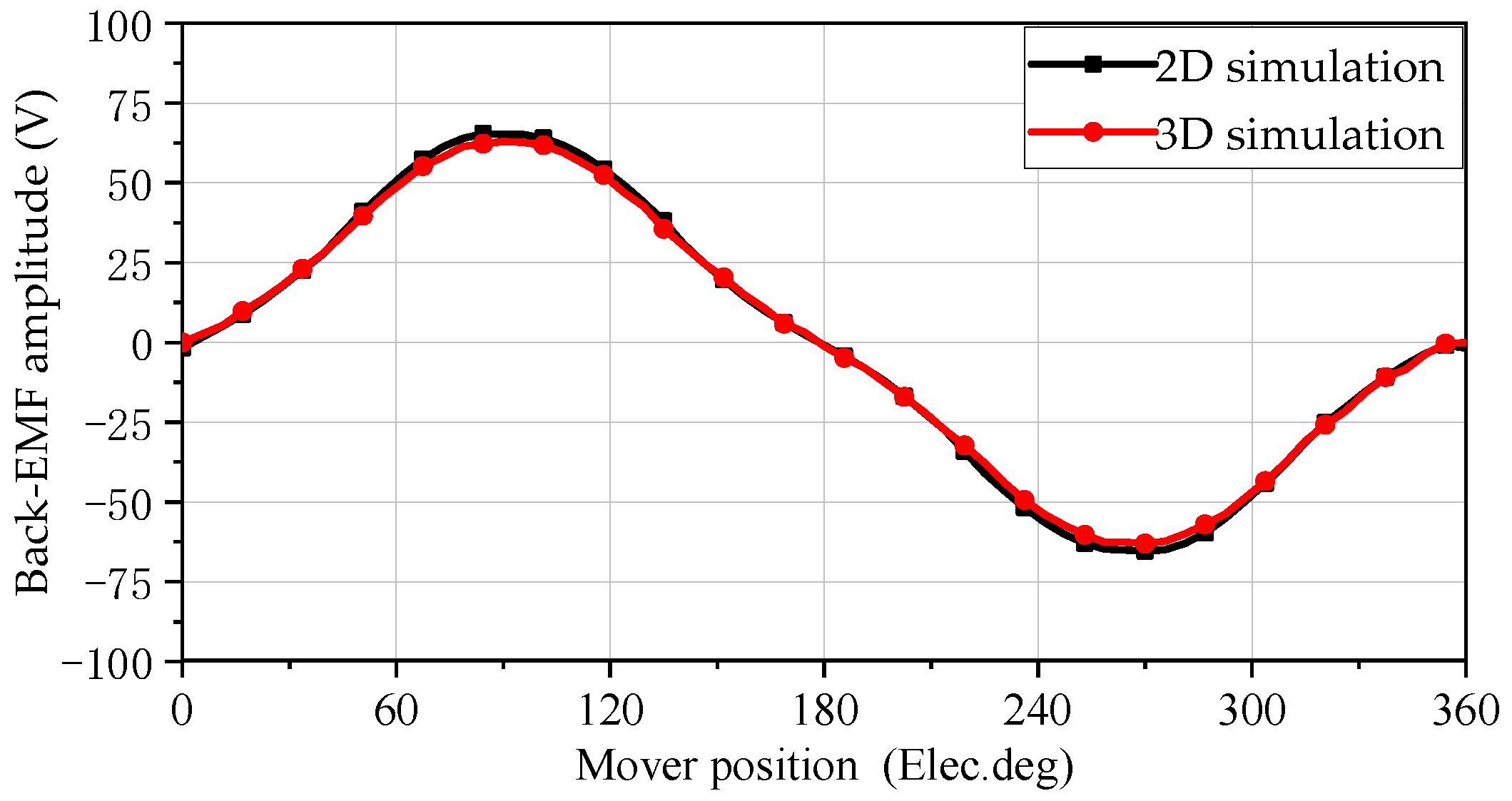
5.3. No-Load Back Electromotive Force
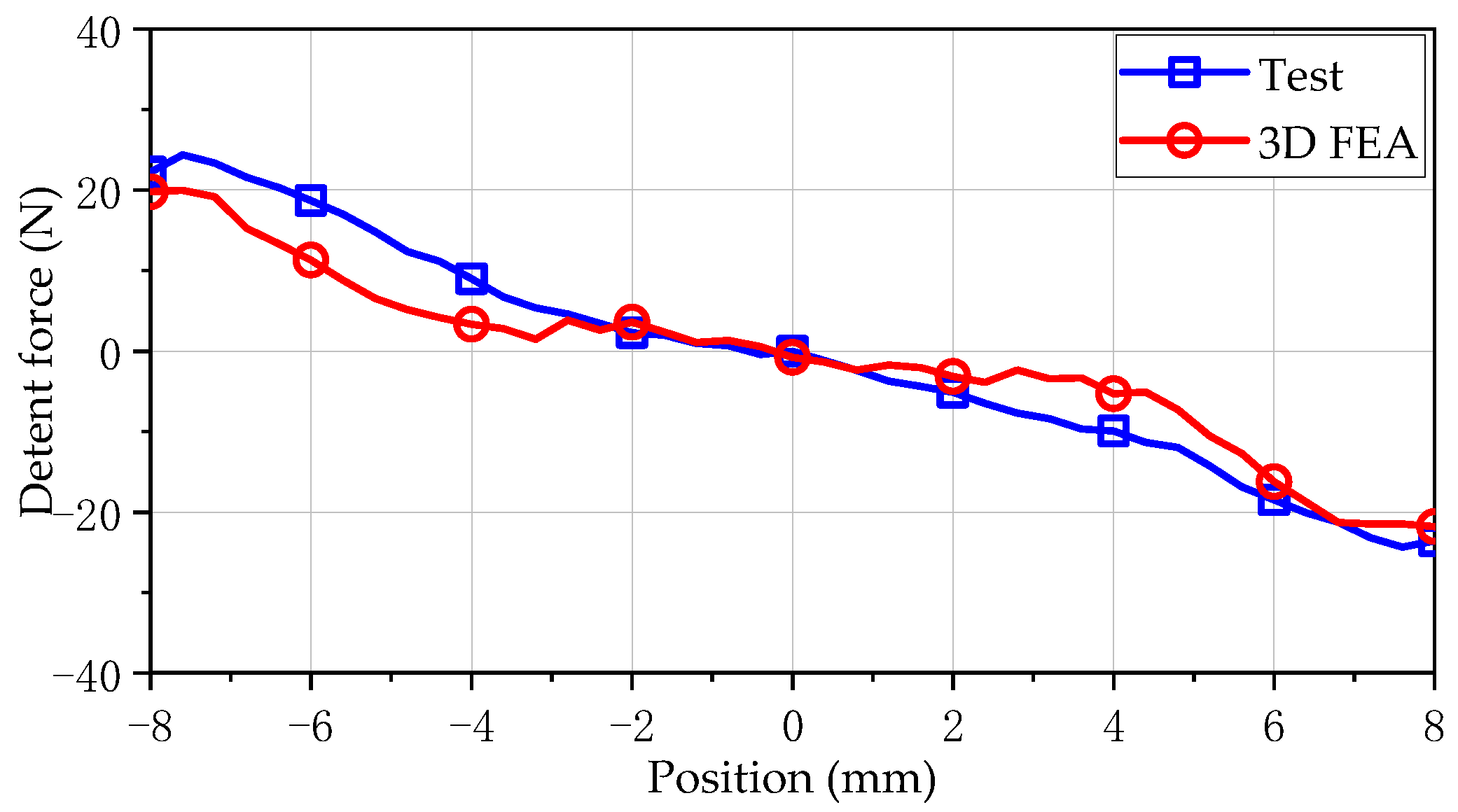
5.4. Detent Force
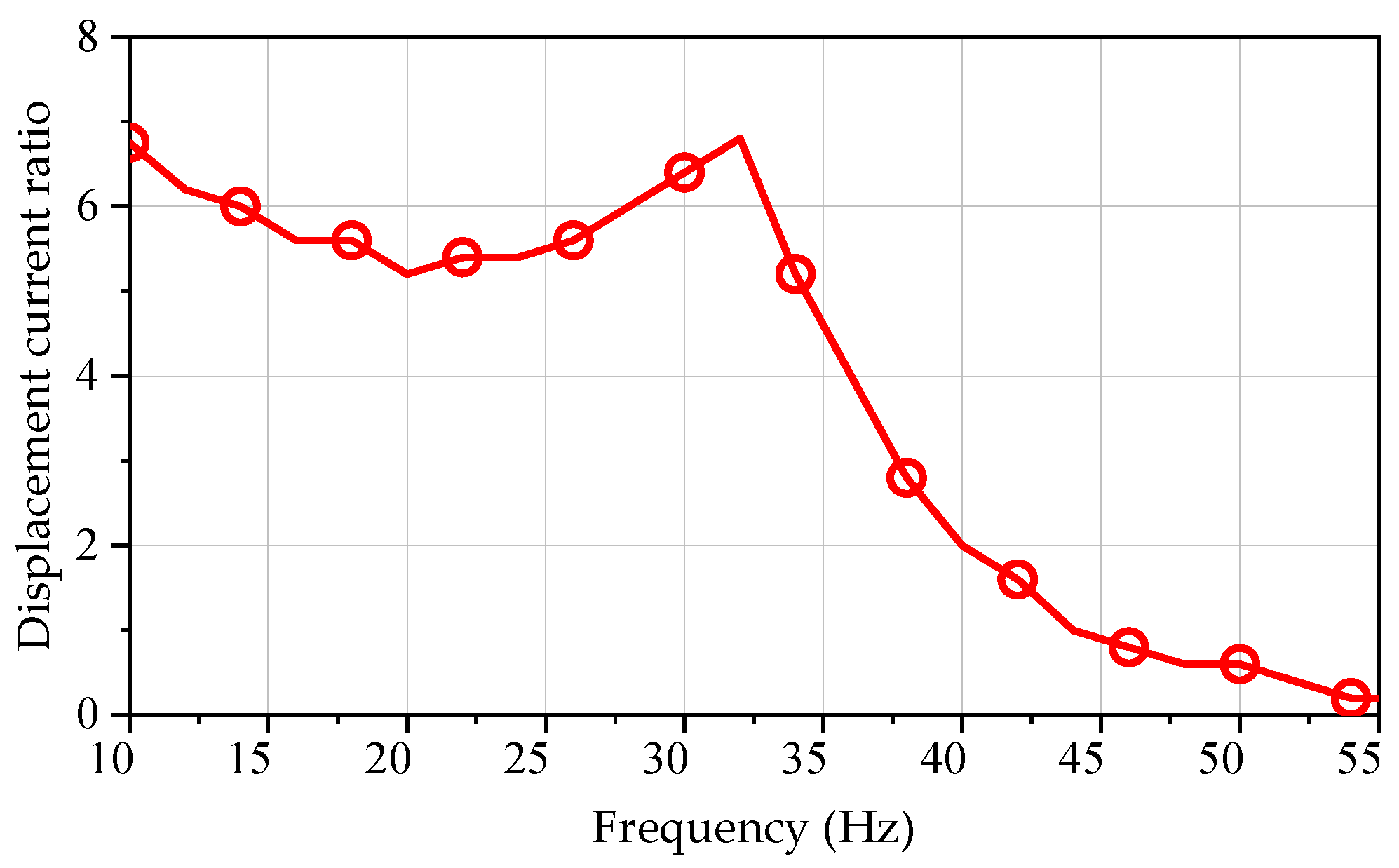
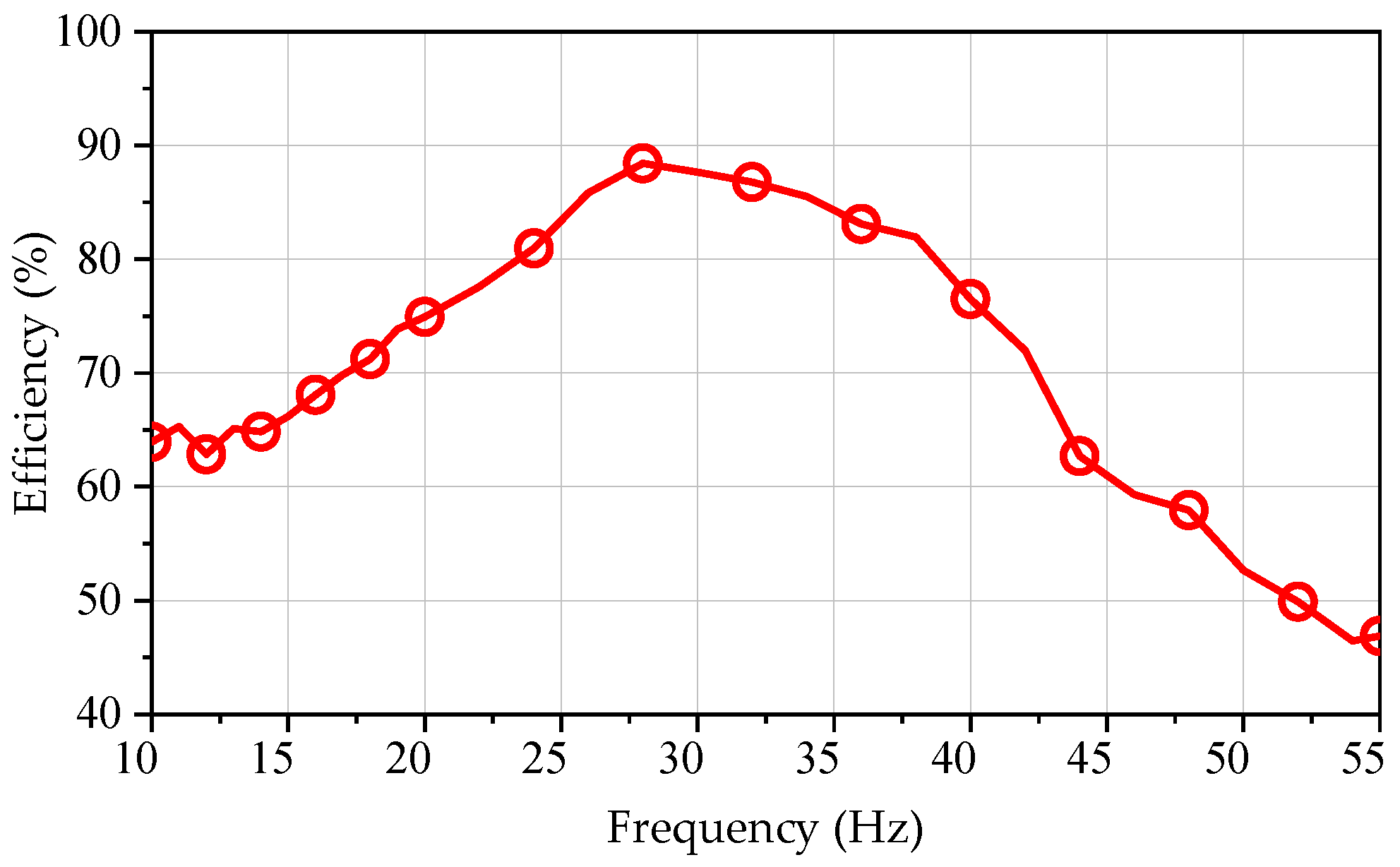
6. Experimental Verification
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; Zhu, Z.Q.; Howe, D. Modeling and analysis of a tubular oscillating permanent-magnet actuator. IEEE Trans. Ind. Electron. 2009, 45, 1961–1970. [Google Scholar] [CrossRef]
- Ahmad, Z.; Hassan, A.; Khan, F.; Lazoglu, I. Design of a high thrust density moving magnet linear actuator with magnetic flux bridge. IET Electr. Power Appl. 2020, 14, 1256–1262. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Chen, X. Analysis of an E-core interior permanent magnet linear oscillating actuator. IEEE Trans. Magn. 2009, 45, 4384–4387. [Google Scholar] [CrossRef]
- Kim, C.-W.; Jang, G.-H.; Seo, S.-W.; Yoon, I.-J.; Lee, S.-H.; Jeong, S.-S.; Choi, J.-Y. Comparison of electromagnetic and dynamic characteristics of linear oscillating actuators with rare-earth and ferrite magnets. IEEE Trans. Magn. 2019, 55, 8203204. [Google Scholar] [CrossRef]
- Kwon, Y.-S.; Kim, W.-J. Detent-force minimization of double-sided interior permanent-magnet flat linear brushless motor. IEEE Trans. Magn. 2016, 52, 8201609. [Google Scholar] [CrossRef]
- Guo, R.; Yu, H.; Wang, Y.; Chen, H.; Liu, X.; Xia, T. Detent force minimization of an improved linear permanent magnet synchronous motor. Int. J. Appl. Electromagn. Mech. 2018, 58, 513–529. [Google Scholar] [CrossRef]
- Hwang, C.-C.; Li, P.-L.; Liu, C.-T. Optimal design of a permanent magnet linear synchronous motor with low cogging force. IEEE Trans. Magn. 2012, 48, 1039–1042. [Google Scholar] [CrossRef]
- Chi, S.; Yan, J.; Shan, L.; Wang, P. Detent force minimizing for moving-magnet-type linear synchronous motor. IEEE Trans. Magn. 2019, 55, 8102005. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Jung, S.-Y. Minimization of outlet edge force using stair shape auxiliary teeth in a stationary discontinuous armature linear permanent magnet motor. IEEE Trans. Magn. 2011, 47, 3228–3231. [Google Scholar] [CrossRef]
- Guan, L.; Liu, B.; Wang, Y.J.; Zhang, J. Performance parameter analysis of flexible plate spring of linear oscillating motor. Mach. Tool Hydraul. 2022, 50, 8–12. [Google Scholar]
- Wang, X.; Xiao, C.; Feng, H. Characteristic analysis and optimization of U-type permanent magnet flux-switching linear motors. Electr. Mach. Control 2021, 25, 132–140. [Google Scholar]
- Cao, R.; Su, E.; Zhang, X. Investigation of linear flux-switching permanent magnet motor with segmented secondary for rail transit. Trans. China Electrotech. Soc. 2020, 35, 1001–1012. [Google Scholar]
- Zhang, C.; Zhang, H.; Ye, P.; Zhang, L. Inductance analysis of two-phase slotless tubular permanent magnet synchronous linear motor. Trans. China Electrotech. Soc. 2021, 36, 1159–1168. [Google Scholar]
- Dongshan, F.; Zeyu, J.; Fuqiang, W.; Xiaojie, W.; Mei, Z. Novel oblique air-gap tubular transverse flux switching permanent magnet linear motors and Its modeling analysis. Proc. CSEE 2021, 42, 5706–5719. [Google Scholar]
- Li, X.; Xu, W.; Ye, C. Novel stator-magnet moving-iron transversal-flux linear oscillatory machine. Proc. CSEE 2021, 37, 6209–6217. [Google Scholar]
- Liang, K. A review of linear compressors for refrigeration. Int. J. Refrig. 2017, 84, 253–273. [Google Scholar] [CrossRef]
- Balanis, A.C. Advanced Engineering Electromagnetics; Wiley: Hoboken, NJ, USA, 1989. [Google Scholar]
- Zienkiewicz, O.C.; Morgan, K. Finite Element and Approximation; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Boldea, I. Linear Electric Machines, Drives and MAGLEVs Handbook; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Xu, W.; Wang, Q.; Li, X.; Liu, Y.; Zhu, J. A novel resonant frequency tracking control for linear compressor based on MRAS method. CES Trans. Electr. Mach. Syst. 2020, 4, 227–236. [Google Scholar] [CrossRef]
- Chun, T.-W.; Ahn, J.-R.; Lee, H.-H.; Kim, H.-G.; Nho, E.-C. A novel strategy of efficiency control for a linear compressor system driven by a PWM inverter. IEEE Trans. Ind. Electron. 2008, 55, 296–301. [Google Scholar] [CrossRef]
- Wei, X.; Yao, B.; Wang, Z.-X.; Zhang, Y.; Peng, Y.-Z.; Sun, Y.-C.; Wang, K.; Wang, H. A robust online junction temperature calibration method for power semiconductors in traction inverter application. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar] [CrossRef]
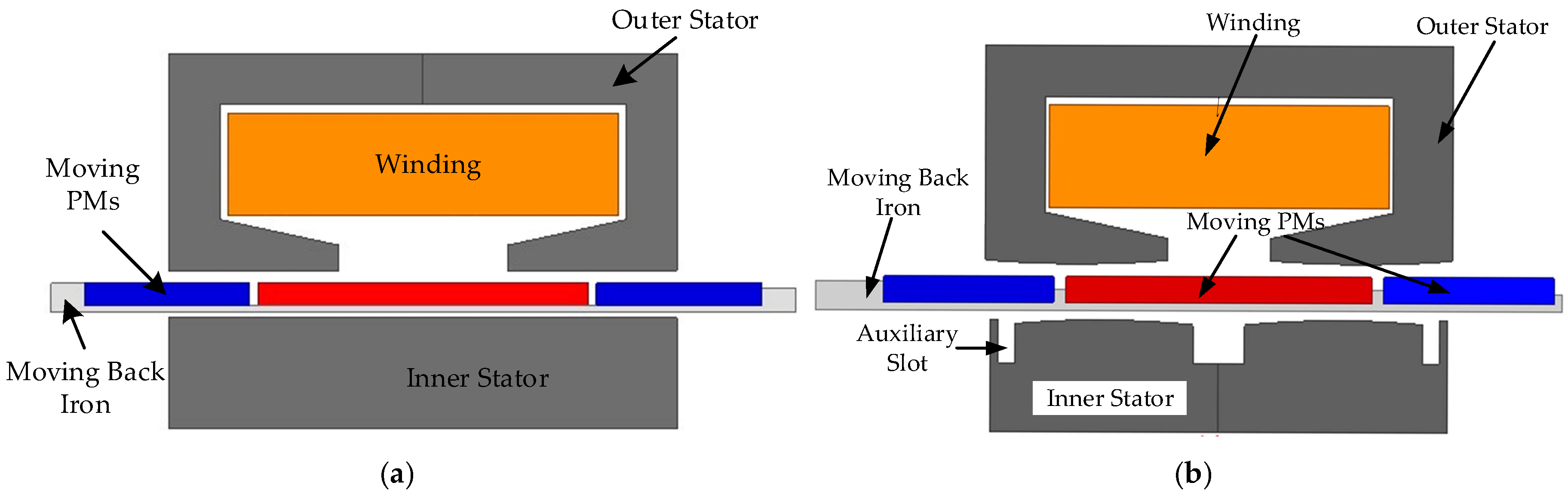

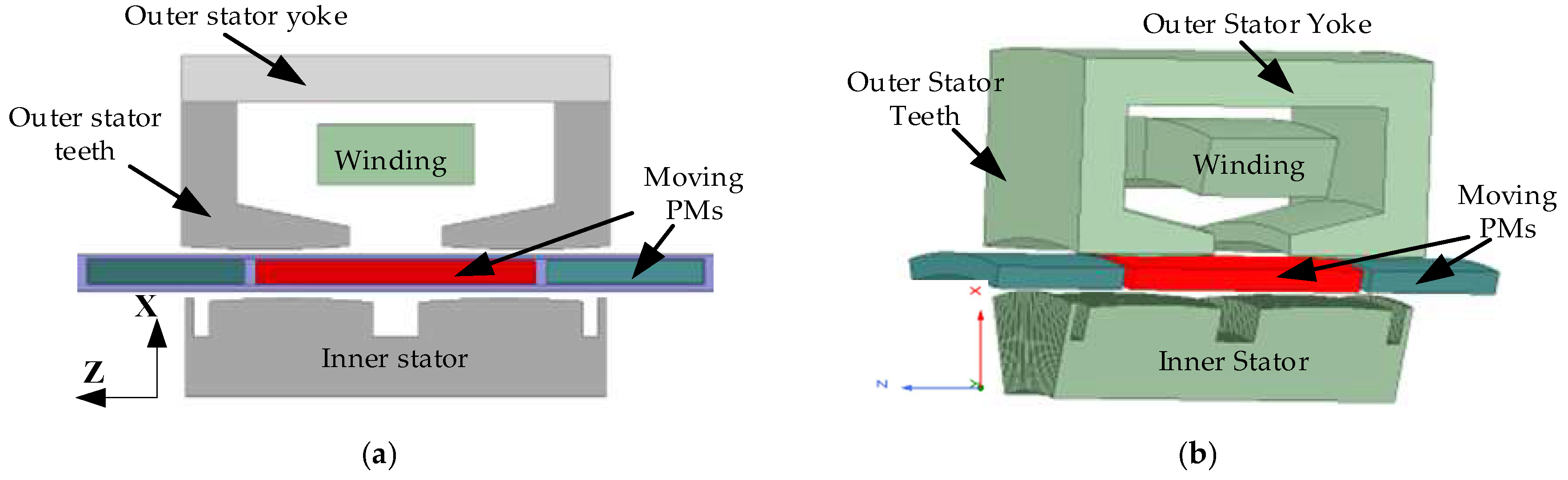
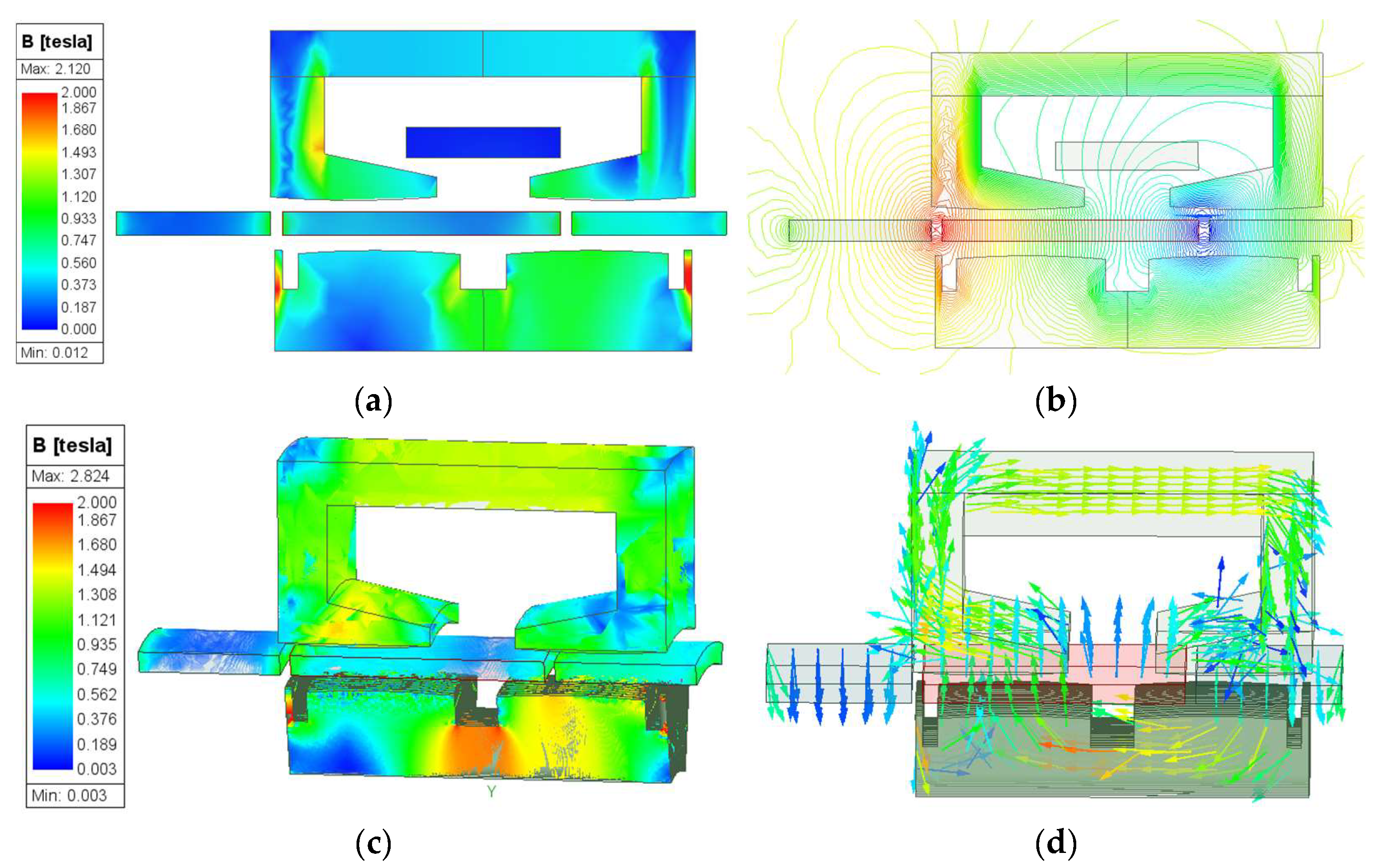
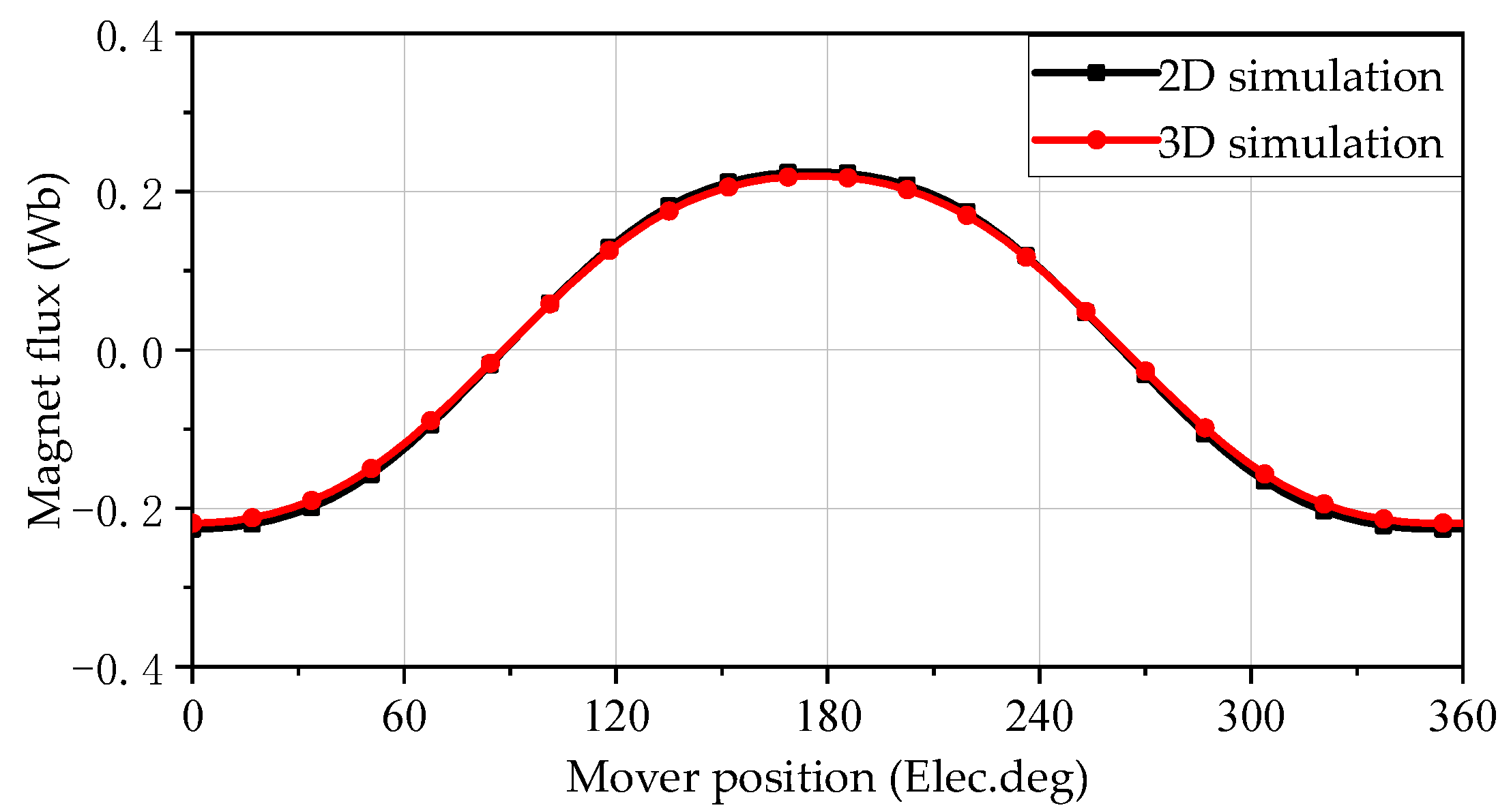




| Parameter | Value | Unit | Parameter | Value | Unit |
|---|---|---|---|---|---|
| Output power | 200 | W | Outer stator height | 25.5 | mm |
| Rated voltage | 60 | V | Back iron height | 6 | mm |
| Rated frequency | 40 | Hz | Slot width | 12 | mm |
| Rated stroke | ±8 | mm | Air gap | 1.5 | mm |
| Thrust | 200 | N | Inner-stator height | 13 | mm |
| Efficiency | 85% | PM height | 3 | mm | |
| Stator length | 55 | mm | Middle PM width | 36 | mm |
| Outer-stator inner diameter | 39.5 | mm | Right and left PM width | 20 | mm |
| Parameter | 2-D | 3-D |
|---|---|---|
| Total number of elements | 22,448 | 333,526 |
| Simulation time | 5 min | 5 h 34 min |
| Error rate | <5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Wang, Z.; Chen, M.; Shen, Z.; Yu, H.; Xu, Z. Finite Element Analysis of Electromagnetic Characteristics of a Single-Phase Permanent Magnet Linear Oscillation Actuator. Sensors 2025, 25, 452. https://doi.org/10.3390/s25020452
Zhang H, Wang Z, Chen M, Shen Z, Yu H, Xu Z. Finite Element Analysis of Electromagnetic Characteristics of a Single-Phase Permanent Magnet Linear Oscillation Actuator. Sensors. 2025; 25(2):452. https://doi.org/10.3390/s25020452
Chicago/Turabian StyleZhang, Hongbin, Zhaoxin Wang, Minshuo Chen, Zhan Shen, Haitao Yu, and Zhike Xu. 2025. "Finite Element Analysis of Electromagnetic Characteristics of a Single-Phase Permanent Magnet Linear Oscillation Actuator" Sensors 25, no. 2: 452. https://doi.org/10.3390/s25020452
APA StyleZhang, H., Wang, Z., Chen, M., Shen, Z., Yu, H., & Xu, Z. (2025). Finite Element Analysis of Electromagnetic Characteristics of a Single-Phase Permanent Magnet Linear Oscillation Actuator. Sensors, 25(2), 452. https://doi.org/10.3390/s25020452






