The Validity and Reliability of the Force Plates and the Linear Position Transducer in Measuring Countermovement Depth and Velocity During Countermovement Jump
Abstract
1. Introduction
2. Methods
2.1. Participants
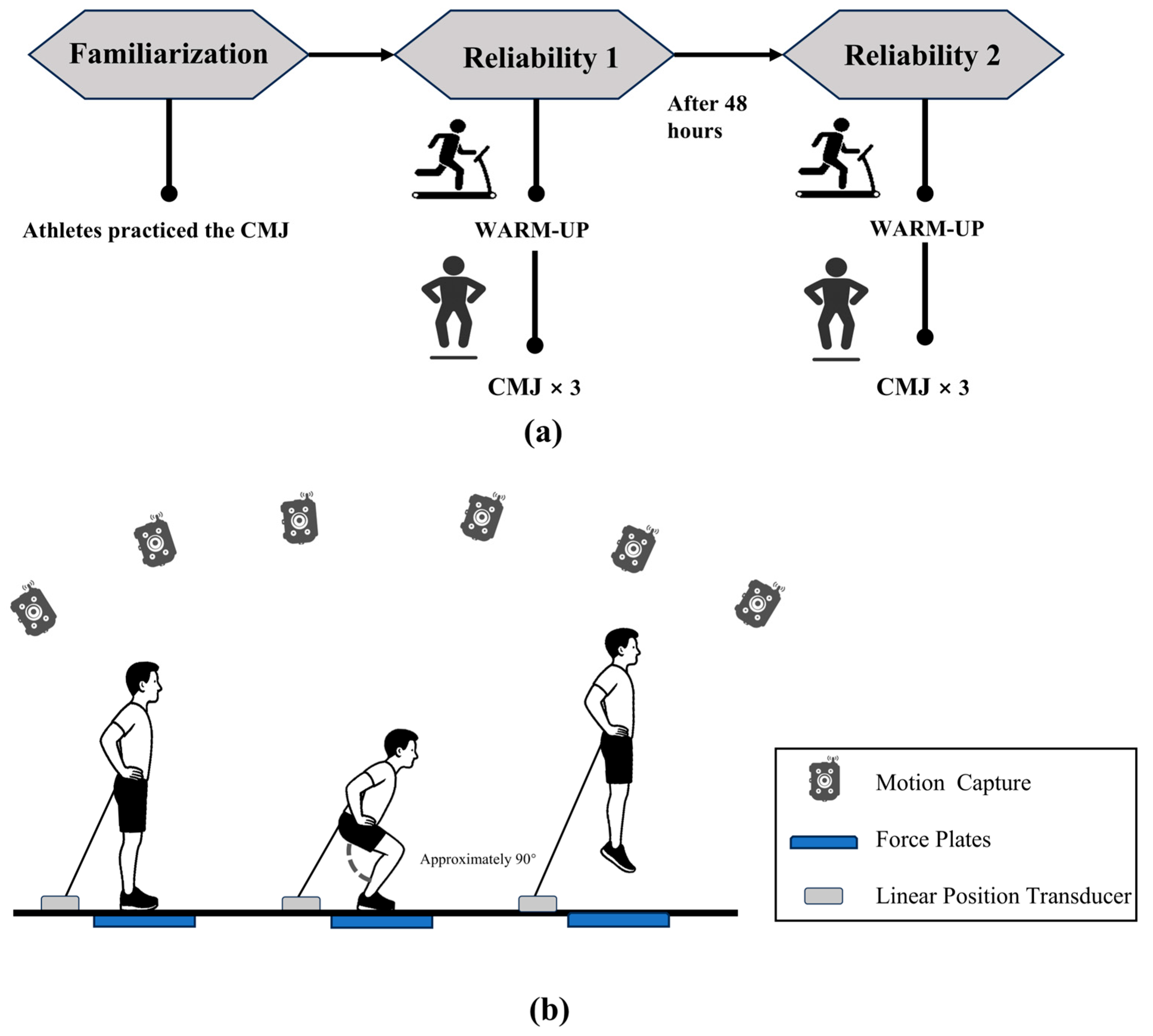
2.2. Study Design
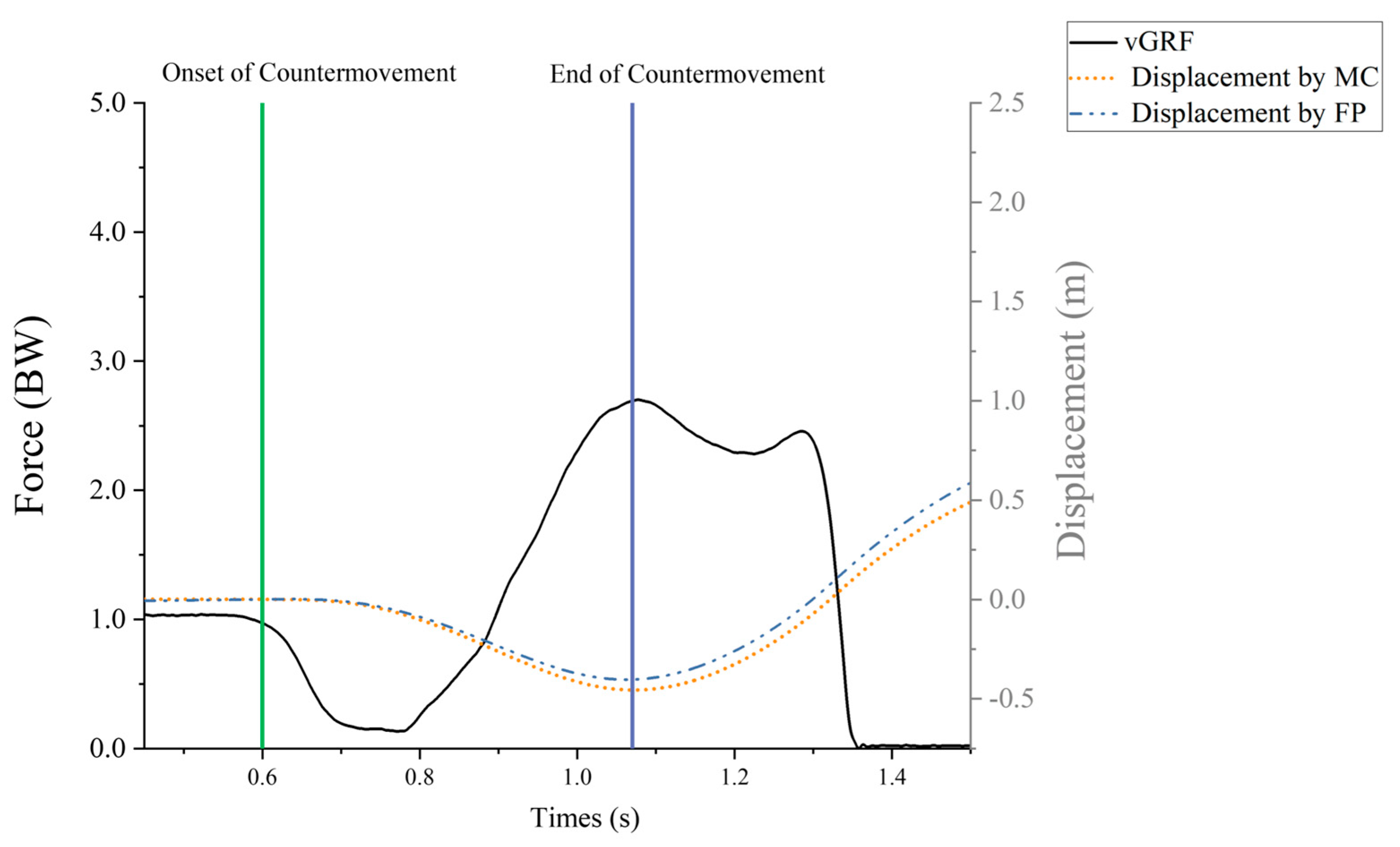
2.3. Data Processing
2.4. Statistical Analysis
3. Results
3.1. Validity
3.2. Test–Retest Reliability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CMJ | Countermovement Jump |
| COM | Centre of Mass |
| vGRF | Vertical Ground Reaction Force |
| CMD | Countermovement Depth |
| CMV | Countermovement Velocity |
| MC | Motion Capture |
| FP | Force Plates |
| LPT | Linear Position Transducer |
| DI | Double Integration Method |
| JH | Jump Height |
| ICC | Intraclass Correlation Coefficient |
Appendix A
| Marker Name | Location/Description |
|---|---|
| H1-H3 | Head (Frontal/Occipital/Temporal, 3 points) |
| C7 | Spinous process of the 7th cervical vertebra |
| T10 | Spinous process of the 10th thoracic vertebra |
| L/R_SAE | Scapula—Acromial Edge |
| L/R_SIA | Scapula—Inferior Angle |
| L/R_HUM | Humeral wand (Left) |
| L/R_HLE | Humerus—Lateral Epicondyle |
| L/R_HME | Humerus—Medial Epicondyle |
| L/R_FAR | Forearm wand |
| L/R_USP | Ulna—Styloid Process |
| L/R_RSP | Radius—Styloid Process |
| L/R_HM2 | Dorsal aspect of the second metacarpal head |
| L/R_IAS | Anterior Superior Iliac Spine |
| L/R_IPS | Posterior Superior Iliac Spine |
| L/R_GT | Greater Trochanter |
| L/R_TH1-4 | Thigh cluster—4 markers |
| L/R_FLE | Femur—Lateral Epicondyle |
| L/R_FME | Femur—Medial Epicondyle |
| L/R_SK1-4 | Shank cluster—4 markers |
| L/R_FAL | Lateral prominence of the lateral malleolus |
| L/R_TAM | Medial prominence of the medial malleolus |
| L/R_FM1 | Dorsal margin of the first metatarsal head |
| L/R_FM2 | Dorsal aspect of the second metatarsal head |
| L/R_FM5 | Dorsal margin of the fifth metatarsal head |
| L/R_TOE | Toe Tip |
| L/R_FCC | Posterior aspect of the calcaneus |
References
- Claudino, J.G.; Cronin, J.; Mezêncio, B.; McMaster, D.T.; McGuigan, M.; Tricoli, V.; Amadio, A.C.; Serrão, J.C. The Countermovement Jump to Monitor Neuromuscular Status: A Meta-Analysis. J. Sci. Med. Sport 2017, 20, 397–402. [Google Scholar] [CrossRef]
- Hughes, S.; Warmenhoven, J.; Haff, G.G.; Chapman, D.W.; Nimphius, S. Countermovement Jump and Squat Jump Force-Time Curve Analysis in Control and Fatigue Conditions. J. Strength Cond. Res. 2022, 36, 2752–2761. [Google Scholar] [CrossRef]
- Bishop, C.; Jordan, M.; Torres-Ronda, L.; Loturco, I.; Harry, J.; Virgile, A.; Mundy, P.; Turner, A.; Comfort, P. Selecting Metrics That Matter: Comparing the Use of the Countermovement Jump for Performance Profiling, Neuromuscular Fatigue Monitoring, and Injury Rehabilitation Testing. Strength Cond. J. 2023, 45, 545–553. [Google Scholar] [CrossRef]
- Harry, J.R.; Paquette, M.R.; Schilling, B.K.; Barker, L.A.; James, C.R.; Dufek, J.S. Kinetic and Electromyographic Subphase Characteristics With Relation to Countermovement Vertical Jump Performance. J. Appl. Biomech. 2018, 34, 291–297. [Google Scholar] [CrossRef]
- Pérez-Castilla, A.; Rojas, F.J.; Gómez-Martínez, F.; García-Ramos, A. Vertical Jump Performance Is Affected by the Velocity and Depth of the Countermovement. Sports Biomech. 2021, 20, 1015–1030. [Google Scholar] [CrossRef]
- Pérez-Castilla, A.; Weakley, J.; García-Pinillos, F.; Rojas, F.J.; García-Ramos, A. Influence of Countermovement Depth on the Countermovement Jump-Derived Reactive Strength Index Modified. Eur. J. Sport Sci. 2021, 21, 1606–1616. [Google Scholar] [CrossRef]
- Pommerell, F.; Boyas, S.; Samozino, P.; Morel, B.; Begue, J.; Rahmani, A.; Peyrot, N. Influence of Countermovement Depth on Net Force, Push-off Time, Vertical Impulse and Performance during Jumping. J. Electromyogr. Kinesiol. 2024, 79, 102945. [Google Scholar] [CrossRef]
- Krzyszkowski, J.; Chowning, L.D.; Harry, J.R. Phase-Specific Verbal Cue Effects on Countermovement Jump Performance. J. Strength Cond. Res. 2022, 36, 3352–3358. [Google Scholar] [CrossRef]
- Xu, J.; Turner, A.; Comyns, T.M.; Chavda, S.; Bishop, C. Effects of External Verbal Cueing on Countermovement Rebound Jump Performance. Sports Biomech. 2024, 1–19. [Google Scholar] [CrossRef]
- Bishop, C.; Turner, A.; Jordan, M.; Harry, J.; Loturco, I.; Lake, J.; Comfort, P. A Framework to Guide Practitioners for Selecting Metrics During the Countermovement and Drop Jump Tests. Strength Cond. J. 2022, 44, 95–103. [Google Scholar] [CrossRef]
- Mao, C.; Li, M.; Li, X.; Li, Z.; Liu, T.; Wang, L.; Zhu, W.; Chen, L.; Sun, Y. The Validity of a Dual-Force Plate for Assessing Counter-Movement Jump Performance. Sensors 2024, 24, 5748. [Google Scholar] [CrossRef]
- O’Donnell, S.; Tavares, F.; McMaster, D.; Chambers, S.; Driller, M. The Validity and Reliability of the GymAware Linear Position Transducer for Measuring Counter-Movement Jump Performance in Female Athletes. Meas. Phys. Educ. Exerc. Sci. 2018, 22, 101–107. [Google Scholar] [CrossRef]
- Wadhi, T.; Rauch, J.T.; Tamulevicius, N.; Andersen, J.C.; De Souza, E.O. Validity and Reliability of the GymAware Linear Position Transducer for Squat Jump and Counter-Movement Jump Height. Sports 2018, 6, 177. [Google Scholar] [CrossRef]
- McMaster, D.T.; Tavares, F.; O’Donnell, S.; Driller, M. Validity of Vertical Jump Measurement Systems. Meas. Phys. Educ. Exerc. Sci. 2021, 25, 95–100. [Google Scholar] [CrossRef]
- Wade, L.; Needham, L.; McGuigan, M.P.; Bilzon, J.L.J. Backward Double Integration Is a Valid Method to Calculate Maximal and Sub-Maximal Jump Height. J. Sports Sci. 2022, 40, 1191–1197. [Google Scholar] [CrossRef]
- Markovic, G.; Dizdar, D.; Jukic, I.; Cardinale, M. Reliability and Factorial Validity of Squat and Countermovement Jump Tests. J. Strength Cond. Res. 2004, 18, 551–555. [Google Scholar] [CrossRef]
- García-López, J.; Morante, J.C.; Ogueta-Alday, A.; Rodríguez-Marroyo, J.A. The Type of Mat (Contact vs. Photocell) Affects Vertical Jump Height Estimated from Flight Time. J. Strength Cond. Res. 2013, 27, 1162–1167. [Google Scholar] [CrossRef]
- Chiu, L.Z.F.; Dæhlin, T.E. Comparing Numerical Methods to Estimate Vertical Jump Height Using a Force Platform. Meas. Phys. Educ. Exerc. Sci. 2020, 24, 25–32. [Google Scholar] [CrossRef]
- Glatthorn, J.F.; Gouge, S.; Nussbaumer, S.; Stauffacher, S.; Impellizzeri, F.M.; Maffiuletti, N.A. Validity and Reliability of Optojump Photoelectric Cells for Estimating Vertical Jump Height. J. Strength Cond. Res. 2011, 25, 556. [Google Scholar] [CrossRef]
- Kozinc, Ž.; Pleša, J. Discrepancy Among Different Methods for Vertical Jump Height Determination and Its Implications for Field-Based Testing: A Narrative Review. Meas. Phys. Educ. Exerc. Sci. 2023, 27, 248–256. [Google Scholar] [CrossRef]
- Xu, J.; Turner, A.; Comfort, P.; Harry, J.R.; McMahon, J.J.; Chavda, S.; Bishop, C. A Systematic Review of the Different Calculation Methods for Measuring Jump Height During the Countermovement and Drop Jump Tests. Sports Med. 2023, 53, 1055–1072. [Google Scholar] [CrossRef]
- Mandic, R.; Jakovljevic, S.; Jaric, S. Effects of Countermovement Depth on Kinematic and Kinetic Patterns of Maximum Vertical Jumps. J. Electromyogr. Kinesiol. 2015, 25, 265–272. [Google Scholar] [CrossRef]
- Wade, L.; Lichtwark, G.A.; Farris, D.J. Comparisons of Laboratory-Based Methods to Calculate Jump Height and Improvements to the Field-Based Flight-Time Method. Scand. J. Med. Sci. Sports 2020, 30, 31–37. [Google Scholar] [CrossRef]
- Fernandes, J.F.T.; Lamb, K.L.; Clark, C.C.T.; Moran, J.; Drury, B.; Garcia-Ramos, A.; Twist, C. Comparison of the FitroDyne and GymAware Rotary Encoders for Quantifying Peak and Mean Velocity During Traditional Multijointed Exercises. J. Strength Cond. Res. 2021, 35, 1760. [Google Scholar] [CrossRef]
- Orange, S.T.; Metcalfe, J.W.; Marshall, P.; Vince, R.V.; Madden, L.A.; Liefeith, A. Test-Retest Reliability of a Commercial Linear Position Transducer (GymAware PowerTool) to Measure Velocity and Power in the Back Squat and Bench Press. J. Strength Cond. Res. 2020, 34, 728. [Google Scholar] [CrossRef]
- van den Tillaar, R.; Nygaard Falch, H.; Larsen, S. Comparison of Velocity and Estimated One Repetition Maximum Measured with Different Measuring Tools in Bench Presses and Squats. Sensors 2024, 24, 7422. [Google Scholar] [CrossRef]
- Xu, J.; Turner, A.; Comyns, T.M.; Chavda, S.; Bishop, C. The Countermovement Rebound Jump: Between-Session Reliability and a Comparison With the Countermovement and Drop Jump Tests. J. Strength Cond. Res. 2024, 38, e150–e159. [Google Scholar] [CrossRef]
- Collins, T.D.; Ghoussayni, S.N.; Ewins, D.J.; Kent, J.A. A Six Degrees-of-Freedom Marker Set for Gait Analysis: Repeatability and Comparison with a Modified Helen Hayes Set. Gait Posture 2009, 30, 173–180. [Google Scholar] [CrossRef]
- Sun, Y.; Wei, S.; Zhong, Y.; Fu, W.; Li, L.; Liu, Y. How Joint Torques Affect Hamstring Injury Risk in Sprinting Swing–Stance Transition. Med. Sci. Sports Exerc. 2015, 47, 373. [Google Scholar] [CrossRef]
- Chiu, L.Z.F.; Salem, G.J. Pelvic Kinematic Method for Determining Vertical Jump Height. J. Appl. Biomech. 2010, 26, 508–511. [Google Scholar] [CrossRef]
- Fathian, R.; Khandan, A.; Chiu, L.Z.F.; Rouhani, H. Assessment of Countermovement Jump with and without Arm Swing Using a Single Inertial Measurement Unit. Sports Biomech. 2024, 23, 2390–2407. [Google Scholar] [CrossRef]
- Lawton, H. Reliability and Validity of the GymAware Optical Encoder to Measure Displacement Data; GymAware: Braddon, Australia, 2020. [Google Scholar]
- Čular, D.; Ivančev, V.; Zagatto, A.M.; Milić, M.; Beslija, T.; Sellami, M.; Padulo, J. Validity and Reliability of the 30-s Continuous Jump for Anaerobic Power and Capacity Assessment in Combat Sport. Front. Physiol. 2018, 9, 543. [Google Scholar] [CrossRef]
- Yu, B.; Gabriel, D.; Noble, L.; An, K.-N. Estimate of the Optimum Cutoff Frequency for the Butterworth Low-Pass Digital Filter. J. Appl. Biomech. 1999, 15, 318–329. [Google Scholar] [CrossRef]
- Harry, J.R.; Blinch, J.; Barker, L.A.; Krzyszkowski, J.; Chowning, L. Low-Pass Filter Effects on Metrics of Countermovement Vertical Jump Performance. J. Strength Cond. Res. 2022, 36, 1459–1467. [Google Scholar] [CrossRef]
- Harry, J.R.; Barker, L.A.; Paquette, M.R. A Joint Power Approach to Define Countermovement Jump Phases Using Force Platforms. Med. Sci. Sports Exerc. 2020, 52, 993–1000. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- Nuzzo, J.L.; Anning, J.H.; Scharfenberg, J.M. The Reliability of Three Devices Used for Measuring Vertical Jump Height. J. Strength Cond. Res. 2011, 25, 2580. [Google Scholar] [CrossRef]
- Moir, G.L. Three Different Methods of Calculating Vertical Jump Height from Force Platform Data in Men and Women. Meas. Phys. Educ. Exerc. Sci. 2008, 12, 207–218. [Google Scholar] [CrossRef]
- Wank, V.; Coenning, C. On the Estimation of Centre of Gravity Height in Vertical Jumping. Ger. J. Exerc. Sport Res. 2019, 49, 454–462. [Google Scholar] [CrossRef]
- Conceição, F.; Lewis, M.; Lopes, H.; Fonseca, E.M.M. An Evaluation of the Accuracy and Precision of Jump Height Measurements Using Different Technologies and Analytical Methods. Appl. Sci. 2022, 12, 511. [Google Scholar] [CrossRef]
- Dias, J.A.; Pupo, J.D.; Reis, D.C.; Borges, L.; Santos, S.G.; Moro, A.R.; Borges, N.G.J. Validity of Two Methods for Estimation of Vertical Jump Height. J. Strength Cond. Res. 2011, 25, 2034. [Google Scholar] [CrossRef] [PubMed]
- Eythorsdottir, I.; Gløersen, Ø.; Rice, H.; Werkhausen, A.; Ettema, G.; Mentzoni, F.; Solberg, P.; Lindberg, K.; Paulsen, G. The Battle of the Equations: A Systematic Review of Jump Height Calculations Using Force Platforms. Sports Med. 2024, 54, 2771–2791. [Google Scholar] [CrossRef] [PubMed]
- Mandic, R.; Knezevic, O.M.; Mirkov, D.M.; Jaric, S. Control Strategy of Maximum Vertical Jumps: The Preferred Countermovement Depth May Not Be Fully Optimized for Jump Height. J. Hum. Kinet. 2016, 52, 85–94. [Google Scholar] [CrossRef] [PubMed]


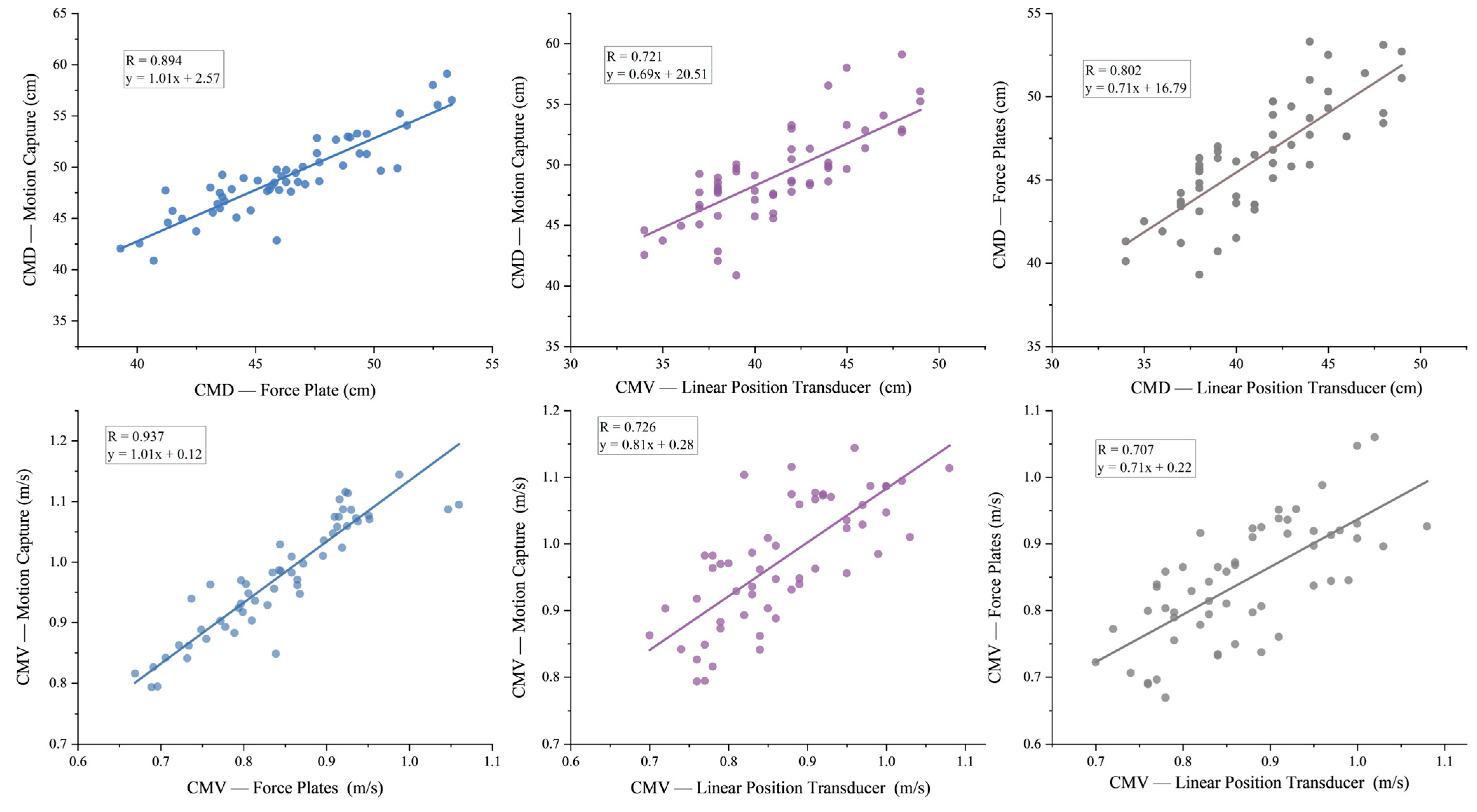
| Variables | MC | FP | LPT | F | p | η2 |
|---|---|---|---|---|---|---|
| CMD (cm) | 49.07 ± 3.85 | 46.26 ± 3.43 | 41.12 ± 4.01 | 254.62 | <0.001 | 0.822 |
| CMV (m/s) | 0.97 ± 0.10 | 0.84 ± 0.09 | 0.87 ± 0.09 | 142.54 | <0.001 | 0.722 |
| Variables | MC vs. FP | MC vs. LPT | FP vs. LPT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| p | 95% CI | p | 95% CI | p | 95% CI | ||||
| CMD (cm) | <0.001 | 2.23 | 3.37 | <0.001 | 6.97 | 8.91 | <0.001 | 4.11 | 6.17 |
| CMV (m/s) | <0.001 | 0.119 | 0.143 | <0.001 | 0.083 | 0.130 | 0.038 | −0.047 | −0.001 |
| Variables | FP | LPT | ||||
|---|---|---|---|---|---|---|
| MAE | RMSE | NRMSE (%) | MAE | RMSE | NRMSE (%) | |
| CMD (cm) | 2.97 | 3.28 | 6.69% | 7.94 | 8.46 | 17.24% |
| CMV (m/s) | 0.07 | 0.09 | 8.17% | 0.06 | 0.07 | 7.54% |
| Variables | Devices | MDC | CV | ICC | 95% CI | p |
|---|---|---|---|---|---|---|
| CMD (cm) | FP | 5.26 | 4.11% | 0.816 | 0.603–0.915 | <0.001 |
| LPT | 4.73 | 4.53% | 0.900 | 0.783–0.954 | <0.001 | |
| CMV (m/s) | FP | 0.14 | 6.11% | 0.809 | 0.587–0.912 | <0.001 |
| LPT | 0.12 | 6.68% | 0.863 | 0.704–0.937 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Ma, W.; Zhang, L.; Zhu, W.; Xie, Q.; Sun, Y. The Validity and Reliability of the Force Plates and the Linear Position Transducer in Measuring Countermovement Depth and Velocity During Countermovement Jump. Sensors 2025, 25, 6542. https://doi.org/10.3390/s25216542
Li Z, Ma W, Zhang L, Zhu W, Xie Q, Sun Y. The Validity and Reliability of the Force Plates and the Linear Position Transducer in Measuring Countermovement Depth and Velocity During Countermovement Jump. Sensors. 2025; 25(21):6542. https://doi.org/10.3390/s25216542
Chicago/Turabian StyleLi, Zheng’ao, Wenyue Ma, Ling Zhang, Wenfei Zhu, Qian Xie, and Yuliang Sun. 2025. "The Validity and Reliability of the Force Plates and the Linear Position Transducer in Measuring Countermovement Depth and Velocity During Countermovement Jump" Sensors 25, no. 21: 6542. https://doi.org/10.3390/s25216542
APA StyleLi, Z., Ma, W., Zhang, L., Zhu, W., Xie, Q., & Sun, Y. (2025). The Validity and Reliability of the Force Plates and the Linear Position Transducer in Measuring Countermovement Depth and Velocity During Countermovement Jump. Sensors, 25(21), 6542. https://doi.org/10.3390/s25216542








