Frugal Self-Optimization Mechanisms for Edge–Cloud Continuum
Abstract
1. Introduction
- Anomaly detection—detection of potential resource utilization abnormalities, which was achieved through density-based analysis of real-time data streams collected from computational nodes
- Adaptive sampling—estimation of the optimal sampling period for the monitoring of resource utilization and power consumption, obtained by analyzing the changes in data distribution with Probabilistic Exponential Moving Average (PEWMA)
2. Related Works
2.1. Frugal Algorithms for Adaptive Sampling
2.2. Frugal Algorithms for Real-Time Anomaly Detection
3. Implemented Approach
3.1. Requirements
- Tailored to operate on data streams: since the self-optimization module receives data from the self-awareness module, its internal mechanisms must be tailored to work on real-time data streams. Therefore, at this stage, methods that utilize large data batches or process entire datasets were excluded from consideration.
- Employ only frugal techniques: all the implemented algorithms should be computationally efficient and require a minimal amount of storage. This requirement was established to enable deploying self-optimization on a wide variety of IEs, including those operating on small edge devices. Consequently, no additional storage for historical data was considered, which eliminated the possibility of implementing some of the more advanced analytical algorithms. However, it should be stressed that this was a design decision rooted in in-depth analysis of pilots, guiding scenarios, and use cases of aerOS and other real-life-anchored projects dealing with ECC.
- Facilitate modular design: all internal parts of the self-optimization should be seamlessly extendable to enable accommodating new requirements, or analyzing new types of monitoring data. Therefore, self-optimization should employ external interfaces that would facilitate the interaction with human operators, or other components of the aerOS continuum. Fulfilling this requirement will allow for generic adaptability of the module since data/metrics to be analyzed may be deployment-specific.
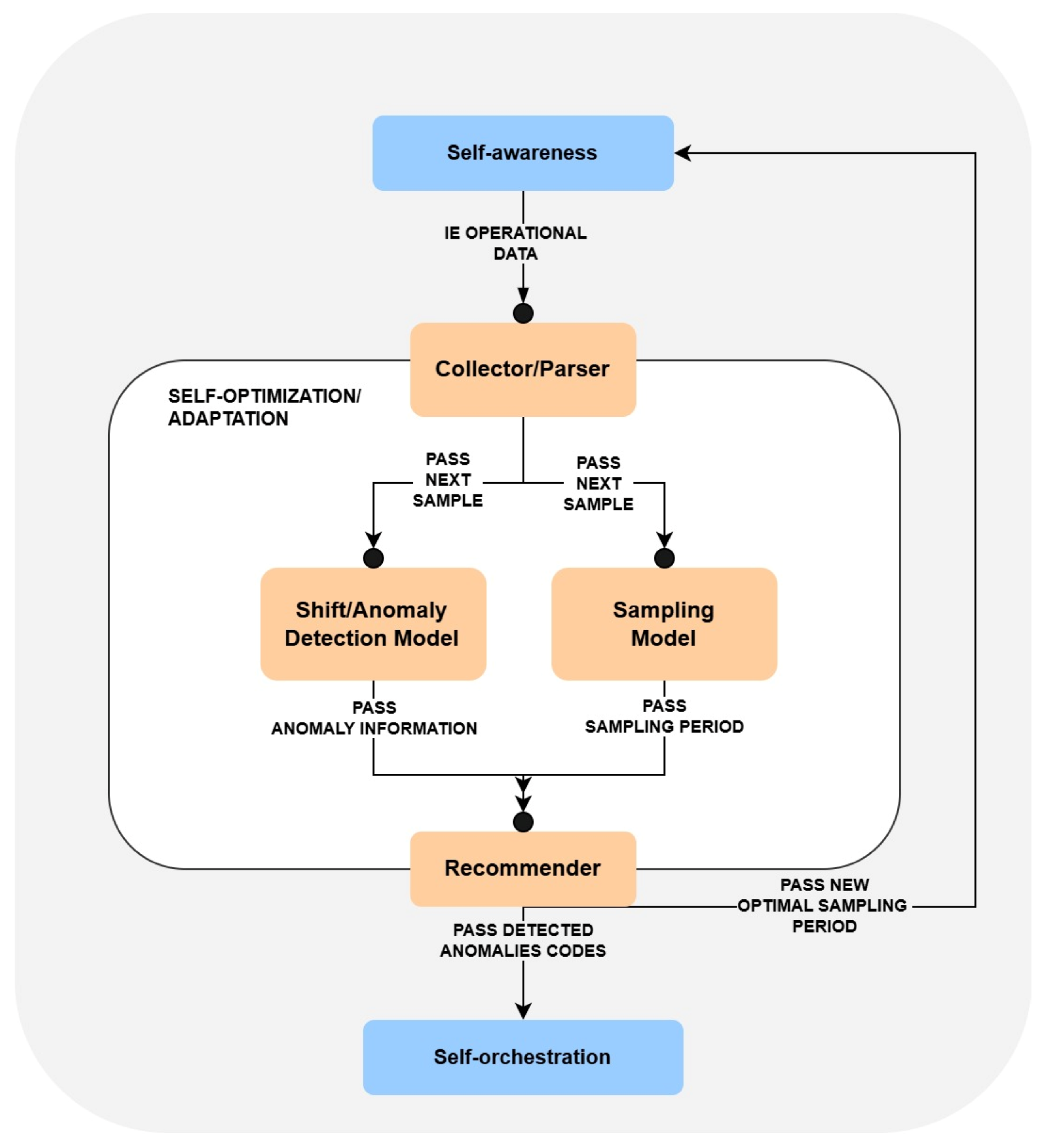
3.2. Self-Optimization Architecture
3.3. Shift/Anomaly Detection Model
3.3.1. Density-Based Anomaly Detection
3.3.2. Model Configuration
3.4. Sampling Model
3.4.1. AdaM Adaptive Sampling
3.4.2. Model Configuration
4. Experimental Validation
- RainMon monitoring dataset (https://github.com/mrcaps/rainmon/blob/master/data/README.md, access date: 24 October 2025): an unlabeled collection of real-world CPU utilization data that consists of 800 observations. It was obtained from the publicly available data corpus of the RainMon research project [50]. The CPU utilization traces of this dataset exhibit non-stationary, highly dynamic behavior, including multiple abrupt spikes. Therefore, it provides an excellent basis for validating the effectiveness of adaptive sampling in capturing critical variations in monitoring data.
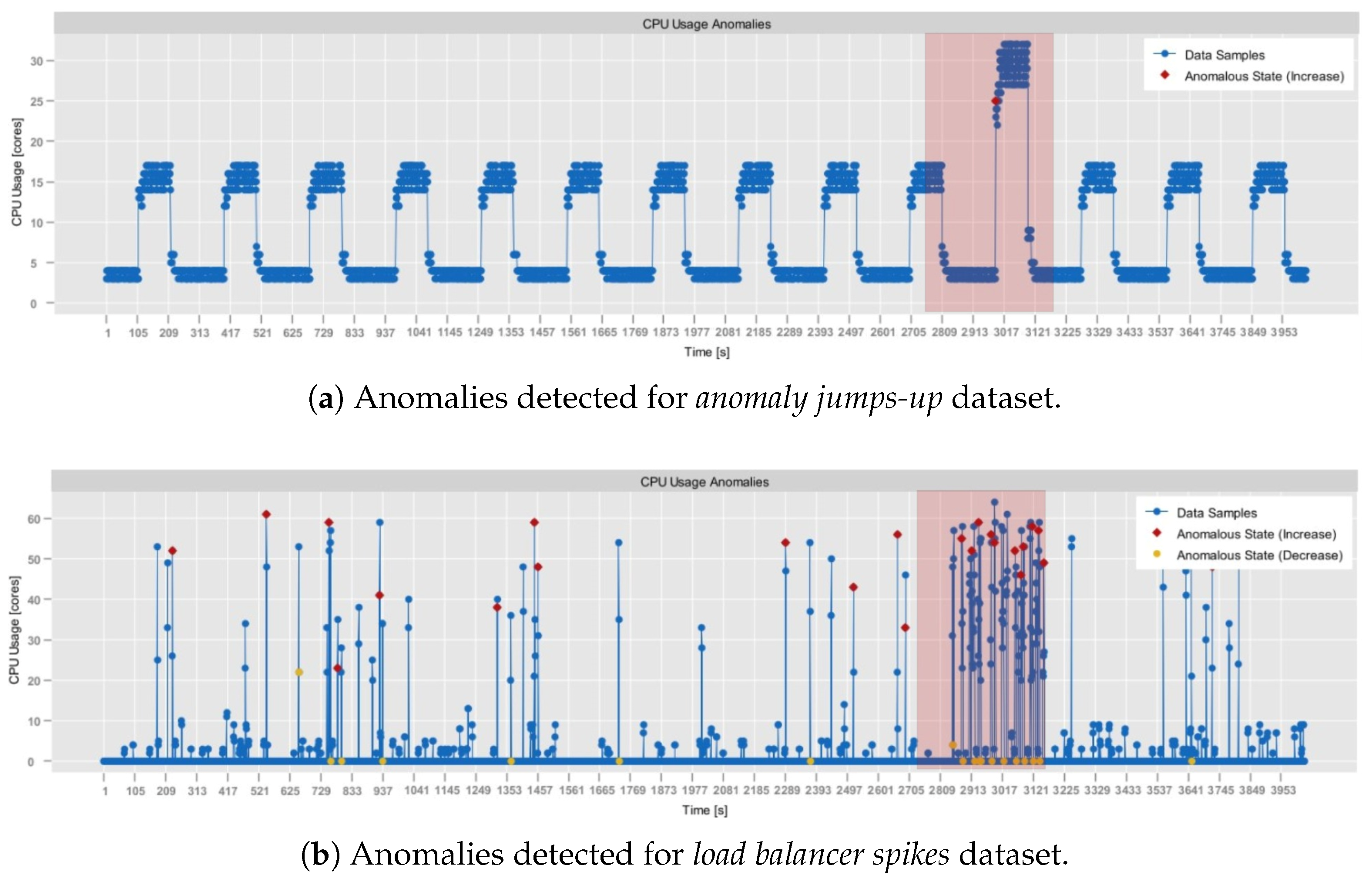
- NAB, synthetic anomaly dataset (anomalies jumps-up) (https://github.com/numenta/NAB/blob/master/data/README.md, access date: 24 October 2025): time-series, labeled, dataset composed of 4032 observations, which was obtained from the NAB data corpus [28]. It features artificially generated anomalies that form a periodic pattern. In particular, in this dataset, CPU usage exhibits regular, continuous bursts of high activity, followed by sharp declines in activity. Consequently, it provides a testbed for anomaly detection, allowing the assessment of its contextual anomaly detection capabilities.
- NAB, synthetic anomaly dataset (load balancer spikes) (https://github.com/numenta/NAB/blob/master/data/README.md, access date: 24 October 2025): similarly to the previous one, a time-series, labeled dataset composed of 4032 observations, which was obtained from the NAB data corpus [28]. It also features artificially generated anomalies, but of different traits than in the anomalies jumps-up dataset. In particular, these represent abrupt individual spikes, providing a basis for the evaluation of both the point-based and the contextual anomaly detection.
- aerOS cluster IE traces: resource utilization traces of a single IE that were collected using the self-awareness component in the aerOS continuum. They span 87 observations obtained during one hour. Although these traces do not exhibit any substantially abrupt behaviors, they were selected for the analysis since they closely resemble the conditions on which the self-optimization algorithms are to operate.
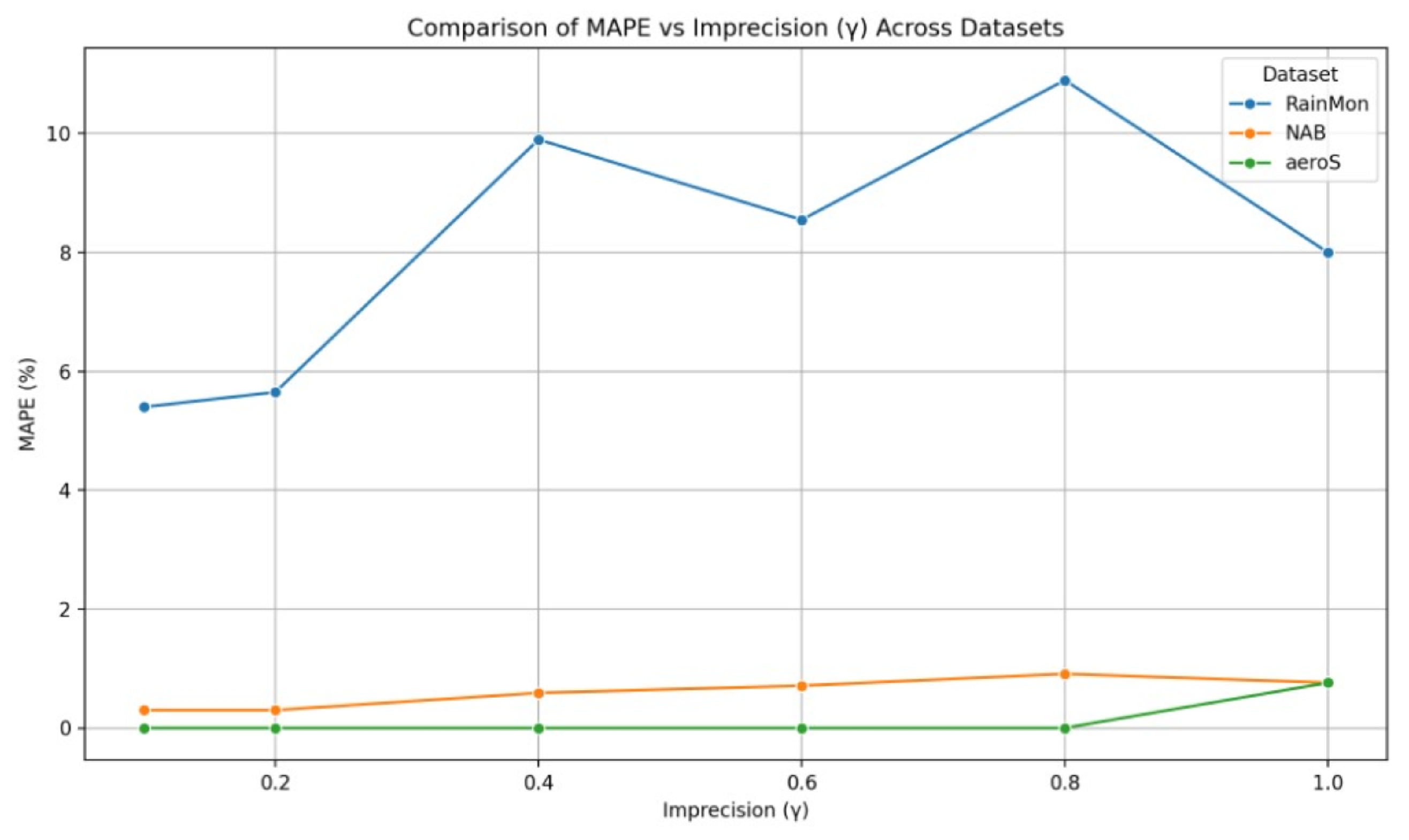
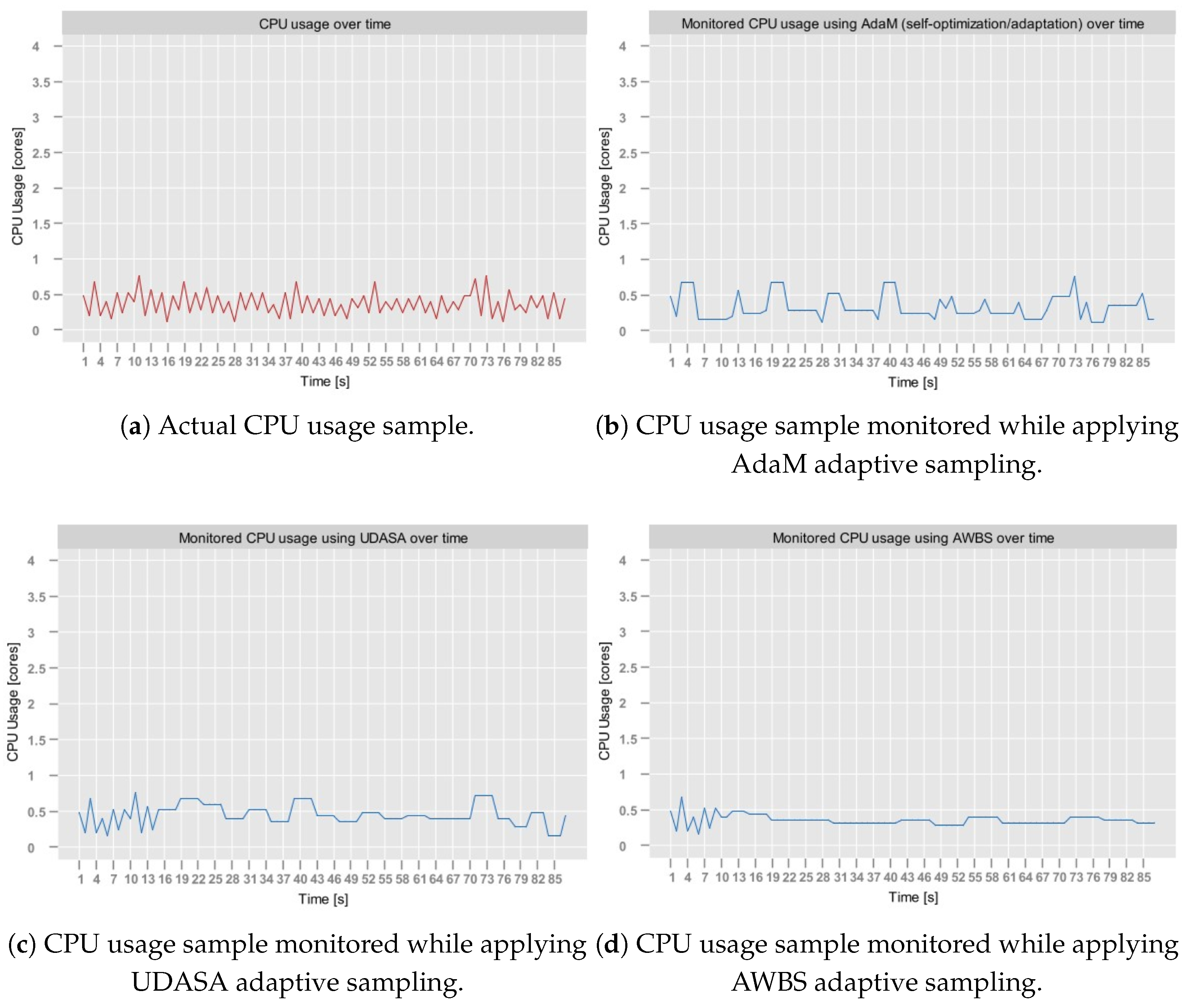
4.1. Sampling Model Verification
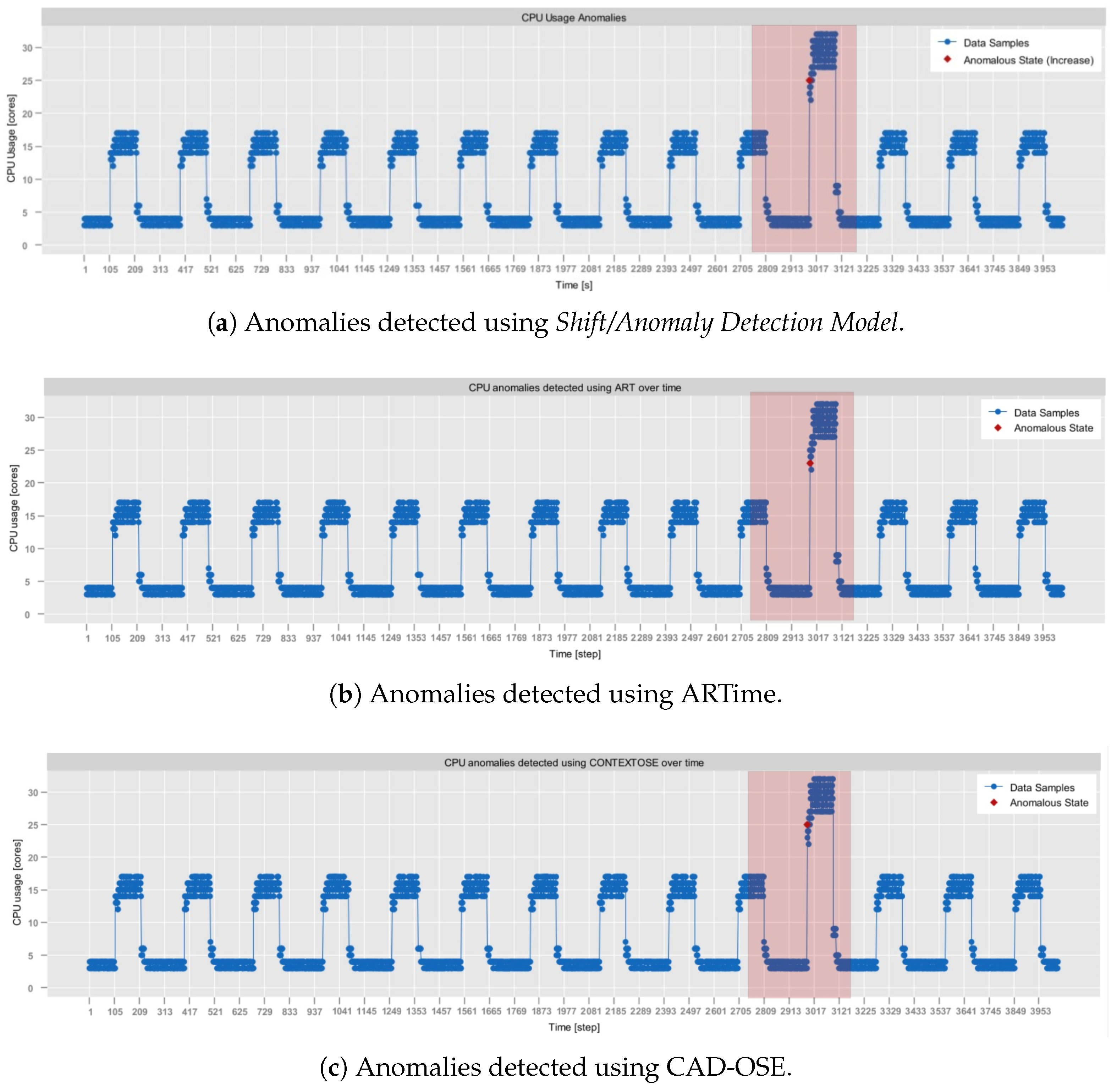
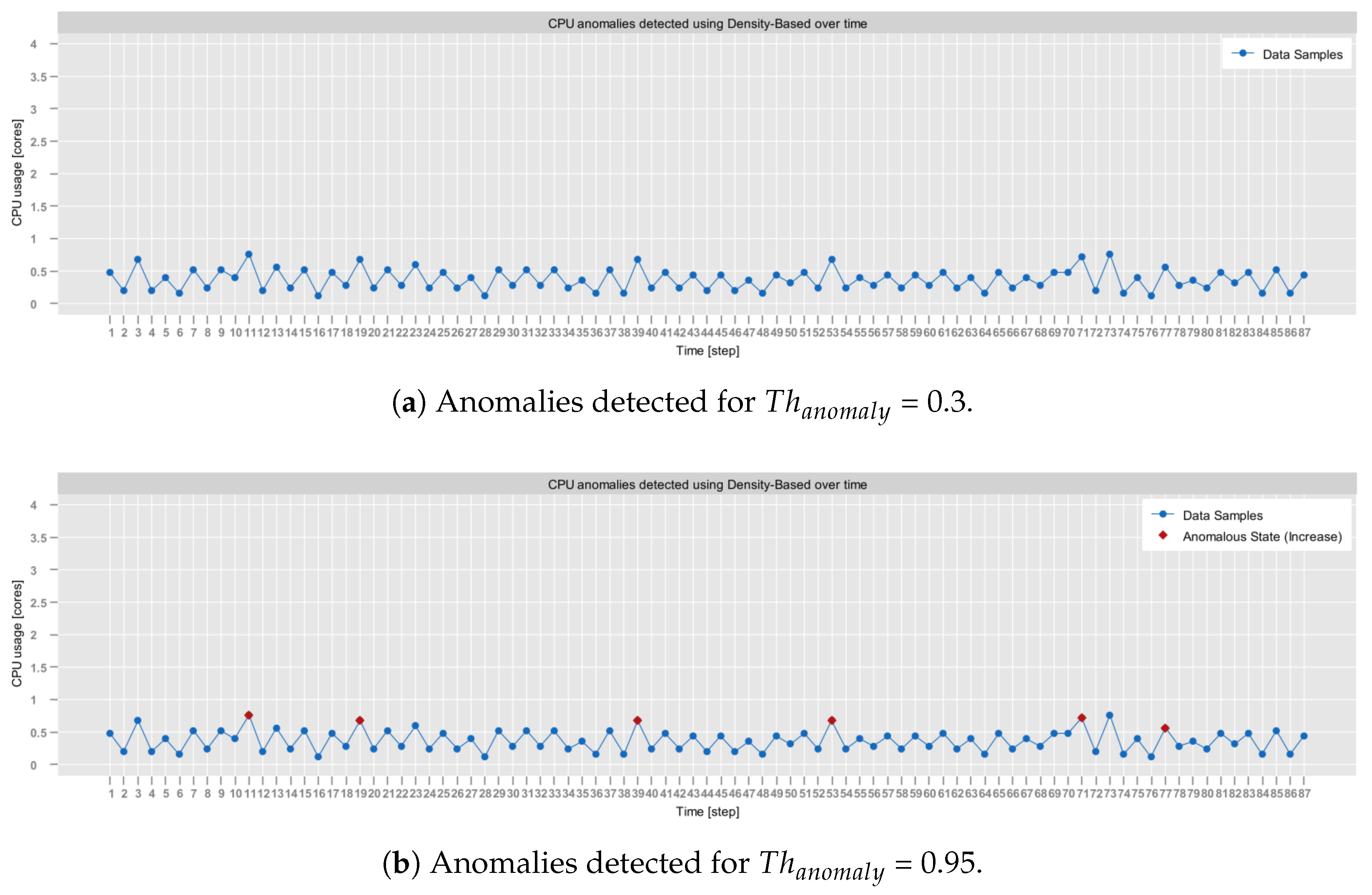
4.2. Shift/Anomaly Detection Model Verification
5. Limitations
6. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| IoT | Internet of Things |
| ECC | Edge–Cloud Continuum |
| SLA | Service Level Agreement |
| NAB | Numenta Anomaly Benchmark |
| PEWMA | Probabilistic Exponential Moving Average |
| HiTL | Human in The Loop |
| IE | Infrastructure Element |
| AWBS | Adaptive Window-Based Sampling |
| UDASA | User-Driven Adaptive Sampling Algorithm |
| QoS | Quality of Service |
| MAD | Median Absolute Deviation |
| AdaM | Adaptive Monitoring Framework |
| MAPE | Mean Absolute Percentage Error |
| SR | Sample Ratio |
| JPM | Joint-Performance Metric |
References
- Gkonis, P.; Giannopoulos, A.; Trakadas, P.; Masip-Bruin, X.; D’Andria, F. A Survey on IoT-Edge-Cloud Continuum Systems: Status, Challenges, Use Cases, and Open Issues. Future Internet 2023, 15, 383. [Google Scholar] [CrossRef]
- Trigka, M.; Dritsas, E. Edge and Cloud Computing in Smart Cities. Future Internet 2025, 17, 118. [Google Scholar] [CrossRef]
- Belcastro, L.; Marozzo, F.; Orsino, A.; Talia, D.; Trunfio, P. Edge-Cloud Continuum Solutions for Urban Mobility Prediction and Planning. IEEE Access 2023, 11, 38864–38874. [Google Scholar] [CrossRef]
- Xu, Y.; He, H.; Liu, J.; Shen, Y.; Taleb, T.; Shiratori, N. IDADET: Iterative Double-Sided Auction-Based Data-Energy Transaction Ecosystem in Internet of Vehicles. IEEE Internet Things J. 2023, 10, 10113–10130. [Google Scholar] [CrossRef]
- Ying, J.; Hsieh, J.; Hou, D.; Hou, J.; Liu, T.; Zhang, X.; Wang, Y.; Pan, Y.T. Edge-enabled cloud computing management platform for smart manufacturing. In Proceedings of the 2021 IEEE International Workshop on Metrology for Industry 4.0 & IoT (MetroInd4.0&IoT), Rome, Italy, 7–9 June 2021; pp. 682–686. [Google Scholar] [CrossRef]
- Boiko, O.; Komin, A.; Malekian, R.; Davidsson, P. Edge-Cloud Architectures for Hybrid Energy Management Systems: A Comprehensive Review. IEEE Sens. J. 2024, 24, 15748–15772. [Google Scholar] [CrossRef]
- Fu, W.; Wan, Y.; Qin, J.; Kang, Y.; Li, L. Privacy-Preserving Optimal Energy Management for Smart Grid With Cloud-Edge Computing. IEEE Trans. Ind. Inform. 2022, 18, 4029–4038. [Google Scholar] [CrossRef]
- Dhifaoui, S.; Houaidia, C.; Saidane, L.A. Cloud-Fog-Edge Computing in Smart Agriculture in the Era of Drones: A systematic survey. In Proceedings of the 2022 IEEE 11th IFIP International Conference on Performance Evaluation and Modeling in Wireless and Wired Networks (PEMWN), Rome, Italy, 8–10 November 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Yousif, M. The Edge, the Cloud, and the Continuum. In Proceedings of the 2022 Cloud Continuum, Los Alamitos, CA, USA, 5 December 2022; pp. 1–2. [Google Scholar] [CrossRef]
- Weinman, J. Trade-Offs Along the Cloud-Edge Continuum. In Proceedings of the 2022 Cloud Continuum, Los Alamitos, CA, USA, 5 December 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 12, pp. 1–7. [Google Scholar] [CrossRef]
- Kong, X.; Wu, Y.; Wang, H.; Xia, F. Edge Computing for Internet of Everything: A Survey. IEEE Internet Things J. 2022, 9, 23472–23485. [Google Scholar] [CrossRef]
- Alalawi, A.; Al-Omary, A. Cloud Computing Resources: Survey of Advantage, Disadvantages and Pricing. In Proceedings of the 2020 International Conference on Data Analytics for Business and Industry: Way Towards a Sustainable Economy (ICDABI), Sakheer, Bahrain, 26–27 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- George, A.S.; George, A.S.H.; Baskar, T. Edge Computing and the Future of Cloud Computing: A Survey of Industry Perspectives and Predictions. Partners Univers. Int. Res. J. 2023, 2, 19–44. [Google Scholar] [CrossRef]
- Azmy, S.B.; El-Khatib, R.F.; Zorba, N.; Hassanein, H.S. Extreme Edge Computing Challenges on the Edge-Cloud Continuum. In Proceedings of the 2024 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Kingston, ON, Canada, 6–9 August 2024; pp. 99–100. [Google Scholar] [CrossRef]
- Vaño, R.; Lacalle, I.; Sowiński, P.; S-Julián, R.; Palau, C.E. Cloud-Native Workload Orchestration at the Edge: A Deployment Review and Future Directions. Sensors 2023, 23, 2215. [Google Scholar] [CrossRef]
- Chiang, Y.; Zhang, Y.; Luo, H.; Chen, T.Y.; Chen, G.H.; Chen, H.T.; Wang, Y.J.; Wei, H.Y.; Chou, C.T. Management and Orchestration of Edge Computing for IoT: A Comprehensive Survey. IEEE Internet Things J. 2023, 10, 14307–14331. [Google Scholar] [CrossRef]
- Karami, A.; Karami, M. Edge computing in big data: Challenges and benefits. Int. J. Data Sci. Anal. 2025, 20, 6183–6226. [Google Scholar] [CrossRef]
- Andriulo, F.C.; Fiore, M.; Mongiello, M.; Traversa, E.; Zizzo, V. Edge Computing and Cloud Computing for Internet of Things: A Review. Informatics 2024, 11, 71. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, C.; Li, X.; Han, Y. Runtime reconfiguration of data services for dealing with out-of-range stream fluctuation in cloud-edge environments. Digit. Commun. Netw. 2022, 8, 1014–1026. [Google Scholar] [CrossRef]
- Sheikh, A.M.; Islam, M.R.; Habaebi, M.H.; Zabidi, S.A.; Bin Najeeb, A.R.; Kabbani, A. A Survey on Edge Computing (EC) Security Challenges: Classification, Threats, and Mitigation Strategies. Future Internet 2025, 17, 175. [Google Scholar] [CrossRef]
- Kephart, J.; Chess, D. The Vision Of Autonomic Computing. Computer 2003, 36, 41–50. [Google Scholar] [CrossRef]
- S-Julián, R.; Lacalle Úbeda, I.; Vaño, R.; Boronat, F.; Palau, C. Self-* Capabilities of Cloud-Edge Nodes: A Research Review. Sensors 2023, 23, 2931. [Google Scholar] [CrossRef] [PubMed]
- Jayakumar, V.K.; Lee, J.; Kim, I.K.; Wang, W. A Self-Optimized Generic Workload Prediction Framework for Cloud Computing. In Proceedings of the 2020 IEEE International Parallel and Distributed Processing Symposium (IPDPS), New Orleans, LO, USA, 18–22 May 2020; pp. 779–788. [Google Scholar] [CrossRef]
- Betancourt, V.P.; Kirschner, M.; Kreutzer, M.; Becker, J. Policy-Based Task Allocation at Runtime for a Self-Adaptive Edge Computing Infrastructure. In Proceedings of the 2023 IEEE 15th International Symposium on Autonomous Decentralized System (ISADS), Mexico City, Mexico, 15–17 March 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Krzysztoń, E.; Rojek, I.; Mikołajewski, D. A Comparative Analysis of Anomaly Detection Methods in IoT Networks: An Experimental Study. Appl. Sci. 2024, 14, 11545. [Google Scholar] [CrossRef]
- De Oliveira, E.A.; Rocha, A.; Mattoso, M.; Delicato, F. Latency and Energy-Awareness in Data Stream Processing for Edge Based IoT Systems. J. Grid Comput. 2022, 20, 27. [Google Scholar] [CrossRef]
- Giouroukis, D.; Dadiani, A.; Traub, J.; Zeuch, S.; Markl, V. A Survey of Adaptive Sampling and Filtering Algorithms for the Internet of Things. In Proceedings of the DEBS ’20: 14th ACM International Conference on Distributed and Event-Based Systems, Montreal, QC, Canada, 13–17 July 2020. [Google Scholar]
- Lavin, A.; Ahmad, S. Evaluating Real-Time Anomaly Detection Algorithms – The Numenta Anomaly Benchmark. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015; pp. 38–44. [Google Scholar] [CrossRef]
- Hafeez, T.; McArdle, G.; Xu, L. Adaptive Window Based Sampling on The Edge for Internet of Things Data Streams. In Proceedings of the 2020 11th International Conference on Network of the Future (NoF), Bordeaux, France, 12–14 October 2020; pp. 105–109. [Google Scholar] [CrossRef]
- Kim-Hung, L.; Le-Trung, Q. User-Driven Adaptive Sampling for Massive Internet of Things. IEEE Access 2020, 8, 135798–135810. [Google Scholar] [CrossRef]
- Singh, S.; Chana, I.; Singh, M.; Buyya, R. SOCCER: Self-Optimization of Energy-efficient Cloud Resources. Clust. Comput. 2016, 19, 1787–1800. [Google Scholar] [CrossRef]
- Kumar, A.; Lal, M.; Kaur, S. An autonomic resource management system for energy efficient and quality of service aware resource scheduling in cloud environment. Concurr. Comput. Pract. Exp. 2023, 35, e7699. [Google Scholar] [CrossRef]
- Mordacchini, M.; Ferrucci, L.; Carlini, E.; Kavalionak, H.; Coppola, M.; Dazzi, P. Self-organizing Energy-Minimization Placement of QoE-Constrained Services at the Edge. In Proceedings of the Economics of Grids, Clouds, Systems, and Services, Virtual Event, 21–23 September 2020; Tserpes, K., Altmann, J., Bañares, J.Á., Agmon Ben-Yehuda, O., Djemame, K., Stankovski, V., Tuffin, B., Eds.; Springer: Cham, Switzerland, 2021; pp. 133–142. [Google Scholar]
- Trihinas, D.; Pallis, G.; Dikaiakos, M.D. AdaM: An adaptive monitoring framework for sampling and filtering on IoT devices. In Proceedings of the 2015 IEEE International Conference on Big Data (Big Data), Santa Clara, CA, USA, 29 October–1 November 2015; pp. 717–726. [Google Scholar] [CrossRef]
- Zhang, D.; Ni, C.; Zhang, J.; Zhang, T.; Yang, P.; Wang, J.; Yan, H. A Novel Edge Computing Architecture Based on Adaptive Stratified Sampling. Comput. Commun. 2022, 183, 121–135. [Google Scholar] [CrossRef]
- Lou, P.; Shi, L.; Zhang, X.; Xiao, Z.; Yan, J. A Data-Driven Adaptive Sampling Method Based on Edge Computing. Sensors 2020, 20, 2174. [Google Scholar] [CrossRef] [PubMed]
- Choi, D.Y.; Kim, S.W.; Choi, M.A.; Geem, Z.W. Adaptive Kalman Filter Based on Adjustable Sampling Interval in Burst Detection for Water Distribution System. Water 2016, 8, 142. [Google Scholar] [CrossRef]
- Hawkins, D.M. Identification of Outliers; Springer: Berlin/Heidelberg, Germany, 1980; Volume 11. [Google Scholar]
- Das, R.; Luo, T. LightESD: Fully-Automated and Lightweight Anomaly Detection Framework for Edge Computing. In Proceedings of the 2023 IEEE International Conference on Edge Computing and Communications (EDGE), Chicago, IL, USA, 2–8 July 2023; pp. 150–158. [Google Scholar] [CrossRef]
- Kim, T.; Park, C.H. Anomaly pattern detection for streaming data. Expert Syst. Appl. 2020, 149, 113252. [Google Scholar] [CrossRef]
- Liu, X.; Lai, Z.; Wang, X.; Huang, L.; Nielsen, P.S. A Contextual Anomaly Detection Framework for Energy Smart Meter Data Stream. In Proceedings of the Neural Information Processing, Vancouver, BC, Canada, 6–12 December 2020; Yang, H., Pasupa, K., Leung, A.C.S., Kwok, J.T., Chan, J.H., King, I., Eds.; Springer: Cham, Switzerland, 2020; pp. 733–742. [Google Scholar]
- Jain, P.; Jain, S.; Zaïane, O.R.; Srivastava, A. Anomaly Detection in Resource Constrained Environments with Streaming Data. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 649–659. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation Forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar] [CrossRef]
- Shirazi, S.N.; Simpson, S.; Gouglidis, A.; Mauthe, A.; Hutchison, D. Anomaly Detection in the Cloud Using Data Density. In Proceedings of the 2016 IEEE 9th International Conference on Cloud Computing (CLOUD), San Francisco, CA, USA, 27 June–2 July 2016; pp. 616–623. [Google Scholar] [CrossRef]
- Garcia-Martin, E.; Bifet, A.; Lavesson, N.; König, R.; Linusson, H. Green Accelerated Hoeffding Tree. arXiv 2022, arXiv:2205.03184. [Google Scholar] [CrossRef]
- Manapragada, C.; Webb, G.I.; Salehi, M. Extremely Fast Decision Tree. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, New York, NY, USA, 19–23 August 2018; KDD ’18. pp. 1953–1962. [Google Scholar] [CrossRef]
- Lu, T.; Wang, L.; Zhao, X. Review of Anomaly Detection Algorithms for Data Streams. Appl. Sci. 2023, 13, 6353. [Google Scholar] [CrossRef]
- OpenFaas. Available online: https://www.openfaas.com/ (accessed on 28 September 2025).
- Angelov, P.; Yager, R. Simplified fuzzy rule-based systems using non-parametric antecedents and relative data density. In Proceedings of the 2011 IEEE Workshop on Evolving and Adaptive Intelligent Systems (EAIS), Paris, France, 14–15 April 2011; pp. 62–69. [Google Scholar] [CrossRef]
- Shafer, I.; Ren, K.; Boddeti, V.N.; Abe, Y.; Ganger, G.R.; Faloutsos, C. RainMon: An integrated approach to mining bursty timeseries monitoring data. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; ACM: New York, NY, USA, 2012. KDD ’12. pp. 1158–1166. [Google Scholar] [CrossRef]
- Contextual Anomaly Detector for NAB. Available online: https://github.com/smirmik/CAD (accessed on 8 May 2025).
- ARTime Anomaly Detector for NAB. Available online: https://github.com/markNZed/ARTimeNAB.jl (accessed on 8 May 2025).





| Algorithm | Adaptation Target | Method | Batch- Based | General Purpose | Extra Storage |
|---|---|---|---|---|---|
| AWBS [29] | window size | moving average | X | X | |
| ApproxECIoT [35] | window size | standard deviation | X | ||
| UDASA [30] | sampling period | MAD | X | X | |
| AdaM [34] | sampling period | PEWMA | X | ||
| Linear Regression [36] | sampling period | linear regression | X | X | X |
| Kalman Sampling [37] | sampling period | Kalman filter | X | X | X |
| Algorithm | Mode | Anomaly Type | Method | Concept Drift | Extra Storage |
|---|---|---|---|---|---|
| LightESD [39] | semi-online | contextual | periodograms | X | X |
| APD-HT/CC [40] | offline | contextual | k-means | X | |
| CAD [41] | semi-online | contextual | LSTM | X | X |
| PiForest [42] | online | point/contextual | decision tree | X | X |
| Density-based [44] | online | point | data density | X | |
| EFDT [45] | online | point | decision tree | X |
| Symbol | Description |
|---|---|
| Observed value at time i. | |
| N | Size of the sample. |
| K | Number of consecutive observations of the same state (i.e., anomalous or normal). |
| Sample mean at the time i. | |
| Sample scalar product at the time i. | |
| Density at the time i. | |
| Average density at the time i. | |
| Difference between consecutive densities at the time i. | |
| Threshold/tolerance weight put on the average density during the transition to the anomalous state. | |
| Threshold/tolerance weight put on the average density during the transition to the normal state. | |
| Window of consecutive observations that must be determined as anomalies in order to switch to the anomalous state. | |
| Window of consecutive observations that must be determined as normal in order to switch to the normal state. |
| Symbol | Description |
|---|---|
| Observed value at time i. | |
| N | Size of the sample. |
| Distance between two consecutive observation at time i. | |
| PEWMA representing the estimated metric stream evolution at time i. | |
| PEWMA of the squared values (second-order statistic) at time i. | |
| Standard deviation at time i. | |
| Moving standard deviation at time i. | |
| Confidence interval that measures the accuracy of metric evolution estimation at time i. | |
| Probability of at time i. | |
| Sampling period estimated at time i. | |
| Minimal sampling period value. | |
| Maximal sampling period value. | |
| Optimal multiplicity that scales the estimated sampling period value. | |
| Imprecision used to calculate the acceptable confidence of the estimation. | |
| Weighting factor put on the value in PEWMA calculation. | |
| Weighting factor put on the probability in PEWMA calculation. |
| Results for RainMon Dataset. | |||
|---|---|---|---|
| MAPE | SR | JPM | |
| 0.1 | 5.40% | 56.62% | 68.98% |
| 0.2 | 5.65% | 47.87% | 73.24% |
| 0.3 | 9.15% | 49.87% | 70.48% |
| 0.4 | 9.9% | 40.12% | 74.99% |
| 0.5 | 9.91% | 37.12% | 76.48% |
| 0.6 | 8.55% | 37.12% | 77.16% |
| 0.7 | 11.92% | 34.62% | 76.72% |
| 0.8 | 10.9% | 37% | 76.05% |
| 0.9 | 10.92% | 36.75% | 76.16% |
| 1.0 | 8% | 45% | 73.5% |
| Results for NAB (Anomaly Jumps-Up) Dataset. | |||
| MAPE | SR | JPM | |
| 0.1 | 0.42% | 49.45% | 75.06% |
| 0.2 | 0.3% | 43.32% | 78.18% |
| 0.3 | 0.34% | 38.29% | 80.67% |
| 0.4 | 0.59% | 33.11% | 83.14% |
| 0.5 | 1.11% | 28.62% | 85.13% |
| 0.6 | 0.71% | 27.38% | 85.94% |
| 0.7 | 0.24% | 27.03% | 86.35% |
| 0.8 | 0.91% | 27.13% | 85.97% |
| 0.9 | 0.44% | 27.33% | 86.11% |
| 1.0 | 0.76% | 30.05% | 84.58% |
| Results for aerOS Dataset. | |||
| MAPE | SR | JPM | |
| 0.1 | 0% | 100% | 50% |
| 0.2 | 0% | 98.85% | 50.57% |
| 0.3 | 0.38% | 93.10% | 53.25% |
| 0.4 | 1.14% | 86.20% | 56.31% |
| 0.5 | 3.06% | 81.60% | 57.65% |
| 0.6 | 4.98% | 60.91% | 66.54% |
| 0.7 | 0.38% | 95.40% | 51.93% |
| 0.8 | 0% | 86.20% | 50.57% |
| 0.9 | 0% | 87.35% | 56.32% |
| 1.0 | 0.76% | 87.35% | 55.94% |
| Results for RainMon Dataset. | |||
|---|---|---|---|
| MAPE | SR | JPM | |
| 500 | 5.27% | 51.37% | 71.67% |
| 1000 | 8.55% | 37.12% | 77.16% |
| 2000 | 14.92% | 29.75% | 77.66% |
| 3000 | 14.28% | 24.37% | 80.67% |
| Results for NAB (Anomaly Jumps-Up) Dataset. | |||
| MAPE | SR | JPM | |
| 500 | 0.64% | 36.48% | 81.43% |
| 1000 | 0.71% | 27.38% | 85.94% |
| 2000 | 0.94% | 23.31% | 87.87% |
| 3000 | 0.74% | 21.97% | 88.64% |
| Results for aerOS Dataset. | |||
| MAPE | SR | JPM | |
| 500 | 0% | 91.95% | 54.022% |
| 1000 | 4.98% | 60.91% | 66.54% |
| 2000 | 1.91% | 75.86% | 61.11% |
| 3000 | 2.68% | 41.37% | 77.96% |
| Results for RainMon Dataset. | |||
|---|---|---|---|
| Algorithm | MAPE | SR | JPM |
| AdaM (self-optimization) | 14.28% | 24.37% | 80.67% |
| UDASA | 9.41% | 37% | 76.79% |
| AWBS | 14.46% | 19% | 83.26% |
| Results for NAB (Anomaly Jumps-Up) Dataset. | |||
| Algorithm | MAPE | SR | JPM |
| AdaM (self-optimization) | 0.74% | 21.97% | 88.64% |
| UDASA | 0.79% | 35.19% | 82.0% |
| AWBS | 1.53% | 16.96% | 90.74% |
| Results for aerOS Dataset. | |||
| Algorithm | MAPE | SR | JPM |
| AdaM (self-optimization) | 2.68% | 41.37% | 77.96% |
| UDASA | 10.34% | 39.08% | 75.28% |
| AWBS | 8.74% | 30.1% | 80.58% |
| Results for NAB (Anomaly Jumps-Up) Dataset. | |
|---|---|
| S | |
| 0.1 | 0% |
| 0.2 | 0% |
| 0.3 | 93.12% |
| 0.4 | 90.61% |
| 0.5 | 87.57% |
| 0.6 | 65.43% |
| 0.7 | 19.15% |
| 0.8 | 9.99% |
| 0.9 | 3.12% |
| Results for NAB (Load Balancer Spikes) Dataset. | |
| S | |
| 0.1 | 0% |
| 0.2 | 73.48% |
| 0.3 | 72.42% |
| 0.4 | 59.89% |
| 0.5 | 44.96% |
| 0.6 | 27.32% |
| 0.7 | 6.73% |
| 0.8 | 1.24% |
| 0.9 | 0.44% |
| Results for Anomaly Jumps-Up Dataset. | |
|---|---|
| Algorithm | S |
| Density-based (self-optimization) | 93.12% |
| CAD-OSE | 93.10% |
| ARTime | 100% |
| Results for NAB (Load Balancer Spikes) Dataset. | |
| Algorithm | S |
| Density-based (self-optimization) | 62.42% |
| CAD-OSE | 52.82% |
| ARTime | 77.10% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wrona, Z.; Wasielewska-Michniewska, K.; Ganzha, M.; Paprzycki, M.; Watanobe, Y. Frugal Self-Optimization Mechanisms for Edge–Cloud Continuum. Sensors 2025, 25, 6556. https://doi.org/10.3390/s25216556
Wrona Z, Wasielewska-Michniewska K, Ganzha M, Paprzycki M, Watanobe Y. Frugal Self-Optimization Mechanisms for Edge–Cloud Continuum. Sensors. 2025; 25(21):6556. https://doi.org/10.3390/s25216556
Chicago/Turabian StyleWrona, Zofia, Katarzyna Wasielewska-Michniewska, Maria Ganzha, Marcin Paprzycki, and Yutaka Watanobe. 2025. "Frugal Self-Optimization Mechanisms for Edge–Cloud Continuum" Sensors 25, no. 21: 6556. https://doi.org/10.3390/s25216556
APA StyleWrona, Z., Wasielewska-Michniewska, K., Ganzha, M., Paprzycki, M., & Watanobe, Y. (2025). Frugal Self-Optimization Mechanisms for Edge–Cloud Continuum. Sensors, 25(21), 6556. https://doi.org/10.3390/s25216556










