Balance Control Method for Bipedal Wheel-Legged Robots Based on Friction Feedforward Linear Quadratic Regulator
Abstract
1. Introduction
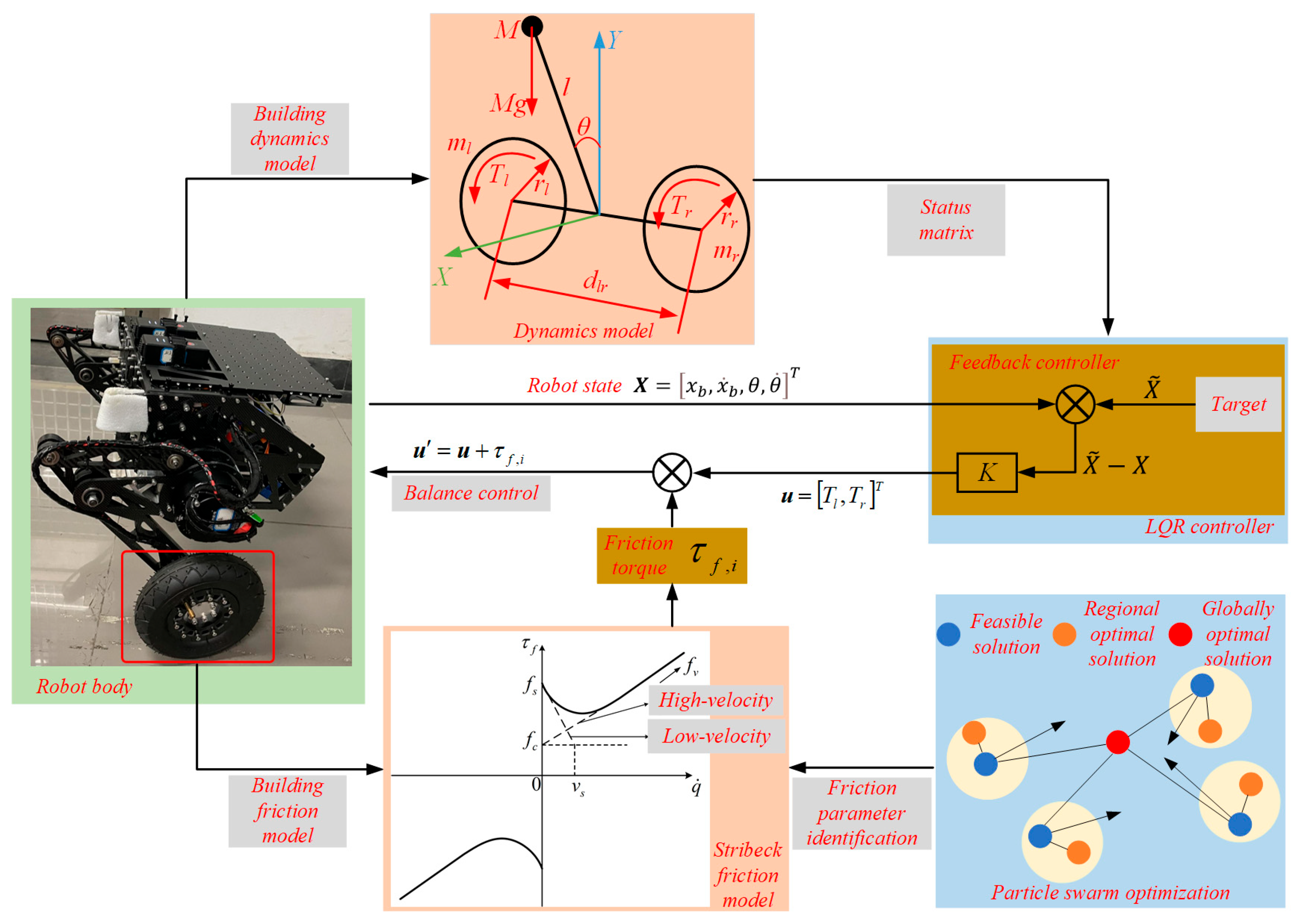
- In response to the challenges of traditional mobile robots in unstructured environments, this paper presents the design of a bipedal wheel-legged robot. To overcome balance and stability control challenges, an LQR balance control algorithm is developed based on a dynamics model. Recognizing the in-wheel motor friction’s significant impact on the dynamics model’s accuracy during low-speed movements, a Stribeck friction identification model is constructed. Building upon this friction model, a friction feedforward LQR balance control algorithm for bipedal wheel-legged robots is proposed to enhance the robot’s stability.
- To optimize the in-wheel motor friction parameters, a uniform-speed motion trajectory is designed to collect identification data. Utilizing the nonlinear friction identification model and data sequence, a PSO algorithm is proposed to identify the optimal friction parameter set.
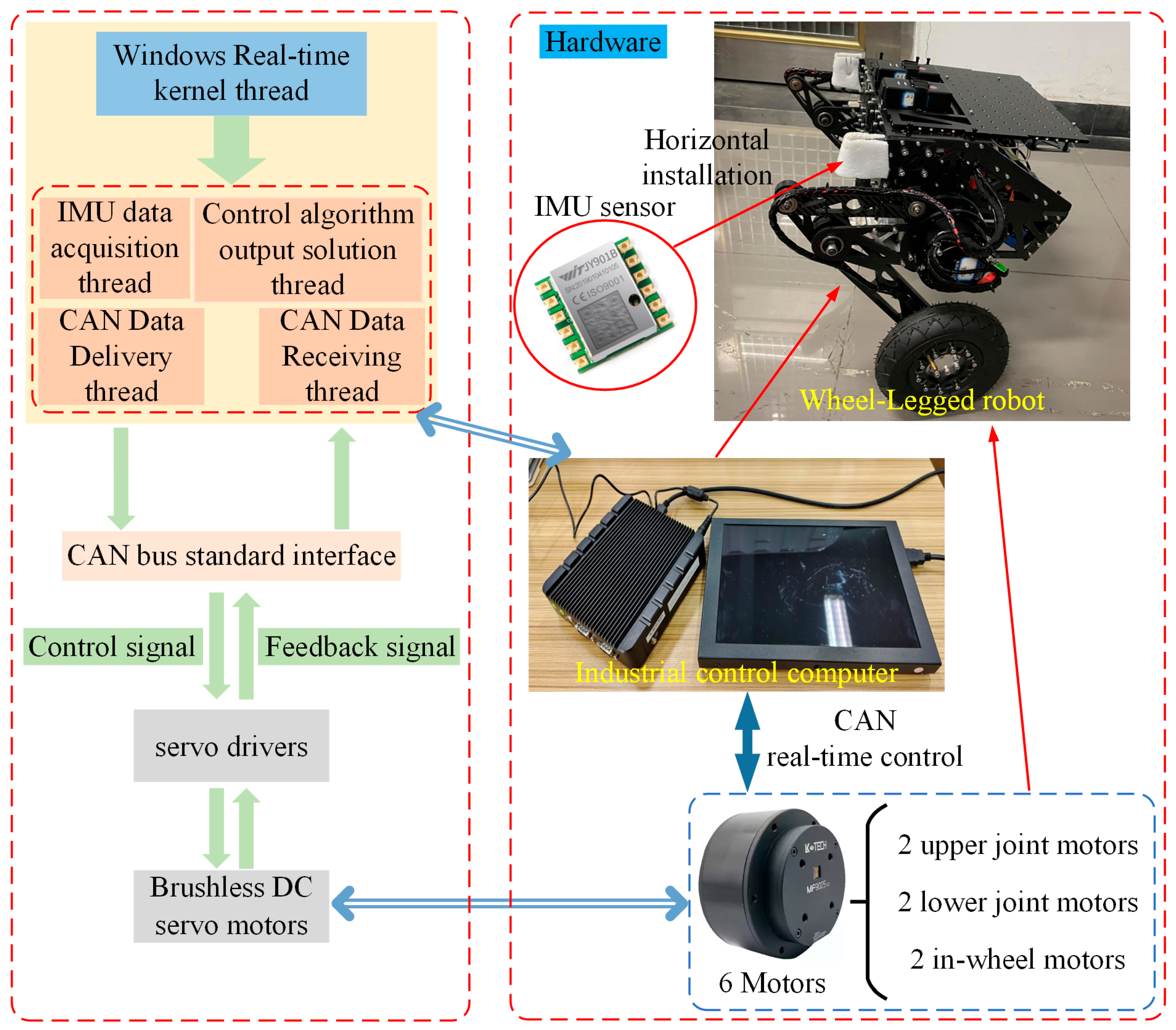
- An experimental platform for the wheel-legged robot is constructed, integrating the bipedal wheel-legged robot with an IMU sensor system and an industrial control computer equipped with a real-time operating system. Experiments on motor friction identification and speed tracking validate the proposed particle swarm optimized in-wheel motor friction parameter set’s effectiveness. Comparative experiments further confirm that the proposed friction feedforward LQR balance control algorithm reduces steady-state oscillations and enhances the robot’s stability.
2. Friction Feedforward LQR Balance Control Algorithm
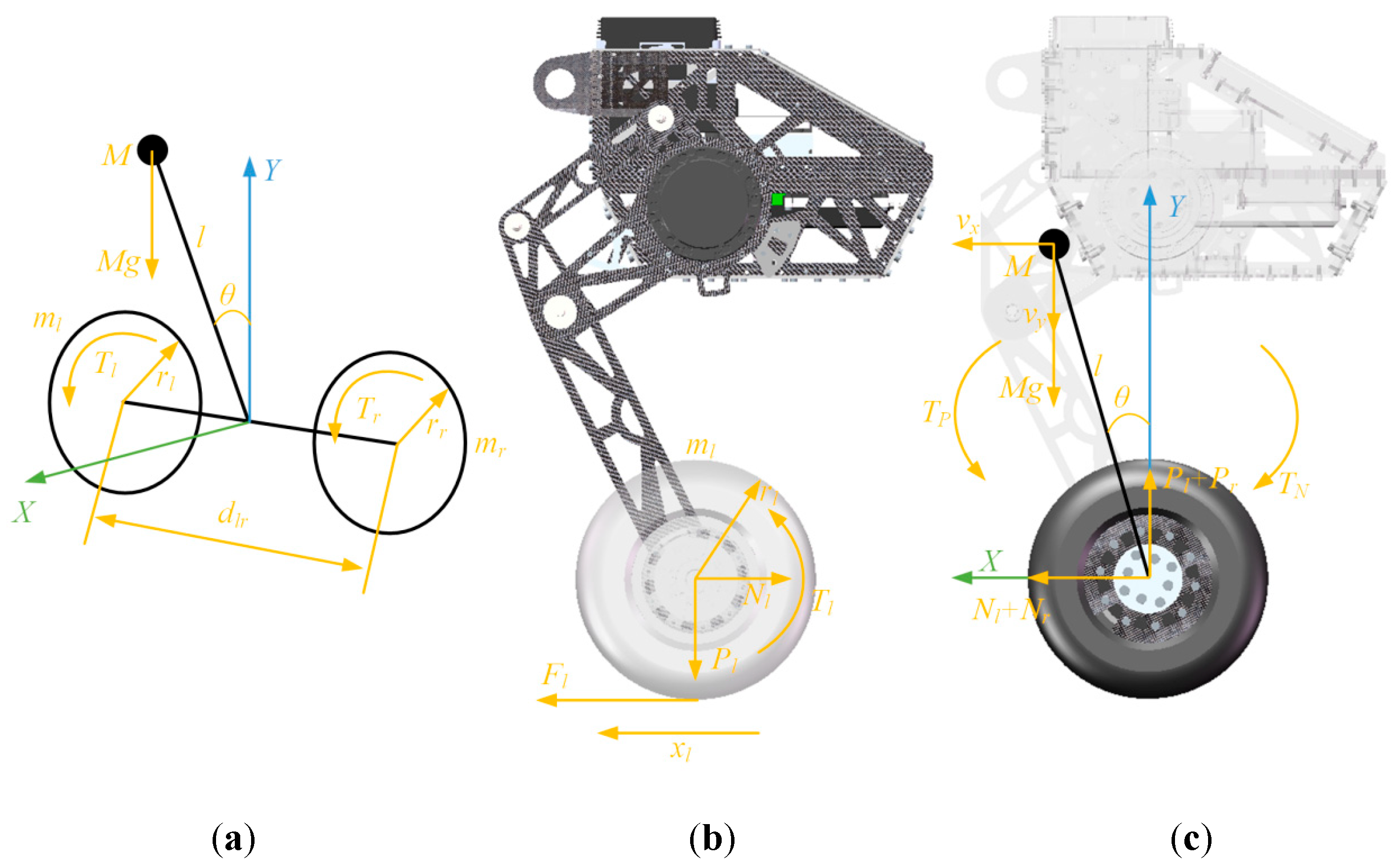
2.1. LQR Balance Controller Based on Dynamics Model
2.2. In-Wheel Motor Stribeck Friction Model
3. PSO for In-Wheel Motor Friction Parameter Identification Model
3.1. Establishing the Friction Identification Dataset
- Control the in-wheel motor i to move at a constant speed , collecting the motion speed and driving torque at a specified frequency during movement.
- Assume that 10 K data points are collected during motion, resulting in data sequences and .
- Remove the first K data points and the last K data points. Divide the remaining eight K stable sequences into eight segments, computing the mean for each segment to obtain eight actual motion speeds .
- Perform the same operation on the driving torque to obtain the corresponding friction torque for each speed .
- Select different motion speeds to generate excitation trajectories and repeat steps 1 to 4 to obtain the friction torques corresponding to different speeds.
- Generate the speed and friction torque sequence , where denotes the total number of data points.
3.2. Friction Parameter Identification Model Based on PSO
| Algorithm 1 Optimization process of particle swarm algorithm |
| Input: Velocity and friction data pair sequence Output: Optimal friction parameter set |
| 1. Initialize iterations t = 0, maximum iterations T 2: Initialize position permissible range xmin, xmax, Initialize velocity permissible range vmin, vmax 3: for particle i = 1 to N do 4: for dimension d = 1 to 6 do 5: Initialize position xid and velocity vid randomly within permissible range 6: end for 7: Initialize particle optimal position with xi 8: Calculate particle i fitness value 9: end for 10: Initialize global optimal position with the particle with the greatest fitness 11: for t = 0 to T do 12: for particle i = 1, N do 13: Calculate particle velocity according to 14: Update particle position according to 15: Update inertia factor 16: if position beyond permissible range then 17: Restores position in last iteration, Inverse velocity, Update position according to new velocity 18: end if 19: Calculate particle i current fitness value 20: if the fitness value is better than in history then 21: Set current fitness value as the 22: end if 23: end for 24: if the optimal fitness value is better than optimal particle in history then 25: Set optima fitness value as the 26: end if 27: if the optimal fitness value is less than the threshold twice break 28: end for 29: Save optimal fitness value as the optimal friction parameter set result |
- Algorithm Initialization:
- 2.
- Iterative Search for Optimal Parameter Solution:
- 3.
- Determination of Iteration Conditions:
4. Experiments and Analysis of Results
4.1. Experimental Platform for Balance Control of Bipedal Wheel-Legged Robot
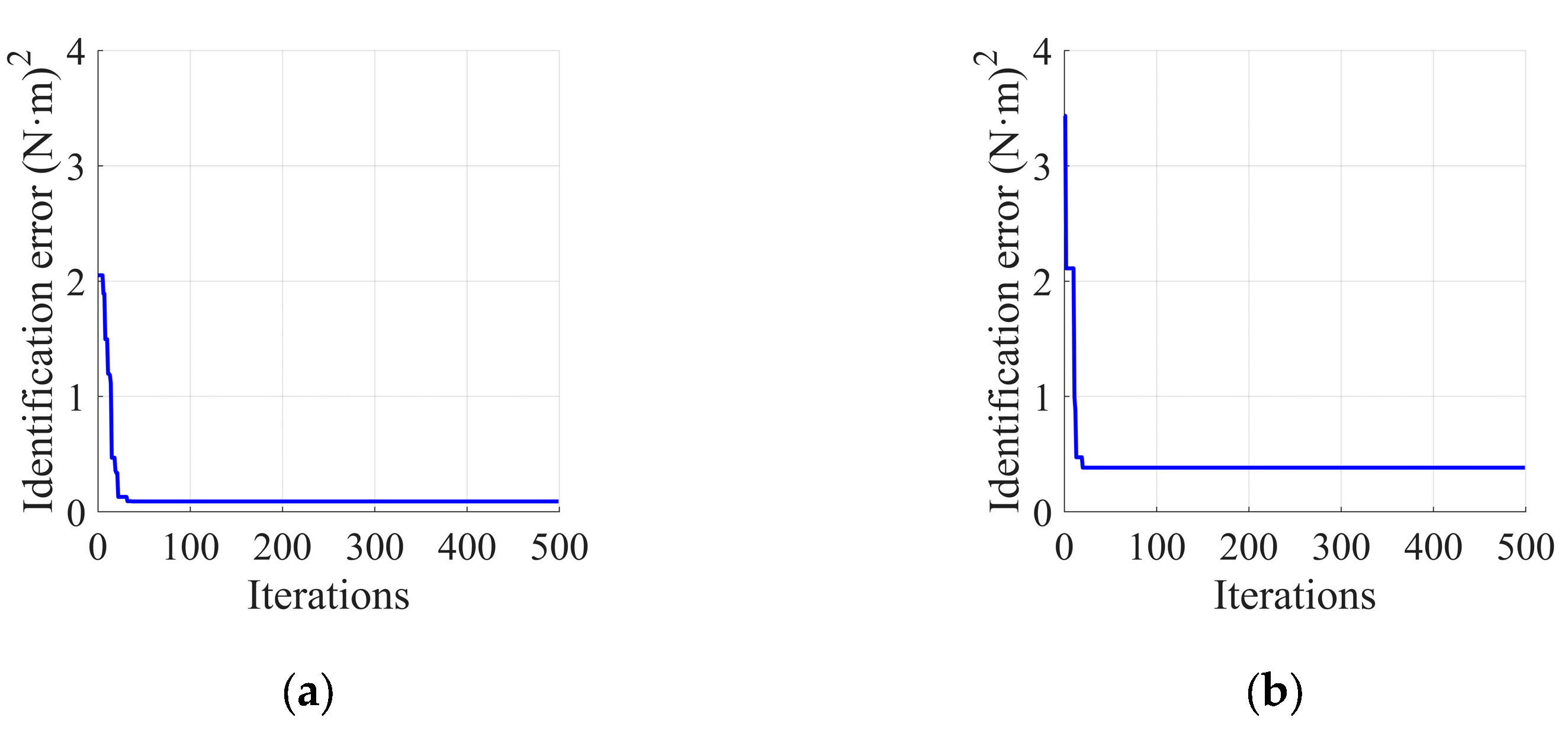
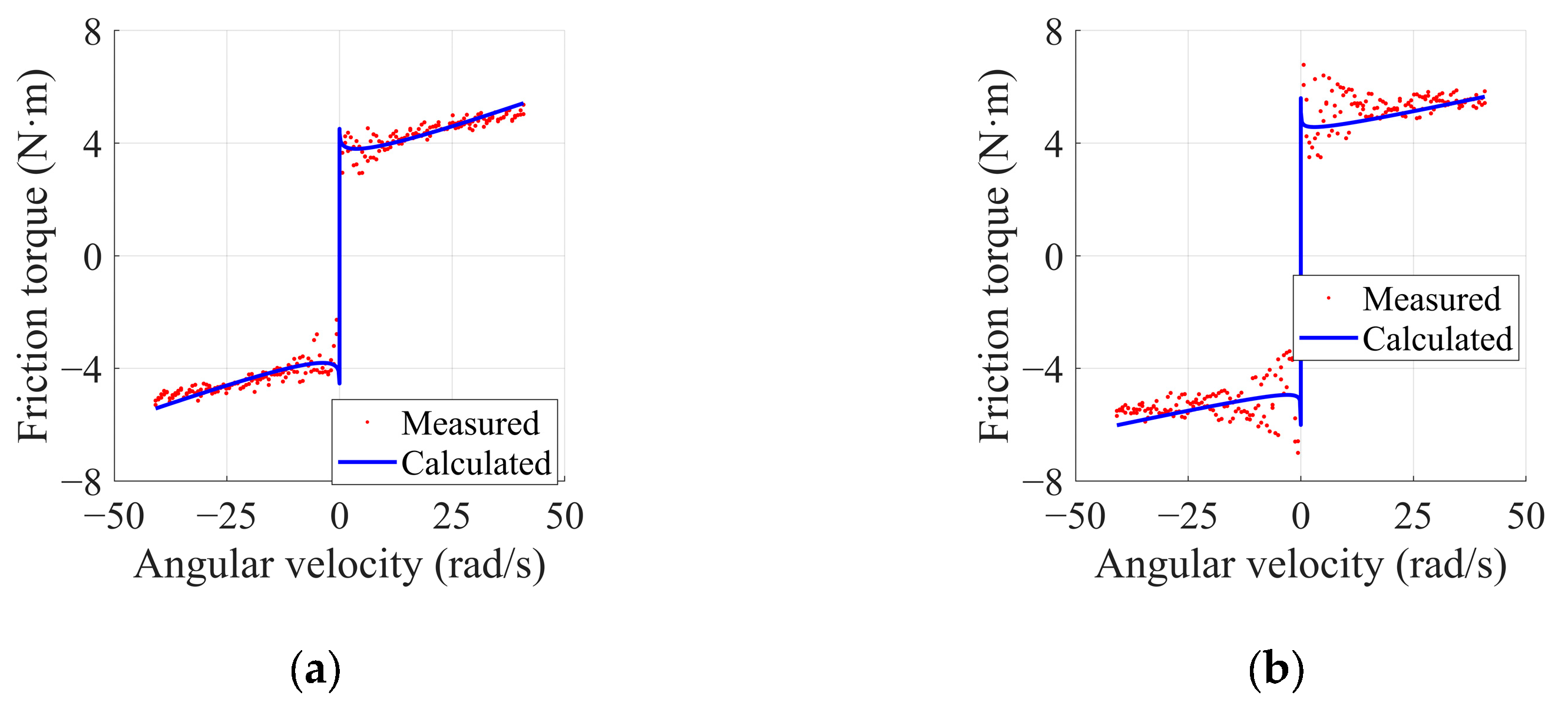
4.2. Experiment and Analysis of Results for Stribeck Friction Parameter Identification Based on PSO
4.3. Verification Experiment of Friction Identification Results Based on Speed Tracking and Analysis of Results
4.4. Experiments and Analysis of Results of Friction Feedforward LQR Balance Control
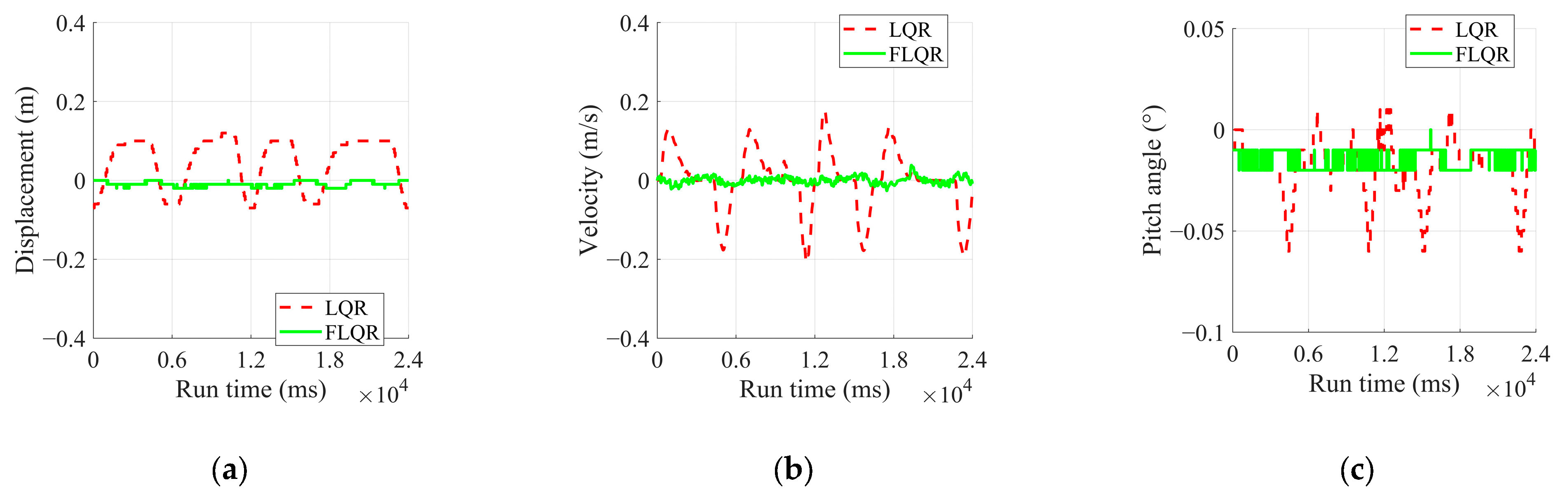
- Flat Ground Steady Point Balance Experiment
- 2.
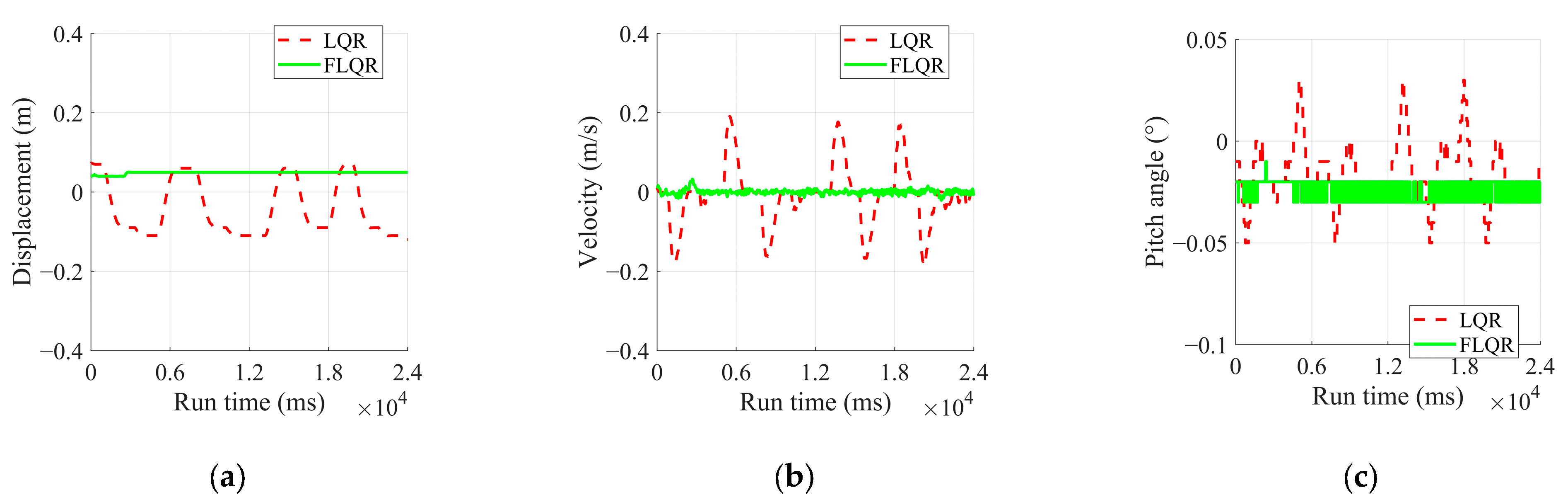
- Single-Sided Bridge Steady Point Balance Experiment
- 3.
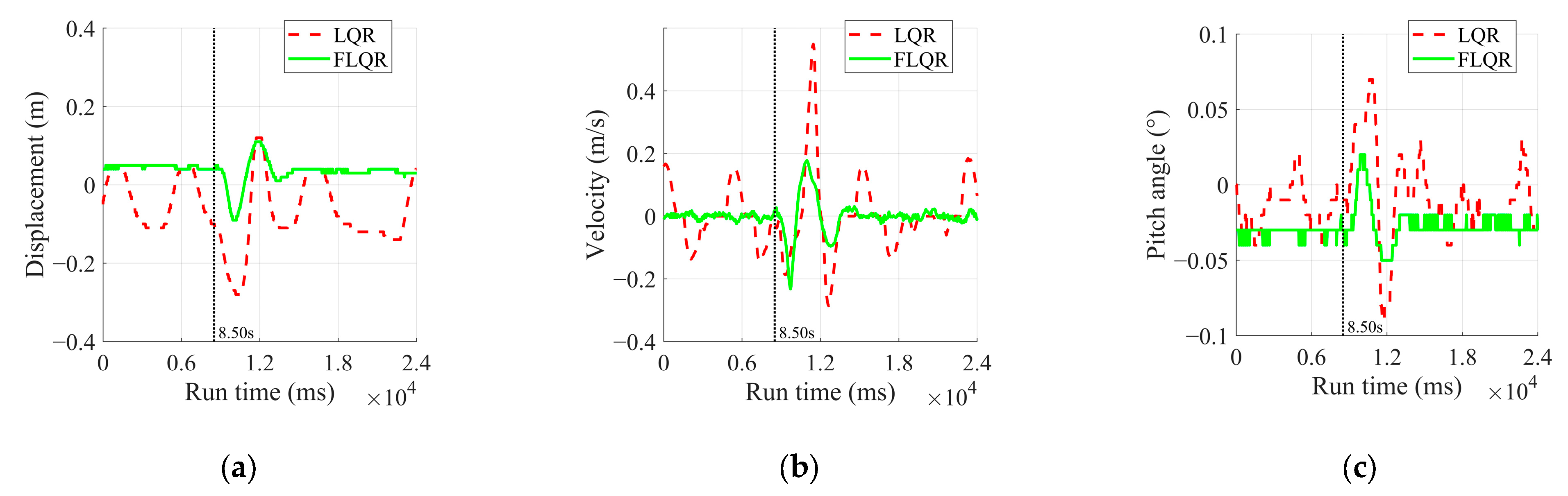
- Disturbance Rejection Experiment
5. Conclusions
- A bipedal wheel-legged robot platform, comprising the robot itself, an IMU sensor, and an industrial control computer with a real-time system, was developed to improve adaptability in unstructured environments. To enhance balance and stability, an LQR balance control algorithm was constructed based on the dynamics model. In-wheel motor friction, which significantly affects model accuracy during low-speed movements, needs to be compensated due to its tendency to cause poor convergence and oscillations. A Stribeck friction identification model for the motor was established, and an FLQR balance control algorithm was proposed to improve the robot’s stability.
- To optimize in-wheel motor friction parameters, a uniform-speed excitation trajectory was designed to collect data for friction identification. Using the nonlinear friction model and data sequences, a Particle Swarm Optimization (PSO) algorithm was employed to determine optimal friction parameters. The minimum standard deviation for friction identification is approximately 0.30, with the computed friction model values closely matching the actual values. The calculated friction torque aligns well with the measured torque. Without friction compensation, the motor could not track the target speed, whereas with friction compensation, the motor successfully tracked the target speed, validating the accuracy and effectiveness of the identification results.
- To validate the effectiveness of the proposed FLQR balance control algorithm in reducing steady-state oscillations and enhancing stability, balance experiments were conducted on flat ground, a single-sided bridge, and under disturbance conditions. The results indicate that the FLQR algorithm achieves effective convergence across these scenarios, with steady-state variance in displacement, velocity, and pitch angle being reduced by at least one order of magnitude compared to the LQR. Additionally, under identical external disturbances, FLQR exhibited a significantly lower disturbance range than LQR, demonstrating its effectiveness in mitigating steady-state oscillations and improving the robot’s robustness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qin, H.; Shao, S.; Wang, T.; Yu, X.; Jiang, Y.; Cao, Z. Review of Autonomous Path Planning Algorithms for Mobile Robots. Drones 2023, 7, 211. [Google Scholar] [CrossRef]
- Fragapane, G.; De Koster, R.; Sgarbossa, F.; Strandhagen, J.O. Planning and control of autonomous mobile robots for intralogistics: Literature review and research agenda. Eur. J. Oper. Res. 2021, 294, 405–426. [Google Scholar] [CrossRef]
- Choudhry, O.A.; Wasim, M.; Ali, A.; Choudhry, M.A.; Iqbal, J. Modelling and robust controller design for an underactuated self-balancing robot with uncertain parameter estimation. PLoS ONE 2023, 18, e0285495. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Sun, Y.; Wen, S.; Cao, K.; Qi, Q.; Zhang, X.; Shen, H.; Chen, G.; Xu, J.; Ji, A. Development of Wheel-Legged Biped Robots: A Review. J. Bionic Eng. 2024, 21, 607–634. [Google Scholar] [CrossRef]
- Feng, X.; Liu, S.; Yuan, Q.; Xiao, J.; Zhao, D. Research on wheel-legged robot based on LQR and ADRC. Sci. Rep. 2023, 13, 15122. [Google Scholar] [CrossRef] [PubMed]
- Pratama, G.N.P.; Yuwono, Y.C.H.; Surjono, H.D.; Sukardiyono, T.; Hidayatulloh, I. Comparing the Efficiency of State-Feedback Controllers in Stabilizing Two-Wheeled Robot. In Proceedings of the 2023 6th International Conference on Information and Communications Technology (ICOIACT), Yogyakarta, Indonesia, 10–11 November 2023; pp. 98–102. [Google Scholar]
- Alihosseini, A.; Dehkordi, N.M.; Sajjadi, M. Designing a free chattering robust nonlinear sliding mode control for underactuated two wheels mobile robots with disturbances and uncertainties. J. Vib. Control 2024, 30, 685–696. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Ri, S.; Xiong, C.; Li, Z.; Kang, Y. High-Order Disturbance-Observer-Based Sliding Mode Control for Mobile Wheeled Inverted Pendulum Systems. IEEE Trans. Ind. Electron. 2020, 67, 2030–2041. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.; Song, S.; Meng, M.Q.H. System design and balance control of a bipedal leg-wheeled robot. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1869–1874. [Google Scholar]
- Raza, F.; Owaki, D.; Hayashibe, M. Modeling and Control of a Hybrid Wheeled Legged Robot: Disturbance Analysis. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Boston, MA, USA, 6–9 July 2020; pp. 466–473. [Google Scholar]
- Kollarcík, A. Modeling and Control of Two-Legged Wheeled Robot. Master’s Thesis, Czech Technical University in Prague, Prague, Czech, 2021. Available online: https://wiki.control.fel.cvut.cz/mediawiki/images/9/92/Dp_2021_kollarcik_adam.pdf (accessed on 8 December 2024).
- Xin, Y.; Chai, H.; Li, Y.; Rong, X.; Li, B.; Li, Y. Speed and Acceleration Control for a Two Wheel-Leg Robot Based on Distributed Dynamics model and Whole-Body Control. IEEE Access 2019, 7, 180630–180639. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Salzmann, C.; Tschopp, F.; Bodie, K.; Gulich, L.; Küng, N.; Mannhart, D.; Pfister, C.; Vierneisel, M.; et al. Ascento: A Two-Wheeled Jumping Robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019. [Google Scholar]
- Zhang, Y.; Zhang, L.; Wang, W.; Li, Y.; Zhang, Q. Design and Implementation of a Two-Wheel and Hopping Robot with a Linkage Mechanism. IEEE Access 2018, 6, 42422–42430. [Google Scholar] [CrossRef]
- Klemm, V.; Morra, A.; Gulich, L.; Mannhart, D.; Rohr, D.; Kamel, M.; de Viragh, Y.; Siegwart, R. LQR-Assisted Whole-Body Control of a Wheeled Bipedal Robot with Kinematic Loops. IEEE Robot. Autom. Lett. 2020, 5, 3745–3752. [Google Scholar] [CrossRef]
- Xin, S.Y.; Vijayakumar, S. Online Dynamic Motion Planning and Control for Wheeled Biped Robots. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; pp. 3892–3899. [Google Scholar]
- Wang, Y.; Xin, Y.; Rong, X.; Li, Y. Whole-body Motion Planning and Control for Underactuated Wheeled-bipdal Robots. In Proceedings of the IEEE International Conference on Robotics and Biomimetics (IEEE ROBIO), Sanya, China, 27–31 December 2021. [Google Scholar]
- Chen, H.; Wang, B.; Hong, Z.; Shen, C.; Wensing, P.M.; Zhang, W. Underactuated Motion Planning and Control for Jumping With Wheeled-Bipedal Robots. IEEE Robot. Autom. Lett. 2021, 6, 747–754. [Google Scholar] [CrossRef]
- Qian, Q.W.; Wu, J.F.; Wang, Z. Dynamic balance control of two-wheeled self-balancing pendulum robot based on adaptive machine learning. Int. J. Wavelets Multiresolut. Inf. Process. 2020, 18, 1941002. [Google Scholar] [CrossRef]
- Raza, F.; Chemori, A.; Hayashibe, M. A New Augmented L1 Adaptive Control for Wheel-Legged Robots: Design and Experiments. In Proceedings of the American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022. [Google Scholar]
- Wang, S.; Cui, L.; Zhang, J.; Lai, J.; Zhang, D.; Chen, K.; Jiang, Z.P. Balance Control of a Novel Wheel-legged Robot: Design and Experiments. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021. [Google Scholar]
- Cui, L.; Wang, S.; Zhang, J.; Zhang, D.; Lai, J.; Zheng, Y.; Jiang, Z.P. Learning-Based Balance Control of Wheel-Legged Robots. IEEE Robot. Autom. Lett. 2021, 6, 7667–7674. [Google Scholar] [CrossRef]
- Zhuang, Y.; Xu, Y.; Huang, B.; Chao, M.; Shi, G.; Yang, X.; Fu, C. Height Control and Optimal Torque Planning for Jumping with Wheeled-Bipedal Robots. In Proceedings of the 6th IEEE International Conference on Advanced Robotics and Mechatronics (ICARM), Chongqing, China, 3–5 July 2021. [Google Scholar]
- Dai, F.; Gao, X.; Jiang, S.; Guo, W.; Liu, Y. A two-wheeled inverted pendulum robot with friction compensation. Mechatronics 2015, 30, 116–125. [Google Scholar] [CrossRef]
- Yang, C.; Lu, W.; Xia, Y. Uncertain optimal attitude control for space power satellite based on interval Riccati equation with non-probabilistic time-dependent reliability. Aerosp. Sci. Technol. 2023, 139, 108406. [Google Scholar] [CrossRef]
- Marques, F.; Flores, P.; Pimenta Claro, J.C.; Lankarani, H.M. A survey and comparison of several friction force models for dynamic analysis of multibody mechanical systems. Nonlinear Dyn. 2016, 86, 1407–1443. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Q.; Wang, Z.; Mo, J.; Jin, W.; Zhu, S. Identification of Stribeck Model Parameters to Accurately Reveal Stick–Slip Characteristics of a Disc–Block Friction System. Tribol. Trans. 2023, 66, 1026–1042. [Google Scholar] [CrossRef]
- Han, Y.; Wu, J.; Liu, C.; Xiong, Z. An Iterative Approach for Accurate Dynamics model Identification of Industrial Robots. IEEE Trans. Robot. 2020, 36, 1577–1594. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]





| Motors | Rated Torque (N ⋅ m) | Rated Speed (RPM) | Power (W) | Control Frequency (Hz) |
|---|---|---|---|---|
| Upper Joint Motors (HaiTai HT8115-J9) | 20 | 120 | 160 | 1000 |
| Lower Joint Motoes (HaiTai H8115-J36) | 54 | 30 | 160 | 1000 |
| In-wheel Motors (LKMTECH MF9025v2) | 2.42 | 490 | 170 | 1000 |
| Parameter | Particle Swarm Size (M) | Learning Factor (c1/c2) | Inertia Factor Upper/Lower Limits | Constraint Factor (α) | Velocity Limit | Number of Iterations |
|---|---|---|---|---|---|---|
| Value | 128 | 1.6/2.0 | 0.9/0.4 | 0.6 | 0.5 | 500 |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Upper | 3 | 10 | 10 | 10 | 2.2 | 10 |
| Lower | 0.01 | 0.01 | 0.01 | 0 | 0 | −10 |
| Left Motor | 0.0338 | 0.0761 | 4.9 × 10−4 | 1.612 | 0.2310 | −0.0016 |
| Right Motor | 0.0406 | 0.0617 | 4.3 × 10−4 | 2.253 | 0.2772 | 0.0014 |
| Type | Method | Range | Mean | Variance |
|---|---|---|---|---|
| Displacement (m) | LQR | −0.07~0.12 | 0.0467 | 0.0645 |
| FLQR | −0.02~0 | −0.0092 | 0.0068 | |
| Velocity (m/s) | LQR | −0.2066~0.1751 | 0 | 0.07 |
| FLQR | −0.0263~0.0384 | 0 | 0.0093 | |
| Pitch angle (°) | LQR | −0.06~0.01 | −0.0188 | 0.0144 |
| FLQR | −0.02~0 | −0.0147 | 0.005 |
| Type | Method | Range | Mean | Variance |
|---|---|---|---|---|
| Displacement (m) | LQR | −0.12~0.07 | −0.0436 | 0.0692 |
| FLQR | 0.03~0.05 | 0.049 | 0.003 | |
| Velocity (m/s) | LQR | −0.1797~0.1907 | −0.0080 | 0.0759 |
| FLQR | −0.0207~0.0324 | 0 | 0.0061 | |
| Pitch angle (°) | LQR | −0.05~0.03 | −0.0158 | 0.0152 |
| FLQR | −0.03~−0.01 | −0.0243 | 0.005 |
| Type | Method | Range or Value of Steady State | Range of Disturbance State |
|---|---|---|---|
| Displacement (m) | LQR | −0.1~0.04 | −0.28~0.11 |
| FLQR | 0.04 | 0.09~0.11 | |
| Velocity (m/s) | LQR | −0.14~0.15 | −0.29~0.55 |
| FLQR | −0.024~0.017 | −0.23~0.17 | |
| Pitch angle (°) | LQR | −0.04~0.03 | −0.09~0.07 |
| FLQR | −0.03 | −0.05~−0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Zhou, R.; Zhang, T.; Zheng, J.; Chen, S. Balance Control Method for Bipedal Wheel-Legged Robots Based on Friction Feedforward Linear Quadratic Regulator. Sensors 2025, 25, 1056. https://doi.org/10.3390/s25041056
Zhang A, Zhou R, Zhang T, Zheng J, Chen S. Balance Control Method for Bipedal Wheel-Legged Robots Based on Friction Feedforward Linear Quadratic Regulator. Sensors. 2025; 25(4):1056. https://doi.org/10.3390/s25041056
Chicago/Turabian StyleZhang, Aimin, Renyi Zhou, Tie Zhang, Jingfu Zheng, and Shouyan Chen. 2025. "Balance Control Method for Bipedal Wheel-Legged Robots Based on Friction Feedforward Linear Quadratic Regulator" Sensors 25, no. 4: 1056. https://doi.org/10.3390/s25041056
APA StyleZhang, A., Zhou, R., Zhang, T., Zheng, J., & Chen, S. (2025). Balance Control Method for Bipedal Wheel-Legged Robots Based on Friction Feedforward Linear Quadratic Regulator. Sensors, 25(4), 1056. https://doi.org/10.3390/s25041056






