CH4, C2H6, and C2H4 Multi-Gas Sensing Based on Mid-Infrared Spectroscopy and SVM Algorithm
Abstract
:1. Introduction
2. Principle and System
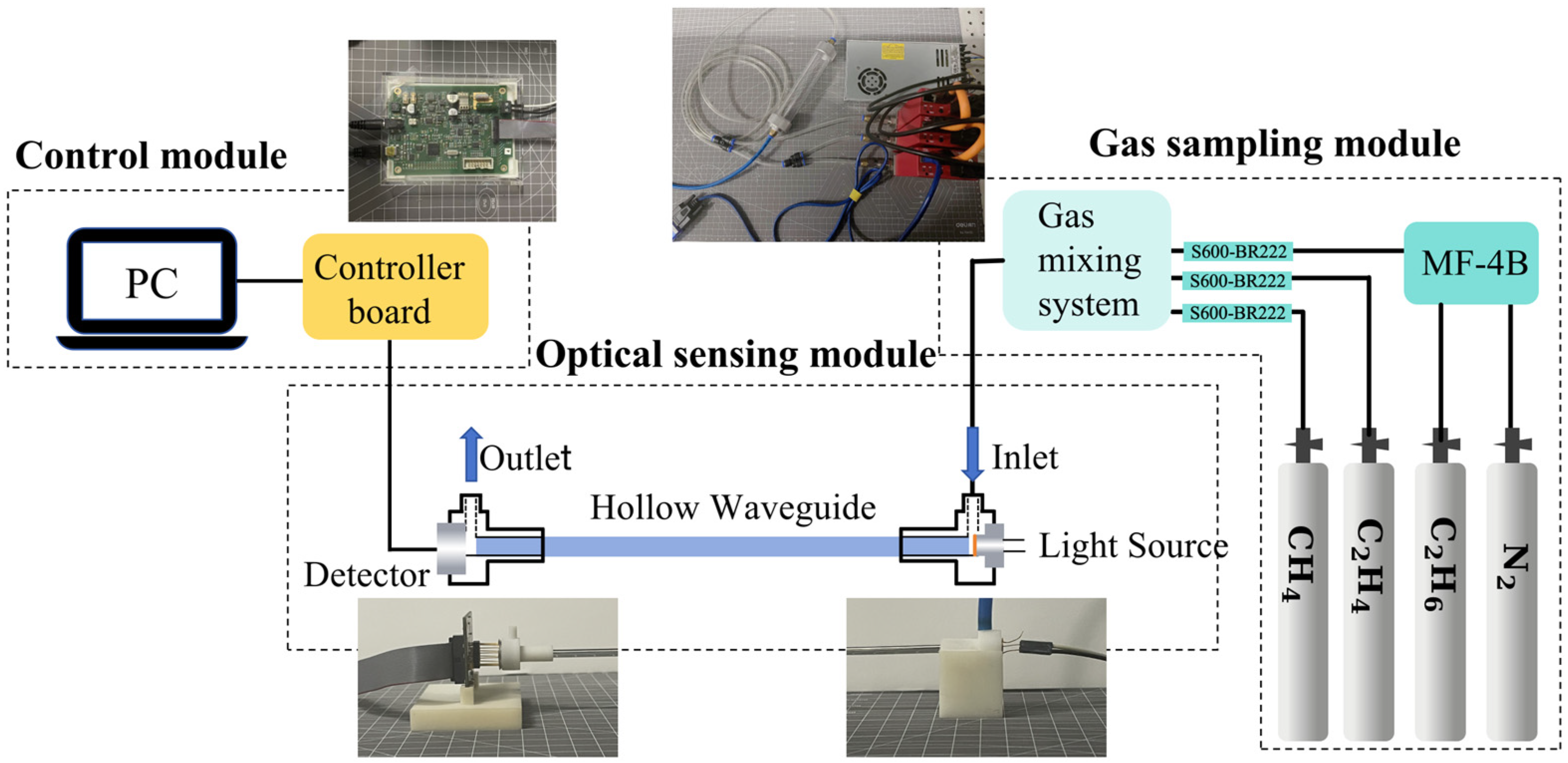
2.1. Sensing System
2.2. Principle
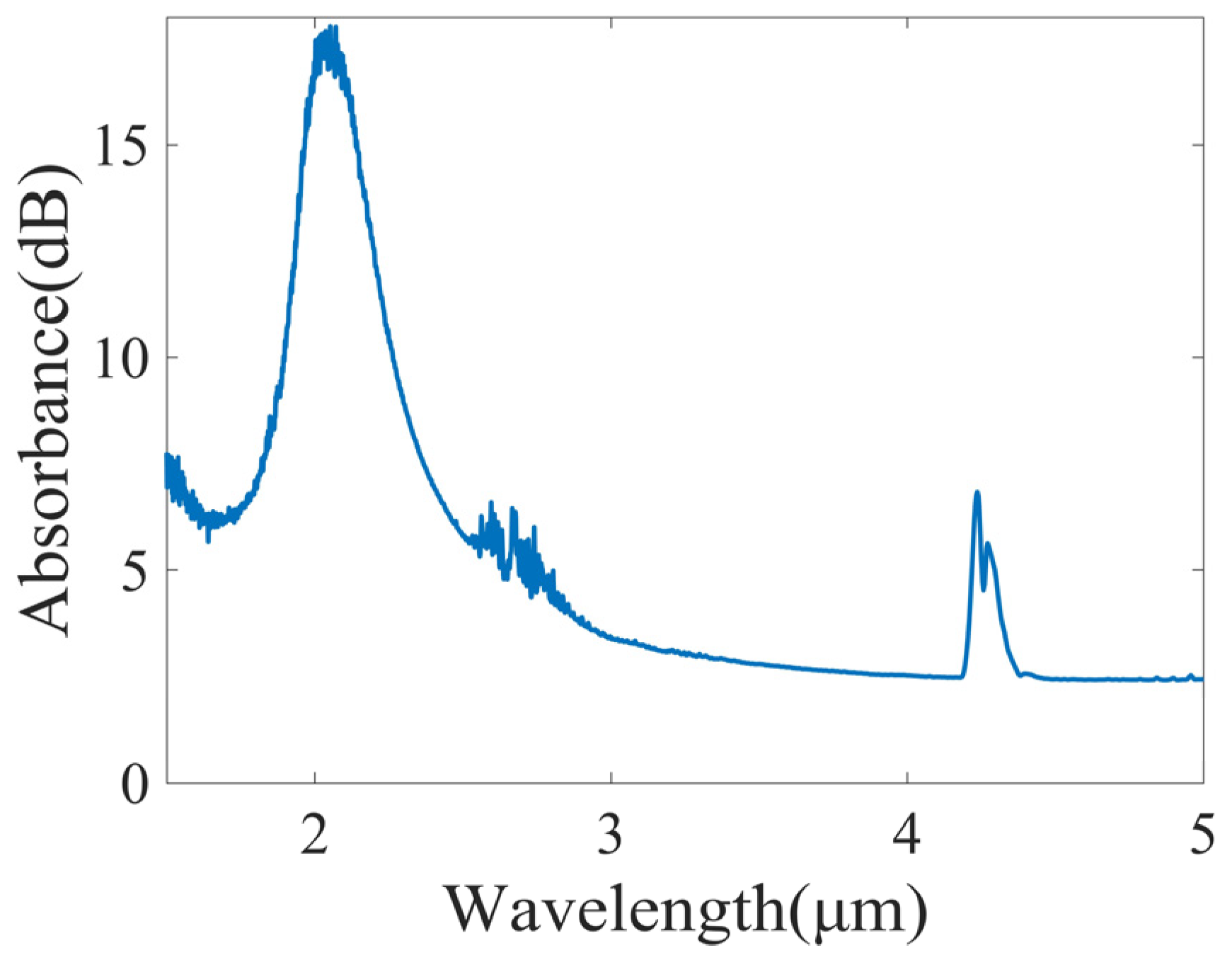
2.2.1. Lambert–Beer’s Law
2.2.2. Support Vector Machine Regression
2.2.3. Evaluation Parameters for SVM
3. Results and Discussion
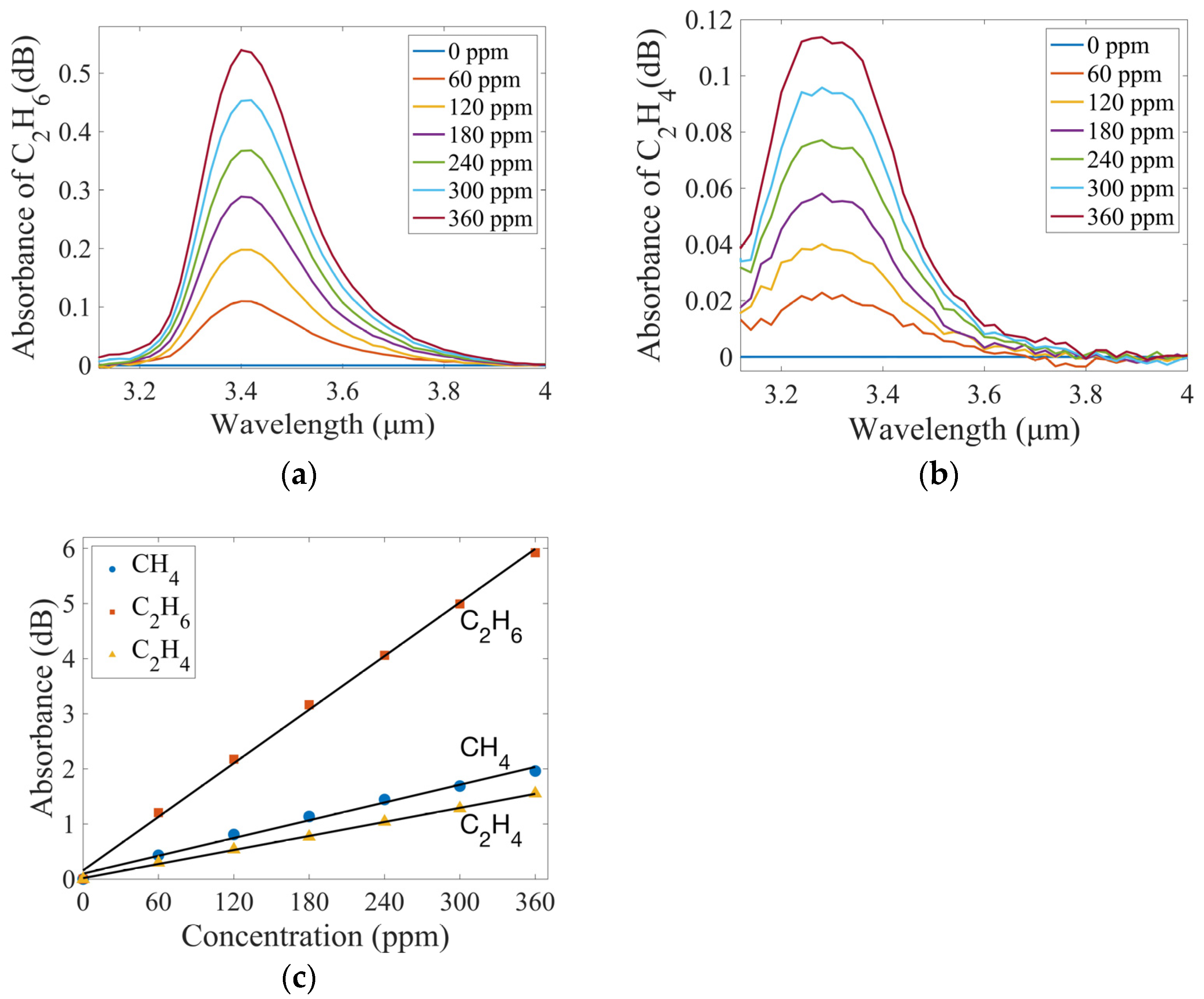
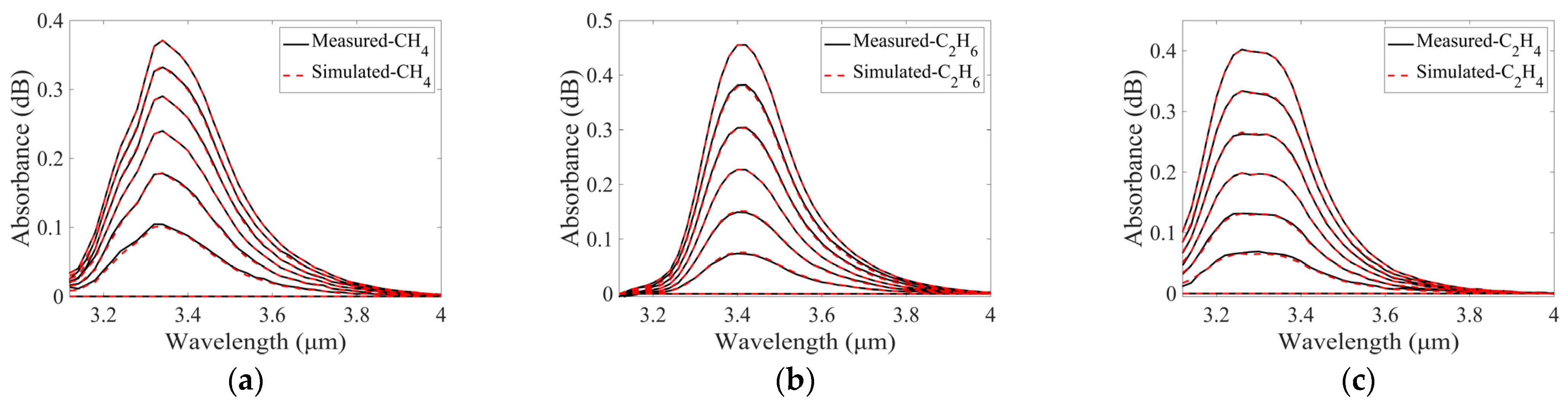
3.1. Measurement and Analysis of Single-Component Gas
| Method | Target Gas | Detection Limit/ Detection Error | Reference | Year |
|---|---|---|---|---|
| FERS | CH4 | 3 ppm | [11] | 2020 |
| H2 | 49 ppm | |||
| FERS | CH4 | 1.2 ppm | [12] | 2022 |
| C2H6 | 2.9 ppm | |||
| C2H4 | 1.6 ppm | |||
| C2H2 | 2.7 ppm | |||
| H2 | 13.8 ppm | |||
| CO | 16.7 ppm | |||
| FERS | CH4 | 1.5 ppm | [13] | 2023 |
| C2H4 | 4.8 ppm | |||
| C2H2 | 3.1 ppm | |||
| CO2 | 9.4 ppm | |||
| CO | 1 ppm | |||
| IR | CH4 | 500 ppm | [14] | 2020 |
| CO2 | 100 ppm | |||
| CO | 500 ppm | |||
| IR | CH4 | 63 ppm | [15] | 2020 |
| CO2 | 2 ppm | |||
| CO | 11 ppm | |||
| IR | CH4 | −0.34%~−0.77% | [16] | 2024 |
| CO2 | −0.40%~−0.26% | |||
| N2O | −0.81%~−0.32% | |||
| IR | CH4 | 7.33 ppm | This work | - |
| C2H6 | 2.13 ppm | |||
| C2H4 | 8.09 ppm |
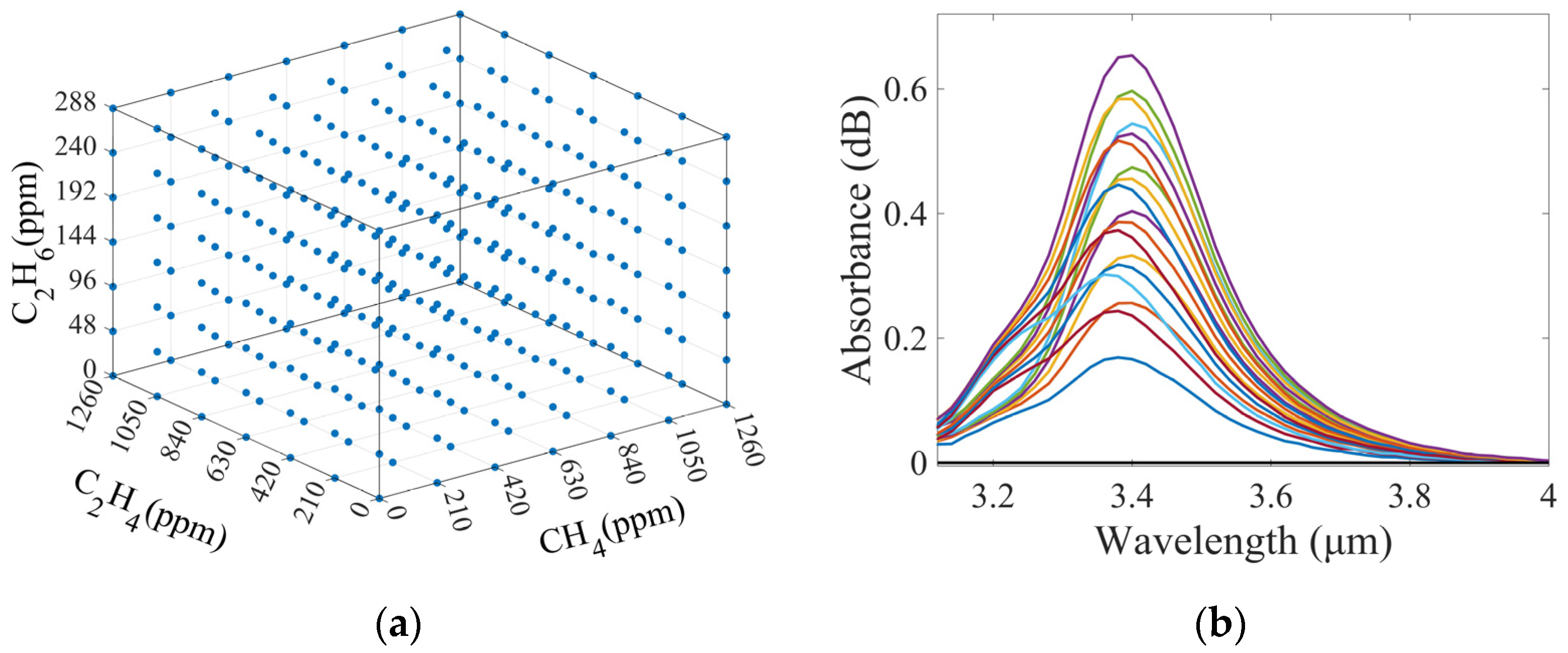
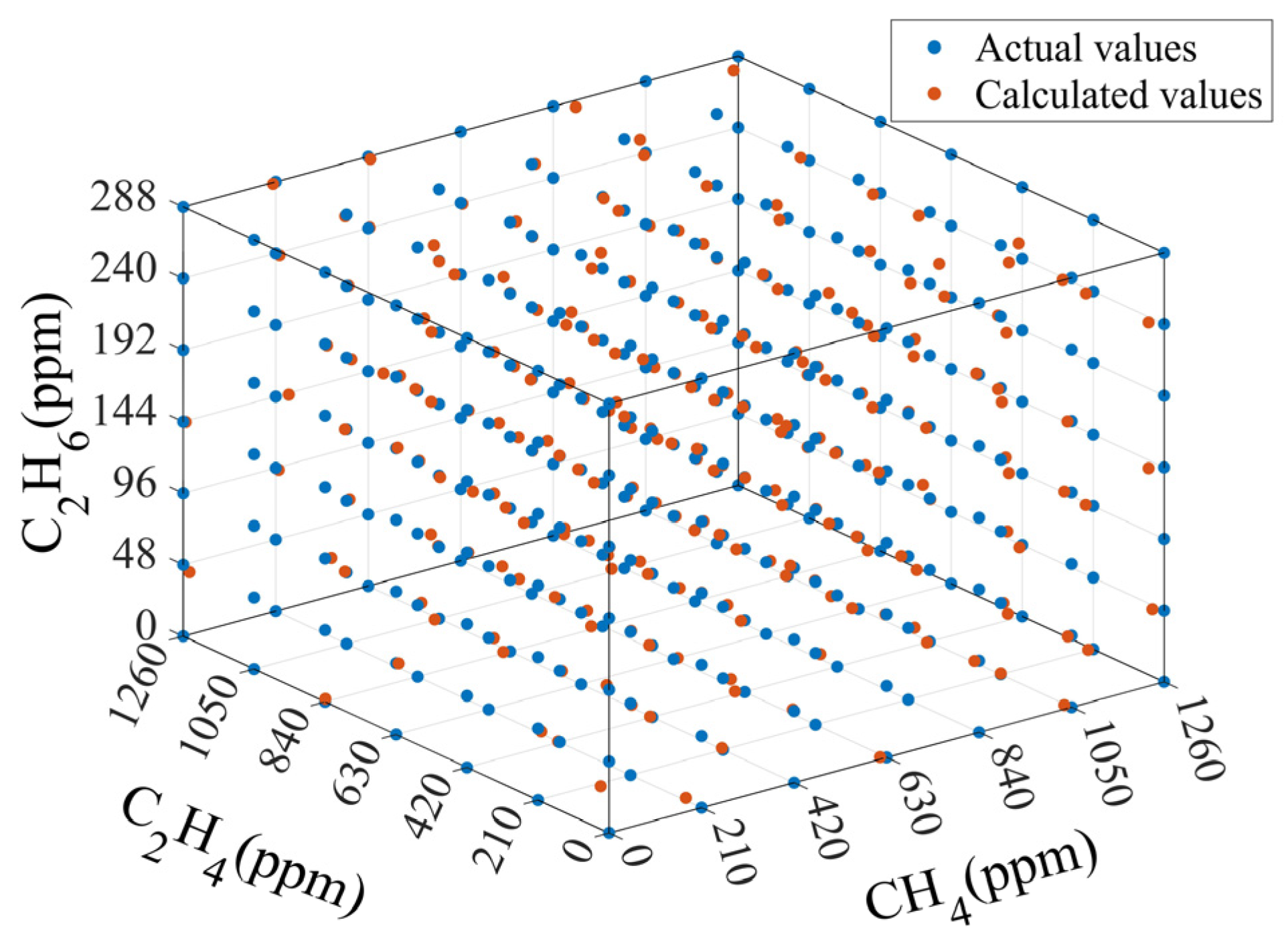
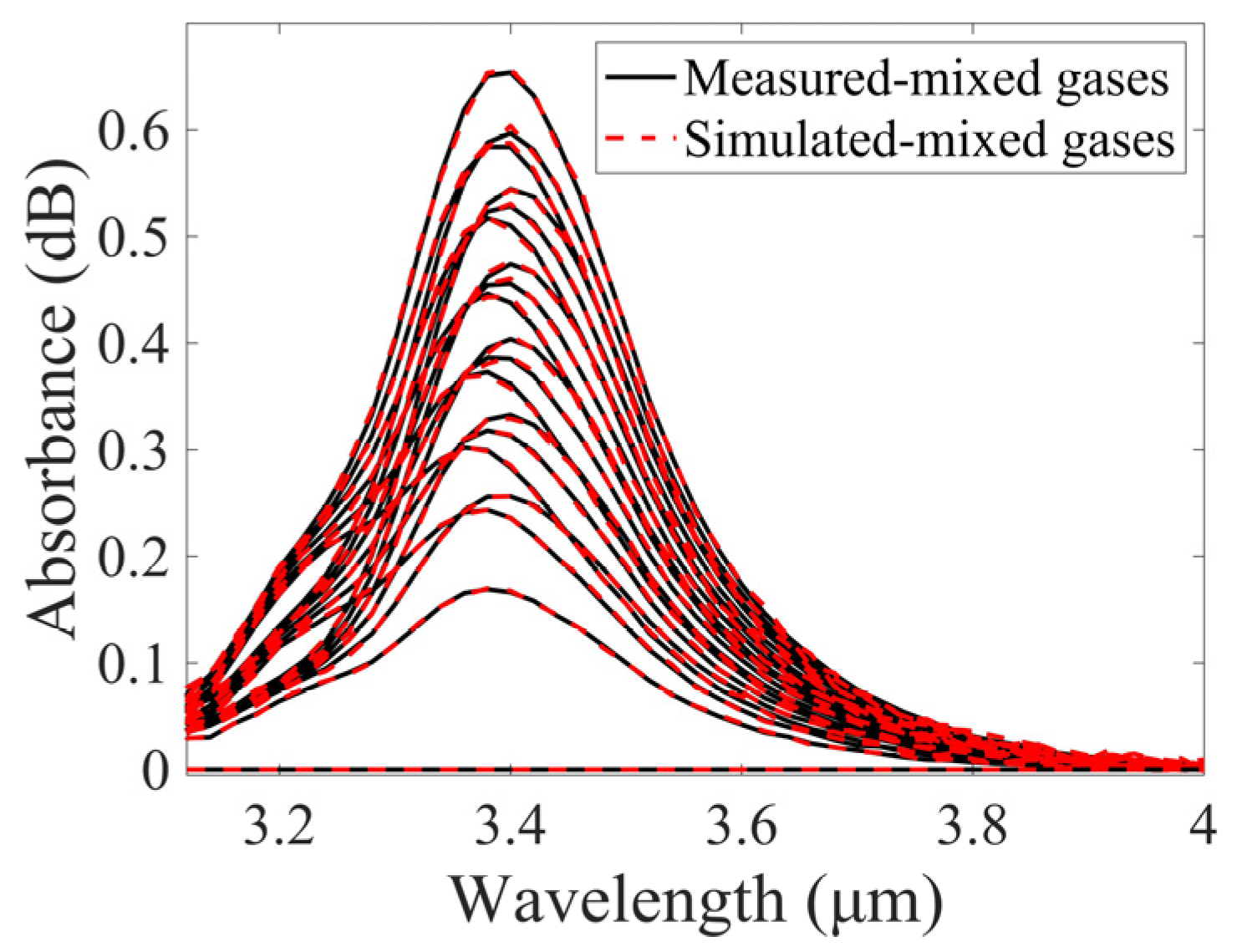
3.2. Measurement and Analysis of Mixed Gases
3.3. Simulation-Assisted Training
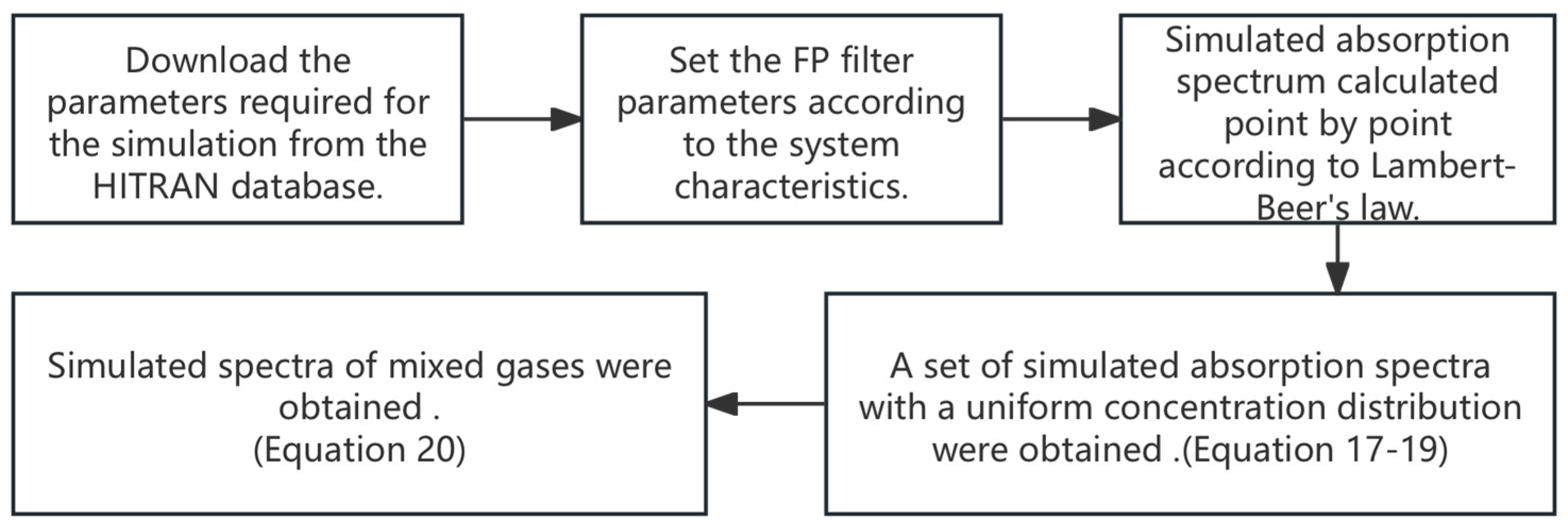
3.3.1. Generation of Simulated Spectra
3.3.2. Selection of Measured Spectra
3.3.3. Simulation Interpolation Method
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FNE | Fluorescence noise elimination |
| FP | Fabry–Pérot |
| FRES | Fiber-enhanced Raman spectroscopy |
| HC-ARF | Hollow-core anti-resonant fiber |
| HWG | Hollow waveguide |
| IR | Infrared spectral absorption |
| LOD | Limit of detection |
| RBF | Radial basis function |
| RMSEC | Root mean square error of calibration |
| RMSEP | Root mean square error of prediction |
| SVM | Support vector machine |
References
- Lee, D.; Lee, D. Environmental gas sensors. IEEE Sens. J. 2001, 1, 214–224. [Google Scholar] [CrossRef]
- Yadav, R.; Sahu, L.K.; Tripathi, N.; Pal, D.; Beig, G.; Jaaffrey, S.N.A. Investigation of emission characteristics of NMVOCs over urban site of western India. Environ. Pollut. 2019, 252, 245–255. [Google Scholar] [CrossRef]
- Melike, D.; Mustafa, O.; Serpil, Y. Source apportionment of biogenic and anthropogenic VOCs in Bolu plateau. Sci. Total Environ. 2020, 731, 139201. [Google Scholar] [CrossRef]
- Tanaka, K.; Akishima, K.; Sekita, M.; Tonokura, K.; Konno, M. Measurement of ethylene in combustion exhaust using a 3.3-μm distributed feedback interband cascade laser with wavelength modulation spectroscopy. Appl. Phys. B 2017, 123, 219. [Google Scholar] [CrossRef]
- Baker, R.W.; Lokhandwala, K. Natural gas processing with membranes: An overview. Ind. Eng. Chem. Res. 2008, 47, 2109–2121. [Google Scholar] [CrossRef]
- Jean, L.M.; Pierre, R. Production, oxidation, emission and consumption of methane by soils: A review. Eur. J. Soil Biol. 2001, 37, 25–50. [Google Scholar] [CrossRef]
- Giuseppe, E.; Paolo, C. Earth’s degassing: A missing ethane and propane source. Science 2009, 323, 478. [Google Scholar] [CrossRef]
- David, A.M. Anthropogenic and biogenic sources of Ethylene and the potential for human exposure: A literature review. Chem.-Biol. Interact. 2015, 241, 10–22. [Google Scholar] [CrossRef]
- Annika, B.; Christian, D.; Andreas, M.; Sebastian, W.; Jurgen, P.; Torsten, F. Comprehensive multi-gas study by means of fiber-enhanced Raman spectroscopy for the investigation of nitrogen cycle processes. Analyst 2024, 149, 1885–1894. [Google Scholar] [CrossRef]
- Nie, Q.; Liu, Z.; Cheng, M.; Pei, S.; Yang, D.; Guo, D.; Yang, M. Review on Hollow-Core Fiber Based Multi-Gas Sensing Using Raman Spectroscopy. Photonic Sens. 2024, 14, 4. [Google Scholar] [CrossRef]
- Andreas, K.; Robert, D.; Sebastian, W.; Christian, D.; Juergen, P.; Torsten, F. Fiber-enhanced Raman gas spectroscopy for the study of microbial methanogenesis. Anal. Chem. 2020, 92, 12564–12571. [Google Scholar] [CrossRef]
- Bai, Y.; Xiong, D.; Yao, Z.; Wang, X.; Zuo, D. Analysis of CH4, C2H6, C2H4, C2H2, H2, CO, and H2S by forward Raman scattering with a hollow-core anti-resonant fiber. J. Raman Spectrosc. 2022, 53, 1023–1031. [Google Scholar] [CrossRef]
- Wan, F.; Kong, W.; Liu, Q.; Wang, P.; Wang, M.; Li, Q.; Yao, X. Fluorescence noise eliminating fiber-enhanced Raman spectroscopy for simultaneous and multi process analysis of intermediate compositions for C2H2 and H2 Production. Anal. Chem. 2023, 95, 8596–8604. [Google Scholar] [CrossRef]
- Tan, X.; Zhang, H.; Li, J.; Wan, H.; Guo, Q.; Zhu, H.; Liu, H.; Yi, F. Non-dispersive infrared multi-gas sensing via nano antenna integrated narrowband detectors. Nat. Commun. 2020, 11, 5245. [Google Scholar] [CrossRef]
- Liu, H.; Shi, Y.; Wang, T. Design of a six-gas NDIR gas sensor using an integrated optical gas chamber. Opt. Express 2020, 28, 11451–11462. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; He, Y.; Zhao, K.; Ji, J.; Li, H.; Jeffrey, M.B. Development and testing of NDIR-based rapid greenhouse gas detection device for dairy farms. Sustainability 2024, 16, 2131. [Google Scholar] [CrossRef]
- Zou, M.; Sun, L.; Wang, X. Multigas sensing based on wavelength modulation spectroscopy using frequency division multiplexing combined with time division multiplexing. IEEE Sens. J. 2022, 22, 12930. [Google Scholar] [CrossRef]
- Fu, L.; You, S.; Li, G.; Fan, Z. Enhancing methane sensing with NDIR technology: Current trends and future prospects. Rev. Anal. Chem. 2023, 42, 20230062. [Google Scholar] [CrossRef]
- Zhou, S.; Liu, N.; Shen, C.; Zhang, L.; He, T.; Yu, B.; Li, J. An adaptive Kalman filtering algorithm based on back-propagation (BP) neural network applied for simultaneously detection of exhaled CO and N2O. Spectrochim. Acta A 2019, 223, 117332. [Google Scholar] [CrossRef] [PubMed]
- Kan, Z.; Zhang, Y.; Luo, L.; Gao, Y. Ultraviolet absorption spectrometry with symmetrized dot patterns and deep learning for quantitative analysis of SO2, H2S, CS2 mixed gases. Eng. Appl. Artif. Intell. 2024, 133, 108366. [Google Scholar] [CrossRef]
- Zhang, B.; Jiang, J.; Zhang, X.; Zhu, X.; Shi, Y. Flexible Hollow Core Fiber Photoacoustic Gas Sensor Based on Embedded Acoustic Resonant Structure. Anal. Chem. 2023, 95, 34. [Google Scholar] [CrossRef] [PubMed]
- Jia, Y.; Jiang, J.; Zhang, B.; Zhao, B.; Yang, Y.; Zhang, X.; Zhu, X.; Shi, Y. Ppb-level CO2 detection with miniaturized gas absorption cell based on low-loss flexible infrared hollow waveguide. Sens. Actuators A Phys. 2023, 363, 114767. [Google Scholar] [CrossRef]
- Chen, Z.; Zeng, J.; He, M.; Zhu, X.; Shi, Y. Portable ppb-level carbon dioxide sensor based on flexible hollow waveguide cell and mid-infrared spectroscopy. Sens. Actuators B Chem. 2022, 359, 131553. [Google Scholar] [CrossRef]
- Yang, Y.; Jiang, J.; Zeng, J.; Chen, Z.; Zhu, X.; Shi, Y. CH4, C2H6, and CO2 multi-gas sensing based on portable mid-infrared spectroscopy and PCA-BP algorithm. Sensors 2023, 23, 1413. [Google Scholar] [CrossRef]






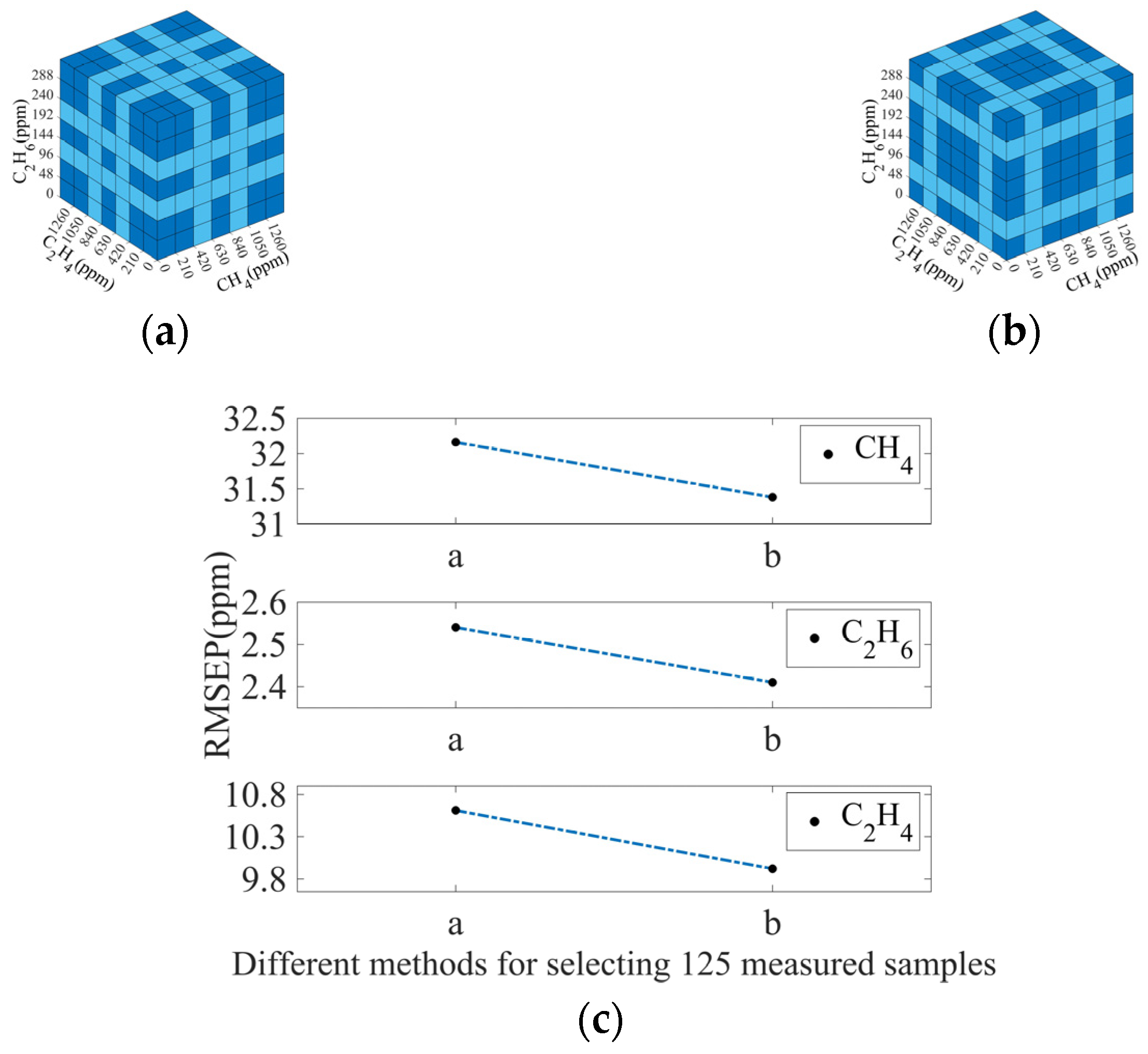
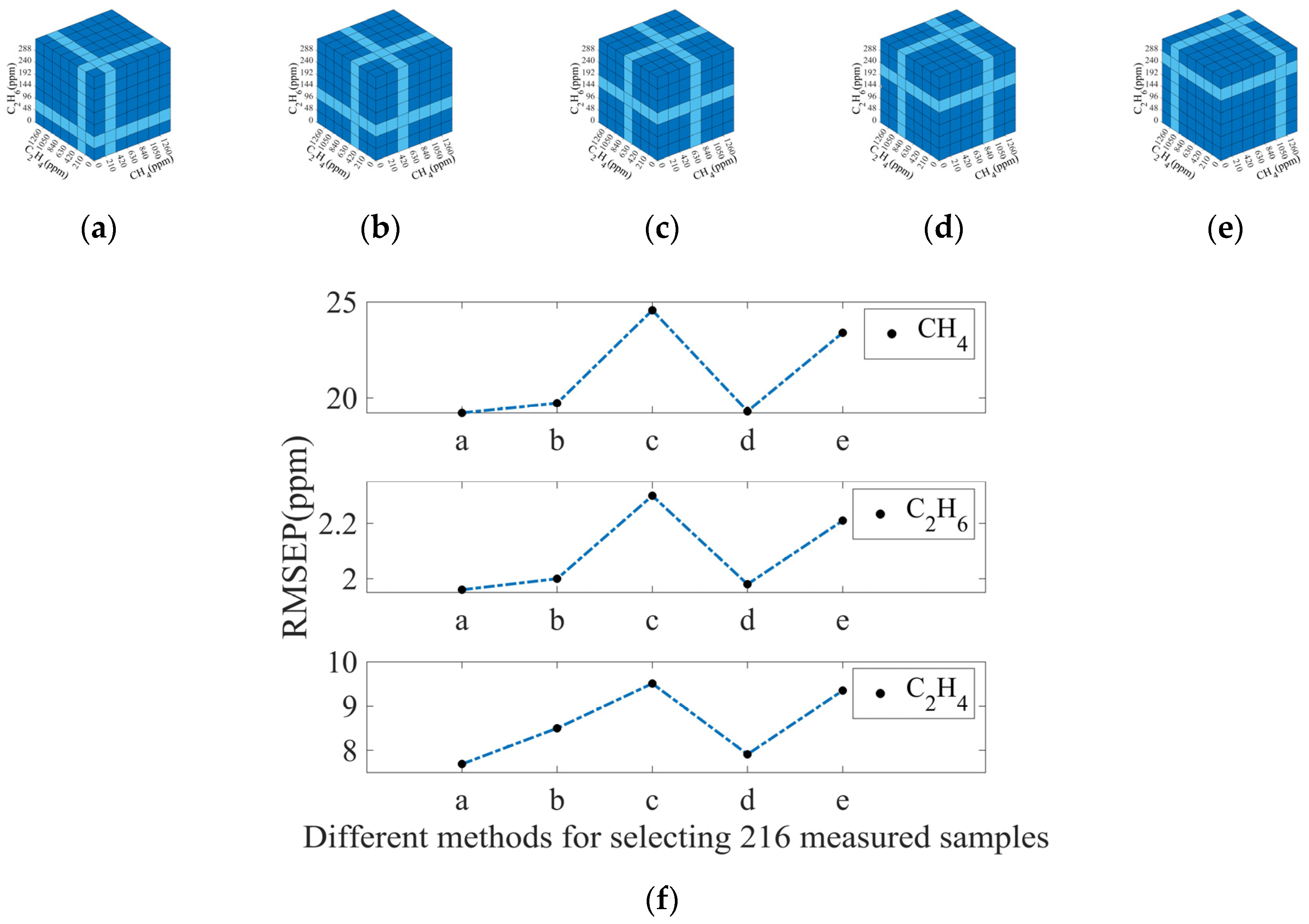




| Gas | RMSEC | RMSEP |
|---|---|---|
| CH4 | 9.97 ppm (0.79%) | 15.91 ppm (1.26%) |
| C2H6 | 0.36 ppm (0.13%) | 1.64 ppm (0.57%) |
| C2H4 | 1.47 ppm (0.12%) | 6.95 ppm (0.55%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, W.; Jia, Y.; Su, X.; Zhao, B.; Jiang, J.; Gao, L.; Zhu, X.; Shi, Y. CH4, C2H6, and C2H4 Multi-Gas Sensing Based on Mid-Infrared Spectroscopy and SVM Algorithm. Sensors 2025, 25, 1427. https://doi.org/10.3390/s25051427
Shao W, Jia Y, Su X, Zhao B, Jiang J, Gao L, Zhu X, Shi Y. CH4, C2H6, and C2H4 Multi-Gas Sensing Based on Mid-Infrared Spectroscopy and SVM Algorithm. Sensors. 2025; 25(5):1427. https://doi.org/10.3390/s25051427
Chicago/Turabian StyleShao, Wenyuan, Yunjiang Jia, Xilian Su, Benlei Zhao, Jiachen Jiang, Limei Gao, Xiaosong Zhu, and Yiwei Shi. 2025. "CH4, C2H6, and C2H4 Multi-Gas Sensing Based on Mid-Infrared Spectroscopy and SVM Algorithm" Sensors 25, no. 5: 1427. https://doi.org/10.3390/s25051427
APA StyleShao, W., Jia, Y., Su, X., Zhao, B., Jiang, J., Gao, L., Zhu, X., & Shi, Y. (2025). CH4, C2H6, and C2H4 Multi-Gas Sensing Based on Mid-Infrared Spectroscopy and SVM Algorithm. Sensors, 25(5), 1427. https://doi.org/10.3390/s25051427







