Design and Characterization of a Self-Oscillating Fluxgate-Based Current Sensor for DC Distribution System Applications
Abstract
1. Introduction
2. Methodology
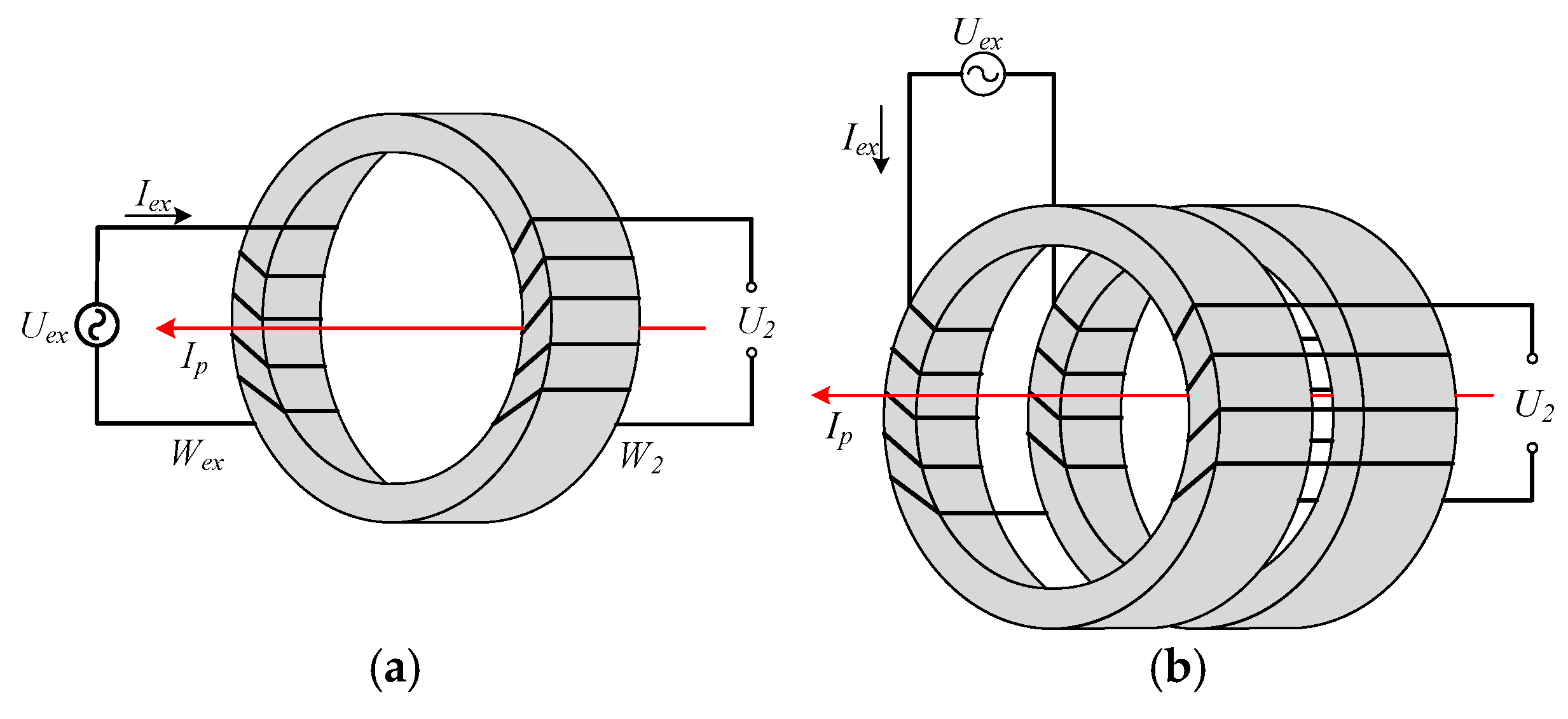
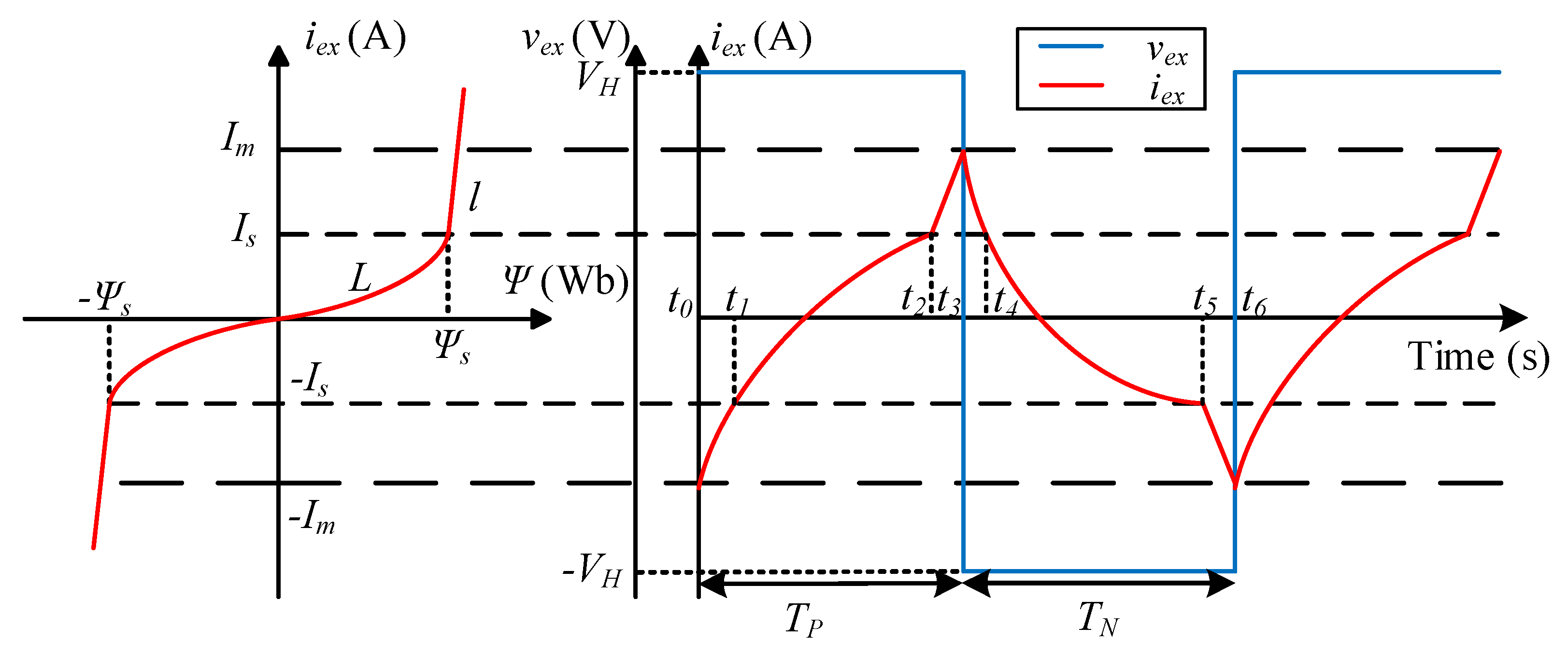
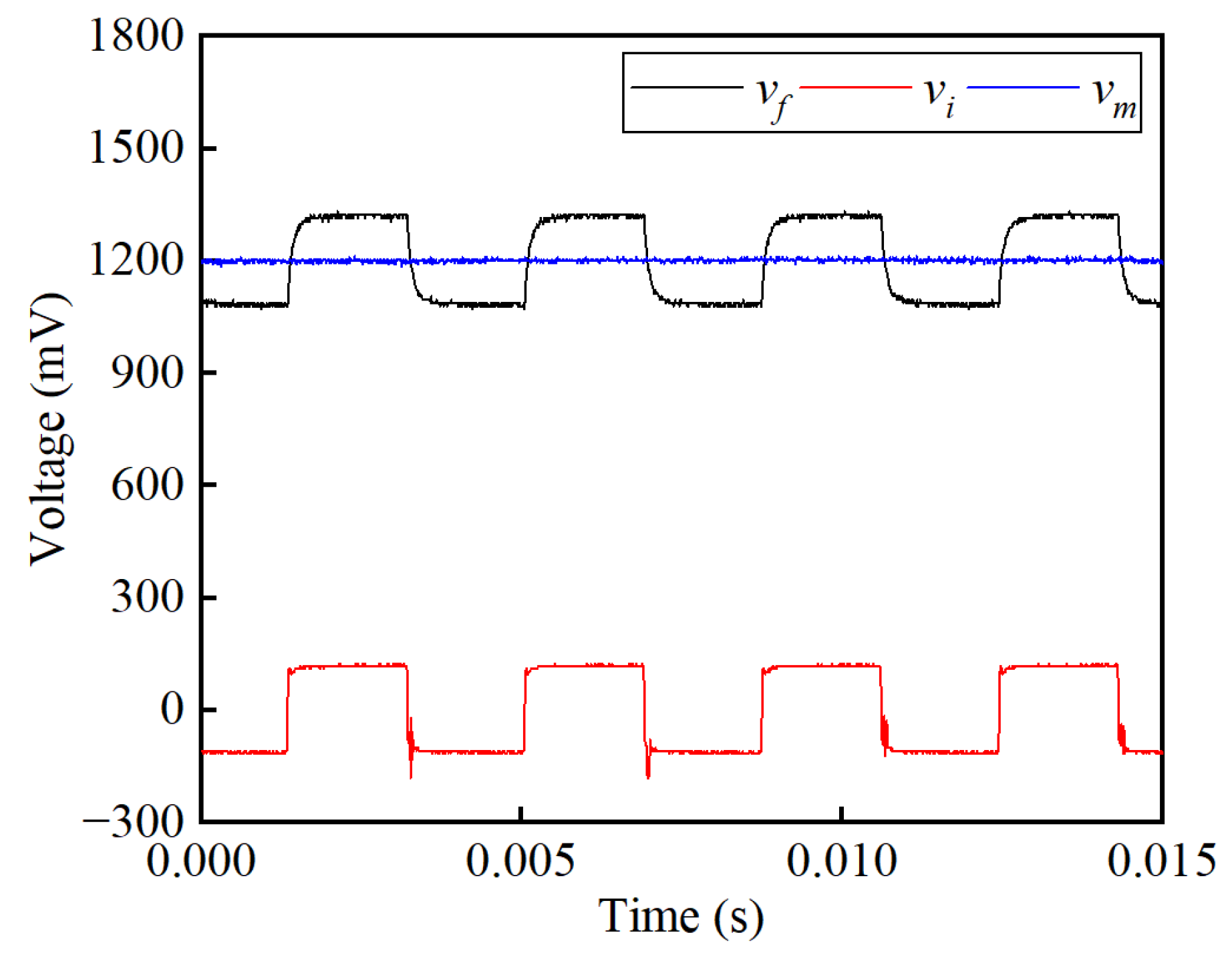
2.1. Measurement Principle
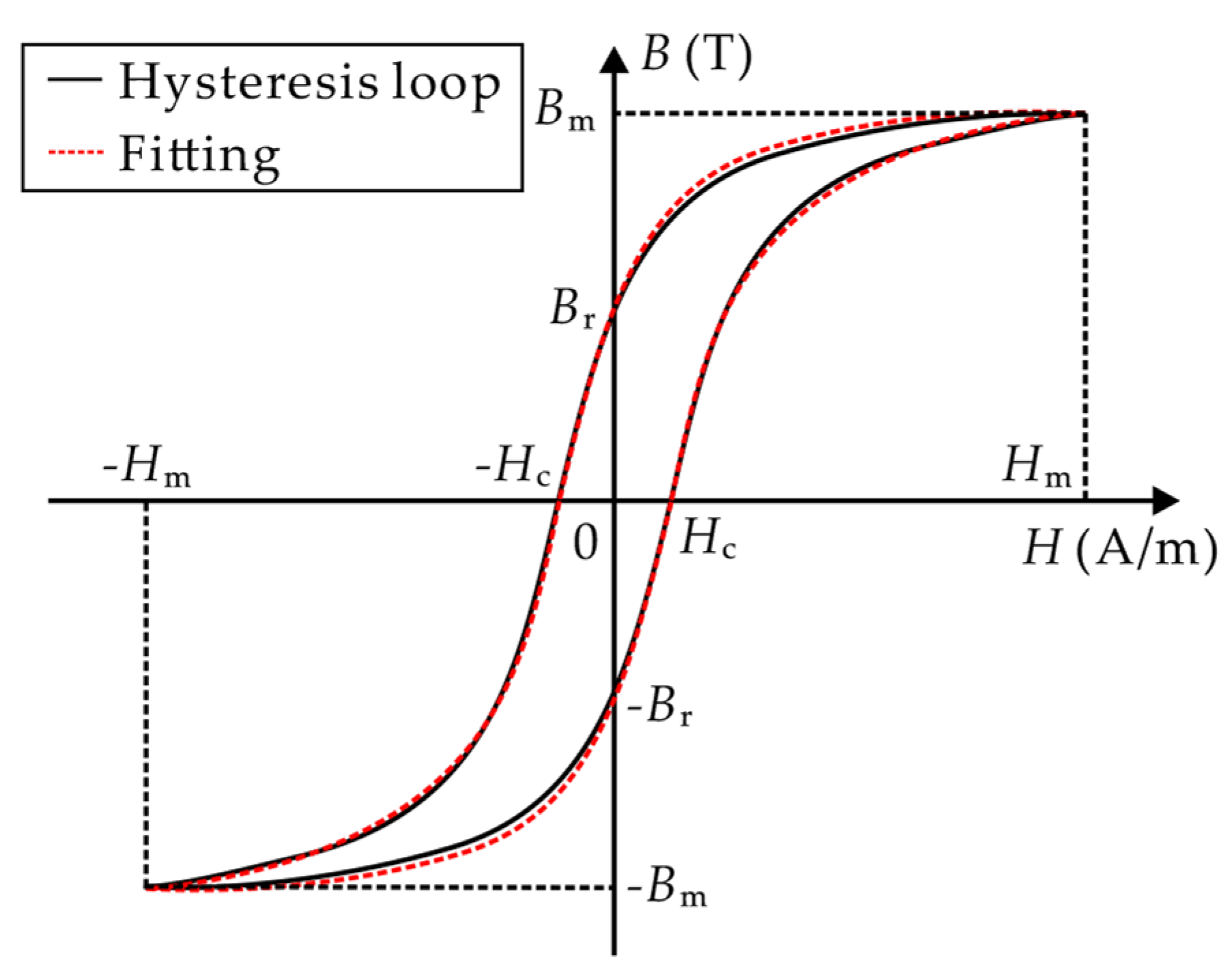
2.2. Analysis of the Transformer Noise and Its Suppression
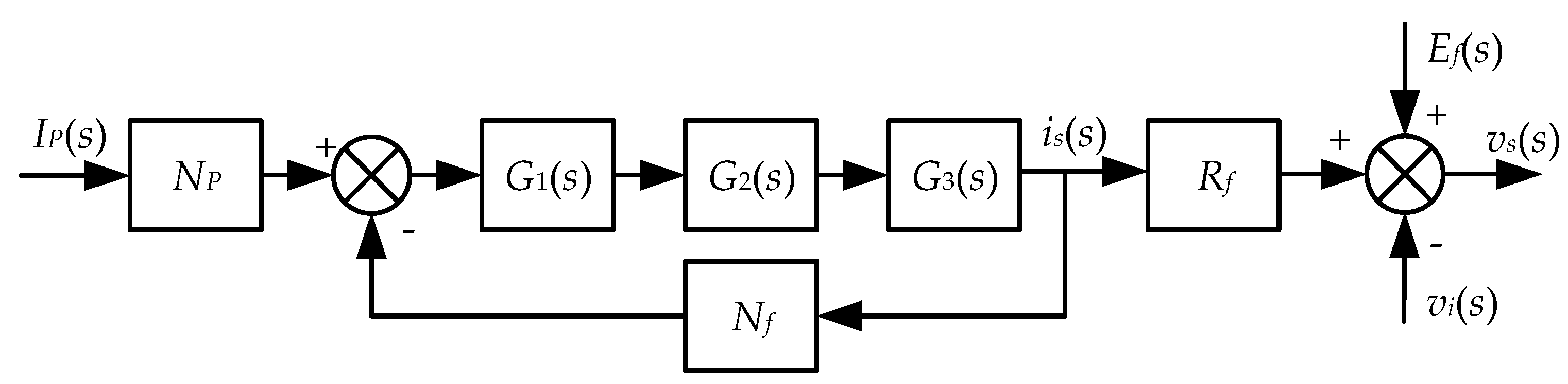
2.3. Derivation of the Transfer Function and Steady Error
3. Design and Realization
3.1. Magnetic Core and Windings
3.2. Circuit Design
3.3. Finished Prototype
4. Experimental Results and Discussion
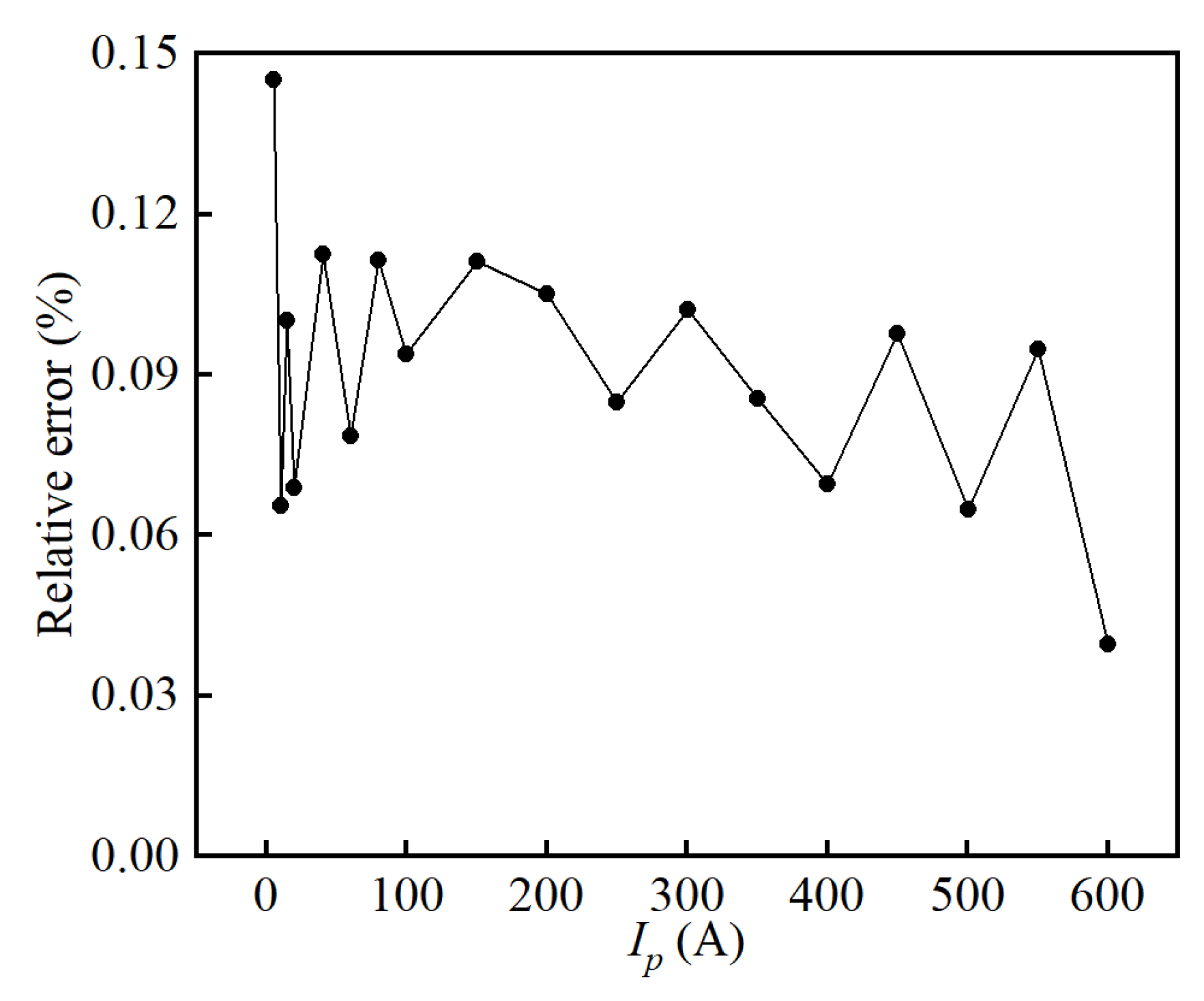
4.1. Linearity
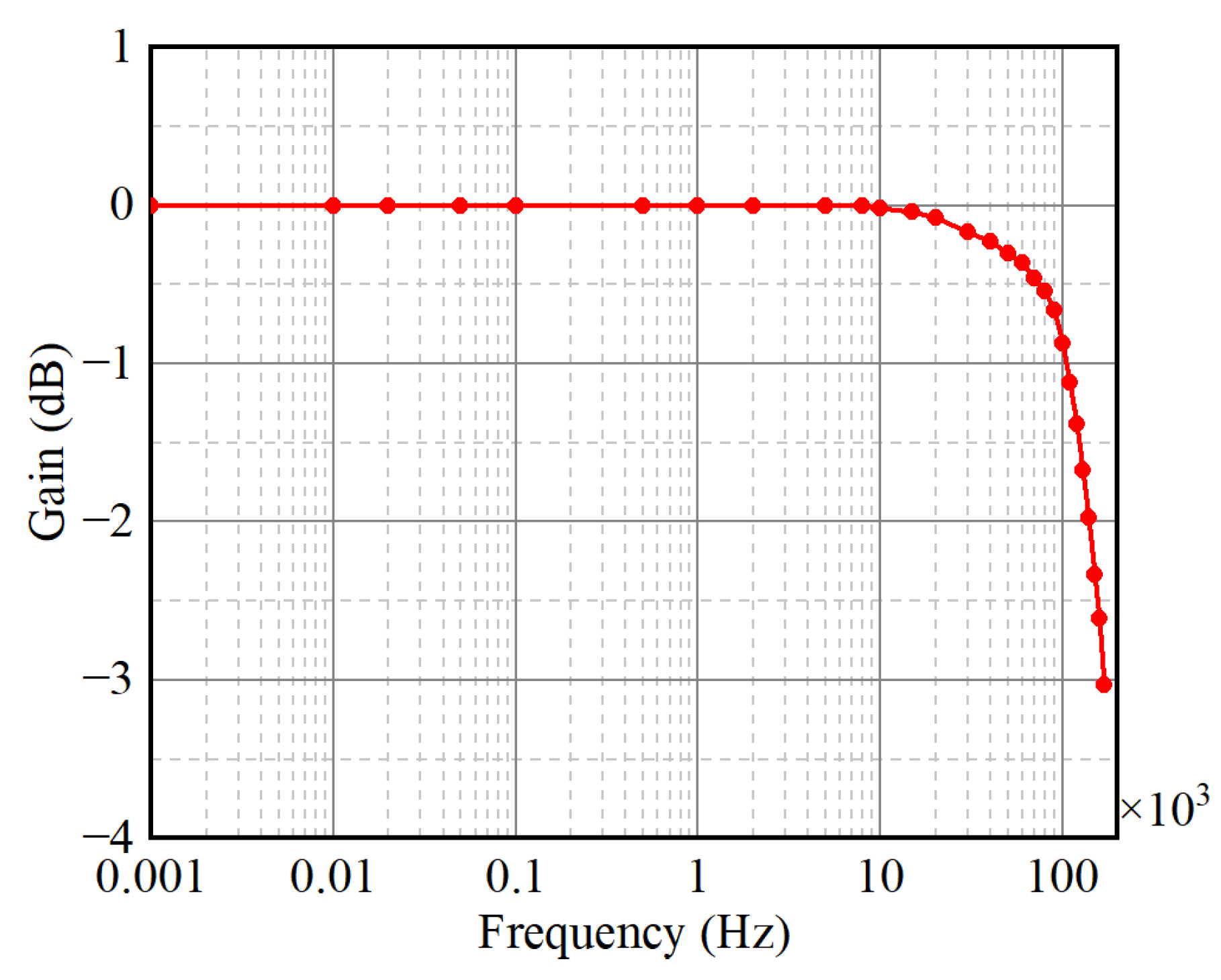
4.2. Small-Signal Bandwidth
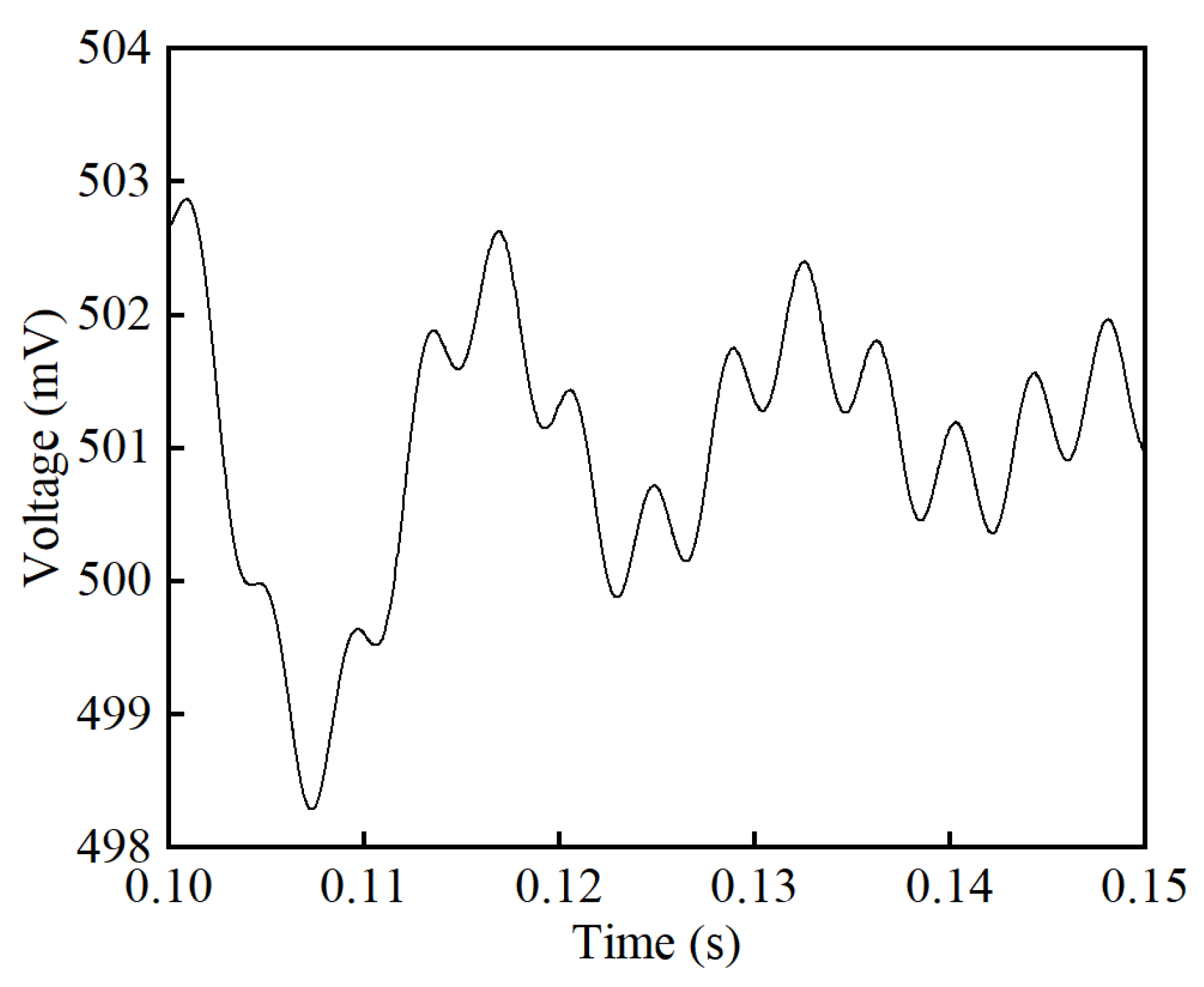
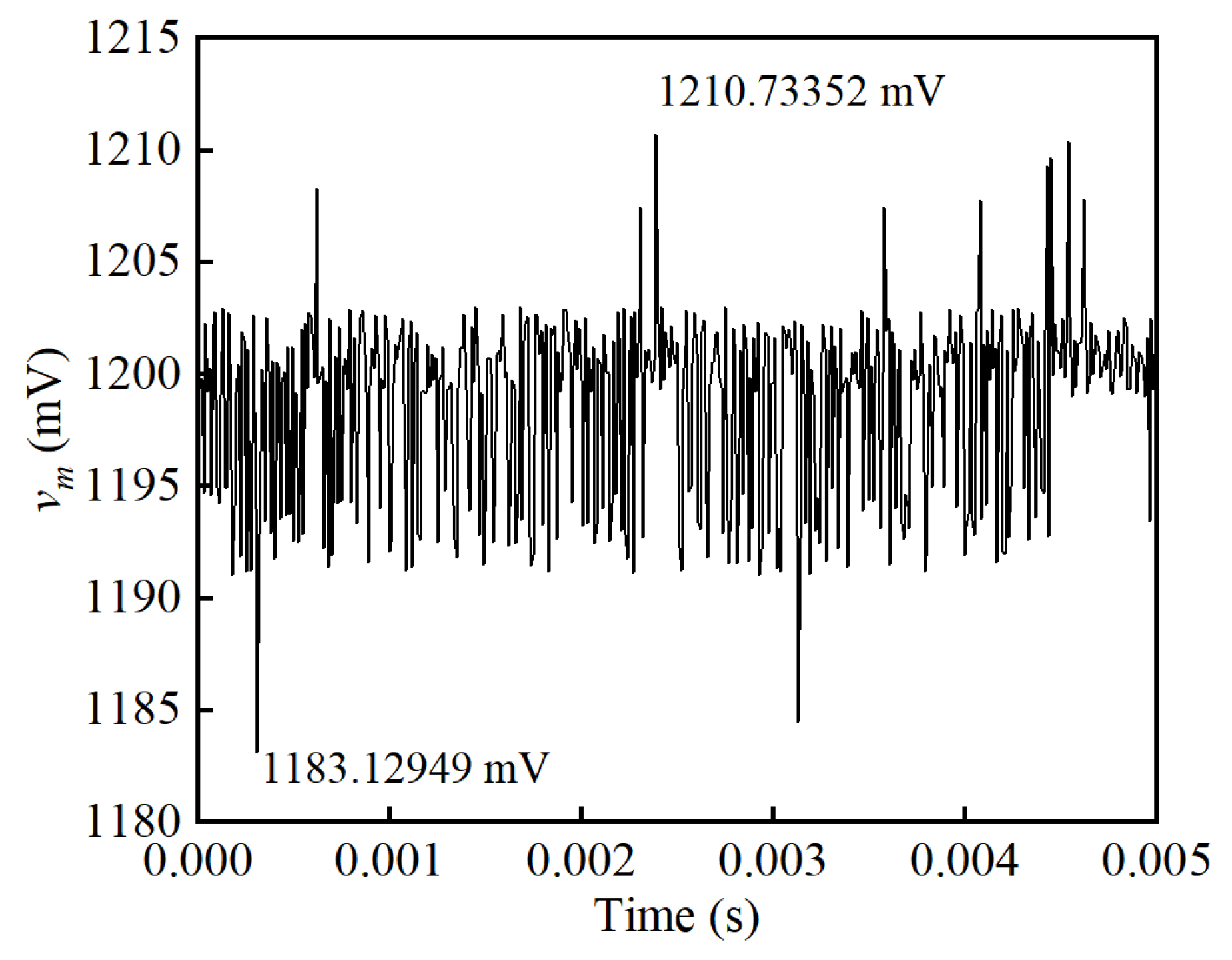
4.3. Output Noise
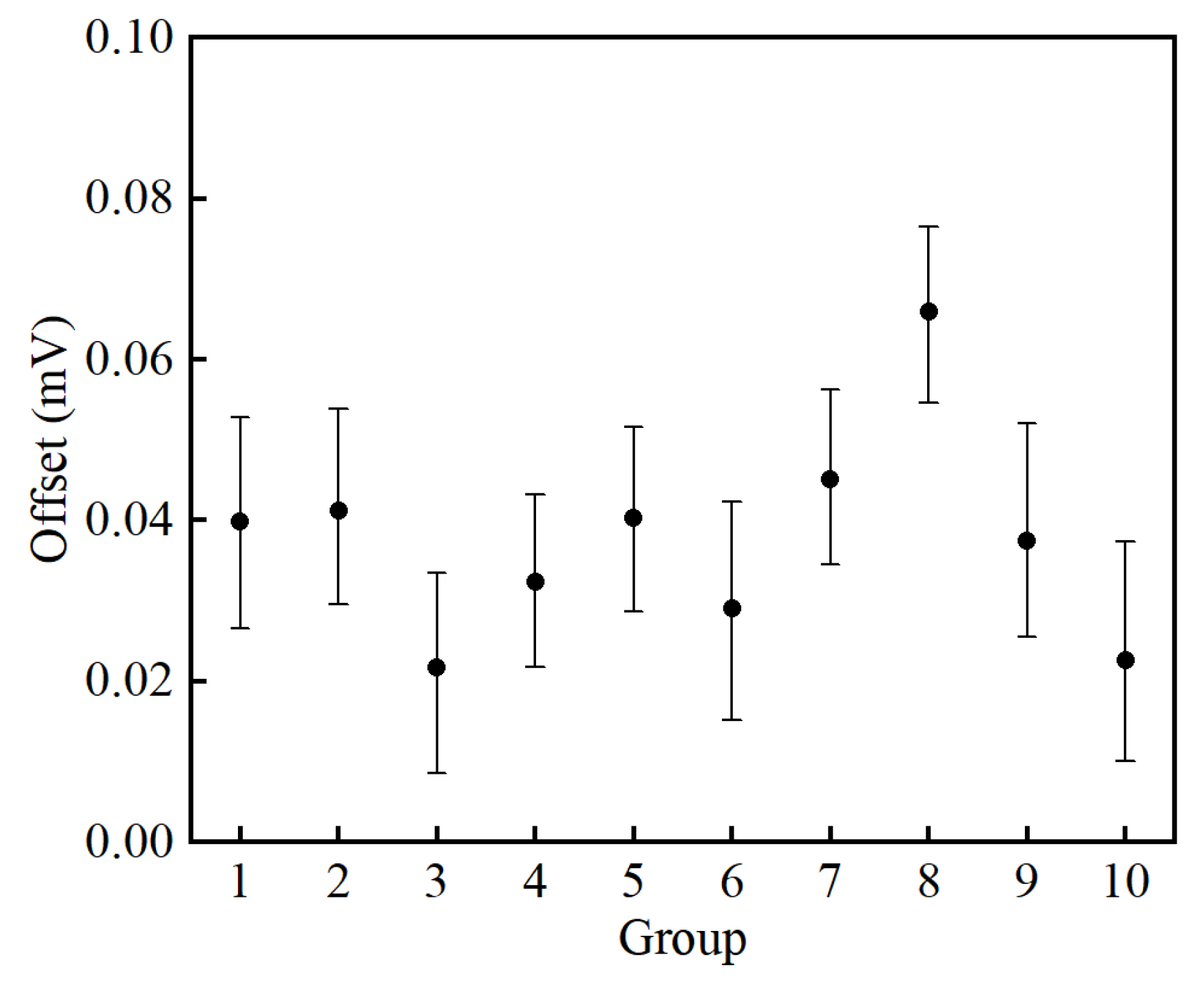
4.4. Power-On Repeatability
4.5. Comparison Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SNR | Singal-to-noise ratio |
| LPF | Low pass filter |
| PI | Proportional-integral |
| PA | Power amplifier |
| DMM | Digital multimeter |
| MCCB | Molded case circuit breaker |
| RMS | Root mean square |
References
- Kebede, A.A.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A Comprehensive Review of Stationary Energy Storage Devices for Large Scale Renewable Energy Sources Grid Integration. Renew. Sustain. Energy Rev. 2022, 159, 112213. [Google Scholar] [CrossRef]
- Li, Y.Z.; Yan, Y.F.; Chen, Y.W.; Zhu, S.P.; Li, X.F. Resistive Onset Determination of Coated Condutors Utilizing a Shunt Current Instead of Voltage Measurement. IEEE Trans. Appl. Supercond. 2025, 35, 4. [Google Scholar] [CrossRef]
- Liu, P.; Wang, W.; Zhou, L.; Zhao, M.C.; Wu, C.H.; He, L.; Liu, H.Y. Development of a Zero-Flux Hall Current Sensor Dedicated for Large-Current Measurement of Superconducting Cable. IEEE Trans. Appl. Supercond. 2025, 35, 5. [Google Scholar] [CrossRef]
- Younis, M.; Abdullah, M.; Dai, S.C.; Iqbal, M.A.; Tang, W.; Sohail, M.T.; Atiq, S.; Chang, H.X.; Zeng, Y.J. Magnetoresistance in 2D Magnetic Materials: From Fundamentals to Applications. Adv. Funct. Mater. 2025, 35, 31. [Google Scholar] [CrossRef]
- Wu, X.; Huang, H.H.; Dou, S.; Peng, L. Research on Magnetically Balanced High-Current TMR Sensor for EAST Poloidal Field Power Supply. IEEE Trans. Magn. 2024, 60, 11. [Google Scholar] [CrossRef]
- Dyankov, G.; Kolev, P.; Eftimov, T.A.; Hikova, E.O.; Kisov, H. Channeled Polarimetry for Magnetic Field/Current Detection. Sensors 2025, 25, 466. [Google Scholar] [CrossRef] [PubMed]
- Garcha, P.; Schaffer, V.; Haroun, B.; Ramaswamy, S.; Wieser, J.; Lang, J.; Chandraksan, A. A Duty-Cycled Integrated-Fluxgate Magnetometer for Current Sensing. IEEE J. Solid-State Circuits 2022, 57, 2741–2751. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, J.; Cheng, S. Research on the Simplified Direct-Current Fluxgate Sensor and its Demodulation. Meas. Sci. Technol. 2019, 30, 075101. [Google Scholar] [CrossRef]
- Ripka, P. Electric Current Sensors: A Review. Meas. Sci. Technol. 2010, 21, 112001. [Google Scholar] [CrossRef]
- Yang, X.; Wen, J.; Chen, M.; Gao, Z.; Xi, L.; Li, Y. Analysis and Design of a Self-Oscillating Bidirectionally Saturated Fluxgate Current Sensor. Measurement 2020, 157, 107687. [Google Scholar] [CrossRef]
- Wei, Y.; Li, C.; Zhao, W.; Xue, M.; Cao, B.; Chu, X.; Ye, C. Electrical Compensation for Magnetization Distortion of Magnetic Fluxgate Current Sensor. IEEE Trans. Instrum. Meas. 2022, 71, 9503409. [Google Scholar] [CrossRef]
- Xiao, X.; Song, H.; Li, H. A High Accuracy AC plus DC Current Transducer for Calibration. Sensors 2022, 22, 2214. [Google Scholar] [CrossRef]
- Ponjavic, M.; Veinovic, S. Low-Power Self-Oscillating Fluxgate Current Sensor Based on Mn-Zn Ferrite Cores. J. Magn. Magn. Mater. 2021, 518, 167368. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, J.; Li, C.; Wang, K.; Shao, H. A Wideband Closed-Loop Residual Current Sensor Based on Self-Oscillating Fluxgate. IEEE Access 2023, 11, 134126–134135. [Google Scholar] [CrossRef]
- Yang, X.; Chen, M.; Jia, Z. Analysis and Design of a Self-Oscillating Quasi-Digital Fluxgate Current Sensor for DC Current Measurement. Rev. Sci. Instrum. 2021, 92, 025001. [Google Scholar] [CrossRef]
- Ponjavic, M.M.; Duric, R.M. Nonlinear Modeling of the Self-Oscillating Fluxgate Current Sensor. IEEE Sens. J. 2007, 7, 1546–1553. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Z.; Li, Z.; Zhang, Y.; He, Q.; Han, B.; Lu, Y. Self-Oscillating Fluxgate-Based Quasi-Digital Sensor for DC High-Current Measurement. IEEE Trans. Instrum. Meas. 2015, 64, 3555–3563. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, Z.; Li, Z.; He, Q.; Lin, F.; Lu, Y. Design and Characterization of a Low-Cost Self-Oscillating Fluxgate Transducer for Precision Measurement of High-Current. IEEE Sens. J. 2016, 16, 2971–2981. [Google Scholar] [CrossRef]
- Li, J.; Ren, W.; Luo, Y.; Zhang, X.; Liu, X.; Zhang, X. Design of Fluxgate Current Sensor Based on Magnetization Residence Times and Neural Networks. Sensors 2024, 24, 3752. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Xie, J.; Ding, T.; Han, X. A New Approach for Solving the False Balance of a Closed-Loop Fluxgate Current Transducer. IEEE Trans. Ind. Electron. 2022, 69, 2147–2152. [Google Scholar] [CrossRef]
- Kusters, N.L.; Moore, W.J.M.; Miljanic, P.N. A Current Comparator for the Precision Measurement of D-C Ratios. IEEE Trans. Commun. Electron. 2013, 82, 204–210. [Google Scholar] [CrossRef]







| Method | Bandwidth | Accuracy | Temperature Drift | Range | Power Dissipation |
|---|---|---|---|---|---|
| Shunt | kHz-MHz | 0.1–2% | 25–300 ppm/K | A-kA | W-kW |
| Hall effect | kHz | 0.5–5% | 50–1000 ppm/K | A-kA | mW |
| Giant magnetoresistance | kHz | 1–10% | 200–1000 ppm/K | mA-kA | mW |
| Tunnel magnetoresistance | kHz | 0.05–3% | 50–200 ppm/K | mA-kA | mW |
| Magneto-optic | kHz-MHz | 0.1–1% | <100 ppm/K | kA-MA | W |
| Fluxgate | kHz | 0.001–0.5% | <50 ppm/K | mA-kA | mW-W |
| Parameter | Description | Value | Unit |
|---|---|---|---|
| μm | Max. magnetic permeability | 84,670 | |
| Bs | Saturation magnetic flux density | 1.069 | T |
| Hc | Coercivity | 0.8488 | A/m |
| do | External diameter of the magnetic core | 38.18 | mm |
| di | Internal diameter of the magnetic core | 29.10 | mm |
| hc | Height of the magnetic core | 8.22 | mm |
| lc | Effective magnetic path length | 78.75 | mm |
| Nex | Exciting winding turns | 225 | |
| Nf | Feedback winding turns | 500 | |
| Ni | Induction winding turns | 500 |
| Parameter | Proposed | Sensor B | Danisense DS400ID | LEM LF 505-S | Unit |
|---|---|---|---|---|---|
| Measurement principle | One-core self-oscillating fluxgate | Three-core self-oscillating fluxgate | One-core fluxgate with modulation circuit | Hall effect | - |
| Nominal current | 600 | 600 | 600 | 500 | A |
| External diameter | 43.81 | 45.79 | 91.5 | 65 | mm |
| Internal diameter | 23.37 | 23.11 | 27.6 | 30.2 | mm |
| Height | 20.54 | 32.54 | 44.5 | 31 | mm |
| Volume | 2.22 × 104 | 3.99 × 104 | 2.66 × 105 | 8.07 × 104 | mm3 |
| Cost/Price | 41.38 | 54.13 | ~400 | ~500 | CNY |
| Current transfer ratio | 500:1 | 500:1 | 2000:1 | 5000:1 | - |
| Excitation frequency | 0.27 | 0.27 | 31.25 | - | kHz |
| Linearity error | 0.07 | 0.01 | 0.0001 | 0.1 | % |
| Relative error | 0.15 | 0.10 | 0.04 | 0.6 | % |
| Small-signal bandwidth | 100 (−1 dB) 170 (−3 dB) | 100 (−1 dB) 170 (−3 dB) | 300 (−3.5 dB) | 100 (−1 dB) | kHz |
| SNR at nominal current | 48.88 | 37.66 | - | - | dB |
| Power-on repeatability | 11.66 | 18.83 | 9 | - | ppm |
| Power consumption at nominal current | 7.1 | 8.5 | 6 | 2.23 | W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Chen, H.; Xu, H.; Li, L. Design and Characterization of a Self-Oscillating Fluxgate-Based Current Sensor for DC Distribution System Applications. Sensors 2025, 25, 2360. https://doi.org/10.3390/s25082360
Chen W, Chen H, Xu H, Li L. Design and Characterization of a Self-Oscillating Fluxgate-Based Current Sensor for DC Distribution System Applications. Sensors. 2025; 25(8):2360. https://doi.org/10.3390/s25082360
Chicago/Turabian StyleChen, Wei, Huaijie Chen, Haibo Xu, and Li Li. 2025. "Design and Characterization of a Self-Oscillating Fluxgate-Based Current Sensor for DC Distribution System Applications" Sensors 25, no. 8: 2360. https://doi.org/10.3390/s25082360
APA StyleChen, W., Chen, H., Xu, H., & Li, L. (2025). Design and Characterization of a Self-Oscillating Fluxgate-Based Current Sensor for DC Distribution System Applications. Sensors, 25(8), 2360. https://doi.org/10.3390/s25082360






