Improvement in and Validation of the Physical Model of an Intelligent Tire Considering the Wear
Abstract
1. Introduction
2. Model Building
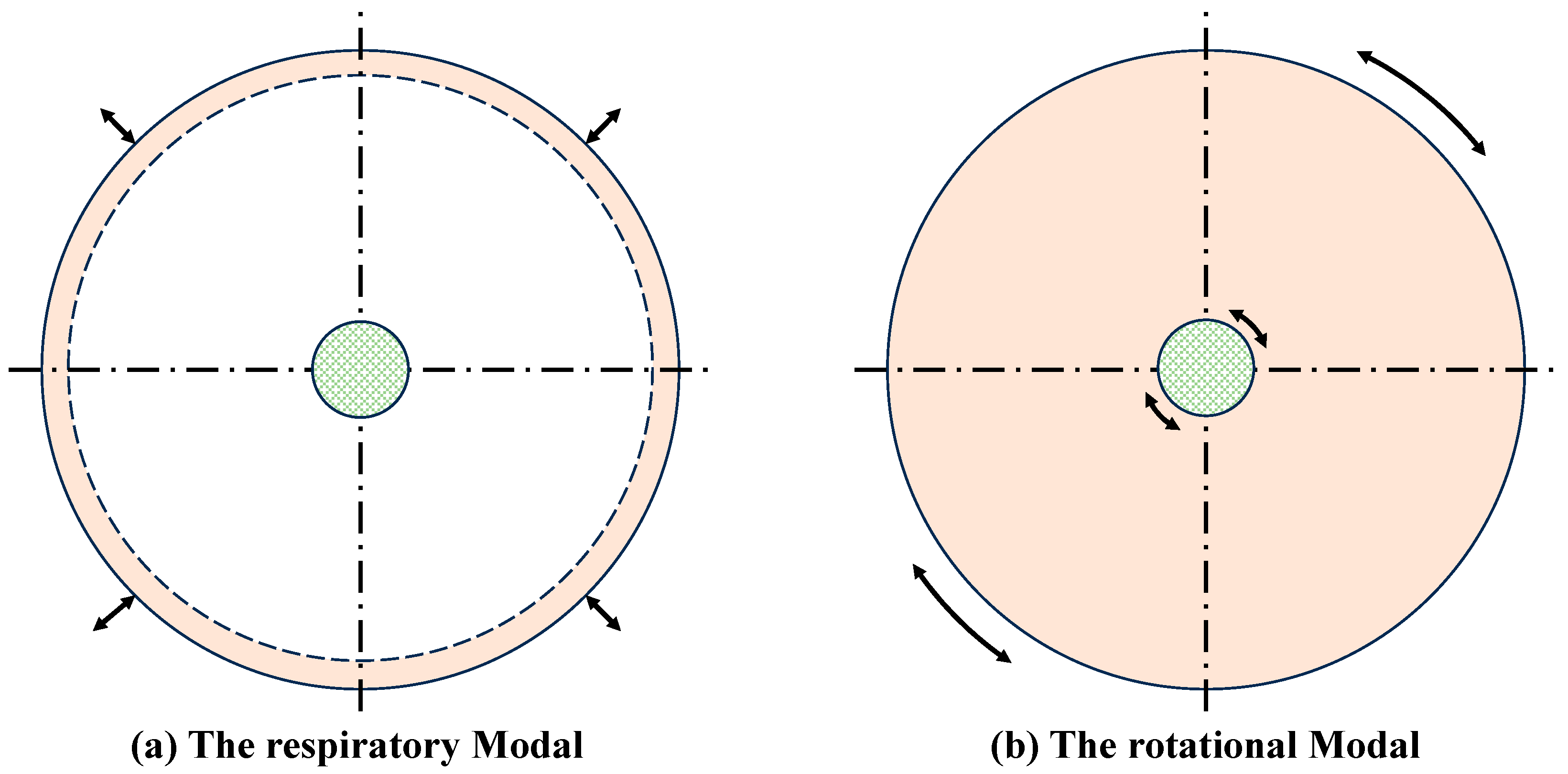
2.1. The Flexible Ring Model
2.2. Model Improvement
2.2.1. Introduction of Tread Wear
2.2.2. Introduction of the Pressure Distribution Function
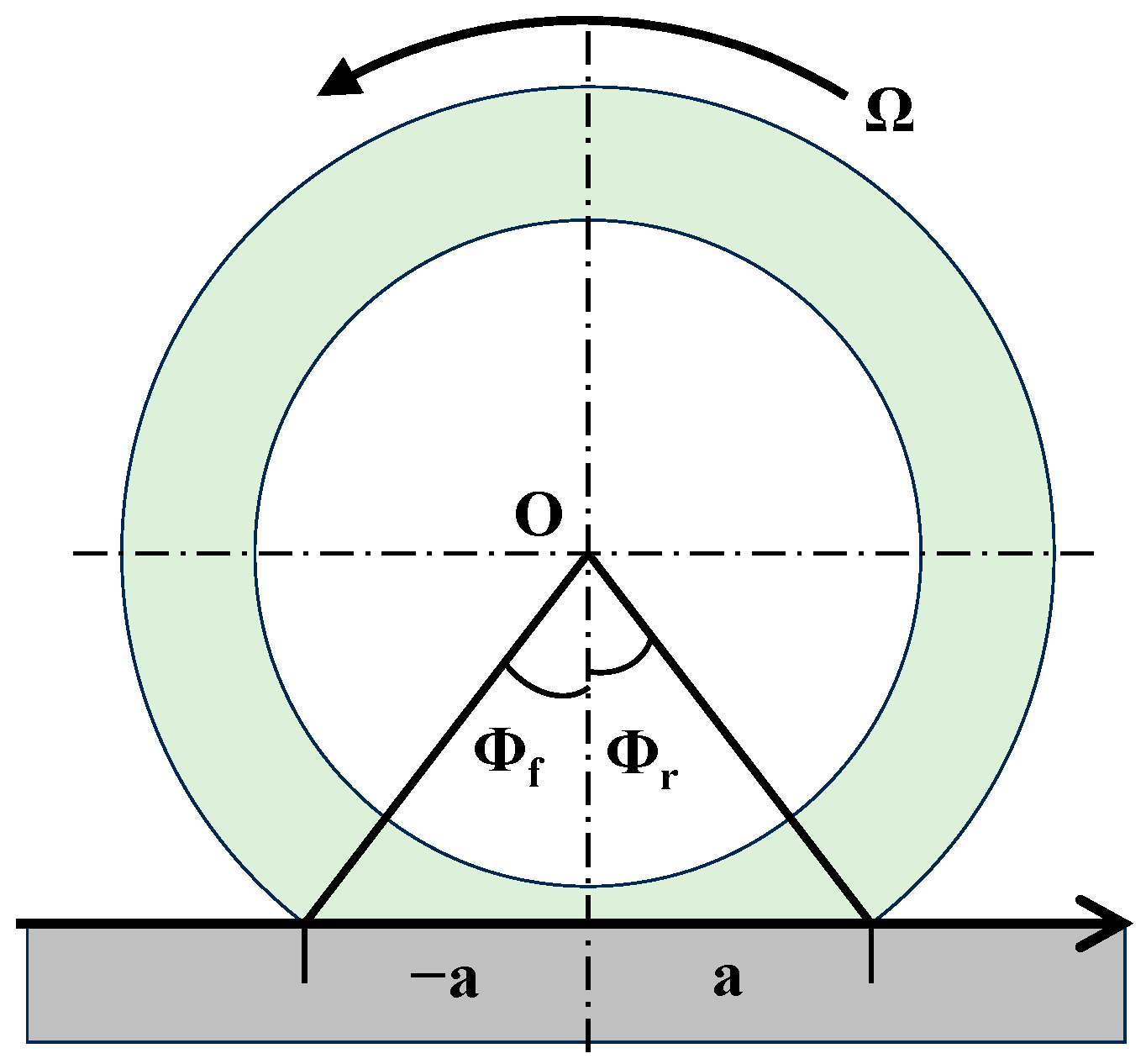
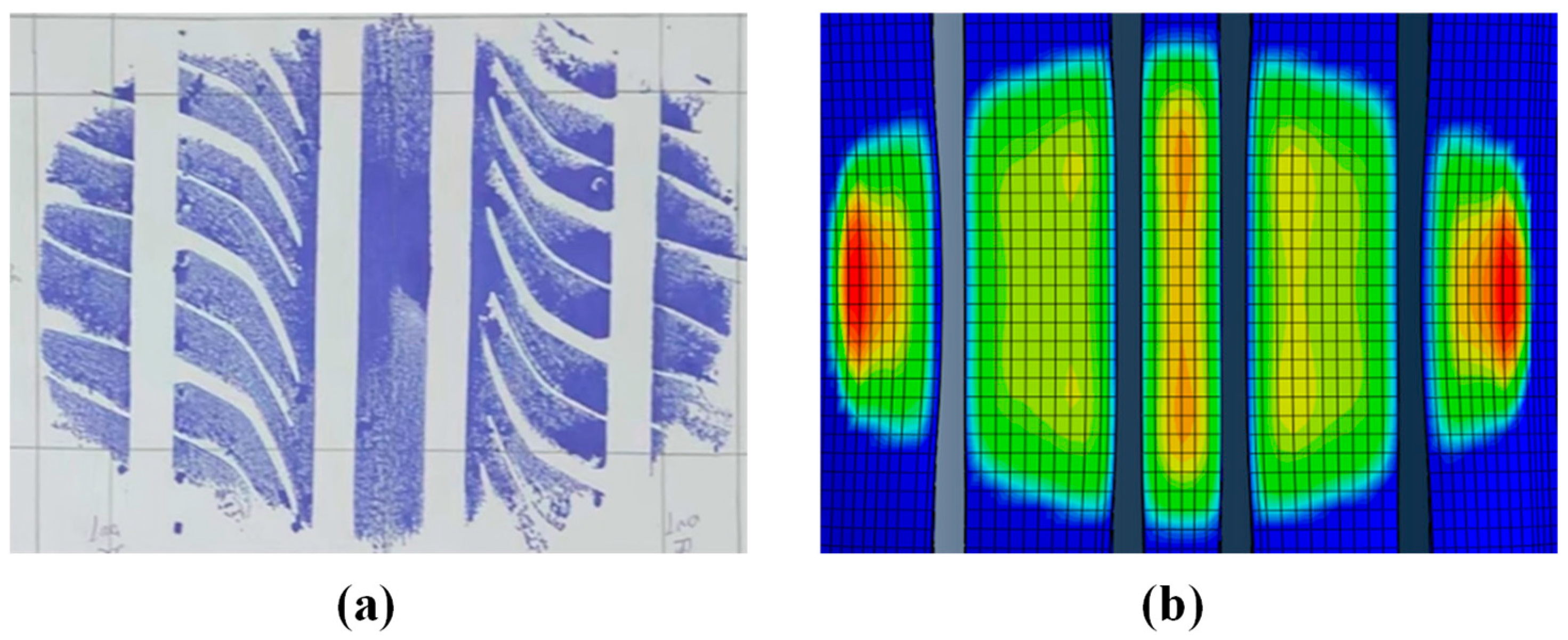
Vertical Force Distribution
Longitudinal Distribution of Forces
3. Model Analysis and Solution
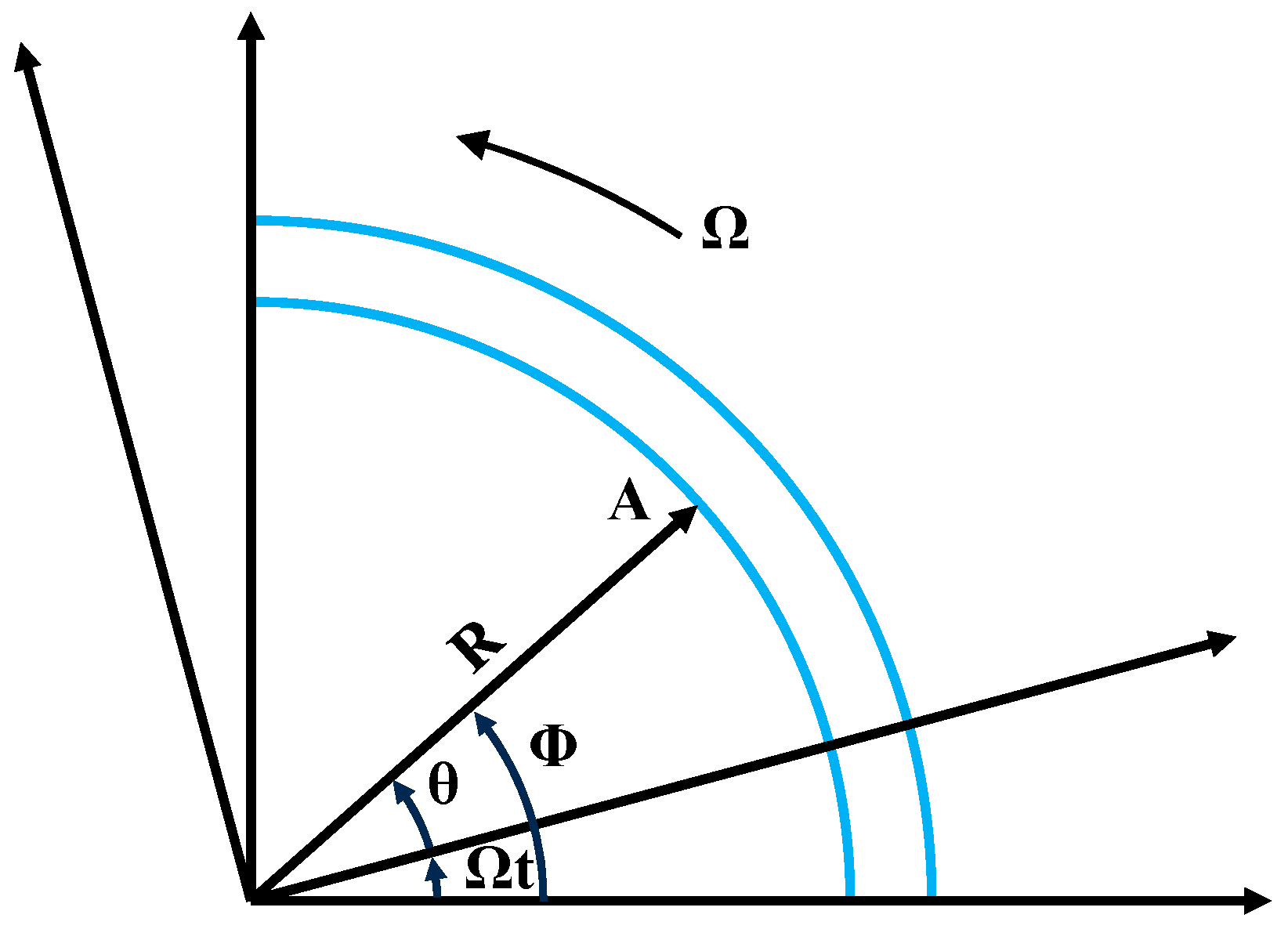
3.1. Energy Equation
3.1.1. Kinetic Energy
3.1.2. Potential Energy
3.1.3. Virtual Work of External Forces
3.1.4. Solution of Motion Equation
3.2. Displacement Expression Solution
3.2.1. Tire Vibration Equation
3.2.2. Tire Response to Concentrated Load
3.2.3. Tire Response to Distributed Load
3.2.4. Circumferential Strain Equation
4. Model Validation
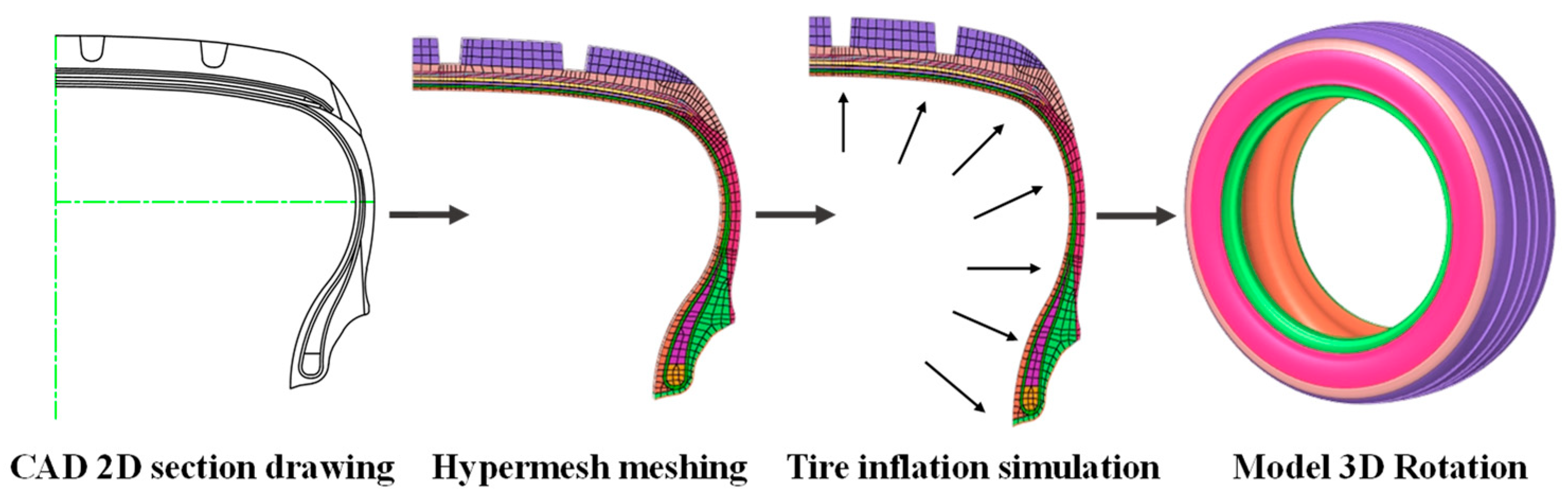
4.1. Parameter Acquisition
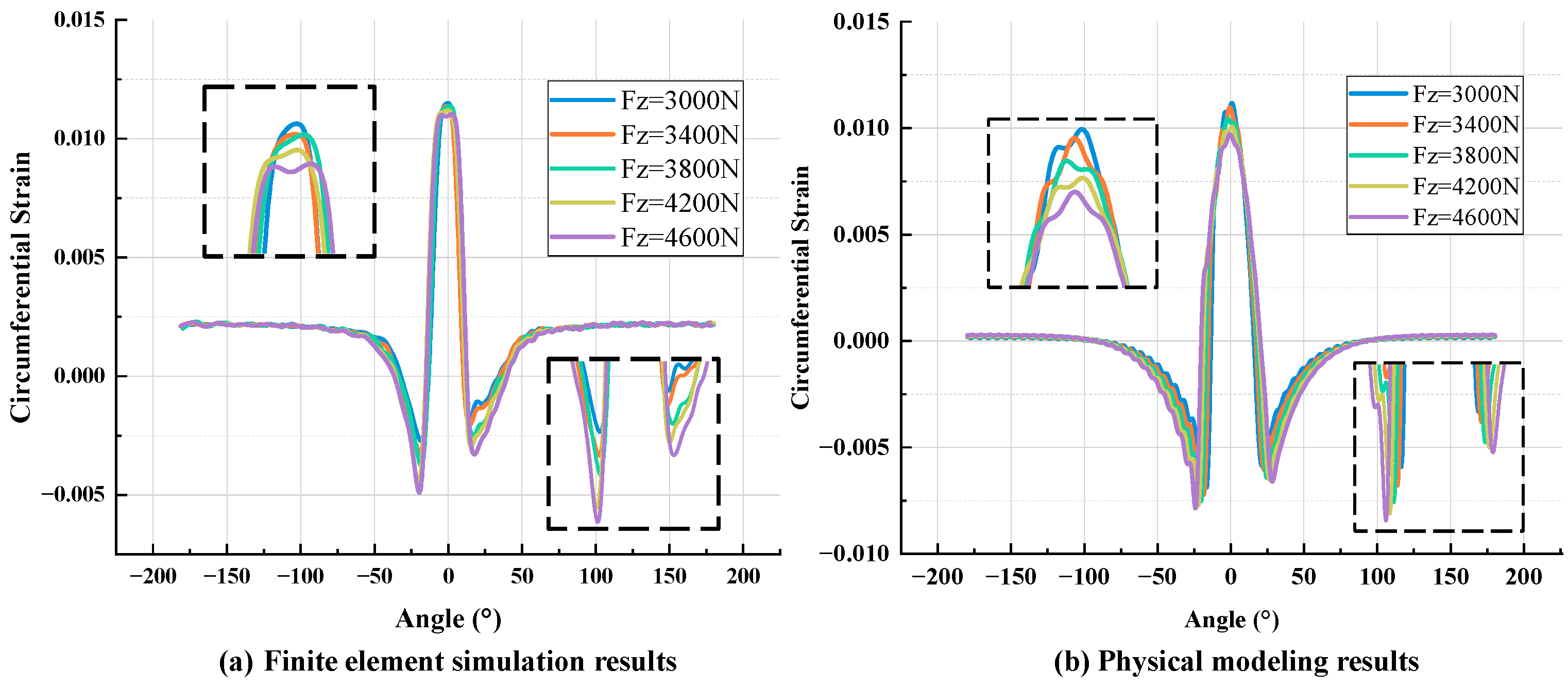
4.2. Finite Element Simulation Verification
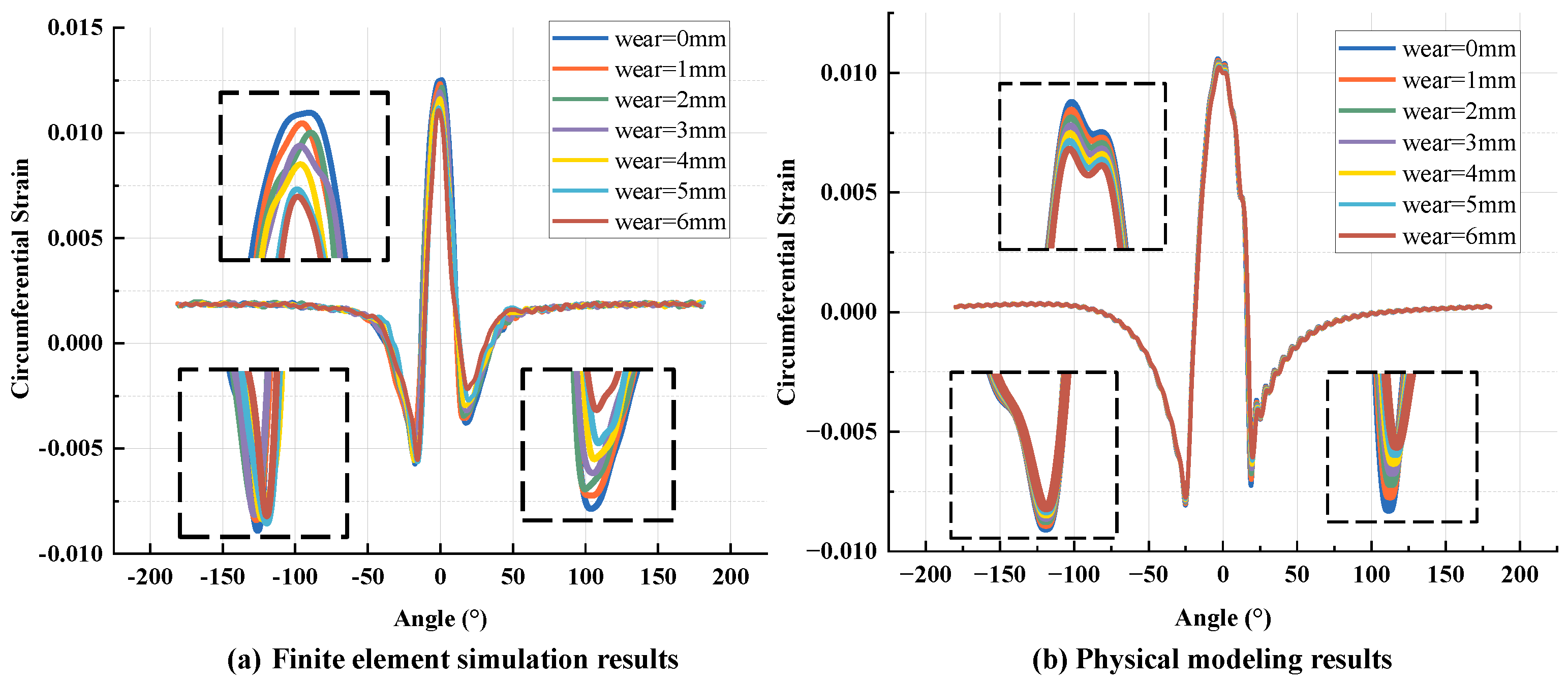
5. Exploring the Effect of Wear on Tire Strain
6. Summary and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Wei, Y.T. Research Progress in Intelligent Tire Technology. In Proceedings of the 2017 Chinese Congress of Theoretical and Applied Mechanics and the 60th Anniversary Celebration of the Chinese Society of Theoretical and Applied Mechanics, Beijing, China, 16 June 2017; pp. 1027–1044. [Google Scholar]
- Xu, N.; Askari, H.; Huang, Y.; Zhou, J.; Khajepour, A. Tire Force Estimation in Intelligent Tires Using Machine Learning. IEEE Trans. Intell. Transp. Syst. 2022, 23, 3565–3574. [Google Scholar] [CrossRef]
- Krier, D.; Zanardo, G.S.; del Re, L. A PCA-Based Modeling Approach for Estimation of Road-Tire Forces by In-Tire Accelerometers. IFAC Proc. Vol. 2014, 47, 12029–12034. [Google Scholar] [CrossRef]
- Tang, Y.; Tao, L.; Li, Y.; Zhang, D.; Zhang, X. Estimation of Tire Side-Slip Angles Based on the Frequency Domain Lateral Acceleration Characteristics inside Tires. Machines 2024, 12, 229. [Google Scholar] [CrossRef]
- Nalawade, R.; Nouri, A.; Gupta, U.; Gorantiwar, A.; Taheri, S. Improved Vehicle Longitudinal Velocity Estimation Using Accelerometer Based Intelligent Tire. Tire Sci. Technol. 2023, 51, 182–209. [Google Scholar] [CrossRef]
- Mendoza-Petit, M.F.; García-Pozuelo, D.; Díaz, V.; Gutiérrez-Moizant, R.; Olatunbosun, O. Automatic Full Slip Detection System Implemented on the Strain-Based Intelligent Tire at Severe Maneuvers. Mech. Syst. Signal Process. 2023, 183, 109577. [Google Scholar] [CrossRef]
- Higuchi, M.; Suzuki, Y.; Sasano, T.; Tachiya, H. Measurement of Road Friction Coefficient Using Strain on Tire Sidewall. Precis. Eng. 2023, 84, 28–36. [Google Scholar] [CrossRef]
- Mendoza-Petit, M.F.; Garcia-Pozuelo, D.; Diaz, V.; Garrosa, M. Characterization of the Loss of Grip Condition in the Strain-Based Intelligent Tire at Severe Maneuvers. Mech. Syst. Signal Process. 2022, 168, 108586. [Google Scholar] [CrossRef]
- Garcia-Pozuelo, D.; Olatunbosun, O.; Yunta, J.; Yang, X.; Diaz, V. A Novel Strain-Based Method to Estimate Tire Conditions Using Fuzzy Logic for Intelligent Tires. Sensors 2017, 17, 350. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, H.; Yang, B.; Ni, S.; Huo, R.; Lian, C. A Spoke Strain-Based Method to Estimate Tire Condition Parameters for Intelligent Tires. Sens. Actuators A Phys. 2024, 367, 115035. [Google Scholar] [CrossRef]
- Ma, S.L. Intelligent Tire Measurement and Control System Based on PVDF Sensors. Master’s Thesis, Tianjin University, Tianjin, China, 2012. [Google Scholar]
- Wei, G.C. Research on Identification of Multi-Dimensional Mechanical Characteristics of Intelligent Tires. Master’s Thesis, Jilin University, Changchun, China, 2024. [Google Scholar]
- Yang, S.; Wang, R.; Shi, R.; Chen, Y.; Lu, J.; Li, Z.; Cao, Y. An Intelligent Tyre System for Road Condition Perception. Int. J. Pavement Eng. 2022, 24, 2096882. [Google Scholar] [CrossRef]
- Sun, X.; Quan, Z.; Cai, Y.; Chen, L.; Li, B. Direct Tire Slip Angle Estimation Using Intelligent Tire Equipped with PVDF Sensors. IEEE/ASME Trans. Mechatron. 2024, 1–11. [Google Scholar] [CrossRef]
- Marsili, R. Measurement of the Dynamic Normal Pressure between Tire and Ground Using PVDF Piezoelectric Films. IEEE Trans. Instrum. Meas. 2000, 49, 736–740. [Google Scholar] [CrossRef]
- Dong, H.; Wang, Z.; Yang, C.; Chang, Y.; Wang, Y.; Li, Z.; Deng, Y.; He, Z. Liquid Metal-Based Flexible Sensing and Wireless Charging System for Smart Tire Strain Monitoring. IEEE Sens. J. 2024, 24, 1304–1312. [Google Scholar] [CrossRef]
- Yue, Y.; Li, X.; Zhao, Z.; Wang, H.; Guo, X. Stretchable Flexible Sensors for Smart Tires Based on Laser-Induced Graphene Technology. Soft Sci. 2023, 3, 13. [Google Scholar] [CrossRef]
- Li, B.; Gu, T.; Quan, Z.; Bei, S.; Zhou, D.; Zhou, X.; Han, X. The Tire Slip Angle Estimation Algorithm Based on Intelligent Tire Technology. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2024, 238, 1589–1608. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, S.; Guo, H.; Wang, B.; Gong, Y.; Zhong, S.; Peng, Y.; Zheng, J.; Xiao, X. On the Performance of Freestanding Rolling Mode Triboelectric Nanogenerators from Rotational Excitations for Smart Tires. Nano Energy 2023, 113, 108595. [Google Scholar] [CrossRef]
- Wang, Z.X. Design of In-Tire Sensing and Tire Force Estimation Based on Triboelectric Nanogenerator. Master’s Thesis, Jilin University, Changchun, China, 2024. [Google Scholar]
- Gao, Q.; Li, W.; Shi, Y.; Liao, W.-H.; Yin, G.; Li, J.; Wang, C.; Qiu, R. A Rotating Auxetic Energy Harvester for Vehicle Wheels. Eng. Struct. 2023, 288, 116190. [Google Scholar] [CrossRef]
- Xu, N.; Zhou, J.; Barbosa, B.H.G.; Askari, H.; Khajepour, A. A Soft Sensor for Estimating Tire Cornering Properties for Intelligent Tires. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 6056–6066. [Google Scholar] [CrossRef]
- Barbosa, B.H.G.; Xu, N.; Askari, H.; Khajepour, A. Lateral Force Prediction Using Gaussian Process Regression for Intelligent Tire Systems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 5332–5343. [Google Scholar] [CrossRef]
- Tang, X.; Shi, Y.; Chen, B.; Longden, M.; Farooq, R.; Lees, H.; Jia, Y. A Miniature and Intelligent Low-Power in Situ Wireless Monitoring System for Automotive Wheel Alignment. Measurement 2023, 211, 112578. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, L.; Huang, C.; Lu, Y.; Wang, C. A Dynamic Tire Model Based on HPSO-SVM. Int. J. Agric. Biol. Eng. 2019, 12, 36–41. [Google Scholar] [CrossRef]
- Viehweger, M.; Vaseur, C.; van Aalst, S.; Acosta, M.; Regolin, E.; Alatorre, A.; Desmet, W.; Naets, F.; Ivanov, V.; Ferrara, A.; et al. Vehicle State and Tyre Force Estimation: Demonstrations and Guidelines. Veh. Syst. Dyn. 2021, 59, 675–702. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, K.-S.; Yoon, Y.-S. Development of a Tire Model Based on an Analysis of Tire Strain Obtained by an Intelligent Tire System. Int. J. Automot. Technol. 2015, 16, 865–875. [Google Scholar] [CrossRef]
- Tong, Z.; Cao, Y.; Wang, R.; Chen, Y.; Li, Z.; Lu, J.; Yang, S. Machine Learning-Driven Intelligent Tire Wear Detection System. Measurement 2025, 242, 115848. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, L.; Jiang, Z.; Zhang, B.; Liu, G.; Shu, Y.; Peng, B. Real-Time Wheel–Rail Friction Coefficient Estimation and Its Application. Veh. Syst. Dyn. 2023, 61, 2598–2612. [Google Scholar] [CrossRef]
- Romano, L.; Strano, S.; Terzo, M. Synthesis and Comparative Analysis of Three Model-Based Observers for Normal Load and Friction Estimation in Intelligent Tyre Concepts. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2021, 235, 1629–1642. [Google Scholar] [CrossRef]
- Min, D.; Wei, Y.; Wang, F.; Lu, B.; Zhu, S. A New Lateral Force Estimator for Intelligent Tires Based on Three-Dimensional Ring Model. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2023, 238, 3680–3691. [Google Scholar] [CrossRef]
- Jeong, D.; Kim, S.; Lee, J.; Choi, S.B.; Kim, M.; Lee, H. Estimation of Tire Load and Vehicle Parameters Using Intelligent Tires Combined with Vehicle Dynamics. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]
- Wu, J.W.; Tao, H.T.; Zhang, F.; Zhang, S.W. Detection Method for Intelligent Tire Wear and Load Based on Wavelet Analysis. Electr. Autom. 2024, 46, 104–107. [Google Scholar]
- Min, D.; Wei, Y.; Zhao, T.; He, J. A Fusion Estimation of Tire Vertical Forces Using Model-Based Tire State Estimators for a Dual-Sensor Intelligent Tire. Proc. Inst. Mech. Eng. Part J. Automob. Eng. 2024, 238, 2146–2159. [Google Scholar] [CrossRef]
- Gao, X.; Xiong, Y.; Liu, W.; Zhuang, Y. Modeling and Experimental Study of Tire Deformation Characteristics under High-Speed Rolling Condition. Polym. Test. 2021, 99, 107052. [Google Scholar] [CrossRef]
- Jeong, D.; Choi, S.B.; Lee, J.; Kim, M.; Lee, H. Tire Dimensionless Numbers for Analysis of Tire Characteristics and Intelligent Tire Signals. Mech. Syst. Signal Process. 2021, 161, 107927. [Google Scholar] [CrossRef]
- Gong, S. A Study of In-Plane Dynamics of Tires, Delft: Delft University of Technology, Faculty of Mechanical Engineering and Marine Technology. 1993. Available online: https://resolver.tudelft.nl/uuid:b564a05b-e580-4171-92f3-d79fdc6bdafc (accessed on 10 June 2023).
- Akasaka, T.; Katoh, M.; Nihei, S.; Hiraiwa, M. Two—Dimensional Contact Pressure Distribution of a Radial Tire. Tire Sci. Technol. 1990, 18, 80–103. [Google Scholar] [CrossRef]
- Yamagishi, K.; Jenkins, J.T. The Circumferential Contact Problem for the Belted Radial Tire. J. Appl. Mech. 1980, 47, 513–518. [Google Scholar] [CrossRef]
- Guo, K. UniTire: Unified Tire Model. J. Mech. Eng. 2016, 52, 90–99. [Google Scholar] [CrossRef]
- Roveri, N.; Pepe, G.; Carcaterra, A. OPTYRE—A New Technology for Tire Monitoring: Evidence of Contact Patch Phenomena. Mech. Syst. Signal Process. 2016, 66–67, 793–810. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Besselink, I. Tire and Vehicle Dynamics, 3rd ed.; Butterworth-Heinemann Elsevier: Waltham, MA, USA, 2012; ISBN 978-0-08-097016-5. [Google Scholar]
- Mavros, G.; Rahnejat, H.; King, P.D. Transient Analysis of Tyre Friction Generation Using a Brush Model with Interconnected Viscoelastic Bristles. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2005, 219, 275–283. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D.; Chen, S.K.; Lin, W.C.; Lu, X.P. The UniTire Model: A Nonlinear and Non-Steady-State Tyre Model for Vehicle Dynamics Simulation. Veh. Syst. Dyn. 2005, 43, 341–358. [Google Scholar] [CrossRef]
- Romano, L. Advanced Brush Tyre Modelling; Springer International Publishing: Cham, Switzerland, 2022; ISBN 978-3-030-98434-2. [Google Scholar]
- Pacejka, H.B. Tire Characteristics and Vehicle Handling and Stability. In Tire and Vehicle Dynamics; Elsevier: Amsterdam, The Netherlands, 2012; pp. 1–58. ISBN 978-0-08-097016-5. [Google Scholar]
- Wei, Y.T.; Liu, Z.; Zhou, F.Q.; Zhao, C.L. Three-Dimensional Ring Model of Tires Considering Out-of-Plane Vibration. J. Vib. Eng. 2016, 29, 795–803. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Kaliske, M.; Wei, Y. Tire Rolling Kinematics Model for an Intelligent Tire Based on an Accelerometer. Tire Sci. Technol. 2020, 48, 287–314. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, K.; Wang, L.; Yang, J.; Bo, L. Influence of the Side Branch Structure Pattern of the Imitation Cat’s Claw Function on the Vibration and Noise of Tires. Stroj. Vestn. J. Mech. Eng. 2023, 69, 49–60. [Google Scholar] [CrossRef]
- Nishiyama, K.; Ishizuki, M.; Mori, T. Strain Measurement-Based Self-Diagnosis of Tire Wear Conditions in Slow Driving Vehicles. In Proceedings of the 2022 IEEE Intelligent Vehicles Symposium (IV), Aachen, Germany, 5 June 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 159–166. [Google Scholar]
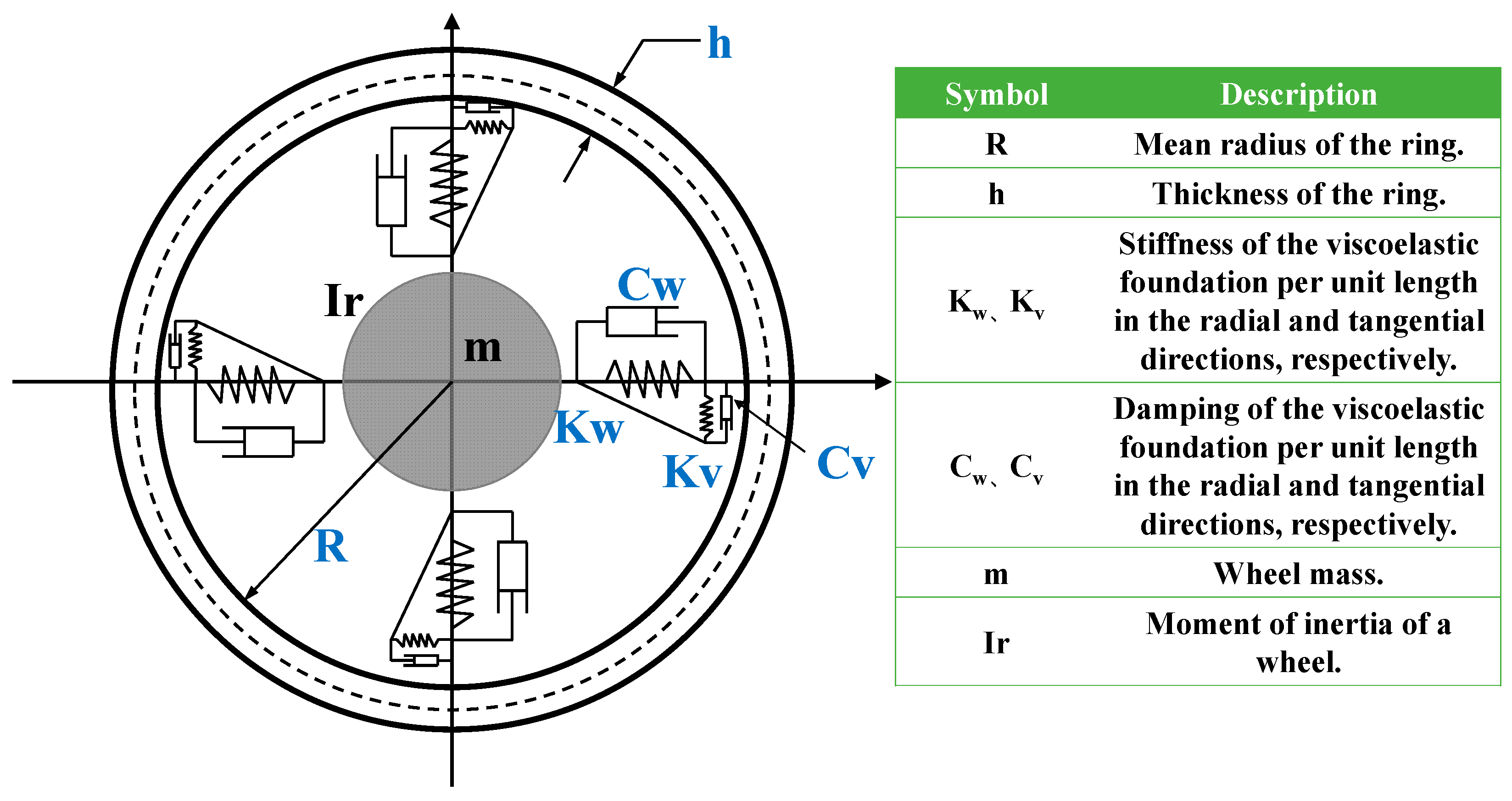
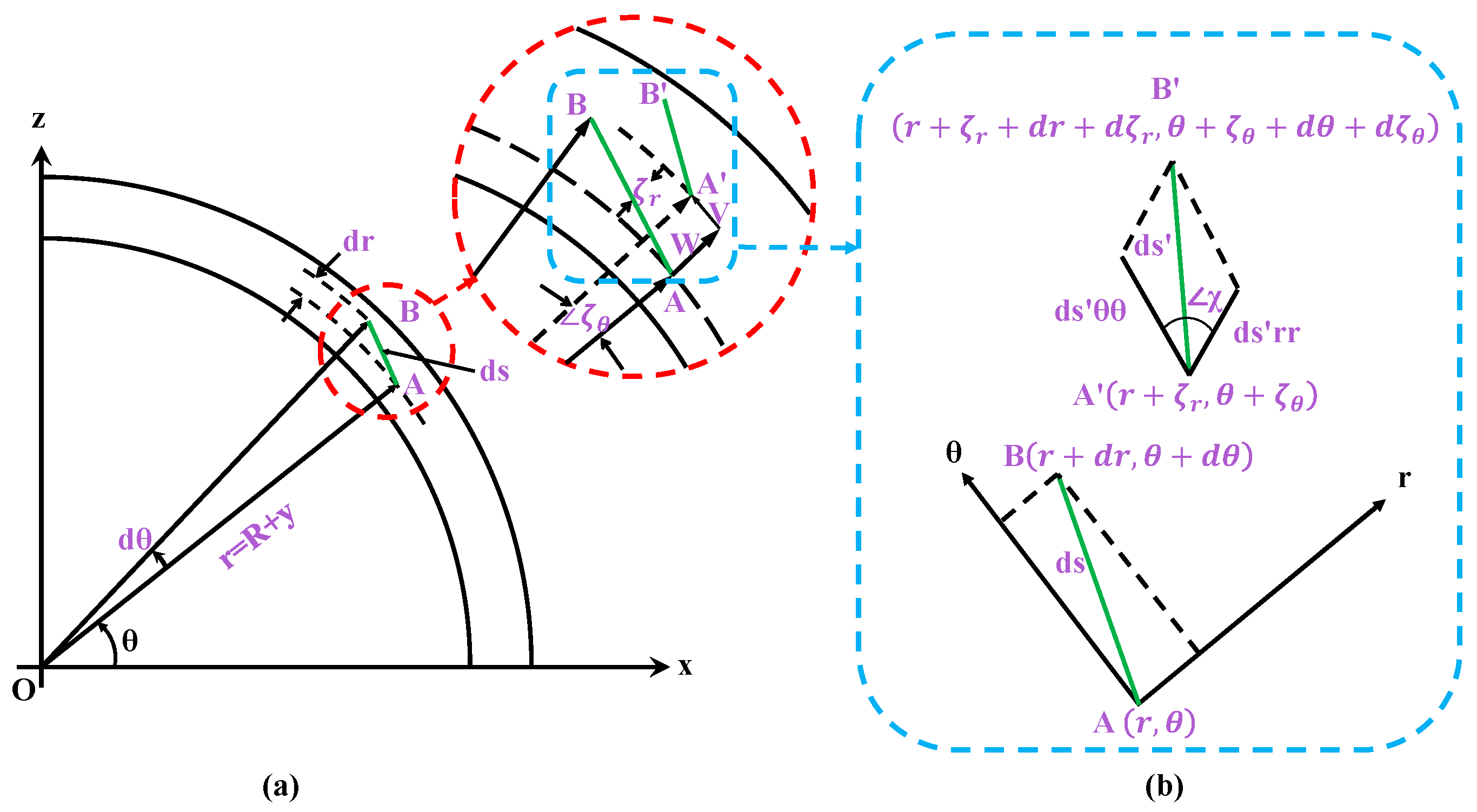
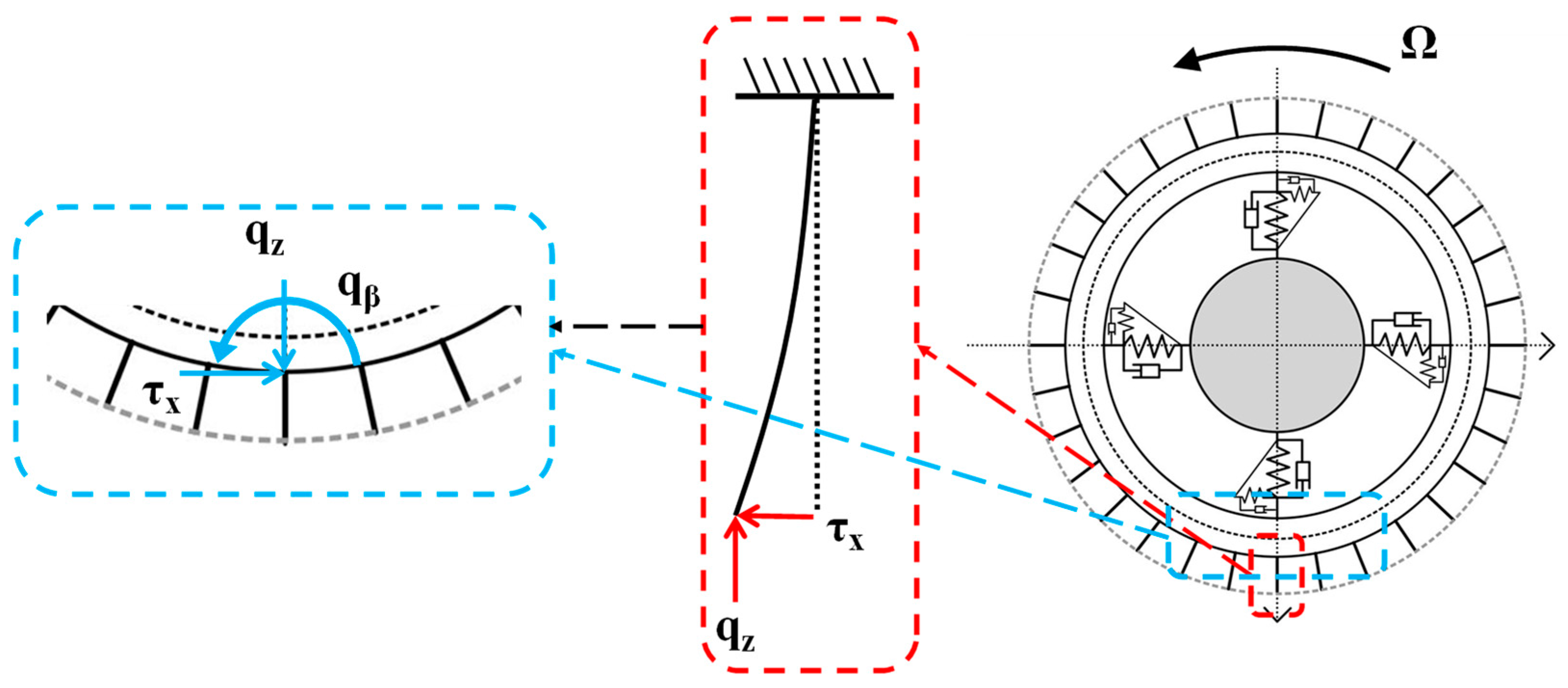
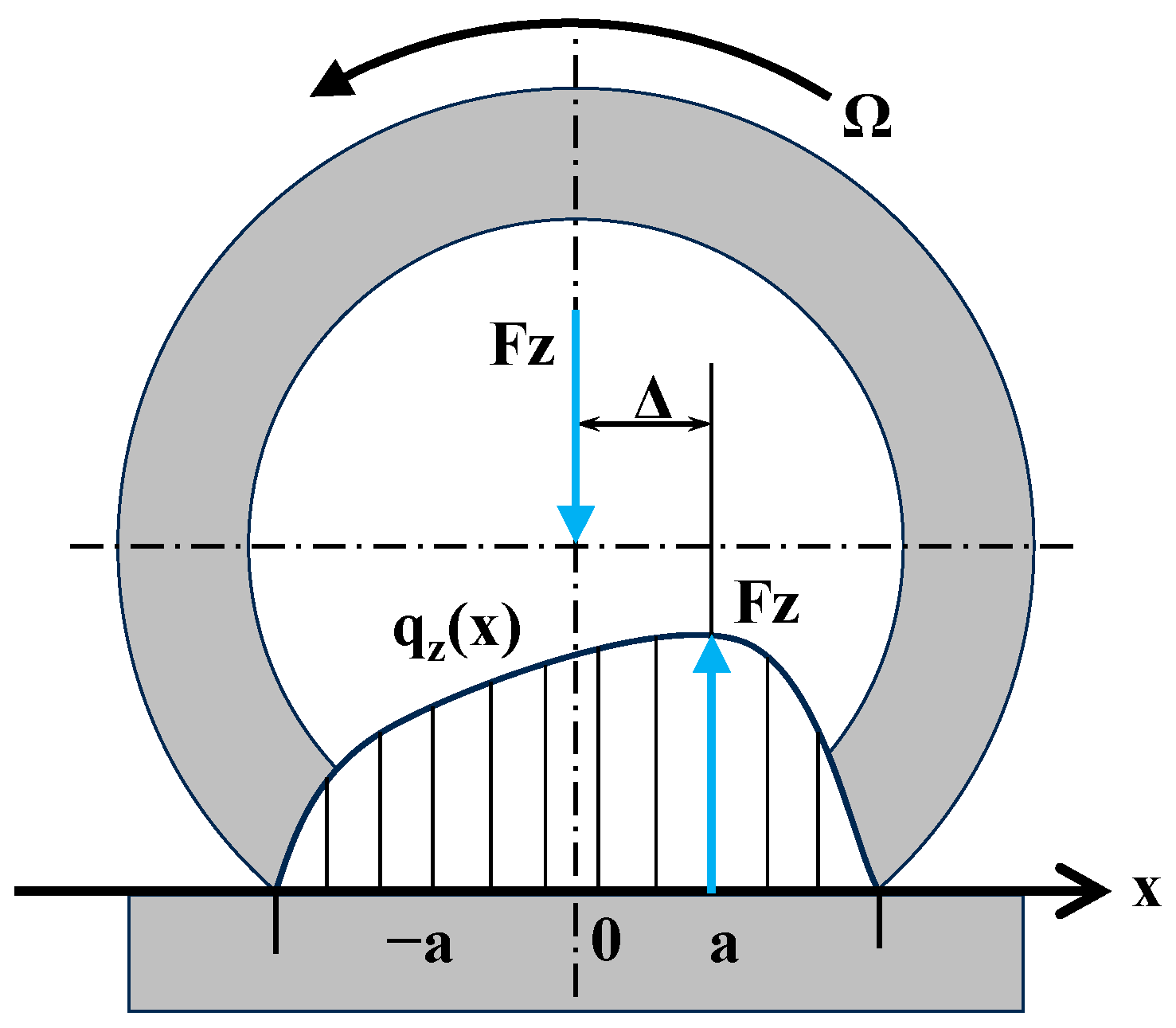


| Parameter Name | Symbols | Value |
|---|---|---|
| Thickness of ring | h (m) | 0.006 |
| Thickness of tread | l (m) | 0.01076 |
| Distance to the inner liner | y (m) | 0.00315 |
| Radius of the ring | R (m) | 0.3023 |
| Width of cross-section | b (m) | 0.189 |
| Area of cross-section | A (m2) | b × h |
| Radial stiffness | kw (N/m) | 9.5 × 105 |
| Tangential stiffness | kv (N/m) | 2.1 × 105 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Li, X.; Jing, Z.; Wang, X.; Zhang, Y. Improvement in and Validation of the Physical Model of an Intelligent Tire Considering the Wear. Sensors 2025, 25, 2490. https://doi.org/10.3390/s25082490
Wang G, Li X, Jing Z, Wang X, Zhang Y. Improvement in and Validation of the Physical Model of an Intelligent Tire Considering the Wear. Sensors. 2025; 25(8):2490. https://doi.org/10.3390/s25082490
Chicago/Turabian StyleWang, Guolin, Xiangliang Li, Zhecheng Jing, Xin Wang, and Yu Zhang. 2025. "Improvement in and Validation of the Physical Model of an Intelligent Tire Considering the Wear" Sensors 25, no. 8: 2490. https://doi.org/10.3390/s25082490
APA StyleWang, G., Li, X., Jing, Z., Wang, X., & Zhang, Y. (2025). Improvement in and Validation of the Physical Model of an Intelligent Tire Considering the Wear. Sensors, 25(8), 2490. https://doi.org/10.3390/s25082490







