Power-Efficient Recycling Folded Cascode Operational Transconductance Amplifier Based on Nested Local Feedback and Adaptive Biasing
Abstract
:1. Introduction
2. Methodology of ERFC OTA
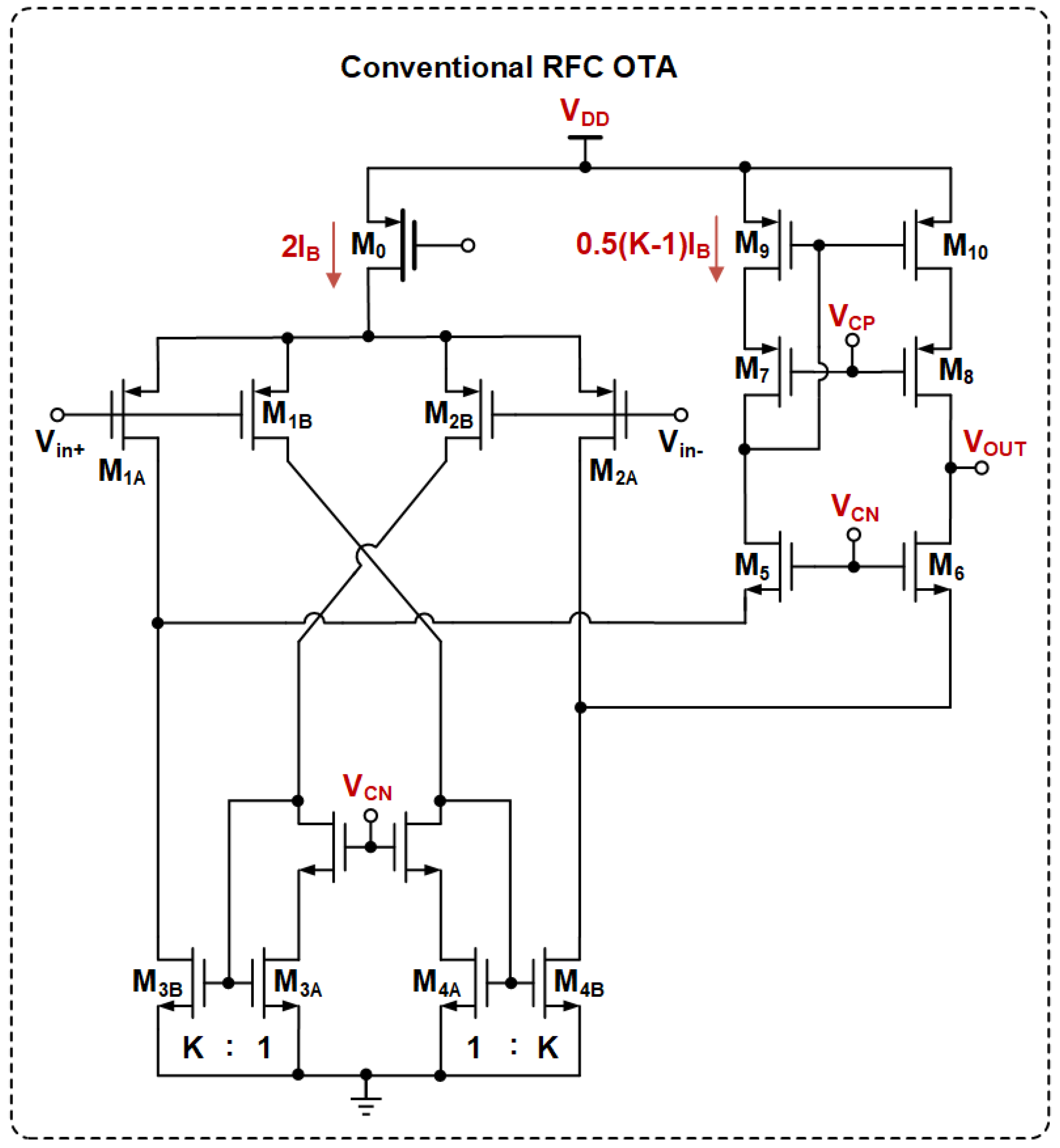
2.1. Limitations of Conventional RFC OTAs
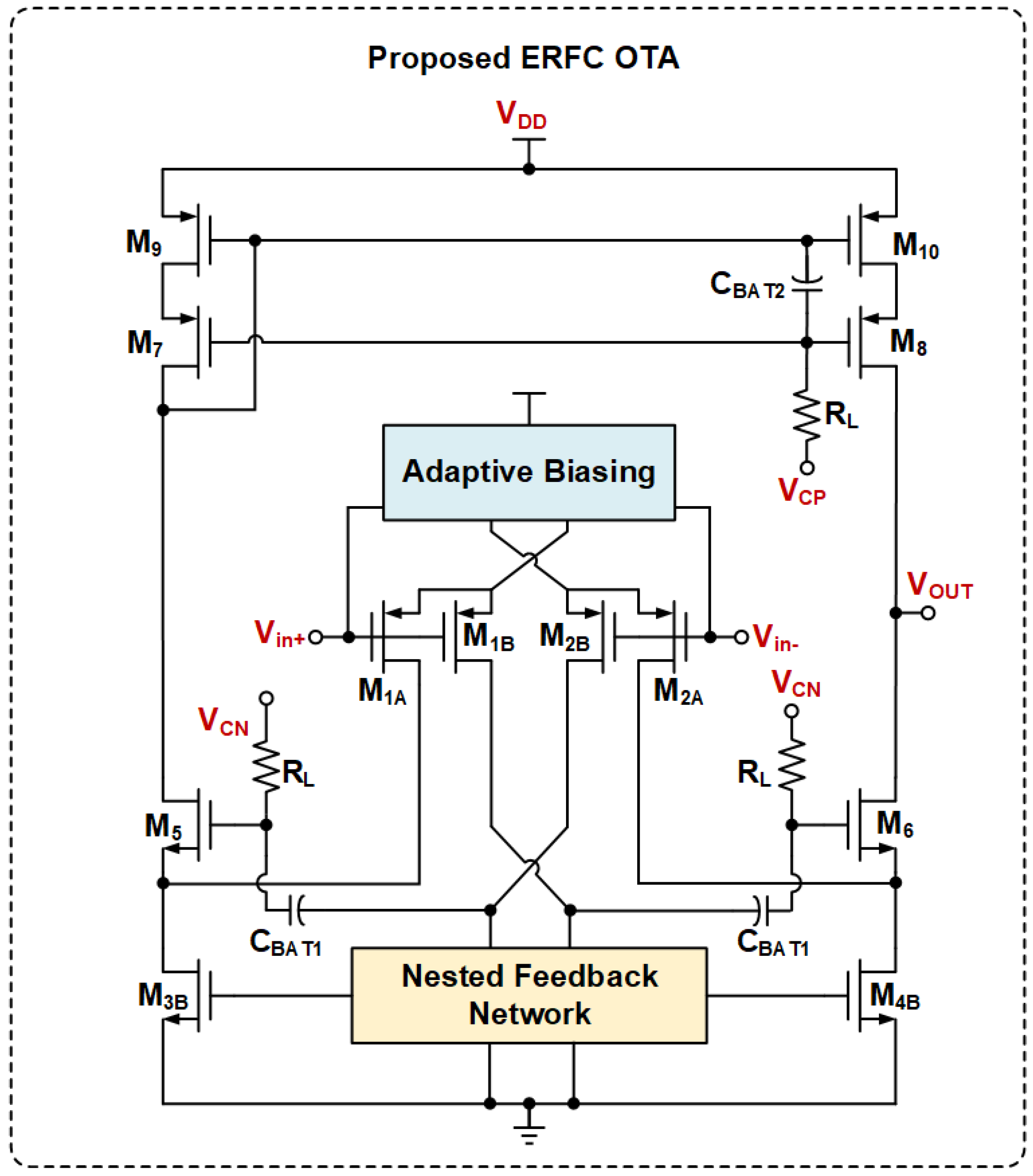
2.2. Concept of ERFC OTA
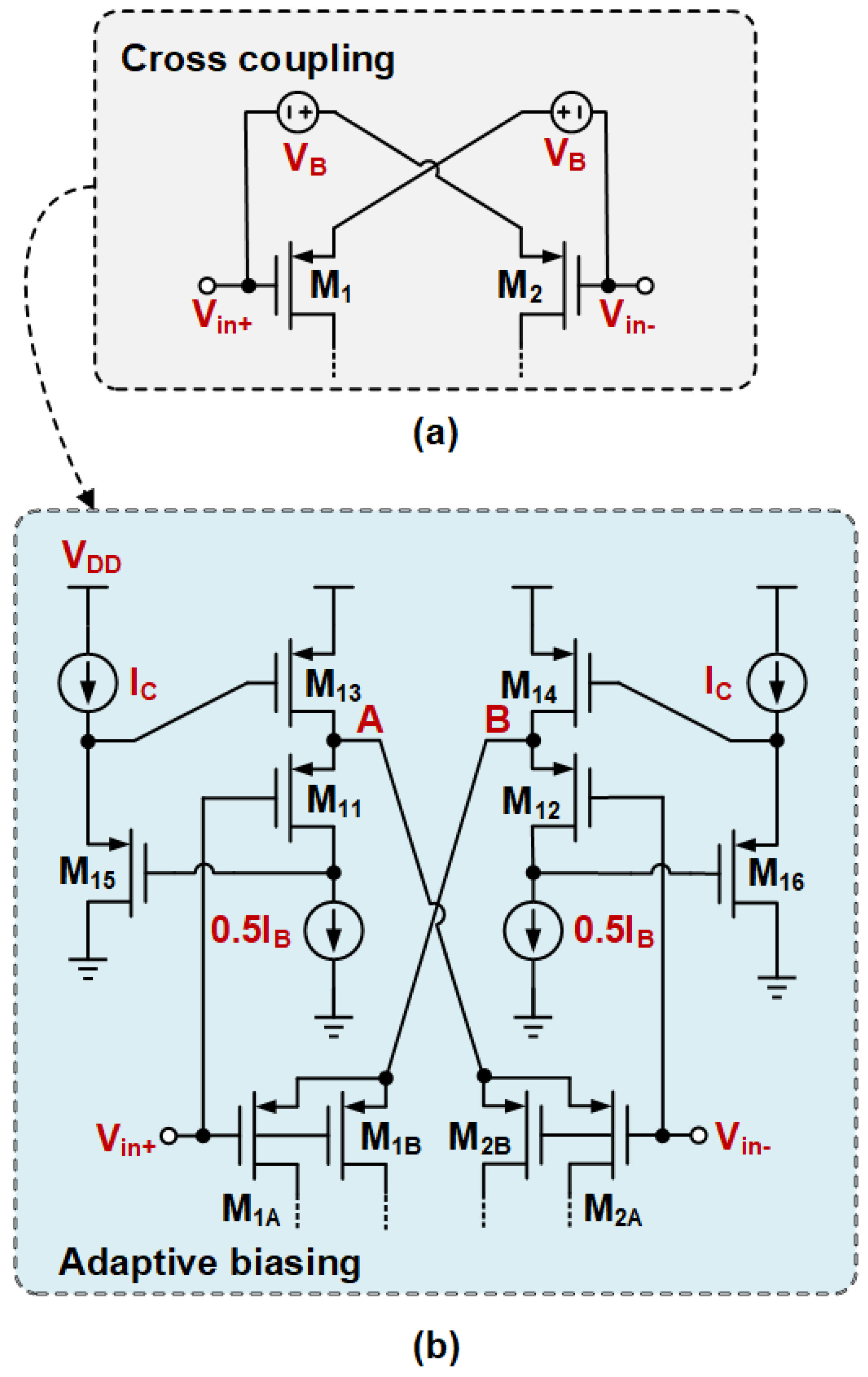
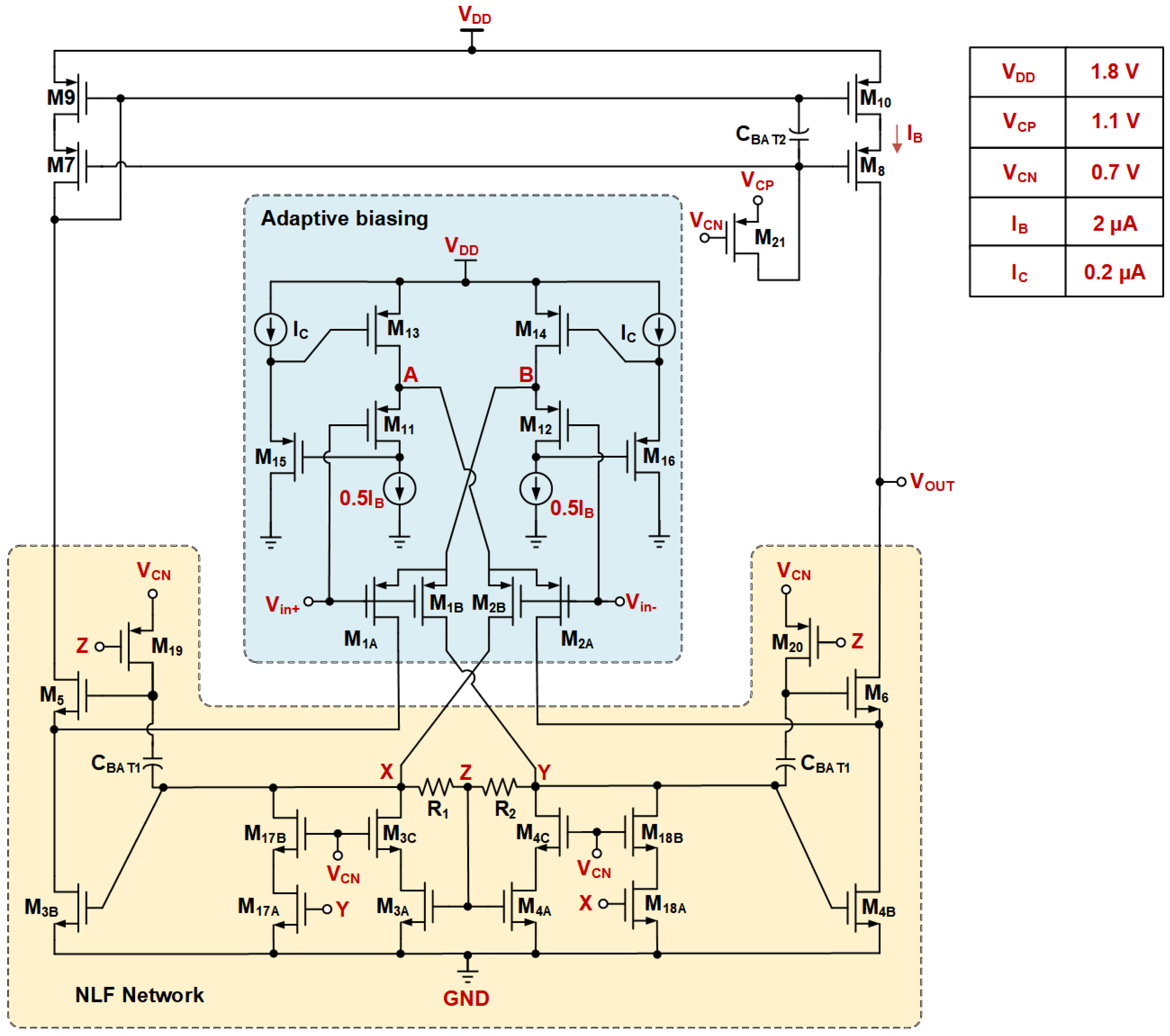
3. Circuit Implementation
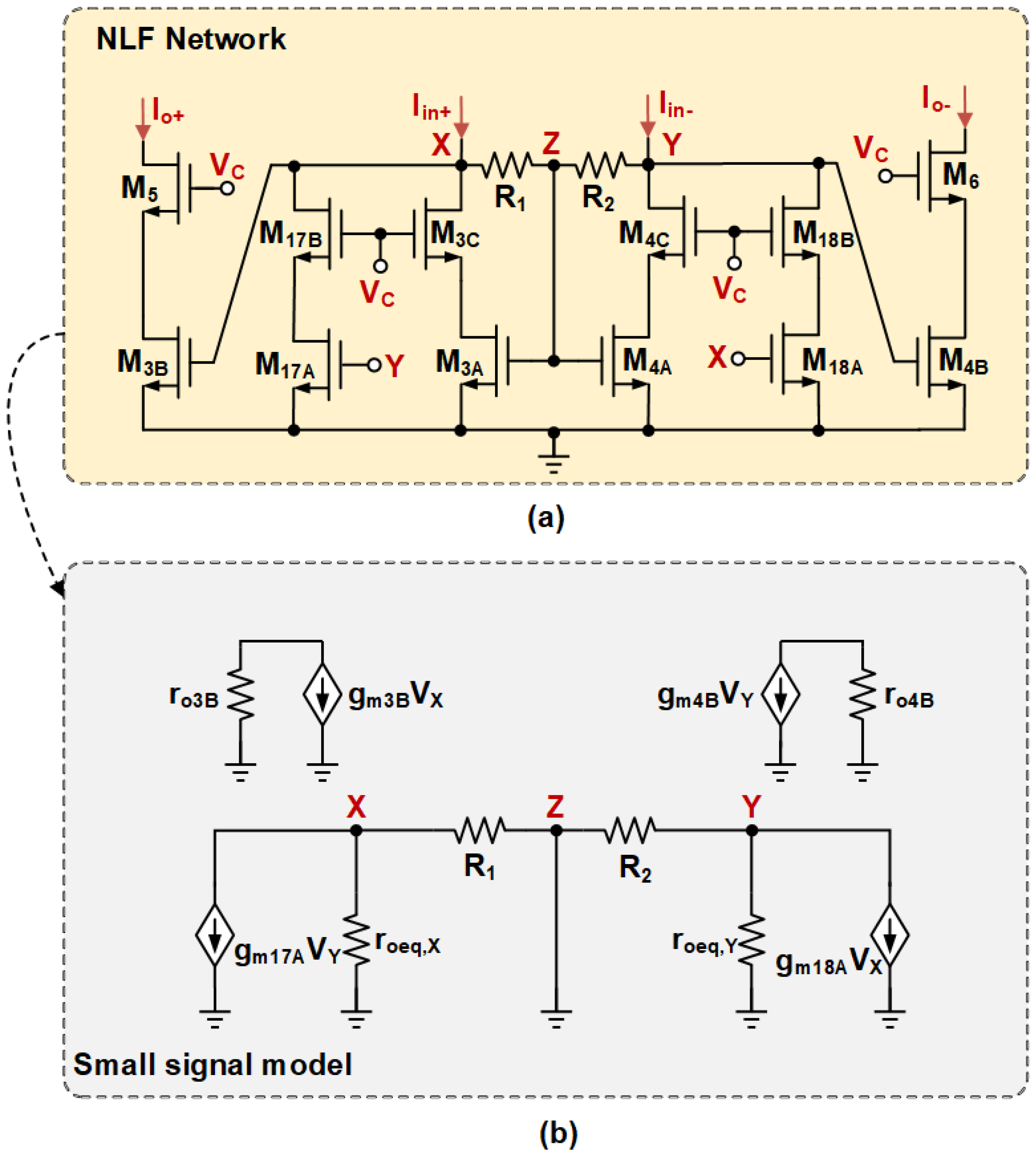
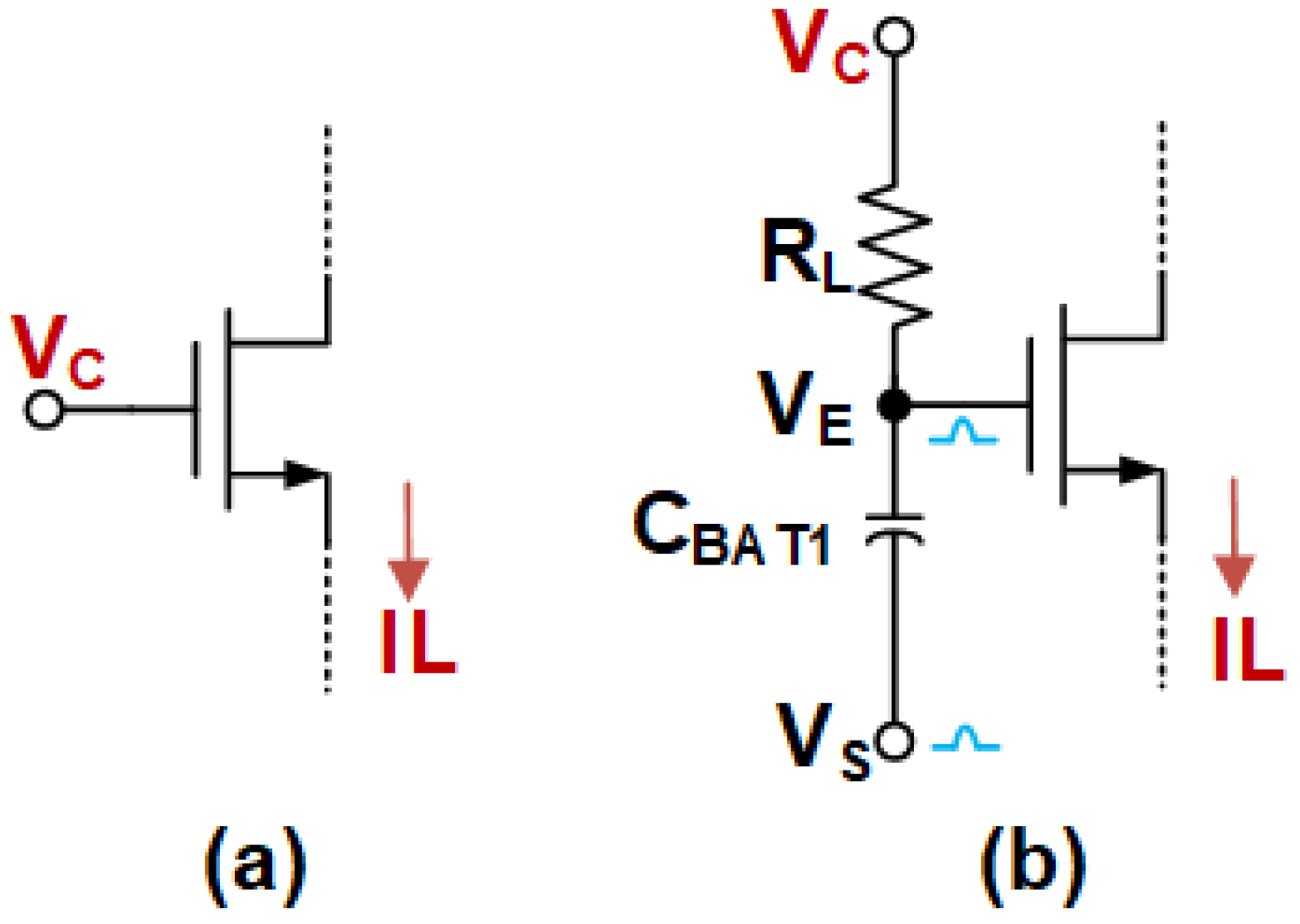
3.1. The ABNLF Technique
3.2. Transistor-Level Implementation
3.3. Small-Signal Analysis
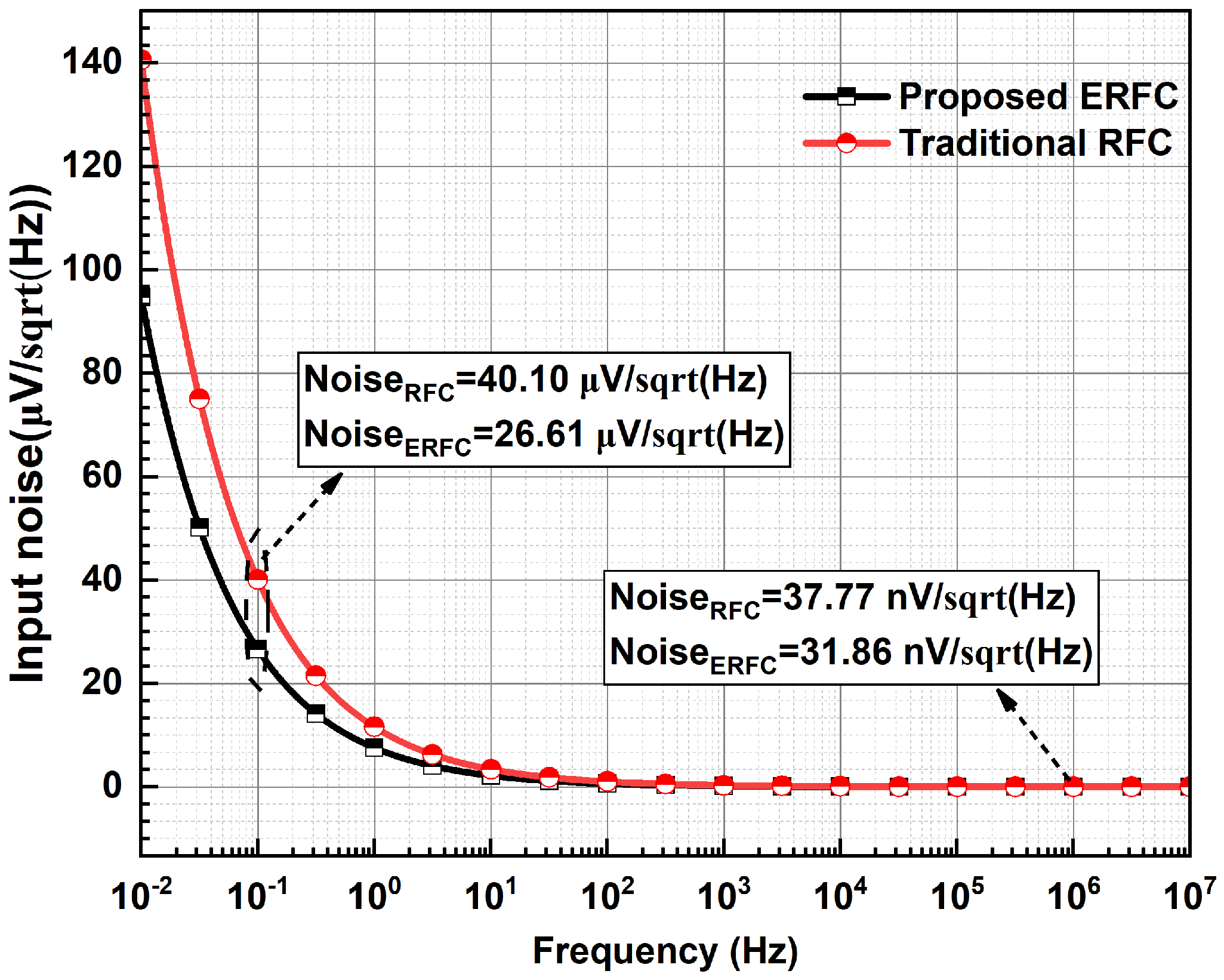
3.4. Noise Analysis
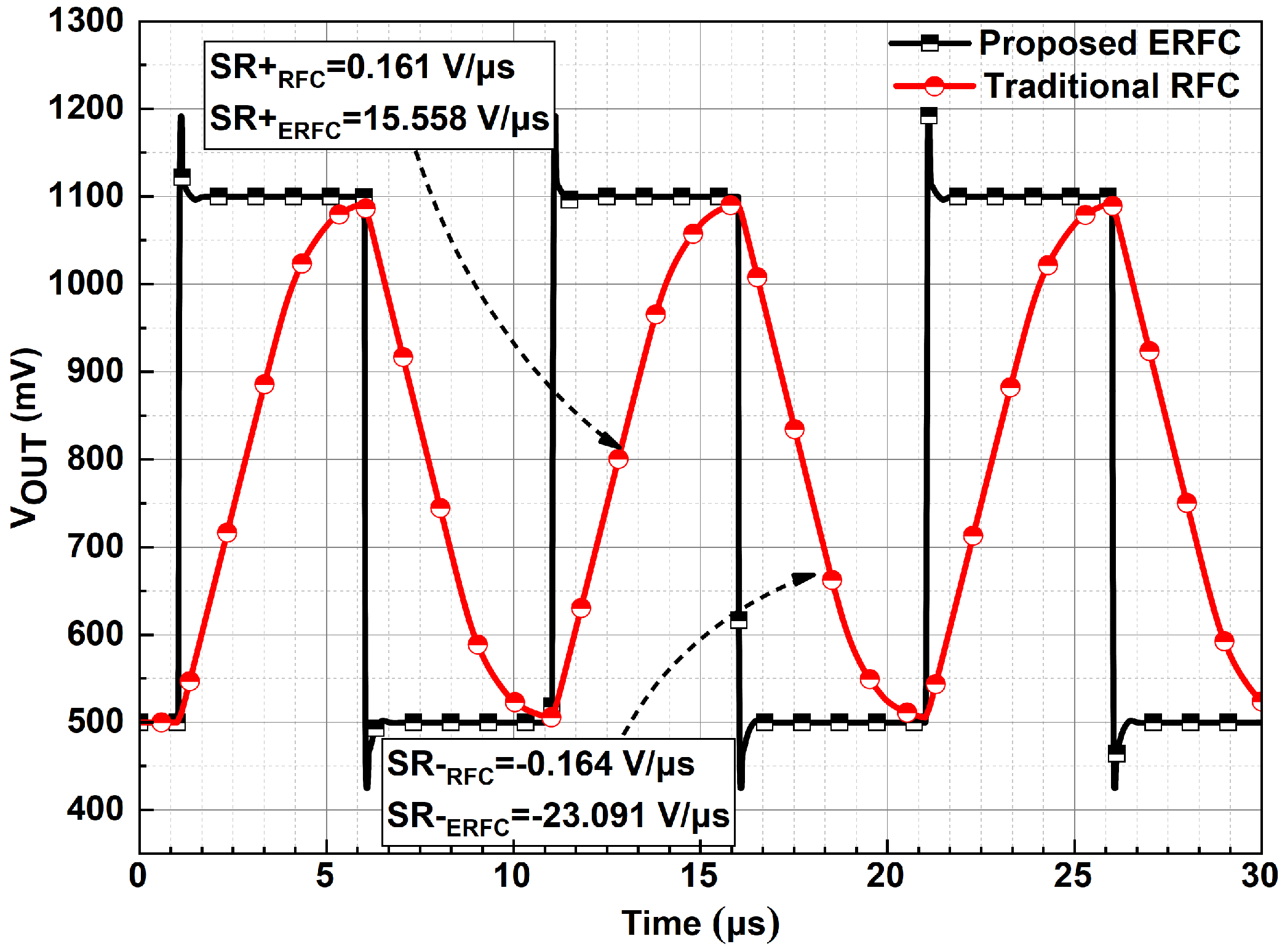
3.5. Large-Signal Response
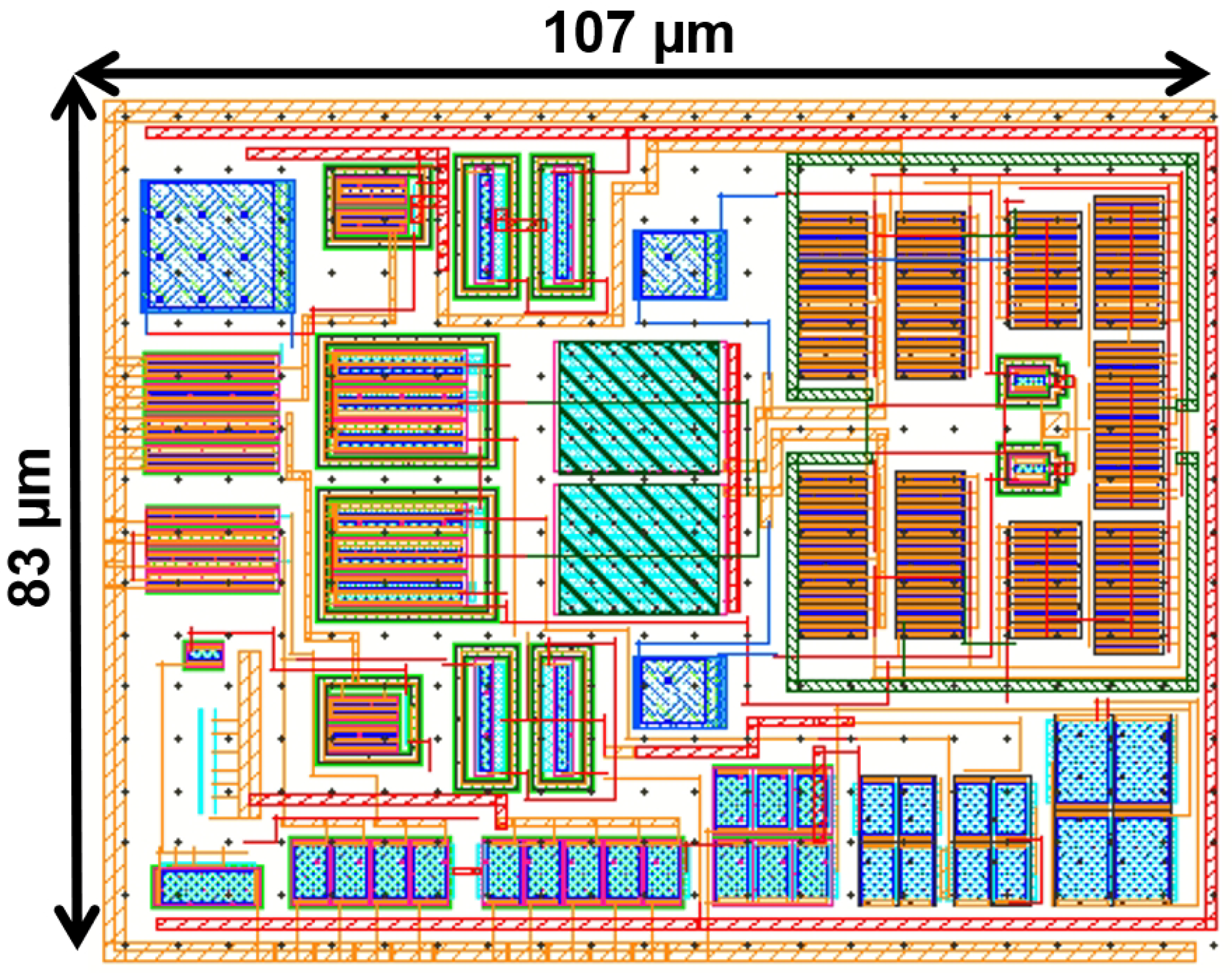
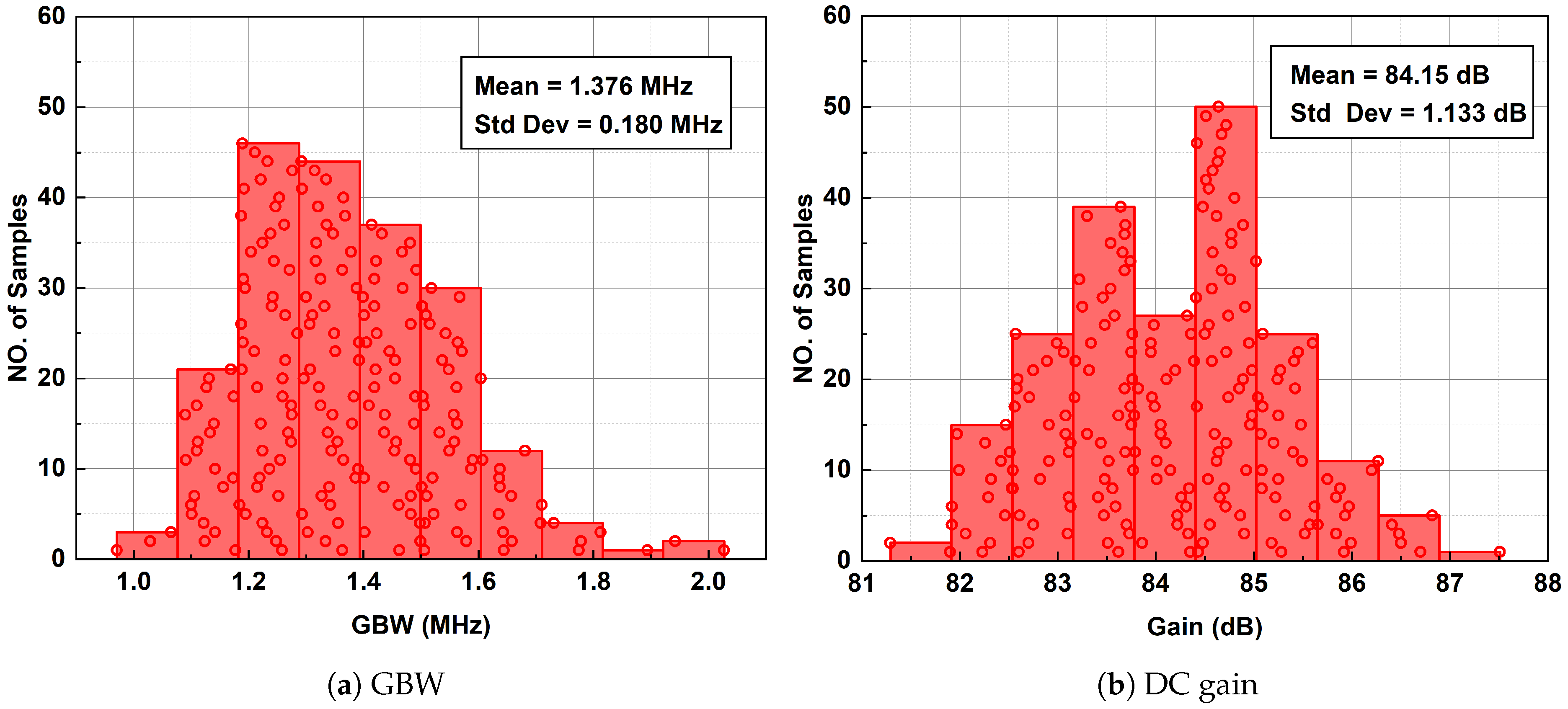
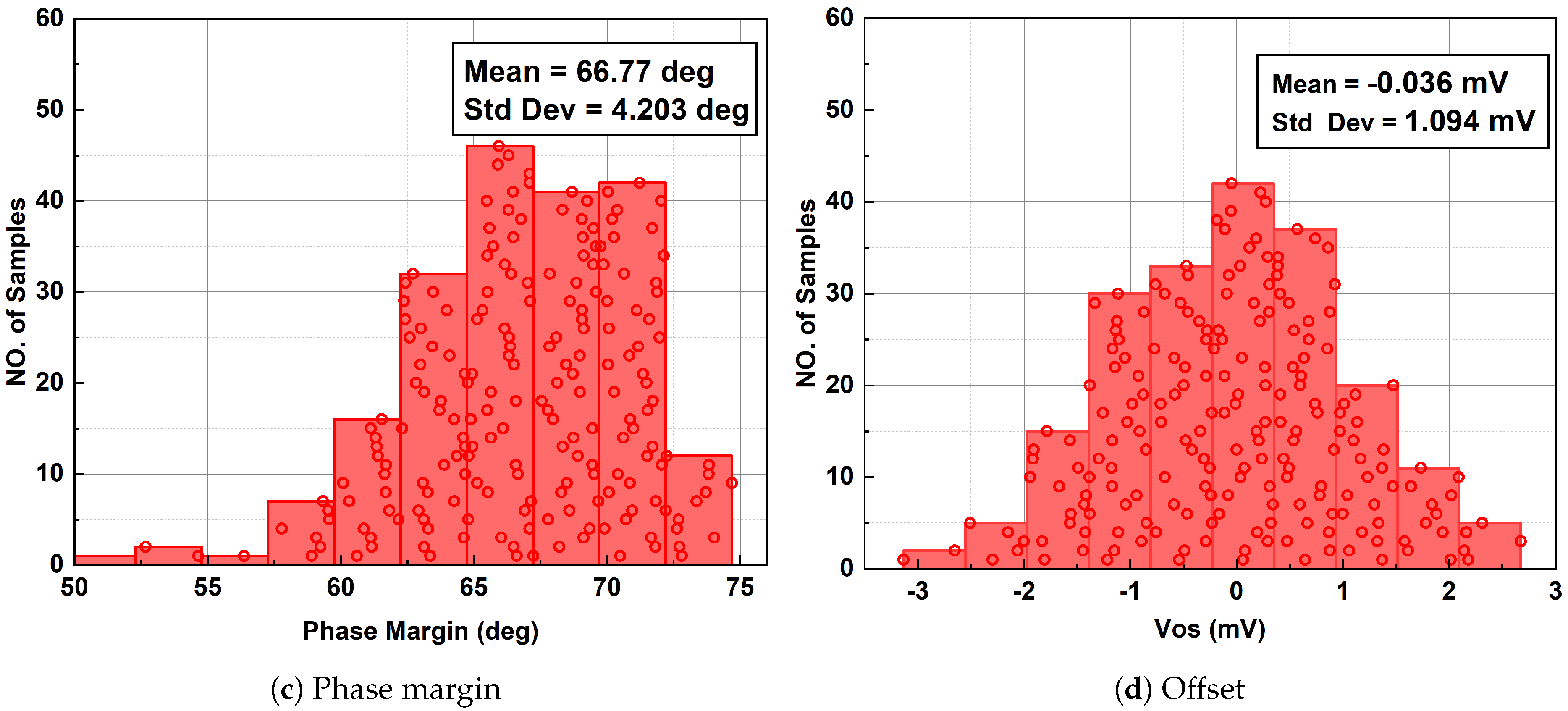
4. Post-Layout Simulations and Comparisons
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Li, S.; Guo, W.; Wen, G.; Sun, N. A 0.029-mm2 17-fJ/Conversion-Step Third-Order CT ΔΣ ADC with a Single OTA and Second-Order Noise-Shaping SAR Quantizer. IEEE J. Solid-State Circuits 2019, 54, 428–440. [Google Scholar] [CrossRef]
- Kulej, T.; Khateb, F.; Kumngern, M. 0.5 V Multiple-Input Fully Differential Operational Transconductance Amplifier and Its Application to a Fifth-Order Chebyshev Low-Pass Filter for Bio-Signal Processing. Sensors 2024, 24, 3013. [Google Scholar] [CrossRef] [PubMed]
- Răducan, C.; Grăjdeanu, A.-T.; Plesa, C.-S.; Neag, M.; Negoiţă, A.; Ţopa, M.D. LDO with Improved Common Gate Class-AB OTA Handles any Load Capacitors and Provides Fast Response to Load Transients. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3740–3752. [Google Scholar] [CrossRef]
- Chen, J.; Sanchez-Sinencio, E.; Silva-Martinez, J. Frequency-dependent harmonic-distortion analysis of a linearized cross-coupled CMOS OTA and its application to OTA-C filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2006, 53, 499–510. [Google Scholar] [CrossRef]
- Zhang, X.; El-Masry, E.I. A Novel CMOS OTA Based on Body-Driven MOSFETs and its Applications in OTA-C Filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 1204–1212. [Google Scholar] [CrossRef]
- Chen, X.; Wang, K.; Liao, H.; Ma, S.; Ma, K. A Power-Efficient Linearized Open-Loop OTA Utilizing Reconfigurable Tail-Resistor Pair. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 2824–2828. [Google Scholar] [CrossRef]
- Akbari, M.; Hussein, S.M.; Hashim, Y.; Khateb, F.; Kulej, T.; Tang, K.-T. Implementation of a Multipath Fully Differential OTA in 0.18-μm CMOS Process. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2023, 31, 147–151. [Google Scholar] [CrossRef]
- Anisheh, S.M.; Abbasizadeh, H.; Shamsi, H.; Dadkhah, C.; Lee, K.-Y. 98-dB Gain Class-AB OTA with 100 pF Load Capacitor in 180-nm Digital CMOS Process. IEEE Access 2019, 7, 17772–17779. [Google Scholar] [CrossRef]
- Li, X.; Hou, B.; Ju, C.; Wei, Q.; Zhou, B.; Zhang, R. A Complementary Recycling Operational Transconductance Amplifier with Data-Driven Enhancement of Transconductance. Electronics 2019, 8, 1457. [Google Scholar] [CrossRef]
- Kim, J.; Song, S.; Roh, J. A High Slew-Rate Enhancement Class-AB Operational Transconductance Amplifier (OTA) for Switched-Capacitor (SC) Applications. IEEE Access 2020, 8, 226167–226175. [Google Scholar] [CrossRef]
- Lv, X.; Zhao, X.; Wang, Y.; Wen, B. An improved non-linear current recycling folded cascode OTA with cascode self-biasing. AEU—Int. J. Electron. Commun. 2019, 101, 182–191. [Google Scholar] [CrossRef]
- Garde, M.P.; Lopez-Martin, A.; Carvajal, R.G.; Ramírez-Angulo, J. Super Class-AB Recycling Folded Cascode OTA. IEEE J. Solid-State Circuits 2018, 53, 2614–2623. [Google Scholar] [CrossRef]
- Assaad, R.S.; Silva-Martinez, J. The Recycling Folded Cascode: A General Enhancement of the Folded Cascode Amplifier. IEEE J. Solid-State Circuits 2009, 44, 2535–2542. [Google Scholar] [CrossRef]
- Assaad, R.; Silva-Martinez, J. Enhancing general performance of folded cascode amplifier by recycling current. Electron. Lett 2007, 43, 1243–1244. [Google Scholar] [CrossRef]
- Li, Y.L.; Han, K.F.; Tan, X.; Yan, N.; Min, H. Transconductance enhancement method for operational transconductance amplifiers. Electron. Lett 2010, 46, 1321–1323. [Google Scholar] [CrossRef]
- Ahmed, M.; Shah, I.; Tang, F.; Bermak, A. An improved recycling folded cascode amplifier with gain boosting and phase margin enhancement. In Proceedings of the 2015 IEEE International Symposium on Circuits and Systems (ISCAS), Lisbon, Portugal, 24–27 May 2015; pp. 2473–2476. [Google Scholar]
- Zhao, X.; Fang, H.; Xu, J. A transconductance enhanced recycling structure for folded cascode amplifier. Analog Integr. Circuits Signal Process 2012, 72, 259–263. [Google Scholar] [CrossRef]
- Dabas, A.; Kumari, S.; Gupta, M.; Yadav, R. Design and Analysis of Class AB RFC OTA with Improved Performance. In Proceedings of the 2022 8th International Conference on Signal Processing and Communication (ICSC), Noida, India, 1–3 December 2022; pp. 582–586. [Google Scholar]
- Yan, Z.; Mak, P.-I.; Martins, R.P. Double recycling technique for folded-cascode OTA. Analog Integr. Circuits Signal Process 2012, 71, 137–141. [Google Scholar] [CrossRef]
- Yavari, M.; Moosazadeh, T. A single-stage operational amplifier with enhanced transconductance and slew rate for switched-capacitor circuits. Analog Integr. Circuits Signal Process 2014, 79, 589–598. [Google Scholar] [CrossRef]
- Ramirez-Angulo, J.; Holmes, M. Simple technique using local CMFB to enhance slew rate and bandwidth of one-stage CMOS op-amps. Electron. Lett 2002, 38, 1409–1411. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Y.; Dong, L. Super current recycling folded cascode amplifier with ultra-high current efficiency. Integration 2018, 62, 322–328. [Google Scholar] [CrossRef]
- Algueta-Miguel, J.M.; Lopez-Martin, A.; Garde, M.P.; De La Cruz, C.A.; Ramirez-Angulo, J. ±0.5 V 15 μW Recycling Folded Cascode Amplifier with 34767 MHz·pF/mA FOM. IEEE Solid-State Circuits Lett. 2018, 1, 170–1731. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Yu, S.S.; Zhao, X.; Trinh, H.; Shi, P. A Robust Local Positive Feedback Based Performance Enhancement Strategy for Non-Recycling Folded Cascode OTA. IEEE Trans. Circuits Syst. I Regul. Pap 2020, 67, 2897–2908. [Google Scholar] [CrossRef]


| ERFC OTA | RFC OTA | ||||
|---|---|---|---|---|---|
| 24 m/0.6 m | 48 m/0.3 m | 24 m/0.6 m | |||
| 18 m/0.3 m | 24 m/0.3 m | 18 m/0.3 m | |||
| 12 m/0.3 m | 30 m/0.3 m | 90 m/0.3 m | |||
| 90 m/0.3 m | 1 m/20 m | 24 m/0.3 m | |||
| 60 m/0.3 m | 3 m/1 m | 60 m/0.3 m | |||
| 24 m/0.3 m | 52 k | 48 m/0.3 m | |||
| Parameter | Traditional RFC OTA | Proposed ERFC OTA |
|---|---|---|
| Supply current (A) | 8 | 10.4 |
| (pF) | 70 | 70 |
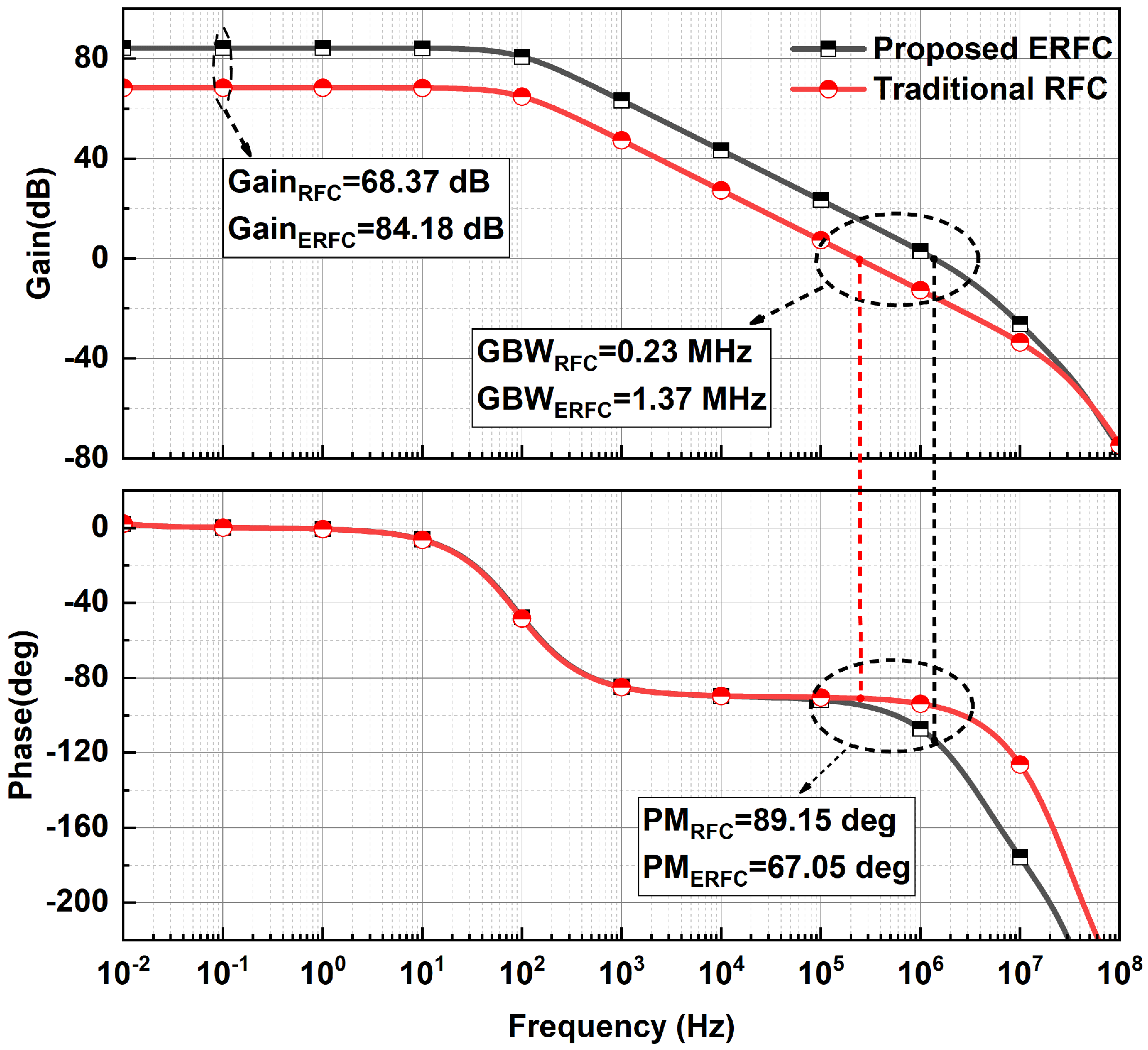
| GBW (MHz) | 0.23 | 1.37 |
| DC gain (dB) | 68.37 | 84.18 |
| Phase margin (∘) | 89.15 | 67.05 |
| Average slew rate (V/s) | 0.16 | 19.32 |
| 1% setting time (s) | 2.945 | 0.473 |
| Input noise (nV/) | 37.77 | 31.86 |
| (MHz pF/A) | 2.01 | 9.22 |
| (V/s) pF/A) | 1.40 | 130.04 |
| Parameter | Corner | VDD | Temp | ||||||
|---|---|---|---|---|---|---|---|---|---|
| FF | SS | SF | FS | TT | −10% | +10% | −40° | +125° | |
| GBW (MHz) | 1.71 | 1.10 | 1.41 | 1.33 | 1.37 | 1.14 | 1.63 | 1.22 | 1.47 |
| PM (∘) | 63.29 | 69.03 | 65.95 | 67.45 | 66.86 | 72.32 | 60.95 | 70.42 | 57.87 |
| Gain (dB) | 83.87 | 84.02 | 84.87 | 83.55 | 84.18 | 82.56 | 85.7 | 84.45 | 82.48 |
| SRav (V/s) | 18.74 | 18.015 | 17.81 | 19.79 | 19.175 | 18.42 | 19.435 | 15.68 | 18.005 |
| STav (ns) | 391.3 | 539.3 | 468.25 | 479.5 | 471.95 | 359.65 | 429.2 | 388.15 | 626.85 |
| Parameter | [7] | [8] | [11] | [12] | [24] | This Work |
|---|---|---|---|---|---|---|
| Supply voltage (V) | 1.8 | 1.8 | 1 | 2 | 0.8 | 1.8 |
| Technology (nm) | 180 | 180 | 180 | 500 | 180 | 180 |
| Supply current (A) | 344 | 800 | 50 | 50 | 45 | 10.4 |
| Load (pF) | 10 | 5.6 | 20 | 70 | 130 | 70 |
| DC gain (dB) | 72.7 | 60.9 | 92.3 | 72.7 | 102.7 | 84.18 |
| GBW (MHz) | 173.3 | 134.2 | 6.51 | 3.4 | 1.12 | 1.37 |
| Phase margin (∘) | 55 | 70.6 | 75.81 | 75.1 | 67.85 | 67.05 |
| Slew rate (V/s) | 139.4 | 94.1 | 15.19 | 19.25 | 1.033 | 19.32 |
| 1% Settling time (ns) | 9.2 | 10.2 | 79.5 | 110 | 555 | 473 |
| Offset voltage (mV) | 7.3 | 7.6 | N/A | N/A | 3.72 | 3.3 |
| Noise 1 MHz (nV/) | 48 | N/A | N/A | 23 | 68.8 | 31.9 |
| (MHz·pF/A) | 5.03 | 0.94 | 2.604 | 4.76 | 3.326 | 9.22 |
| ((V/s)·pF/A) | 4.07 | 0.66 | 6.07 | 26.95 | 2.98 | 130.04 |
| Measured/simulated | Meas. | Sim. | Sim. | Meas. | Meas. | Sim. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C.; Cai, P.; Li, J.; Xie, J.; Luo, Z. Power-Efficient Recycling Folded Cascode Operational Transconductance Amplifier Based on Nested Local Feedback and Adaptive Biasing. Sensors 2025, 25, 2523. https://doi.org/10.3390/s25082523
Wu C, Cai P, Li J, Xie J, Luo Z. Power-Efficient Recycling Folded Cascode Operational Transconductance Amplifier Based on Nested Local Feedback and Adaptive Biasing. Sensors. 2025; 25(8):2523. https://doi.org/10.3390/s25082523
Chicago/Turabian StyleWu, Chunkai, Peng Cai, Jinghu Li, Jin Xie, and Zhicong Luo. 2025. "Power-Efficient Recycling Folded Cascode Operational Transconductance Amplifier Based on Nested Local Feedback and Adaptive Biasing" Sensors 25, no. 8: 2523. https://doi.org/10.3390/s25082523
APA StyleWu, C., Cai, P., Li, J., Xie, J., & Luo, Z. (2025). Power-Efficient Recycling Folded Cascode Operational Transconductance Amplifier Based on Nested Local Feedback and Adaptive Biasing. Sensors, 25(8), 2523. https://doi.org/10.3390/s25082523