Analytical Formulation of Relationship Between Sensors and Euler Angle Errors for Arbitrary Stationary Alignment Based on Accelerometer and Magnetometer
Abstract
1. Introduction
2. Materials and Methods
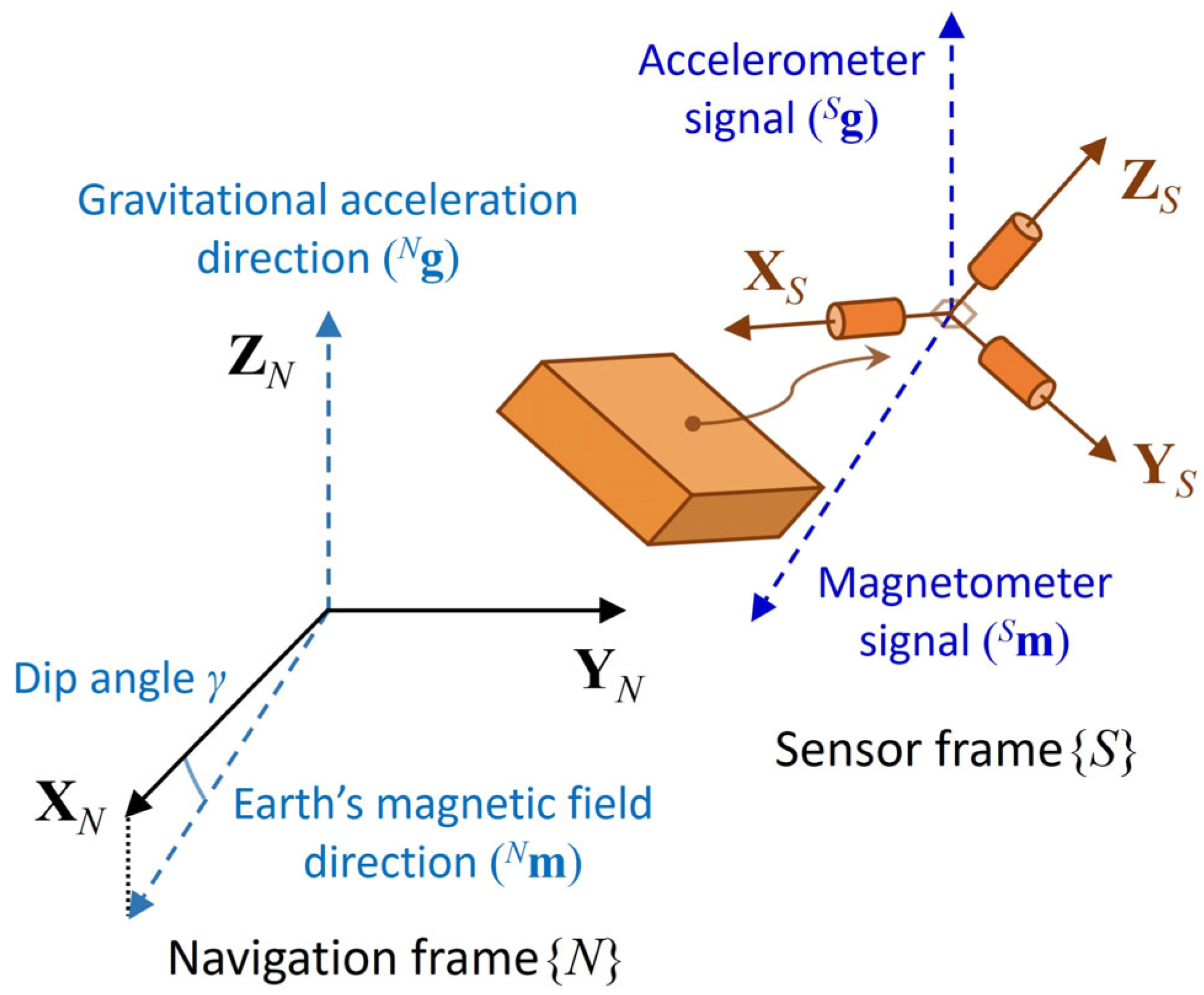
2.1. Three-Axis Attitude Determination (TRIAD)
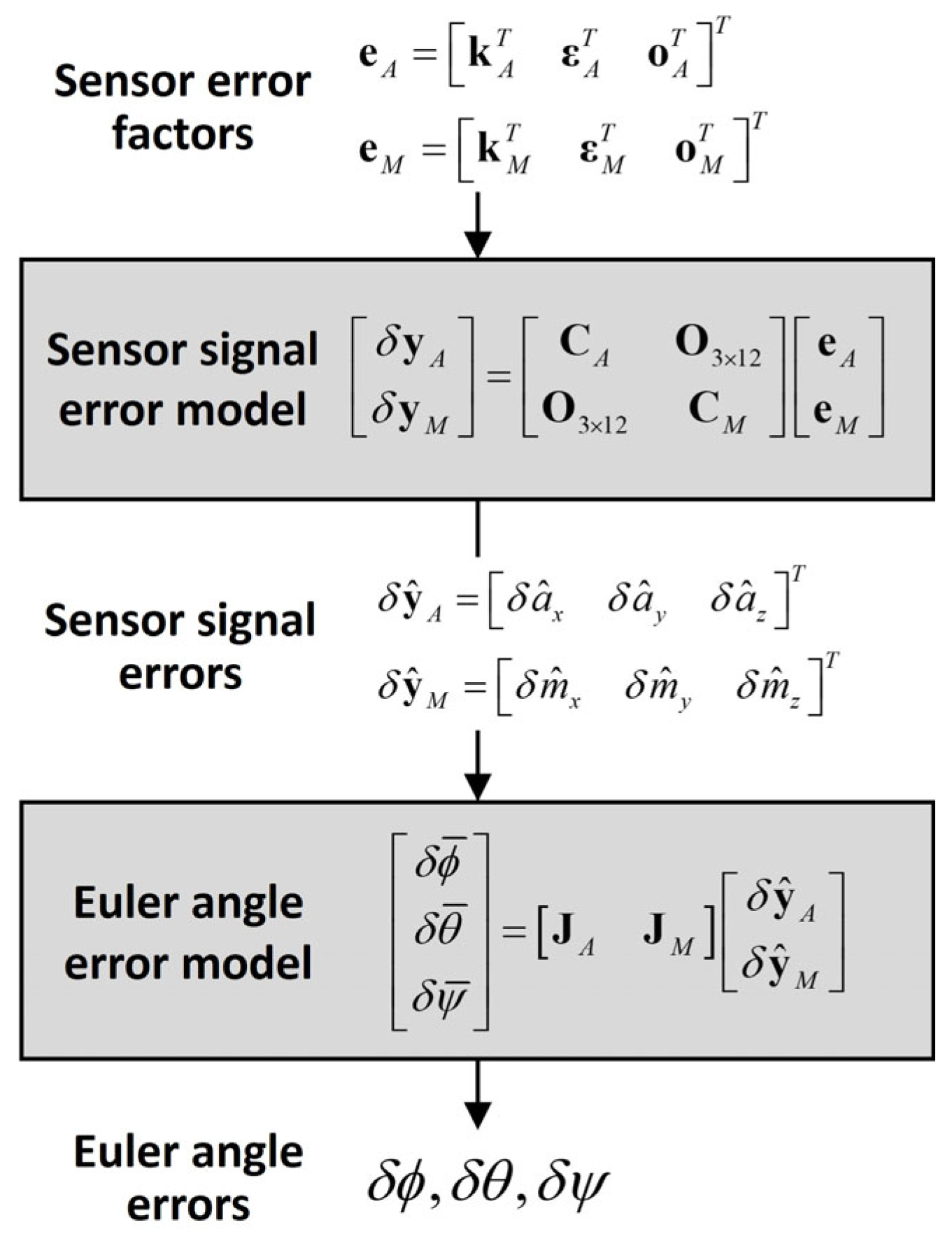
2.2. Sensor Error Model
2.3. Euler Angle Error Model
3. Results
3.1. Simulation Test
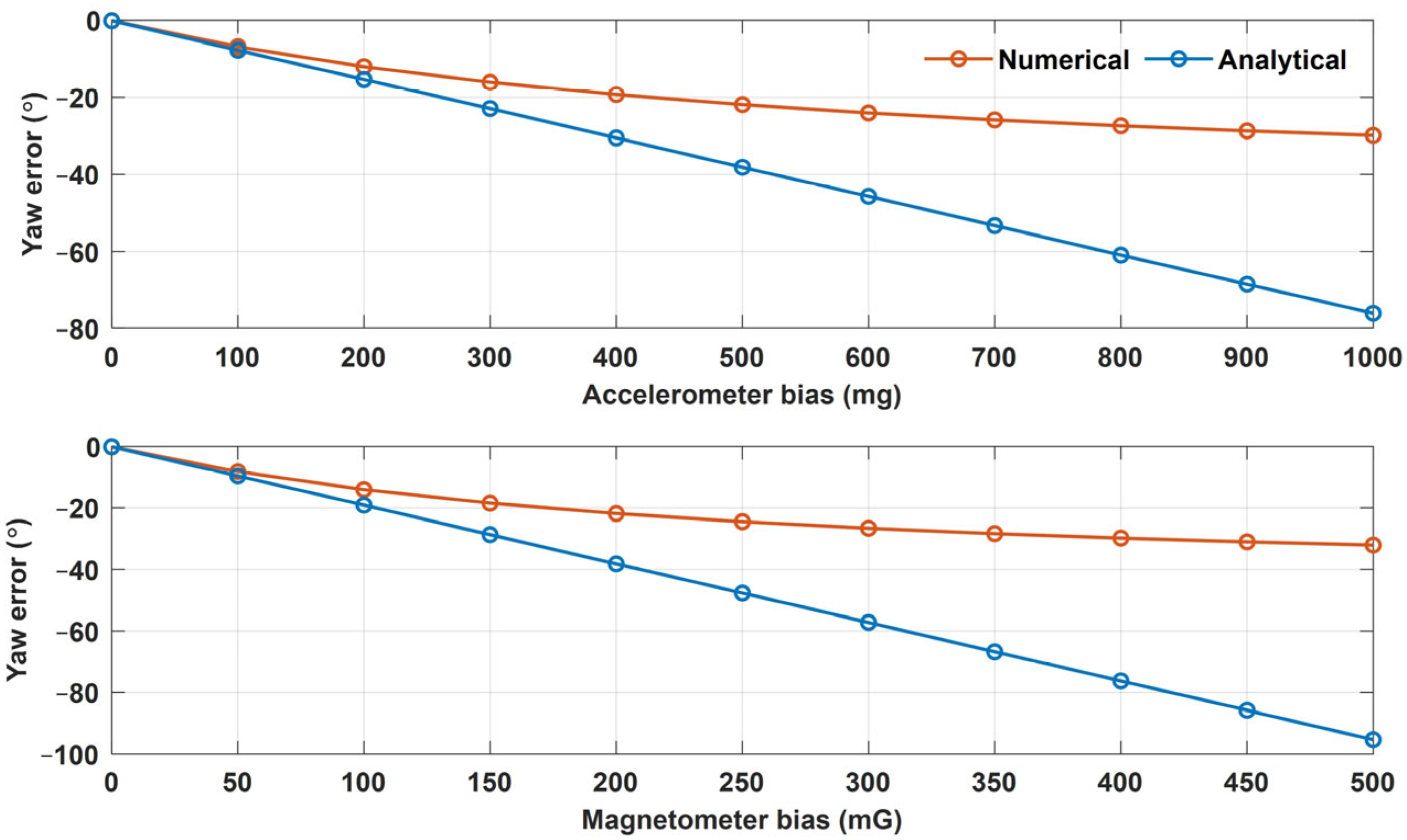
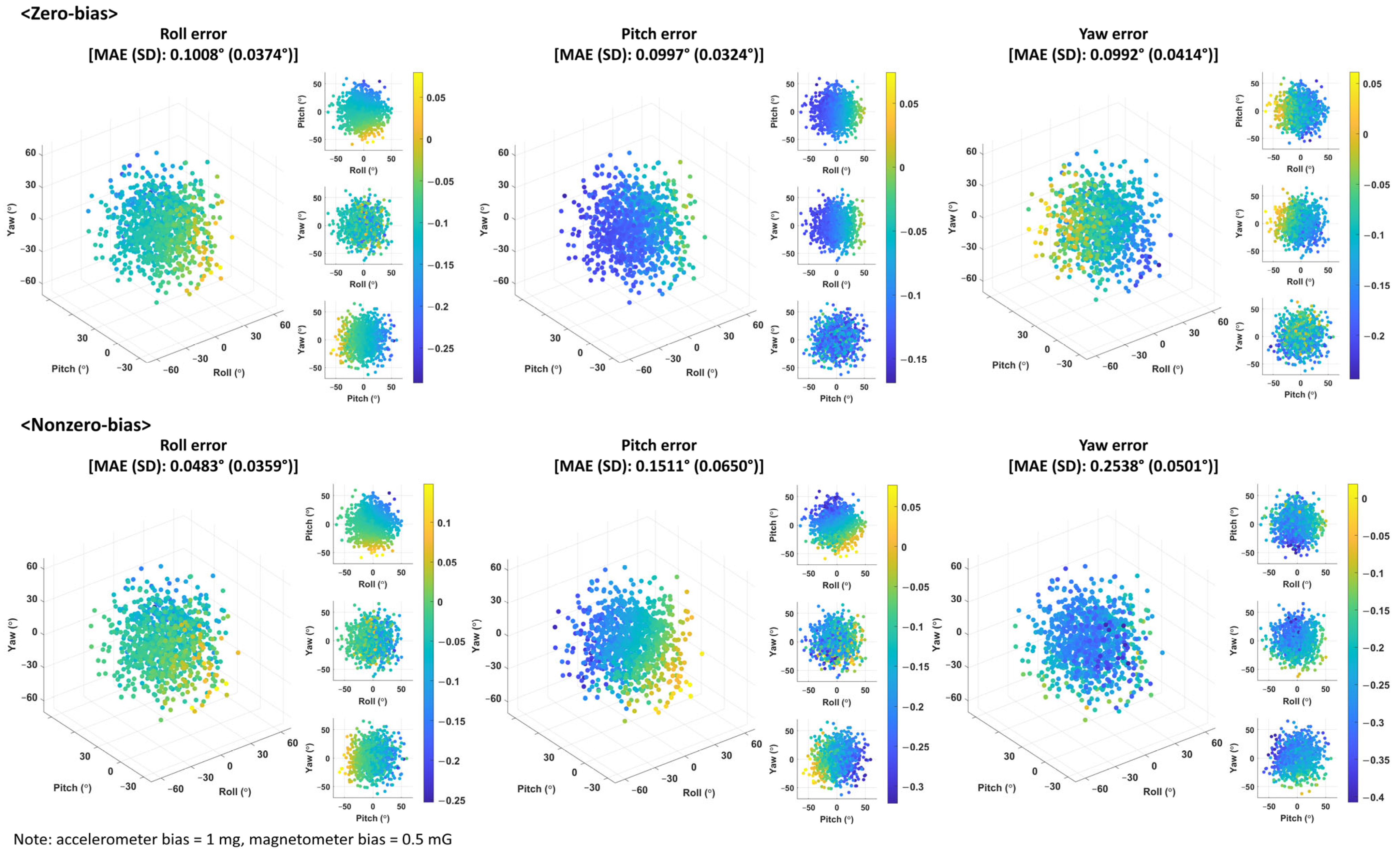
3.2. Analysis of Results
4. Conclusions
- (i)
- The analytical formulation for arbitrary stationary alignment conditions: Unlike the previous studies that analyzed errors in sensor-aligned situations in which the Euler angles were 0°, this study presents a method for analyzing the Euler angle error in sensor-misaligned situations in which the Euler angles are arbitrary. This generalization is crucial for practical applications because the errors vary depending on sensor orientation. The ability to analyze and describe these errors across arbitrary alignment conditions is a key contribution that distinguishes this work.
- (ii)
- The linear relationship between the sensor error factors and the Euler angle errors: The previous studies have primarily focused on describing the relationship between the sensor signal and Euler angle errors. In contrast, our work goes further by deriving a linear relationship between the sensor error factors (e.g., biases and misalignments) and the Euler angle errors. This distinction is meaningful because it simplifies the interpretation and analysis of the propagation of specific sensor error factors into attitude estimation errors. To the best of our knowledge, this is the first study to present an analytical formulation of the relationship between sensor and Euler angle errors for an arbitrary stationary alignment based on accelerometers and magnetometers. Although this study does not directly propose calibration or compensation methods, the presented framework serves as a foundation for future research aimed at optimizing error mitigation strategies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Marina, H.G.; Pereda, F.J.; Giron-Sierra, J.M.; Espinosa, F. UAV attitude estimation using unscented Kalman filter and TRIAD. IEEE Trans. Ind. Electron. 2011, 59, 4465–4474. [Google Scholar] [CrossRef]
- Thienel, J.; Sanner, R.M. A coupled nonlinear spacecraft attitude controller and observer with an unknown constant gyro bias and gyro noise. IEEE Trans. Autom. Control 2003, 48, 2011–2015. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Z.; Xiong, J.; Lv, K. Adaptive UAV navigation method based on AHRS. Sensors 2024, 24, 2518. [Google Scholar] [CrossRef] [PubMed]
- Jørgensen, E.K.; Fossen, T.I.; Bryne, T.H.; Schjølberg, I. Underwater position and attitude estimation using acoustic, inertial, and depth measurements. IEEE J. Ocean. Eng. 2019, 45, 1450–1465. [Google Scholar] [CrossRef]
- Lee, J.K.; Park, E.J. Minimum-order Kalman filter with vector selector for accurate estimation of human body orientation. IEEE Trans. Robot. 2009, 25, 1196–1201. [Google Scholar]
- Lee, J.K.; Park, E.J. A fast quaternion-based orientation optimizer via virtual rotation for human motion tracking. IEEE Trans. Biomed. Eng. 2008, 56, 1574–1582. [Google Scholar] [CrossRef]
- Lee, C.J.; Lee, J.K. Inertial motion capture-based wearable systems for estimation of joint kinetics: A systematic review. Sensors 2022, 22, 2507. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, X.; Hu, D.; Li, T.; Lian, J. Strapdown inertial navigation system algorithms based on dual quaternions. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 110–132. [Google Scholar]
- Rogne, R.H.; Bryne, T.H.; Fossen, T.I.; Johansen, T.A. On the usage of low-cost MEMS sensors, strapdown inertial navigation, and nonlinear estimation techniques in dynamic positioning. IEEE J. Ocean. Eng. 2020, 46, 24–39. [Google Scholar] [CrossRef]
- Huang, C.; Hendeby, G.; Fourati, H.; Prieur, C.; Skog, I. MAINS: A Magnetic Field Aided Inertial Navigation System for Indoor positioning. IEEE Sens. J. 2024, 24, 15156–15166. [Google Scholar] [CrossRef]
- Savage, P.G. Strapdown inertial navigation integration algorithm design part 1: Attitude algorithms. J. Guid. Control Dyn. 1998, 21, 19–28. [Google Scholar] [CrossRef]
- Sabatini, A.M. Quaternion-based strap-down integration method for applications of inertial sensing to gait analysis. Med. Biol. Eng. Comput. 2005, 43, 94–101. [Google Scholar] [CrossRef] [PubMed]
- Yun, X.; Bachmann, E.R.; McGhee, R.B. A simplified quaternion-based algorithm for orientation estimation from earth gravity and magnetic field measurements. IEEE Trans. Instrum. Meas. 2008, 57, 638–650. [Google Scholar]
- Kuga, H.K.; Carrara, V. Attitude determination with magnetometers and accelerometers to use in satellite simulator. Math. Probl. Eng. 2013, 2013, 401282. [Google Scholar] [CrossRef][Green Version]
- Wu, J.; Zhou, Z.; Fourati, H.; Cheng, Y. A super fast attitude determination algorithm for consumer-level accelerometer and magnetometer. IEEE Trans. Consum. Electron. 2018, 64, 375–381. [Google Scholar] [CrossRef]
- Silva, F.O.; Menezes Filho, R.P.; Vieira, L.A.; Kuga, H.K.; de Barros, E.A. Three-axis attitude determination with pseudo-bias estimation from gravity/magnetic vector observations. J. Guid. Control Dyn. 2020, 43, 2237–2257. [Google Scholar] [CrossRef]
- Lee, J.K.; Park, E.J.; Robinovitch, S.N. Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions. IEEE Trans. Instrum. Meas. 2012, 61, 2262–2273. [Google Scholar] [CrossRef]
- Lee, J.K. A parallel attitude-heading Kalman filter without state-augmentation of model-based disturbance components. IEEE Trans. Instrum. Meas. 2019, 68, 2668–2670. [Google Scholar] [CrossRef]
- Kok, M.; Schön, T.B. A fast and robust algorithm for orientation estimation using inertial sensors. IEEE Signal Process. Lett. 2019, 26, 1673–1677. [Google Scholar] [CrossRef]
- Laidig, D.; Seel, T. VQF: Highly accurate IMU orientation estimation with bias estimation and magnetic disturbance rejection. Inf. Fusion 2023, 91, 187–204. [Google Scholar] [CrossRef]
- Weber, D.; Gühmann, C.; Seel, T. RIANN—A robust neural network outperforms attitude estimation filters. AI 2021, 2, 444–463. [Google Scholar] [CrossRef]
- Choi, J.S.; Lee, C.J.; Lee, J.K. A parallel recurrent neural network for robust inertial and magnetic sensor-based 3D orientation estimation. IEEE Access 2023, 11, 89685–89693. [Google Scholar] [CrossRef]
- Black, H.D. A passive system for determining the attitude of a satellite. AIAA J. 1964, 2, 1350–1351. [Google Scholar] [CrossRef]
- Shuster, M.D.; Oh, S.D. Three-axis attitude determination from vector observations. J. Guid. Control Dyn. 1981, 4, 70–77. [Google Scholar] [CrossRef]
- Fang, J.C.; Wan, D.J. A fast initial alignment method for strapdown inertial navigation system on stationary base. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1501–1504. [Google Scholar] [CrossRef]
- Silva, F.O.; Hemerly, E.M.; Leite Filho, W.C.; Kuga, H.K. A fast in-field coarse alignment and bias estimation method for stationary intermediate-grade IMUs. IEEE Trans. Instrum. Meas. 2018, 67, 831–838. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, B.; Wang, L.; Wei, Q.; Zhang, R. A novel method for fast stationary initial alignment based on extended measurement information. IEEE Access 2019, 7, 165873–165883. [Google Scholar] [CrossRef]
- Klein, I.; Bar-Shalom, Y. INS fine alignment with low-cost gyroscopes: Adaptive filters for different measurement types. IEEE Access 2021, 9, 79021–79032. [Google Scholar] [CrossRef]
- Senobari, M.S. A new method for accurate alignment and calibration of strapdown INS. Measurement 2023, 216, 112943. [Google Scholar] [CrossRef]
- Hajiyev, C.; Guler, D.C. Review on gyroless attitude determination methods for small satellites. Prog. Aerosp. Sci. 2017, 90, 54–66. [Google Scholar] [CrossRef]
- Unsal, D.; Demirbas, K. Estimation of deterministic and stochastic IMU error parameters. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposiu, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 862–868. [Google Scholar]
- Farrell, J.A.; Silva, F.O.; Rahman, F.; Wendel, J. IMU Error Modeling Tutorial: INS state estimation with real-time sensor calibration. IEEE Control Syst. Mag. 2021, 42, 40–66. [Google Scholar] [CrossRef]
- Lee, D.; Lee, S.; Park, S.; Ko, S. Test and error parameter estimation for MEMS-based low cost IMU calibration. Int. J. Precis. Eng. Manuf. 2011, 12, 597–603. [Google Scholar] [CrossRef]
- Tedaldi, D.; Pretto, A.; Menegatti, E. A robust and easy to implement method for IMU calibration without external equipment. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 3042–3049. [Google Scholar]
- Wang, B.; Ren, Q.; Deng, Z.; Fu, M. A self-calibration method for nonorthogonal angles between gimbals of rotational inertial navigation system. IEEE Trans. Ind. Electron. 2014, 62, 2353–2362. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, Y.; Yu, X.; Fan, H.; Wei, G.; Wang, L.; Fan, Z.; Wang, G.; Luo, H. A system-level calibration method including temperature-related error coefficients for a strapdown inertial navigation system. Meas. Sci. Technol. 2021, 32, 115117. [Google Scholar] [CrossRef]
- Zhao, G.; Tan, M.; Wang, X.; Liang, W.; Gao, S.; Chen, Z. Research on IMU calibration model based on polar decomposition. Micromachines 2023, 14, 697. [Google Scholar] [CrossRef]
- Zheng, T.; Xu, A.; Xu, X.; Liu, M. Modeling and compensation of inertial sensor errors in measurement systems. Electronics 2023, 12, 2458. [Google Scholar] [CrossRef]
- Silva, F.O.; Hemerly, E.M.; Waldemar Filho, C.L. Error analysis of analytical coarse alignment formulations for stationary SINS. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1777–1796. [Google Scholar] [CrossRef]
- Silva, F.O.; Paiva, L.P.; Carvalho, G.S. Error analysis of accelerometer and magnetometer-based stationary alignment. Sensors 2021, 21, 2040. [Google Scholar] [CrossRef]
- Britting, K. Inertial Navigation Systems Analysis; John Wiley & Sons: Washington, DC, USA, 1971; pp. 65–69. ISBN 0-471-10485-X. [Google Scholar]


| Error Factor | Accelerometer (Axis) | Magnetometer (Axis) |
|---|---|---|
| Scale error | 0.1% (X, Y, Z) | 0.1% (X, Y, Z) |
| Installation error | 0.1° (YZ, ZY, XZ, ZX, XY, YX) | 0.1° (YZ, ZY, XZ, ZX, XY, YX) |
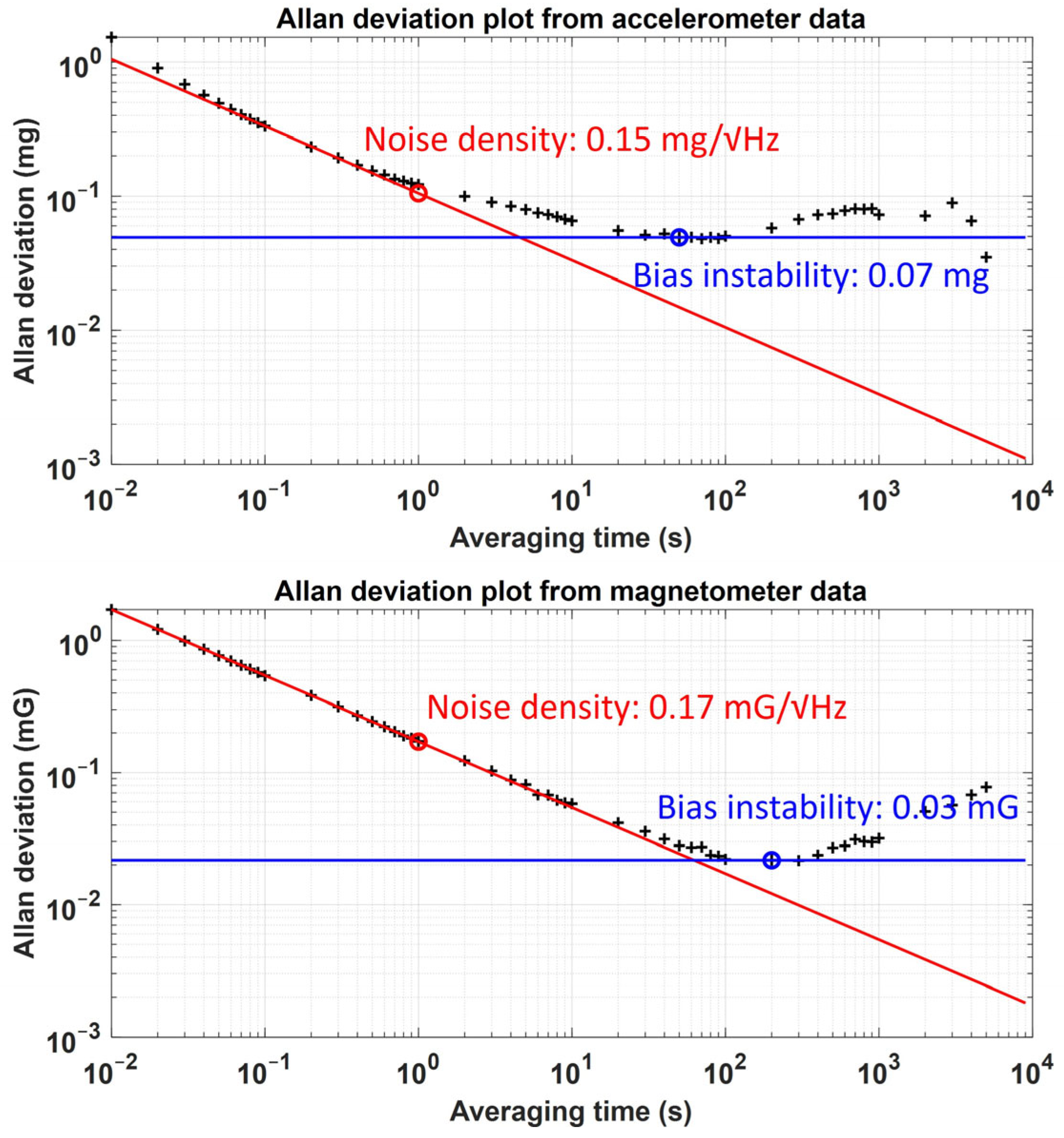
| Noise density | 0.15 mg/√Hz (X, Y, Z) | 0.17 mG/√Hz (X, Y, Z) |
| Bias instability | 0.07 mg (X, Y, Z) | 0.03 mG (X, Y, Z) |
| Constant bias | 0–1 mg (X, Y, Z) | 0–0.5 mG (X, Y, Z) |
| X | Y | Z | |
|---|---|---|---|
| Accelerometer [mg] | 1.6916 (1.5095) | −1.6894 (1.4652) | 0.8443 (1.5098) |
| Magnetometer [mG] | −0.4570 (1.7111) | 1.2875 (1.6604) | −1.0525 (1.7097) |
| X | Y | Z | |
|---|---|---|---|
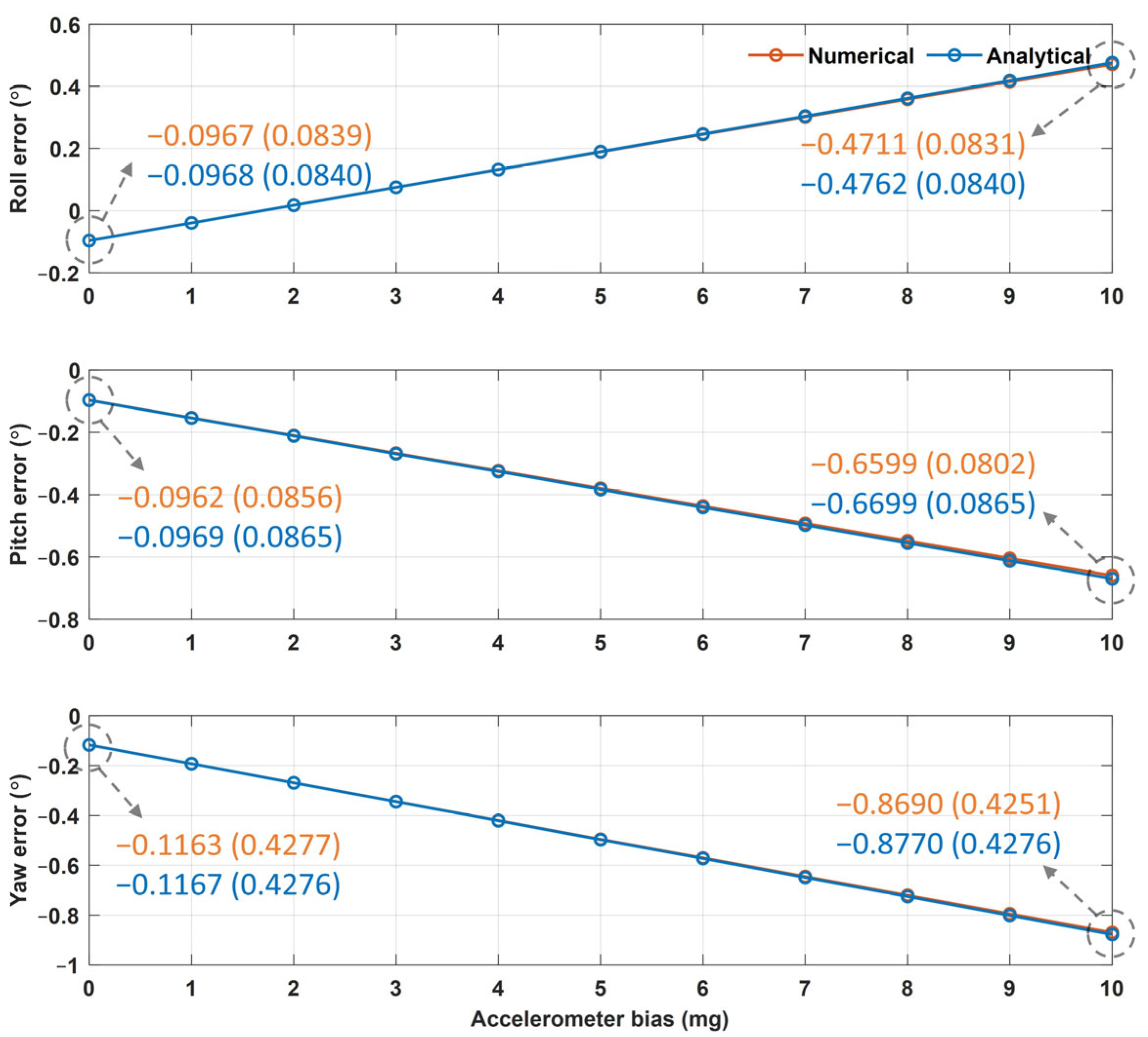
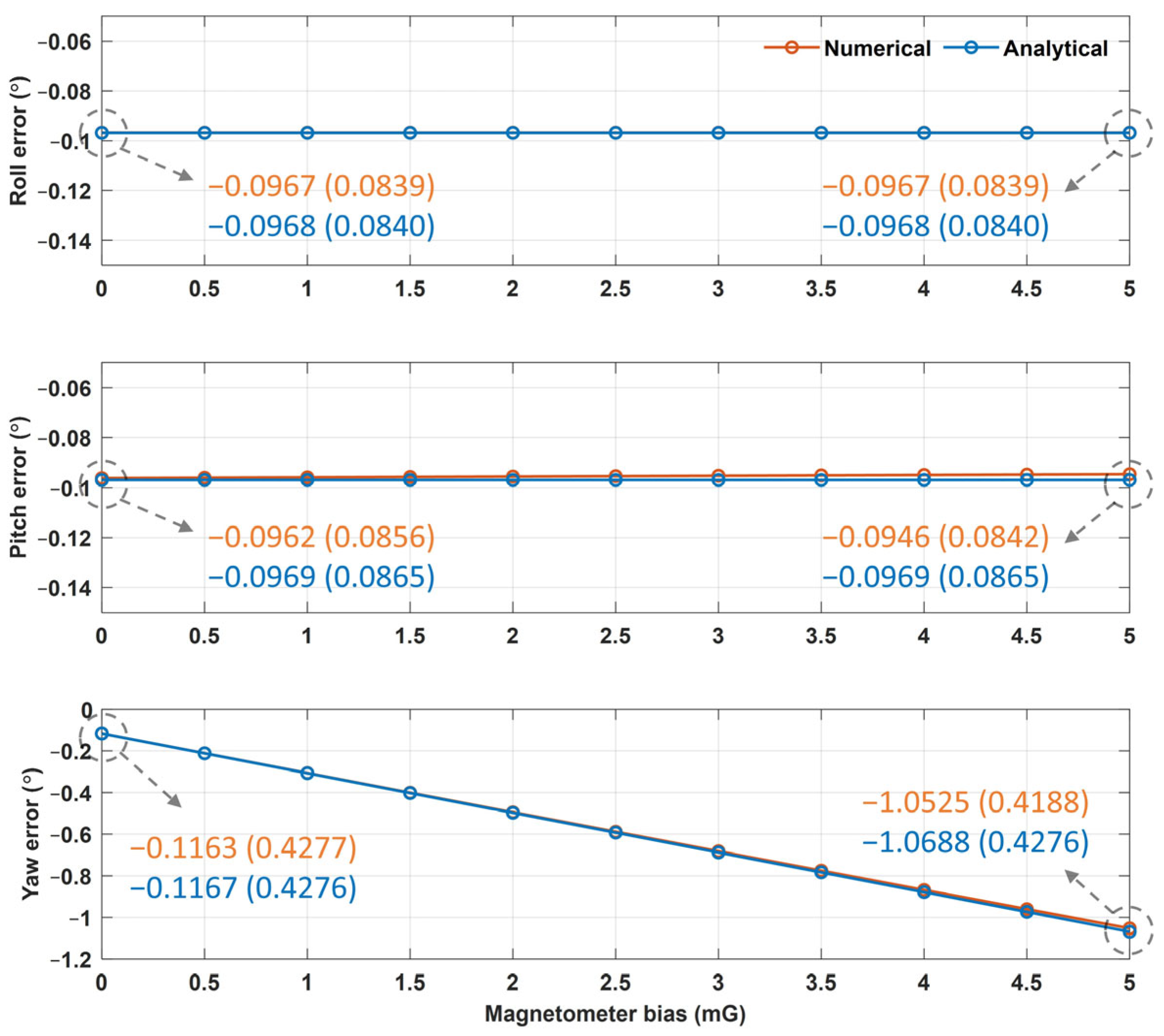
| Numerical approach | −0.0967 (0.0839) | −0.0962 (0.0856) | −0.1163 (0.4277) |
| Analytical approach | −0.0968 (0.0840) | −0.0969 (0.0865) | −0.1167 (0.4276) |
| Mean absolute difference (×10−3) | 0.1476 | 0.8107 | 2.4411 |
| Euler Angle (Roll/Pitch/Yaw) | Roll Error | Pitch Error | Yaw Error | |||
|---|---|---|---|---|---|---|
| Acc | Mag | Acc | Mag | Acc | Mag | |
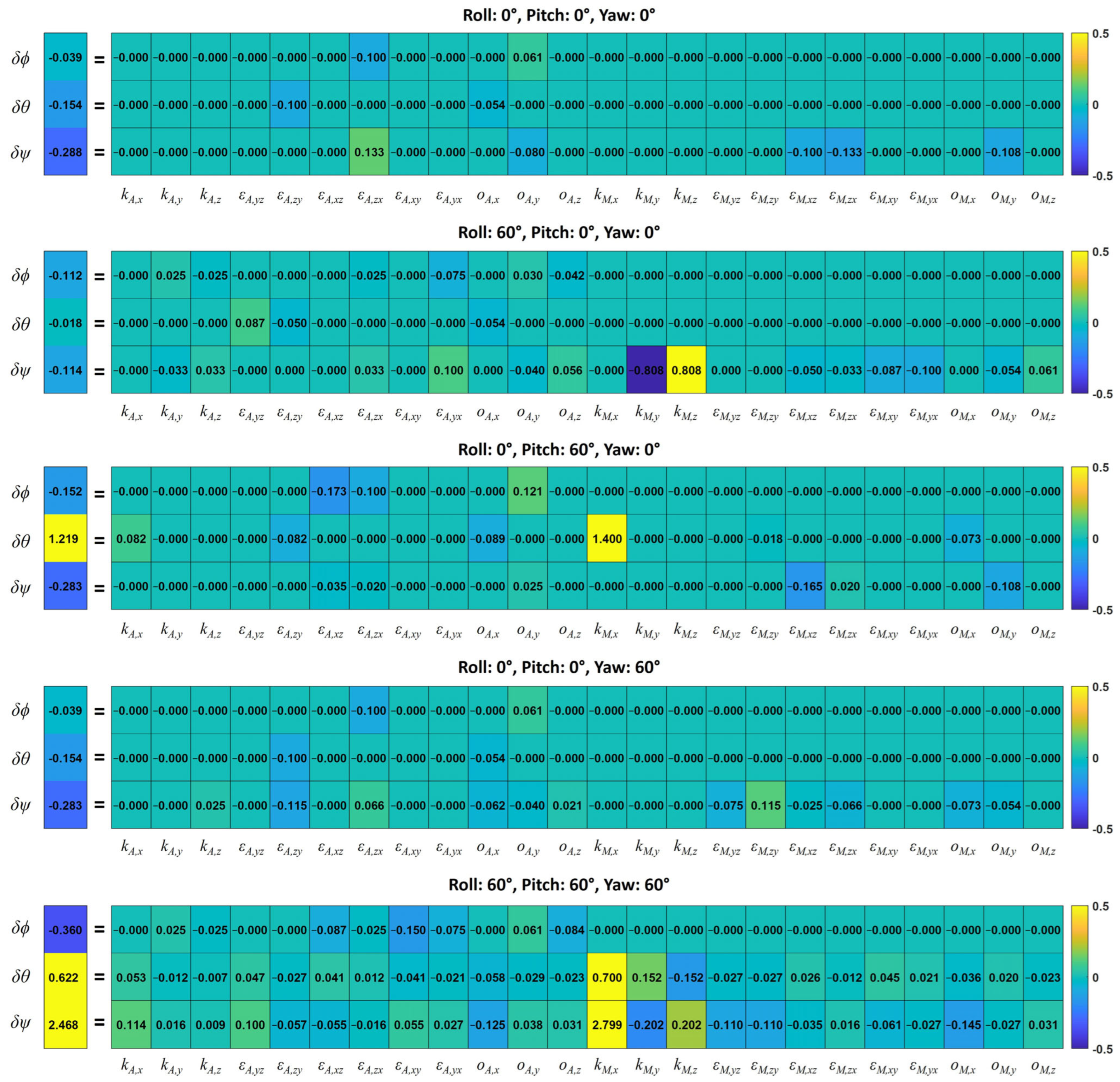
| 0/0/0 | −0.0395 | 0.0000 | −0.1542 | 0.0000 | 0.0524 | −0.3404 |
| 60/0/0 | −0.1118 | 0.0000 | −0.0176 | 0.0000 | 0.1484 | −0.2620 |
| 0/60/0 | −0.1522 | 0.0000 | −0.0900 | 1.3094 | −0.0308 | −0.2523 |
| 0/0/60 | −0.0395 | 0.0000 | −0.1542 | 0.0000 | −0.1052 | −0.1778 |
| 60/60/60 | −0.3602 | 0.0000 | −0.0642 | 0.6862 | 0.1368 | 2.3310 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.J.; Lee, J.K. Analytical Formulation of Relationship Between Sensors and Euler Angle Errors for Arbitrary Stationary Alignment Based on Accelerometer and Magnetometer. Sensors 2025, 25, 2593. https://doi.org/10.3390/s25082593
Lee CJ, Lee JK. Analytical Formulation of Relationship Between Sensors and Euler Angle Errors for Arbitrary Stationary Alignment Based on Accelerometer and Magnetometer. Sensors. 2025; 25(8):2593. https://doi.org/10.3390/s25082593
Chicago/Turabian StyleLee, Chang June, and Jung Keun Lee. 2025. "Analytical Formulation of Relationship Between Sensors and Euler Angle Errors for Arbitrary Stationary Alignment Based on Accelerometer and Magnetometer" Sensors 25, no. 8: 2593. https://doi.org/10.3390/s25082593
APA StyleLee, C. J., & Lee, J. K. (2025). Analytical Formulation of Relationship Between Sensors and Euler Angle Errors for Arbitrary Stationary Alignment Based on Accelerometer and Magnetometer. Sensors, 25(8), 2593. https://doi.org/10.3390/s25082593





