Ammonia Optical Sensing by Microring Resonators
Abstract
:1. Introduction
2. Sensing Principle
3. Device Sensitivity
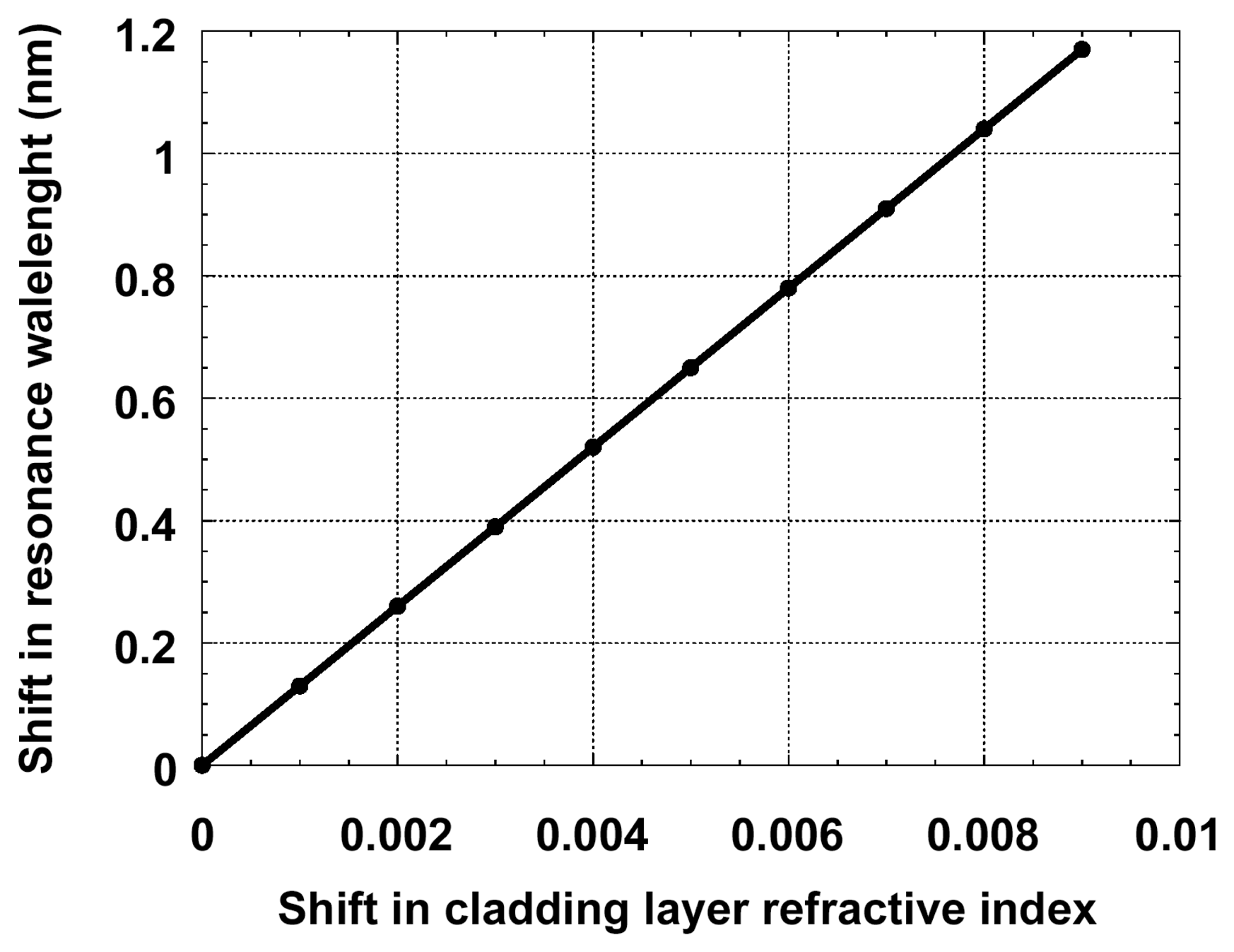
4. Sensor Design and Simulation
5. Conclusions
Acknowledgments
References
- Timmer, B.; Olthuis, W.; van den Berg, A. Ammonia sensors and their applications–a review. Sens. Actuators B, Chem. 1994, 107, 666–677. [Google Scholar]
- Kearney, D.J.; Hubbard, T.; Putnam, D. Breath ammonia measurement in Helicobacter pylori infection. Digest. Dis. Sci. 2002, 47, 2523–2530. [Google Scholar]
- Seiyama, T.; Kato, A.; Fujiishi, K.; Nagatani, M. A new detector for gaseous components using semiconductive thin films. Anal. Chem. 1962, 34, 1502–1503. [Google Scholar]
- Prasad, A.K.; Gouma, P.I.; Kubinski, D.J.; Visser, J.H.; Soltis, R.E.; Schmitz, P.J. Reactively sputtered MoO3 films for ammonia sensing. Thin Solid Films 2003, 436, 46–51. [Google Scholar]
- Meyerhoff, M.E. Polymer membrane electrode-based potentiometric ammonia gas sensor. Anal. Chem. 1980, 52, 1532–1534. [Google Scholar]
- Kumar, P.S.; Scaria, A.V.; Vallabhan, C.P.G.; Nampoori, V.P.N.; Radhakrishnan, P. Long-period grating in multimode fiber for ammonia gas detection. Proc. SPIE 2004, 5279, 331–335. [Google Scholar]
- Cai, Q.Y.; Jain, M.K.; Grimes, C.A. A wireless, remote query ammonia sensor. Sens. Actuators B, Chem. 2001, 77, 614–619. [Google Scholar]
- Scorsone, E.; Christie, S.; Persaud, K.C.; Simon, P.; Kvasnik, F. Fiber optic evanescent sensing of gaseous ammonia with two forms of a new near-infrared dye in comparison to phenol red. Sens. Actuators B, Chem. 2003, 90, 37–45. [Google Scholar]
- Cao, W.; Duan, Y. Optical fiber-based evanescent ammonia sensor. Sens. Actuators B, Chem. 2005, 110, 252–259. [Google Scholar]
- Brandenburg, A.; Edelhaeuser, R.; Werner, T.; He, H.; Wolfbeis, O.S. Ammonia Detection via Integrated Optical Evanescent Wave Sensors. Microchim. Acta 1995, 121, 95–105. [Google Scholar]
- Passaro, V.M.N.; Dell'Olio, F.; Casamassima, B.; De Leonardis, F. Guided-wave Optical Biosensors. Sensors 2007, 7, 508–538. [Google Scholar]
- Luff, B.J.; Harris, R.D.; Wilkinson, J.S.; Wilson, R.; Schiffrin, D.J. Integrated-optical directional coupler biosensor. Opt. Lett. 1996, 21, 618–620. [Google Scholar]
- Prieto, F.; Sepulveda, B.; Calle, A.; Llobera, A.; Domynguez, C.; Abad, A.; Montoya, A.; Lechuga, L.M. An integrated optical interferometric nanodevice based on silicon technology for biosensor applications. Nanotechnology 2003, 14, 907–912. [Google Scholar]
- Clerc, D.; Lukosz, W. Integrated optical output grating coupler as bio chemical sensor. Sens. Actuators B, Chem. 1994, 19, 581–586. [Google Scholar]
- Krioukov, E.; Greve, J.; Otto, C. Performance of integrated optical microcavities for refractive index and fluorescence sensing. Sens. Actuators B, Chem. 2003, 90, 58–67. [Google Scholar]
- Chao, C.-Y.; Fung, W.; Guo, L.J. Polymer Microring Resonators for Biochemical Sensing Applications. IEEE J. Sel. Topics in Quantum Electron. 2006, 12, 134–142. [Google Scholar]
- Yalçyn, A.; Popat, K.C.; Aldridge, J.C.; Desai, T.A.; Hryniewicz, J.; Chbouki, N.; Little, B.E.; King, O.; Van, V.; Chu, S.; Gill, D.; Anthes-Washburn, M.; Unlu, M.S.; Goldberg, B.B. Optical Sensing of Biomolecules Using Microring Resonators. IEEE J. Sel. Topics in Quantum Electron. 2006, 12, 148–155. [Google Scholar]
- De Vos, K.; Bartolozzi, I.; Schacht, E.; Bienstman, P.; Baets, R. Silicon-on-Insulator microring resonator for sensitive and label-free biosensing. Optics Express 2007, 15, 7610–7615. [Google Scholar]
- Sarkisov, S.S.; Diggs, D.E.; Adamovsky, G.; Curley, M.J. Single-arm double-mode double-order planar waveguide interferometric sensor. Appl. Opt. 2001, 40, 349–359. [Google Scholar]
- 3D Mode Solver by Optiwave Corp. ©, single license; 2005.
- Dell'Olio, F.; Passaro, V.M.N.; De Leonardis, F. Surface Sensitivity Optimization of a Microring Resonator for Biochemical Sensing. Int. Conf. on Tran. Opt. Net. (ICTON) Proc, Nottingham, 18-22 June, 2006; 4, pp. 128–131.
- OptiFDTD by Optiwave Corp. ©, ver. 7.0, single license; 2005.
- Sarkisov, S.S.; Wilkosz, A.; Venkateswarlu, P. Nonlinear optical waveguides based on polymeric films doped with phthalocyanines. Proc. SPIE 1996, 2693, 523–531. [Google Scholar]







© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Passaro, V.M.N.; Dell’Olio, F.; De Leonardis, F. Ammonia Optical Sensing by Microring Resonators. Sensors 2007, 7, 2741-2749. https://doi.org/10.3390/s7112741
Passaro VMN, Dell’Olio F, De Leonardis F. Ammonia Optical Sensing by Microring Resonators. Sensors. 2007; 7(11):2741-2749. https://doi.org/10.3390/s7112741
Chicago/Turabian StylePassaro, Vittorio M. N., Francesco Dell’Olio, and Francesco De Leonardis. 2007. "Ammonia Optical Sensing by Microring Resonators" Sensors 7, no. 11: 2741-2749. https://doi.org/10.3390/s7112741
APA StylePassaro, V. M. N., Dell’Olio, F., & De Leonardis, F. (2007). Ammonia Optical Sensing by Microring Resonators. Sensors, 7(11), 2741-2749. https://doi.org/10.3390/s7112741



