A New Method to Define the VI-Ts Diagram Using Subpixel Vegetation and Soil Information: A Case Study over a Semiarid Agricultural Region in the North China Plain
Abstract
:1. Introduction
2. Study Area and Data Collection
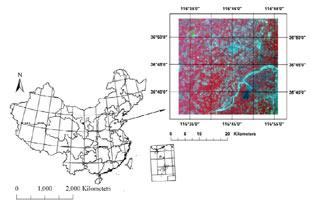
2.1. Study Area and Ground Data Collection
2.2. Satellite Data Collection and Processing
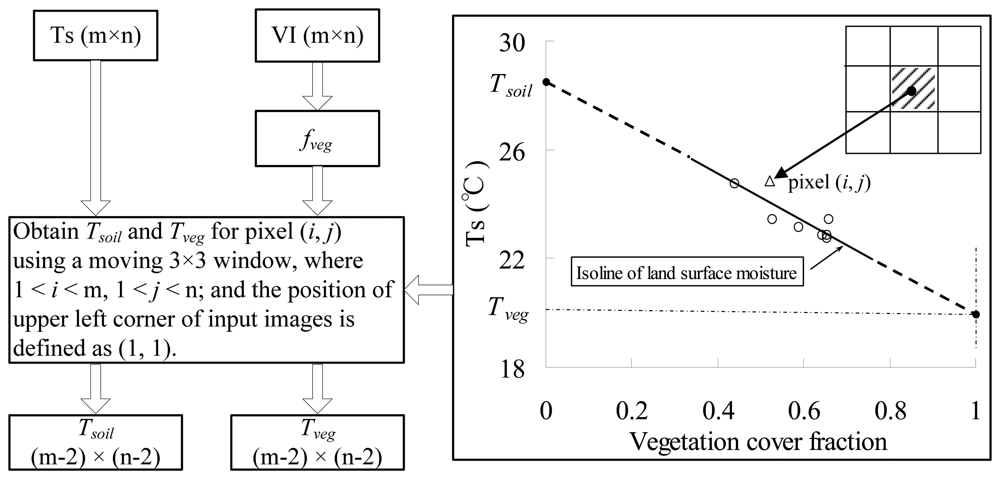
3. Method for Estimating the Component Surface Temperatures of Vegetation and Soil
4. Results
4.1. Obtaining MODIS-Tveg and MODIS-Tsoil using the proposed approach
4.2 Validations of MODIS-Tveg and MODIS-Tsoil obtained using the proposed approach
4.2.1 Validation using the Normalized 90 m-ASTER-Ts on May 9, 2003
4.2.2 Validation using ground data across the whole year of 2003
4.3 Comparisons of the Proposed and Traditional Methods for Defining the VI-Ts Diagram
4.3.1 Comparisons based on the Normalized 90 m-ASTER-Ts on May 9 2003
4.3.2 Comparisons based on MODIS data through the whole year of 2003
5. Discussion
5.1 Issues about the Bias between MODIS-Ts and ASTER-Ts
5.2 Issues about the Approach of Obtaining Tveg and Tsoil
5.3 Issues about Obtaining Wet and Dry Points
5.4 Issues about the Definition of the VI-Ts Diagram
6. Conclusions
Acknowledgments
References
- Boegh, E.; Soegaard, H.; Thomsen, A. Evaluating evapotranspiration rates and surface conditions using Landsat TM to estimate atmospheric resistance and surface resistance. Remote Sens. Environ. 2002, 79, 329–343. [Google Scholar]
- Nishida, K.; Nemani, R.R.; Running, S.W.; Glassy, J.M. An operational remote sensing algorithm of land surface evaporation. J. Geophys. Res. 2003, 108, 4270–4284. [Google Scholar]
- Venturini, V.; Bisht, G.; Islam, S.; Jiang, L. Comparison of evaporative fractions estimated from AVHRR and MODIS sensors over South Florida. Remote Sens. Environ. 2004, 93, 77–86. [Google Scholar]
- Smith, R.C.G.; Choudhury, B.J. Analysis of normalized difference and surface temperature observations over southeastern Australia. Int. J. Remote Sens. 1991, 12, 2021–2044. [Google Scholar]
- Nemani, R.R.; Pierce, L.; Running, S.W.; Goward, S. Developing satellite-derived estimates of surface moisture status. J. Appl. Meteorol. 1993, 32, 548–557. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An interpretation of methodologies for indirect measurement of soil water content. Agr. Forest Meteorol. 1995, 77, 191–205. [Google Scholar]
- Gillies, R.R.; Carlson, T.N.; Cui, J.; Kustas, W.P.; Humes, K.S. A verification of the ‘triangle’ method for obtaining surface soil water content and energy fluxes from remote measurements of the Normalized Difference Vegetation Index (NDVI) and surface radiant temperature. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature / vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar]
- Verstraeten, W. W.; Veroustraete, F.; Feyen, J. Estimating evapotranspiration of European forests from NOAA-imagery at satellite overpass time: Towards an operational processing chain for integrated optical and thermal sensor data products. Remote Sens. Environ. 2005, 96, 256–276. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ. 1981, 11, 221–229. [Google Scholar]
- Cain, S. Bayesian-based subpixel brightness temperature estimation from multichannel infrared GOES radiometer data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 188–201. [Google Scholar]
- Xu, X.; Chen, L.; Zhuang, J. Genetic inverse algorithm for retrieval of component temperature of mixed pixel by multi-angle thermal infrared remote sensing data. Sci. China,Ser. D 2001, 44(4), 363–372. [Google Scholar]
- Zhang, R.; Sun, X.; Liu, J. Determination of regional distribution of crop transpiration and soil water use efficiency using quantitative remote sensing data through inversion. Sci.China, Ser. D 2003, 46, 10–22. [Google Scholar]
- Sokal, R.R.; Thomson, J.D. Applications of spatial autocorrelation in ecology. In Developments in Numerical Ecology; NATO ASI Series; Legendre, P., Legendre, L., Eds.; Springer-Verlag: Berlin, Germany, 1987; Vol. G14. [Google Scholar]
- Lannoy, G.J.M.D.; Verhoest, N.E.C.; Houser, P.R.; Gish, T.J.; Meirvenne, M.V. Spatial and temporal characteristics of soil moisture in an intensively monitored agricultural field (OPE). J. Hydrol. 2006, 331, 719–730. [Google Scholar]
- Das, N.N.; Mohanty, B.P. Temporal dynamics of PSR-based soil moisture across spatial scales in an agricultural landscape during SMEX02: A wavelet approach. Remote Sens. Environ. 2008, 112, 522–534. [Google Scholar]
- Wang, Q.; Watanabe, M.; Ouyang, Z. Simulation of water and carbon fluxes using BIOME-BGC model over crops in China. Agr. Forest Meteorol. 2005, 131, 209–224. [Google Scholar]
- Loheide, S.P., II; Gorelick, S.M. A local-scale, high-resolution evapotranspiration mapping algorithm (ETMA) with hydroecological applications at riparian meadow restoration site. Remote Sens. Environ. 2005, 98, 182–200. [Google Scholar]
- Zhang, R.; Sun, X.; Wang, W.; Xu, J.; Zhu, Z.; Tian, J. An operational two-layer remote sensing model to estimate surface flux in regional scale: Physical background. Science in China, Ser. D-Earth Science 2005, 48 suppl., 225–244. [Google Scholar]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, S.; Hook, S.; Kahle, A. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1113–1126. [Google Scholar]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar]
- Wolfe, R.E.; Nishihama, M.; Fleig, A.J.; Kuyper, J.A.; Roy, D.P.; Storey, J.C.; Patt, F.S. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sens. Environ. 2002, 83, 31–49. [Google Scholar]
- Iwasaki, A.; Fujisada, H. ASTER geometric performance. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2700–2706. [Google Scholar]
- Buheaosier; Tsuchiya, K.; Kaneko, M.; Sung, S. J. Comparison of image data acquired with AVHRR, MODIS, ETM+ and ASTER over Hokkaido, Japan. Adv. Space Res. 2003, 32, 2211–2216. [Google Scholar]
- Jacob, F.; Petitcolin, F.; Schmugge, T.; Vermote, É.; French, A.; Ogawa, K. Comparison of land surface emissivity and radiometric temperature derived from MODIS and ASTER sensors. Remote Sens. Environ. 2004, 90, 137–152. [Google Scholar]
- Liu, Y.; Hiyama, T.; Yamaguchi, Y. Scaling of land surface temperature using satellite data: A case examination on ASTER and MODIS products over a heterogeneous terrain area. Remote Sens. Environ. 2006, 105, 115–128. [Google Scholar]
- Jimēnez-Muñoz, J.C.; Sobrino, J.A.; Gillespie, A.; Sabol, D.; Gustafson, W.T. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006, 103, 474–487. [Google Scholar]
- Choudhury, B.J.; Ahmed, N.U.; Idso, S.B.; Reginato, R.J.; Daughtry, CTM. Relations between evaporation coefficients and vegetation indices studied by model simulations. Remote Sens. Environ. 1994, 50, 1–17. [Google Scholar]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar]
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fraction vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar]
- Archer, N.A.L.; Jones, H.G. Integrating hyperspectral imagery at different scales to estimate component surface temperatures. Int. J. Remote Sens. 2006, 27, 2141–2159. [Google Scholar]
- Hébrard, O.; Voltz, M.; Andrieux, P.; Moussa, R. Spatio-temporal distribution of soil surface moisture in a heterogeneously farmed Mediterranean catchment. J. Hydrol. 2006, 329, 110–121. [Google Scholar]
- Lu, D.; Weng, Q. Spectral mixture analysis of ASTER images for examining the relationship between urban thermal features and biophysical descriptors in Indianapolis, Indiana, USA. Remote Sens. Environ. 2006, 104, 157–167. [Google Scholar]
- Small, C. Comparative analysis of urban reflectance and surface temperature. Remote Sens. Environ. 2006, 104, 168–189. [Google Scholar]
- Karnieli, A.; Bayasgalan, M.; Bayarjargal, Y.; Agam, N.; Khudulmur, S.; Tucker, C.J. Comments on the use of the vegetation health index over Mongolia. Int. J. Remote Sens. 2006, 27, 2017–2024. [Google Scholar]
- Kawashima, S. Relation between vegetation, surface-temperature, and surface composition in the Tokyo region during winter. Remote Sens. Environ. 1994, 50, 52–60. [Google Scholar]
- Smith, R.C.G.; Choudhury, B.J. Analysis of normalized difference and surface temperature observations over southeastern Australia. Int. J. Remote Sens. 1991, 12, 2021–2044. [Google Scholar]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature related drought indices over North America. Geophys. Res. Lett. 2007, 34, L24406. [Google Scholar]











| Dataset | Resolution | Size (pixel×pixel) | Min. | Max. | Mean | Stdev* | Range |
|---|---|---|---|---|---|---|---|
| 15 m-ASTER-NDVI | 15 m | 2336×2158 | 0.03 | 0.74 | 0.40 | 0.11 | 0.71 |
| MODIS-NDVI | 1000 m | 35×33 | 0.07 | 0.85 | 0.44 | 0.09 | 0.78 |
| 90 m-ASTER-Ts (°C) | 90 m | 390×359 | 17.85 | 46.85 | 25.97 | 2.29 | 29.00 |
| 1 km-ASTER-Ts (°C) | 1000 m | 35×33 | 20.40 | 34.37 | 26.19 | 1.63 | 13.97 |
| MODIS-Ts (°C) | 1000 m | 35×33 | 20.05 | 27.15 | 22.81 | 0.86 | 7.10 |
| Year/Month/Day | MODIS-NDVI | MODIS-Ts (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Mean | Stdev | Range | Min. | Max. | Mean | Stdev | Range | |
| 2003/3/27 | 0.05 | 0.49 | 0.3 | 0.07 | 0.44 | 11.79 | 25.91 | 21.05 | 1.85 | 14.12 |
| 2003/4/25 | 0.1 | 0.86 | 0.46 | 0.11 | 0.75 | 17.95 | 24.49 | 20.63 | 0.93 | 6.54 |
| 2003/4/30 | 0.1 | 0.81 | 0.48 | 0.11 | 0.7 | 19.95 | 27.63 | 2.42 | 0.82 | 7.68 |
| 2003/5/13 | 0.15 | 0.75 | 0.5 | 0.1 | 0.6 | 24.79 | 35.17 | 28.17 | 1.19 | 10.38 |
| 2003/6/24 | 0 | 0.66 | 0.31 | 0.05 | 0.66 | 29.61 | 38.35 | 35.18 | 1.46 | 8.74 |
| 2003/6/28 | 0 | 0.44 | 0.32 | 0.05 | 0.44 | 30.29 | 40.55 | 36.16 | 1.58 | 10.26 |
| 2003/7/26 | 0.18 | 0.93 | 0.76 | 0.11 | 0.75 | 28.35 | 32.85 | 30.19 | 0.44 | 4.5 |
| 2003/9/21 | 0.17 | 0.87 | 0.69 | 0.12 | 0.7 | 24.13 | 3.81 | 26.23 | 0.93 | 6.68 |
| 2003/10/21 | 0.03 | 0.61 | 0.29 | 0.06 | 0.59 | 18.35 | 22.79 | 20.99 | 0.68 | 4.44 |
| 2003/10/23 | 0 | 0.55 | 0.27 | 0.06 | 0.55 | 14.67 | 19.63 | 16.95 | 0.94 | 4.96 |
| 2003/11/22 | 0.01 | 0.52 | 0.27 | 0.05 | 0.51 | 6.45 | 8.97 | 7.74 | 0.4 | 2.52 |
| 2003/12/26 | 0 | 0.46 | 0.24 | 0.05 | 0.46 | 2.55 | 7.89 | 4.94 | 1.12 | 5.34 |
| Year/Month/Day | R2 | |
|---|---|---|
| Mean | Stdev | |
| 2003/3/27 | 0.56 | 0.19 |
| 2003/4/25 | 0.59 | 0.22 |
| 2003/4/30 | 0.57 | 0.20 |
| 2003/5/9 | 0.59 | 0.21 |
| 2003/5/13 | 0.63 | 0.20 |
| 2003/6/24 | 0.60 | 0.21 |
| 2003/6/28 | 0.57 | 0.20 |
| 2003/7/26 | 0.60 | 0.21 |
| 2003/9/21 | 0.60 | 0.19 |
| 2003/10/21 | 0.60 | 0.17 |
| 2003/10/23 | 0.61 | 0.18 |
| 2003/11/22 | 0.58 | 0.17 |
| 2003/12/26 | 0.55 | 0.18 |
| Pixels | Mean | Stdev | Range | Min. | Max. | |
|---|---|---|---|---|---|---|
| 90 m-ASTER-Tveg-N (°C) | 356 | 20.72 | 0.68 | 3.36 | 19.42 | 22.78 |
| MODIS-Tveg (°C) | 356 | 21.24 | 1.05 | 3.41 | 19.53 | 22.94 |
| 90 m-ASTER-Tsoil-N (°C) | 549 | 24.78 | 2.05 | 9.17 | 20.28 | 29.45 |
| MODIS-Tsoil (°C) | 549 | 23.98 | 1.01 | 6.38 | 21.92 | 28.30 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sun, Z.; Wang, Q.; Matsushita, B.; Fukushima, T.; Ouyang, Z.; Watanabe, M. A New Method to Define the VI-Ts Diagram Using Subpixel Vegetation and Soil Information: A Case Study over a Semiarid Agricultural Region in the North China Plain. Sensors 2008, 8, 6260-6279. https://doi.org/10.3390/s8106260
Sun Z, Wang Q, Matsushita B, Fukushima T, Ouyang Z, Watanabe M. A New Method to Define the VI-Ts Diagram Using Subpixel Vegetation and Soil Information: A Case Study over a Semiarid Agricultural Region in the North China Plain. Sensors. 2008; 8(10):6260-6279. https://doi.org/10.3390/s8106260
Chicago/Turabian StyleSun, Zhigang, Qinxue Wang, Bunkei Matsushita, Takehiko Fukushima, Zhu Ouyang, and Masataka Watanabe. 2008. "A New Method to Define the VI-Ts Diagram Using Subpixel Vegetation and Soil Information: A Case Study over a Semiarid Agricultural Region in the North China Plain" Sensors 8, no. 10: 6260-6279. https://doi.org/10.3390/s8106260
APA StyleSun, Z., Wang, Q., Matsushita, B., Fukushima, T., Ouyang, Z., & Watanabe, M. (2008). A New Method to Define the VI-Ts Diagram Using Subpixel Vegetation and Soil Information: A Case Study over a Semiarid Agricultural Region in the North China Plain. Sensors, 8(10), 6260-6279. https://doi.org/10.3390/s8106260