The pH Response and Sensing Mechanism of n-Type ZnO/Electrolyte Interfaces
Abstract
:1. Introduction
- Energy levels in semiconductors and electrolytes
- The electrical double layer
- Mapping of the semiconductor band edge positions relative to solution redox levels (pH-sensing).
- The role of surface states.
2. Energy Levels in Semiconductors and Liquids
2.1. Electron Energy Levels in Semiconductors and the Energy Band Model
2.2. Solution-Redox Levels
2.3. n-Type Semiconductor-Electrolyte Systems at Equilibrium
3. The Electrical Double Layer
- B = a conversion factor from moles/liter to μC/cm2 of charge.
- A = the surface area of ZnO immersed in the solution (cm3/liter)
- F = the Faraday constant
- [Concentration] = moles/liter
- C = the bulk concentration
- Z = the charge of the supporting electrolyte counter ion in the diffusion layer.
- ψd = the mean potential at the start of the diffusion layer.
4. n-Type Semiconductor-Electrolyte Interface: Physical
- The space charge region in the semiconductor, bounded on one side by the surface of the semiconductor and decaying into the electrode bulk. The length of the space charge region depends on the doping density. There is a characteristic region inside the semiconductor within which the charge would have been removed by the equilibration process. Beyond this boundary, the ionized donors (for an n-type semiconductor), have their compensating charge (electrons), and the semiconductor as a whole is electrically neutral. This layer is the space charge region, also known as the depletion layer, so termed because the layer is depleted of the majority carrier.
- The Helmholtz region. This region adjacent to the semiconductor surface is measured from the plane through the center of the surface atoms of the semiconductor to the Helmholtz plane (the plane through the center of the ions of the electrolyte at their point of closest approach to the semiconductor surface) and is typically 0.3–0.6 nm in thickness.
- The space charge region in the electrolyte, bounded on one side by the outer Helmholtz plane and decaying into the bulk of the electrolyte. This region is also called the Gouy diffuse layer.
5. n-Type Semiconductor-Electrolyte Interfaces (without Surface States)
5.1. Total Potential Difference Across the Interface
5.2. The Differential Capacitance of the Space Charge Layer
5.3. Measurement of Differential Capacitance
5.3.1. Applied potential
- At a certain potential, the Fermi energy lies at the same energy as the solution redox potential (see Figure 6b). There is no net transfer of charge, and there is no band bending. This potential is therefore referred to as the flatband potential (Efb).
- For an n-type semiconductor, depletion regions arise at potentials positive of the flatband potential (see Figure 6a).
- For n-type semiconductors at potentials negative of the flatband potential, there is now an excess of the majority charge carrier (electrons) in this space charge region, which is referred to as an accumulation region (see Figure 6c).
5.3.2. Mott-schottky plots and flat band potentials
5.3.3. Heavily doped n-type semiconductors (ND > 1020 cm−3)
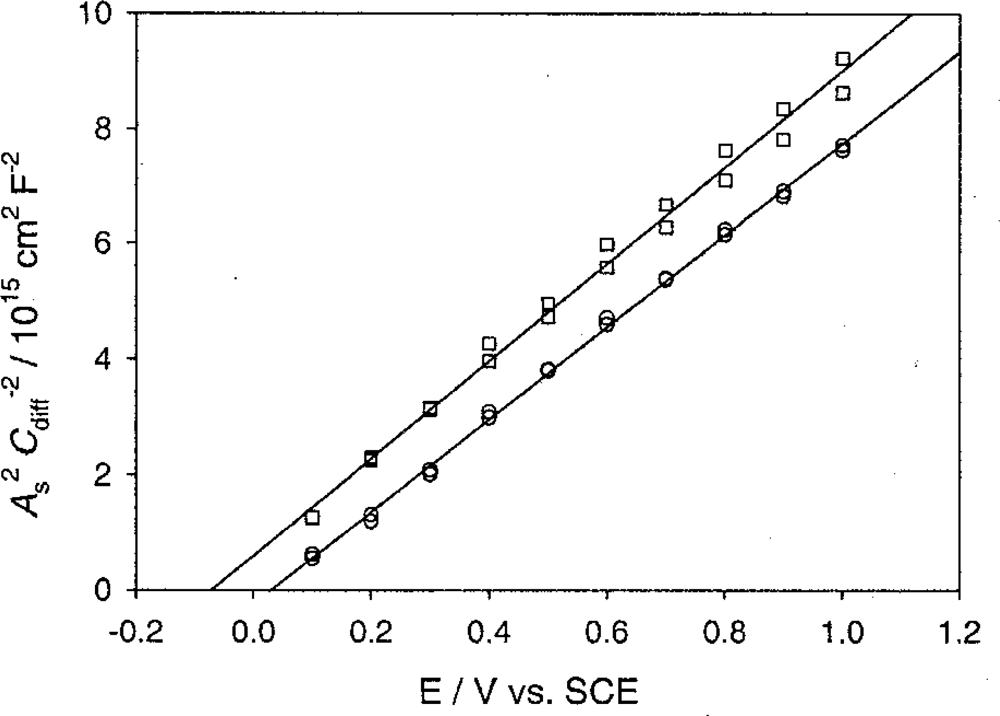
5.4. n-Type ZnO Nanowire-Electrolyte Interface
6. n-Type Semiconductor-Electrolyte Interfaces (with Surface States)
6.1. Fermi Level Pinning
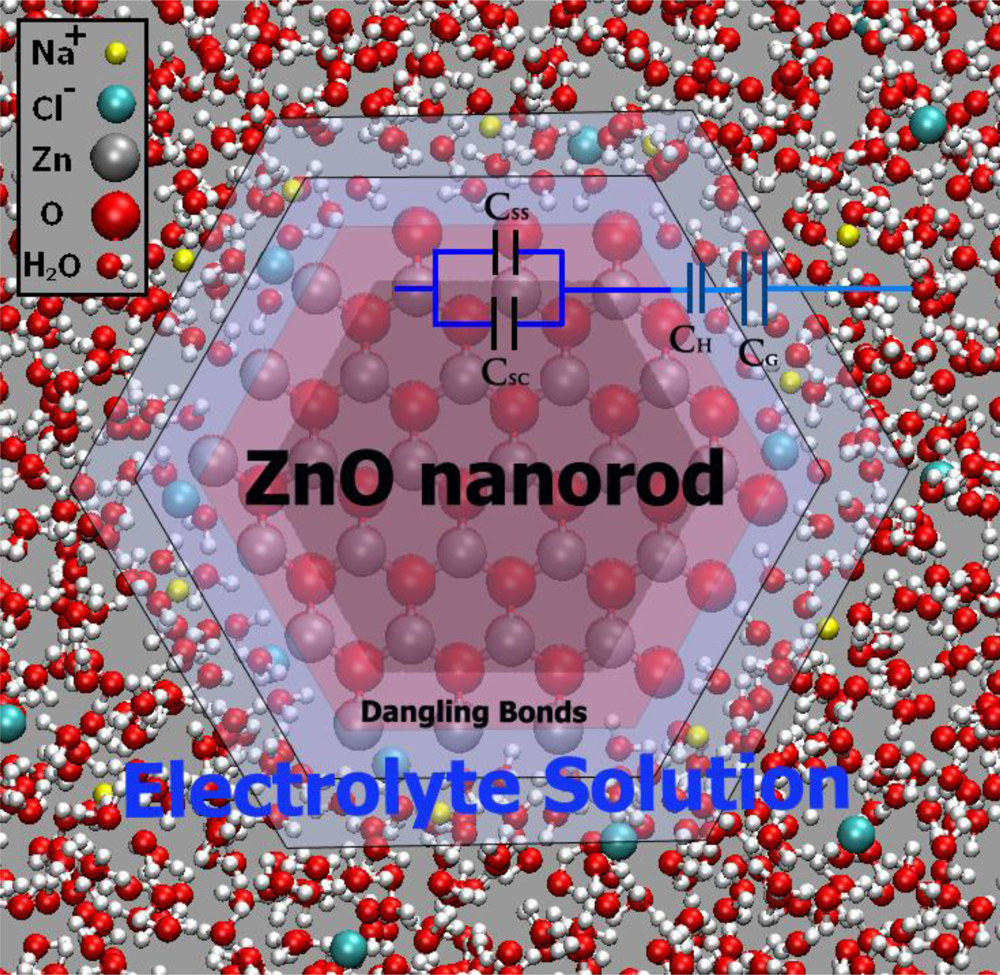
6.2. Electrochemical Potential of n-Type ZnO Nanorod Electrodes (Potentiometric Measurements)
7. n-Type ZnO Sensing Mechanism
7.1. Surface Composition and Variation in PZC
7.2. Interface Mechanism
- At pH < 9: On the first contact of ZnO with the aqueous solution, adsorption of H+ on ≡ZnOH groups and chemisorption of Cl− on ≡Zn ions near the surface takes place. Of the charges transferred to the ZnO by these processes, only the negative charges imparted by Cl− chemisorption are mobile (ZnO is an electronic semiconductor). These charges thus distribute themselves over the surface region (Figure 19a).
- At pH > 9: On the first contact of ZnO with the aqueous solution, ≡ZnOH groups combine with OH− ions, forming ≡ZnO−. Again, the negative charge imparted by this process to the ZnO forms a space charge region (Figure 19b).
7.2.1. Adsorption of Water on the (0001)–Zn and (0001̄) – O Surfaces
7.2.2. Adsorption of Water on the (101̄0)-ZnO Surfaces
8. Conclusions and Perspectives
References and Notes
- Kittel, C. Introduction to Solid State Physics, 7th ed; John Wiley & Sons, Inc: New York, NY, USA, 1996; pp. 244–255. [Google Scholar]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2007; pp. 12–30. [Google Scholar]
- Gerischer, H. Semiconductor electrode reactions. In Advances in Electrochemistry and Electrochemical Engineering: Electrochemistry, 1st ed; Delahay, P., Tobias, C., Eds.; Interscience (Wiley): New York, NY, USA, 1961; Volume 1, pp. 139–232. [Google Scholar]
- Bard, A.J. Photoelectrochemistry and heterogeneous photo-catalysis at semiconductors. J. Photochem 1979, 10, 59–75. [Google Scholar]
- Gerischer, H. Semiconductor electrochemistry. In Physical Chemistry: An Advanced Treatise, 1st ed; Eyring, H., Henderson, D., Jost, W., Eds.; Academic Press: New York, NY, USA, 1970; Volume 9A, pp. 463–542. [Google Scholar]
- Gerischer, H.Z. Uber den ablauf von redoxreaktionen an metallen und an halbleitern I: allgemeines zum elecktronenubergang zwischen einem festkorper und einem redoxelektrolyten. Z. Phys. Chem. (Frankfurt) 1960, 26, 223–247. [Google Scholar]
- Gerischer, H.Z. Uber den ablauf von redoxreaktionen an metallen und an halbleitern. Z. Phys. Chem. (Frankfurt) 1961, 27, 48–79. [Google Scholar]
- Nozik, A.J. Photoelectrochemistry: applications to solar energy conversion. Annu. Rev. Phys. Chem 1978, 29, 189–222. [Google Scholar]
- Memming, R. Processes at semiconductor electrodes. In Comprehensive Treatise of Electrochemistry, 1st ed; Conway, B.E., Bockris, J.O’M., Yeager, E., Khan, S.U.M., White, R.E., Eds.; Plenum Press: New York, NY, USA, 1983; Volume 7, pp. 529–533. [Google Scholar]
- Gerischer, H.Z. Uber den ablauf von redoxreaktionen an metallen und an halbleitern II: metall-elektroden. Z. Phys. Chem. (Frankfurt) 1960, 26, 325–338. [Google Scholar]
- Gerischer, H. Principles of electrochemistry. In The CRC Handbook of Solid State Electrochemistry, 1st ed; Gellings, P.J., Bouwmeester, H.J.M., Eds.; CRC Press Inc.: Boca Raton, FL, USA, 1997; pp. 30–50. [Google Scholar]
- Gerischer, H. Electrochemical photo and solar cells-principles and some experiments. J. Electroanal. Chem. Interfacial Electrochem 1975, 58, 263–274. [Google Scholar]
- Gerischer, H.; Tributsch, H. Elektrochemische untersuchungen zur spektralen sensibilisierung von ZnO-einkristallen. Ber. Bunsenges. Phys. Chem 1968, 72, 437–445. [Google Scholar]
- Cop, A.; Kovacevic, D.; Dragic, T.; Kallay, N. Evaluation of equilibrium parameters characterizingmetal oxide/electrolyte solution interface. Colloids and Surface A: Physicochem. Eng. Aspects 2003, 230, 159–165. [Google Scholar]
- Trimbos, H.F.A.; Stein, H.N. The ZnO/aqueous solution interface I: capacity of the double layer. J. Colloid Interface Sci 1988, 77, 386–396. [Google Scholar]
- Davis, J.A.; James, R.O.; Leckie, J.O. Surface ionization and complexation at the oxide/water interface I: computation of electrical double layer properties in simple electrolytes. J. Colloid Interface Sci 1978, 63, 480–499. [Google Scholar]
- Healy, T.W.; Jellett, V.R. Adsorption-coagulation reactions of Zn II: Hydrolyzed species at the zinc oxide-water interface. J. Colloid Interface Sci 1967, 24, 41–46. [Google Scholar]
- Yates, D.E.; Levine, S.; Healy, T.W. Site-binding model of the electrical double layer at the oxide/water interface. J. Chem. Soc. Faraday Trans. I 1974, 70, 1807–1818. [Google Scholar]
- Sprycha, R. Surface charge and adsorption of background electrolyte ions at anatase/electrolyte interface. J. Colloid Interface Sci 1984, 102, 173–185. [Google Scholar]
- Hames, R.O.; Davis, J.A.; Leckie, J.O. Computer simulation of the conductormetric and potentiometric titrations of the surface groups on ionizable latexes. J. Colloid Interface Sci 1978, 65, 331–344. [Google Scholar]
- Bootsma, G.A.; De Rooij, N.F.; Van Silfhout, A. The solid/liquid interface. Sen. Actuat 1981, 1, 111–136. [Google Scholar]
- Green, M. Electrochemistry of the semiconductor-electrolyte electrode I: the electrical double layer. J. Chem. Phys 1959, 31, 200–203. [Google Scholar]
- Tan, M.X.; Laibinis, P.E.; Nguyen, S.T.; Kesselman, J.M.; Stanton, C.E.; Lewis, N.S. Principles and applications of semiconductor photoelectrochemistry. In Progress in Inorganic Chemistry; Karlin, K.D., Ed.; John Wiley & Sons: New York, NY, USA, 1994; Volume 41, pp. 21–144. [Google Scholar]
- Gerischer, H. The impact of semiconductors on the concepts of electrochemistry. Electrochim. Acta 1990, 35, 1677–1699. [Google Scholar]
- Piasecki, W. The influence of surface potential on quantities measuring for metal oxide/electrolyte solution interface: theoretical study based on 1-pK and 2-pK surface charging models. Phys. Chem. Chem. Phys 2003, 5, 713–719. [Google Scholar]
- Dewald, J.F. The charge distribution at the zinc oxide-electrolyte interface. J. Phys. Chem. Solids 1960, 14, 155–161. [Google Scholar]
- Nozik, A.J.; Memming, R. Physical chemistry of semiconductor liquid interface. J. Phys. Chem 1996, 100, 13061–13078. [Google Scholar]
- Morrison, S.R. The Chemical Physics of Surfaces; Plenum Publishing Corporation: New York, NY, USA, 1990; pp. 54–293. [Google Scholar]
- Morrison, S.R. Electrochemistry at Semiconductor and Oxidized Metal Electrodes; Plenum Press: New York, NY, USA, 1980. [Google Scholar]
- Pleskowr, Y.V.; Gurevich, Y.Y. Semiconductor Photoelectrochemistry; Consultants Bureau: New York, NY, USA, 1986. [Google Scholar]
- Lewis, N.S. Progress in understanding electron transfer reactions at semiconductor/liquid interfaces. J. Phys. Chem 1998, 102, 4843–4855. [Google Scholar]
- Licht, S. Semiconductor electrodes and photoelectrochemistry. In Encyclopedia of Electrochemistry; Bard, A.J., Stratmann, M., Eds.; Wiley-VCH Verlag: Weinheim, Germany, 2002; Volume 6. [Google Scholar]
- Blok, L.; De Bruyn, P.L. The ionic double layer at the ZnO/solution interface III: comparison of calculated and experimental differential capacities. J. Colloid Interface Sci 1970, 32, 533–538. [Google Scholar]
- Friedmann, J.; Fruhwirth, O.; Herzog, G.W. Capacitances and losses of ZnO/Borax electrolyte and corroding Zn/Borax electrolyte contacts. Surf. Technol 1978, 6, 469–478. [Google Scholar]
- Logtenberg, E.H.P.; Stein, H.N. Surface sharge and coagulation of aqueous ZnO dispersions. J. Colloid Interface Sci 1986, 109, 190–200. [Google Scholar]
- Schubert, E.F.; Kuo, J.M.; Kopf, R.F.; Jordan, A.S. Fermi-level-pinning-induced impurity redistribution in semiconductors during epitaxial growth. Phys. Rev. B 1990, 42, 1364–1368. [Google Scholar]
- Gabouze, N.; Fotouhi, B.; Gorochov, O.; Cachet, H.; Yao, N.A. Flatband potential shift of n-type GaAs in CH3CN containing different redox reagents. J. Electroanal. Chem 1987, 237, 289–293. [Google Scholar]
- Schmuki, P.; Bohni, H.; Bardwell, J. In situ characterization of anodic silicon oxide films by AC impedance measurements. J. Electrochem. Soc 1995, 142, 1705–1712. [Google Scholar]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods, 2nd ed; John Wiley & Sons, Inc: New York, NY, USA, 2001. [Google Scholar]
- Zoski, C.G. Handbook of Electrochemistry, 1st ed; Elsevier: Amsterdam, The Netherlands, 2007; pp. 329–390. [Google Scholar]
- Hamann, T.W.; Gstrein, F.; Brunschwing, B.S.; Lewis, N.S. Measurement of the driving force dependence of interfacial charge transfer rate constants in response to pH charges at n-ZnO/H2O interfaces. Chem. Phys 2006, 326, 15–23. [Google Scholar]
- Arutyunyan, V.M. Physical properties of the semiconductor-electrolyte interface. Sov. Phys. Usp 1989, 32, 521–542. [Google Scholar]
- Kovacs, I.K.; Horvai, G. Possibilities of chemical sensing at the semiconductor/electrolyte interface. Sens. Actuat. B 1994, 18–19, 315–320. [Google Scholar]
- Pettinger, B.; Schöppel, H.R.; Yokoyama, T.; Gerischer, H. Tunneling processes at highly doped ZnO electrode in aqueous electrolytes II: electron exchange with the valence band. Ber. Bunsenges. Phys. Chem 1974, 78, 1024–1030. [Google Scholar]
- Uosaki, K.; Kita, H. Effects of the Helmholtz layer capacitance on the potential distribution at semiconductor/electrolyte interface and the linearity of the Mott-Schottky plot. J. Electrochem. Soc 1983, 130, 895–897. [Google Scholar]
- De Gryse, R.; Gomes, W.P.; Cardon, F.; Vennik, J. On the interpretation of Mott-Schottky plots determined at semiconductor/electrolyte systems. J. Electrochem. Soc 1975, 122, 711–712. [Google Scholar]
- Parthasarathy, M.; Ramgir, N.S.; Sathe, B.R.; Mulla, I.S.; Pillai, V.K. Surface-state-mediated electron transfer at nanostructured ZnO multipod/electrolyte interfaces. J. Phys. Chem. C 2007, 111, 13092–13102. [Google Scholar]
- Tornow, J.; Schwarzberg, K. Electrical response of wet chemically grown ZnO nanorods for photovoltaic application. Mater. Res. Soc. Symp. Proc 2006, 974. 0974-CC10-27.. [Google Scholar]
- Mora-Sero, I.; Fabregat-Santiago, F.; Denier, B.; Bisquert, J. Determination of carrier density of ZnO nanowires by electrochemical technique. Appl. Phys. Lett 2006, 89, 203117. [Google Scholar]
- Makarova, M.V.; Macunova, K.; Krtil, P. The effect of cationic disorder on the optical and electrochemical behavior of nanocrystalline ZnO prepared from precursors. J. Solid State Electrochem 2006, 10, 320–328. [Google Scholar]
- Qu, F.; Morais, P.C. An oxide semiconductor nanoparticle in an aqueous medium: a surface charge density investigation. J. Phys. Chem. B 2000, 104, 5232–5236. [Google Scholar]
- Redmond, G.; O’Keeffe, A.; Burgess, C.; MacHale, C.; Fitzmaurice, D. Spectroscopic determination of the flatband potential of transparent nanocrystalline ZnO films. J. Phys. Chem 1993, 97, 11081–11086. [Google Scholar]
- Schmidt-Mende, L.; MacManus-Driscoll, J.L. ZnO nanostructures defects and devices. Mater. Today 2007, 10, 40–48. [Google Scholar]
- Adamson, A.W.; Gast, A.P. Physical Chemistry of Surfaces, 6th ed; John Wiley & Sons, Inc: New York, NY, USA, 1997. [Google Scholar]
- Somorjai, G.A. Introduction to Surface Chemistry and Catalysis; John Wiley & Sons: New York, NY, USA, 1994. [Google Scholar]
- Oekermann, T.; Schlettwein, D.; Jaeger, N.I. Role of surface states and adsorbates in time-resolved photocurrent measurements and photovoltage generation at phthalocyaninatozic II-photocathodes. J. Electroanal. Chem 1999, 462, 222–234. [Google Scholar]
- Van Meirhaeghe, R.L.; Cardon, F.; Gomes, W.P. A quantitative expression for partial Fermi level pinning at semiconductor/redox electrolyte interfaces. J. Electroanal. Chem 1985, 188, 287–291. [Google Scholar]
- Bard, A.J.; Bocarsly, A.B.; Fan, F-R.F.; Ealton, E.G.; Wrighton, M.S. The concept of Fermi level pinning at semiconductor/liquid junctions: consequences for energy conversion efficiency and selection of solution redox couples in solar devices. J. Am. Chem. Soc 1980, 102, 3671–3677. [Google Scholar]
- Bardeen, J. Surface states and rectification at a metal semi-conductor contact. Phys. Rev 1947, 71, 717–727. [Google Scholar]
- Mead, C.A.; Spitzer, W.G. Fermi level position at metal-semiconductor interfaces. Phys. Rev. A 1964, 134, A713–A716. [Google Scholar]
- McGill, T.C. Phenomenology of metal-semiconductor electrical barriers. J. Vac. Sci. Technol 1974, 11, 935–942. [Google Scholar]
- Kurtin, S.; McGill, T.C.; Mead, C.A. Fundamental transition in the electronic nature of solids. Phys. Rev. Lett 1969, 22, 1433–1436. [Google Scholar]
- Rajeshwar, K. Fundamentals of semiconductor electrochemistry and photoelectrochemistry. In Encyclopedia of Electrochemistry; Licht, S., Ed.; Wiley-VCH: Weinheim, Germany, 2001; pp. 3–53. [Google Scholar]
- Liao, Z.; Liu, K.; Zhang, J.; Xu, J.; Yu, D. Effect of surface states on electron transport in individual ZnO nanowires. Phys. Lett. A 2007, 367, 207–210. [Google Scholar]
- Jones, F.; Leonard, F.; Talin, A.A. Electrical conduction and photoluminescence properties of solution-grown ZnO nanowires. J. Appl. Phys 2007, 102, 014305. [Google Scholar]
- Green, M. Modern Aspects of Electrochemistry; Bockris, J.O’M., Ed.; Plenum: New York, NY, USA, 1959; Volume 2, pp. 356–381. [Google Scholar]
- Tamm, I.E. A possible kind of electron binding on crystal surfaces. Z. Phys 1932, 76, 76849–76850. [Google Scholar]
- Shockley, W. On the surface states associated with a periodic potential. Phys. Rev 1939, 56, 317–323. [Google Scholar]
- Gerischer, H. Semiconductor electrochemistry. In Physical Chemistry: An Advanced Treatise; Eyring, H., Henderson, D., Jost, W., Eds.; Academic Press: New York, NY, USA, 1970; Volume IXA, pp. 463–542. [Google Scholar]
- Greene, L.E.; Law, M.; Goldberger, J.; Kim, F.; Johnson, J.C.; Zhang, Y.; Saykally, R.J.; Yang, P. Low-temperature wafer-scale production of ZnO nanowire arrays. Angew. Chem. Int. Ed 2003, 42, 3031–3034. [Google Scholar]
- Vayssieres, L.; Keis, K.; Lindquist, S-E.; Hagfeldt, A. Purpose-build anisotropic metal oxide material: 3D highly oriented microrod. J. Phys. Chem. B 2001, 105, 3350–3352. [Google Scholar]
- Li, Q.; Kumar, V.; Li, Y.; Zhang, H.; Marks, T.J.; Chang, R.P.H. Fabrication of ZnO nanorods and nanotubes in aqueous solutions. Chem. Mater 2005, 17, 1001–1006. [Google Scholar]
- Al-Hilli, S.; Öst, A.; Strålfors, P.; Willander, M. ZnO nanorods as an intracellular sensor for pH measurements. J. Appl. Phys 2007, 102, 084304. [Google Scholar]
- Parks, G.A.; De Bruyn, P.L. The zero point of charge of oxides. J. Phys. Chem 1960, 66, 967–973. [Google Scholar]
- Blok, L.; De Bruyn, P.L. The ionic double layer at the ZnO solution interface II: composition model of the surface. J. Colloid Interface Sci 1970, 32, 527–532. [Google Scholar]
- Blok, L.; De Bruyn, P.L. The ionic double layer at the ZnO solution interface I: the experimental point of zero charge. J. Colloid Interface Sci 1970, 32, 518–526. [Google Scholar]
- Trimbos, H.F.A.; Stein, H.N. The ZnO/aqueous solution interface II: mechanism of the slow process. J. Colloid Interface Sci 1980, 77, 397–407. [Google Scholar]
- Nosker, R.W.; Mark, P.; Levine, J.D. Polar surfaces of wurtzite and zincblende lattices. Surf. Sci 1970, 19, 291–317. [Google Scholar]
- Wander, A.; Schedin, F.; Steadman, P.; Norris, A.; McGrath, R.; Turner, T.S.; Thornton, G.; Harrison, N.M. Stability of polar oxide surfaces. Phys. Rev. Lett 2001, 86, 3811–3814. [Google Scholar]
- Meyer, B. First principle study of the polar O-terminated ZnO surface in thermodynamic equilibrium with oxygen and hydrogen. Phys. Rev. B 2004, 69, 045416. [Google Scholar]
- Wander, A.; Harrison, N.M. The stability of polar oxide surfaces: The interaction of H2O with ZnO (0001) and ZnO (0001-). J. Chem. Phys 2001, 115, 2312–2316. [Google Scholar]
- Meyer, B.; Marx, D.; Dulub, O.; Diebold, U.; Kunat, M.; Langenberg, D.; Woll, C. Partial dissociation of water leads to stable superstructure on the surface of zinc oxide. Angew. Chem. Int. Ed 2004, 43, 6642–6645. [Google Scholar]
- Dulub, O.; Meyer, B.; Diebold, U. Observation of the dynamical change in a water monolayer adsorbed on a ZnO surface. Phys. Rev. Lett 2005, 95, 136101. [Google Scholar]
- Yan, Y.; Al-Jassim, M.M. Structure and energetic of water adsorbed on the ZnO (101̄0) surface. Phys. Rev. B 2005, 72, 235406. [Google Scholar]




















© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Al-Hilli, S.; Willander, M. The pH Response and Sensing Mechanism of n-Type ZnO/Electrolyte Interfaces. Sensors 2009, 9, 7445-7480. https://doi.org/10.3390/s90907445
Al-Hilli S, Willander M. The pH Response and Sensing Mechanism of n-Type ZnO/Electrolyte Interfaces. Sensors. 2009; 9(9):7445-7480. https://doi.org/10.3390/s90907445
Chicago/Turabian StyleAl-Hilli, Safaa, and Magnus Willander. 2009. "The pH Response and Sensing Mechanism of n-Type ZnO/Electrolyte Interfaces" Sensors 9, no. 9: 7445-7480. https://doi.org/10.3390/s90907445
APA StyleAl-Hilli, S., & Willander, M. (2009). The pH Response and Sensing Mechanism of n-Type ZnO/Electrolyte Interfaces. Sensors, 9(9), 7445-7480. https://doi.org/10.3390/s90907445



