Investigation on a Large-Scale Braceless-TLP Floating Offshore Wind Turbine at Intermediate Water Depth
Abstract
:1. Introduction
2. Model Description
2.1. Physical Model Description
2.2. Numerical Modeling
2.2.1. Aerodynamics
2.2.2. Hydrodynamics
2.2.3. Mooring Dynamics
3. Results and Discussions
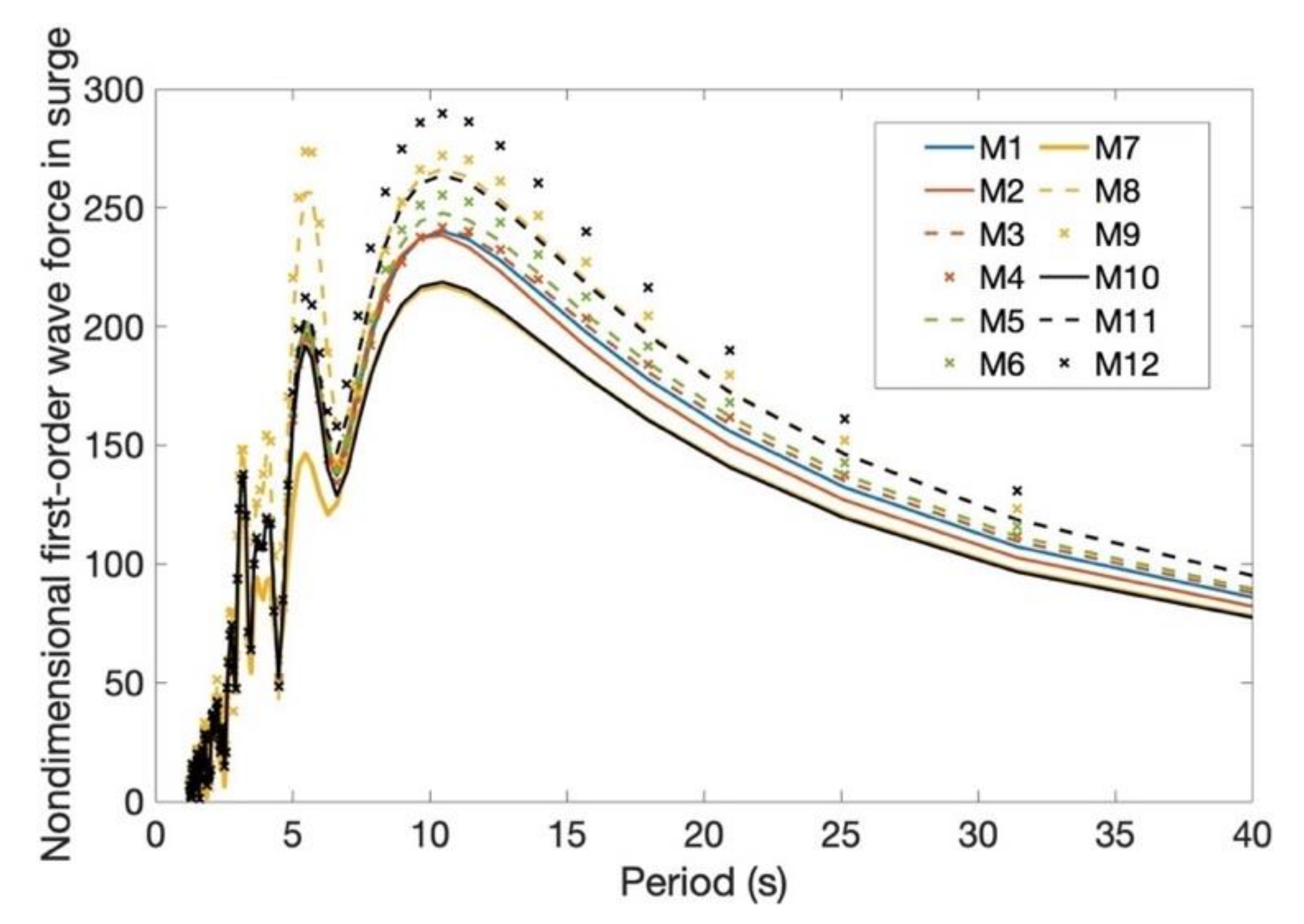
3.1. Hydrodynamic Analysis of Floating Platform
3.2. Coupled Analysis of FOWT
3.2.1. Free-Decay Tests
3.2.2. Response Amplitude Operators
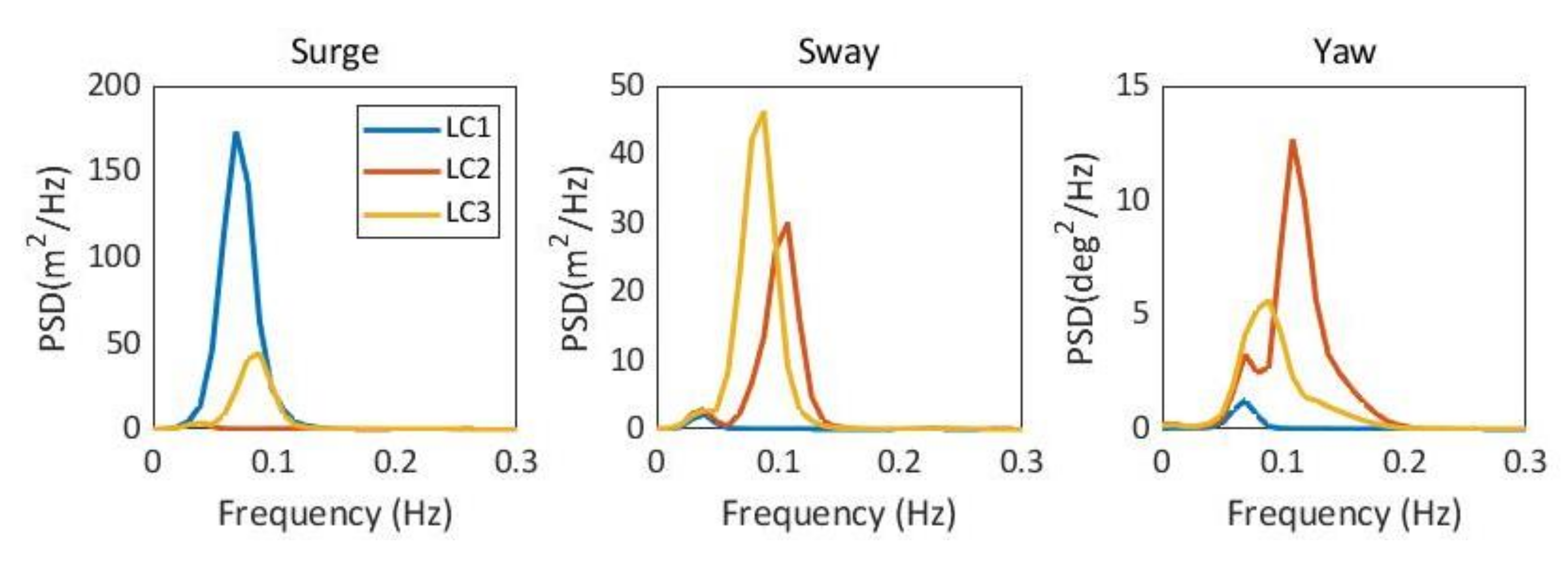
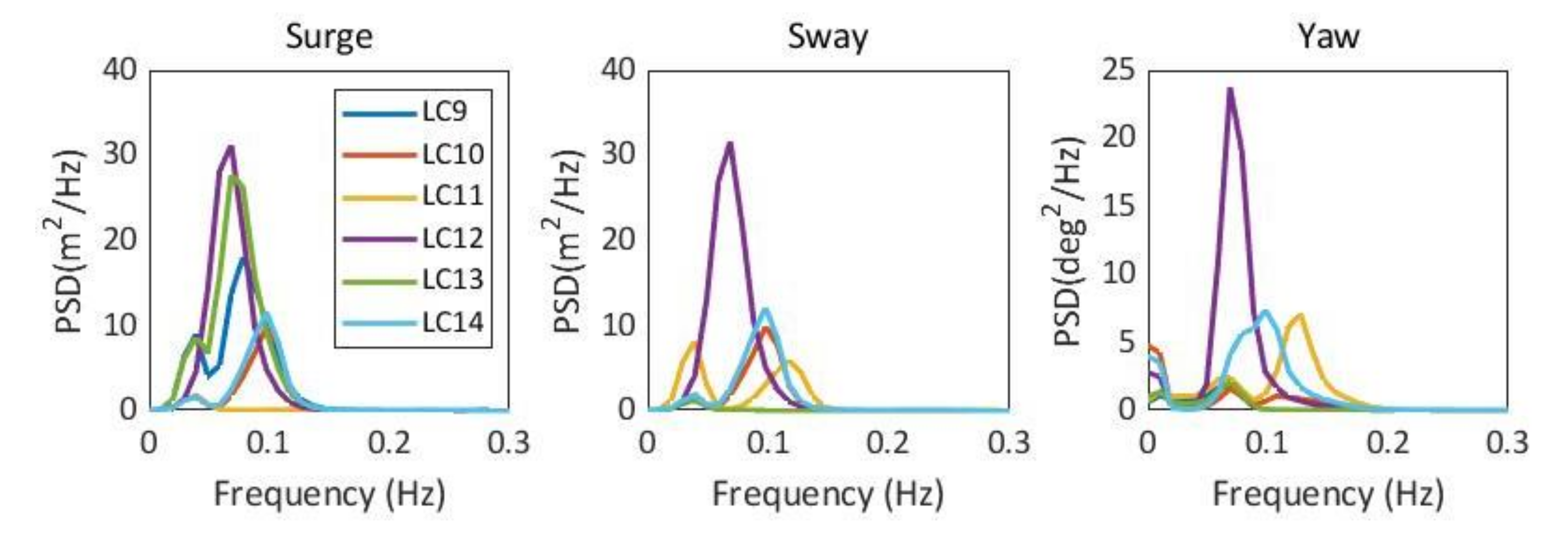
3.2.3. Responses to Wind–Wave Combined Effects
4. Conclusions
- (1)
- The natural periods of the platform in surge/way, heave, pitch/roll, and yaw were 26.4 s, 1.3 s, 2 s, and 19.7 s, which satisfied the standard given by DNV-RP-0268.
- (2)
- The RAOs of the platform were derived from the time series responses excited by white noise waves. The platform showed small RAO in heave and pitch, illustrating good stability of the structure in the corresponding DOFs.
- (3)
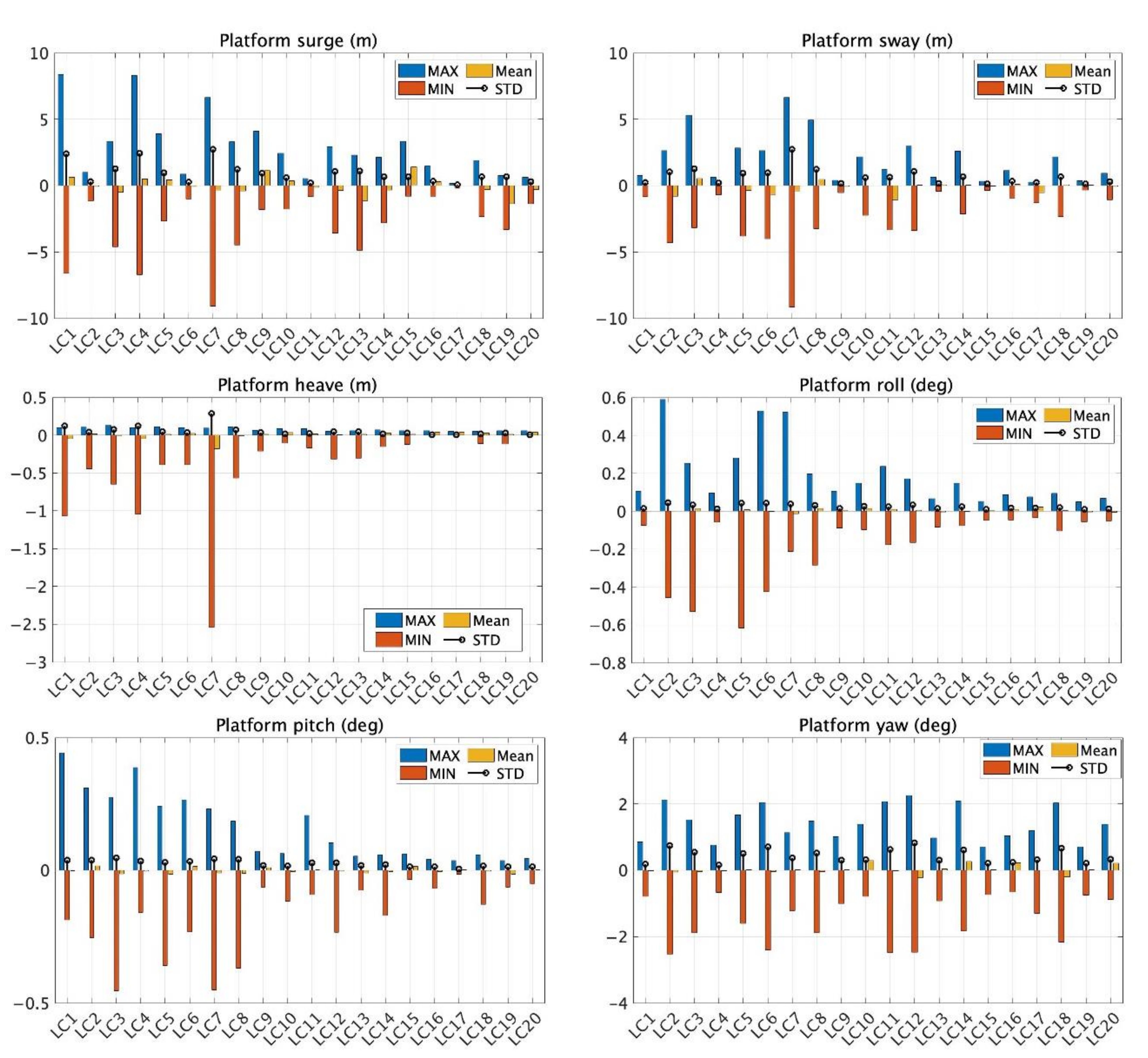
- The effects of wind and waves on the responses of the FOWT were investigated. A total of 20 load cases were utilized combining different environmental parameters. The results showed that the FOWT can survive under the most extreme 100-year-return wind–wave combined environments.
- (4)
- The maximum surge displacement was 15% of the designed water depth, which was smaller than the admissible offset to the water depth ratio of 23%.
- (5)
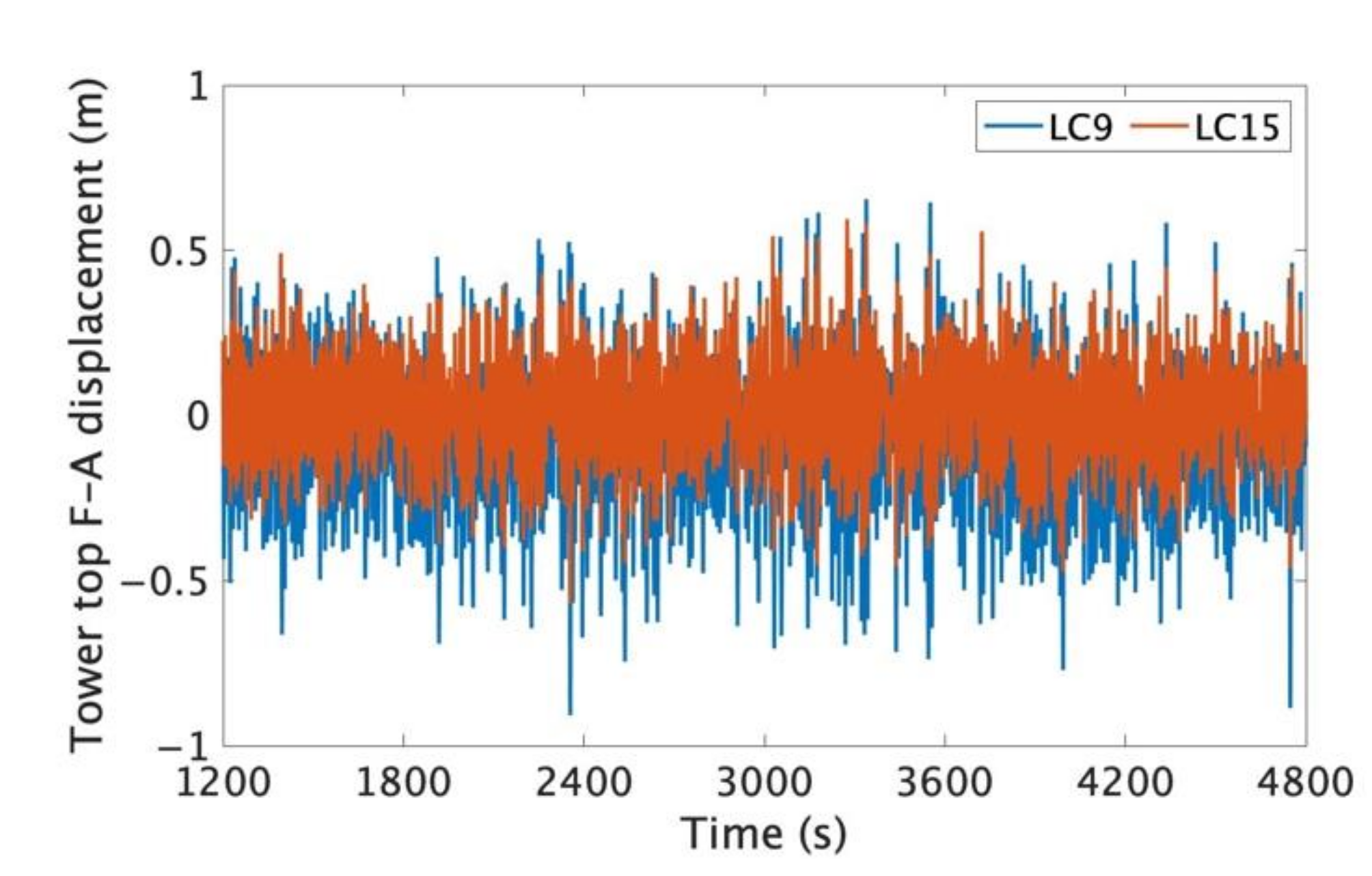
- The tower top displacements were in the similar order as that calculated for a 10-MW wind turbine supported by the monopile foundation, indicating that the RNA was not affected by the motion of the floating platform.
- (6)
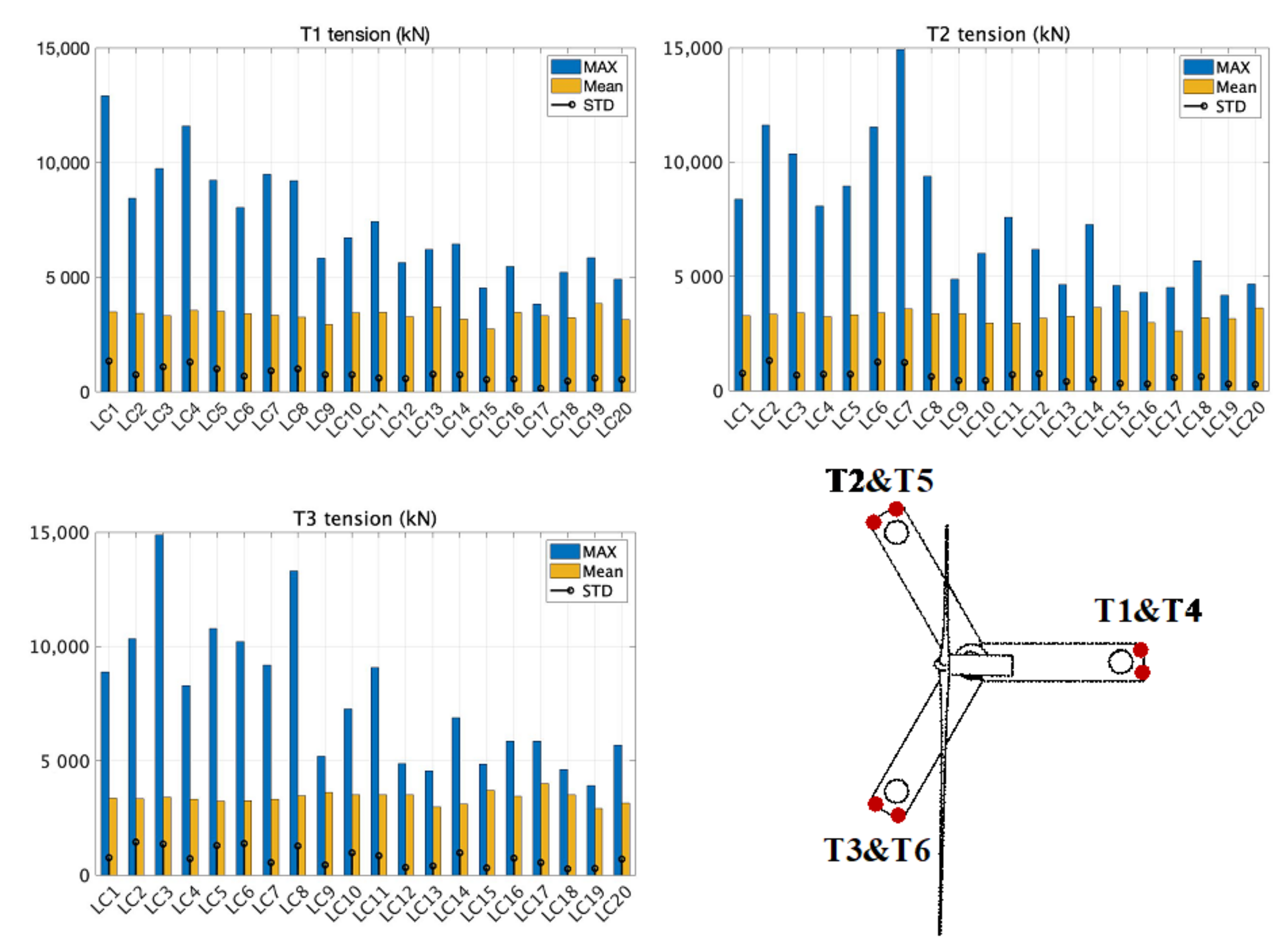
- The largest tension force was 14,923 kN, which was observed in the 50-year-return load case. As the tendons experienced relatively high-tension forces, it was vital for TLP to select proper materials for station-keeping to avoid damage of the tendon due to the high-tension force. All six tendons remained tense during the simulation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Q. Design and Dynamic Analysis of a Steel Pontoon-Type Semi-Submersible Floater Supporting the DTU 10MW Reference Turbine. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2014. [Google Scholar]
- Li, J.; Shi, W.; Zhang, L.; Michailides, C.; Li, X. Wind-Wave Coupling Effect on the Dynamic Response of a Combined Wind-Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 1101. [Google Scholar] [CrossRef]
- GWEC. Global Offshore Wind Report 2021; GWEC: Brussels, Belgium, 2021. [Google Scholar]
- Wang, Y.; Shi, W.; Michailides, C.; Wan, L.; Kim, H.; Li, X. WEC shape effect on the motion response and power performance of a combined wind-wave energy converter. Ocean. Eng. 2022, accepted. [Google Scholar]
- Matha, D. Model Development and Loads Analysis of an Offshore Wind Turbine on a Tnesion Leg Platform, with a Comparison to Other Floating Turbine Concepts; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2009. [Google Scholar]
- Speight, J.G. Subsea and Deepwater Oil and Gas Science and Technology; Gulf Professional Publishing: Oxford, UK, 2015. [Google Scholar]
- Withee, J.E. Fully Coupled Dynamic Analysis of a Floating Wind Turbine System. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; NREL: Jefferson County, CO, USA, 2005. [Google Scholar]
- Vita, L.; Ramachandran, G.K.V.; Krieger, A.; Kvittem, M.I.; Merino, D.; Cross-Whiter, J.; Ackers, B.B. Comparison of Numerical Models and Verification Against Experimental Data, Using Pelastar TLP Concept. In Proceedings of the ASME 2015 34th International Conference on Ocean, Offshore and Arctic Engineering, St. John’s, NL, Canada, , 31 May–5 June 2015. [Google Scholar]
- Zhao, Y.; Yang, J.; He, Y. Preliminary Design of a Multi-Column TLP Foundation for a 5-MW Offshore Wind Turbine. Energies 2012, 5, 3874. [Google Scholar] [CrossRef]
- Zhao, Y.; She, X.; He, Y.; Yang, J.; Peng, T.; Kou, Y. Experimental Study on New Multi-Column Tension-Leg-Type Floating Wind Turbine. China Ocean. Eng. 2018, 32, 123–131. [Google Scholar] [CrossRef]
- Ding, H.; Han, Y.; Zhang, P.; Le, C.; Liu, J. Dynamic Analysis of a New Type of Floating Platform for Offshore Wind Turbine. In Proceedings of the the Twenty-Sixth (2016) International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- Oguz, E.; Day, A.H.; Clelland, D.; Incecik, A.; Dai, S.; Lopez, J.A.; González, G.; Sánchez, G.D. Experimental Study of a TLP Offshore Floating Wind Turbine. In Proceedings of the ICMT, Harbin, China, 16–18 July 2016. [Google Scholar]
- Ren, Y.; Vengatesan, V.; Shi, W. Dynamic Analysis of a Multi-column TLP Floating Offshore Wind Turbine with Tendon Failure Scenarios. Ocean Eng. 2022, 245, 110472. [Google Scholar] [CrossRef]
- Copple, R.; Capanoglu, C. Tension Leg Wind Turbine (TLWT) Conceptual Design Suitable for a Wide Range of Water Depths. In Proceedings of the the Twenty-Fourth International Ocean and Polar Engineering Conference, Busan, Korea, 15–20 June 2014. [Google Scholar]
- Zhao, Z.; Shi, W.; Wang, W.; Qi, S.; Li, X. Dynamic analysis of a novel semi-submersible platform for a 10 MW wind turbine in intermediate water depth. Ocean Eng. 2021, 237, 109688. [Google Scholar] [CrossRef]
- Luan, C.; Gao, Z.; Moan, T. Design and analysis of a braceless steel 5-MW semi-submersible wind turbine. In Proceedings of the 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Peng, Z.; Zhao, H.; Li, X. New ductile fracture model for fracture prediction ranging from negative to high stress triaxiality. Int. J. Plast. 2021, 145, 103057. [Google Scholar] [CrossRef]
- Luan, C. Design and analysis for a steel braceless semi-submersible hull for supporting a 5-MW horizontal axis wind turbine. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2018. [Google Scholar]
- Bortolotti, P.; Dykes, K.; Merz, K.; Zahle, F. IEA Wind Task 37 on Systems Engineering in Wind Energy. In WP2.1 Reference Wind Turbines; National Renewable Energy Laboratory: Golden, CO, USA, 2019. [Google Scholar]
- DNVGL. DNVGL-RP-0286 Coupled Analysis of Floating Wind Turbines; DNVGL: Bærum, Norway, 2019. [Google Scholar]
- DNVGL. DNVGL-OS-E301 Position Mooring; DNVGL: Bærum, Norway, 2015. [Google Scholar]
- Jonkman, J.; Buhl, J.M.L. TurbSim User’s Guide; NREL/TP-500-39797; National Renewable Energy Laboratory: Golden, CO, USA, 2006. [Google Scholar]
- Hsu, S.A.; Meindl, E.A.; Gilhousen, D.B. Determining the Power-Low Wind-Profile Exponent under Near-Neutral Stability Conditions at Sea. J. Appl. Meteorol. Climatol. 1994, 33, 757–765. [Google Scholar] [CrossRef] [Green Version]
- Masciola, M. MAP++ Documentation—Release 1.15; National Renewable Energy Laboratory: Golden, CO, USA, 2018. [Google Scholar]
- ANSYS, I.; ANSYS AQWA, Librium. NAUT and Tether Manuals. Electrical Source. Available online: https://cyberships.files.wordpress.com/2014/01/aqwa_ref.pdf (accessed on 15 October 2021).
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, National Renewable Energy Laboratory, Golden, CO, USA, 2007. [Google Scholar]
- Masciola, M.; Jonkman, J.; Robertson, A. Implementation of a Multisegmented, Quasi-Static Cable Model. In Proceedings of the International Ocean (Offshore) and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Wu, H.; Zhao, Y.; He, Y.; Shao, Y.; Mao, W.; Han, Z.; Huang, C.; Gu, X.; Jiang, Z. Transient response of a TLP-type floating offshore wind turbine under tendon failure conditions. Ocean Eng. 2021, 220, 108486. [Google Scholar] [CrossRef]
- Hall, M.; Buckham, B.; Crawford, C. Evaluating the importance of mooring line model fidelity in floating offshore wind turbine simulations. Wind Energy 2014, 17, 1835–1853. [Google Scholar] [CrossRef]
- Ramachandran, G.K.V.; Robertson, A.; Jonkman, J.M.; Masciola, M.D. Investigation of Response Amplitude Operators for Floating Offshore Wind Turbines. In Proceedings of the The 23rd International Ocean, Offshore and Polar Engineering Conference, Anchorage, AK, USA, 30 June–5 July 2013. [Google Scholar]
- Campanile, A.; Piscopo, V.; Scanardella, A. Mooring design and selection for floating offshore wind turbines on intermediate and deep water depths. Ocean. Eng. 2018, 148, 349–360. [Google Scholar] [CrossRef]
- Xi, R.; Du, X.; Wang, P.; Xu, C.; Zhai, E.; Wang, S. Dynamic analysis of 10 MW monopile supported offshore wind turbine based on fully coupled model. Ocean. Eng. 2021, 234, 109346. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Wind Regime | IEC class 1A |
| Cut-in wind speed | 4 m/s |
| Cut-out wind speed | 25 m/s |
| Rated wind speed | 11 m/s |
| Rotor diameter | 198.0 m |
| Hub diameter | 4.6 m |
| Hub Height | 119 m |
| Minimum rotor speed | 6.0 rpm |
| Maximum rotor speed | 8.68 rpm |
| Maximum tip speed | 90.0 m/s |
| Hub overhang | 7.1 m |
| Shaft tilt angle | 6.0 deg. |
| Blade Mass | 47,700 kg |
| Nacelle mass | 542,600 kg |
| Tower mass | 628,442 kg |
| Dimension | Value |
|---|---|
| Pontoon length | 36.4 m |
| Pontoon width | 9 m |
| Pontoon height | 5 m |
| Main column diameter | 8.3 m |
| Main column height | 36 m |
| Freeboard height | 10 m |
| Side column diameter | 5.5 m |
| Side column height | 41 m |
| Hull thickness | 0.015 m |
| Draft | 26 m |
| Platform mass (including ballast) | 4047 ton |
| Platform center of mass below SWL | 9.29 m |
| Platform pitch/roll moment of inertia | 1.65 × 109 kg m2 |
| Platform yaw moment of inertia | 3.02 × 109 kg m2 |
| Displacement | 7328 ton |
| Unstretched tendon length | 33.98 m |
| Tendon dry weight | 116.027 kg/m |
| Tendon axial stiffness | 1.8 × 109 N |
| Prototype | Draft | Pontoon Width | Pontoon Height | Column Diameter |
|---|---|---|---|---|
| M1 | 26 | 9 | 5 | 6.5 |
| M2 | 24 | 9 | 5 | 6.5 |
| M3 | 28 | 9 | 5 | 6.5 |
| M4 | 30 | 9 | 5 | 6.5 |
| M5 | 26 | 10 | 5 | 6.5 |
| M6 | 26 | 11 | 5 | 6.5 |
| M7 | 26 | 9 | 5 | 5.5 |
| M8 | 26 | 9 | 5 | 7.5 |
| M9 | 26 | 9 | 5 | 8.5 |
| M10 | 26 | 9 | 4 | 6.5 |
| M11 | 26 | 9 | 6 | 6.5 |
| M12 | 26 | 9 | 7 | 6.5 |
| Mode | Period (s) | Standard (s) |
|---|---|---|
| Surge/sway | 26.4 | 15–60 |
| Heave | 1.3 | 1–2 |
| Roll/pitch | 2 | 2–5 |
| Yaw | 19.7 | 8–20 |
| Load Case | Return Period (Year) | HS (m) | TP (s) | VHub (m/s) | Direction (°) |
|---|---|---|---|---|---|
| LC1 | 100 | 9.07 | 13.3 | 38.13 | 0 |
| LC2 | 8.45 | 9.3 | 44.18 | 90 | |
| LC3 | 9.38 | 11.4 | 41.45 | 225 | |
| LC4 | 50 | 8.96 | 13.5 | 34.16 | 0 |
| LC5 | 8.45 | 10.4 | 36.78 | 45 | |
| LC6 | 8.13 | 9.3 | 40.05 | 90 | |
| LC7 | 8.69 | 16.4 | 35.55 | 135 | |
| LC8 | 9.07 | 11.5 | 37.79 | 225 | |
| LC9 | 5 | 5.10 | 11.1 | 20.77 | 0 |
| LC10 | 6.21 | 9.8 | 24.92 | 45 | |
| LC11 | 5.94 | 8.2 | 24.96 | 90 | |
| LC12 | 5.47 | 13.6 | 23.37 | 135 | |
| LC13 | 4.99 | 12.2 | 20.15 | 180 | |
| LC14 | 6.42 | 10 | 24.82 | 225 | |
| LC15 | 2 | 3.50 | 10.8 | 15.22 | 0 |
| LC16 | 4.22 | 8.7 | 19.17 | 45 | |
| LC17 | 3.68 | 7 | 17.4 | 90 | |
| LC18 | 4.34 | 12.2 | 18.76 | 135 | |
| LC19 | 3.81 | 10.4 | 15.64 | 180 | |
| LC20 | 4.11 | 8.3 | 18.79 | 225 |
| Tendon Load Case | T1 | T2 | T3 |
|---|---|---|---|
| LC1 | 32.79 | 37.10 | 35.83 |
| LC2 | 32.50 | 32.32 | 32.00 |
| LC3 | 32.29 | 32.43 | 32.39 |
| LC4 | 34.63 | 45.13 | 49.09 |
| LC5 | 32.30 | 32.66 | 31.67 |
| LC6 | 45.52 | 32.35 | 32.01 |
| LC7 | 32.32 | 32.89 | 32.87 |
| LC8 | 32.31 | 42.73 | 32.96 |
| LC9 | 435.78 | 1467.05 | 1990.44 |
| LC10 | 32.87 | 72.36 | 32.50 |
| LC11 | 34.80 | 32.76 | 32.43 |
| LC12 | 1266.67 | 550.78 | 2025.45 |
| LC13 | 845.87 | 1728.30 | 1637.50 |
| LC14 | 43.72 | 761.69 | 32.96 |
| LC15 | 919.79 | 2272.05 | 2577.92 |
| LC16 | 1307.90 | 1853.66 | 287.31 |
| LC17 | 2686.97 | 798.93 | 2222.04 |
| LC18 | 1461.90 | 956.23 | 2372.19 |
| LC19 | 1673.04 | 2068.80 | 1745.74 |
| LC20 | 1265.52 | 2071.74 | 408.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Ren, Y.; Shi, W.; Li, X. Investigation on a Large-Scale Braceless-TLP Floating Offshore Wind Turbine at Intermediate Water Depth. J. Mar. Sci. Eng. 2022, 10, 302. https://doi.org/10.3390/jmse10020302
Zhou Y, Ren Y, Shi W, Li X. Investigation on a Large-Scale Braceless-TLP Floating Offshore Wind Turbine at Intermediate Water Depth. Journal of Marine Science and Engineering. 2022; 10(2):302. https://doi.org/10.3390/jmse10020302
Chicago/Turabian StyleZhou, Yiming, Yajun Ren, Wei Shi, and Xin Li. 2022. "Investigation on a Large-Scale Braceless-TLP Floating Offshore Wind Turbine at Intermediate Water Depth" Journal of Marine Science and Engineering 10, no. 2: 302. https://doi.org/10.3390/jmse10020302
APA StyleZhou, Y., Ren, Y., Shi, W., & Li, X. (2022). Investigation on a Large-Scale Braceless-TLP Floating Offshore Wind Turbine at Intermediate Water Depth. Journal of Marine Science and Engineering, 10(2), 302. https://doi.org/10.3390/jmse10020302







