GPU-Accelerated Multi-Objective Optimal Planning in Stochastic Dynamic Environments
Abstract
:1. Introduction
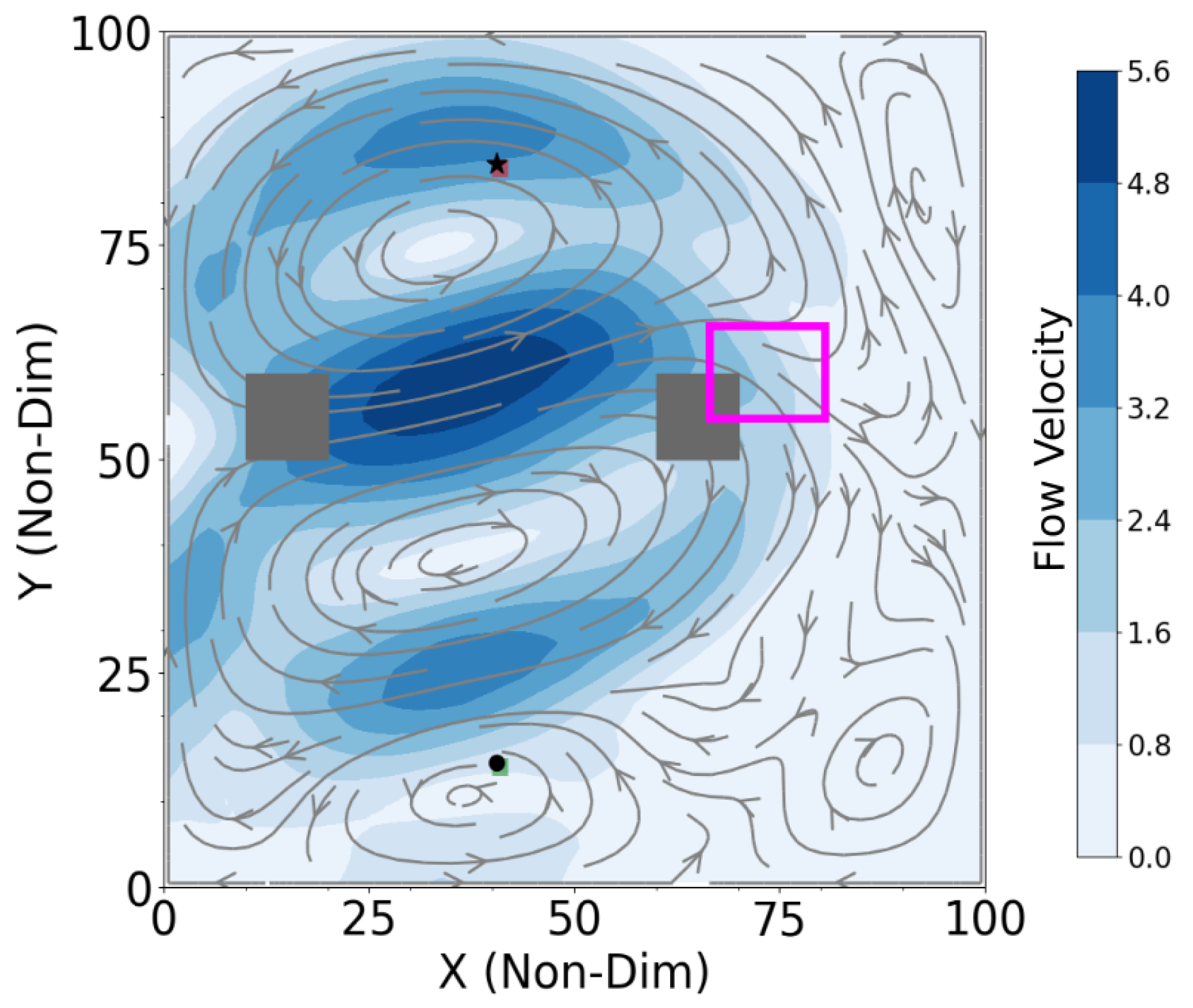
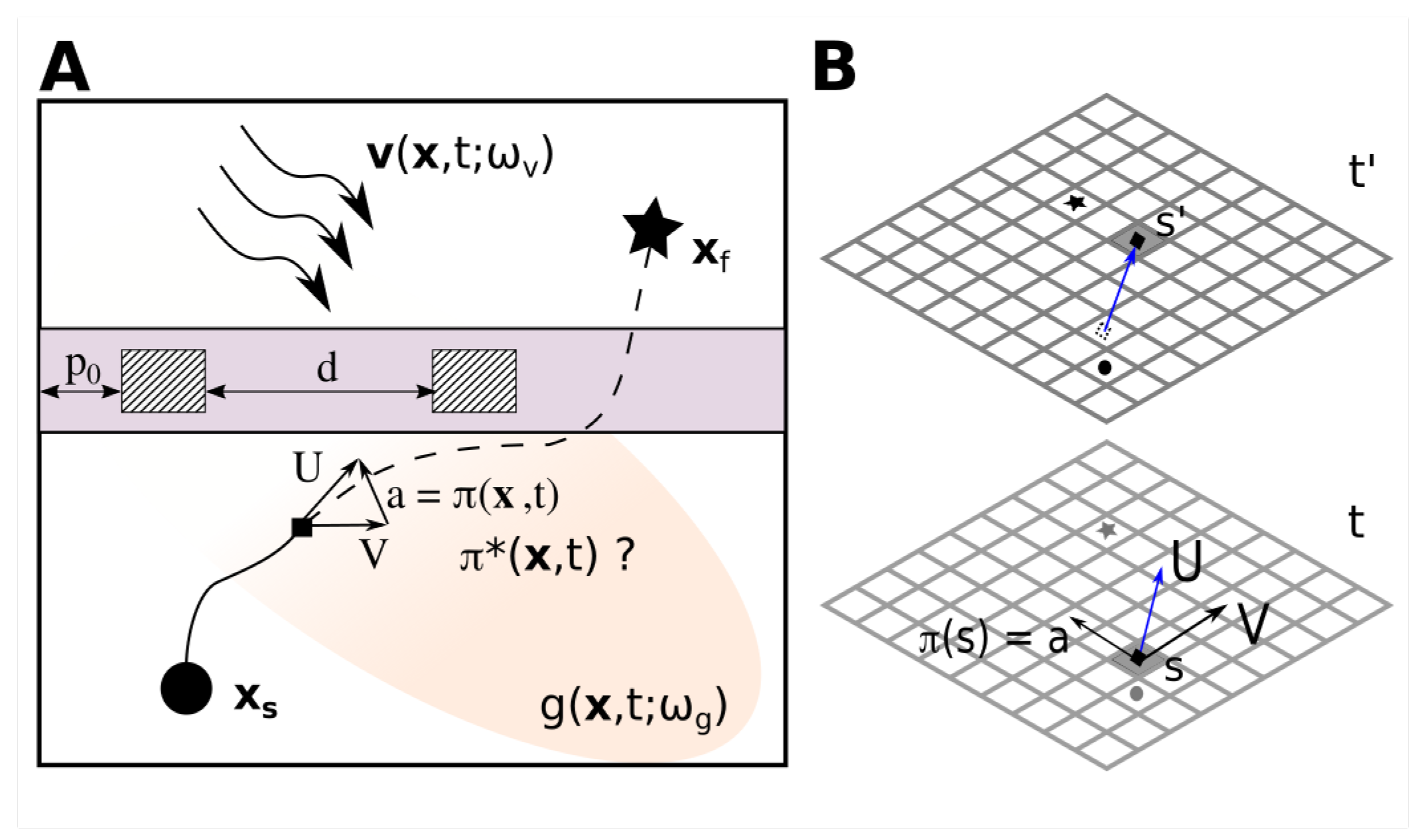
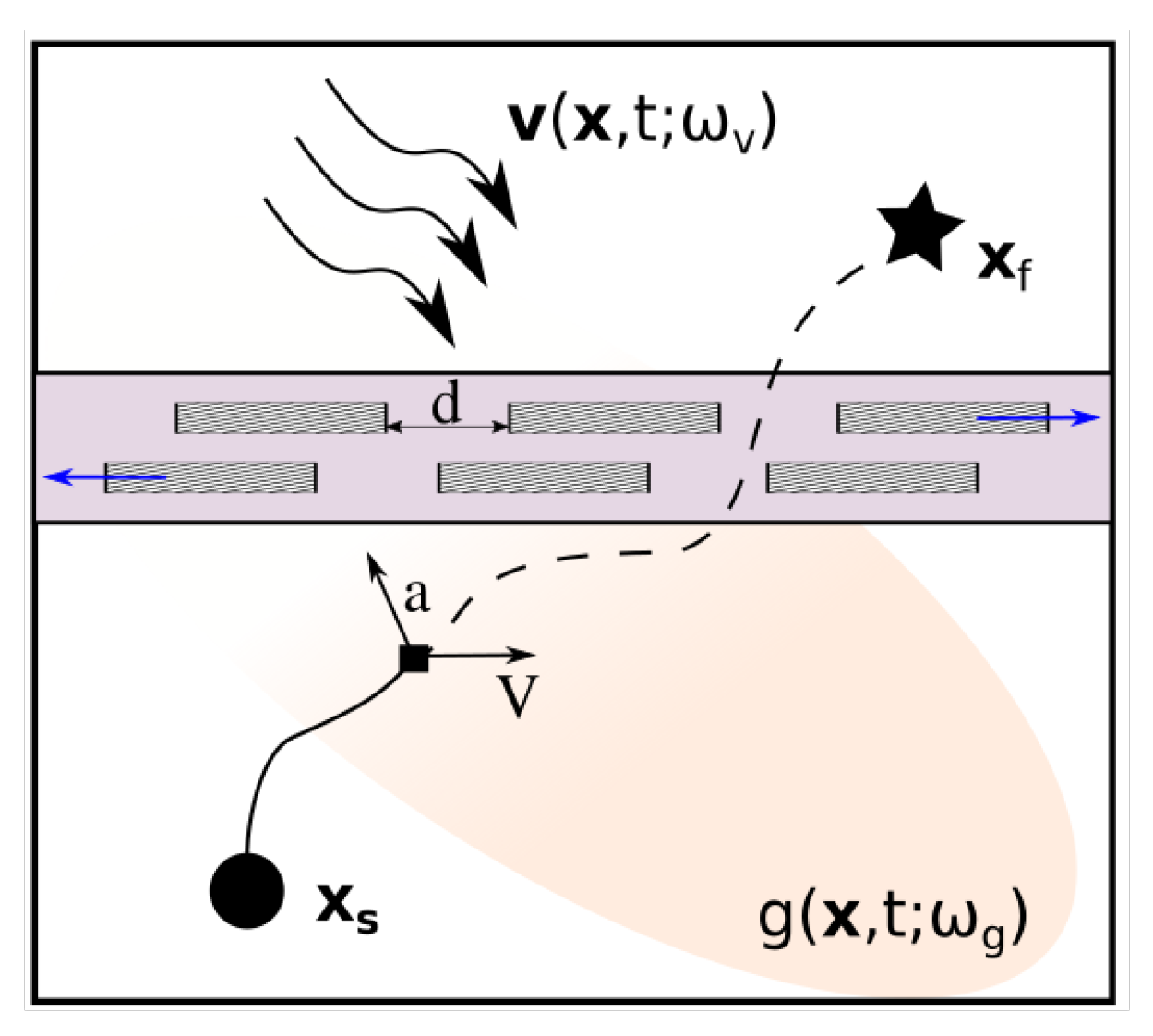
1.1. Problem Statement
1.2. Prior Work
2. Optimal Path Planning with MDPs
3. Multi-Objective Planning
3.1. Multi-Objective Reward Formulation
3.2. GPU Accelerated Algorithm
| Algorithm 1: GPU Accelerated Planning Algorithm. |
| Input: |
| Output: {},{} |
| 1: Copy data to GPU; |
| 2: Allocate GPU memory for intermediate data, and ; |
| 3: for () do |
| 4: for do |
| 5: Compute , and ; |
| 6: Count number of times is reached for given (); |
| 7: Allocate memory for ; |
| 8: Reduce the count data to a sparse STM ; |
| 9: Compute and through sample mean and store in , ; |
| 10: , ; |
| 11: end for |
| 12: end for |
| 13: ; |
| 14: for α in range () do |
| 15: Compute |
| 16: ; |
| 17: end for |
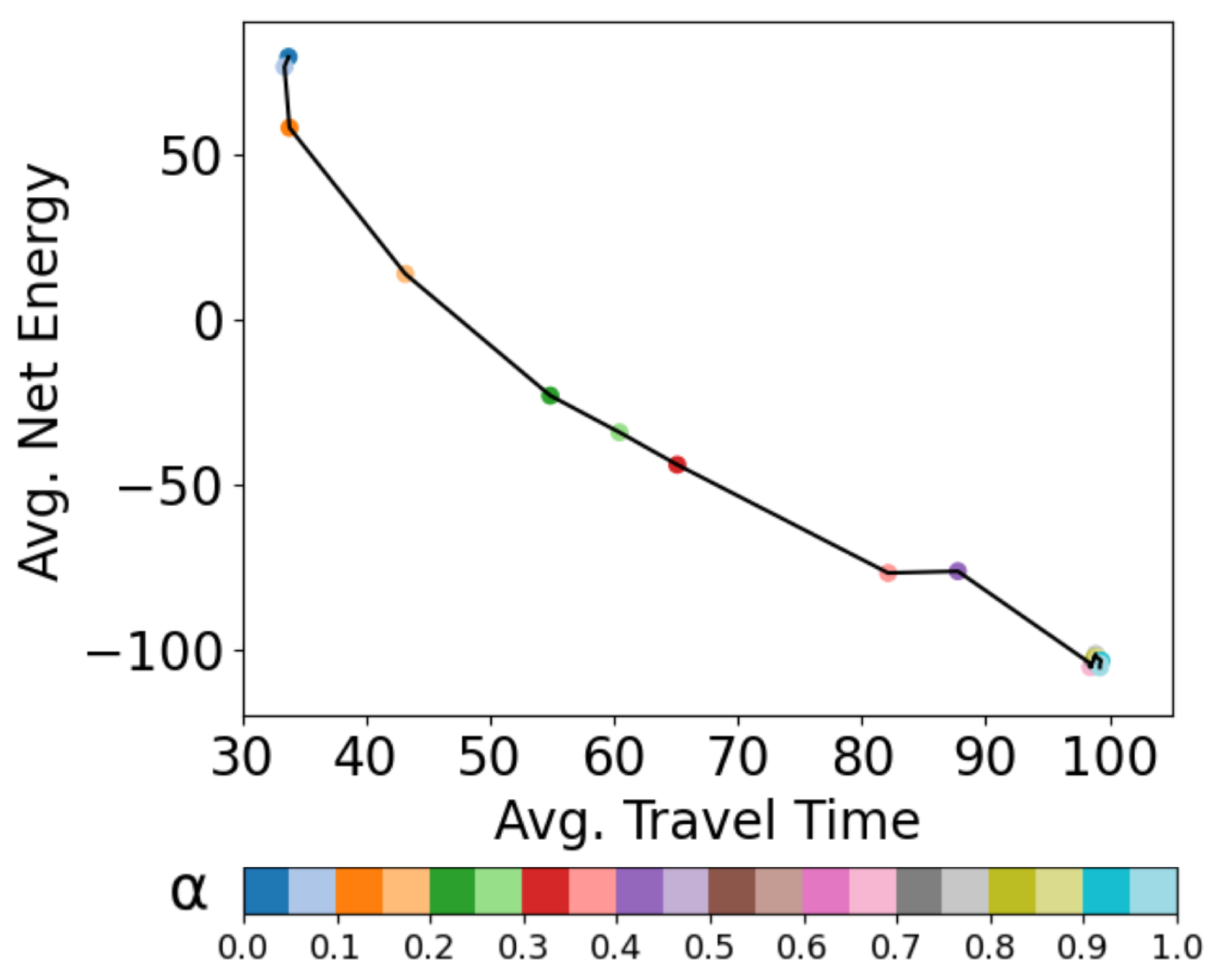
3.3. Operating Curves
4. Applications
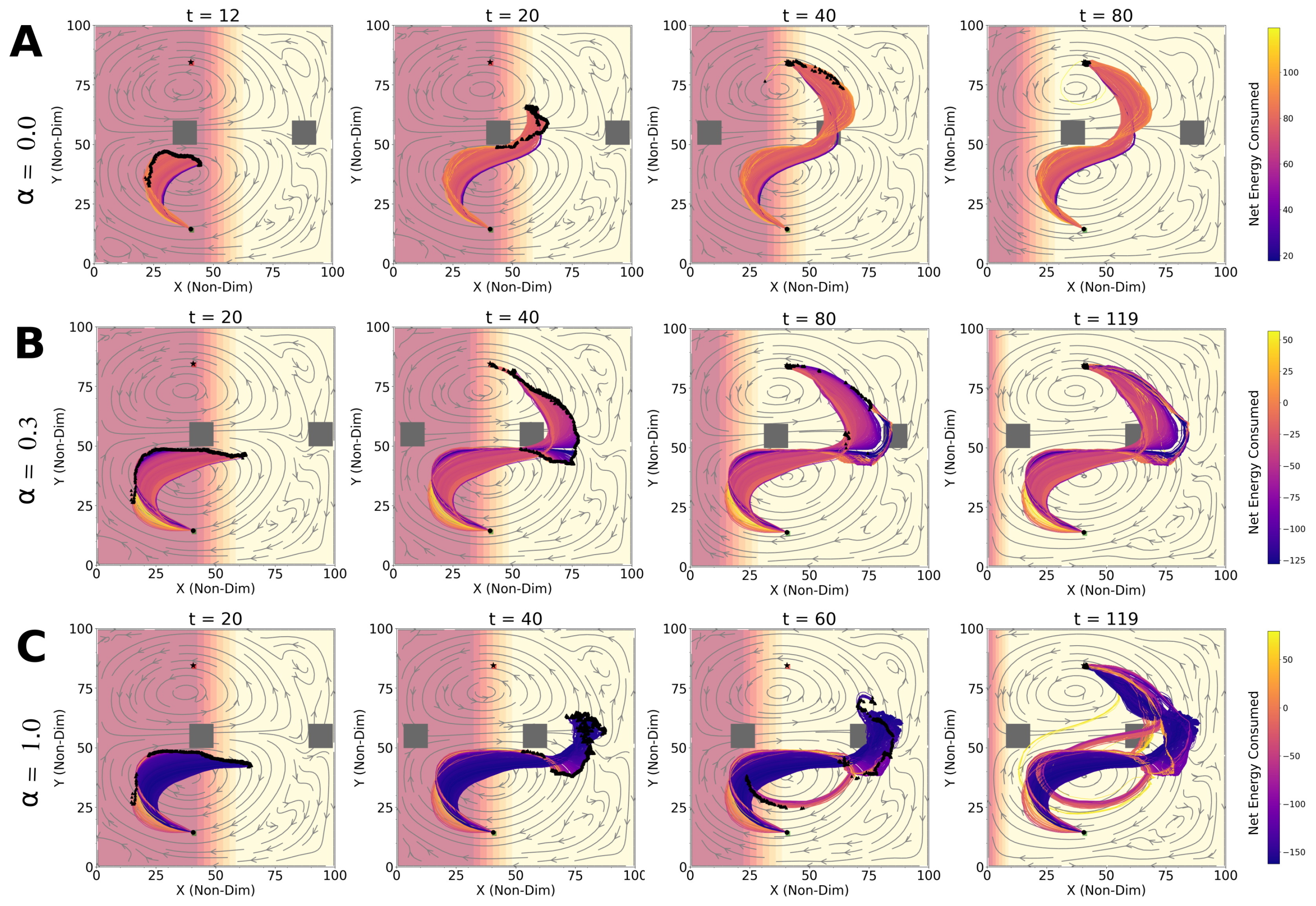
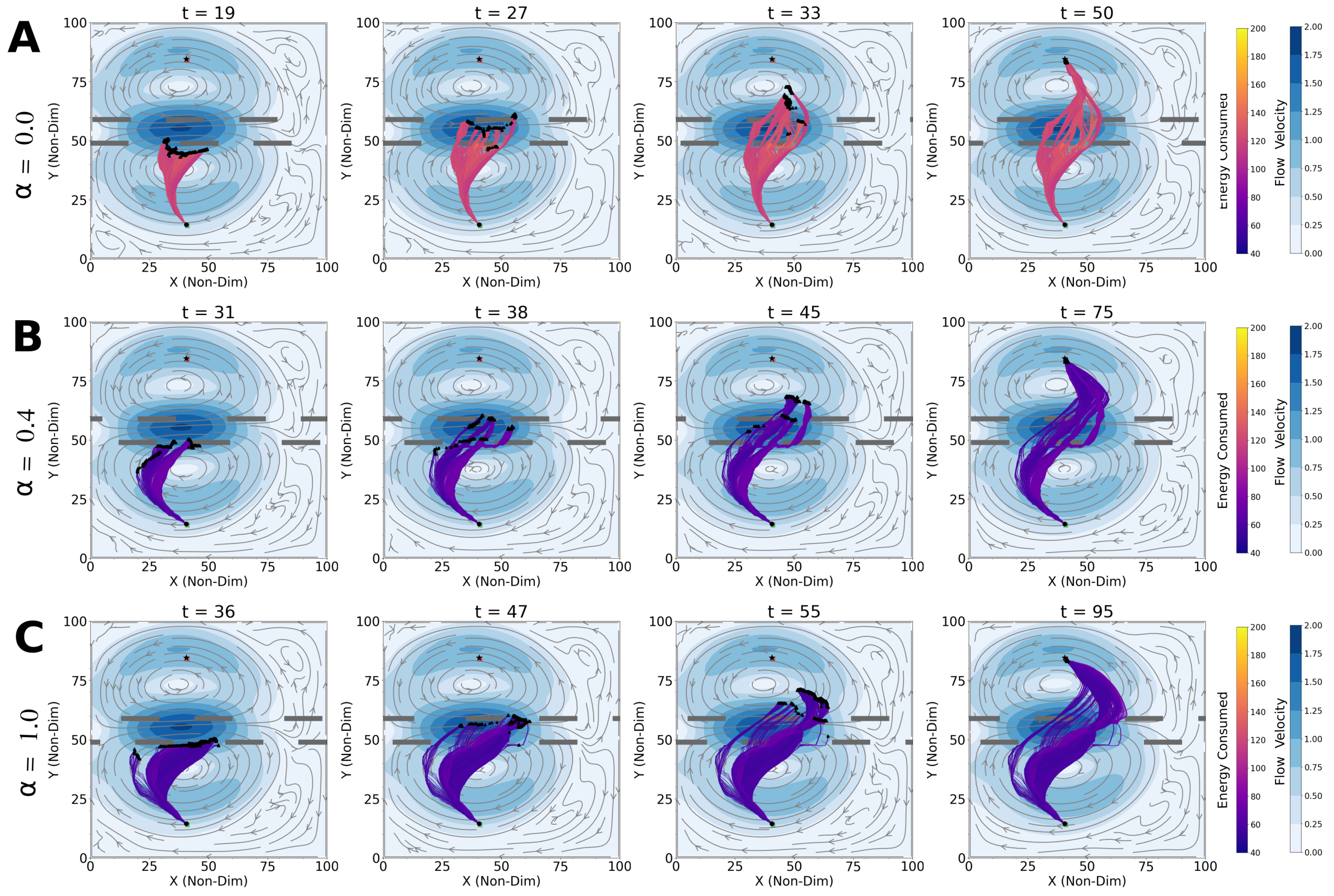
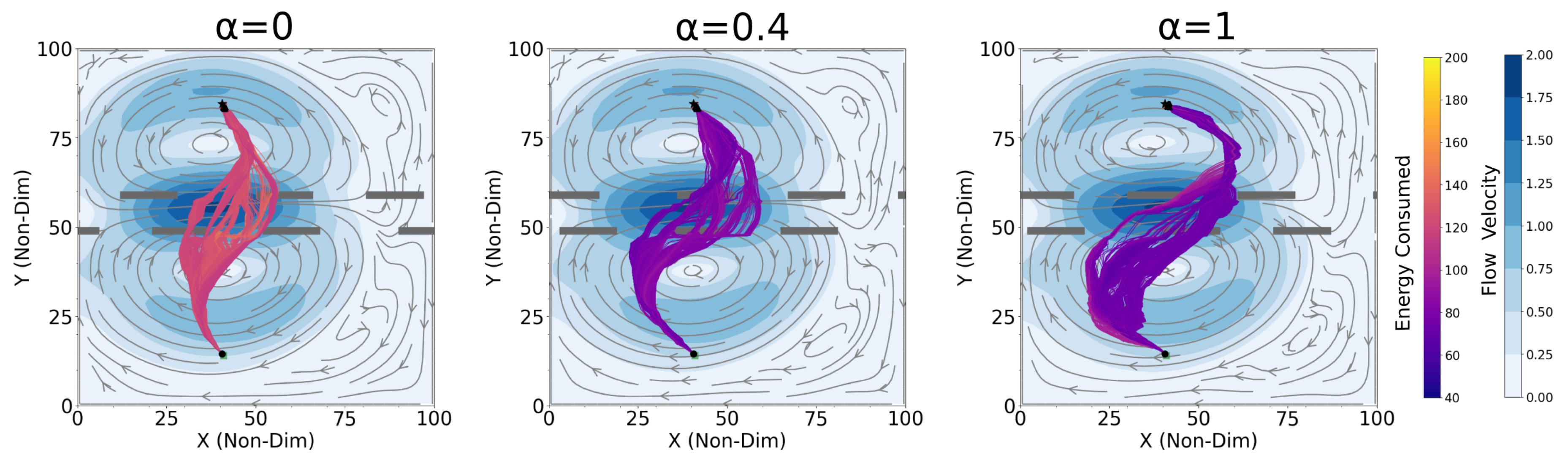
4.1. Optimal Time and Net Energy Missions
4.2. Optimal Time and Energy Missions with Unknown
4.3. Shipping Channel Crossing Problem
4.4. Computational Efficiency
4.5. Discussion and Future Extension
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| MDP | Markov Decision Process |
| POMDP | Partially Observable Markov Decision Process |
| CMDP | Constrained Markov Decision Process |
| MOMDP | Multi-Objective Markov Decision Process |
| RL | Reinforcement Learning |
| GPU | Graphical Processing Unit |
| CUDA | Compute Unified Device Architecture |
| DO | Dynamically Orthogonal |
| QG | Quasi-Geostrophic |
| STM | State Transition Matrix |
| ADCP | Acoustic Doppler Current Profiler |
Appendix A
| Figure Number | URL |
|---|---|
| Figure 3A | https://youtu.be/wn7VoLGuDl0, accessed on 4 April 2022 |
| Figure 3B | https://youtu.be/9QTuTSBzg3Y, accessed on 4 April 2022 |
| Figure 3C | https://youtu.be/Da4mIU691A8, accessed on 4 April 2022 |
| Figure 4B | https://youtu.be/3V_GnrsOVaA, accessed on 4 April 2022 |
| Figure 4C | https://youtu.be/hX6Qmm2WSJ4, accessed on 4 April 2022 |
| Figure 7A | https://youtu.be/9bmKnY0LE5c, accessed on 4 April 2022 |
| Figure 7B | https://youtu.be/MTUUQaHrxJc, accessed on 4 April 2022 |
| Figure 7C | https://youtu.be/ZMv-31RTyvY, accessed on 4 April 2022 |
Appendix B
References
- Sherman, J.; Davis, R.; Owens, W.; Valdes, J. The autonomous underwater glider “Spray”. IEEE J. Ocean. Eng. 2001, 26, 437–446. [Google Scholar] [CrossRef] [Green Version]
- Bellingham, J.G.; Rajan, K. Robotics in remote and hostile environments. Science 2007, 318, 1098–1102. [Google Scholar] [CrossRef] [Green Version]
- Subramani, D.N.; Haley, P.J., Jr.; Lermusiaux, P.F.J. Energy-optimal Path Planning in the Coastal Ocean. JGR Oceans 2017, 122, 3981–4003. [Google Scholar] [CrossRef]
- Kularatne, D.; Hajieghrary, H.; Hsieh, M.A. Optimal Path Planning in Time-Varying Flows with Forecasting Uncertainties. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1–8. [Google Scholar]
- Pereira, A.A.; Binney, J.; Hollinger, G.A.; Sukhatme, G.S. Risk-aware Path Planning for Autonomous Underwater Vehicles using Predictive Ocean Models. J. Field Robot. 2013, 30, 741–762. [Google Scholar] [CrossRef]
- Lermusiaux, P.F.J.; Haley, P.J., Jr.; Jana, S.; Gupta, A.; Kulkarni, C.S.; Mirabito, C.; Ali, W.H.; Subramani, D.N.; Dutt, A.; Lin, J.; et al. Optimal Planning and Sampling Predictions for Autonomous and Lagrangian Platforms and Sensors in the Northern Arabian Sea. Oceanography 2017, 30, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Rathbun, D.; Kragelund, S.; Pongpunwattana, A.; Capozzi, B. An evolution based path planning algorithm for autonomous motion of a UAV through uncertain environments. In Proceedings of the 21st Digital Avionics Systems Conference, Irvine, CA, USA, 27–31 October 2002; Volume 2, pp. 8D2-1–8D2-12. [Google Scholar] [CrossRef]
- Wang, T.; Le Maître, O.P.; Hoteit, I.; Knio, O.M. Path planning in uncertain flow fields using ensemble method. Ocean. Dyn. 2016, 66, 1231–1251. [Google Scholar] [CrossRef]
- Kewlani, G.; Ishigami, G.; Iagnemma, K. Stochastic mobility-based path planning in uncertain environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 1183–1189. [Google Scholar] [CrossRef]
- Chowdhury, R.; Subramani, D.N. Physics-Driven Machine Learning for Time-Optimal Path Planning in Stochastic Dynamic Flows. In Proceedings of the International Conference on Dynamic Data Driven Application Systems, Boston, MA, USA, 2–4 October 2020; Springer: Cham, Switzerland, 2020; pp. 293–301. [Google Scholar]
- Anderlini, E.; Parker, G.G.; Thomas, G. Docking Control of an Autonomous Underwater Vehicle Using Reinforcement Learning. Appl. Sci. 2019, 9, 3456. [Google Scholar] [CrossRef] [Green Version]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. Feasibility study of a constrained Dijkstra approach for optimal path planning of an unmanned surface vehicle in a dynamic maritime environment. In Proceedings of the 2018 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Torres Vedras, Portugal, 25–27 April 2018; pp. 117–122. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Xiang, X. Improved Astar Algorithm for Path Planning of Marine Robot. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 5410–5414. [Google Scholar] [CrossRef]
- Singh, Y.; Sharma, S.; Sutton, R.; Hatton, D.; Khan, A. A constrained A* approach towards optimal path planning for an unmanned surface vehicle in a maritime environment containing dynamic obstacles and ocean currents. Ocean Eng. 2018, 169, 187–201. [Google Scholar] [CrossRef] [Green Version]
- Ferguson, D.; Stentz, A. The Delayed D* Algorithm for Efficient Path Replanning. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 2045–2050. [Google Scholar] [CrossRef]
- Vagale, A.; Oucheikh, R.; Bye, R.T.; Osen, O.L.; Fossen, T.I. Path planning and collision avoidance for autonomous surface vehicles I: A review. J. Mar. Sci. Technol. 2021, 26, 1292–1306. [Google Scholar] [CrossRef]
- Subramani, D.N.; Wei, Q.J.; Lermusiaux, P.F.J. Stochastic Time-Optimal Path-Planning in Uncertain, Strong, and Dynamic Flows. Comp. Methods Appl. Mech. Eng. 2018, 333, 218–237. [Google Scholar] [CrossRef]
- Subramani, D.N.; Lermusiaux, P.F.J. Energy-optimal Path Planning by Stochastic Dynamically Orthogonal Level-Set Optimization. Ocean. Model. 2016, 100, 57–77. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, R.; Subramani, D. Optimal Path Planning of Autonomous Marine Vehicles in Stochastic Dynamic Ocean Flows using a GPU-Accelerated Algorithm. arXiv 2021, arXiv:2109.00857. [Google Scholar]
- Andersson, J. A Survey of Multiobjective Optimization in Engineering Design; Department of Mechanical Engineering, Linktjping University: Linköping, Sweden, 2000. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Stewart, R.H.; Palmer, T.S.; DuPont, B. A survey of multi-objective optimization methods and their applications for nuclear scientists and engineers. Prog. Nucl. Energy 2021, 138, 103830. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]
- Brownlee, J. Clever Algorithms: Nature-Inspired Programming Recipes; Lulu Press: Morrisville, NC, USA, 2011. [Google Scholar]
- Roijers, D.M.; Vamplew, P.; Whiteson, S.; Dazeley, R. A survey of multi-objective sequential decision-making. J. Artif. Intell. Res. 2013, 48, 67–113. [Google Scholar] [CrossRef] [Green Version]
- Perny, P.; Weng, P. On finding compromise solutions in multiobjective Markov decision processes. In ECAI 2010; IOS Press: Amsterdam, The Netherlands, 2010; pp. 969–970. [Google Scholar]
- Wray, K.H.; Zilberstein, S.; Mouaddib, A.I. Multi-objective MDPs with conditional lexicographic reward preferences. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Geibel, P. Reinforcement learning for MDPs with constraints. In Proceedings of the European Conference on Machine Learning, Berlin, Germany, 18–22 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 646–653. [Google Scholar]
- Zaccone, R.; Ottaviani, E.; Figari, M.; Altosole, M. Ship voyage optimization for safe and energy-efficient navigation: A dynamic programming approach. Ocean. Eng. 2018, 153, 215–224. [Google Scholar] [CrossRef]
- White, C.C.; Kim, K.W. Solution procedures for vector criterion Markov Decision Processes. Large Scale Syst. 1980, 1, 129–140. [Google Scholar]
- Lee, T.; Kim, Y.J. GPU-based motion planning under uncertainties using POMDP. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 4576–4581. [Google Scholar]
- Lee, T.; Kim, Y.J. Massively parallel motion planning algorithms under uncertainty using POMDP. Int. J. Robot. Res. 2016, 35, 928–942. [Google Scholar] [CrossRef]
- Spaan, M.T.; Vlassis, N. Perseus: Randomized point-based value iteration for POMDPs. J. Artif. Intell. Res. 2005, 24, 195–220. [Google Scholar] [CrossRef]
- Pineau, J.; Gordon, G.; Thrun, S. Anytime point-based approximations for large POMDPs. J. Artif. Intell. Res. 2006, 27, 335–380. [Google Scholar] [CrossRef]
- Shani, G.; Pineau, J.; Kaplow, R. A survey of point-based POMDP solvers. Auton. Agents Multi-Agent Syst. 2013, 27, 1–51. [Google Scholar] [CrossRef]
- Wray, K.H.; Zilberstein, S. A parallel point-based POMDP algorithm leveraging GPUs. In Proceedings of the 2015 AAAI Fall Symposium Series, Arlington, VA, USA, 12–14 November 2015. [Google Scholar]
- Barrett, L.; Narayanan, S. Learning all optimal policies with multiple criteria. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; pp. 41–47. [Google Scholar]
- Rao, D.; Williams, S.B. Large-scale path planning for underwater gliders in ocean currents. In Proceedings of the Australasian Conference on Robotics and Automation (ACRA), Sydney, Australia, 2–4 December 2009; pp. 2–4. [Google Scholar]
- Fernández-Perdomo, E.; Cabrera-Gámez, J.; Hernández-Sosa, D.; Isern-González, J.; Domínguez-Brito, A.C.; Redondo, A.; Coca, J.; Ramos, A.G.; Fanjul, E.Á.; García, M. Path planning for gliders using Regional Ocean Models: Application of Pinzón path planner with the ESEOAT model and the RU27 trans-Atlantic flight data. In Proceedings of the OCEANS’10 IEEE SYDNEY, Sydney, Australia, 24–27 May 2010; pp. 1–10. [Google Scholar]
- Smith, R.N.; Chao, Y.; Li, P.P.; Caron, D.A.; Jones, B.H.; Sukhatme, G.S. Planning and implementing trajectories for autonomous underwater vehicles to track evolving ocean processes based on predictions from a regional ocean model. Int. J. Robot. Res. 2010, 29, 1475–1497. [Google Scholar] [CrossRef] [Green Version]
- Al-Sabban, W.H.; Gonzalez, L.F.; Smith, R.N. Wind-energy based path planning for unmanned aerial vehicles using markov decision processes. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 784–789. [Google Scholar]
- Subramani, D.N.; Lermusiaux, P.F.J.; Haley, P.J., Jr.; Mirabito, C.; Jana, S.; Kulkarni, C.S.; Girard, A.; Wickman, D.; Edwards, J.; Smith, J. Time-Optimal Path Planning: Real-Time Sea Exercises. In Proceedings of the Oceans ’17 MTS/IEEE Conference, Aberdeen, UK, 19–22 June 2017. [Google Scholar] [CrossRef]
- Lolla, T.; Lermusiaux, P.F.J.; Ueckermann, M.P.; Haley, P.J., Jr. Time-Optimal Path Planning in Dynamic Flows using Level Set Equations: Theory and Schemes. Ocean. Dyn. 2014, 64, 1373–1397. [Google Scholar] [CrossRef] [Green Version]
- Sapsis, T.P.; Lermusiaux, P.F.J. Dynamically orthogonal field equations for continuous stochastic dynamical systems. Phys. D Nonlinear Phenom. 2009, 238, 2347–2360. [Google Scholar] [CrossRef]
- Ueckermann, M.P.; Lermusiaux, P.F.J.; Sapsis, T.P. Numerical schemes for dynamically orthogonal equations of stochastic fluid and ocean flows. J. Comput. Phys. 2013, 233, 272–294. [Google Scholar] [CrossRef] [Green Version]
- Subramani, D.N.; Lermusiaux, P.F.J. Risk-Optimal Path Planning in Stochastic Dynamic Environments. Comp. Methods Appl. Mech. Eng. 2019, 353, 391–415. [Google Scholar] [CrossRef]
- Lermusiaux, P.F.J.; Subramani, D.N.; Lin, J.; Kulkarni, C.S.; Gupta, A.; Dutt, A.; Lolla, T.; Haley, P.J., Jr.; Ali, W.H.; Mirabito, C.; et al. A Future for Intelligent Autonomous Ocean Observing Systems. J. Mar. Res. 2017, 75, 765–813. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.; Duda, M.; Barker, D.; et al. A Description of the Advanced Research WRF Model Version 4; Technical Report; National Center for Atmospheric Research: Boulder, CO, USA, 2019. [Google Scholar]
- Tolman, H. User Manual and System Documentation of WAVEWATCH III TM Version 3.14; Technical Report; MMAB: College Park, MD, USA, 2009. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- NVIDIA; Vingelmann, P.; Fitzek, F.H. CUDA, Release: 10.2.89, 2020. Available online: https://developer.nvidia.com/cuda-toolkit (accessed on 1 February 2022).
- Sapio, A.; Bhattacharyya, S.S.; Wolf, M. Efficient solving of Markov decision processes on GPUs using parallelized sparse matrices. In Proceedings of the 2018 Conference on Design and Architectures for Signal and Image Processing (DASIP), Porto, Portugal, 10–12 October 2018; pp. 13–18. [Google Scholar]
- Gangopadhyay, A. Introduction to Ocean Circulation and Modeling; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Cushman-Roisin, B.; Beckers, J.M. Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Podder, T.K.; Sibenac, M.; Bellingham, J.G. Applications and Challenges of AUV Docking Systems Deployed for Long-Term Science Missions; Monterey Bay Aquarium Research Institute: Moss Landing, CA, USA, 2019. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdhury, R.; Navsalkar, A.; Subramani, D. GPU-Accelerated Multi-Objective Optimal Planning in Stochastic Dynamic Environments. J. Mar. Sci. Eng. 2022, 10, 533. https://doi.org/10.3390/jmse10040533
Chowdhury R, Navsalkar A, Subramani D. GPU-Accelerated Multi-Objective Optimal Planning in Stochastic Dynamic Environments. Journal of Marine Science and Engineering. 2022; 10(4):533. https://doi.org/10.3390/jmse10040533
Chicago/Turabian StyleChowdhury, Rohit, Atharva Navsalkar, and Deepak Subramani. 2022. "GPU-Accelerated Multi-Objective Optimal Planning in Stochastic Dynamic Environments" Journal of Marine Science and Engineering 10, no. 4: 533. https://doi.org/10.3390/jmse10040533
APA StyleChowdhury, R., Navsalkar, A., & Subramani, D. (2022). GPU-Accelerated Multi-Objective Optimal Planning in Stochastic Dynamic Environments. Journal of Marine Science and Engineering, 10(4), 533. https://doi.org/10.3390/jmse10040533







