2.1. Experimental Protocol
Eleven (11) healthy male volunteers (age: 30.97 ± 7.15 years; height: 1.81 ± 0.06 m; weight: 77.34 ± 9.22 kg; body mass index (BMI): 23.60 ± 2.41 kg/m) participated in the measurements performed at the Human Performance Laboratory, at the Department of Health Science and Technology, Aalborg University, Aalborg, Denmark. The experiment was performed in accordance with the ethical guidelines of The North Denmark Region Committee on Health Research Ethics, and participants provided full written informed consent, prior to the experiment.
The core system used in this study is an IMC system (Xsens MVN Link, Xsens Technologies BV, Enschede, The Netherlands [
26]) powered by the matching software (Xsens MVN Studio version 4.2.4), delivering data at 240 Hz. The 17 IMU modules were mounted on a tight-fitting Lycra suit on the following segments: head, sternum, pelvis, upper legs, lower legs, feet, shoulders, upper arms, forearms and hands [
22,
27] (
Figure 1). In addition, an OMC system, including eight infrared high-speed cameras (Oqus 300 series, Qualisys AB, Gothenburg, Sweden [
28]), was used to capture 53 retro-reflective markers mounted on the body. The placement of the markers on the body is shown in
Figure A1 and described in
Table A1 in the
Appendix section. Furthermore, three FPs (AMTI, Advanced Mechanical Technology, Inc., Watertown, MA, USA), embedded in the floor of the laboratory, recorded GRF&Ms (
Figure 2). A combination of the OMC and FP systems (lab-based system) was used as a reference for comparison to the IMC-derived GRF&M predictions. To synchronize the IMC-based and lab-based systems, the Xsens sync station was used. The sampling frequency of the camera-based system was set to 240 Hz and that of FPs to 2400 Hz.
Before starting the recordings, the body dimensions of each subject were assessed and applied in the Xsens MVN software. Particularly, the heights of the ankle, knee, hip and top of head from the ground, the widths of the shoulder and pelvis, as well as the length of the foot were measured using a conventional tape with the subject in an upright posture [
30]. These measurements were used to calibrate the IMC system using a steady upright posture, known as the neutral pose or n-pose [
22]. The software classifies the quality of the calibration as “poor”, “fair”, “acceptable” or “good” based on the steadiness of the subject and the homogeneity of magnetic field around the IMUs at the time of the calibration. The calibration process was repeated before each set of walking speed trials and until the indication “good” was achieved in all cases, to maximize the quality of IMC.
Between the completion of the instrumentation setup and the start of the measurements, the subjects were given a five-minute acclimatisation period, to feel comfortable in the wearable equipment. Throughout the whole experiment, subjects remained barefoot, without wearing any type of footwear, apart from a thin strap wrapped around each foot to firmly mount the inertial measurement unit on these segments.
Gait at a self-selected normal (NW), fast (FW) and slow (SW) speed were measured. FW and SW speeds were instructed to the subjects as at least 20% higher or lower than their mean baseline NW speed, respectively. Particularly, the actual mean walking speeds performed were m/s for NW, m/s for FW (NW + 23%) and m/s for SW (NW − 33%). To prevent the generation of additional external forces, the use of handrails or contact with any other external objects was not allowed. Before each task was recorded, subjects were given oral instructions and practiced the respective movement patterns. At least five successful trials per walking speed were obtained. A trial was considered successful when the right (left) foot hit one of the FPs completely, followed by a complete hit of the left (right) foot on the next FP. This definition ensures that FPs capture both right and left feet successfully within a stride.
2.2. Data Processing: IMC System
Xsens MVN estimates the orientation of segments by combining the orientations of individual IMUs with a biomechanical model of the human body. The orientation of each IMU is obtained by fusing accelerometer, gyroscope and magnetometer signals using an extended Kalman filter [
31]. To relate the sensor orientations to segment orientations, a sensor-to-segment calibration procedure is performed. In this procedure, called n-pose, the subject is asked to stand in a known n-pose for a few seconds. The estimated transformation is applied and considered constant during a recording session.
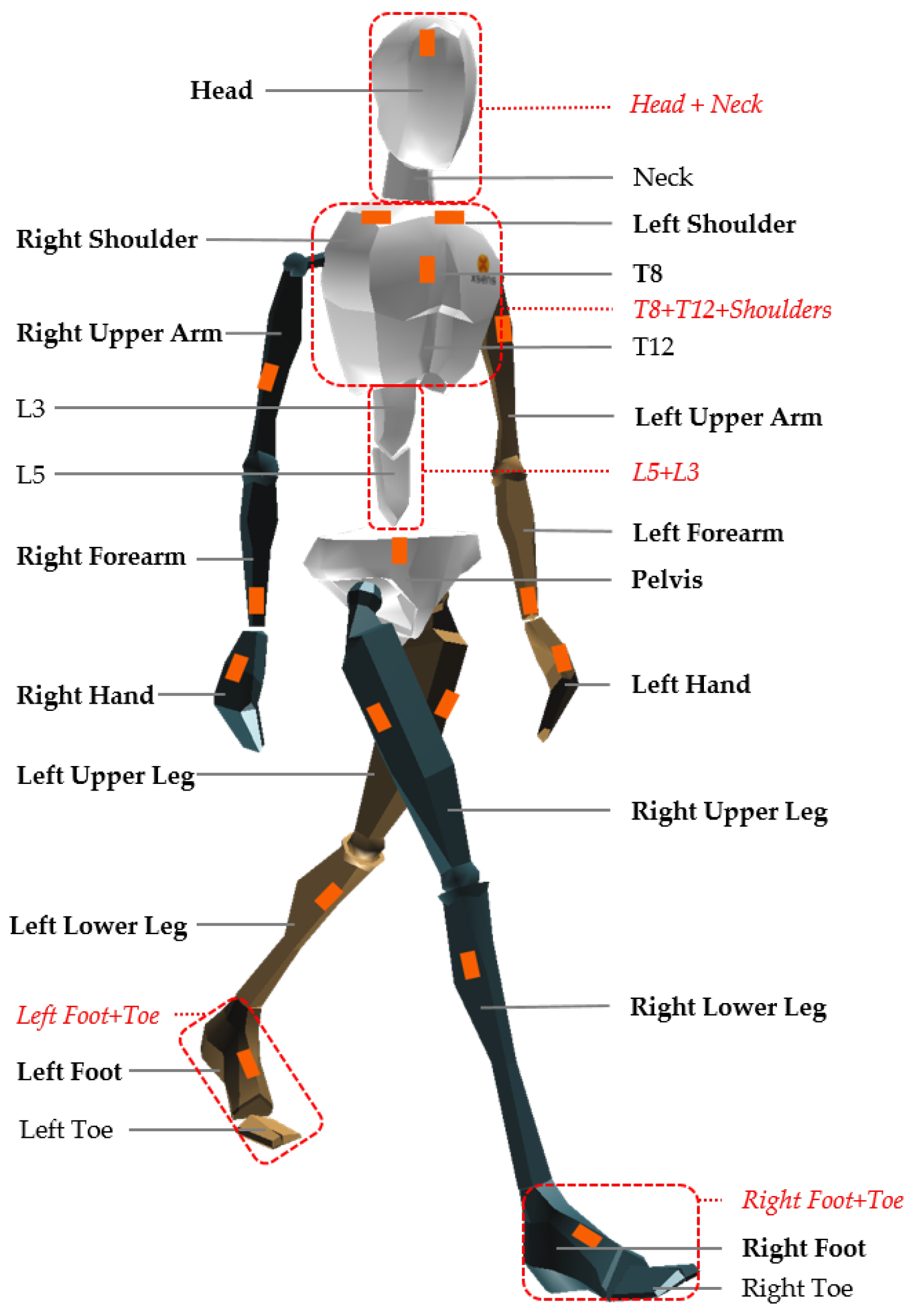
We developed a program in MATLAB to assess the kinetic values from IMC-derived kinematics. By default, Xsens MVN Studio uses 17 IMU sensors to derive the kinematics of 23 segments as shown in
Figure 1. Due to lack of literature reporting inertial parameters and relative center of mass positions for these exact segments, the original kinematic model has been adjusted to match the definitions of the 16-segment model reported by De Leva, 1996. To achieve this adaptation, 5 new rigid body segments were defined by merging specific given segments:
Head-neck segment, formed by constraining the relative movement between head and neck segments. Kinematics were derived from the orientation of the IMU mounted on the head.
Upper trunk segment, formed by constraining the relative movement between T8 and T12, T8 and right shoulder and T8 and left shoulder segments. Kinematics were derived from the orientation of the IMU mounted on the sternum.
Middle trunk segment, formed by constraining the relative movement between L3 and L5 segments. Kinematics were derived from interpolation between the upper trunk and pelvis segment.
Foot-toe, formed by constraining the relative movement between foot and toe segments. Kinematics were derived from the orientation of the IMU mounted on the foot.
The segment definitions of the pelvis, upper legs, lower legs, hands, forearms and upper arms remained unchanged (
Figure 1;
Table 1).
For the analysis, two coordinate systems were defined:
the global coordinate system of the IMC system (), in which the anterior axis points to the magnetic north, the vertical axis matches the direction of the gravitational acceleration and the lateral axis perpendicular to these axes, such that a right-handed coordinate frame is formed
the walking coordinate system (), which is defined by the same vertical, but has the anterior axes pointing in the walking direction, which means the difference between the two systems is only a rotation around the vertical; the walking direction was derived from known initial and final positions of the pelvis segment and assuming that the subjects walked approximately in a straight line throughout the trial
Knowing the kinematics and inertial properties of the segments of the biomechanical model, we estimated the total external force based on the Newton equations of motion:
where
denotes the total three-dimensional external force,
N the total number of segments,
the mass of each segment,
the linear acceleration in the center of mass of each segment and
.
In a similar way, we calculated the total external moment from Euler’s equation:
where
denotes the total three-dimensional external moment,
the number of end points in each segment (joints and external contact points),
and
the angular velocities and angular accelerations of each segment, respectively. The inertia tensor around the center of mass of each segment is denoted by
, the position vectors between the center of mass and the end points denoted by
and the resultant force in the end points of each segment described by
. All variables are expressed in the global coordinate system of the IMC system (
).
Segment linear accelerations exported from the Xsens MVN Studio software were expressed in the origin of each segment as described in detail in the manual of the IMC system [
22]. To apply these variables in Equation (
1), a translation to the segment’s center of mass was required, defined as:
The position vectors between the center of mass and the origin of each segment
and the inertial parameters of the body segments
and
were calculated through scaled anthropometric data, based on adjustments to Zatsiorsky–Seluyanov’s inertial parameters reported by De Leva [
29]. The total body mass of the subjects includes their actual body mass plus the mass of the wearable instrumentation. The added mass of the inertial motion capture system was in total 390 g (seventeen IMUs of 10 g each, one wireless communication pack of 150 g and one battery of 70 g). These additional masses were initially subtracted from the total measured mass before calculating the net mass of each segment and then added individually to each of the corresponding body segments. The resulting mass was input to the calculation of the moment of inertia from the radii of gyration. The effect of the wearable equipment in the radii of gyration was assumed to be negligible.
Segment angular velocities , angular accelerations and linear accelerations of the origins , provided by Xsens MVN software, were filtered using a second-order Butterworth zero-phase low-pass filter with a cut-off frequency of 6 Hz.
Our major assumption was that the GRF&Ms are the only significant external loads present. Thus, the total external force (moment) derived from Newton (Euler) equations of motion (Equations (
1) and (
2)) balances the sum of forces (moments) applied on both left and right lower limbs:
and
where
(
) and
(
) are the ground reaction forces (moments) applied on the left and right foot, respectively.
During the single support phase, the result of the computation is the GRF&M applied on the foot, which is in contact with the ground. The resulting GRM is expressed about the external contact point on that foot, which is chosen as the projection of the ankle joint on the ground. However, during the phase of double support, the system of equations is indeterminate. To overcome this, we applied a distribution algorithm based on a smooth transition assumption function (
), which was constructed from empirical data similarly to previous studies [
19,
20]. The curves of the measured GRF&M during the second double support phase were averaged for all steps. Subsequently, a cubic spline interpolation function was used to generate the
. The generated function curves were compared to the ones proposed by Ren et al. [
19] and shown in
Figure 3. A direct comparison to the function of Villeger et al. [
20] was not possible, because that study calculated the GRM about a fixed point on the plate and not with respect to the body.
The distribution function
was expressed in the coordinate system
. Since the input variables of the Newton–Euler equations were expressed in
, the same applied to the calculated vectors
and
. Therefore, before applying the distribution function, we rotated the force and moment vectors from the coordinate system
to
, resulting in two new vectors
and
. The GRF&Ms applied on the left and right lower limbs are shown in
Table 2, where
and
are the components of
for the GRF and GRM, respectively. Both functions depend on time
relative to the timing of gait events denoted by
,
for heel-strike and
,
for toe-off events for the right or left lower limb, respectively. The behavior of the components of
and
that was used in this implementation is illustrated in
Figure 3.
To distinguish between the phases of single and double stance, we used a gait event detection algorithm based on a threshold in the norm of the velocities of the heel (
) and the toe (
). The positions of the heel and toe points were provided by Xsens MVN Studio, and the velocity threshold (
) was set equal to the norm of the average velocity of the pelvis segment for each trial. The state of the gait cycle at time
t is shown in
Figure 4.
An overview of the algorithmic steps used in our study is shown in
Figure 5.
2.3. Data Analysis: Reference Lab System
The Qualisys Track Manager 2.2 software package was used to process the three-dimensional positions of the markers and the GRF&Ms recorded using the FPs [
28]. For each subject, a model for the automatic identification of markers was created, to assist the marker labeling across trials, and gaps were filled in the missing marker trajectories using a visual preview option. The marker trajectories were filtered using a second-order, zero-phase Butterworth low-pass filter with a cut-off frequency of 6 Hz, following the recommendations of the literature [
1]. A biomechanical model composed of 16 segments, as described in
Table 1, was constructed from the marker trajectories, with segment coordinate frames based on recommendations of the International Society of Biomechanics [
32,
33]. A custom script was developed in MATLAB R2015a (The MathWorks Inc.; Natick, MA, USA) to downsample the measured GRF&Ms by a factor of 10 to match the sampling rate of the OMC system. Similarly to Ren et al. [
19], no filtering was applied to the processed GRF&Ms.
To compare the OMC data with the IMC data, all quantities expressed in the OMC lab coordinate frame () were rotated to the coordinate frame based on the walking direction (). Similar to the transformation applied to the IMC, is defined by a rotation around the vertical of , and the walking direction was derived from known initial and final positions of the pelvis segment.
In addition, the timing of the reference gait events (heel strike and toe-off) was identified and logged automatically, using a 5 N threshold on the vertical force measured by each FP. The steps that were only partially captured by the FPs were recognized and excluded based on the horizontal positions of the heel and toe markers during gait events. Due to the limited number of FPs, heel strike events used to denote the end of the gait cycle were not always available directly from the force data. In such cases, a velocity-based gait event detection, driven by the marker data, was used, similarly to
Figure 4. The method performed with an error of 12 ± 10 ms in heel strike detection across all walking speeds.
The ground reaction force (GRF) was normalized to body weight and the ground reaction moment (GRM) to body weight times body height. In addition, for each step, the time was normalized to 100% of the gait cycle, defined by two consecutive heel contacts of the same foot. Finally, the six components of the measured and predicted GRF&Ms were compared, per walking speed and in total. The GRM was calculated about the projection of the ankle joint on the ground.
To evaluate the accuracy of our method, we used absolute (RMSE) and relative (rRMSE) root mean square errors, as defined by Ren et al. [
19]. The agreement between the measured and predicted data normalized to the gait cycle was derived from Pearson’s correlation coefficients, which were categorized as weak
, moderate
, strong
and excellent
, according to previous studies [
16,
34].
Furthermore, we calculated the curve magnitude (M) and phase (P) percentage differences, based on the technique proposed by Sprague and Geers [
35]. Out of 525 measured steps in total, 432 valid steps were included, and 93 steps were excluded due to incomplete stepping on the FPs.
In addition to the analysis over a whole gait cycle, we calculated the
ρ, RMSE and rRMSE of the GRF&M throughout three sub-phases:
DS1: first double stance phase of the ipsilateral foot, between a heel strike of the ipsilateral foot and a toe-off of the contralateral foot.
DS2: second double stance phase of the ipsilateral foot, between a heel strike of the contralateral foot and a toe-off of the ipsilateral foot.
SS: single stance phase of the ipsilateral foot, between a toe-off of the contralateral foot and heel strike of the contralateral foot.
Moreover, we analyzed the absolute and relative peak differences between the predicted and measured curves. The stance phase has been divided into three phases: early stance
, middle stance
and late stance
, where
is the duration of the stance phase and
t is the time initialized at the beginning of each stance phase. Within these phases, the following peaks have been sought for both predicted and measured values:
In the early stance (ES) phase: the maximum values of lateral and vertical GRF and minimum value of anterior GRF.
In the middle stance (MS) phase: the minimum value of the vertical GRF.
In the late stance (LS) phase: the maximum values of the GRF components and transverse GRM and the minimum values of frontal and sagittal GRM components.
Finally, we compared the center of pressure (COP) and frictional torque estimates to the FP measurements. To derive these values for the right foot, we used the following equations:
where
and
are the anterior and lateral positions of the center of pressure on the ground with respect to the projection of the right ankle joint on the ground.
is the frictional torque,
,
and
the anterior, lateral and vertical GRF, respectively, and
,
and
the frontal, sagittal and transverse GRM, respectively, calculated about the projection of the right ankle joint on the ground. The COP was calculated and analyzed per foot during stance phase, when
was greater than 5 N. In the same way, the calculations for the left foot were performed. All variables are used in the equations individually for both right and left foot and are expressed in the coordinate system
.
In our implementation, the estimates of GRF&M depend highly on the performance of the gait event detection. Particularly, during the double support phase, the GRF&Ms applied on the ipsilateral foot are driven by the smooth transition assumption function. This is represented by a curve, which is based on the magnitude of each GRF&M component during the last single support frame and assumes zero magnitude on the last frame of double support. Thus, we evaluated the sensitivity of the heel strike and toe-off detection while using the original thresholds, compared to 10% higher and 10% lower than that.
We additionally performed a sensitivity analysis to investigate the effect of the selection of the cut-off frequency used in the second-order Butterworth low-pass filter. The change in the root mean square errors of each component of the GRF&M was used to indicate the impact of the selection in the final estimates.