Life Cycle Assessment under Uncertainty: A Scoping Review

Abstract

Today, life cycle assessment (LCA) is the most widely used approach to model and calculate the environmental impacts of products and processes. The results of LCAs are often said to be deterministic, even though the real-life applications are uncertain and vague. The uncertainty, which may be simply ignored, is one of the key factors influencing the reliability of LCA outcomes. Numerous sources of uncertainty in LCA are classified in various ways, such as parameter and model uncertainty, choices, spatial variability, temporal variability, variability between sources and objects, etc. Through a scoping review, the present study aims to identify and assess the frequency with which LCA studies reflect the uncertainty and what are the tools to cope with the uncertainty to map the knowledge gaps in the field to reveal the challenges and opportunities to have a robust LCA model. It is also investigated which database, methodology, software, etc., have been used in the life cycle assessment process. The results indicate that the most significant sources of uncertainty were in the model and process parameters, data variability, and the use of different methodologies and databases. The probabilistic approach or stochastic modeling, using numerical methods such as Monte Carlo simulation, was the dominating tool to cope with the uncertainty. There were four dominant LCA methodologies: CML, ReCiPe, IMPACT 2002+, and TRACI. The most commonly used LCA software and databases were SimaPro^® and Ecoinvent^®, respectively.

1. Introduction

In the new economic context that has emerged in recent years, the environmental impact of products and services has become a vital concern. To measure and assess these impacts, several tools and frameworks can be utilized, such as life cycle assessment (LCA), environmental impact assessment (EIA), environmental risk assessment (ERA), material flow analysis (MFA), strategic environmental assessment (SEA), cost–benefit analysis (CBA), and the ecological footprint (EF) method [1]. LCA is one of the most well-known approaches [2]. The LCA methodology [3,4] is widely used to assess the environmental impact of products and services [5]. Ultimately, LCA as a deterministic model [6] aims to provide appropriate information for decisions leading to economies’ environmental improvement [7], and it has been shown to be a viable technique for documenting the environmental considerations that must be considered in decision making towards sustainability [8]. Because of the limitations inherent in data collection and modeling of the impacts, the LCA technique identifies potential environmental impacts but does not predict absolute or precise impacts in this context [9]. On the other hand, particular issues in the methodology necessitate the LCA practitioner to decide and choose among different possibilities in the study. This freedom of choice can occasionally result in significantly disparate outcomes, leading to uncertainty [5]. Due to the analysis’s nature, the uncertainty arises from the scarce and imprecise nature of available data and simplified model assumptions [6]. In a fundamental sense, uncertainty exists in many forms throughout the LCA process [10].

As a result, in a scenario comparison, the uncertainty in LCA outcomes might mislead decision makers [11]. One of the first things which might be defined while discussing uncertainties, is the concept of uncertainty itself. There are many ways to define uncertainty, and finding a fully satisfying definition that may be difficult to agree upon seems challenging. Finnveden et al. [12] proposed one definition: “the discrepancy between a measured or calculated quantity and that quantity’s true value”. In LCA, the most common causes of uncertainty include the variability and quality of data (parameter uncertainty), a variety of methodological choices (scenario uncertainty), and impact assessment methodologies (model uncertainty) [13]. On the other hand, the LCA approach necessitates various decisions and assumptions, such as system boundaries, functional units, the time horizon of emissions, stakeholder interpretation of results, human behavior, etc. Such choices are debatable and affect the result directly [12].

Moreover, decision makers can perceive uncertain outcomes in various ways based on their preferences, timing, and framing of the choice scenario, among other variables [10]. The literature distinguishes between the sources (e.g., data, choices, and relations) and types of uncertainty. For instance, data variability, inconsistency across alternatives, and the incorrect relationship between a pollutant emission and its environmental impact are examples of uncertainty types [5]. Before delving more into uncertainty, reviewing the difference between variability and uncertainty is necessary. Uncertainty is associated with a lack of information: either no data are available, or the available data are incorrect or vague. On the other hand, variability can be described as a data quality necessary for heterogeneity [14] or the multiple values at different locations, periods, or distances [15]. Heijungs and Huijbregts [14] reviewed approaches to treating uncertainty in LCA. According to several studies described in their study,

Table 1. Classification of uncertainties according to different authors.

Types of Uncertainties	Ref.
Systematic errors and random errors	[16]
Parameter uncertainty, model uncertainty, uncertainty due to choices, spatial variability, temporal variability, and variability between sources and objects	[17]
Data uncertainty, model uncertainty, and completeness uncertainty	[18]
Aleatory uncertainty, epistemic uncertainty, parameter uncertainty, data uncertainty, model uncertainty, ambiguity, and volitional uncertainty	[19]
Statistical variation, subjective judgment, linguistic imprecision, variability, inherent randomness, disagreement, and approximation	[20]
Ignoring non-linear processes, lack of process data, no spatial details on emissions, no temporal details on emissions, sum emissions, ignoring non-linear processes, no information on substance properties, no interactions with other pollutants, no modeling of metabolites, and no information on the sensitivity of the receiving environment	[21]

lists a few classifications of uncertainties.

Through a scoping review and following the PRISMA guidelines, the present study aims to identify and assess the frequency with which LCA studies reflect the uncertainty to identify the gaps within the examined papers to reveal the challenges and opportunities to have a robust model. The study’s proposed research questions are:

• What are the most recent studies’ main sources of uncertainties and their related probability distribution functions (PDF)?
• What methods/tools have been employed to cope with these uncertainties?
• Which database, methodology, software, etc., have been used in life cycle assessments?

The article is organized as follows: Section 1 demonstrates the definition, characteristics, and importance of considering uncertainty in the context of LCA; Section 2 describes the research methodology; Section 3 presents the results and descriptive analysis; Section 4 answers the research questions and discusses them; and Section 5 concludes the review.

2. Research Design

2.1. A Scoping Review

The present study adopted a scoping review’s methodological framework proposed by Arksey and O’Malley [22] and Peters et al. [23] to analyze and summarize the history of uncertainty in the LCA context and recognize the contrasts between the many primary forms that already exist. In addition, the development areas with the most potential were identified by reviewing and assessing previous studies. This methodology was employed because it is more rigorous than a literature review. It entails multiple structured searches and a rigorous search process [24]. The process includes reporting on the papers found in each step in a PRISMA flow diagram [25]. The PRISMA flow diagram is well-established reporting template methodology for scoping reviews [26,27]. This method is neither a mapping review nor a systematic review because there is no intention to evaluate the identified literature critically. A descriptive and qualitative thematic analysis is presented instead.

Figure 1 illustrates the research process following these six steps: (1) defining the search string and eligibility criteria; (2) performing the search; (3) ensuring that the corpus is comprehensive and that the search string is correct; (4) preparation of the final corpus; (5) article screening; and (6) data extraction.

2.2. Review Procedure

The following steps were conducted under the scoping review protocol (PRISMA) illustrated in Figure 1:

• Three research questions were defined (see Section 1).
• In order to begin the search, several attempts and errors were made using available scientific databases (Web of Science (WoS), Scopus, and ScienceDirect).

  Table 2. Initial strings used in databases.

  Database	String
  Web of Science (WoS)	ALL = (((((life AND cycle) OR (environmental AND impact) OR LCA) AND(fuzzy OR bias* OR uncertain* OR variability OR sensitivity))))
  Scopus	TITLE-ABS-KEY((((life AND cycle) OR (environmental AND impact) OR LCA) AND (fuzzy OR bias* OR uncertain* OR variability OR sensitivity)))
  ScienceDirect	((((“life cycle” ) OR (“environmental impact”) OR LCA) AND (fuzzy OR uncertainty OR variability OR sensitivity)))

  provides the search strings. The initial search was not limited to this level. Scopus, ScienceDirect, and all WoS categories were searched for titles, abstracts, and keywords. As a result, 120,232, 86,106, and 7433 documents (in all categories) were listed in WoS, Scopus, and ScienceDirect, respectively. Asterisks (*) are frequently used to broaden a search by indicating terms with identical first letters [27]. For example, uncertain* can find uncertain, uncertainty, uncertainties, etc.
• Due to the very high number of obtained articles in the initial search, the year of the studies was limited to the title only. Therefore, the remaining articles dropped to 824, 1213, and 290 for WoS, Scopus, and ScienceDirect.
• Because of significant interest among researchers during the past decade, limiting the string to the most recent studies (last four years), the number of studies between 2019–2022 dropped to 247, 316, and 82 in WoS, Scopus, and ScienceDirect.
• In addition, the language of the studies was limited to English. Consequently, only a few documents were eliminated. The remaining studies became 246, 311, and 82 for WoS, Scopus, and ScienceDirect, respectively.
• As a final step at the screening stage, the string was tailored to achieve more accurate results, and the number of remaining documents was reduced to 76, 101, and 39 (216 documents in total) for WoS, Scopus, and ScienceDirect, respectively. The tailored string is as follows:
  ((((life AND cycle AND assessment) OR LCA) AND (fuzzy OR uncertain* OR variability OR sensitivity)))
• The list contained many duplicates. Therefore, after trimming the list and removing duplicates using Microsoft Excel^® v2016 (Microsoft, USA), 112 documents were left, and 104 remained.
• The eligibility of the studies was assessed at two stages by title and full-text screening. In the title-screening stage, four documents, and in the full-text screening, eight articles, were considered non-relevant and were eliminated from the list. All in all, the list consisted of 92 publications.
• In the last step, adding an article, the final list reached 93 publications.

Once the bibliographic information was extracted, the collected articles were categorized based on the following features. The main categories are year, country, and sector addressed in the study, method, and tools. The results are summarized in the tables given in Section 3. Following the PRISMA methodology, Figure 2 illustrates the screening process results to present the retained articles and studies at each stage.

3. Results

This section provides the descriptive information associated with the latest studies on applying uncertainty analysis in LCA.

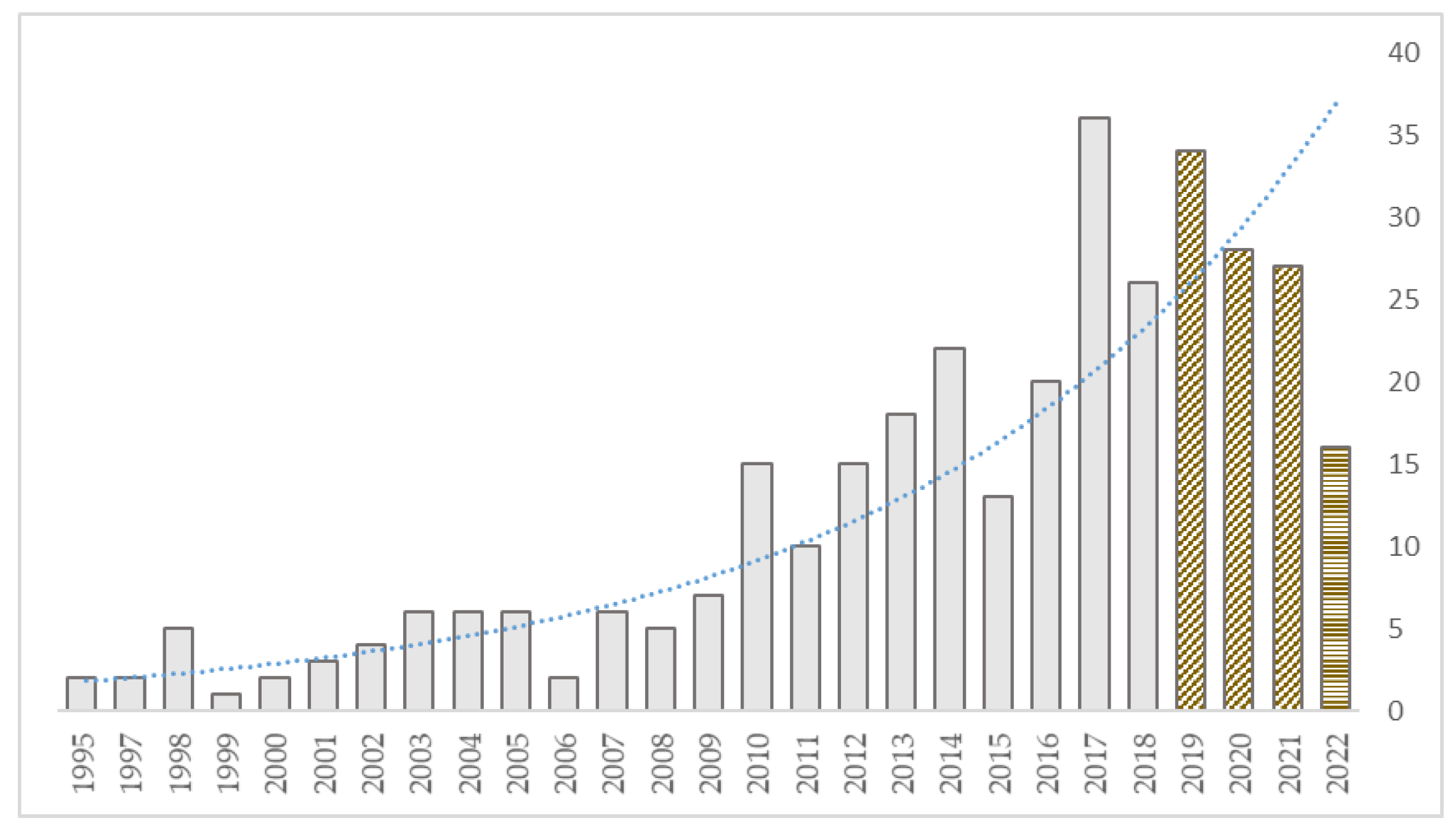
3.1. Year-Wise Analysis

The year-wise analysis provides an overview of the research’s progress and shows the researchers’ interest. It may be challenging to find a clear trend based on recent studies. As part of the research period, 1995–2018 were added to understand better how interest in this topic has evolved. Figure 3 illustrates the number of published studies since 1995 (extracted from Scopus based on the tailored string). There has been an accelerated interest in LCA-related studies focusing on uncertainty. The highest contributions belong to 2017, with 36 studies, followed by 34 publications in 2019. Although there are 16 listed publications within early August 2022, it is expected to have many more upcoming publications. The significant drop in 2020 and 2021 may be due to the COVID-19 pandemic when it reached its peak.

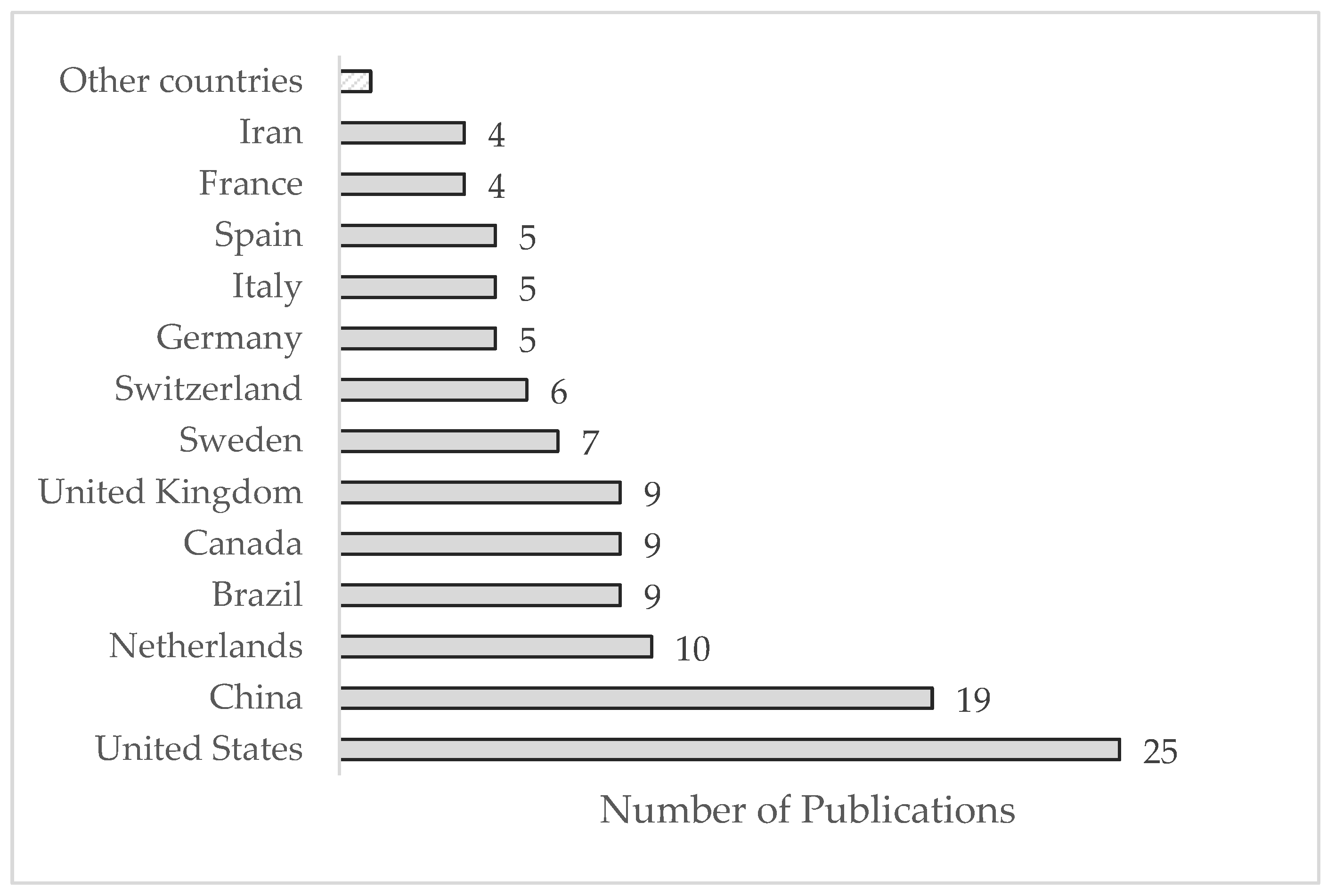
3.2. Country-Wise Analysis

Country-wise analysis of the selected publications shows that 31 countries contributed to this topic (2019–2022). As seen in Figure 4, the highest contribution belongs to the United States with 25 studies, followed by China with 19, the Netherlands with 10, and Brazil and Canada with 9 studies each. A total of eighteen countries were involved in only three studies or fewer that were categorized as “Other Countries”.

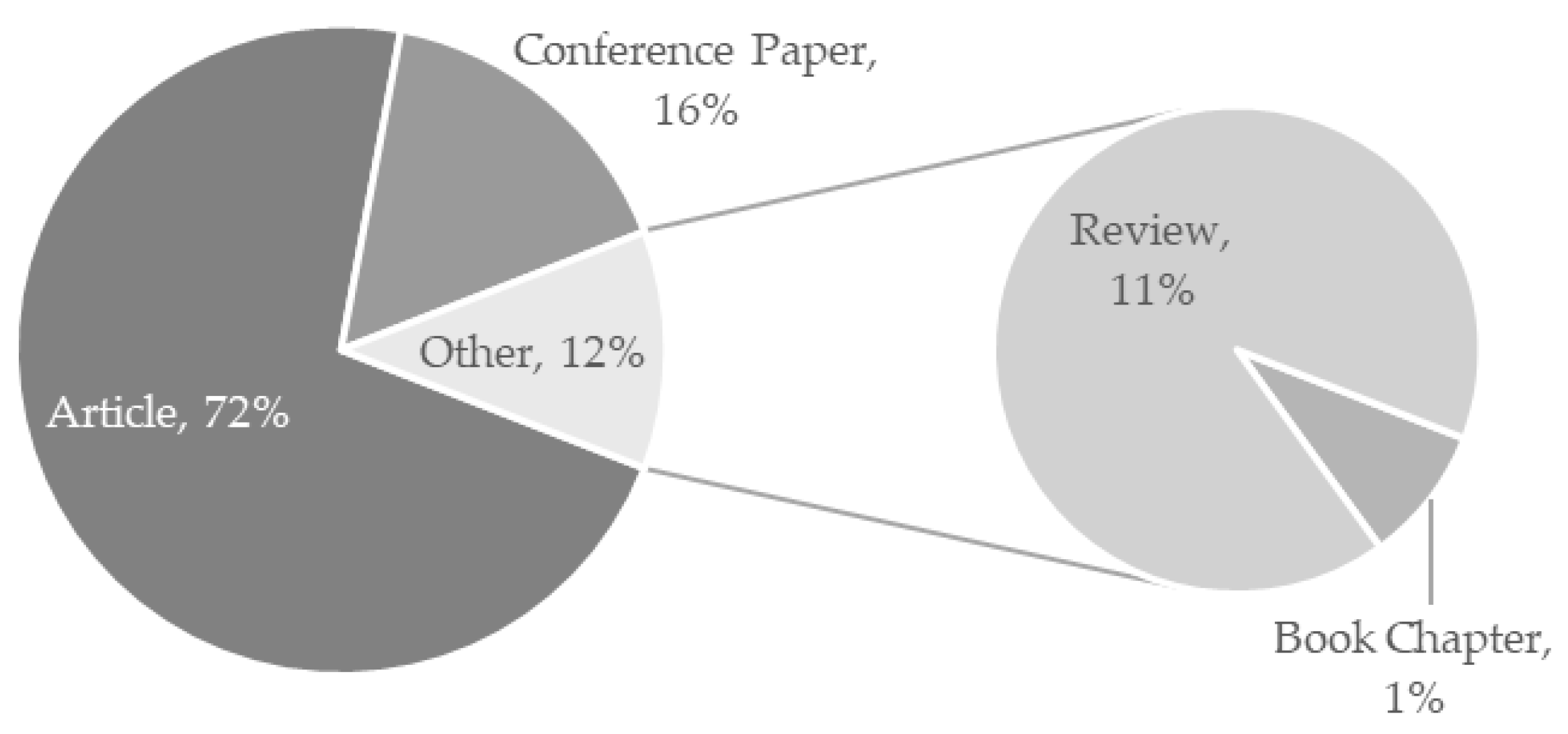
3.3. Classification Based on Document Type

This review considered all types of publications, as discussed earlier. According to Figure 5, there were four types of documents. Articles received the highest rank of 72%, followed by conference papers with a ranking of 16%. Review documents accounted for only 11% of all documents (nine studies), and book chapters made up the smallest percentage (1%).

3.4. Classification Based on the Subject Area

Based on the extracted data from Scopus, 16 different subject areas cover uncertainty and LCA. Environmental sciences, engineering, and energy-related topics lead this list by 30, 19, and 12 percent (see

Table 3. Subject areas in the selected publications.

Subject Area	%	Subject Area	%
Environmental science	30	Earth and planetary sciences	3
Engineering	19	Chemistry	3
Energy	12	Biochemistry, genetics, and molecular biology	2
Social sciences	8	Mathematics	2
Computer science	5	Economics, econometrics, and finance	1
Business, management, and accounting	4	Agricultural and biological Sciences	1
Material science	4%	Decision sciences	1%
Chemical engineering	4%	Physics and astronomy	1%

).

4. Discussion

To answer the research questions, a comprehensive content-based analysis was conducted. The following section summarizes 93 selected research studies conducted during the preceding four years. Among 104 selected studies belonging to the period between 2019 to Aug 2022, 93 studies were considered relevant to the topic.

Table 4. Life cycle thinking approaches under uncertainty and their frequency.

Life Cycle Assessment (LCA)	57	Other References Than Those Listed Below
Comparative life cycle assessment (CLCA)	4	[28,29,30,31]
Life cycle assessment (LCA) and life cycle cost assessment (LCCA)	3	[32,33,34]
Life cycle sustainability assessment (LCSA) (including environmental, economic, and social impacts)	3	[35,36,37]
Energy, economic, and environmental life cycle (EEELC)	2	[38,39]
Hybrid life cycle assessment (HLCA) (which is a combination of the process- and IO-based LCA)	1	[40]
Probabilistic life cycle assessment (PLCA)	1	[41]
Dynamic life cycle assessment (DLCA)	1	[42]
Full-scale life cycle assessment (FSLCA)	1	[43]
Life cycle assessment and techno-economic analysis (TEA)	1	[44]
Screening-level life cycle assessment (SLLCA)	1	[45]
Bottom-up-based life cycle assessment (BULCA)	1	[46]
Integrated life cycle assessment and analytic hierarchy process (AHP)	1	[47]
Economic input–output (EIO)-based life cycle assessment	1	[48]
Life cycle sustainability assessment (environmental, economic, and social impacts) combined with technical life cycle assessment (TLCA)	1	[49]
Reviews	9	[1,13,50,51,52,53,54,55,56]
Other	5	[57,58,59,60,61]
Total	93

provides a breakdown of different aspects of life cycle thinking and their frequency in the selected publications.

As seen in Section 3.3. there were nine review articles on this topic. Piano and Benini [50] reviewed approaches for assessing uncertainty as part of the life cycle assessment. Specifically, they discussed stochastic uncertainty as well as epistemic uncertainty when analyzing uncertainty and sensitivity, as well as assessing knowledge quality. The following issues were identified by the authors: (1) most articles primarily addressed uncertainty during the life cycle inventory (LCI) phase, failing to consider other phases of LCA; (2) the assessments of uncertainty analysis (UA) and sensitivity analysis (SA) were usually conducted independently; (3) uncertainty parameters were typically selected based on their effect on the LCA output (thereby confusing the mean with uncertainty); (4) SAs were often conducted one factor at a time (local sensitivity analysis), which overlooks the interaction between parameters; (5) uncertainty communication terminology has been misused frequently by confusing uncertainty appraisal with uncertainty allocation; (6) pedigree coefficients for data quality assessment were also misinterpreted by translating them into multiplicative coefficients that defined the probability distributions of input parameters; and, finally, (7) a significant gap exists between state-of-the-art methodologies and commonly used methodologies in life cycle assessment studies. Feng et al. [51] conducted a comprehensive systematic review to address uncertain sources of whole-building life cycle assessment (WBLCA) and solutions to these problems. According to the selected publications, they concluded that uncertainties could be attributed to a variety of factors, including life cycle stages, used database, life cycle inventory assessment (LCIA) methods, functional units, system boundaries, input parameters, characterization factors, practitioners’ knowledge and experience, human activities, and uncertainty methods. Therefore, eight different solutions and variations were proposed, of which Monte Carlo simulation (MCS) and sensitivity analysis were the most common. Through a systematic review, Michiels and Geeraerd [52] investigated the approaches already employed to determine if uncertainty or variability dominates LCA results. In their 562 selected papers, there was no consistency in the definitions and viewpoints of the phrases uncertainty and variability, as noted during the research’s preliminary phase. Different types of uncertainty and variability were classified based on the data’s goal, scope, definition, and quality. They concluded that the most critical consideration was that uncertainty and variability were considered in some manner. Even though some studies focus on separating uncertainty from variability, others appear to have done so by accident or as an afterthought. The uncertainty analysis methods were categorized as follows:

• Characterization via multiple scenarios, predefined changes, ranges around a default value or probability distributions;
• Uncertainty and variability propagation via Monte Carlo simulations;
• Local sensitivity analysis via scenario analysis, one-at-a-time approach, or the multiplier method;
• Screening method via the method of elementary effects;
• Global sensitivity analysis by calculating rank correlation coefficients or regression coefficients;
• Visualization via coefficients of variation, summary statistics, ranges, contribution to variance percentages, sensitivity indices, and critical parameters.

Through LCA, Geller et al. [53] compared uncertainty factors such as different energy sources and several hydropower plants with differing characteristics. Lima et al. [1] critically reviewed the relationship between uncertainty analysis and life cycle assessment in 64 scientific publications addressing the biorefineries’ systems. Bamber et al. [13] conducted a review study to determine and assess the reported frequency of uncertainty in LCA studies (including attributional and consequential LCA and any combinations of these two). Moreover, they investigated whether or not the generally used methodologies for uncertainty assessment in attributional LCA and the types of uncertainty that have been evaluated are also appropriate in consequential life cycle modelling scenarios. Zara et al. [54] systematically reviewed 35 papers to investigate approaches to handling uncertainty and sensitivity analysis in LCAs at the neighborhood scale to identify inconsistencies, limitations, and challenges. Igos et al. [55] reviewed the methods for treating uncertainty in LCA, including characterization of uncertainty sources, propagation to results (uncertainty analysis), analysis of their effects (sensitivity analysis), and communication about uncertainty. Building life cycle assessment and life cycle cost results were reviewed by Giorgi et al. [56] concerning existing service life values for building elements.

4.1. Uncertainty Analysis Methods

The selected studies utilized various tools and methods to address uncertainty in the earlier discussed LCA methods. In the following section, we try to provide a comprehensive answer to the research questions.

Table 5. Uncertainty and sensitivity analysis methods.

Uncertainty Analysis Methods	Freq	Reference
Monte Carlo simulation (MCS)	14	[28,31,37,40,45,62,63,64,65,66,67,68,69,70]
Sensitivity analysis (SA)	11	[44,47,60,71,72,73,74,75,76,77,78]
Fuzzy multi-criteria decision making (F-MCDM)	7	[33,35,36,49,79,80,81]
Monte Carlo simulation + sensitivity analysis	8	[29,41,82,83,84,85,86]
Scenario analysis (ScA)	4	[30,87,88,89]
Variability analysis (VA)	4	[90,91,92,93]
Monte Carlo simulation + global sensitivity analysis	3	[34,94,95]
Global sensitivity analysis (GSA)	3	[43,96,97]
Statistical analysis (StA)	2	[98,99]
Gaussian process regression (GPR)	1	[100]
Fuzzy Delphi (F-Del)	1	[61]
Global sensitivity analysis + local sensitivity analysis (LSA)	1	[57]
Fuzzy rough set theory (F-RST)	1	[101]
Global sensitivity analysis + Regression (Reg)	1	[46]
Uncertainty estimation GHG protocol (UE-GHG)	1	[102]
Bayesian fuzzy mathematics (BFM) + sensitivity analysis	1	[103]
Monte Carlo simulation + logarithmic mean Divisia index (LMDI) decomposition method	1	[104]
Quantitative risk assessment (QRA)	1	[105]
Quantitative and qualitative analysis (QQA)	1	[58]
Adaptive neuro-fuzzy inference system (ANFIS) + Multi-objective genetic algorithm (MOGA)	1	[38]
Uncertainty propagation (UP)	1	[48]
Pedigree approach (PA)	1	[106]
DQI semi-quantitative approach (DQI-SQA) + MCS + GSA	1	[107]
Decision choices procedure (DCP)	1	[108]
Variation mode and effect analysis (VMEA) + MCS	1	[109]
Monte Carlo simulation + scenario analysis	1	[110]
Monte Carlo simulation + scenario analysis + GSA	1	[111]
Monte Carlo simulation + contribution analysis (CA) + sensitivity analysis + multiple regression (MReg)	1	[112]
Interval analysis (IA) + Bayesian inference (BI) + LSA	1	[113]
Adaptive neuro-fuzzy inference system (ANFIS)	1	[39]
Taylor’s first-order approximation (TFOA)	1	[114]
MCS + limited Taylor series expansion (LTSE)	1	[115]
Novel system-level approach (NSLA) + Monte Carlo simulation	1	[116]
Monte Carlo Simulation + sensitivity analysis + multi-criteria decision analysis (MCDA)	1	[42]
Monte Carlo simulation + convolution theory (CT)	1	[117]
Fuzzy synthetic evaluation (FSE)	1	[32]

lists the main uncertainty quantification methods and their frequency in the selected studies. As seen in Table 5, Monte Carlo simulation as a single method dominates the list with 15 studies, followed by sensitivity analysis with 11 studies. Each method is suitable to cope with specific sources of uncertainty. For this reason, several methods have been employed in most studies which will be discussed in the following.

4.1.1. Monte Carlo-Based Analysis

Monte Carlo simulations use random sampling and statistical modeling to estimate mathematical functions and simulate complex systems’ behavior [118]. This technique develops probabilistic models for real-world processes to estimate specific average properties, such as mathematical expectations, variance, and covariance. The main steps to performing a Monte Carlo simulation are random number generation, simulation of the random values with more complicated distribution, and calculations [119]. The following section shows that the Monte Carlo approach was used directly for uncertainty quantification or indirectly in other methods, such as global sensitivity analysis (GSA).

As seen in Table 5, 14 studies have employed Monte Carlo simulation as the dominating method. In the development of cassava ethanol, Jiao et al. [62] assessed the uncertainty of energy efficiency and environmental performance in a cassava ethanol plant in China by Monte Carlo as a single method. Through a hybrid life cycle assessment (HLCA), Perkins and Suh [40] answer the question, “how do the accuracy benefits of hybridization weigh against precision costs?” by using the environmental assessment of Swedish fashion consumption as the case study. They applied Monte Carlo simulation by randomly varying each process data based on its distribution. This study was limited to existing probability distribution function (PDF) data from Ecoinvent v3.1 and CEDA v5. Based on data from a firm in eastern China, Wang et al. [64] conducted a Monte Carlo simulation for the stochastic research of life cycle inventory (LCI) about the production process of polyester yarn in the textile industry. An analysis of the life cycle of a warm asphalt rubber pavement built with three typical warm additives, organic wax, surfactant additive, and zeolite, incorporating uncertainty analysis, was performed by Cao et al. [29] to identify the long-term energy savings potential of WMA technologies in Asphalt rubber pavements and quantify the life cycle energy consumption. A Monte Carlo simulation was conducted to quantify and propagate the four categories of uncertainty: material energy consumption, equipment energy consumption, mixing temperature reduction, and material transportation distance. Messagie et al. [65] employed Monte Carlo analysis to calculate the different effects the parameter has on the calculated environmental impact. Specifically, MCS was used to incorporate the variability and uncertainty of the foreground and background data in vehicle technologies. Alyaseri and Zhou [66] showed the impact of uncertainty from the life cycle inventory assessment method on LCA outcomes by using MCS and a case-study-based approach on three wastewater sludge treatment processes, multiple hearth incineration, and two proposed alternative processes: fluid bed incineration and anaerobic digestion. Based on hydrologic analysis and LCA, Tavakol-Davani [67] identified critical uncertainty sources in designing an ecologically sustainable urban drainage system. The objective of the uncertainty analysis was to describe and analyze the relative contributions of unreliability, incompleteness, technological difference, geographical and temporal variation in LCIA data, as well as natural variability in hydrologic data. Using high-throughput computing and Morse-Scale regression models, uncertainties were evaluated using a robust Monte Carlo technique. It is reported that as a limitation, model structural and decision uncertainties were not considered. Through LCA, Kumar and Krishna [73] evaluated the uncertainties in environmental impacts of contaminated-site remediation options using MCS to assess the range of predicted environmental consequences for the provided uncertainty in transportation distances associated with the execution of the remedial option. To capture the uncertainties associated with economic, environmental, and social pillars during the life cycle of pavement alternatives, Zheng et al. [37] proposed an uncertainty-based LCSA framework. Based on the identification and characterization of uncertainties, Monte Carlo simulations were applied to determine the probabilistic LCSA results associated with eight impact categories. A case study was conducted to assess the uncertainty associated with hot mix asphalt pavement, warm mix asphalt pavement, and reclaimed pavement. Scricca et al. [68] aimed to quantify a major source of uncertainty in the LCA of red wine using the Monte Carlo approach implemented in the SimaPro software. Baaqel et al. [69] proposed a strategy for integrating foreground and background uncertainty in the life cycle assessment (LCA) of low-technology-readiness processes and products. The suggested methodological structure incorporated uncertainty modeling, Monte Carlo sampling, process simulation, and environmental assessment. Uncertainty was propagated through the background and foreground inventories and, ultimately, to the environmental damages for each realization of uncertainty. Using MCS, Wolff and Duffy [70] presented a structured uncertainty management method to improve uncertainty reporting in LCA in the case study of Irish apartment development. The three-dimensional uncertainty classification in LCA was further developed in this study. Using ISO 14044, the classification was integrated into an uncertainty management technique that consists of five stages: identification, classification, quantification, reduction, and reporting, and was included in the iterative processes of a life cycle assessment. A comparative assessment of sixteen cement-treated base mixtures, with or without recycled asphalt pavement, and varying cement percentages, production processes, and recycling procedures was performed by Bressi et al. [31]. Assuming that the assumed distributions are representative of the actual conditions, MCS was used to propagate the uncertainties of the input into the LCA outputs to reduce the likelihood of drawing incorrect and misguided conclusions. Heiguns [28] used MCS to select a best product alternative. They did not discuss approaches for classical multi-criteria decision making (MCDM) methods. Gaudreault et al. [45] compared the possible environmental benefits and costs of several management alternatives for wood ash, including agricultural land application, forest soil amendment, usage in forest roads, use in concrete and mortar, and landfilling, using a screening-level LCA technique. For each management choice and impact category contribution, quantitative contributions of groups of unit processes to indicator scores were computed by MCS.

The studies cited above used MCSs to quantify the system’s uncertainty. Not only was MCS used in conjunction with other uncertainty analysis methods, but it was also used as a secondary method to handle the main methods such as global sensitivity analysis and decision choice procedure (DCP), etc. [43,57,103,108]. Table 6 provides the uncertainty analysis methods and software in the selected studies.

4.1.2. Sensitivity Analysis

Sensitivity analysis (SA) is commonly used to evaluate the significance of each parameter of the model on the system’s behavior [120]. In a numerical model, SA is a technique that assesses the effect of uncertainty on one or more input variables on output variables [121]. Furthermore, sensitivity analysis is useful for guiding experimental analysis, model reduction, and parameter estimation. The two main types of sensitivity analysis are local and global sensitivity analysis. Local sensitivity analysis examines the impact of small perturbations on model outputs. In contrast, global sensitivity analysis approaches are used to investigate how large variations in model parameters can affect model outputs [122].

Similar to MCS, sensitivity analysis (including global sensitivity analysis) was addressed in 14 studies (Table 5). Liang et al. [44] conducted a sensitivity and techno-economic analysis of shale gas development based on LCA. Using estimated ultimate recovery prediction models as a basis for economic evaluation, this paper established the estimated ultimate recovery evaluation procedure. The influence of investment and geology–engineering factors were studied using SA. Cucurachi et al. [43] developed a practical software implementation and theoretical basis that combines moment-independent global sensitivity analysis with uncertainty analysis, which can be easily used in large-scale LCA models. Jolivet et al. [57] provided the LCA community with practical tools to create parametric inventories and investigated the model uncertainty. Both local and global sensitivity analysis were used to contrast insights into the significance of each variable in the variety of environmental consequences. Ferronato et al. [78] improved the recycling rate in municipal solid waste LCA using sensitivity analysis. The analysis consisted of ten parameters and a scenario assessment regarding the increase in recycling rates. It was reported that the environmental impacts were mostly sensitive to the use of plastic bags, landfill gas collection efficiency, the replacement rate of virgin materials, and the transportation distances of collected waste. Jaxa-Rozen [97] highlighted three innovative approaches that build on variance-based global sensitivity analysis and can offer novel insights on uncertainty in typical LCA applications with non-normal output distributions, interactions between model inputs, and trade-offs between environmental impacts. Using distribution-based global sensitivity analysis, spectral clustering, and patient rule induction methods, they identified influential model inputs, trade-offs, and decision-relevant interactions for the case of geothermal-heating networks. Andrade et al. [77] compared four agricultural models with different complexity levels and tested their suitability and sensitivity in LCA. Through LCA, Dabaieh [76] assessed the carbon impact of a minus carbon experimental refugee house in Sweden using SimaPro^® (PRé Consultants, Netherlands) and GaBi^® (sphere, USA) software. Through two case studies, Wu et al. [75] evaluated the sensitivity of LCA analysis on a hybrid-timber building. In Case 1, the focus was on changes in the volume of wood materials, whereas in Case 2, the focus was on simultaneous changes in the volumes of wood, steel, and concrete materials. In the context of phosphorus recovery from wastewater in Metro Manila, Pausta et al. [47] evaluated the holistic environmental performance scores of the following scenarios based on the LCA framework integrated with the analytic hierarchy Process (AHP). Using the sensitivity analysis, the overall environmental impact score was evaluated using different input parameters for the LCI analysis and priority weights for the AHP method. Helmers et al. [74] compared the environmental impacts of petrol, diesel, natural gas, and electric vehicles using a process-based attributional LCA and sensitivity analysis of six parameters (size of car, emission profile, fossil fuel choice, electricity choices during battery production and use phase, battery size and battery second use, and mileage). Through a global sensitivity analysis, Patouillard et al. [96] prioritized regionalization efforts in LCA. The objective of regionalization in LCA is to improve the representativeness of LCA results and reduce uncertainty caused by spatial variations. A stepwise methodology was proposed for LCA practitioners to prioritize data collection for regionalization based on a global sensitivity analysis (GSA) that used Sobol indices for quantifying global sensitivity. To solve major environmental concern in Brunei due to the overuse of petroleum, Hossain et al. [72] conducted a comprehensive LCA of alternative biofuels such as bioethanol production from microalgae. Chàfer et al. [71] compared the LCA of a pneumatic municipal waste collection system and traditional truck collection through sensitivity analysis of the influence of the energy sources. In their analysis, six different waste collection systems and five energy sources (Spanish energy mix 2008, hydropower, photovoltaic, wind, and a renewable energy mix) were analyzed.

4.1.3. Fuzzy Multi-Criteria Decision Making

The concept of MCDM describes the process of selecting the most suitable alternative among predetermined alternatives by evaluating them based on a multitude of factors [123]. A fuzzy MCDM model evaluates alternative capabilities in the context of selected criteria with the help of a committee of decision makers. The suitability of alternatives is weighed against criteria, and the importance weights of criteria are represented by fuzzy numbers [124]. There is a wide range of fuzzy MCDM studies in the literature, such as fuzzy AHP, fuzzy ANP, fuzzy TOPSIS, fuzzy PROMETHEE, combined fuzzy MCDM methods, fuzzy DEMATEL, etc.

In the selected studies, only seven studies addressed fuzzy MCDM methods. Dewalker and Shastri [33] proposed a comprehensive fuzzy MCDM framework with LCA and LCCA approaches to selecting the most appropriate wastewater treatment system (WWT) for multi-level residential buildings. In their framework, fuzzy AHP and fuzzy TOPSIS were used to assess criteria and indicators and the final ranking of alternatives. Fetanat et al. [49] combined life cycle sustainability assessment (LCSA) and fuzzy MCDM to prioritize the industries’ flare technologies. By merging the SWARA–WASPAS [125,126] method with fuzzy evaluation, a novel fuzzy MCDM strategy capable of addressing linguistic factors in the decision-making matrix was developed. Figueiredo et al. [35] used the LCSA approach and fuzzy AHP as a decision-making tool to choose sustainable materials for construction projects. As part of the proposed framework, fuzzy AHP was selected as the MCDA method because the problem of material choice often involves subjectivity, uncertainty, and ambiguity, all of which are best handled by fuzzy logic. By applying fuzzy–technique for order of preference by similarity to ideal solution (TOPSIS) to the life cycle sustainability assessment (LCSA) methodology, Zanchi et al. [36] integrated environmental, economic, and social assessment (LCSA) results. This study aimed to evaluate the usefulness of the LCSA methodology as a tool for supporting the design phase, providing solutions tailored to its application in the automotive sector. Farooque et al. [81] adapted fuzzy DEMATEL to analyze the barriers of blockchain-based LCA in China. It was expected that the emerging blockchain technology would significantly improve the effectiveness and efficiency of life cycle assessments, widely used to evaluate the environmental impact of products and processes. Through an integrated LCSA and MCDA approach, Angelo and Marujo [80] discussed how to consider uncertainties inherent in LCSA in decision making using the ELECTRE [127] methodology. Macioł and Rębiasz [79] assessed the potential for aggregating LCA results using knowledge-based methods. This study investigated two classical, multi-criteria decision-making methods (AHP and TOPSIS), conventional reasoning (crisp), and Mamdani’s fuzzy inference method [128]. Table 6 shows detailed information about the selected studies’ methods and the software/tools used to cope with them. The reviews were excluded from the list.

Table 6. Uncertainty analysis methods and tools in the selected studies.

Main Approach	Via	Software	Ref
FSE	Questionnaire survey		[32]
MCS	MCS sampling		[28]
StA	Four-way ANOVA		[99]
MCS			[31]
GSA	MCS	Python	[43]
GPR	Hamiltonian MCS, mean absolute percentage error (MAPE)	Python package GPFlow	[100]
MCS + SA	MCS via bootstrap resampling and parametric distribution fitting		[41]
Fuzzy MCDM	FAHP, FTOPSIS, SA		[33]
ScA	sensitivity, scenario screening		[89]
MCS + SA		Crystal Ball	[86]
VA	Scenario analysis		[93]
UE-GHG			[102]
GSA + LSA	GSA via Sobol’s method and MCS	python (Brightway2)	[57]
SA			[44]
Fuzzy MCDM	Novel technique		[49]
ScA			[88]
MCS + GSA	Sobol’s method		[34]
BFM + SA	BFM combined with MCS, geometric mean and geometric standard deviation	OpenLCA 1.10	[103]
SA	Interval analysis, scenario analysis		[78]
Fuzzy MCDM	Fuzzy AHP		[35]
MCS + SA	SA via scenario analysis		[129]
MCS + LMDI	MCS via the Pedigree method	Python	[104]
GSA	Variance-based GSA via Sobol indices and MCS + spectral clustering and scenario discovery		[97]
VA	variability analysis + pedigree matrix		[92]
MCS	MCS + DQI + DQR	Rstudio	[70]
Fuzzy MCDM	Fuzzy TOPSIS		[36]
QRA	Logic tree diagram + scenario analysis		[105]
SA	SA and scenario analysis		[77]
QQA	ANOVA and one-sided t-tests		[58]
MCS	MCS sampling, scenario analysis	Matlab	[69]
MCS + SA	MCS via “what-if” scenario, SA via contribution to variance	Python	[85]
ScA			[30]
VA			[91]
ANFIS + MOGA		Matlab	[38]
MCS + GSA			[95]
MCS + SA			[45]
MCS + SA	SA via rank acceptability index (RAI), MCS via pedigree matrix, outranking via PROMETHEE II		[84]
SA			[76]
UP	via variance of the output uncertainty	Matlab	[48]
MCS + GSA	GSA via a variance-based method, Sobol method, and bootstrapping	Rstudio	[94]
MCS		Sima Pro	[68]
PA	Survey		[106]
Fuzzy MCDM	Fuzzy DEMATEL		[81]
StA	via data quality indicators (DQIs)		[98]
MCS	Data quality indicator (DQI) based on the pedigree matrix approach		[37]
VA			[90]
DQI-SQA + MCS + GSA	Stochastic modeling via MCS GSA via analysis of key issues DOI via pedigree matrix	Sima Pro, Crystal Ball	[107]
DCP	via MCS		[108]
SA		Athena IE4B	[75]
SA + ScA	Other methods: MCDM via AHP, sampling via space-filling Latin hypercube design	JMP software	[47]
MCS + SA			[83]
SA			[74]
GSA + Reg	GSA via Morris and Sobol indices method, regression via multiparameter linear regression ANOVA analysis	Rstudio and Excel VBA	[46]
MCS + SA	Stochastic modeling via MCS		[82]
MSC		SimaPro v8.5	[73]
MCS	MCS via HTC and interpreted by Morse scale regression models		[67]
GSA	GSA via Sobol indices, MCS, and pedigree matrix approach	Brightway 2	[96]
MCS + SA + ScA		SimaPro 8.0	[66]
SA		Microsoft Excel	[72]
MCS			[65]
SA			[71]
MCS + ScA + GSA	Stochastic modeling via MCS GSA via contribution to variance	Brightway 2	[111]
MCS	pedigree matrix		[29]
MCS + CA + SA + MReg		SimaPro 8.4	[112]
ScA	SA		[87]
VMEA + MCS			[109]
MCS	MCS		[64]
IA + BI + LSA	Direct sampling via MCS Machine learning surrogate model Introduced model correction method via orthogonal polynomial basis functions		[113]
ANFIS		Matlab (R2016b)	[39]
MCS	Pedigree approach	Matlab	[40]
MCS	MCS	@RISK 7.5	[63]
SA		PestLCI 2.0	[60]
TFOA		Matlab	[114]
MCS + LTSE			[115]
NSIA + MCS	Pedigree matrix, SA	SimaPro 8.2	[116]
Fuzzy MCDM			[80]
FRST			[101]
MCS + SA + MCDA			[42]
MCS + CT	Pedigree matrix		[117]
Fuzzy MCDM	Via AHP, TOPSIS, conventional (crisp) reasoning method, and Mamdani’s fuzzy inference method		[79]
MCS		@RISK 7.5	[62]
MCS + ScA	Stochastic modeling via MCS	Matlab	[110]
F-Del	Survey		[61]

Table 6. Uncertainty analysis methods and tools in the selected studies.

Main Approach	Via	Software	Ref
FSE	Questionnaire survey		[32]
MCS	MCS sampling		[28]
StA	Four-way ANOVA		[99]
MCS			[31]
GSA	MCS	Python	[43]
GPR	Hamiltonian MCS, mean absolute percentage error (MAPE)	Python package GPFlow	[100]
MCS + SA	MCS via bootstrap resampling and parametric distribution fitting		[41]
Fuzzy MCDM	FAHP, FTOPSIS, SA		[33]
ScA	sensitivity, scenario screening		[89]
MCS + SA		Crystal Ball	[86]
VA	Scenario analysis		[93]
UE-GHG			[102]
GSA + LSA	GSA via Sobol’s method and MCS	python (Brightway2)	[57]
SA			[44]
Fuzzy MCDM	Novel technique		[49]
ScA			[88]
MCS + GSA	Sobol’s method		[34]
BFM + SA	BFM combined with MCS, geometric mean and geometric standard deviation	OpenLCA 1.10	[103]
SA	Interval analysis, scenario analysis		[78]
Fuzzy MCDM	Fuzzy AHP		[35]
MCS + SA	SA via scenario analysis		[129]
MCS + LMDI	MCS via the Pedigree method	Python	[104]
GSA	Variance-based GSA via Sobol indices and MCS + spectral clustering and scenario discovery		[97]
VA	variability analysis + pedigree matrix		[92]
MCS	MCS + DQI + DQR	Rstudio	[70]
Fuzzy MCDM	Fuzzy TOPSIS		[36]
QRA	Logic tree diagram + scenario analysis		[105]
SA	SA and scenario analysis		[77]
QQA	ANOVA and one-sided t-tests		[58]
MCS	MCS sampling, scenario analysis	Matlab	[69]
MCS + SA	MCS via “what-if” scenario, SA via contribution to variance	Python	[85]
ScA			[30]
VA			[91]
ANFIS + MOGA		Matlab	[38]
MCS + GSA			[95]
MCS + SA			[45]
MCS + SA	SA via rank acceptability index (RAI), MCS via pedigree matrix, outranking via PROMETHEE II		[84]
SA			[76]
UP	via variance of the output uncertainty	Matlab	[48]
MCS + GSA	GSA via a variance-based method, Sobol method, and bootstrapping	Rstudio	[94]
MCS		Sima Pro	[68]
PA	Survey		[106]
Fuzzy MCDM	Fuzzy DEMATEL		[81]
StA	via data quality indicators (DQIs)		[98]
MCS	Data quality indicator (DQI) based on the pedigree matrix approach		[37]
VA			[90]
DQI-SQA + MCS + GSA	Stochastic modeling via MCS GSA via analysis of key issues DOI via pedigree matrix	Sima Pro, Crystal Ball	[107]
DCP	via MCS		[108]
SA		Athena IE4B	[75]
SA + ScA	Other methods: MCDM via AHP, sampling via space-filling Latin hypercube design	JMP software	[47]
MCS + SA			[83]
SA			[74]
GSA + Reg	GSA via Morris and Sobol indices method, regression via multiparameter linear regression ANOVA analysis	Rstudio and Excel VBA	[46]
MCS + SA	Stochastic modeling via MCS		[82]
MSC		SimaPro v8.5	[73]
MCS	MCS via HTC and interpreted by Morse scale regression models		[67]
GSA	GSA via Sobol indices, MCS, and pedigree matrix approach	Brightway 2	[96]
MCS + SA + ScA		SimaPro 8.0	[66]
SA		Microsoft Excel	[72]
MCS			[65]
SA			[71]
MCS + ScA + GSA	Stochastic modeling via MCS GSA via contribution to variance	Brightway 2	[111]
MCS	pedigree matrix		[29]
MCS + CA + SA + MReg		SimaPro 8.4	[112]
ScA	SA		[87]
VMEA + MCS			[109]
MCS	MCS		[64]
IA + BI + LSA	Direct sampling via MCS Machine learning surrogate model Introduced model correction method via orthogonal polynomial basis functions		[113]
ANFIS		Matlab (R2016b)	[39]
MCS	Pedigree approach	Matlab	[40]
MCS	MCS	@RISK 7.5	[63]
SA		PestLCI 2.0	[60]
TFOA		Matlab	[114]
MCS + LTSE			[115]
NSIA + MCS	Pedigree matrix, SA	SimaPro 8.2	[116]
Fuzzy MCDM			[80]
FRST			[101]
MCS + SA + MCDA			[42]
MCS + CT	Pedigree matrix		[117]
Fuzzy MCDM	Via AHP, TOPSIS, conventional (crisp) reasoning method, and Mamdani’s fuzzy inference method		[79]
MCS		@RISK 7.5	[62]
MCS + ScA	Stochastic modeling via MCS	Matlab	[110]
F-Del	Survey		[61]

More than 30 percent of studies used two or more methods to handle the LCA-related uncertainties. In other words, different uncertainties can be quantified using different methods, and only one approach can be used to study a specific uncertainty. Based on Table 5 and Table 6, it is evident that probabilistic approaches, and more specifically MCS, were by far the most commonly used tools to deal with uncertainty. MCS was used as a single method or in combination with other methods such as convolution theory, MCDM, scenario analysis, limited Taylor series expansion, and sensitivity analysis. After MCS, sensitivity analysis (global and local), fuzzy MCDM, and scenario and variability analysis showed the highest interest. Although Monte Carlo simulation is the dominating method in uncertainty analysis in LCA (directly or indirectly), it has some disadvantages. It is costly in time and hardware, specifically in very high iterations. On the other hand, choosing a good PDF in many cases is challenging and has significant uncertainty inside. According to Table 6, several software tools were used to quantify the system uncertainties. Some employed commercial software such as @RISK (Palisade, USA), SimaPro^® (PRé Consultants, Netherlands), Crystal Ball^® (Oracle, USA), Matlab^® (MathWorks, USA), python, and Brightway to perform the Monte Carlo simulations. As part of the sensitivity analysis, other software such as PestLCI v2.0 (developed by Dijkman, Birkved, and Hauschild, Denmark), Brightway, Microsoft Excel^® (Microsift, USA) JMP^® (SAS, UK), Athena IE4B^® (Athena Software, Canada), Rstudio^® (Rsudio, USA) and Python were used.

4.2. Sources of Uncertainty and PDFs

Many factors contribute to uncertainty, encompassing a wide variety of circumstances [130]. Mahdavi-Hezavehi et al. [131] categorized uncertainty sources into six classes, namely: model, adaptation function, goals, environment, resources, and managed system uncertainties. Uncertainty analysis in LCA involves estimating a confidence interval for the results based on the uncertainty of all parameters and model selections of the modelled product system [13]. Different sources of uncertainty were reported in the selected studies. A significant source of uncertainty was the variation in model parameters, the choice of a database used, and estimations. Moreover, errors in data, measurements, and methodology were reported in [70,83,114].

Defining a proper probability distribution function, however, proved to be challenging.

Table 7. Uncertain sources’ distribution functions.

Normal	[27,34,37,39,41,43,57,63,64,65,67,69,73,86,108,110,116]
Lognormal	[28,40,41,63,65,66,67,70,82,83,96,106,107,109,110,115,116]
Triangular	[31,41,45,57,62,65,98,107,110]
Uniform	[34,41,57,65,70,95,110,113]
Beta	[57,96,116]
Gamma	[41,67]
BETA-PERT	[85,110]
n-Normal	[100]
Weibull	[41]
Exponential	[41]
Fixed	[57]
Statistic weight	[57]
PAWN	[97]
t	[28]
Spatial	[96]

lists 15 different PDFs and their frequency in the selected studies. Normal and lognormal distributions with 17 studies followed by triangular and uniform distributions were dominating. The sources of uncertainty reported in the selected studies are summarized in

Table 8. Sources of uncertainties reported in the selected studies.

Uncertainty Sources	Ref
Importance of suitability indicators and criteria.	[32]
Randomly selected specimens of products.	[28]
Crop/feedstock, land-use change, modelling approach, and greenhouse gas metrics.	[99]
Possible variations in quantities and construction methods, appropriateness and quality of the data reliability, completeness, temporal correlation, geographical correlation, and other technological correlations.	[31]
Uncertainty parameters described in the Ecoinvent 3.6 database.	[43]
Temporal and geographical variations.	[100]
Variability in model predictions quantifies non-linear interactions.	[41]
Short and long-term variations in electricity production.	[89]
Inventory variation and parameter uncertainty.	[86]
Variability in the cultivation and conversion processes due to different types of feedstocks.	[93]
Uncertainty of emission units and uncertainty of activity data and emission factor.	[102]
Reservoir parameters and economic parameters.	[44]
Uncertainties due to different LCIA methods	[88]
Data missing in the database, complexity, and discreteness of environmental factors.	[103]
Variability in energy consumption, fuel consumption, transportation distances, etc.	[78]
Input data are inherited from their collection through various data sources.	[129]
All the variables involved in a model.	[104]
Model parameters.	[97]
Process parameters.	[92]
Errors in emissions data, measurement, bill of quantities and costs, database quantities, and choice of Ecoinvent dataset.	[70]
“The aggregation of emissions in the inventory, regardless of the geographic and temporal context; (ii) the linear modeling of environmental effects; and (iii) the estimation of characterization factors without considering the fate of the substances and the characteristics of the receiving environment”.	[105]
Emission factors and model parameters.	[77]
Nine uncertain parameters in the (foreground) process model, five of which correspond to unit-operating conditions (e.g., temperature and pressure), and the other four of which are thermophysical properties (e.g., density and the heat of formation).	[69]
Model parameters.	[85]
Different electricity mixes, the trade-off between the collecting and sorting phase, assumptions, and parameter variability.	[30]
Temporal variability of inventory data.	[91]
Predict output parameters from energy inputs to establish the optimum inputs necessary for canola production.	[38]
Critical process parameters and governing life cycle environmental impacts.	[95]
Model parameters, the generalizability of the results, different management options obtained, the quantitative contribution of groups of unit processes to the indicator scores, and beneficial use.	[45]
Importance coefficient weights, uncertainty in characterized results and weights, and communication of results via a probabilistic ranking.	[84]
Impact of input uncertainties (selection of material from the database and the method) on the total GWP impact with and without sequestration.	[76]
Life cycle model quality, data uncertainty in environmental impact, technology matrix, and LCA results.	[48]
Different types of uncertainty (technical and other) for the service life of building elements.	[94]
Environmental impact parameters.	[68]
Parameter and nonparametric uncertainties associated with the technical, methodological, and epistemic dimensions of a data set.	[106]
From technical reasons and natural variability, parameter and scenario uncertainty.	[98]
Model parameters.	[37]
Regional variability.	[90]
Variability in input data.	[107]
“Choice uncertainty present in LCA when used as decision support, as well as to mitigate subjective interpretations of the numerical results leading to arbitrary decisions”.	[108]
Wood materials volumetrically change, and the volumetric percentage of each major building material.	[75]
Variation in the input parameters in the life cycle inventory (LCI) analysis and the priority weights for the AHP method concerning the overall environmental impact score.	[47]
The uncertainties related to the LCI data location considered by comparing LCI regionalized data to Brazil (B-LCI) and global market data, the uncertainties from errors obtained in data collection, and data quality indicators through the pedigree matrix approach.	[83]
Size of the car (small vs. mid-sized, carbon footprint only), emission profile (laboratory-based vs. real-world); fossil fuel choice (diesel, petrol, or natural gas); electricity choices during battery production and use phase; battery size and battery second use; and mileage (150,000 and 200,000 km).	[74]
Key model inputs.	[46]
Service life calculation, design, technological change, repair cost and availability of parts, household affluence, residual and resale values, aesthetic and functional quality, fashion, advertising, and social pressure.	[82]
Estimating the range of expected values of the environmental impacts for the specified variability in the uncertainty in transportation distances involved in the remedial option implementation.	[73]
Unreliability, incompleteness, technological difference, and spatial and temporal variation in life cycle impact assessment (LCIA) data, as well as the natural variability in hydrologic data.	[67]
Model parameters.	[96]
Variation in input data of the LCA model.	[66]
Influential variability.	[72]
Insufficient knowledge of the true value of a parameter; uncertainty in life cycle impact assessment due to normalization, weighting, and methodology.	[65]
Influence of the energy source.	[71]
The large variety of materials, subjective choices, and long lifespans introduce parameter, scenario, and model uncertainties throughout the life cycle.	[111]
Material energy consumption, equipment energy consumption, mixing temperature reduction, and material transportation distance.	[29]
The efficiency of the feeding system, or the distance from the harbor to the farm; feed; and fuel variability.	[112]
Different scenarios.	[87]
Emission factors only, emission factors + material amounts, and emission factors + material amounts + expected service life.	[109]
Model parameters.	[64]
Input variability, model parameter, and model–form uncertainties,	[113]
Predicted values of output energy, environmental impacts, and economic profit.	[39]
Process data.	[40]
Statistical variation in use-stage parameters upon the output from impact assessment.	[63]
Soil variations with the ultimate goal of increasing the robustness of the modeling in LCA studies.	[60]
Associated margins of error due to methodological ambiguity.	[114]
Probability distributions of the input parameters, the uncertainty of the network model, and assumptions made.	[115]
Identified sources through sensitivity analysis.	[116]
Any factor that affects the LCA results in the final step since some parameters are assumed in the modeling.	[101]
Lack of data over the complete value chain associated with nascent nano-enabled products, data quantity, quality, impact assessment, and stakeholder behavior and valuation variations.	[42]
Uncertainty information of an Ecoinvent dataset (“wheat grain, feed production, organic”).	[117]
Process and input data.	[62]
Parameter, scenario, and model uncertainties.	[110]
Uncertainty in survey responses.	[61]

. The most significant sources of uncertainties reported in the studies were uncertainty in model and process parameters, data variability, and uncertainty due to using different methodologies and databases.

4.3. Life Cycle Assessment

As listed in Table 4, different life cycle thinking approaches were investigated. Generally, different methodologies and databases are available to assess life cycle impacts. According to

Table 9. LCA’s software, databases, and methodologies in the selected studies.

LCA Software	Database	Methodology	Ref
SimaPro v8.3.0.0		ReCiPe endpoint, input–output LCA	[32]
Open LCA v1.9	Ecoinvent	CML v4.4 2015	[31]
An implemented open source LCA software	Ecoinvent 3.6		[43]
	Agribalyse v1.3, World Food Database v3.5.1		[100]
	Ecoinvent 3.4		[89]
Open LCA	Ecoinvent 3.4	ReCiPe Midpoint	[86]
	Ecoinvent 3.6	ILCD 2.0 Midpoint	[93]
	Ecoinvent and CLCD-Q	IPCC	[102]
	Ecoinvent 3.4	ILCD 2.0	[57]
SimaPro v8.5	US LCI database, Ecoinvent 3.4	IMPACT 2002+, BEES+, CML 2, EDP, GHG protocol, and IPCC100	[88]
	Ecoinvent		[34]
OpenLCA v1.10	Ecoinvent and Bedec		[103]
WRATE v4	WRATE v4	CML 2001	[78]
TRACI v2.1, Microsoft Excel	GaBi database		[35]
		IMPACT 2002+ midpoint, endpoint, and single as the baseline-score impact, CML 2001, GWP 100a, TRACI 2, EPD 2007, BEES	[129]
OpenLCA	Ecoinvent		[104]
OpenLCA v1.10	Ecoinvent 3.5	CML 2016 H midpoint method	[97]
		CML 2016, ReCiPe 2016	[92]
	Ecoinvent 3.1		[70]
			[36]
Gabi v8.0	Ecoinvent 3.4	ILCD v1.09	[105]
SimaPro v8.5		ILCD 2011 midpoint	[77]
SimaPro v9.0	Ecoinvent 3.5	ReCiPe 2016 midpoint/endpoint	[69]
AECO Software	Ecoinvent 3.6	ReCiPe 2008	[85]
	Ecoinvent	CML, ReCiPe endpoint	[30]
			[91]
SimaPro v8.0.3	Ecoinvent 3.0	CML-IA	[38]
BioSTEAM-LCA	Ecoinvent, USDA-Ag data, Forwast, and GREET Model	Integrating CML 2001, CED, CExD, EDP, EDIP, EDIP 2003, EPS 2000, IPCC 2001, 2007, and 2013, Impact 2002+, ReCiPe (2008, midpoint, and endpoint approaches), USEtox, and TRACI 2.0	[95]
	DATASMART (US LCI v1.60 and Ecoinvent 2.2)	TRACI 2	[45]
SimaPro PhD version	Ecoinvent 3.0	CML-IA 2001 and ReCipE (H) Midpoint	[84]
SimaPro and GaBi	SimaPro, Ecoinvent and GaBi databases	LCIA–CML 2001 and ILCD 50	[76]
	Ecoinvent		[48]
	DUREE database, KBOB database		[94]
SimaPro v8.4	PR e Consultants and Ecoinvent	IPCC 2013 GWP 100a	[68]
	Ecoinvent		[106]
	Ecoinvent		[98]
		TRACI 2.0	[37]
	GreenConcrete LCA Tool	TRACI Midpoint	[90]
SimaPro	Ecoinvent 3.2	ReCiPe 2016	[107]
Athena IE4B	Athena IE4B	TRACI 2.1	[75]
		IMPACT 2002+	[47]
OpenLCA v1.6.3	Ecoinvent 3.3		[83]
Umberto v5.6	Ecoinvent (Ei) 2.2	ReCiPe 2012	[74]
Excel-based LCA model			[46]
	KBOB database, DUREE		[82]
SimaPro v8.5	SimaPro v8.5	TRACI	[73]
GaBi v6	Ecoinvent 2.2	TRACI	[67]
Brightway v2	Ecoinvent 3.3	IMPACT World+:	[96]
SimaPro v8.0	Ecoinvent	ReCipe 2008, Ecoindicator 99, and IMPACT +2002	[66]
	Ecoinvent	EDIP, Ecoindicator 99, EPS, IMPACT +2002	[65]
	Ecoinvent 3.0	Ecoindicator 99 and the IPCC 2003 GWP	[71]
SimaPro v7.3	Ecoinvent 3.2	CML 2001 v.2.05	[111]
	Ecoinvent, U.S. Life Cycle Inventory Database, and other references		[29]
SimaPro v8.4	Ecoinvent 3.4 and Agri-footprint 4.0	CML-baseline	[112]
SimaPro v7.3	Ecoinvent 3.2	Cumulative Energy Demand (CED) and CML 2001 v.2.05	[87]
	Ecoinvent		[109]
	Ecoinvent 3.3	CML	[39]
	Ecoinvent 3.1, CEDA 5 input-output LCA database	Global Warming Potential 100	[40]
	GREET2	IPCC 2006	[63]
	NREL U.S. LCI		[114]
	Ecoinvent 2.2 and 3.3	ReCiPe Midpoint	[115]
SimaPro v8.2	Ecoinvent 3	TRACI 2.0	[116]
		ReCiPe2016	[101]
FineChem		TCLP	[42]
UMBERTO	Ecoinvent	CML 2001	[117]
		CML 2001,EDIP	[79]
eFootprint	Chinese Life Cycle Database		[62]

, only 36 studies described the 14 pieces of software they used. By far, SimaPro^® was the most frequently used LCA software in 15 studies. SimaPro^® was followed by OpenLCA by six; Gabi^® by three; and Umberto^® by two studies. The remaining ten software/tools were contributed by one study. Several other widely used applications, such as OneClickLCA^®, Mobius^®, and Ecochain^®, were not used in addition to those listed in Table 9. The environmental calculations performed by all LCA software are based on a database. There are many databases available and they are continually updating their databases. As seen in Table 9, Ecoinvent^® was the dominating database among the 21 databases used in the selected studies. Ecoinvent’s greatest strength is its completeness and transparency. Using data from Ecoinvent, the LCA practitioner can be confident that all relevant aspects of the supply chain have been considered.

In LCIA, a number of methods are employed to translate emissions and resource extractions into a limited number of environmental impact scores using so-called characterization factors. Characterization factors can be derived in two ways: at the midpoint and endpoint, giving different levels of detail. Climate change or acidification are midpoint indicators focusing on specific environmental problems. In comparison, endpoint indicators assess the environmental impact at three higher aggregation levels: human health, biodiversity, and resource scarcity. As seen in Table 9, researchers utilized different methodologies to conduct LCA studies and were particularly interested in using ReCiPe, CML, IMPACT 2002+, and TRACI.

Although Monte Carlo simulation is now a much-used scientific tool for problems, it also has disadvantages: it may require colossal processing and computing resources; it does not give exact solutions; outcomes are only as good as the model and inputs utilized; and it needs programming or software to be applied. As a knowledge gap and in a mathematical sense, fuzzy set theory is an essential approach that avoids expensive and time-consuming simulations, such as Monte Carlo or global sensitivity analysis. Finding the sources of uncertainty, establishing suitable fuzzy values, and performing sensitivity analysis are the most crucial processes for developing a viable model utilizing fuzzy set theory to describe uncertainty.

5. Conclusions and Perspectives

To model and calculate the environmental impacts of products and processes, life cycle assessment (LCA) is widely used today. Although assessing and communicating uncertainty is well-recognized in scientific research, studies on uncertainty in LCAs are still infrequent compared to published studies on LCAs. By conducting a scoping review, the current study aims to determine and assess the frequency with which LCA studies reflect uncertainty in order to reveal the challenges and opportunities involved in developing a robust model. In total, 93 studies from 2019–August 2022 were comprehensively reviewed. The results indicate that the most significant sources of uncertainty reported in the studies were uncertainty in the parameters of the models and processes, data variability, and uncertainties resulting from the use of different methodologies and databases. These uncertainties were mostly modeled by normal, lognormal, triangular, and uniform distributions. In order to quantify the uncertainty of the system, the Monte Carlo methodology (probabilistic approach), either alone or in combination with other methods, was the predominant method. The majority of the studies, however, relied heavily on sensitivity analyses. SimaPro^® and Ecoinvent^® were the most commonly used LCA software and database, respectively. In the LCA studies, researchers used a variety of methodologies and were particularly interested in using ReCiPe, CML, IMPACT 2002+, and TRACI, and both midpoints and endpoints approaches were used. Despite being the dominant method in uncertainty analysis in LCA studies, Monte Carlo simulation has some disadvantages. This process is time- and hardware-intensive, particularly when many iterations are involved. Furthermore, it is sensitive to PFDs, and it can be challenging to define a proper PFD for uncertain parameters.

As a result of this review, the following suggestions have been made. A comprehensive uncertainty analysis should be included in all published LCA studies. With the advent of new industrial challenges, a greater focus should be placed on uncertainty in all industries, specifically emerging industries such as IT data centers and electric vehicle batteries. In addition, it is recommended to use probabilistic approaches rather than probabilistic ones, specifically fuzzy set theory, to avoid costly simulations.