Abstract
New curriculum reform across the United States requires teacher educators to rapidly develop and implement professional development (PD) for K-12 teachers, newly assigned to teach computer science (CS). One of the many inherent challenges in providing valuable PD is knowing what it is that novice CS teachers most need. This quantitative research study was designed to inform the iterative development of a K-12 CS Teaching Endorsement program offered at a small college in the rural Rocky Mountain west, based on participants’ perceptions of the program, before and after attempting to teach the CS curriculum provided by the endorsement program. The overarching research question guiding this study is: What differences might exist between teachers’ perceived needs for CS-based professional development before and after actual classroom teaching experiences with CS? To pursue this question, the following null hypothesis was tested: H0: No measurable change exists in teachers’ perceptions regarding the impact of PD before and after teaching. The research study used a 29-item Likert-style survey, organized into categories to measure participants’ perceptions across five subscales. Thirteen teachers completed the targeted K-12 CS Endorsement program in May and July 2021, seven of whom subsequently taught CS in K-12 schools for the first time. Of these seven, 100% participated in this research study. After gaining classroom experience, the survey results showed very few differences before and after the endorsement program. These results suggest that CS-based PD can be more effective if the PD better targets enhancing teachers’ confidence in teaching actual students and providing more useful classroom-ready instructional materials rather than targeting improving teachers’ knowledge of CS concepts.
1. Introduction
As the digital information age defining this century rapidly unfolds, so do the immediate professional development (PD) needs of K-12 teachers. Nowhere, perhaps, is this more disruptive than in the rapidly emerging domain of computer science (CS) instruction [1]. Many states across the United States are struggling with how to best respond to education reform calls for increasing the quantity and quality of CS education, spanning the entire K-12 grade bands [2]. Wyoming, like many other states, is initiating CS teaching deliverables across its school districts. These changes are being influenced through multi-year, multi-agency, state-government-backed initiatives that are still being constructed, even as CS is made available to public-school students across the state [3]. A vital component of this Wyoming initiative is preparing the state’s K-12 schoolteachers to implement CS concepts in their classrooms.
Few existing in-service teachers were ever formally trained on how to teach CS during their undergraduate teacher preparation programs. In response, some states have relied on professional computer scientists as content experts to lead CS instruction in schools [4]. In contrast, Wyoming certified teachers across all disciplines of content are charged with this task. Such a scenario leaves wide open the question of how to best support teachers in teaching CS concepts for which they have little to no experience in teaching. Naturally, one way for teachers to prepare for this challenge is by completing a K-12 CS endorsement program as a PD experience at an institution of higher education. In Wyoming, in cooperation with the state government’s Professional Teaching Standards Board (PTSB), several institutions of higher education have created endorsement programs designed to fulfill the new requirements for teachers to become a certified Wyoming K-12 teacher by earning a K-12 CS endorsement. Such an approach to creating highly qualified teachers allows teachers the opportunity to teach K-12 CS immediately [5].
Northwest College (NWC), a two-year college located in the rural Rocky Mountain west, offers one such CS endorsement program. NWC’s program consists of 15 semester credits offered over the course of three to four semesters and is delivered using a cohort model [6]. The first NWC K-12 CS Endorsement program began in June 2020, with 13 certified teachers graduating in May and July of 2021. Of these 13 teachers, 7 went on to teach CS in K-12 schools the Fall of 2021; all 7 of these were surveyed for this research study.
Given how new these educational reforms are, there exists an open question as to how to best prepare teachers to teach CS. In particular, it is unclear from the existing literature base precisely what it is that new CS teachers most need. It is to this end that this research study was designed. Because CS education is not yet a fixture in Wyoming, the experiences of the teachers who have completed the endorsement program and subsequently taught CS informs the NWC faculty development team as they continue to iteratively modify the curriculum and structure of the K-12 CS endorsement program to better serve the immediate needs of Wyoming’s new cadre of K-12 teachers assigned to teach CS.
1.1. Purpose of the Study
The purpose of this study was to examine the relationship between in-service teachers’ perceptions of the NWC K-12 CS endorsement program at two points in time: before and after actual K-12 classroom experience teaching CS. The study design is most easily envisioned as two surveys, pre and post. Survey 1: Pre-Classroom Implementation was completed between July and August, 2021, after the participants had completed the K-12 CS endorsement program. Survey 2: Post-Classroom Implementation was completed between December 2021 and January 2022 after the participants had taught CS for one semester. The purpose of the research study was to identify areas where teachers’ perceptions of the endorsement program were less favorable after they used the material to teach CS, as measured across five subscales, described below.
1.2. Research Question
To inform the CS PD design team about which aspects of the endorsement program merit further examination in order to improve the program, the following research question was posed: What differences might exist between teachers’ perceived needs for CS-based PD before and after actual classroom teaching experiences with CS? To answer this question, the following null hypothesis was tested for each of five subscales:
H0: No measurable change exists in teachers’ perceptions regarding the impact of the PD before and after teaching.
2. Review of Related Literature
The scholarly domain of how best to train teachers to teach covers a literature landscape spanning more than 100 years. In recent decades, authors, such as Shulman [7] and those who echo his ideas eloquently, have argued that each discipline’s conceptual domain is sufficiently different, that each one needs to be systematically studied on its own. In this sense, developing a scholarly understanding of what new CS teachers perceive they need in order to be high-quality CS teachers would naturally seem to be an important scholarly endeavor. CS education scholars agree. Burrows [8] and Hewson [9] found that a connection needs to be established between PD and learning outcomes. These authors’ review of the literature identified a clear need to study the evolution and implementation of K-12 CS education in a systematic manner.
This research study focuses on one aspect of the gap identified by Burrows [8] and Hewson [9]: comparing teachers’ perception of how well the endorsement program prepared them to teach K-12 CS, before and after they actually taught. In this literature review, the reader’s attention is directed to this gap and, finally, this research study is contextualized within the current body of literature.
2.1. K-12 Teachers’ Perceptions and Experiences in Teaching Computer Science
The literature review for this topic builds on a process presented extensively elsewhere in “Identifying implementation challenges for a new computer science curriculum in rural western regions of the United States” [10]. However, in this research study, the authors have a different focus on K-12 teachers’ perceptions and experiences. Because implementation of universal K-12 CS education in Wyoming begins in the Fall of 2022, the PD curriculum is evolving over time and is informed by the participants in this study. The researchers delved into this topic, believing that the expectations and experiences of the first classroom teachers to earn CS endorsements should become an integral part of the CS outcomes and can help construct the practices that Wyoming will ultimately use to shape K-12 CS education in the future. Yadav et al. [11] discussed the current trend of educating non-computer scientists to teach CS and focused on these teachers’ perspectives as they deliver the CS curriculum. Their findings are important to this research study because Wyoming has accepted a similar model of training STEM and non-STEM teachers alike to implement CS education. Yadav and colleagues [11] cite the teachers’ lack of adequate CS training and the isolation they feel from often working alone as challenges. In Wyoming, allowing teachers to work in cohorts may help them develop a community of other non-STEM CS teachers to mitigate this challenge.
The Wyoming Department of Education [12] has adopted seven performance standards for CS. These standards are broader than coding and computational thinking (CT) alone [13]. The literature on CS and CT in K-12 classrooms addresses this breadth and also the teachers’ role in K-12 CS education. Astrachan and Briggs [14] discussed the importance of the creative and intellectual aspects of CS, while ChanLin [15], Borowczak and Burrows [13], and Lee and colleagues [16] focused on teachers’ perceptions of the importance of integrating CS into their classrooms. Goode [17] studied the role of teachers in teaching CS. She explored the applicability of PD models and asserted that curriculum alone is not enough: teachers require well-constructed PD and support to teach CS effectively. In this way, she separated and related the knowledge of CS from the practice of teaching CT. In follow-up research, Goode, Margolis, and Chapman [18] set up the connection between educational research related to PD for CS and CT teachers, describing the Exploring Computer Science PD model. The state’s Department of Education (WDE) CS Standards [19] reflect a similar breadth, not limited to CT and CS, but teaching collaboration and inclusivity as well. Collaboration and inclusivity were initially addressed by using a cohort model for the NWC K-12 CS endorsement program, by forming learning communities within cohort participants.
Researchers in different areas of the United States have studied different PD models and programming environments in relation to their effectiveness in preparing in-service teachers to deliver K-12 CS education. Gray and colleagues [20] described statewide PD models for teacher preparation for CS teaching in Alabama. The project, entitled CS4Alabama, is a year-long PD using a teacher leader model of mentoring new CS teachers. Continuing along this line of research, Lee’s team [16] made connections between established STEM subject areas and CS integration, describing a model for in-service teacher PD that is valuable for integrating CS by making connections between STEM fields and other areas of study. Similarly, Borowczak and Burrows [13] studied NetLogo as a platform for teacher PD for integrating CS into the curriculum. The results revealed that classroom applications were limited to topics addressed in the PD. Connecting this research to teachers’ perceptions before and after teaching may illuminate some ideas for broadening classroom applications.
In summary, the goal of the endorsement program this study is targeting is two-fold. First, the program should prepare teachers for classroom experiences. Second, the PD experience will be improved by using teachers’ feedback. This approach should bridge the distance between pre-teaching and post-teaching experiences as part of the distance to the connection between PD and learning outcomes.
2.2. Contextualization of Research
2.2.1. How Is Quality PD Created?
“A bridge, like professional development, is a critical link between where one is, and where one wants to be” [21] (p. 2). In the matter of Wyoming’s K-12 CS initiative, the bridge is the distance between content and performance standards [19] and learning outcomes. The specific span of the bridge addressed in this research study is the link between completing the PD and teaching CS.
The researchers studied the literature as a foundation for developing NWC’s K-12 CS endorsement program. This PD was designed based upon Content and Performance Standards, enumerated by Wyoming Department of Education [19], which, in turn, was written using the overarching goals set forth by the Wyoming legislature [22]. Specifically, in 2020, a committee was empaneled by the WDE and, in 2021, published a report identifying seven CS practices; the NWC K-12 CS endorsement program was based on these practices. These practices are enumerated by the Wyoming Department of Education [19]. Through this process, the design of NWC’s K-12 CS endorsement program is connected to Wyoming’s newly developed K-12 CS standards. Additionally, the expectations and the design of the PD are consistent with the seven principles of excellent professional development identified and enumerated by Loucks-Horsley [21]. A main focus of this research is to create effective, consistently deliverable PD to provide Wyoming K-12 teachers with experiences that will facilitate the delivery of K-12 CS education in all Wyoming schools, as described below.
A major structural element of effective PD is instructional scaffolding. Instructional scaffolding is a structured approach to education, in which support is provided to help students master foundational tasks based on student experiences and knowledge. Belland [23] lists four key features of instructional scaffolding: first, temporary support is provided as students are engaging with problems. Second, scaffolding needs to lead to skill gain, such that students can function independently in the future; third, scaffolding builds on what students already know; and fourth, students meaningfully participate in a target task to gain understanding of what success at the task means. As described by Kleickmann et al. [24], instructional scaffolding addresses the fact that higher-level skills (here, CS, CT and coding) are impossible to teach without first teaching the basics (here, filing systems, shortcut keys, and other elements specific to different platforms). Each step requires instructional scaffolding in order to prepare participants for the next element of the PD, which is consistent with Belland’s [23] and Kleickmann et al.’s [24] findings. These authors address the need to create an instructional scaffold to systematically build on foundational skills in order to facilitate learning new skills with no knowledge gaps.
The seminal work on professional development for K-12 teachers, “Designing Professional Development for Teachers of Science and Mathematics”, by Susan Loucks-Horsley and colleagues [25], has served as a foundational work for designing PD since the first edition was published over two decades ago (1999). The late Loucks-Horsley highlighted seven principles common to effective PD experiences for STEM teachers, revolving around clarity related to teaching, broadening opportunities for teachers, mirroring/modeling instructional methods for the teachers to use with their students, encouraging teachers to form learning communities with other STEM teachers, developing leadership among teachers, teaching or linking across the curriculum, and continually assessing the professional development process [25].
To be sure, high-quality PD is best based on a foundation of structure and content. Based on the academic literature, Burrows and colleagues [26] cite six best practices for developing successful PD. These practices are enumerated in Table 1.

Table 1.
Best practices for developing successful PD.
Darling-Hammond and colleagues [37] state that many PD experiences are ineffective in supporting changes when connected to teacher practices and student learning. To identify the features of effective professional development, they reviewed 35 research studies to identify the features of effective PD. From this review, they identified that most effective PDs share seven features. They are content focused, incorporate active learning, support collaboration, use models and modeling of effective practice, provide coaching and expert support, offer opportunities for feedback and reflection, and are of sustained duration.
Foundational misconceptions can create barriers to successful PD. One such misconception surrounding the term model was uncovered by Reynolds, Burrows, and Borowczak [38]. In 2018, these authors conducted a two-week-long STEM PD for in-service teachers. One goal of the PD was to help participants use computer science modeling in their classrooms. Although instruction on modeling was presented throughout the PD, follow-up discourse among participants revealed that they did not move past their prior conception of the term model. When participants heard this term, their attention was directed to their previous understanding of model and away from the meaning of model as a CS concept. Because of this fundamental misunderstanding, the CS modeling that was taught had no schema to attach to in the participants’ views, which led to the disconnect. This unexpected misconception highlights how important fundamental concepts can be and how future learning can be impeded by a lack of foundational understanding by participants in a PD.
2.2.2. Literature Gap
In Wyoming the State’s Department of Education outlines scripted content and performance standards for guidance and direction to school districts; in turn, the districts are charged with the responsibility for implementing education for all students with fidelity. Student learning is assessed by measuring learning outcomes, with certified teachers serving as the conduit between standards, curriculum implementation, and student learning outcomes. In this way, PD can be imagined to be serving as one span of the bridge between standards and learning outcomes.
Because Wyoming’s education initiative is still being implemented, it is crucial that the effectiveness of the K-12 CS endorsement program is continually evaluated to achieve maximum efficiency. By relating teachers’ perceptions before and after they use this material to teach, faculty development teams should be able to deliver more effective curricula based upon input received at critical junctions between PD and learning outcomes.
The lack of connection between PD and learning outcomes has been identified as a gap in the literature. As articulated by Hewson [9] and reaffirmed by Burrows [8]: “Although PD among STEM teachers has been studied and connected to national standards, a gap exists in studying PD in a systematic manner, especially in regard to the connection between PD and learning outcomes”. By collecting teachers’ perceptions of the effectiveness of the endorsement program before teaching and comparing the results to their perceptions after they used the material to teach, researchers can better focus on this critical junction. This focus contributes to understanding this span of the gap in the literature.
3. Materials and Methods
In this section the researchers describe the participants, then provides an explanation of the type of data collected for analysis and the current state of research in analyzing data in a valid manner. The types of statistical tests performed are then explained in this context.
3.1. Participants
The participants in this study were purposefully selected from the members of the first cohort of NWC’s K-12 Computer Science Endorsement program. The seven participants were selected because they earned their K-12 CS endorsements then taught CS in Wyoming K-12 schools. Because they had completed the PD then subsequently taught the material, they met the specific criteria of understanding the PD at two points in time, before and after classroom implementation. Although 13 professional educators completed the program and earned a state-level endorsement to teach K-12 CS in Wyoming in May and July 2021, only 7 of these 13 taught CS after earning their endorsements. All seven of these cohort members participated in this research study. Of the remaining six cohort members, three are no longer employed as educators and three are educators who are not teaching computer science, and because the remaining six did not meet the specific criteria, they were not chosen for this study.
The participant ages range from 31 years to 60 years. Of the seven participants, three are female and four are male. Two of the participants teach elementary school, two teach middle school, and three teach high school. All participants live in rural Wyoming and work in the Wyoming K-12 education system as full-time, in-service teachers. The participants were certified in a diversity of disciplines including: science, social science, business, career and technical education/vocational education, library/digital studies, and computer science. They are also part of extracurricular activities in that some coach and sponsor sports and activities, including track, basketball, football, and Girls Who Code. All seven participants earned a bachelor’s degree, while four have also attained master’s degrees in education. None of the participants has a degree in engineering or computer science.
3.2. Survey Instrument
A quantitative research design was used to examine the differences in teachers’ perceptions of the quality of the endorsement program before and after teaching computer science. The survey instrument used comprised 29 Likert-type items, arranged into 5 subscales. All measures were based on a traditional, forced-choice, five-point Likert rating scale, ranging from 1—strongly disagree to 5—strongly agree.
The survey instrument was constructed from three existing instruments: Burrows [8], code.org, [39], and the Friday Institute, [40]. Established survey instruments were chosen as the basis of the combined survey instrument to support reliability and validity. Slight modifications were made to equate rating scales and to increase specificity for NWC’s K-12 CS endorsement program. Otherwise, the instruments were unchanged. These three existing survey instruments, as well as the composite instrument used in this research study, are provided in Appendix A.
3.3. Quantitative Analysis Using Likert Data
Quantitative research methods allow for the systematic study of data in a consistent and replicable manner [41]. This quantitative research study employed a survey instrument administered two times to the same participants, then compared the responses using dependent t-tests. The survey instrument comprised 29 Likert-type items, organized into five subscales. Boone and Boone [42] addressed the difference between Likert-type items and Likert scales. Likert-type items are ordinal data, meaning that the difference between choices on the scale does not have an equal or even quantifiable difference, only that each is greater than or less than the one before. However, when Likert-type items are combined into scales, the scales become interval data ([42,43]).
A Likert scale is a “structured and reasoned whole” that, if anchored properly from “strongly disagree” to “strongly agree”, can be treated as interval or ratio data. The relationship of Likert-type items to Likert scales corresponds to the relationship of atom to molecule, in that the second is made of the first, yet takes on characteristics greater than the sum of the parts [44] (p. 109).
Individual Likert-type items are not suitable for data analysis using inferential statistics; they must be combined into Likert scales to represent a construct or perception before quantitative research methods can be employed. Likert scales are interval data that represent a construct, or idea, which can then be analyzed using quantitative methods. Data analysis procedures including t-tests and regression procedures are appropriate for interval data whereas only descriptive statistics are recommended for ordinal data [42]. General agreement exists that a Likert scale must consist of four or more Likert-type items ([42,44,45]).
The literature search validates the use of Likert data for analysis using quantitative research methods ([42,43]). Likert-type items must first be organized into Likert scales that represent a construct. Each scale should consist of four or more Likert-type items ([42,44,45]). For this study, 29 Likert items were organized into five Likert scales. Variables for each scale were created using SPSS. Each of these five scales was tested for reliability, data distribution, statistical significance, and effect size. These scales and their corresponding variable names are described in Table 2 below. Further, also listed are descriptive statistics for each Likert scale before and after classroom implementation (Survey 1 and Survey 2).

Table 2.
Description of scales and correlation to variables with descriptive statistics (Survey 1: Pre-Classroom Implementation and Survey 2: Post-Classroom Implementation).
3.4. Validity and Reliability
Validity refers to the appropriateness of conclusions drawn from a research study [46] and reliability refers to the consistency of results produced by a survey instrument [41]. The manner in which validity and reliability are established in this research study is discussed below.
3.4.1. External Validity
The survey instrument was constructed from three established survey instruments. The instruments were chosen to support validity. Slight modifications were made to equate the rating scales and to increase specificity toward NWC’s K-12 CS endorsement program. The participants in this pilot study represent a small number; power analysis estimates the sample size required for the survey to reach a power level of 80%. When a power level of 80% is attained through additional data collection, the results will have a sufficient statistical power to merit generalization. Table 4 addresses statistical power for this pilot study and the necessary sample size required for a power level of 80%.
To further support the validity of the survey instrument, the researchers conducted a concurrent validity study. Three of the participants were contacted by telephone and asked to complete the survey again verbally as a “talk aloud.” The participants were purposefully selected to represent each grade band (elementary, middle school, and high school). This extra precautionary step bolsters the validity of the survey instrument. In this “talk aloud”, participants clarified their perceptions of the survey instrument, specifically addressing the anchoring of the items between “strongly disagree” and “strongly agree”, as well as the perception that choices on the scale are evenly distributed. The participants confirmed these assumptions, thus, reinforcing the validity of the instrument. The validity study lends weight to the notion that the participants’ scores on the survey can be interpreted the same way as was intended by the researchers.
3.4.2. Construct Validity: How Well the Research Study Targets the Correct Questions
The Likert-type items on each established survey used were carefully considered by the researchers. Questions were modified slightly to address specific questions regarding NWC’s K-12 CS endorsement program. Aside from these modifications, the essential construction of each survey instrument remained unchanged.
3.4.3. Statistical Validity: Appropriateness of Statistical Tests Used for Analysis
Dependent t-tests compare the means of dependent samples. Here, Survey 1 and Survey 2 were conducted with the same participants, then matched for their pre-classroom implementation and post-classroom implementation responses.
3.4.4. Inter-Item Reliability: A Measure of Internal Consistency
Likert-type items that measure the same construct should be positively correlated. One method to measure internal consistency is calculating Cronbach’s alpha for a scale [41]. Cronbach’s alpha is an estimate of internal consistency that can be derived from the scores of a Likert scale or variable [45]. Reliability is associated with a Cronbach’s alpha value of 0.70 or greater [47]. Each of the five scales used in this study had a Cronbach’s alpha of 0.7 or greater, for both Survey 1 and Survey 2 results. See Table 3 for individual values of Cronbach’s alpha.

Table 3.
Cronbach’s alpha for each Likert scale, Survey 1: Pre-classroom implementation and Survey 2: Post-classroom implementation.
3.5. Procedure
The authors created the survey instrument using Survey Monkey (http://www.surveymonkey.com, accessed on 5 October 2022). The research study received IRB approval and a link to the survey instrument was distributed to all CS endorsement program participants through email. The survey instrument was then self-administered by the participants. All participants signed informed consent before taking the survey. The survey instrument was distributed at two points in time: first, after the PD was completed but before the participants taught computer science (Survey 1: Pre-classroom Implementation) and second, after the participants had taught computer science for one semester (Survey 2: Post-Classroom Implementation). All seven participants returned Survey 1 and Survey 2. The average time required to complete the survey was approximately fourteen minutes.
4. Results
This research study compares teachers’ perceptions of the effectiveness of NWC’s K-12 CS endorsement program, before and after classroom implementation. A research question guided the inquiry: What differences might exist between teachers’ perceived needs for CS-based professional development, before and after actual classroom teaching experiences with CS? To answer this question, the following null hypothesis was tested: H0: No measurable change exists in teachers’ perceptions regarding the impact of the PD before and after teaching.
H0 was tested on the five separate Likert subscales. Based on the results of statistical testing, H0 was rejected for only one subscale: perception of PD relationship to teaching CS (Identified by scale/variable name S1a). This result was statistically significant on a one-tailed test and indicates that a Type I error has less than a 5% chance of occurrence. Testing on the other four Likert scales failed to reject or accepted H0.
On average, participants had a lower perception after teaching CS of the relationship on Survey 2: Post-classroom implementation between the endorsement program’s relationship to teaching CS (M = 4.086, SD = 0.7105) than they did on Survey 1: Pre-classroom implementation (M = 4.343, SD = 0.5623). This difference, 0.257, BCa 95% CI (−1.605, 0.042), was significant t(6) = −2.274, p = 0.032, and represented a small- to medium-sized effect, d = 0.3197. BCa 95% CI refers to the range of the 95% bootstrap confidence interval [47].
Finding or not finding a real, meaningful difference between Survey 1: (Pre-Classroom Implementation) and Survey 2: (Post-Classroom Implementation) informs the researchers when deciding whether or not to reject the null hypothesis. Here, the overall finding is that teachers expected to be more prepared to teach CS before they actually implemented CS in their classrooms. This analysis is based on the results of several statistical tests, centered on analyzing the Likert data and finding meaningful conclusions. A summary of the decisions made is presented here.
4.1. Parametric and Non-Parametric Tests
Parametric tests are extremely robust in terms of analysis of interval data. Monte Carlo studies conducted by Glass [48] showed no resulting bias when ANOVA was used with Likert scale data and Field [47] (p. 168) explains that the “assumption of normality” is often incorrectly interpreted to mean that data must be normally distributed to use parametric testing methods. In practice, parametric tests can be used effectively for many types of non-normally distributed data. This conclusion seems to be inharmonious with underlying mathematical theory; however, many studies in the social sciences have very few scores that deviate greatly from the central score and this simplifies the application of statistical theory, depending on the assumption of normal data distribution [48]. Therefore, parametric data analysis methods have a wide range of applicability, including Likert scale data [44].
It is sometimes assumed that data must be normally distributed to be analyzed using parametric tests. A review of the literature on this topic ([44,48]) indicates that parametric tests are often robust enough to use with non-normal data.
Dependent t-tests were used to understand the differences in the mean of teachers’ perceptions before and after classroom implementation [47]. Dependent t-tests were conducted on data from Survey 1 and Survey 2 to determine if perceptions had changed based on classroom implementation. If a non-parametric test was determined to be appropriate, Wilcoxon’s sign test was used.
4.2. Type I Error: Significance Level
A type I error is a “false-positive” error, referring to the probability of rejection of a true null hypothesis. This occurs when a research study compares two populations that are NOT different yet incorrectly finds them to be different or when researchers “see a difference where none exits” [49].
This research study uses a 95% confidence level (p < 0.05) in determining if a type I error has occurred. Significance level is the confidence in the answer. Using a significance level cutoff of 0.05 means there is a 5% chance that our results are not significant, indicating a Type I or false-positive error. In other words, significance level tells us whether Survey 1 and Survey 2 are 95% likely to be truly different from each other. Since the purpose of the research study is to identify negative perceptions that would lead to curricular changes, the researchers used one-tailed tests.
4.3. Type II Error: Statistical Power
A type II error is a “false-negative” error, referring to a failure to reject a false null hypothesis. This is referred to as beta. To find beta, the researchers first calculate statistical power, which indicates the probability of detecting an error that is actually present. The generally accepted power value is 0.8, meaning there is a 20% probability of making a type II error [47].
Field [47] (p. 70) suggests using power (1-beta) of 0.8 and a significance (alpha) of less than 0.05. This means the researchers have 80% confidence that the test will find a significant difference (type II error).
4.4. Effect Size
Does a difference between populations exist? Significance level does not tell the whole story [41] (p. 26). Effect size, measured by Cohen’s d (with Hedge’s correction), provides the researcher an indication of whether the difference between populations is important. Effect size, as measured by Cohen’s d (with Hedge’s correction), is an indication of whether the difference matters. Typically, a medium effect size is considered to correspond to |d| > 0.5 [50].
4.5. Number of Participants and Power Analysis
Due to the small number of participants, power analysis suggests a larger sample is needed. In this pilot study, every available participant is represented in the data. Each participant was purposefully selected based upon the special criteria of teaching CS after completing the endorsement program and these participants constitute the full distribution as it was known. For this reason, it is the authors’ judgement that the results are valid. However, as each new cohort completes the endorsement program, surveys will be distributed to them, pre-classroom implementation and post-classroom implementation, and the data collected will be continually aggregated and analyzed.
Table 4 summarizes these factors to determine whether the differences found on each Likert scale represent a meaningful difference in terms of Type I error (probability value), Type II error (statistical power), whether the difference between Survey 1 and Survey 2 is important (effect size), and the sample size needed for statistical power of 80% for each of the five scales.

Table 4.
Summary of statistical test results.
5. Discussion
In this research study, teachers’ perceptions of the effectiveness of NWC’s K-12 CS endorsement program were compared at two points in time: after they had completed the endorsement program (Survey 1: Pre-Classroom Implementation) and after they had taught CS (Survey 2: Post-Classroom Implementation). The survey instrument used comprised 29 Likert-type items, categorized into five subscales to represent constructs. The purpose of this study was to identify areas where teachers had a lower perception of the endorsement program after they taught CS, indicating areas requiring further study for curricular or structural changes, so that the team could create the most effective PD possible.
One Likert scale, described as perception of PD relationship to teaching CS and identified as scale/variable S3a, showed a statistically significant negative change: in other words, the teachers expected to be more prepared to teach CS before they actually implemented CS in their classrooms. This is an indication of an area requiring examination and further study by the faculty development team as they modify the endorsement program for future participants.
In order to focus future research on specific areas needing improvement, the Likert-type items comprising Scale S3a are enumerated below. Four of these items show a decrease from Survey 1 to Survey 2 and the decrease in one of these items (“I am planning to make use of the ideas/content from this PD in my classroom”) is statistically significant, indicating an area of PD where improvement is needed. The perception of PD relationship to teaching CS Likert scale consisted of five Likert items, shown in Table 5:

Table 5.
Likert-type items comprising perception of PD relationship to teaching CS scale.
As detailed in Table 5, participants experienced a statistically significant decrease in their perceptions of their plans to use ideas/content from the endorsement program in their classrooms. This is a specific area of future study for the faculty development team to investigate when making curricular and structural changes to the program. One might assume that what teachers most need is foundational knowledge, but one interpretation of these data is that teachers feel like they need proven classroom-ready activities appropriate for their particular teaching environment, which can vary tremendously among participants.
Limitations
It is important to address concerns about the small number of participants in this quantitative research study. All seven teachers who met the criteria of teaching CS after completing the PD participated and constitute the entire study distribution as it was known. This lends more confidence in the research than if this small number had represented a sample of a larger population; however, the researchers plan continued research with future teachers who complete the endorsement program in order to increase the statistical power of the sample. Moreover, statistical significance is more difficult to achieve with small numbers of participants, lending even further weight to the interpretation of the results. In the end, however, the data acquired from the “talk aloud” confirmation interviews reassure the research team that their interpretations of the Likert-scale data are correct.
This small study motivates the need to conduct a larger study to inform the PD developers to improve the curriculum and structure of the K-12 CS PD. These results serve as a partial connection to bridge the gap identified in the literature between PD and learning outcomes. As a next step, the researchers recommend that detailed interviews be conducted with participants to determine specifically how their plans to use ideas/contents shifted negatively after actually teaching. For future cohorts, the survey instrument will be modified based on needs identified in this study and participants in future studies will continue to provide information to the faculty development team to inform decisions about future changes to NWC’s K-12 CS endorsement program.
Two recommended changes to the survey instrument were identified through the administration of the pilot study. First, the survey lacked a unique identifier to connect participants’ responses in Survey 2 to their original responses in Survey 1. Connecting respondents is necessary for dependent t-test analysis; here, it was accomplished through comparing personal/demographic data. This would likely be unsuccessful and laborious with a large number of participants. Second, the Likert responses from the original survey from the Friday Institute [40] included a “not applicable” response choice. The literature addressing the use of Likert data for quantitative analysis recommends anchoring the response choices between “strongly agree” and “strongly disagree”. The inclusion of a “not applicable” response choice could have resulted in an inconsistent response scale and the need to cull responses. The researchers plan to remove this choice.
6. Conclusions
Overall, the finding of this study is that teachers expected to be more prepared to teach CS before they implemented CS in their classrooms.
The research question, “What differences might exist between teachers’ perceived needs for CS-based professional development before and after actual classroom teaching experiences with CS?” guided this study. To answer this question, the following null hypothesis was tested: H0: No measurable change exists in teachers’ perceptions regarding the impact of the PD before and after teaching.
Based on the results of statistical testing, H0 was rejected for one subscale: perception of PD relationship to teaching CS. This result was statistically significant on a one-tailed test and indicates that a Type I error has less than a 5% chance of occurrence. Testing on the other four Likert scales failed to reject or accept H0.
On average, participants had a lower perception after teaching CS of the relationship on Survey 2: Post-classroom implementation between the endorsement program’s relationship to teaching CS than they did on Survey 1: Pre-classroom implementation. The difference was statistically significant.
Dunning [51] defines “meta-ignorance” as a human tendency to overestimate our understanding of issues exceeding our actual knowledge. The realm of “unknown unknowns” that gives rise to this overestimation is known as the Dunning–Kruger effect and may contribute to the self-overestimation of participants’ preparedness to teach before they actually taught. Simply put, they did not know what they did not know before they taught CS and overestimated their preparedness. Their actual experiences teaching illuminated what they did not learn in the PD.
The data from this first-steps research study strongly suggest that teachers completing the CS endorsement program felt less prepared after classroom implementation of CS than before doing so. This is an area of focus for faculty development teams as they modify the content and structure of endorsement programs for future participants. The first teachers to complete the K-12 CS endorsement program will assuredly be leaders and mentors within their schools and districts, so their experiences are foundational, not only for themselves but for future K-12 CS teachers as well.
The researchers view this work as the initial phase of a longitudinal study. The first cohort comprised only seven teachers who completed the CS endorsement program then subsequently taught CS in Wyoming’s K-12 schools. While these participants constitute the full distribution as it was known, the small number results in a strong possibility of a Type II (“false-negative”) error, resulting in a failure to reject a false null hypothesis [47]. In a Type II error, cases that are statistically significant would be overlooked. For this research study, it means that one or more of the Likert scales would not be identified as having a significant decrease between Survey 1 and Survey 2 and would, therefore, not be studied by the researchers when additional study would in fact be merited.
The results serve as a guide for the faculty development team when deciding where to implement modifications to the endorsement program; however, a larger sample is needed to reach the statistical power sought. Participants from future cohorts will be surveyed to get a sufficiently large sample size.
Two changes to the survey instrument are indicated: first, a unique identifier will be added in order to correlate responses between Survey 1 and Survey 2 and second, the Likert scale will be anchored between “strongly disagree” and “strongly agree” by removing the “not applicable” choice. These changes will be made to the survey instrument, then the study will be resubmitted for IRB approval before administering the survey instrument in August 2022. Participants’ responses from future cohorts will be collected with the updated survey instrument, then aggregated with responses from the pilot study to increase statistical power.
Directions for future research include classroom implementation fidelity studies, in which researchers observe participants’ classrooms. These observations could provide rich data to expand the current understanding of the effectiveness of the PD and to direct researchers toward specific curricular modifications. Another future area of study indicated is discourse analysis among the participants. Open-ended questions and/or guided discussions could be conducted either face to face or remotely and researchers could then study participants’ responses in the social context of discussion among educational professionals. This research is the third study of a three-study research project and examines a critical juncture between PD and learning outcomes. Future research will be required to fully bridge this gap.
Author Contributions
Conceptualization, A.C.B.B., A.K.N.; methodology, A.K.N., T.F.S.; validation, A.C.B.B., T.F.S., A.K.N.; formal analysis, A.K.N., T.F.S.; investigation, A.K.N.; data curation, A.K.N.; writing—original draft preparation, A.K.N.; writing—review and editing, A.C.B.B., T.F.S.; supervision, A.K.N., A.C.B.B., T.F.S.; project administration, A.K.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This research project qualified for exempt review and is approved by the University of Wyoming Institutional Review Board. The Approval code is referenced as Protocol #20210715AN03085 in the letter dated 15 July 2021. The letter further notes that exempt protocols are approved for a maximum of three years.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Survey Instruments
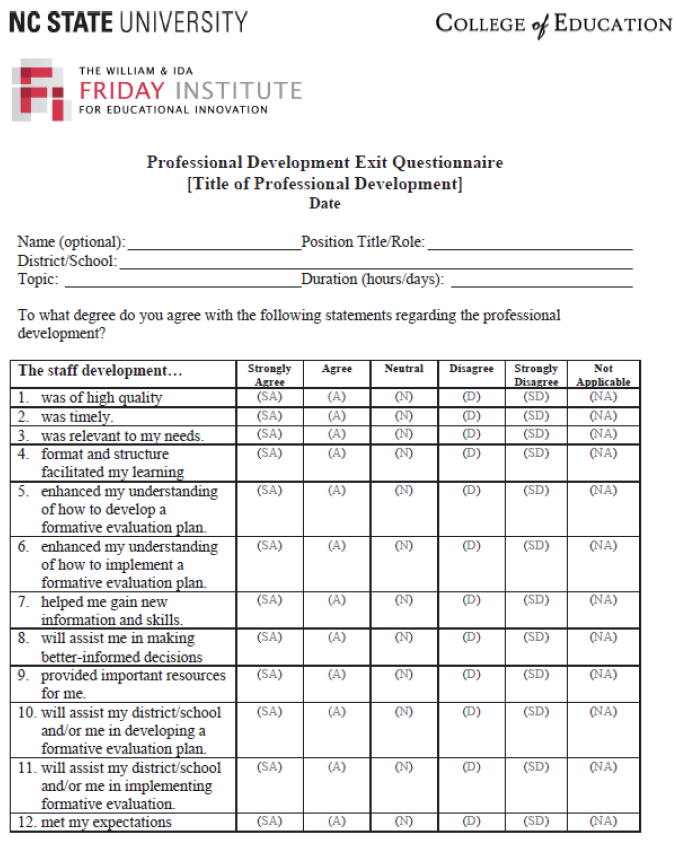 |
| Survey Instrument A2: Burrows, A.C. |
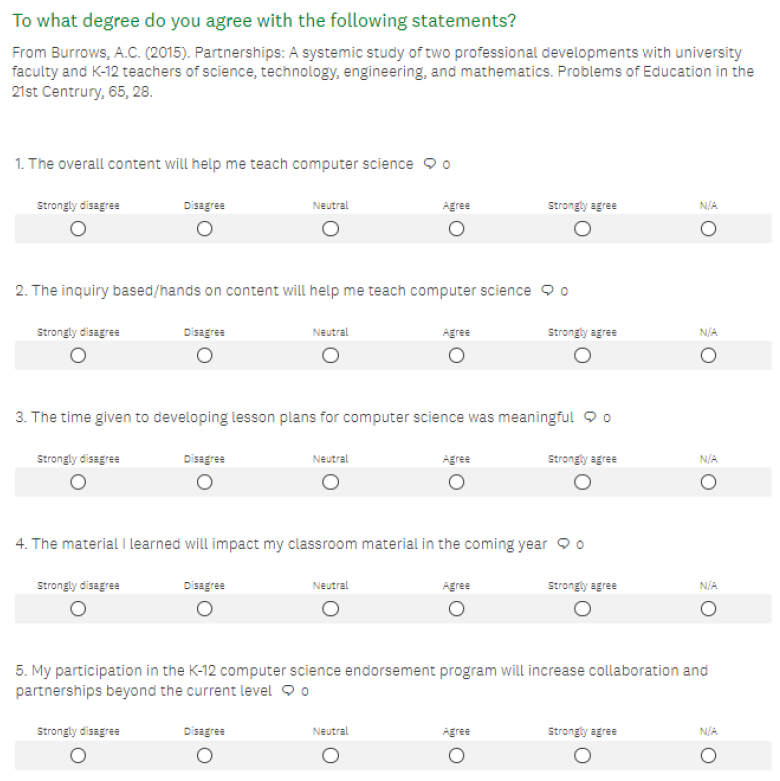 |
| Survey Instrument A3: Code.org |
 |
| Composite Survey Instrument A4: Survey Monkey |
 |
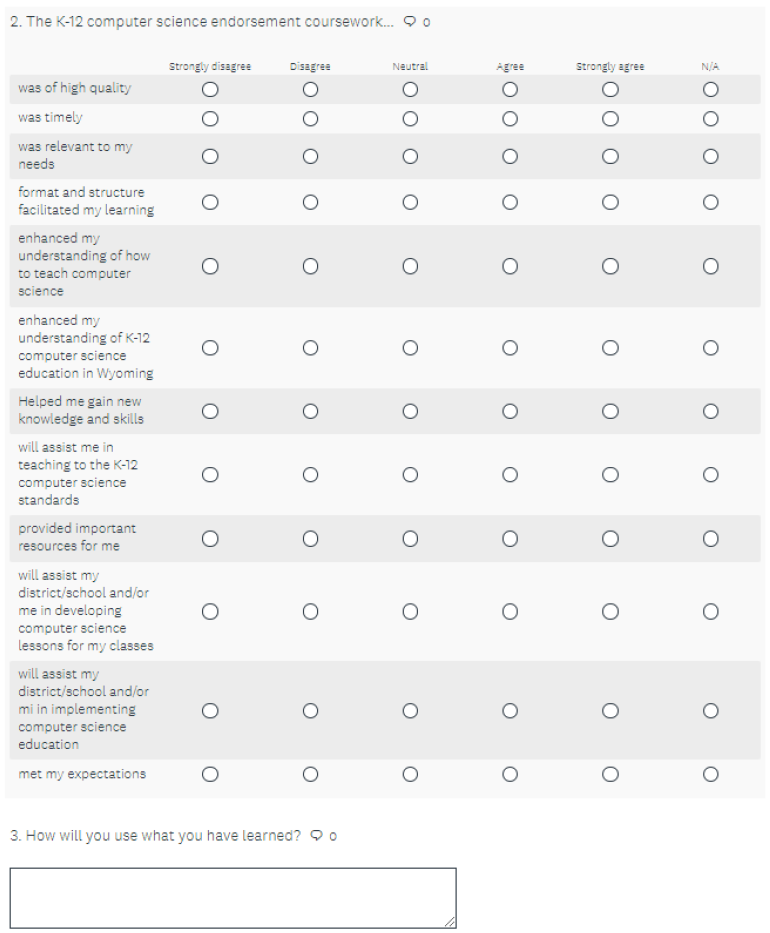 |
 |
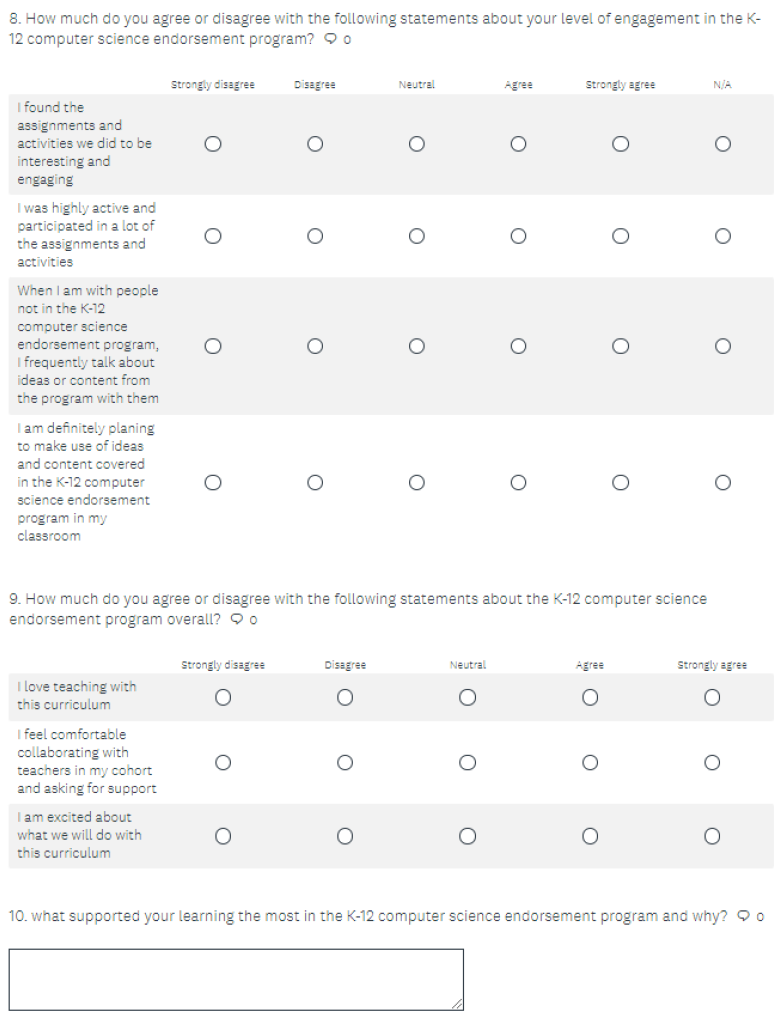 |
 |
 |
References
- Menekse, M. Computer science teacher professional development in the United States: A review of studies published between 2004 and 2014. Comput. Sci. Educ. 2015, 25, 325–350. [Google Scholar] [CrossRef]
- Hubwieser, P.; Armoni, M.; Giannakos, M.N.; Mittermeir, R.T. Perspectives and visions of computer science education in primary and secondary (K-12) schools. ACM Trans. Comput. Educ. 2014, 14, 1–9. [Google Scholar] [CrossRef]
- Graf, D. WySLICE Program Introduced to Educators Across the State. Wyoming News Now. Available online: https://www.wyomingnewsnow.tv/2021/04/21/wyslice-program-introduced-to-educators-across-the-state/ (accessed on 21 April 2021).
- Zendler, A.; Spannagel, C.; Klaudt, D. Marrying content and process in computer science education. IEEE Trans. Educ. 2010, 54, 387–397. [Google Scholar] [CrossRef]
- Professional Teaching Standard Board. Item 6.b: Computer science endorsement program approval applications. In Proceedings of the Minutes of the Regular Meeting of the Wyoming PTSB, Virtual Event, 27 January 2020.
- Northwest College. 2020–2021 Northwest College Catalog. Available online: https://catalog.nwc.edu/content.php?catoid-12&navoid=1370 (accessed on 10 December 2020).
- Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Burrows, A.C. Partnerships: A systemic study of two professional developments with university faculty and K-12 teachers of science, technology, engineering, and mathematics. Probl. Educ. 21st Century 2015, 65, 28–38. Available online: https://www.proquest.com/docview/2343798161?pq-origsite=gscholar&fromopenview=true (accessed on 5 October 2022). [CrossRef]
- Hewson, P.W. Teacher professional development in science: A case study of the primary science programme’s CTI course. In Proceedings of the 15th Annual Conference of the Southern African Association for Research in Mathematics, Science, and Technology Education, Maputo, Mozambique, January 2007; Available online: https://www.psp.org.za/wp-content/uploads/2015/07/Casestudy-on-PSP-Prof-Hewson-07.pdf (accessed on 5 October 2022).
- Northrup, A.K.; Burrows, A.C.; Slater, T.F. Identifying implementation challenges for a new computer science curriculum in rural western regions of the United States. Probl. Educ. 21st Century 2022, 80, 353–370. [Google Scholar] [CrossRef]
- Yadav, A.; Gretter, S.; Hambrusch, S.; Sands, P. Expanding computer science education in schools: Understanding teacher experiences and challenges. Comput. Sci. Educ. 2016, 26, 235–254. [Google Scholar] [CrossRef]
- Wyoming Department of Education. Available online: https://edu.wyoming.gov (accessed on 15 May 2022).
- Borowczak, M.; Burrows, A.C. Ants go marching—Integrating computer science into teacher professional development with NetLogo. Educ. Sci. 2019, 9, 66. [Google Scholar] [CrossRef]
- Astrachan, O.; Briggs, A. The CS principles project. ACM Inroads 2012, 3, 38–42. [Google Scholar] [CrossRef]
- ChanLin, L.J. Perceived importance and manageability of teachers toward the factors of integrating computer technology into classrooms. Innov. Educ. Teach. Int. 2007, 44, 45–55. [Google Scholar] [CrossRef]
- Lee, I.; Grover, S.; Martin, F.; Pillai, S.; Malyn-Smith, J. Computational thinking from a disciplinary perspective: Integrating computational thinking in K-12 science, technology, engineering, and mathematics education. J. Sci. Educ. Technol. 2020, 29, 1–8. [Google Scholar] [CrossRef]
- Goode, J. If you build teachers, will students come? The role of teachers in broadening computer science learning for urban youth. J. Educ. Comput. Res. 2007, 36, 65–88. [Google Scholar] [CrossRef]
- Goode, J.; Margolis, J.; Chapman, G. Curriculum is not enough: The educational theory and research foundation of the exploring computer science professional development model. In Proceedings of the 45th ACM Technical Symposium on Computer Science Education, Atlanta, GA, USA, 5–8 March 2014; pp. 493–498. [Google Scholar] [CrossRef]
- Wyoming Department of Education. 2020 Wyoming Computer Science Content & Performance Standards (WYCPS). Available online: https://edu.wyoming.gov/wp-content/uploads/2021/04/2020-CS-WYCPS-with-all-PLDs-effective-04.07.21.pdf (accessed on 7 April 2021).
- Gray, J.; Haynie, K.; Packman, S.; Boehm, M.; Crawford, C.; Muralidhar, D. A mid-project report on a statewide professional development model for CS principles. In Proceedings of the 46th ACM Technical Symposium on Computer Science Education, Kansas City, MO, USA, 4–7 March 2015; pp. 380–385. [Google Scholar] [CrossRef]
- Loucks-Horsley, S.; Stiles, K.E.; Mundry, S.; Love, N.; Hewson, P.W. Designing Professional Development for Teachers of Science and Mathematics; Corwin Press: Thousand Oaks, CA, USA, 1999. [Google Scholar]
- Wyoming 2018 Senate File 29. Education-Computer Science and Computational Thinking. Available online: https://www.wyoleg.gov/2018/Enroll/SF0029.pdf (accessed on 1 July 2018).
- Belland, B.R. Instructional Scaffolding in STEM Education: Strategies and Efficacy Evidence; Springer Nature: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kleickmann, T.; Tröbst, S.; Jonen, A.; Vehmeyer, J.; Möller, K. The effects of expert scaffolding in elementary science professional development on teachers’ beliefs and motivations, instructional practices, and student achievement. J. Educ. Psychol. 2016, 108, 21–42. [Google Scholar] [CrossRef]
- Loucks-Horsley, S.; Stiles, K.E.; Mundry, S.; Love, N.; Hewson, P.W. Designing Professional Development for Teacher of Science and Mathematics, 3rd ed.; Corwin Press: Thousand Oaks, CA, USA, 2010. [Google Scholar]
- Burrows, A.C.; Di Pompeo, M.A.; Myers, A.D.; Hickox, R.C.; Borowczak, M.; French, D.A.; Schwortz, A.C. Authentic science experiences: Pre-collegiate science educators’ successes and challenges during professional development. Probl. Educ. 21st Century 2016, 70, 59. [Google Scholar] [CrossRef]
- Crippen, K. Argument as professional development: Impacting teacher knowledge and beliefs about science. J. Sci. Teach. Educ. 2012, 23, 847–866. [Google Scholar] [CrossRef]
- Loucks-Horsley, S.; Stiles, K.E.; Mundry, S.; Love, N.; Hewson, P.W. Designing Professional Development for Teachers of Science and Mathematics; Corwin Press: Thousand Oaks, CA, USA, 2003. [Google Scholar]
- Penuel, W.; Fishman, B.; Yamaguchi, R.; Gallagher, L. What makes professional development effective: Strategies that foster curriculum implementation. Am. Educ. Res. J. 2007, 44, 921–958. [Google Scholar] [CrossRef]
- Zozakiewicz, C.; Rodriguez, A.J. Using sociotransformative constructivism to create multicultural and gender-inclusive classrooms an intervention project for teacher professional development. Educ. Policy 2007, 21, 397–425. [Google Scholar] [CrossRef]
- Burrows, A.C.; Breiner, J.; Keiner, J.; Behm, C. Biodiesel and integrated STEM: Vertical alignment of high school biology/biochemistry and chemistry. J. Chem. Educ. 2014, 91, 1379–1389. [Google Scholar] [CrossRef]
- Jackson, J.K.; Ash, G. Science achievement for all: Improving science performance and closing achievement gaps. J. Sci. Teach. Educ. 2012, 23, 723–744. [Google Scholar] [CrossRef]
- Stolk, M.; DeJong, O.; Bulte, A.; Pilot, A. Exploring a framework for professional development in curriculum innovation: Empowering teachers for designing context-based chemistry education. Res. Sci. Educ. 2011, 41, 369–388. [Google Scholar] [CrossRef][Green Version]
- Marshall, J.C.; Alston, D.M. Effective, sustained inquiry-based instruction promotes higher science proficiency among all groups: A 5-year analysis. J. Sci. Teach. Educ. 2014, 25, 807–821. [Google Scholar] [CrossRef]
- Spuck, T. Putting the “authenticity” in science learning. In Einstein Fellows: Best Practices in STEM Education; Spuck, T., Jenkins, L., Dou, R., Eds.; Peter Lang: New York, NY, USA, 2014; pp. 118–156. [Google Scholar]
- Zeidler, D.L. Socioscientific Issues as a Curriculum emphasis: Theory, research, and Practice. In Handbook of Research on Science Education; Lederman, N.G., Abell, S.K., Eds.; Routledge: London, UK, 2022; Volume II, pp. 697–726. [Google Scholar] [CrossRef]
- Darling-Hammond, L.; Hyler, M.E.; Gardner, M. Effective Teacher Professional Development; Learning Policy Institute: Palo Alto, CA, USA, 2007; Available online: https://learningpolicyinstitute.org/product/teacher-prof-dev (accessed on 5 May 2022).
- Reynolds, T.; Burrows, A.C.; Borowczak, M. Confusion over models: Exploring Discourse in a STEM professional development. SAGE Open 2022, 12, 21582440221097916. [Google Scholar] [CrossRef]
- Code.org Computer Science Principles Teacher Post-Academic Year Workshop Survey. Available online: https://drive.google.com/file/d/1Rnhul8D2G-5rUjevvcGiePKl4LGFBDNF/view (accessed on 25 May 2021).
- The Friday Institute for Educational Innovation. Professional Development Exit Questionnaire. Available online: https://www.fi.ncsu.edu/resource-library/ (accessed on 15 December 2013).
- Fallon, M. Writing up Quantitative Research in the Social and Behavioral Sciences; Brill: Leiden, The Netherlands, 2019. [Google Scholar]
- Boone, H.N.; Boone, D.A. Analyzing likert data. J. Ext. 2012, 50, 1–5. [Google Scholar]
- Harpe, S.E. How to analyze Likert and other rating scale data. Curr. Pharm. Teach. Learn. 2015, 7, 836–850. [Google Scholar] [CrossRef]
- Carifio, J.; Perla, R.J. Ten common misunderstandings, misconceptions, persistent myths and urban legends about Likert scales and Likert response formats and their antidotes. J. Soc. Sci. 2007, 3, 106–116. [Google Scholar] [CrossRef]
- Adeniran, A.O. Application of Likert scale’s type and Cronbach’s alpha analysis in an airport perception study. Sch. J. Appl. Sci. Res. 2019, 2, 1–5. [Google Scholar]
- Morling, B. Research Methods in Psychology Evaluating a World of Information, 2nd ed.; W.W. Norton & Company: New York, NY, USA, 2015. [Google Scholar]
- Field, A. Discovering Statistics Using IBM SPSS Statistics, 4th ed.; SAGE Publications: Thousand Oaks, CA, USA, 2013. [Google Scholar]
- Glass, G.V.; Peckham, P.D.; Sanders, J.R. Consequences of Failure to Meet Assumptions Underlying the Fixed Effects Analyses of Variance and Covariance. Rev. Educ. Res. 1972, 42, 237–288. [Google Scholar] [CrossRef]
- Corporatefinanceinstitute.com. What Is a Type I Error? Available online: https://corporatefinanceinstitute.com/resources/knowledge/other/type-i-error/ (accessed on 15 May 2022).
- Corporatefinanceinstitute.com. What Is a Type II Error? Available online: https://corporatefinanceinstitute.com/resources/knowledge/other/type-ii-error/ (accessed on 15 May 2022).
- Dunning, D. The Dunning–Kruger effect: On being ignorant of one’s own ignorance. In Advances in Experimental Social Psychology; Academic Press: Cambridge, MA, USA, 2011; Volume 44, pp. 247–296. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
