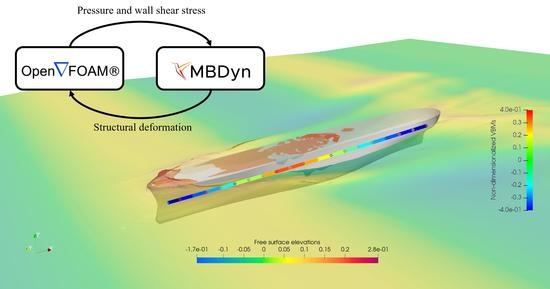
1. Introduction
Ships can experience slamming impacts while operating at high speeds, in severe sea states, or both. Severe slamming events can result in not only enormous local impact pressure but also hull girder global whipping responses, which is critical for the ultimate strength evaluation of a ship structure. El Moctar [
1] presented a statistical report from the International Union of Marine Insurance [
2] stating that approximately
of ship losses of all total losses, between 2001 to 2015, were associated with ships encountering harsh weather.
An increase in ship size tends to make the hull more “flexible” and leads to the wave encounter frequency being closer to the ship’s wetted natural frequency. In such resonance frequency, comparatively small vibration-induced loads are superposed to the wave-induced load that may significantly violate the ship motions and deform the ship structure. This phenomenon is called the ship’s hydroelastic effect, which is particularly important in determining design wave loads and structure strength evaluation of large ships [
3]. The prediction of slamming loads on a deformable ship is a very challenging subject due to the strongly nonlinear free surface and the structure elastic behaviour. In such cases, the deformed ship structure interacts with the surrounding flow fields, which form a fully coupled fluid–structure interaction (FSI) system against the traditional rigid ship assumption. Hirdaris [
4], Jiao [
5], and Bakti [
6] also supported this point of view, showing that the rigid body model may lead to inaccurate predictions of hydrodynamic loadings as well as the global ship motions. Therefore, as suggested by Hirdaris [
4], a fully coupled FSI approach was used in this study to predict the flexible ship motions and hydrodynamic loads of an S175 containership in extreme wave conditions.
Over the past decade, the theoretical and numerical methods for predicting ship seakeeping performance based on hydroelasticity theory have gained momentum. To account for both fluid and structural features, the partitioned approach was adopted most commonly, in which the wave-structure system was divided into the fluid and structure parts and solved iteratively. The pioneering work of Bishop [
7] developed a linear FSI model on the basis of 2D potential flow theory and a linear beam model on a monohull. Within this framework, the flexible structural characteristics of the ship was idealised as an elastic beam and interacted with the fluid forces, which were calculated from the strip theory. The theory was subsequently extended by Bishop [
8] to a generalised beam model for floating vehicles or more complicated shapes. The three-dimensional hydroelasticity theory was established in the early 1980s by Bishop [
8]; since then, a great deal of progress has been made in the development and applications of the hydroelasticity analysis on ship structures based on the potential theory [
6,
9,
10,
11,
12,
13].
The potential flow theory provides an efficient insight into the initial design stage of shipbuilding; however, it cannot reproduce some important physical phenomena, such as wave breaking and viscous effects. As El Moctar [
1] stated, the use of potential flow theory was questionable when applied to extreme wave conditions because the viscosity effects become critical for modelling large free-surface elevation waves. Therefore, the fully nonlinear computational fluid dynamics (CFD) method, which makes use of the Reynolds averaged Navier–Stokes (RANS) equations, is commonly used to investigate ship seakeeping in harsh seaways as an alternative. Extensive research has been proposed and validated the performance of the CFD method on the studies of ship seakeeping performance under different conditions—for example, coupled ship motions in deep water [
14,
15], ship resistance in restricted shallow water [
16], and ship manoeuvring in irregular waves [
17], to name a few.
The majority of current CFD studies on ship seakeeping were proposed by modelling fluid flow around a rigid ship. Although global ship motions and external loadings can be routinely obtained by CFD simulations, the hull section loads, e.g., vertical bending moment and shearing force, used for wave loads analysis cannot be directly obtained. Therefore, the CFD method can be further coupled with a structure solver to study the dynamic responses of a flexible ship on a free surface. In some cases, CFD and the finite element analysis (FEA) are coupled for the hydroelastic simulations based on a one-way coupling approach [
18] or a two-way coupling approach [
19]. The differences between one-way and two-way coupling methods on ship wave loads and hydroelastic responses were investigated by Lakshmynarayanana [
18] and Takami [
20] by using a commercial co-simulation interface (Star-CCM+ & ABAQUS). According to their results, the one-way coupling approach should not be used for the studies of the ringing and whipping phenomenon because the added mass effects in the elastic deformation are not accounted for, and it may result in an underestimate of the high vibratory components as well as the wave loads. Generally, there are three types of structure modelling of ship in the FEA: the pure-beam model, the beam-shell model, and the full ship model. First, the pure-beam model was built based on beam theory, i.e., Euler–Bernoulli beam or a Timoshenko beam, in which the ship’s elastic deformations are computed by solving the beam equation of motions and external forces. El Moctar [
1] proposed a study based on the Timoshenko beam model and coupled with a CFD model by a two-way coupling method to investigate the wave-induced structural loads of three containerships in regular and deterministic wave sequences. Their numerical results including the dynamics loads and structural vibrations agreed well with the experiments, which assessed the feasibility of using the beam model and transient RANS solver to obtain the short-term statistical measures of nonlinear ship responses. Secondly, the beam-shell model requires a more complex design in FEA, in which the ship geometrical models in the CFD and FEA solvers should be topologically equal. The wet hull surface is generated by using the shell elements and is kinematically constrained with the beam nodes in such a model. Prior to the FSI simulations, the structural modal analysis has to be applied to calibrate the beam profiles [
5,
19]. Such an FEA model was coupled with a CFD solver based on a two-way coupling approach through co-simulation interface (Star-CCM+ & ABAQUS) by Lakshmynarayanana [
21], Lakshmynarayanana [
22], and Jiao [
5] to predict the motions, wave loads, and hydroelastic vibrations of an S175 containership in waves with forward speeds. Their results, including global ship motions and vertical bending moments in different regular wave conditions, were comprehensively analysed and validated with the existing experimental results [
23]. The third method is the full ship model, which discretises the whole ship and substructure by using the finite shell elements in the FEA software. This method is capable of accounting for the complex deformation behaviours of the ship and predicting local stress distributions; however, it is computationally very demanding. Ma [
24] modelled the full ship with sandwich composite material by using ANSYS and coupled it with CFX through the ANSYS workbench. Their FSI results were further studied with stress analysis, which revealed that the most vulnerable region in the sandwich plate structure was the core-skin interface near the girder.
However, the abovementioned CFD–FEA coupling method requires significant computational efforts [
6,
21], making it difficult to extend applications to more complex wave conditions. Recently, a CFD–DMB method was first proposed by Lu [
25] on the investigation of the hydroelastic behaviour of a large VLF. The DMB model has a similar setup with the traditional hydroelastic experiments. In this approach, the ship hull is divided into multiple floating rigid sections, whereas a stiffness matrix based on an Euler–Bernoulli (EB) beam theory, equivalently representing the structure’s stiffness, is employed to connect ship neighbouring sections. In this method, only a one-dimensional beam is modelled in the structural solver, and it can significantly save computational time and effort compared with the CFD–FEA method. Based on the above design, the dynamic motion of the ship is both affected by the hydrodynamic forces from fluid solver and restricted by the deformation conditions of the equivalent beam properties from the structural solver. Such a CFD–DMB coupling approach has been applied successfully in the literature—for example, flexible wind turbine blades [
26] and aircraft wings [
27]. However, in these applications, a single-phase solver is applied to calculate the air forces at the geometry surface with a low mass ratio. For multiphase cases, the DMB method has been successfully employed by Li [
28] on the dynamic motion of a close-loop WEC array in waves. Lu [
25] investigated the hydroelasticity of very large floating structures (VLFs) in waves, which was solved in both frequency [
29] and time domains [
30]. Recently, Bakti [
6] studied the forward speed effects on the elastic responses of an analytical Wigley hull by using a BEM–DMB coupling method in both regular and irregular waves. According to their results, a noticeable increase of ship vertical bending moments occurs when the ship speed increases due to the whipping phenomenon.
Most ship hydroelastic research in the literature was presented in regular wave conditions. However, regular waves are unrepresentative of actual extreme events, as stated by Ning [
31]. On the other hand, random wave simulations require very long runs in order to capture the near-extreme events because they are so rare in any random wave series. In practice, the focused wave theory is used as an alternative to a long-term irregular wave. The concept of the focused wave was first proposed by Davis [
32] by modulation of a series of conventional sinusoidal wave trains generated from a prescribed wave spectrum and superimposing the crests. Since then, experiments and numerical investigations have been carried out by using the focused wave groups to replace the irregular waves in the nonlinear wave–wave interaction studies. For example, T. E. Baldock [
33] created wave focus events through the superposition of regular wave trains based on the linear wave theory and investigated the effects of nonlinearity of wave–wave interactions. Ning [
31] studied the propagation of the focused wave groups with different incident wave parameters and compared the solutions between the first- and second-order wave theory. Recently, the focused wave theory has been adopted to investigate wave-structure problems and predict extreme loads on offshore structures. These studies were initially focused on a simple floater [
34], and then extended to complex floating structures, such as wave energy converters (WECs) [
35] or semi-submersible wind turbine foundations [
36,
37]. Zhou [
38] and Zhou [
39] further extended their applications of studying the dynamic motions of a fully coupled aero-hydro-moored version of a floating offshore wind turbine (FOWT) subject to focused wave conditions.
To the best of the authors’ knowledge, the research using transient FSI simulations to investigate ship hydroelasticity in extreme wave conditions is very limited in number and scope. The reasons for this mainly stem from the computational burdens of determining maximum values of ship responses in irregular waves through direct simulation by using Navier–Stokes equations. In this study, we overcome such issues by studying ship hydroelastic behaviour and slamming loads in extreme waves based on the CFD–DMB method and focused wave theory. It is expected that the results obtained from this improved and validated numerical tools can provide a more precise and more detailed insight into the physical phenomena of the ship dynamic motions and its hydrodynamic loads in real sea states. The results proposed in this study could also help to assess the structural integrity of the ship longitudinal strength, which serves as an improved technique by which to evaluate unconventional ship designs.
The rest of this paper is organised as follows. In
Section 2, the numerical setup and the methodology used in the present study are discussed. In
Section 3, the verification and sensitivity studies are presented for focused waves and the CFD–DMB model. In
Section 4, the numerical results for the study on the dynamic motions of a flexible S175 ship in regular wave conditions are presented. In
Section 5, a comprehensive comparison of the ship global motion and hydroelastic behaviours between focused and regular waves are presented. The discussion and conclusions are drawn in the final section.