Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection
Abstract
:1. Introduction
2. Numerical Simulation Methodology
2.1. 1D Pipeline Calculation Methodology
2.2. 3D Flow Simulation Methodology
2.3. Fluid–Structure Interaction Analysis Methodology
3. Numerical Simulation of the Fluid Flow
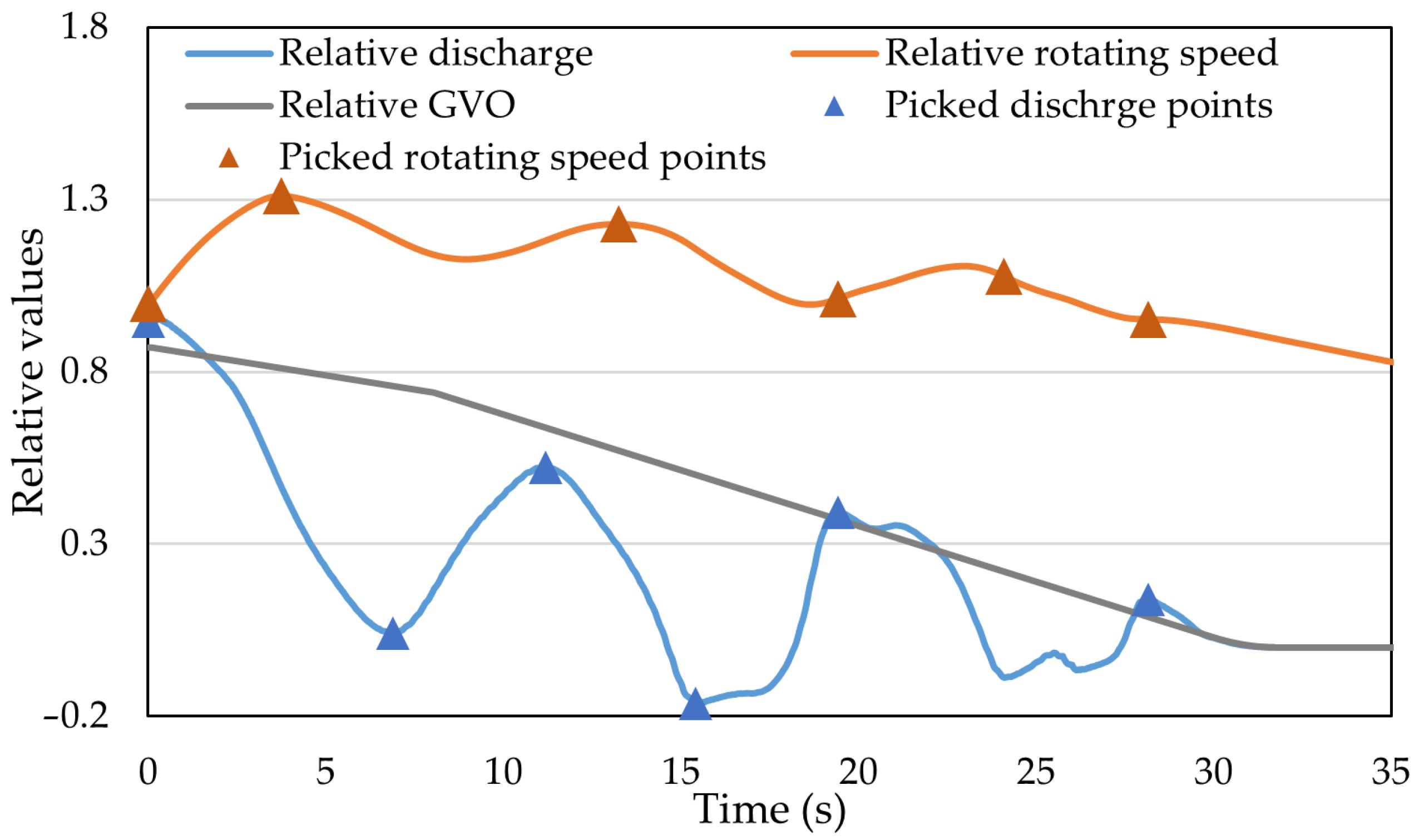
3.1. 1D Simulation on Pipeline Flow
3.2. 3D CFD Simulation
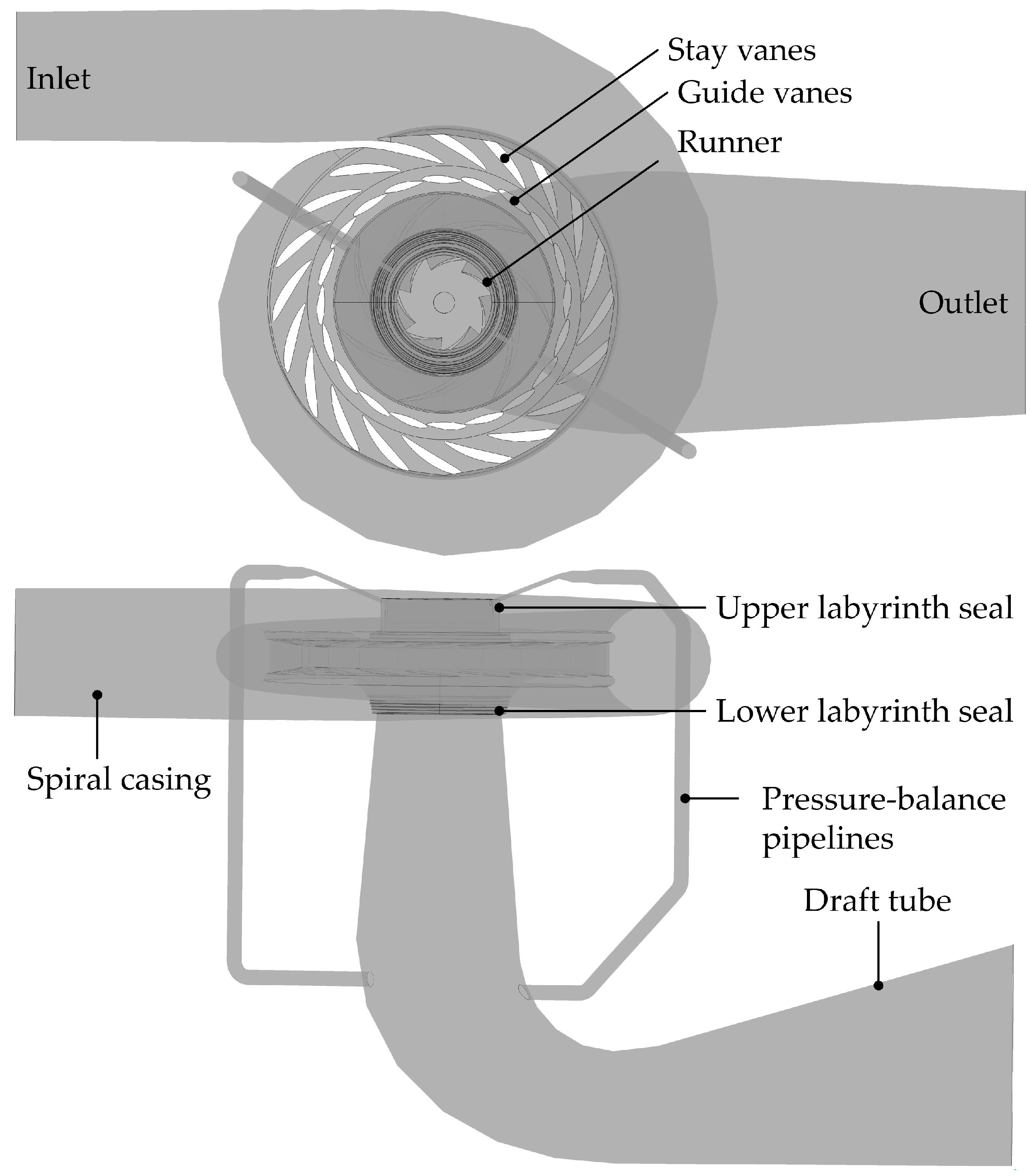
3.2.1. 3D Model of Flow Calculation
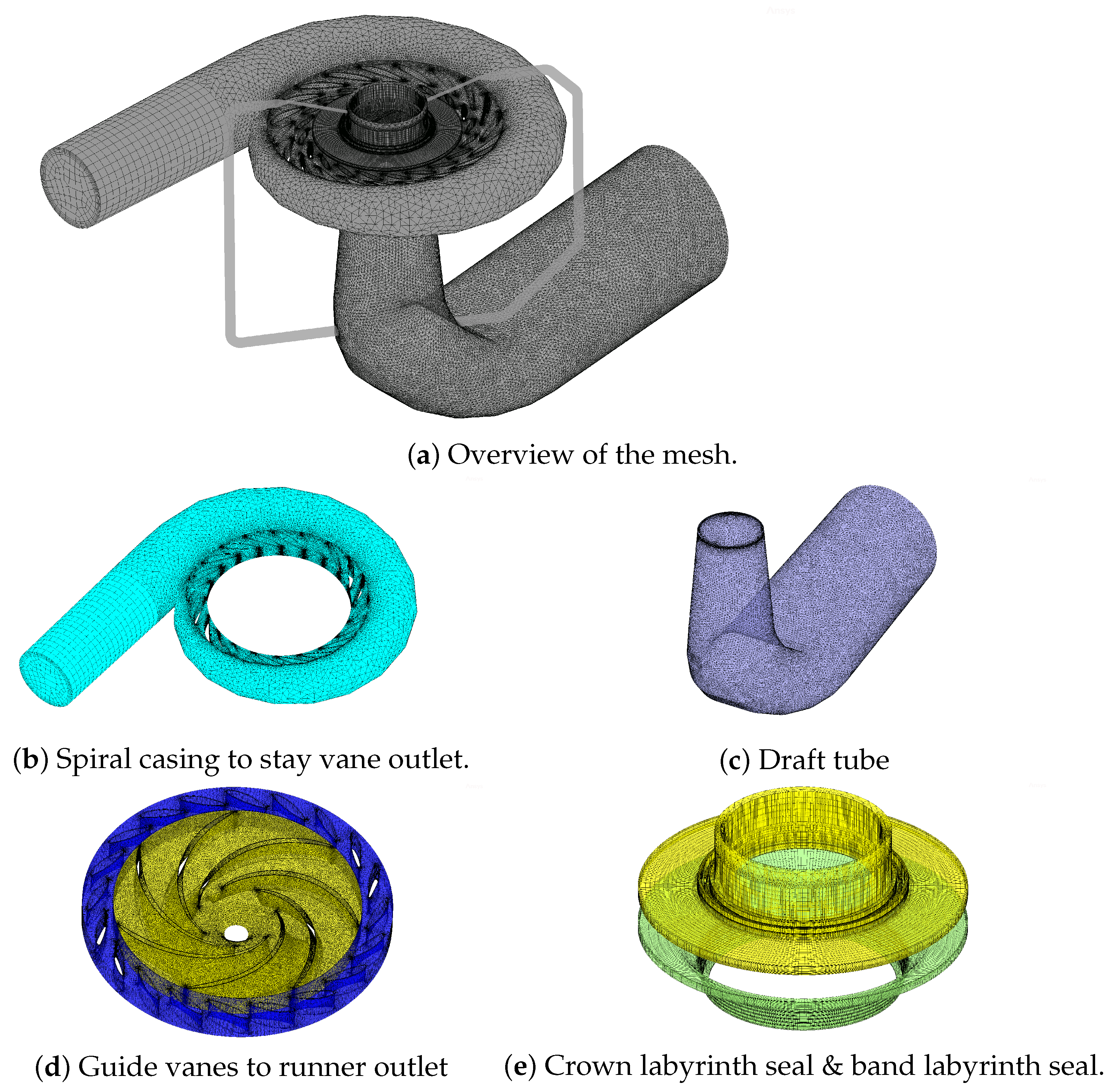
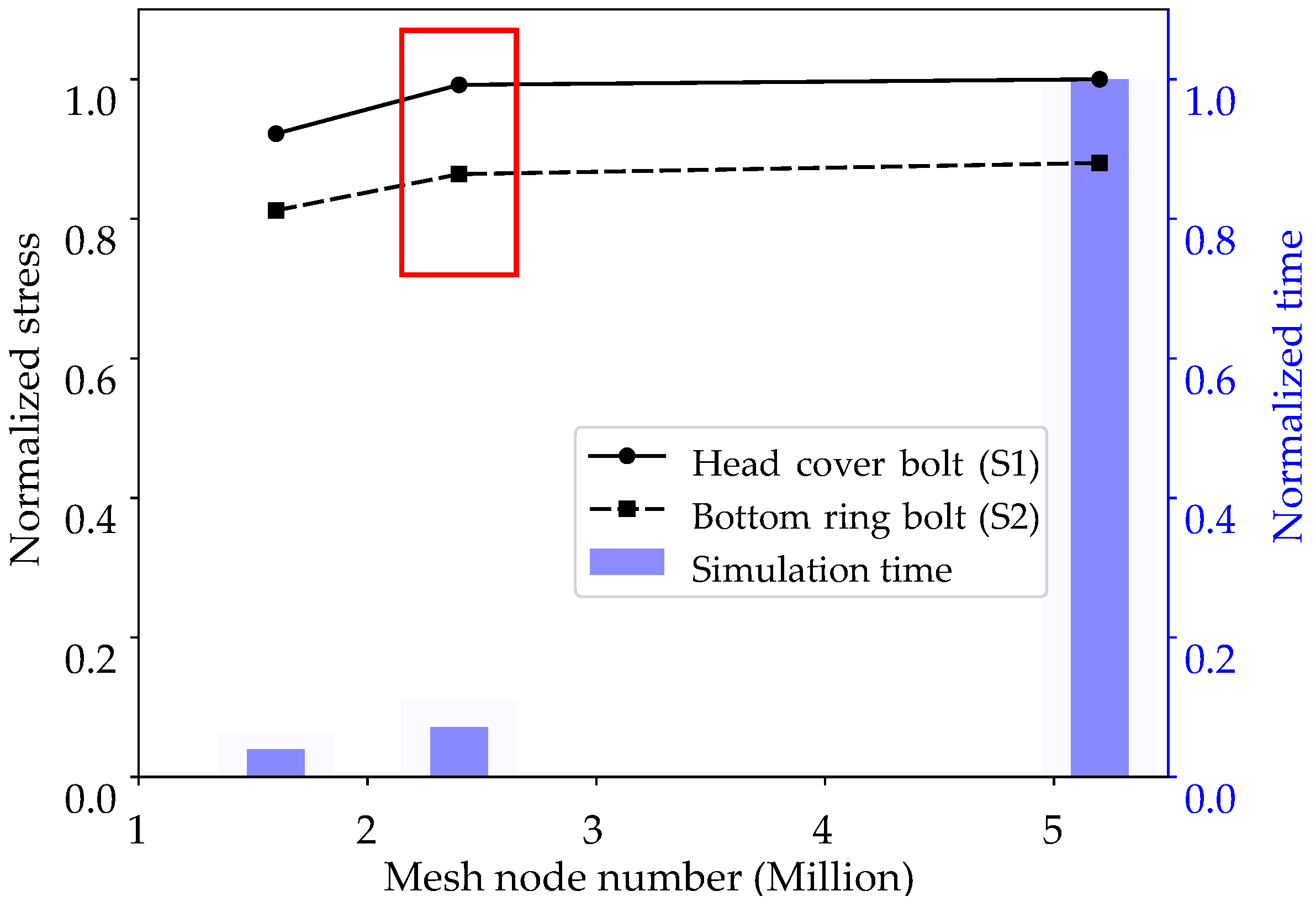
3.2.2. Mesh Independence Analysis of the 3D Flow Calculation
3.3. 3D Fluid Simulation Results
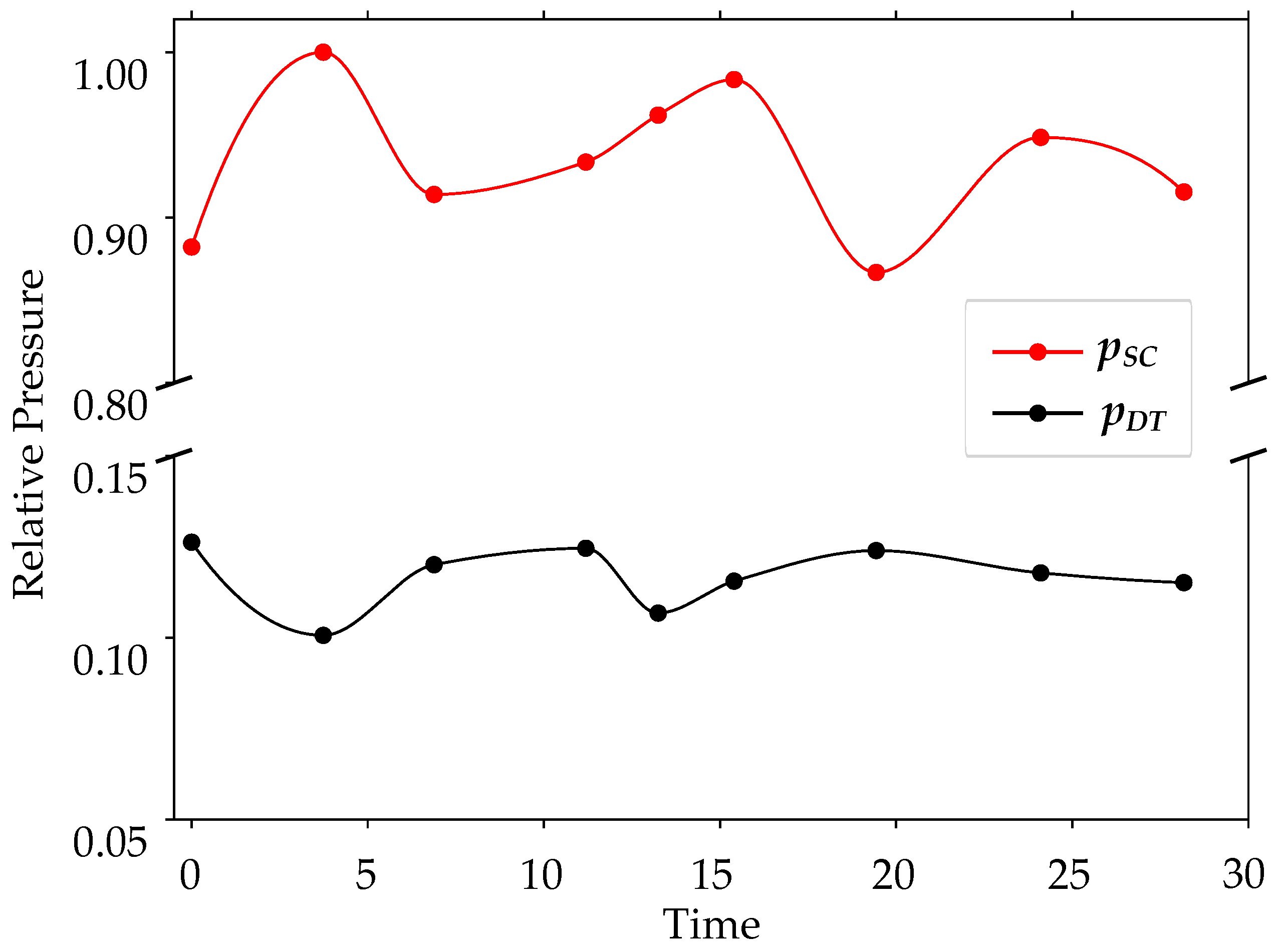
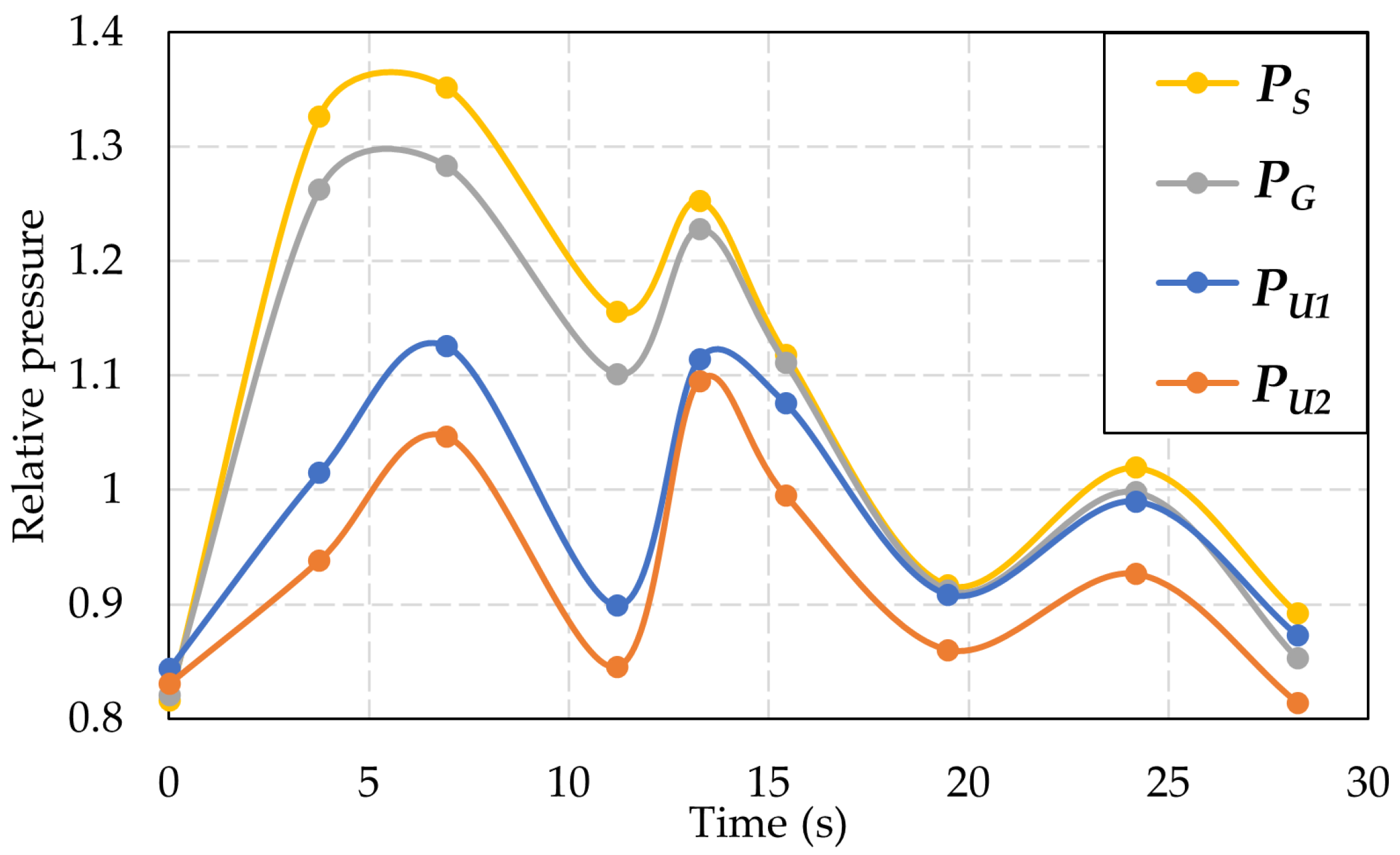
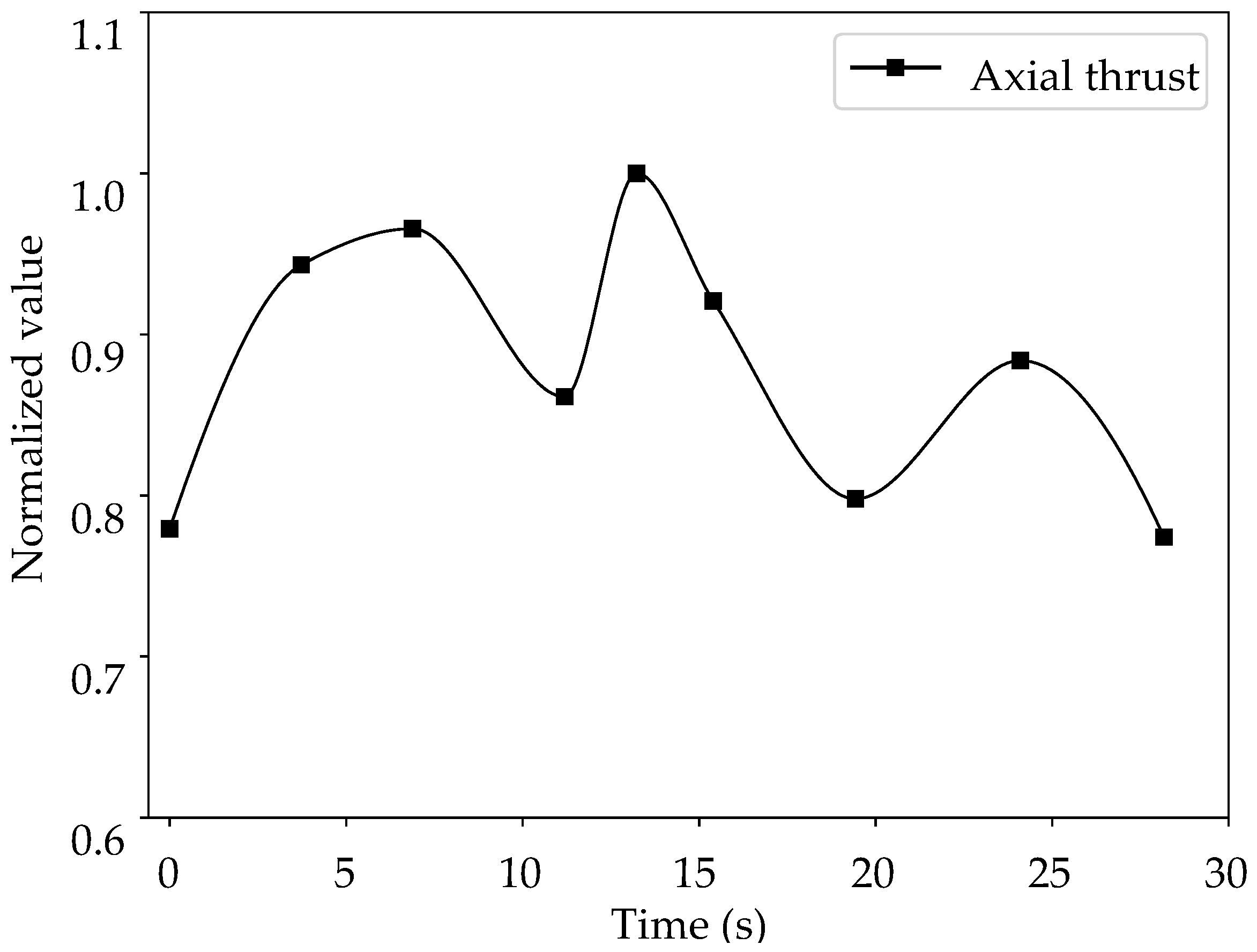
3.3.1. Pressure Variation at the Monitoring Points
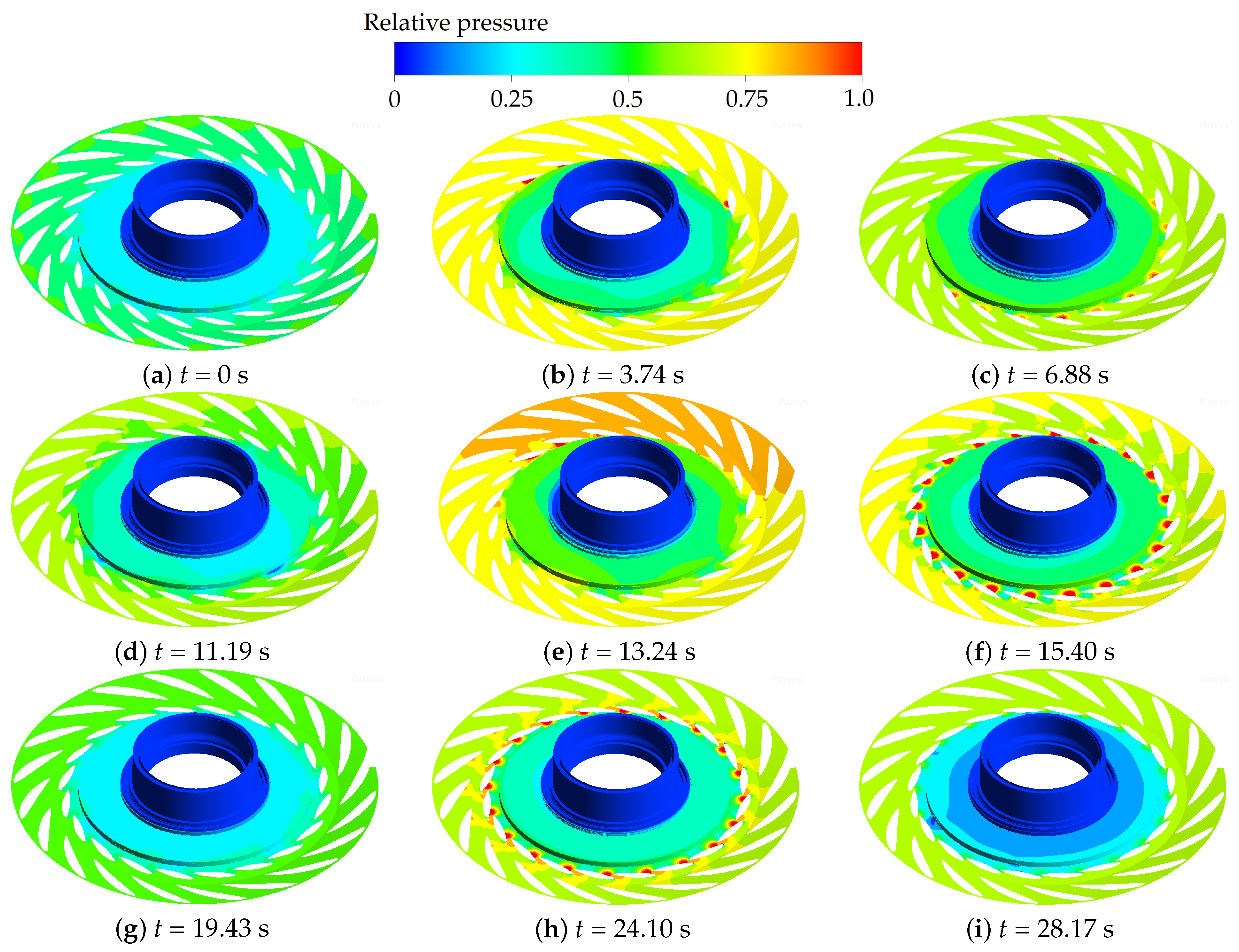
3.3.2. Flow Pattern Change in the Runner Passage
3.3.3. Result of Pressure Variation
4. Flow-Induced Dynamic Behavior of Structures
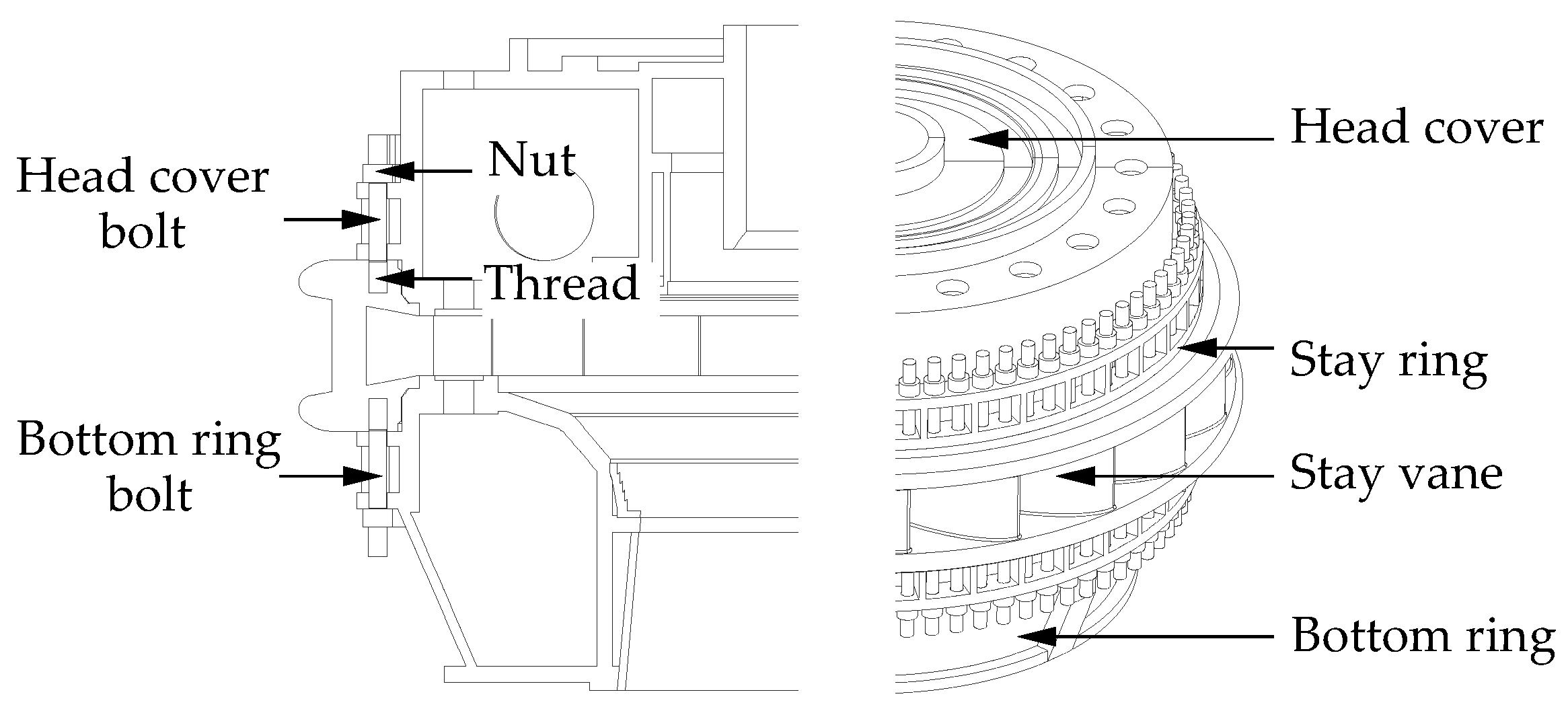
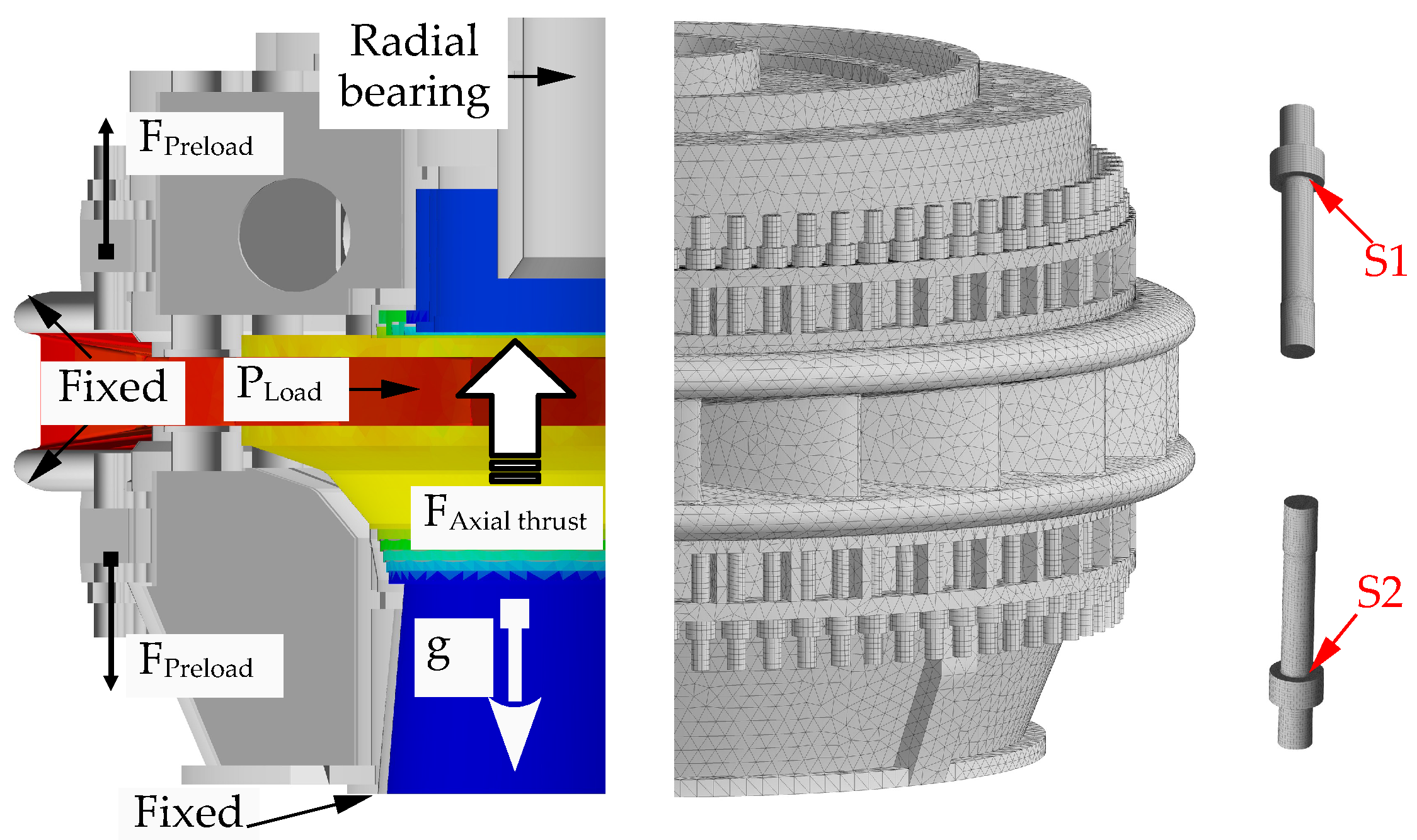
4.1. Simulation Setup and Mesh Independence Analysis
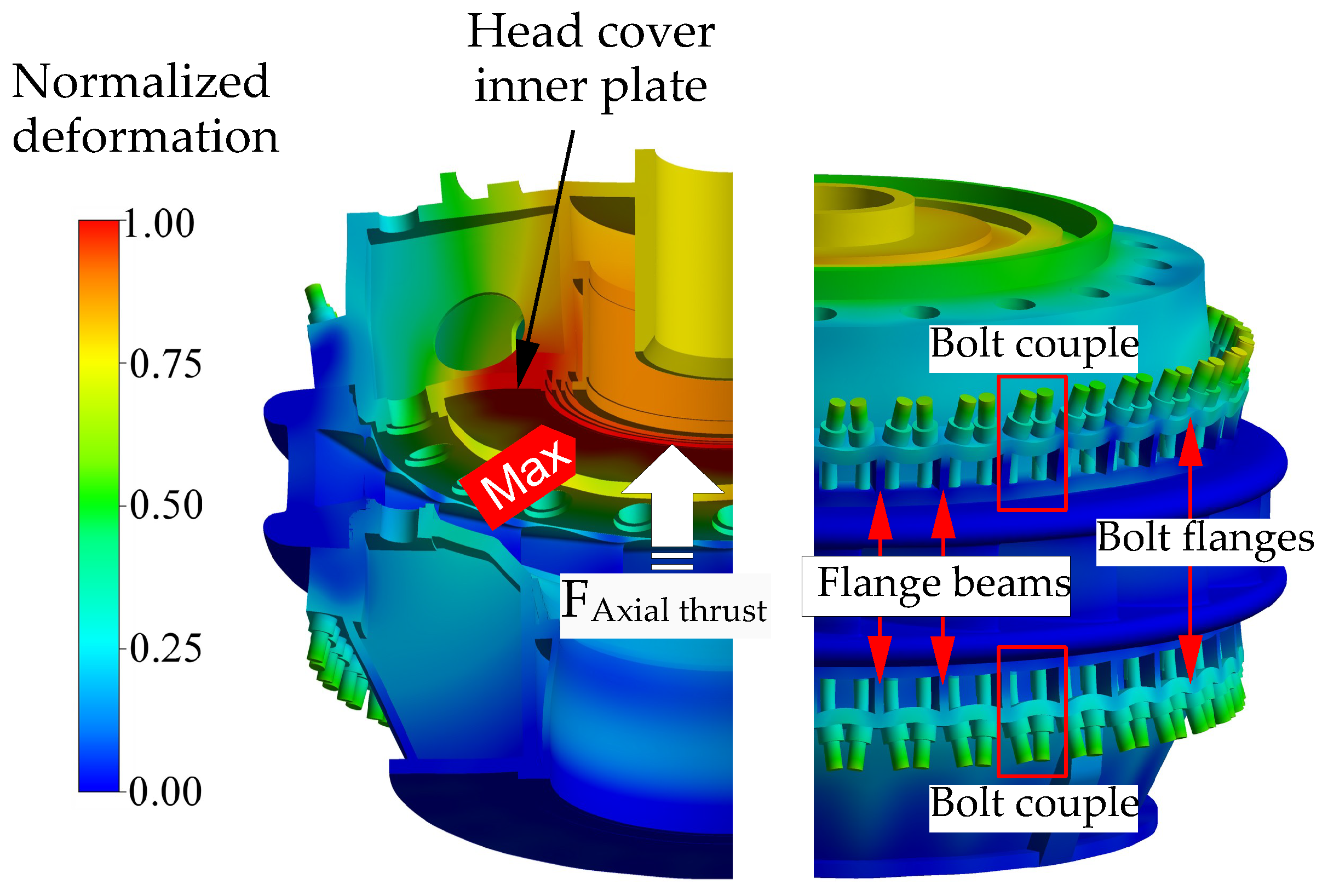
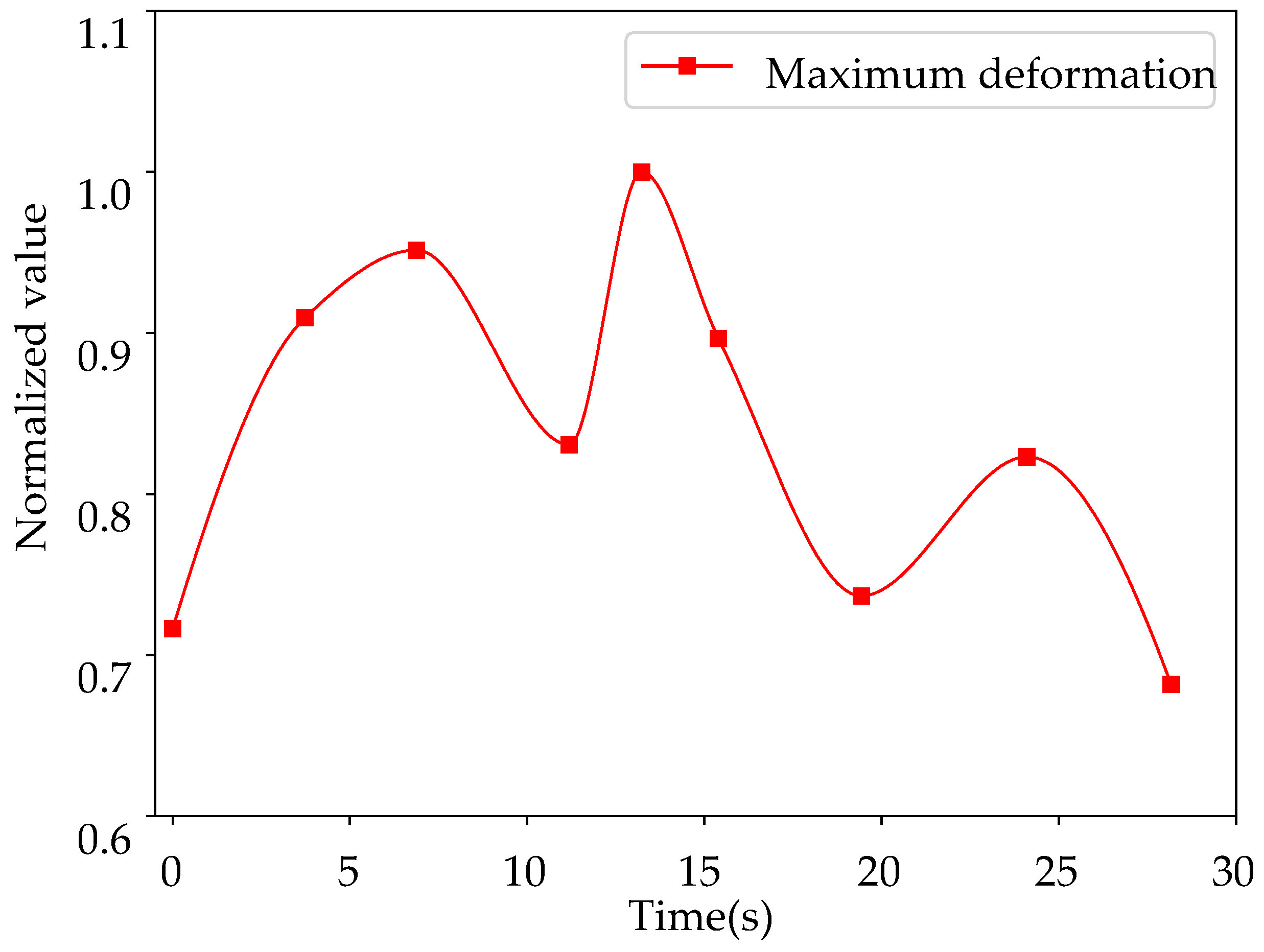
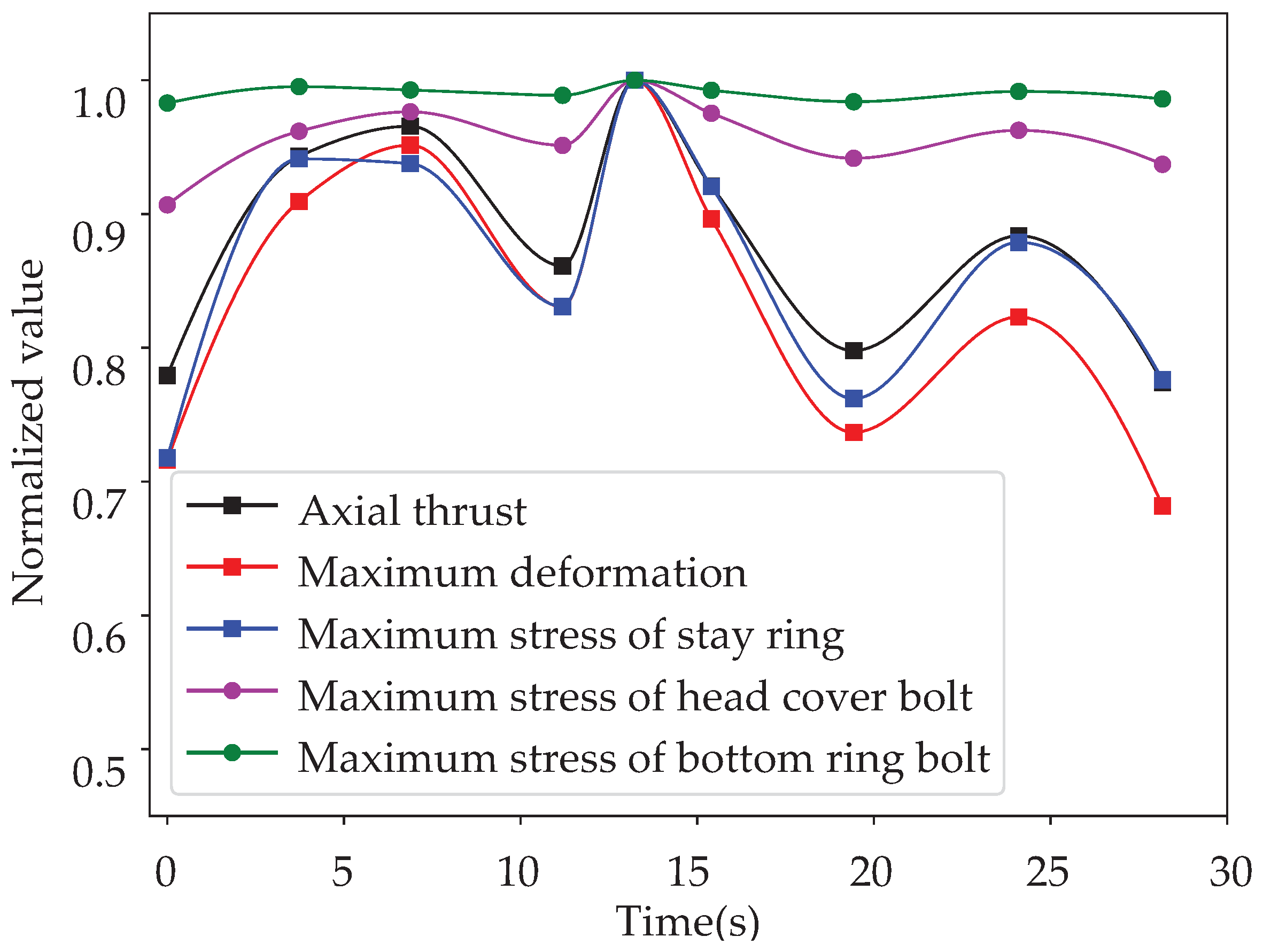
4.2. Results and Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PSPS | Pumped storage power station |
| CFD | Computational fluid dynamics |
| FEM | Finite element method |
| FSI | Fluid–structure interaction |
| FVM | Finite volume method |
| PT | Pump-turbine |
References
- Zhao, W. Improved Condition Monitoring of Hydraulic Turbines Based on Artificial Intelligence Techniques. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2021. [Google Scholar]
- Zhao, W.; Presas, A.; Egusquiza, M.; Valentín, D.; Egusquiza, E.; Valero, C. On the use of Vibrational Hill Charts for improved condition monitoring and diagnosis of hydraulic turbines. Struct. Health Monit. 2022, 21, 14759217211072409. [Google Scholar] [CrossRef]
- Zhao, W.; Egusquiza, M.; Valero, C.; Valentín, D.; Presas, A.; Egusquiza, E. On the use of artificial neural networks for condition monitoring of pump-turbines with extended operation. Measurement 2020, 163, 107952. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Y.; Wang, Z. A review on fatigue damage mechanism in hydro turbines. Renew. Sustain. Energy Rev. 2016, 54, 1–14. [Google Scholar] [CrossRef]
- Casanova, F.; Mantilla, C. Fatigue failure of the bolts connecting a Francis turbine with the shaft. Eng. Fail. Anal. 2018, 90, 1–13. [Google Scholar] [CrossRef]
- Peltier, R.; Boyko, A.; Popov, S.; Krajisnik, N. Investigating the Sayano-Shushenskaya hydro power plant disaster. Power 2010, 154, 48. [Google Scholar]
- Egusquiza, E.; Valero, C.; Huang, X.; Jou, E.; Guardo, A.; Rodriguez, C. Failure investigation of a large pump-turbine runner. Eng. Fail. Anal. 2012, 23, 27–34. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Yang, J.; Wang, W.; Qu, J.; Huang, X.; Zhao, W. Research on the Flow-Induced Stress Characteristics of Head-Cover Bolts of a Pump-Turbine during Turbine Start-Up. Energies 2022, 15, 1832. [Google Scholar] [CrossRef]
- Song, X.j.; Yao, R.; Chao, L.; Wang, Z.w. Study of the formation and dynamic characteristics of the vortex in the pump sump by CFD and experiment. J. Hydrodyn. 2021, 33, 1202–1215. [Google Scholar] [CrossRef]
- Luo, Y.; Chen, F.; Chen, L.; Wang, Z.; Yu, J.; Zhu, X.; Zhao, Z.; Ren, S.; Li, J.; Lu, X. Study on stresses of head cover bolts in a pump turbine based on FSI. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 804, p. 042062. [Google Scholar]
- Luo, Y.; Chen, F.; Chen, L.; Wang, Z.; Yu, J.; Luo, C.; Zhao, Z.; Ren, S.; Li, J.; Deng, D. Stresses and relative stiffness of the head cover bolts in a pump turbine. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 493, p. 012113. [Google Scholar]
- Chen, F.; Chen, L.; Wang, Z.; Yu, J.; Luo, C.; Zhao, Z.; Ren, S.; Li, J.; Deng, D. Computation of static stresses of the head cover bolts in a pump turbine. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2019; Volume 493, p. 012143. [Google Scholar]
- Chen, L.; Li, H.; Yu, J.; Luo, Y.; Wang, Z.; Zhu, X.; Zhao, Z.; Lu, X. Stress analysis of screw connection of key structural components in pump turbine. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 804, p. 032037. [Google Scholar]
- Brekke, H. Performance and safety of hydraulic turbines. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2010; Volume 12, p. 012061. [Google Scholar]
- Huang, X.; Chamberland-Lauzon, J.; Oram, C.; Klopfer, A.; Ruchonnet, N. Fatigue analyses of the prototype Francis runners based on site measurements and simulations. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 012014. [Google Scholar]
- He, Q.; Huang, X.; Yang, M.; Yang, H.; Bi, H.; Wang, Z. Fluid–Structure Coupling Analysis of the Stationary Structures of a Prototype Pump Turbine during Load Rejection. Energies 2022, 15, 3764. [Google Scholar] [CrossRef]
- He, L.; Wang, Z.; Kurosawa, S.; Nakahara, Y. Resonance investigation of pump-turbine during startup process. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 032024. [Google Scholar]
- Kolšek, T.; Duhovnik, J.; Bergant, A. Simulation of unsteady flow and runner rotation during shut-down of an axial water turbine. J. Hydraul. Res. 2006, 44, 129–137. [Google Scholar] [CrossRef]
- Ciocan, G.D.; Iliescu, M.S.; Vu, T.C.; Nennemann, B.; Avellan, F. Experimental study and numerical simulation of the FLINDT draft tube rotating vortex. J. Fluids Eng. 2007, 129, 146–158. [Google Scholar] [CrossRef]
- Huang, X.; Oram, C.; Sick, M. Static and dynamic stress analyses of the prototype high head Francis runner based on site measurement. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2014; Volume 22, p. 032052. [Google Scholar]
- Goyal, R.; Cervantes, M.J.; Gandhi, B.K. Characteristics of Synchronous and Asynchronous modes of fluctuations in Francis turbine draft tube during load variation. Int. J. Fluid Mach. Syst. 2017, 10, 164–175. [Google Scholar] [CrossRef]
- Mao, Z.; Tao, R.; Chen, F.; Bi, H.; Cao, J.; Luo, Y.; Fan, H.; Wang, Z. Investigation of the starting-up axial hydraulic force and structure characteristics of pump turbine in pump mode. J. Mar. Sci. Eng. 2021, 9, 158. [Google Scholar] [CrossRef]
- Münch, C.; Ausoni, P.; Braun, O.; Farhat, M.; Avellan, F. Fluid–structure coupling for an oscillating hydrofoil. J. Fluids Struct. 2010, 26, 1018–1033. [Google Scholar] [CrossRef]
- Benra, F.K.; Dohmen, H.J. Comparison of pump impeller orbit curves obtained by measurement and FSI simulation. In Proceedings of the ASME Pressure Vessels and Piping Conference, San Antonio, TX, USA, 22–26 July 2007; Volume 42827, pp. 41–48. [Google Scholar]
- Kato, C.; Yoshimura, S.; Yamade, Y.; Jiang, Y.Y.; Wang, H.; Imai, R.; Katsura, H.; Yoshida, T.; Takano, Y. Prediction of the noise from a multi-stage centrifugal pump. In Proceedings of the Fluids Engineering Division Summer Meeting, Houston, TX, USA, 19–23 June 2005; Volume 41987, pp. 1273–1280. [Google Scholar]
- Jiang, Y.; Yoshimura, S.; Imai, R.; Katsura, H.; Yoshida, T.; Kato, C. Quantitative evaluation of flow-induced structural vibration and noise in turbomachinery by full-scale weakly coupled simulation. J. Fluids Struct. 2007, 23, 531–544. [Google Scholar] [CrossRef]
- Mandair, S.; Morissette, J.; Magnan, R.; Karney, B. MOC-CFD coupled model of load rejection in hydropower station. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 774, p. 012021. [Google Scholar]
- Zhou, D.; Chen, H.; Kan, K.; Yu, A.; Binama, M.; Chen, Y. Experimental study on load rejection process of a model tubular turbine. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 774, p. 012036. [Google Scholar]
- Fu, X.; Li, D.; Wang, H.; Zhang, G.; Li, Z.; Wei, X. Dynamic instability of a pump-turbine in load rejection transient process. Sci. China Technol. Sci. 2018, 61, 1765–1775. [Google Scholar] [CrossRef]




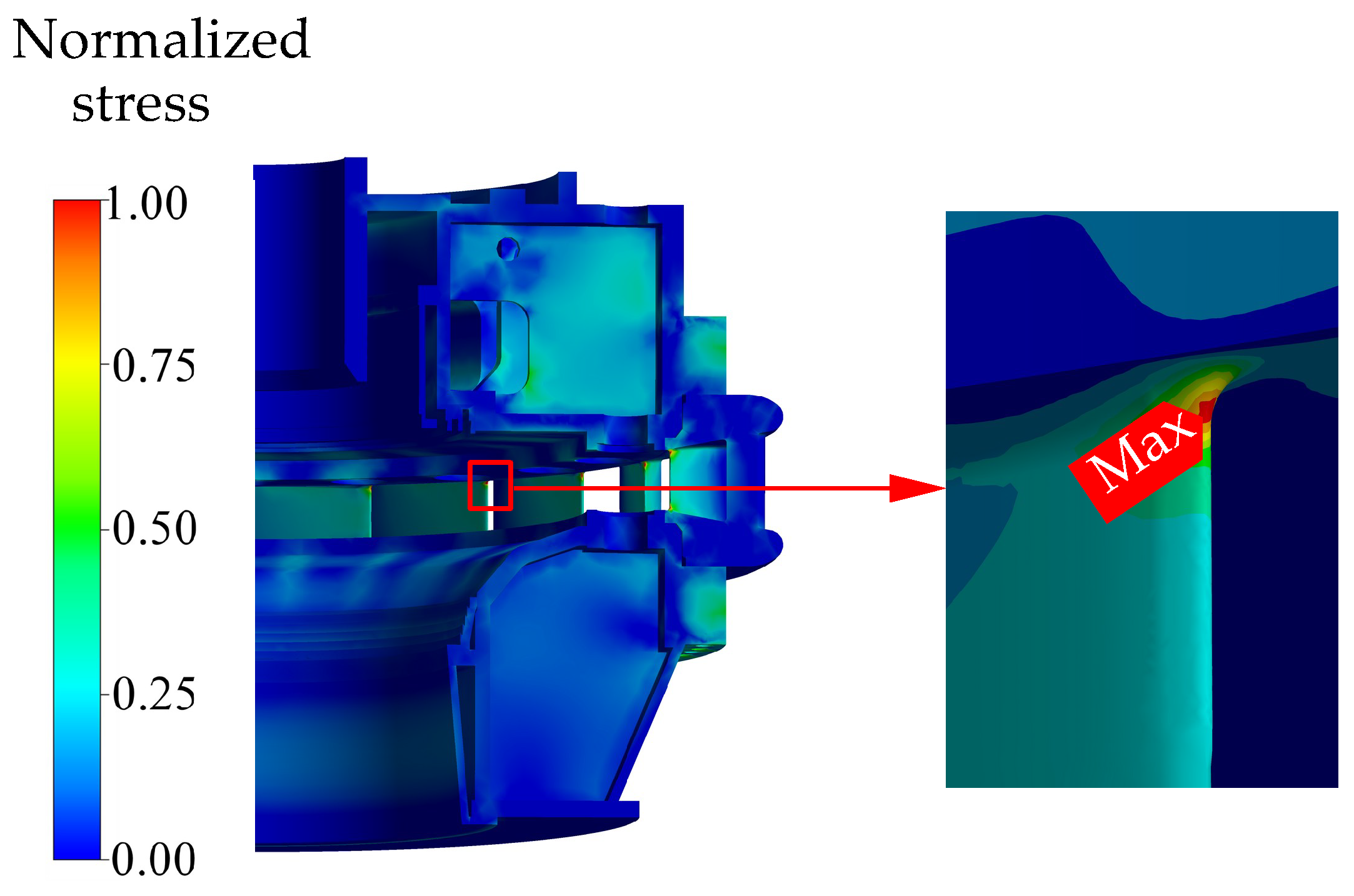
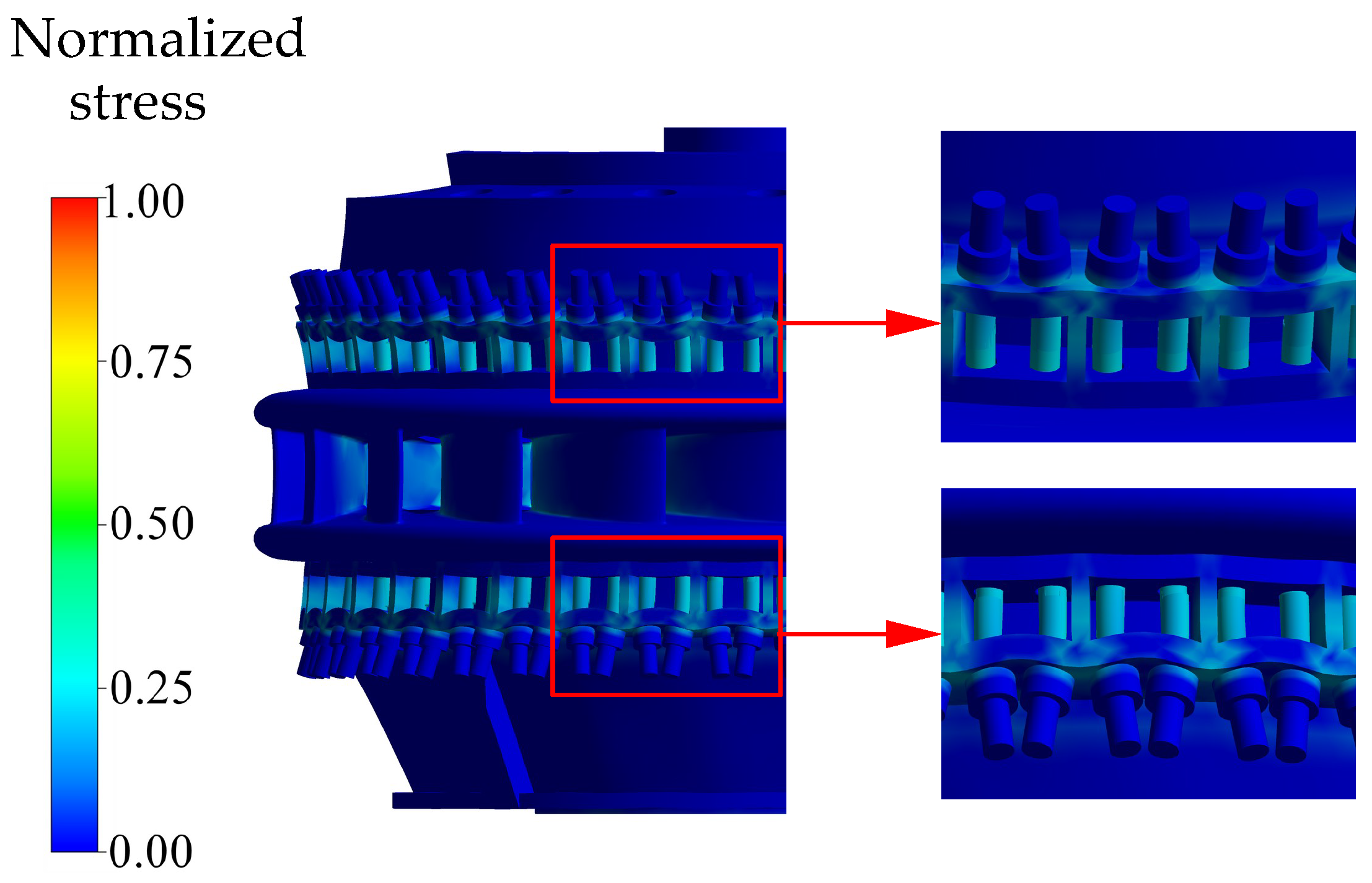
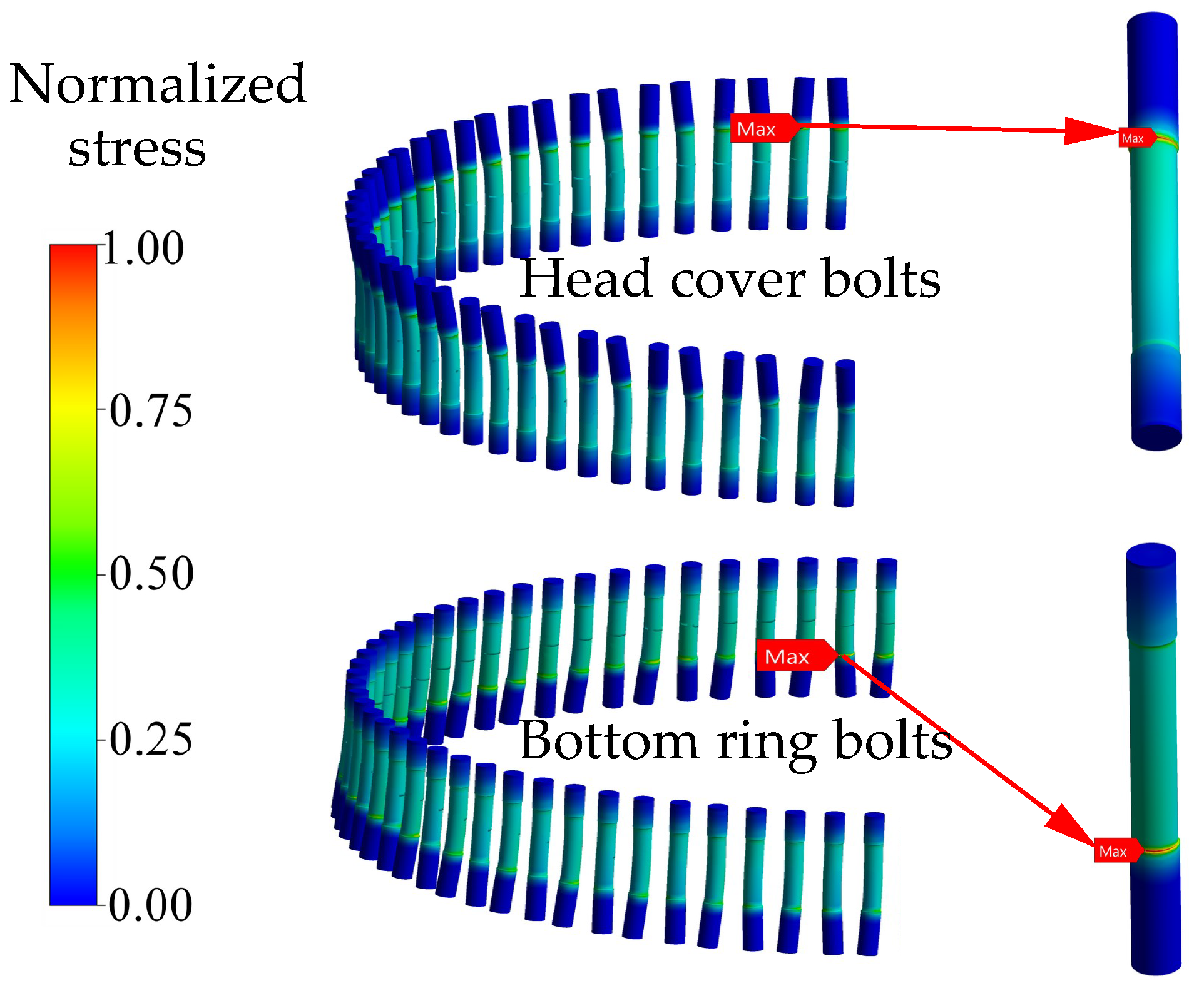
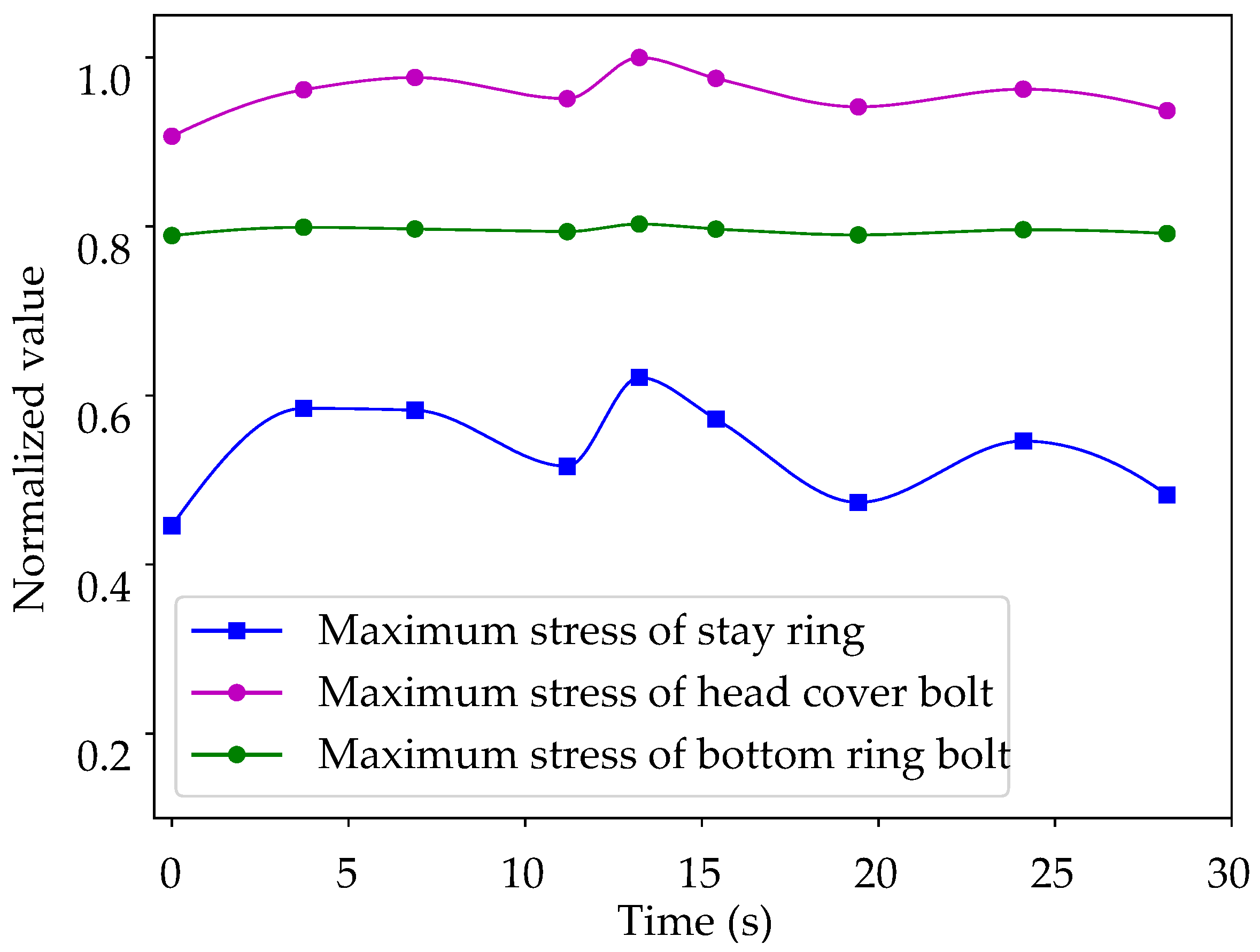
| Flow Domain | Elements () |
|---|---|
| Spiral casing and Stay vane | 3.26 |
| Guide Vane | 0.27 |
| Runner | 3.63 |
| Draft tube | 0.60 |
| Labyrinth seal and Pressure-balance pipelines | 0.40 |
| Total | 8.16 |
| Property | Value |
|---|---|
| Elastic modulus [Pa] | 2.1 × |
| Poisson’s ratio [-] | 0.3 |
| Density [kg·m ] | 7850 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Huang, X.; Yang, M.; Yang, H.; Bi, H.; He, Q.; Wang, Z. Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection. Machines 2022, 10, 1130. https://doi.org/10.3390/machines10121130
Zhao W, Huang X, Yang M, Yang H, Bi H, He Q, Wang Z. Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection. Machines. 2022; 10(12):1130. https://doi.org/10.3390/machines10121130
Chicago/Turabian StyleZhao, Weiqiang, Xingxing Huang, Mengqi Yang, Haixia Yang, Huili Bi, Qilian He, and Zhengwei Wang. 2022. "Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection" Machines 10, no. 12: 1130. https://doi.org/10.3390/machines10121130
APA StyleZhao, W., Huang, X., Yang, M., Yang, H., Bi, H., He, Q., & Wang, Z. (2022). Flow-Induced Dynamic Behavior of Head-Cover Bolts in a Prototype Pump-Turbine during Load Rejection. Machines, 10(12), 1130. https://doi.org/10.3390/machines10121130









