Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control
Abstract
:1. Introduction
2. Notation and Mathematical Background
3. Problem Formulation
4. Costate Estimation for Problem P
4.1. First-Order Optimality Conditions of Problem P
4.2. KKT Conditions of Problem
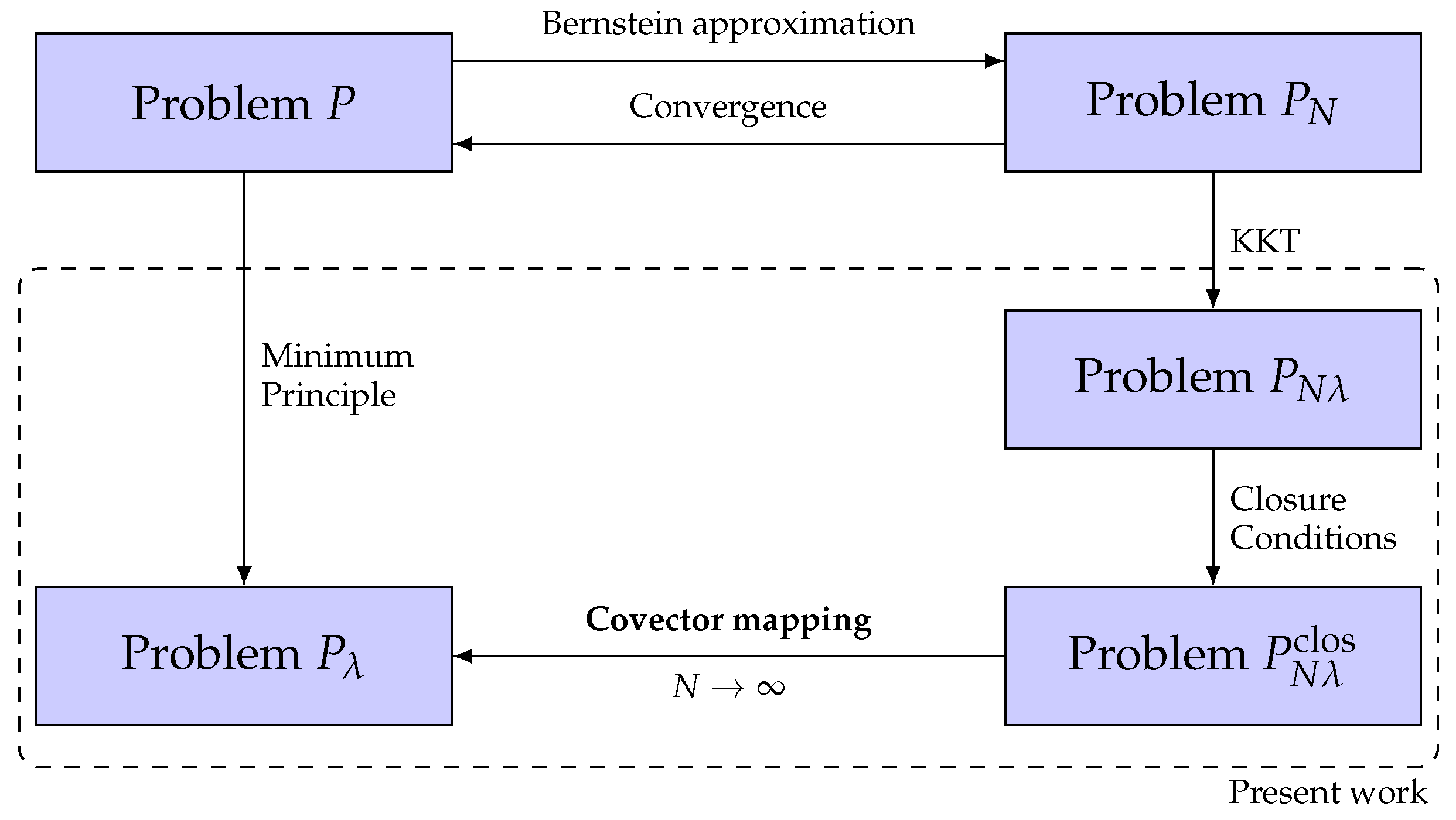
5. Feasibility and Consistency of Problem
6. Numerical Examples
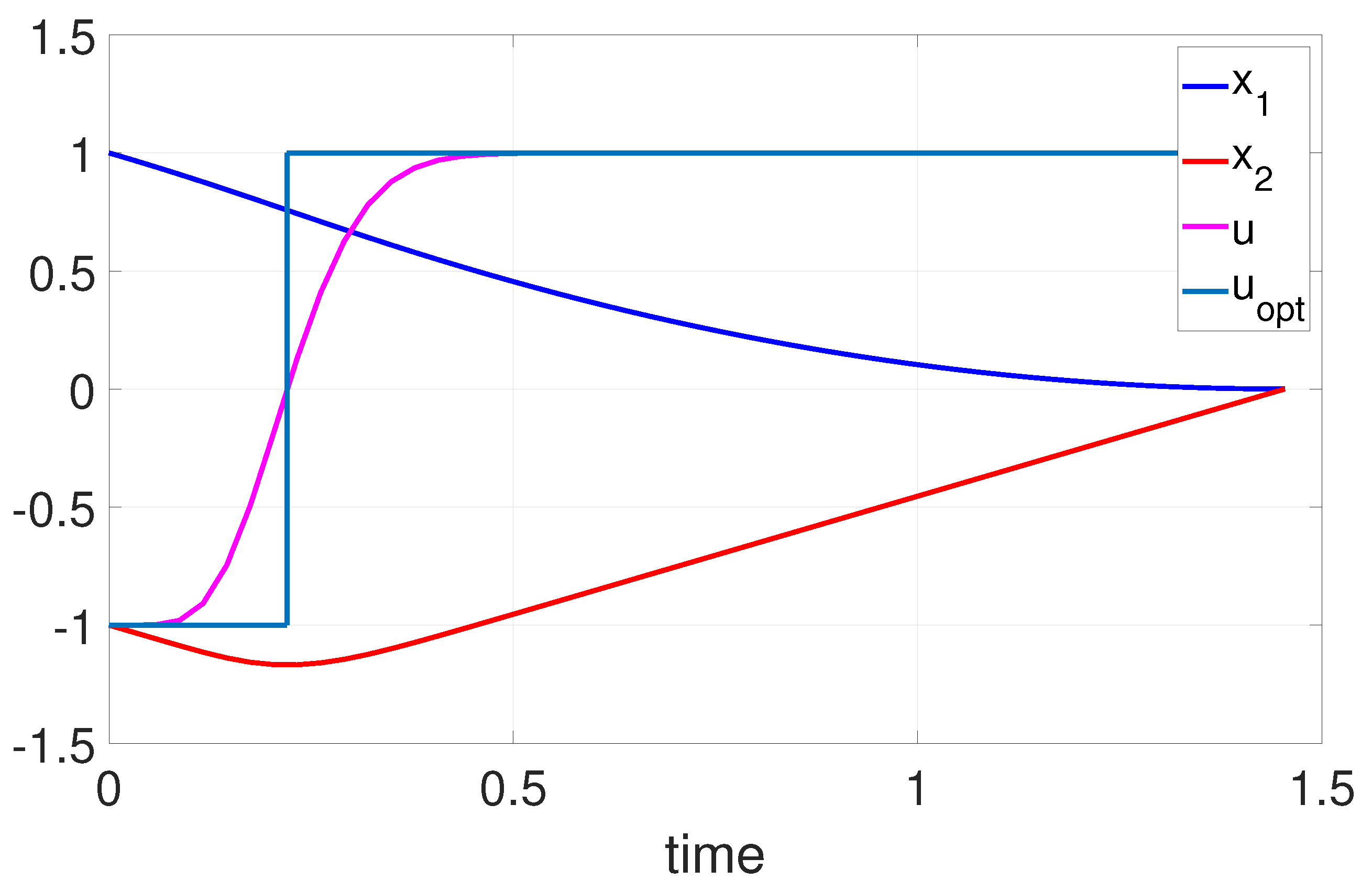
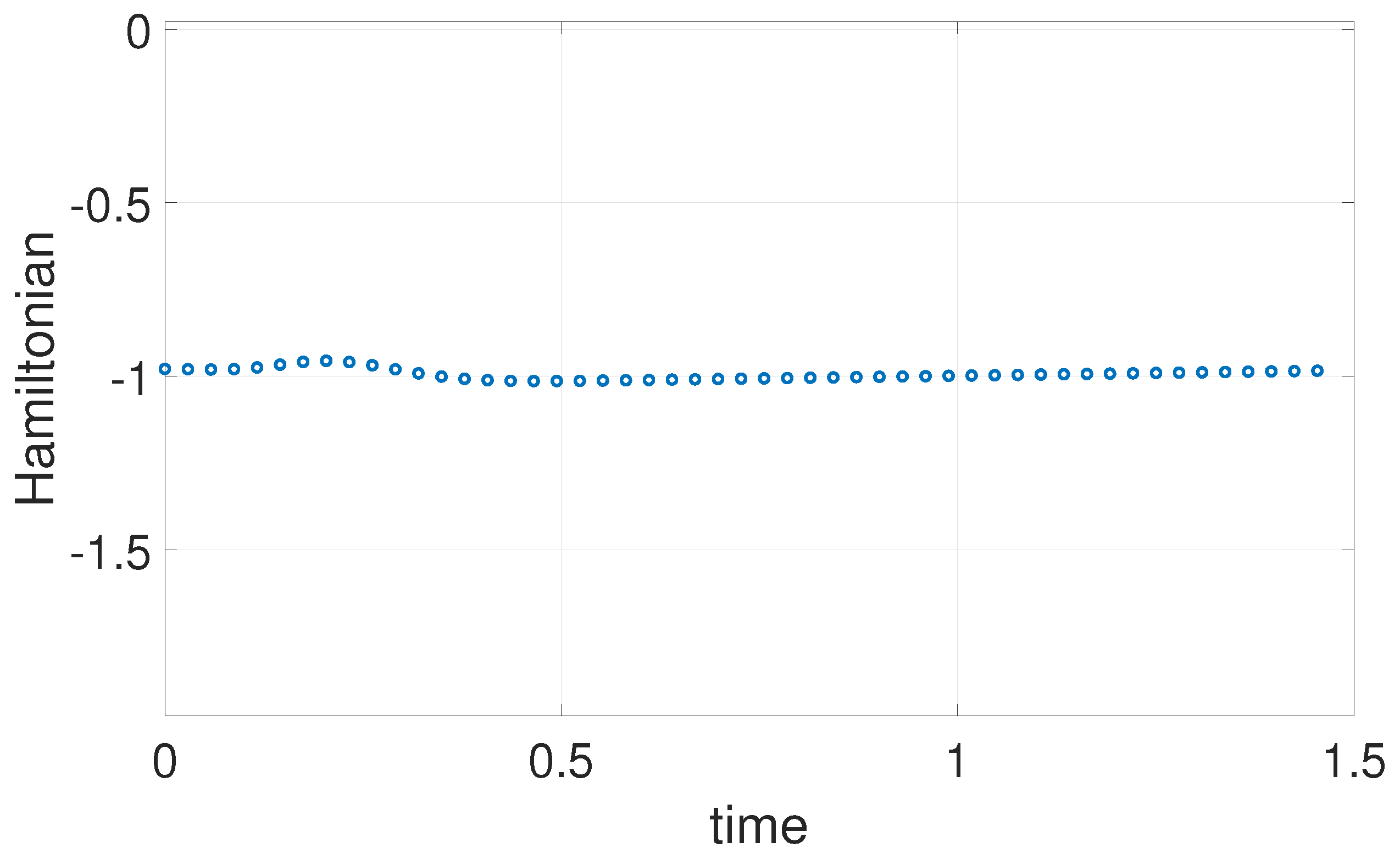
6.1. Example 1: 1D Minimum Time Problem
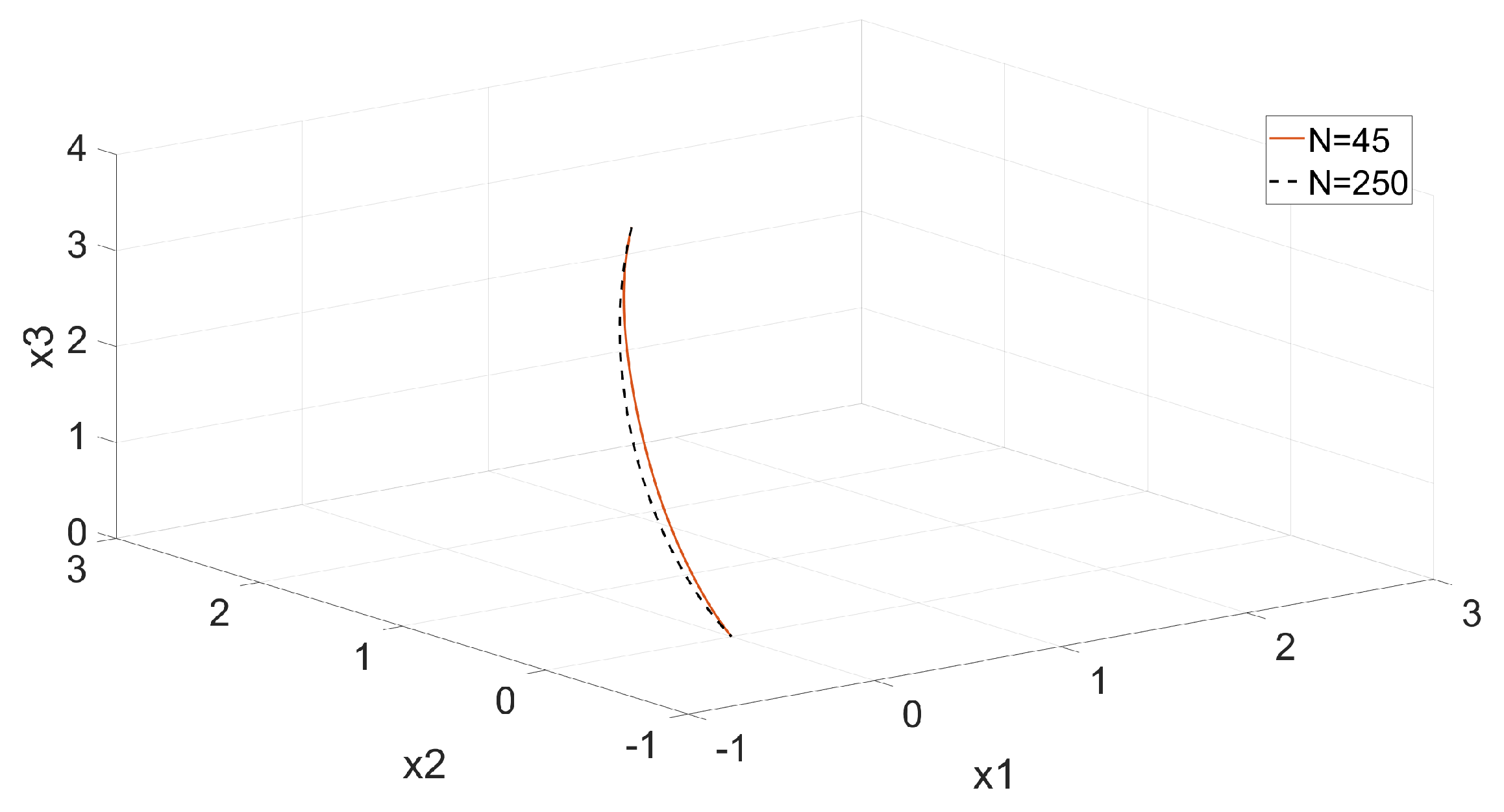
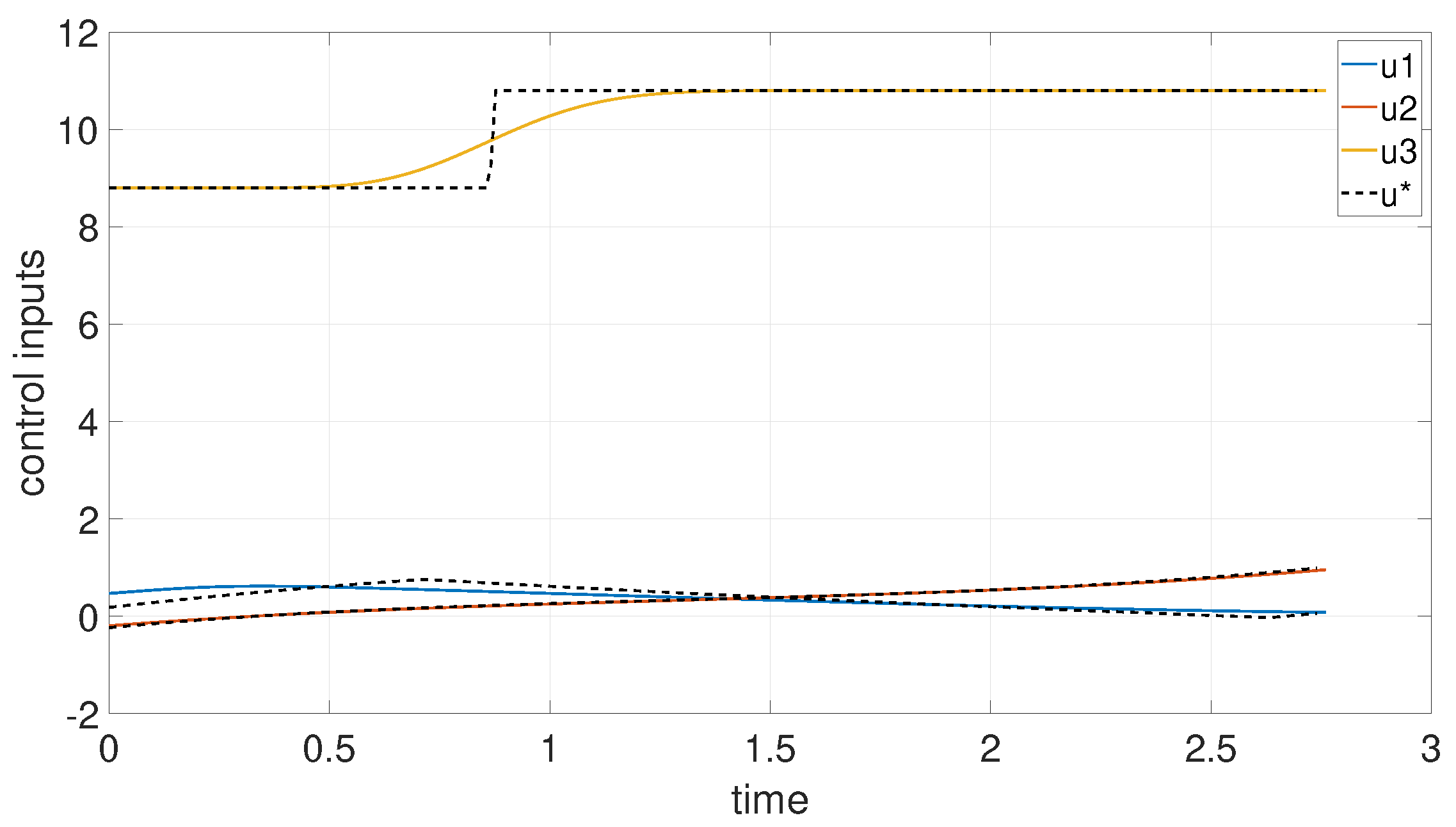
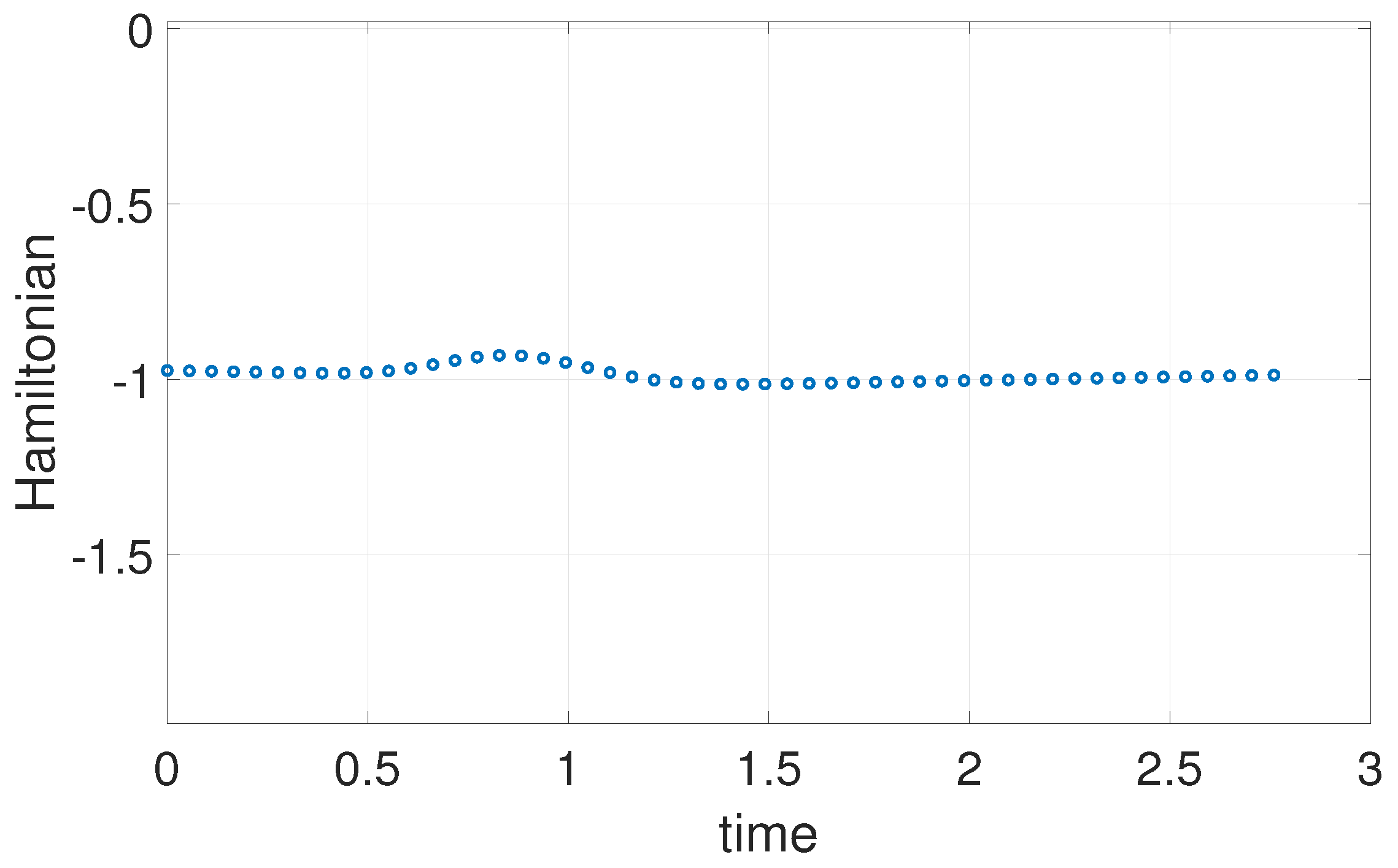
6.2. Example 2: 3D Minimum Time Problem
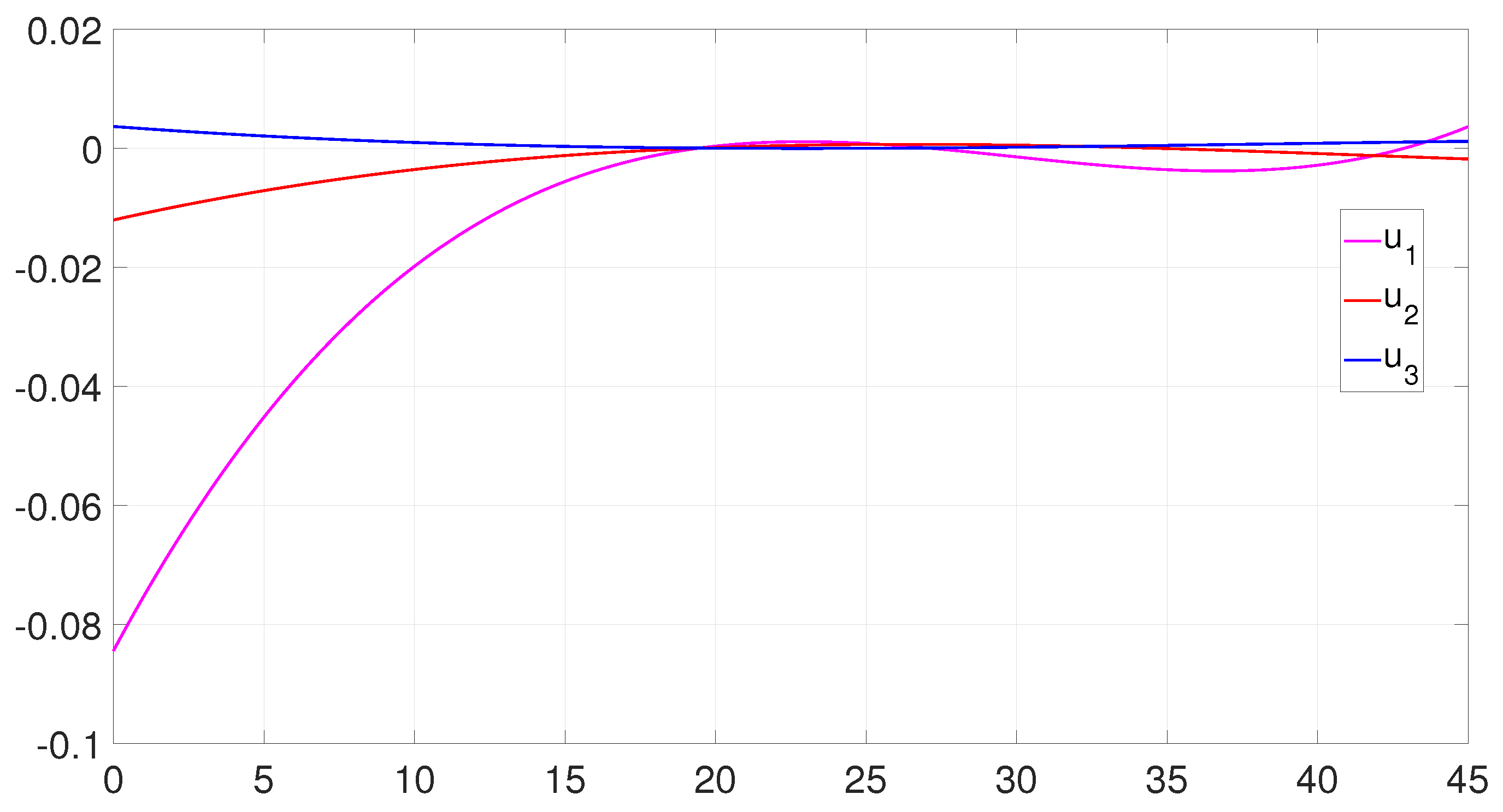
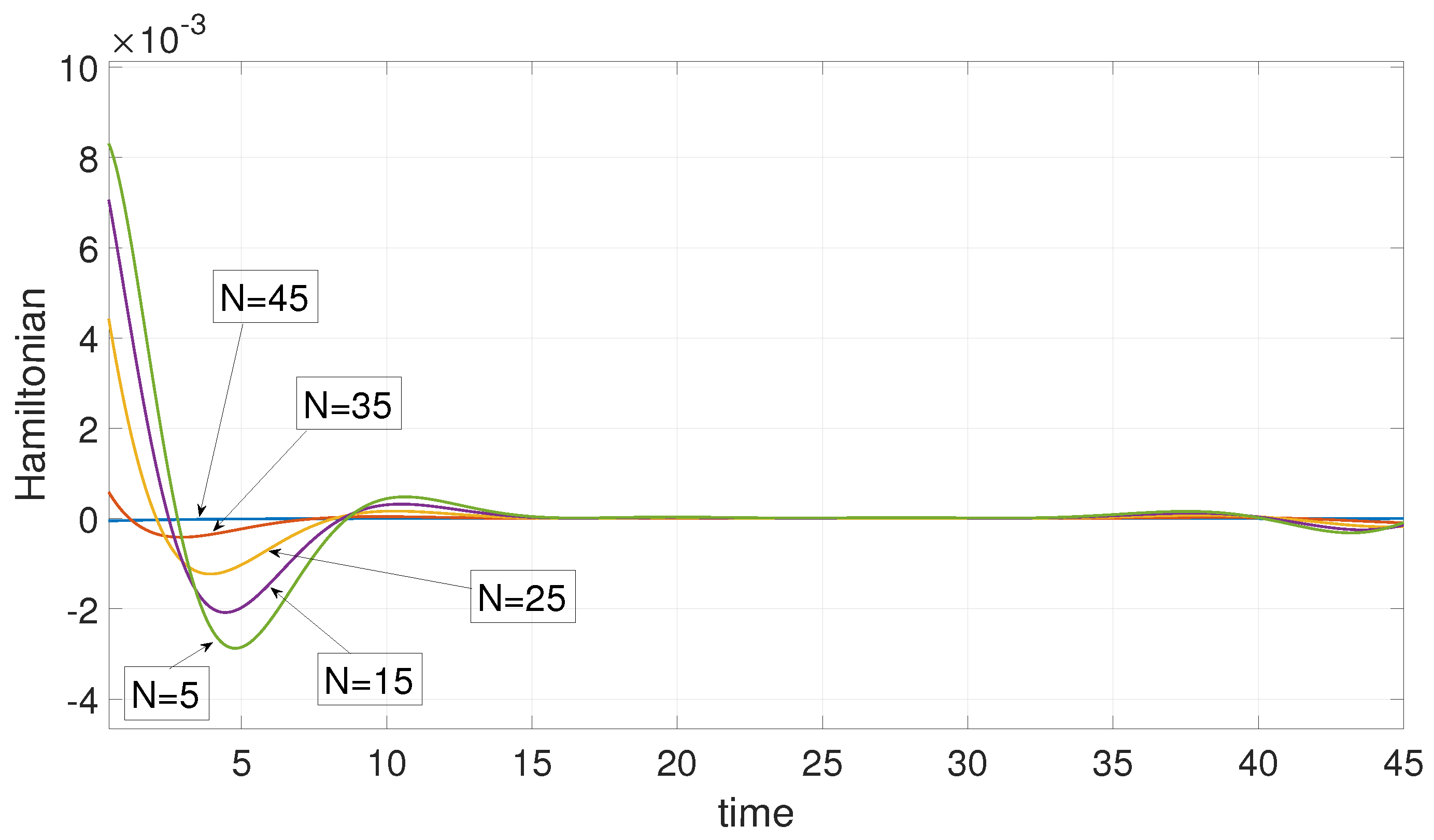
7. Defense against a Swarm Attack
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Equation (34)
References
- Ng, J.; Bräunl, T. Performance comparison of bug navigation algorithms. J. Intell. Robot. Syst. 2007, 50, 73–84. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Autonomous Robot Vehicles; Springer: Berlin/ Heidelberg, Germany, 1986; pp. 396–404. [Google Scholar]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Choset, H.M. Principles of Robot Motion: Theory, Algorithms, and Implementation; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Latombe, J.C. Robot Motion Planning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 124. [Google Scholar]
- Betts, J.T. Survey of numerical methods for trajectory optimization. J. Guid. Control Dyn. 1998, 21, 193–207. [Google Scholar] [CrossRef] [Green Version]
- Von Stryk, O.; Bulirsch, R. Direct and indirect methods for trajectory optimization. Ann. Oper. Res. 1992, 37, 357–373. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Cichella, V. Cooperative Autonomous Systems: Motion Planning and Coordinated Tracking Control for Multi-Vehicle Missions. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2018. [Google Scholar]
- Cichella, V.; Kaminer, I.; Dobrokhodov, V.; Xargay, E.; Choe, R.; Hovakimyan, N.; Aguiar, A.P.; Pascoal, A.M. Cooperative Path-Following of Multiple Multirotors over Time-Varying Networks. IEEE Trans. Autom. Sci. Eng. 2015, 12, 945–957. [Google Scholar] [CrossRef]
- Sun, X.; Cassandras, C.G. Optimal dynamic formation control of multi-agent systems in constrained environments. Automatica 2016, 73, 169–179. [Google Scholar] [CrossRef] [Green Version]
- Walton, C.; Kaminer, I.; Gong, Q.; Clark, A.H.; Tsatsanifos, T. Defense against adversarial swarms with parameter uncertainty. Sensors 2022, 22, 4773. [Google Scholar] [CrossRef]
- Rao, A.V. A survey of numerical methods for optimal control. Adv. Astronaut. Sci. 2009, 135, 497–528. [Google Scholar]
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2010. [Google Scholar]
- Conway, B.A. A survey of methods available for the numerical optimization of continuous dynamic systems. J. Optim. Theory Appl. 2012, 152, 271–306. [Google Scholar] [CrossRef]
- Becerra, V.M. Solving complex optimal control problems at no cost with PSOPT. In Proceedings of the 2010 IEEE International Symposium on Computer-Aided Control System Design, Yokohama, Japan, 8–10 September 2010; pp. 1391–1396. [Google Scholar]
- Febbo, H.; Jayakumar, P.; Stein, J.L.; Ersal, T. NLOptControl: A modeling language for solving optimal control problems. arXiv 2020, arXiv:2003.00142. [Google Scholar]
- Patterson, M.A.; Rao, A.V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive Gaussian quadrature collocation methods and sparse nonlinear programming. ACM Trans. Math. Softw. (TOMS) 2014, 41, 1–37. [Google Scholar] [CrossRef] [Green Version]
- Rutquist, P.E.; Edvall, M.M. Propt—Matlab Optimal Control Software; Tomlab Optimization Inc.: Washington, DC, USA, 2010. [Google Scholar]
- Ross, I.M. Enhancements to the DIDO Optimal Control Toolbox. arXiv 2020, arXiv:2004.13112. [Google Scholar]
- Andersson, J.A.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Fahroo, F.; Ross, I.M. On discrete-time optimality conditions for pseudospectral methods. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006; p. 6304. [Google Scholar]
- Bollino, K.; Lewis, L.R.; Sekhavat, P.; Ross, I.M. Pseudospectral optimal control: A clear road for autonomous intelligent path planning. In Proceedings of the AIAA Infotech@ Aerospace 2007 Conference and Exhibit, Rohnert Park, CA, USA, 7–10 May 2007; p. 2831. [Google Scholar]
- Gong, Q.; Lewis, R.; Ross, M. Pseudospectral motion planning for autonomous vehicles. J. Guid. Control. Dyn. 2009, 32, 1039–1045. [Google Scholar] [CrossRef]
- Bedrossian, N.S.; Bhatt, S.; Kang, W.; Ross, I.M. Zero-propellant maneuver guidance. IEEE Control. Syst. 2009, 29. [Google Scholar]
- Bollino, K.; Lewis, L.R. Collision-free multi-UAV optimal path planning and cooperative control for tactical applications. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 7134. [Google Scholar]
- Bedrossian, N.; Bhatt, S.; Lammers, M.; Nguyen, L.; Zhang, Y. First Ever Flight Demonstration of Zero Propellant Maneuver (TM) Attitute Control Concept. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007; p. 76734. [Google Scholar]
- Ross, I.M.; Karpenko, M. A review of pseudospectral optimal control: From theory to flight. Annu. Rev. Control. 2012, 36, 182–197. [Google Scholar] [CrossRef]
- Polak, E. Optimization: Algorithms and Consistent Approximations; Springer: Berilin, Germany, 1997. [Google Scholar]
- Fahroo, F.; Ross, I.M. Costate estimation by a Legendre pseudospectral method. J. Guid. Control Dyn. 2001, 24, 270–277. [Google Scholar] [CrossRef]
- Darby, C.L.; Garg, D.; Rao, A.V. Costate estimation using multiple-interval pseudospectral methods. J. Spacecr. Rocket. 2011, 48, 856–866. [Google Scholar] [CrossRef]
- Hager, W.W. Runge-Kutta methods in optimal control and the transformed adjoint system. Numer. Math. 2000, 87, 247–282. [Google Scholar] [CrossRef]
- Grimm, W.; Markl, A. Adjoint estimation from a direct multiple shooting method. J. Optim. Theory Appl. 1997, 92, 263–283. [Google Scholar] [CrossRef]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N. Optimal Motion Planning for Differentially Flat Systems Using Bernstein Approximation. IEEE Control Syst. Lett. 2018, 2, 181–186. [Google Scholar] [CrossRef]
- Kielas-Jensen, C.; Cichella, V. BeBOT: Bernstein polynomial toolkit for trajectory generation. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Venetian Macao, Macau, 3–8 November 2019; pp. 3288–3293. [Google Scholar]
- Kielas-Jensen, C.; Cichella, V.; Berry, T.; Kaminer, I.; Walton, C.; Pascoal, A. Bernstein Polynomial-Based Method for Solving Optimal Trajectory Generation Problems. Sensors 2022, 22, 1869. [Google Scholar] [CrossRef] [PubMed]
- Ricciardi, L.A.; Vasile, M. Direct transcription of optimal control problems with finite elements on Bernstein basis. J. Guid. Control Dyn. 2018. [Google Scholar] [CrossRef]
- Choe, R.; Puig-Navarro, J.; Cichella, V.; Xargay, E.; Hovakimyan, N. Cooperative Trajectory Generation Using Pythagorean Hodograph Bézier Curves. J. Guid. Control Dyn. 2016, 39, 1744–1763. [Google Scholar] [CrossRef]
- Ghomanjani, F.; Farahi, M.H. Optimal control of switched systems based on Bezier control points. Int. J. Intell. Syst. Appl. 2012, 4, 16. [Google Scholar] [CrossRef]
- Huo, M.; Yang, L.; Peng, N.; Zhao, C.; Feng, W.; Yu, Z.; Qi, N. Fast costate estimation for indirect trajectory optimization using Bezier-curve-based shaping approach. Aerosp. Sci. Technol. 2022, 126, 107582. [Google Scholar] [CrossRef]
- Zhao, Z.; Kumar, M. Split-bernstein approach to chance-constrained optimal control. J. Guid. Control Dyn. 2017, 40, 2782–2795. [Google Scholar] [CrossRef]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A.M. Optimal Multi-Vehicle Motion Planning using Bernstein Approximants. IEEE Trans. Autom. Control 2020. [Google Scholar] [CrossRef]
- Schwartz, A.; Polak, E. Consistent approximations for optimal control problems based on Runge–Kutta integration. SIAM J. Control Optim. 1996, 34, 1235–1269. [Google Scholar] [CrossRef]
- Bojanic, R.; Cheng, F. Rate of convergence of Bernstein polynomials for functions with derivatives of bounded variation. J. Math. Anal. Appl. 1989, 141, 136–151. [Google Scholar] [CrossRef]
- Popoviciu, T. Sur l’approximation des fonctions convexes d’ordre supérieur. Mathematica 1935, 10, 49–54. [Google Scholar]
- Sikkema, P. Der wert einiger konstanten in der theorie der approximation mit Bernstein-Polynomen. Numer. Math. 1961, 3, 107–116. [Google Scholar] [CrossRef]
- Powell, M.J.D. Approximation Theory and Methods; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Floater, M.S. On the convergence of derivatives of Bernstein approximation. J. Approx. Theory 2005, 134, 130–135. [Google Scholar] [CrossRef]
- Hartl, R.F.; Sethi, S.P.; Vickson, R.G. A survey of the maximum principles for optimal control problems with state constraints. SIAM Rev. 1995, 37, 181–218. [Google Scholar] [CrossRef]
- Garg, D.; Patterson, M.A.; Francolin, C.; Darby, C.L.; Huntington, G.T.; Hager, W.W.; Rao, A.V. Direct trajectory optimization and costate estimation of finite-horizon and infinite-horizon optimal control problems using a Radau pseudospectral method. Comput. Optim. Appl. 2011, 49, 335–358. [Google Scholar] [CrossRef] [Green Version]
- Gong, Q.; Ross, I.M.; Kang, W.; Fahroo, F. Connections between the covector mapping theorem and convergence of pseudospectral methods for optimal control. Comput. Optim. Appl. 2008, 41, 307–335. [Google Scholar] [CrossRef]
- Singh, B.; Bhattacharya, R.; Vadali, S.R. Verification of optimality and costate estimation using Hilbert space projection. J. Guid. Control Dyn. 2009, 32, 1345–1355. [Google Scholar] [CrossRef]
- Kirk. Optimal Control Theory: An Introduction; Prentice-Hall: Hoboken, NJ, USA, 1970. [Google Scholar]
- Ogren, P.; Fiorelli, E.; Leonard, N.E. Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment. IEEE Trans. Autom. Control 2004, 49, 1292–1302. [Google Scholar] [CrossRef] [Green Version]
- Washburn, A.; Kress, M. Combat Modeling; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Walton, C.; Lambrianides, P.; Kaminer, I.; Royset, J.; Gong, Q. Optimal motion planning in rapid-fire combat situations with attacker uncertainty. Naval Res. Logist. 2018, 65, 101–119. [Google Scholar] [CrossRef]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A. Bernstein approximation of optimal control problems. arXiv 2018, arXiv:1812.06132. [Google Scholar]
- Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A.M. Consistent approximation of optimal control problems using Bernstein polynomials. In Proceedings of the 2019 IEEE 58th Conference on Decision and Control (CDC), Nice, France, 11–13 December 2019; pp. 4292–4297. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cichella, V.; Kaminer, I.; Walton, C.; Hovakimyan, N.; Pascoal, A. Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control. Machines 2022, 10, 1132. https://doi.org/10.3390/machines10121132
Cichella V, Kaminer I, Walton C, Hovakimyan N, Pascoal A. Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control. Machines. 2022; 10(12):1132. https://doi.org/10.3390/machines10121132
Chicago/Turabian StyleCichella, Venanzio, Isaac Kaminer, Claire Walton, Naira Hovakimyan, and António Pascoal. 2022. "Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control" Machines 10, no. 12: 1132. https://doi.org/10.3390/machines10121132
APA StyleCichella, V., Kaminer, I., Walton, C., Hovakimyan, N., & Pascoal, A. (2022). Consistency of Approximation of Bernstein Polynomial-Based Direct Methods for Optimal Control. Machines, 10(12), 1132. https://doi.org/10.3390/machines10121132







