Optimizing Propagation of Staphylococcus aureus Infecting Bacteriophage vB_SauM-phiIPLA-RODI on Staphylococcus xylosus Using Response Surface Methodology
Abstract
:1. Introduction
2. Materials and Methods
2.1. Bacterial Strains, Bacteriophage and Media
2.2. Biofilm Removal by Phage phiIPLA-RODI Propagated on S. xylosus CTC1642 and S. aureus IPLA1
2.3. One-Step Growth Curve
2.4. Bacteriophage Amplification: Conventional Phage Propagation
2.5. Bacteriophage Amplification: Phage Propagation for Optimization Purposes
2.6. Experimental Design
2.7. Analysis of Results, Model Validation, and Final Response Surface (RS) Equation
2.8. Statistical Analysis
3. Results
3.1. PhiIPLA-RODI Infects Food-Grade S. xylosus Strains and Other Staphylococcal Species
3.2. Identification of Experimental Factors Affecting Phage Yield
3.3. Response Surface Model for Phage phiIPLA-RODI Yield
3.4. Validation of RSM
3.5. Final Equations for the Phage Production and Phage Amplification Ratio
4. Discussion
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hennekinne, J.A.; de Buyser, M.L.; Dragacci, S. Staphylococcus aureus and its food poisoning toxins: Characterization and outbreak investigation. FEMS Microbiol. Rev. 2012, 36, 815–836. [Google Scholar] [CrossRef] [PubMed]
- European Food Safety Authority (EFSA); European Centre for Disease Prevention and Control (ECDC). The European Union summary report on trends and sources of zoonoses, zoonotic agents and food-borne outbreaks in 2015. EFSA J. 2016, 14, 4634. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention (CDC). National Outbreak Reporting System (NORS); Centers for Disease Control and Prevention (CDC): Atlanta, GA, USA, 2017.
- Le Loir, Y.; Baron, F.; Gautier, M. Staphylococcus aureus and food poisoning. Genet. Mol. Res. 2003, 2, 63–76. [Google Scholar] [PubMed]
- Davis, S.L.; Perri, M.B.; Donabedian, S.M.; Manierski, C.; Singh, A.; Vager, D.; Haque, N.Z.; Speirs, K.; Muder, R.R.; Robinson-Dunn, B.; et al. Epidemiology and outcomes of community-associated methicillin-resistant Staphylococcus aureus infection. J. Clin. Microbiol. 2007, 45, 1705–1711. [Google Scholar] [CrossRef] [PubMed]
- Enright, M.C.; Robinson, D.A.; Randle, G.; Feil, E.J.; Grundmann, H.; Spratt, B.G. The evolutionary history of methicillin-resistant Staphylococcus aureus (MRSA). Proc. Natl. Acad. Sci. USA 2002, 99, 7687–7692. [Google Scholar] [CrossRef] [PubMed]
- Loomba, P.S.; Taneja, J.; Mishra, B. Methicillin and vancomycin resistant S. aureus in hospitalized patients. J. Glob. Infect. Dis. 2010, 2, 275–283. [Google Scholar] [CrossRef] [PubMed]
- Tarai, B.; Das, P.; Kumar, D. Recurrent challenges for clinicians: Emergence of methicillin-resistant Staphylococcus aureus, vancomycin resistance, and current treatment options. J. Lab. Physicians 2013, 5, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Suetens, C.; Hopkins, S.; Kolman, J.; Diaz, L.; European Centre for Disease Prevention and Control (ECDC). Point Prevalence Survey of Healthcare-Associated Infections and Antimicrobial Use in European Acute Care Hospitals; European Centre for Disease Prevention and Control (ECDC): Stockholm, Sweden, 2013.
- Munita, J.M.; Bayer, A.S.; Arias, C.A. Evolving resistance among Gram-positive pathogens. Clin. Infect. Dis. 2015, 61 (Suppl. 2), S48–S57. [Google Scholar] [CrossRef] [PubMed]
- Kutter, E.; De Vos, D.; Gvasalia, G.; Alavidze, Z.; Gogokhia, L.; Kuhl, S.; Abedon, S.T. Phage therapy in clinical practice: Treatment of human infections. Curr. Pharm. Biotechnol. 2010, 11, 69–86. [Google Scholar] [CrossRef] [PubMed]
- Cooper, C.J.; Khan Mirzaei, M.; Nilsson, A.S. Adapting drug approval pathways for bacteriophage-based therapeutics. Front. Microbiol. 2016, 7, 1209. [Google Scholar] [CrossRef] [PubMed]
- Vandenheuvel, D.; Lavigne, R.; Brüssow, H. Bacteriophage Therapy: Advances in Formulation Strategies and Human Clinical Trial. Annu. Rev. Virol. 2015, 2, 599–618. [Google Scholar] [CrossRef] [PubMed]
- García, P.; Rodríguez-Rubio, L.; Rodríguez, A.; Martínez, B. Food biopreservation: Promising strategies using bacteriocins, bacteriophages and endolysins. Trends Food Sci. Technol. 2010, 21, 373–382. [Google Scholar] [CrossRef] [Green Version]
- Aminov, R.; Caplin, J.; Chanishvili, N.; Coffey, A.; Cooper, I.; de Vos, D.; Doška, J.R.; Friman, V.P.; Kurtböke, I.; Pantůček, R.; et al. Application of bacteriophages. Microbiol. Aust. 2017, 38, 63–66. [Google Scholar] [CrossRef]
- Gutiérrez, D.; Vandenheuvel, D.; Martínez, B.; Rodríguez, A.; Lavigne, R.; García, P. Two Phages, phiIPLA-RODI and phiIPLA-C1C, lyse mono- and dual-species staphylococcal biofilms. Appl. Environ. Microbiol. 2015, 81, 3336–3348. [Google Scholar] [CrossRef] [PubMed]
- Kelly, D.; McAuliffe, O.; Ross, R.P.; Coffey, A. Prevention of Staphylococcus aureus biofilm formation and reduction in established biofilm density using a combination of phage K and modified derivatives. Lett. Appl. Microbiol. 2012, 54, 286–291. [Google Scholar] [CrossRef] [PubMed]
- Alves, D.R.; Gaudion, A.; Bean, J.E.; Perez Esteban, P.; Arnot, T.C.; Harper, D.R.; Kot, W.; Hansen, L.H.; Enright, M.C.; Jenkins, A.T. Combined use of bacteriophage K and a novel bacteriophage to reduce Staphylococcus aureus biofilm formation. Appl. Environ. Microbiol. 2014, 80, 6694–6703. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.K.; Bowers, J.; Koeris, M.S. Advancing bacteriophage-based microbial diagnostics with synthetic biology. Trends Biotechnol. 2013, 31, 325–327. [Google Scholar] [CrossRef] [PubMed]
- Warner, C.M.; Barker, N.; Lee, S.W.; Perkins, E.J. M13 bacteriophage production for large-scale applications. Bioprocess Biosyst. Eng. 2014, 37, 2067–2072. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2017; pp. 489–568. ISBN 978-1-119-11347-8. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Multiple Response Optimization. In Response Surface Methodology Process and Product Optimization Using Designed Experiments, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 325–368. ISBN 978-1-118-91601-8. [Google Scholar]
- Grieco, S.H.; Wong, A.Y.; Dunbar, W.S.; MacGillivray, R.T.; Curtis, S.B. Optimization of fermentation parameters in phage production using response surface methodology. J. Ind. Microbiol. Biotechnol. 2012, 39, 1515–1522. [Google Scholar] [CrossRef] [PubMed]
- Gutierrez, D.; Delgado, S.; Vazquez-Sanchez, D.; Martinez, B.; Cabo, M.L.; Rodriguez, A.; Herrera, J.J.; Garcia, P. Incidence of Staphylococcus aureus and analysis of associated bacterial communities on food industry surfaces. Appl. Environ. Microbiol. 2012, 8, 8547–8554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gutiérrez, D.; Ruas-Madiedo, P.; Martínez, B.; Rodríguez, A.; García, P. Effective removal of staphylococcal biofilms by the endolysin LysH5. PLoS ONE 2014, 9, e107307. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, D.; Martínez, B.; Rodríguez, A.; García, P. Isolation and characterization of bacteriophages infecting Staphylococcus epidermidis. Curr. Microbiol. 2010, 61, 601–608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myers, R.H.; Montgomery, D.C. Response surface methodology, 2nd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Pirnay, J.P.; Blasdel, B.G.; Bretaudeau, L.; Buckling, A.; Chanishvili, N.; Clark, J.R.; Corte-Real, S.; Debarbieux, L.; Dublanchet, A.; De Vos, D.; et al. Quality and safety requirements for sustainable phage therapy products. Pharm. Res. 2015, 32, 2173–2179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santos, S.B.; Fernandes, E.; Carvalho, C.M.; Sillankorva, S.; Krylov, V.N.; Pleteneva, E.A.; Shaburova, O.V.; Nicolau, A.; Ferreira, E.C.; Azeredo, J. Selection and characterization of a multivalent Salmonella phage and its production in a nonpathogenic Escherichia coli strain. Appl. Environ. Microbiol. 2010, 76, 7338–7342. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El Haddad, L.; Ben Abdallah, N.; Plante, P.L.; Dumaresq, J.; Katsarava, R.; Labrie, S.; Corbeil, J.; St-Gelais, D.; Moineau, S. Improving the safety of Staphylococcus aureus polyvalent phages by their production on a Staphylococcus xylosus strain. PLoS ONE 2014, 9, e102600. [Google Scholar] [CrossRef] [PubMed]
- Hyman, P.; Abedon, S.T. Practical methods for determining phage growth parameters. Methods Mol. Biol. 2009, 501, 175–202. [Google Scholar] [CrossRef] [PubMed]
- Santos, S.B.; Carvalho, C.; Azeredo, J.; Ferreira, E.C. Population dynamics of a Salmonella lytic phage and its host: Implications of the host bacterial growth rate in modelling. PLoS ONE 2014, 9, e102507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Denes, T.; Wiedmann, M. Environmental responses and phage susceptibility in foodborne pathogens: Implications for improving applications in food safety. Curr. Opin. Biotechnol. 2014, 26, 45–49. [Google Scholar] [CrossRef] [PubMed]
- Bryan, D.; El-Shibiny, A.; Hobbs, Z.; Porter, J.; Kutter, E.M. Bacteriophage T4 Infection of stationary phase E. coli: Life after log from a phage perspective. Front. Microbiol. 2016, 7, 1391. [Google Scholar] [CrossRef] [PubMed]
- Kasman, L.M.; Kasman, A.; Westwater, C.; Dolan, J.; Schmidt, M.G.; Norris, J.S. Overcoming the phage replication threshold: A mathematical model with implications for phage therapy. J. Virol. 2002, 76, 5557–5564. [Google Scholar] [CrossRef] [PubMed]
- Payne, R.J.; Jansen, V.A. Pharmacokinetic principles of bacteriophage therapy. Clin. Pharmacokinet. 2003, 42, 315–325. [Google Scholar] [CrossRef] [PubMed]


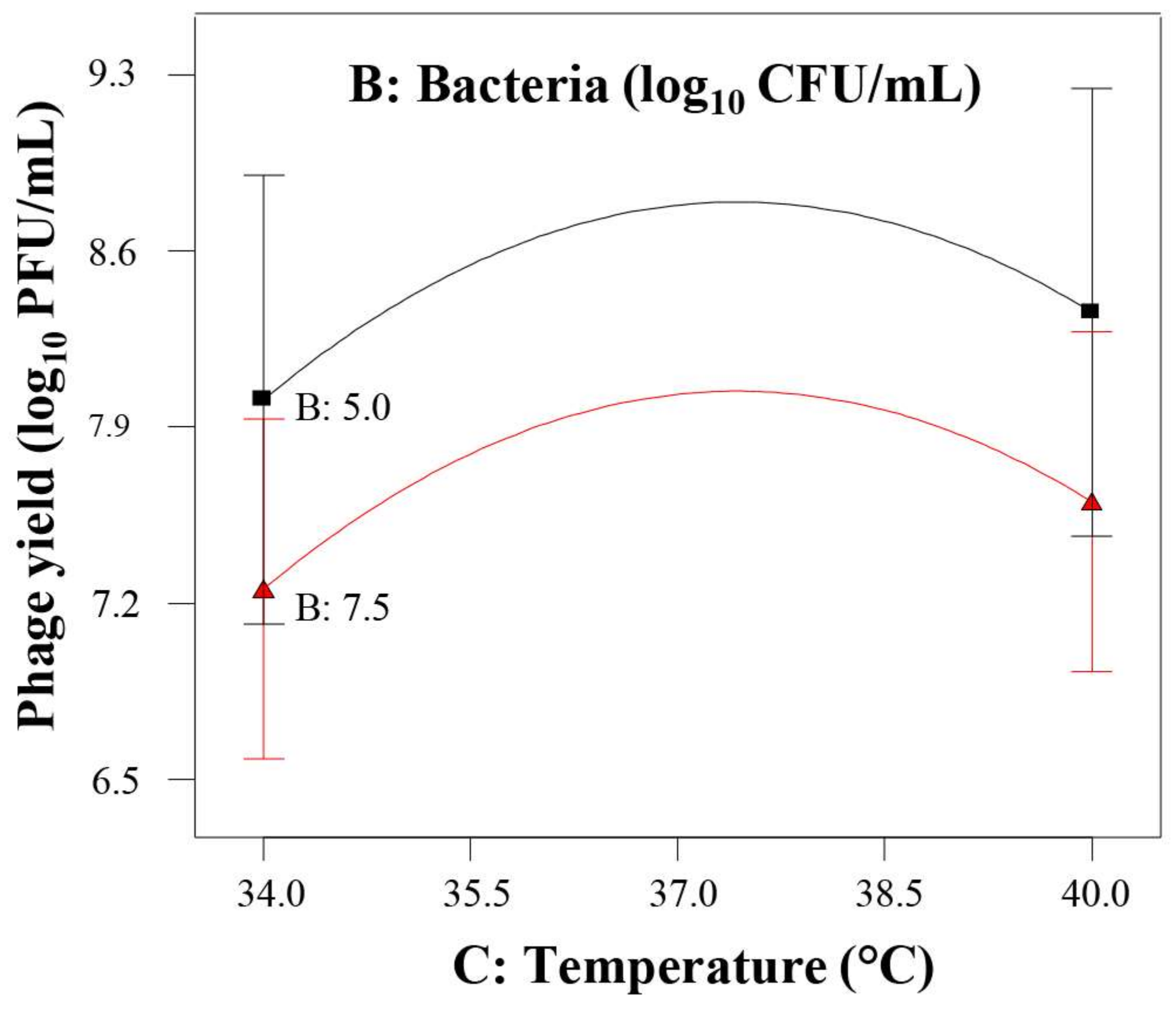
 ) and phage multiplication ratio (
) and phage multiplication ratio (  ), as a function of initial bacterial populations (
), as a function of initial bacterial populations (  ) and phage titers (
) and phage titers (  ), using the desirability approach as implemented in Design Expert.
), using the desirability approach as implemented in Design Expert.
 ) and phage multiplication ratio (
) and phage multiplication ratio (  ), as a function of initial bacterial populations (
), as a function of initial bacterial populations (  ) and phage titers (
) and phage titers (  ), using the desirability approach as implemented in Design Expert.
), using the desirability approach as implemented in Design Expert.
| 1st Tentative Design (Central Composite) | 2nd Design (D-Optimal) a | 3rd Design (Central Composite) b | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Runs | Phage Titer | Bacterial Concentration | Temperature (°C) | Agitation (rpm) | Phage Yield | Phage Titer | Bacterial Concentration | Temperature (°C) | Phage Yield | Phage Titer | Bacterial Concentration | Phage Yield |
| 1 | 7.39 | 7.56 | 24.2 | 67 | 5.53 | 8.00 | 5.78 | 40.0 | 7.42 | 7.00 | 6.85 | 8.4 |
| 2 | 6.50 | 7.28 | 29.0 | 135 | 5.67 | 6.00 | 5.95 | 34.0 | 6.61 | 6.50 | 7.72 | 9.0 |
| 3 | 6.50 | 8.27 | 29.0 | 135 | 4.37 | 7.19 | 7.45 | 37.6 | 8.43 | 6.50 | 7.35 | 9.3 |
| 4 | 5.61 | 6.96 | 33.8 | 67. | 6.66 | 7.19 | 6.30 | 34.0 | 6.86 | 6.50 | 6.05 | 8.5 |
| 5 | 5.00 | 7.53 | 29.0 | 135 | 4.86 | 6.00 | 7.44 | 34.0 | 7.57 | 7.21 | 7.61 | 8.9 |
| 6 | 5.61 | 7.99 | 33.8 | 203 | 4.08 | 7.18 | 6.48 | 37.8 | 7.37 | 5.79 | 7.41 | 9.1 |
| 7 | 6.50 | 7.51 | 29.0 | 135 | 5.79 | 8.00 | 6.81 | 40.0 | 7.81 | 6.00 | 8.15 | 3.7 |
| 8 | 6.50 | 7.62 | 29.0 | 135 | 6.00 | 8.00 | 5.66 | 36.1 | 8.27 | 7.00 | 8.11 | 8.3 |
| 9 | 6.50 | 7.38 | 21.0 | 135 | 5.51 | 6.00 | 6.66 | 37.6 | 8.05 | 6.50 | 7.61 | 9.0 |
| 10 | 6.50 | 6.25 | 29.0 | 135 | 6.13 | 6.00 | 7.82 | 40.0 | 8.12 | 6.50 | 7.34 | 9.0 |
| 11 | 6.50 | 7.57 | 29.0 | 135 | 5.68 | 6.00 | 7.43 | 40.0 | 8.27 | 6.00 | 6.29 | 8.7 |
| 12 | 8.00 | 7.11 | 29.0 | 135 | 6.80 | 8.00 | 7.48 | 34.0 | 8.04 | 6.50 | 7.53 | 9.1 |
| 13 | 5.61 | 7.88 | 24.2 | 203 | 4.23 | 6.00 | 5.77 | 34.0 | 7.58 | 6.50 | 8.40 | 4.1 |
| 14 | 7.39 | 7.01 | 24.2 | 203 | 7.06 | 6.70 | 5.86 | 40.0 | 7.54 | |||
| 15 | 5.61 | 6.99 | 24.2 | 67 | 5.25 | |||||||
| 16 | 6.50 | 7.04 | 29.0 | 20 | 5.02 | |||||||
| 17 | 6.50 | 7.11 | 29.0 | 135 | 5.26 | |||||||
| 18 | 6.50 | 6.85 | 37.0 | 135 | 8.13 | |||||||
| 19 | 7.39 | 7.15 | 33.8 | 203 | 7.34 | |||||||
| 20 | 7.39 | 7.70 | 33.8 | 67 | 6.83 | |||||||
| 21 | 6.50 | 7.18 | 29.0 | 250 | 6.43 | |||||||
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F Value | p-Value (Prob > F) |
|---|---|---|---|---|---|
| Model | 16.99 | 4 | 4.25 | 12.45 | <0.0001 significant |
| A-Phage | 4.46 | 1 | 4.46 | 13.09 | 0.0023 |
| B-Bacteria | 0.78 | 1 | 0.78 | 2.28 | 0.1508 |
| C-Temperature | 3.62 | 1 | 3.62 | 10.62 | 0.0049 |
| B2 | 1.21 | 1 | 1.21 | 3.56 | 0.0775 |
| Residual | 5.46 | 16 | 0.34 | ||
| Cor total | 22.44 | 20 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 2.51 | 4 | 0.63 | 4.59 | 0.0271 |
| B-Bacteria | 0.13 | 1 | 0.13 | 0.91 | 0.3644 |
| C-Temperature | 0.30 | 1 | 0.30 | 2.19 | 0.1734 |
| B2 | 0.52 | 1 | 0.52 | 3.76 | 0.0844 |
| C2 | 0.86 | 1 | 0.86 | 6.28 | 0.0336 |
| Residual | 1.23 | 9 | 0.14 | ||
| Cor total | 3.75 | 13 |
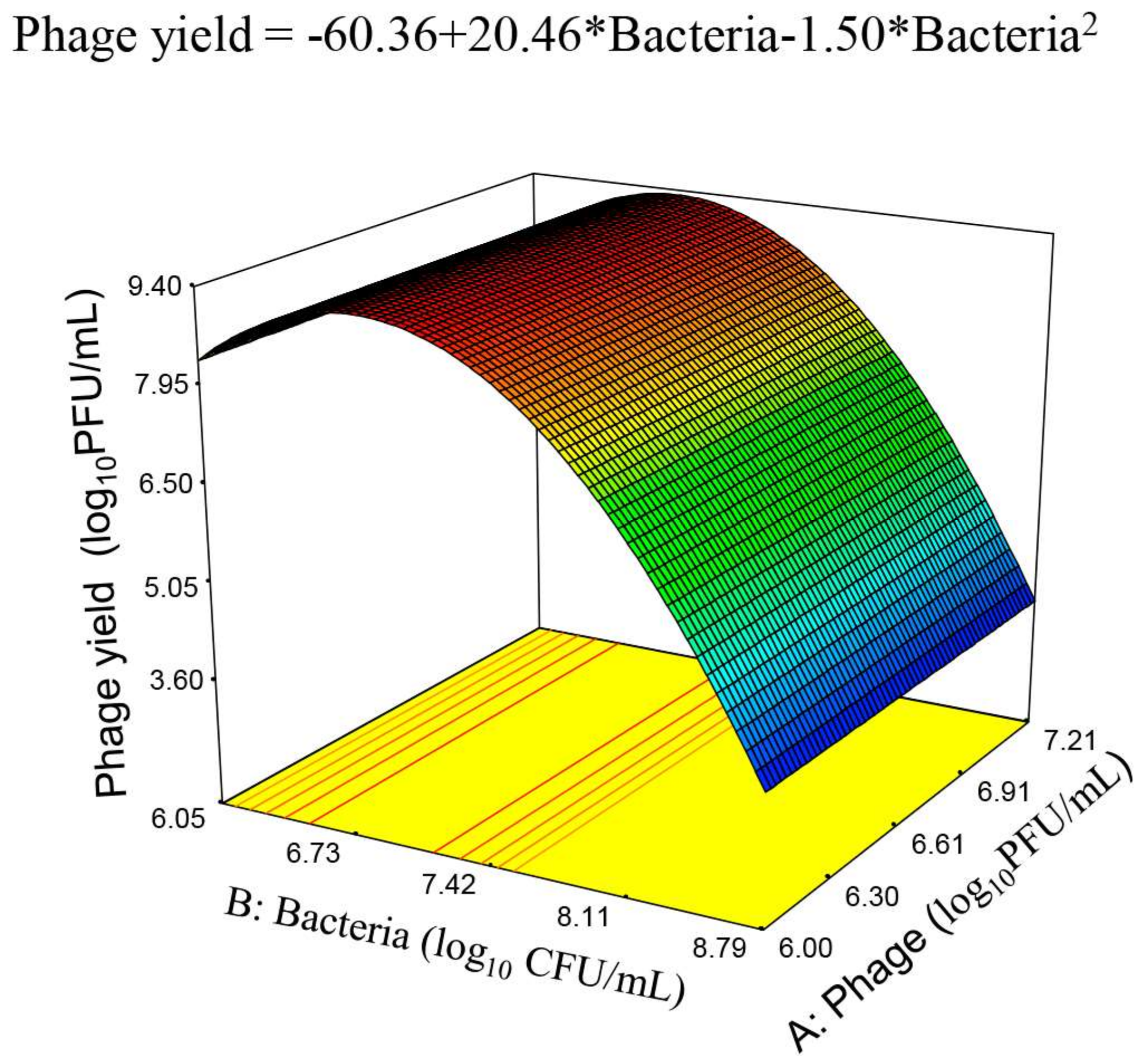
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 37.26 | 2 | 18.63 | 20.01 | <0.0001 significant |
| B-Bacteria | 2.15 | 1 | 2.15 | 2.30 | 0.1455 |
| B2 | 18.16 | 1 | 18.16 | 19.50 | 0.0003 |
| Residual | 1.04 | 18 | 0.058 | ||
| Lack of fit | 0.78 | 16 | 0.049 | 0.37 | 0.9042 not significant |
| Pure error | 0.26 | 2 | 0.13 | ||
| Cor total | 4.03 | 19 |
| Initial Bacteria Population | Initial Phage Titer | Phage Yield, Validation Experiments | Predicted Phage Yield, RS 3rd Design | Predicted Phage Yield, RS Enlarged 3rd Design a |
|---|---|---|---|---|
| 7.51 | 6.50 | 8.8 ± 0.1 | 8.6 ± 0.5 | 8.7 ± 0.3 |
| 7.42 | 6.50 | 8.8 ± 0.1 | 8.7 ± 0.5 | 8.8 ± 0.3 |
| 7.63 | 6.50 | 8.8 ± 0.1 | 8.3 ± 0.5 | 8.4 ± 0.3 |
| 7.56 | 6.50 | 8.7 ± 0.1 | 8.5 ± 0.5 | 8.5 ± 0.3 |
| 7.72 | 6.50 | 8.8 ± 0.1 | 8.1 ± 0.5 | 8.2 ± 0.3 |
| 7.62 | 6.50 | 8.8 ± 0.1 | 8.3 ± 0.5 | 8.4 ± 0.3 |
| 7.35 | 6.50 | 8.6 ± 0.1 | 8.9 ± 0.5 | 8.9 ± 0.3 |
| 7.28 | 6.50 | 8.5 ± 0.1 | 9.0 ± 0.5 | 9.0 ± 0.3 |
| 7.39 | 6.50 | 8.8 ± 0.1 | 8.8 ± 0.5 | 8.9 ± 0.3 |
| Source | Sum of Squares | Degrees of Freedom | Mean Square | F Value | p-Value Prob > F |
|---|---|---|---|---|---|
| Model | 37.26 | 2 | 18.63 | 20.01 | <0.0001 significant |
| B-Bacteria | 2.15 | 1 | 2.15 | 2.30 | 0.1455 |
| B2 | 18.16 | 1 | 18.16 | 19.50 | 0.0003 |
| Residual | 1.04 | 18 | 0.058 | ||
| Lack of fit | 0.78 | 16 | 0.049 | 0.37 | 0.9042 not significant |
| Pure error | 0.26 | 2 | 0.13 | ||
| Cor total | 4.03 | 19 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Menéndez, E.; Arroyo-López, F.N.; Martínez, B.; García, P.; Garrido-Fernández, A.; Rodríguez, A. Optimizing Propagation of Staphylococcus aureus Infecting Bacteriophage vB_SauM-phiIPLA-RODI on Staphylococcus xylosus Using Response Surface Methodology. Viruses 2018, 10, 153. https://doi.org/10.3390/v10040153
González-Menéndez E, Arroyo-López FN, Martínez B, García P, Garrido-Fernández A, Rodríguez A. Optimizing Propagation of Staphylococcus aureus Infecting Bacteriophage vB_SauM-phiIPLA-RODI on Staphylococcus xylosus Using Response Surface Methodology. Viruses. 2018; 10(4):153. https://doi.org/10.3390/v10040153
Chicago/Turabian StyleGonzález-Menéndez, Eva, Francisco Noé Arroyo-López, Beatriz Martínez, Pilar García, Antonio Garrido-Fernández, and Ana Rodríguez. 2018. "Optimizing Propagation of Staphylococcus aureus Infecting Bacteriophage vB_SauM-phiIPLA-RODI on Staphylococcus xylosus Using Response Surface Methodology" Viruses 10, no. 4: 153. https://doi.org/10.3390/v10040153
APA StyleGonzález-Menéndez, E., Arroyo-López, F. N., Martínez, B., García, P., Garrido-Fernández, A., & Rodríguez, A. (2018). Optimizing Propagation of Staphylococcus aureus Infecting Bacteriophage vB_SauM-phiIPLA-RODI on Staphylococcus xylosus Using Response Surface Methodology. Viruses, 10(4), 153. https://doi.org/10.3390/v10040153







