Viral Phrenology
Abstract
1. Introduction
2. Materials and Methods
2.1. Virus Library
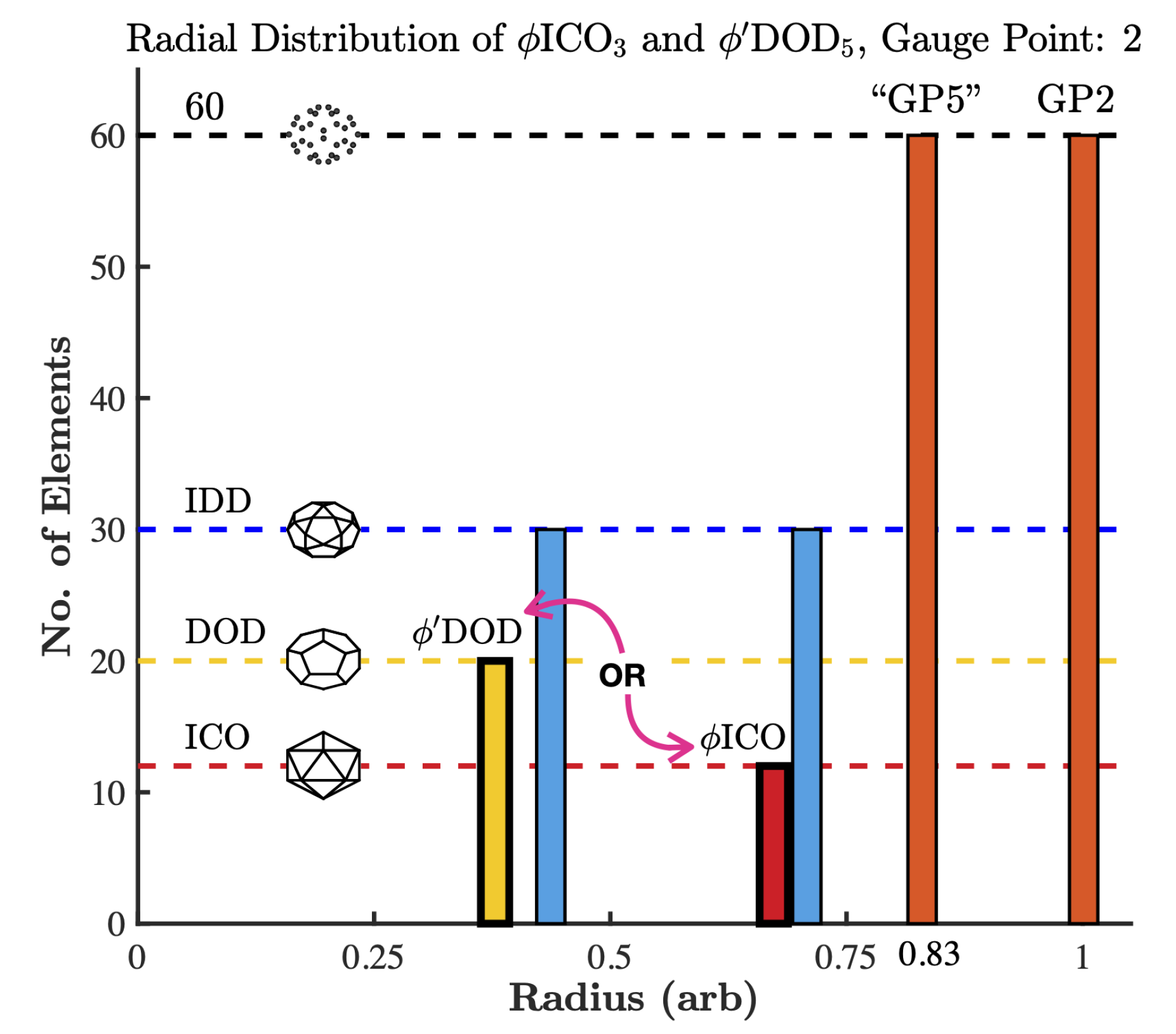
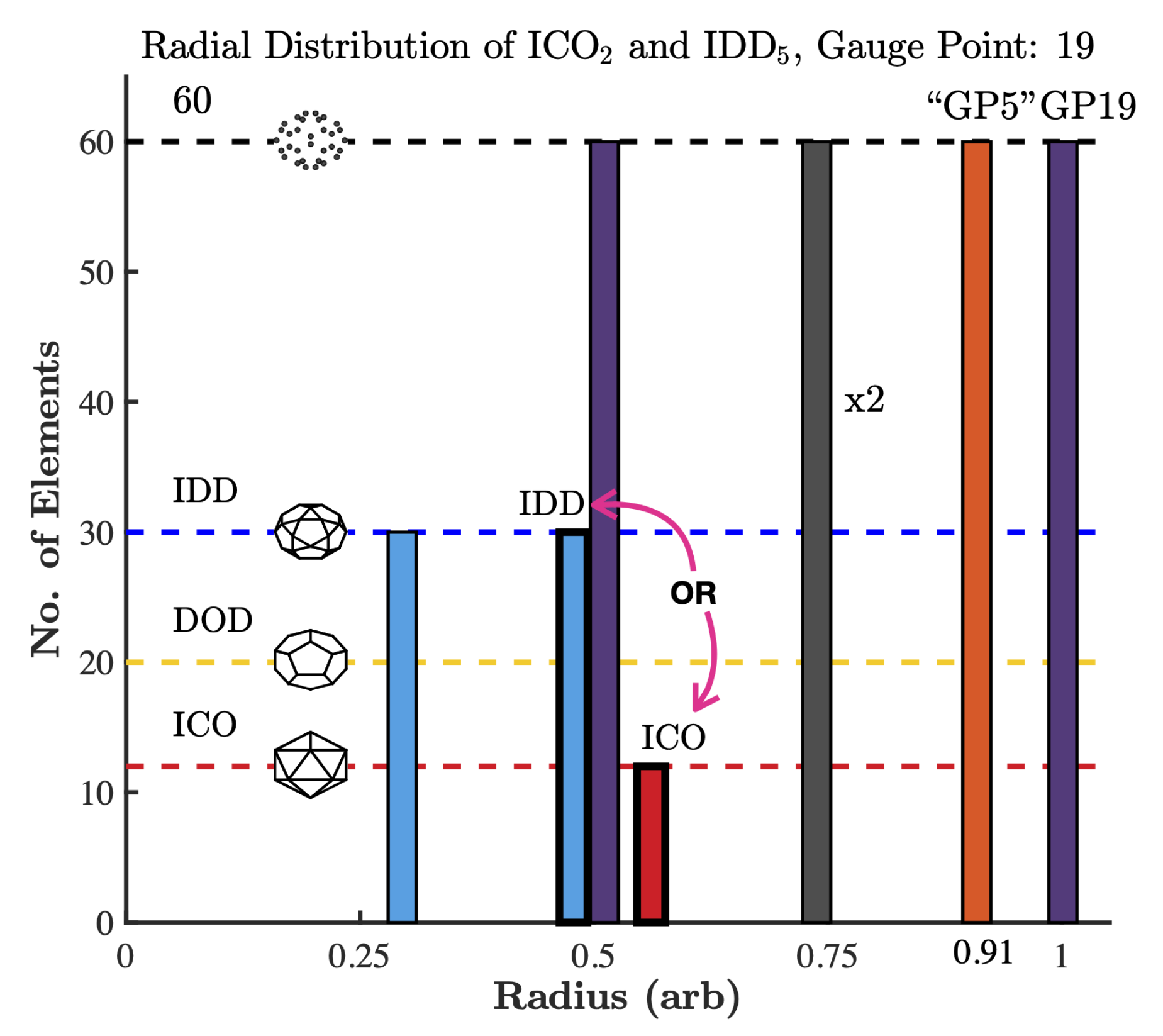
2.2. Point Arrays
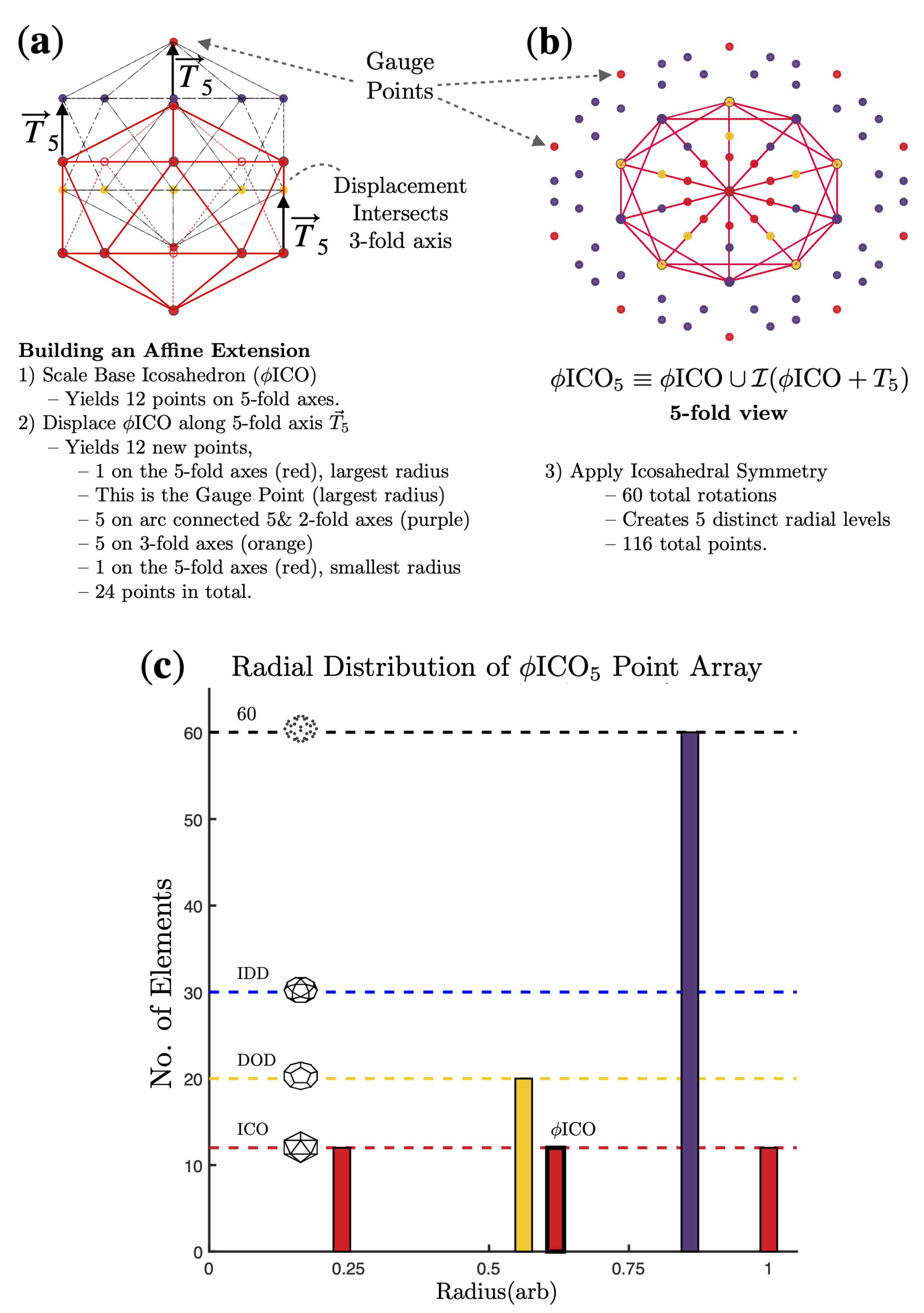
3. Results
3.1. Gauge Point vs. Triangulation Number
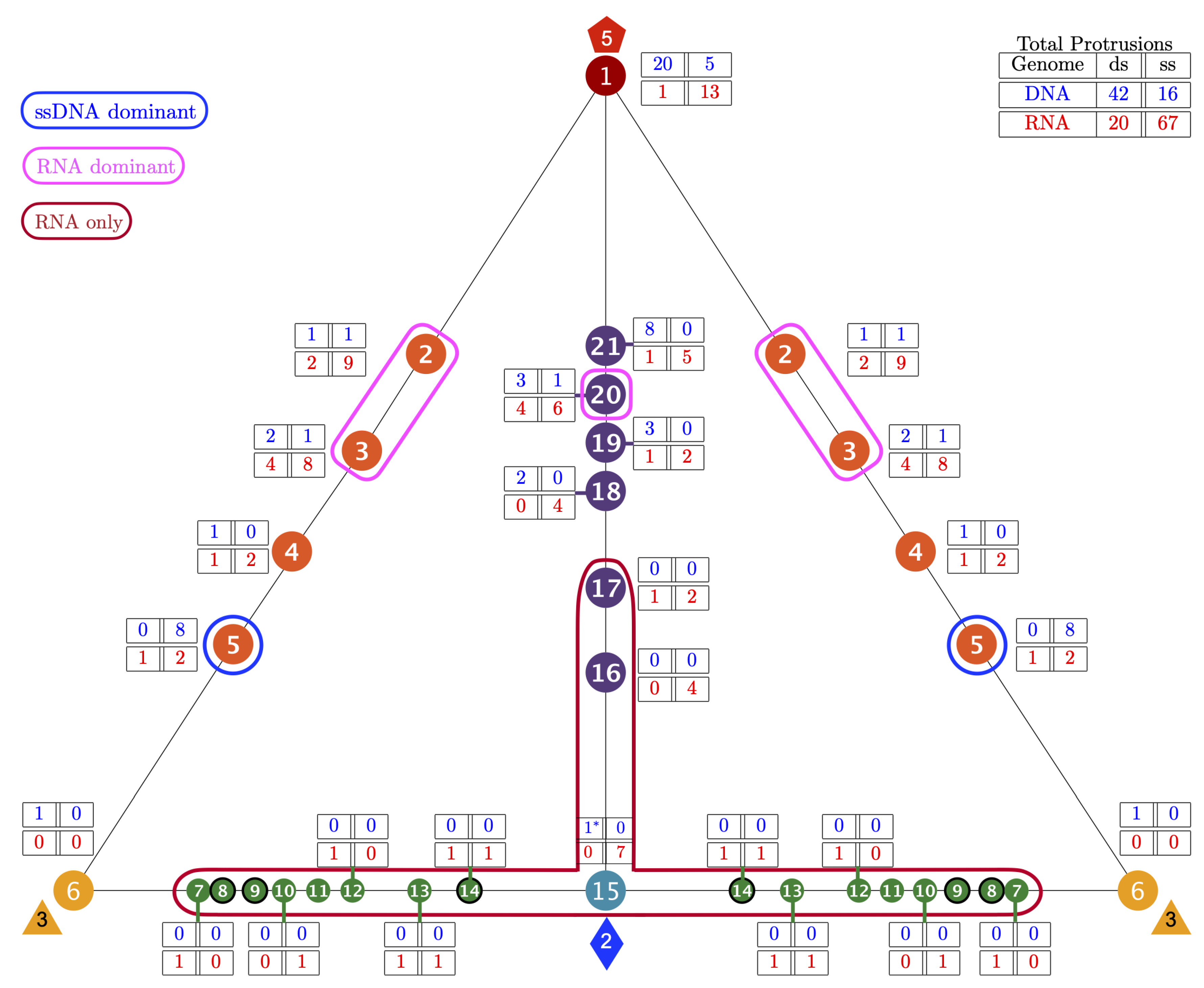
3.2. Gauge Point vs. Genome
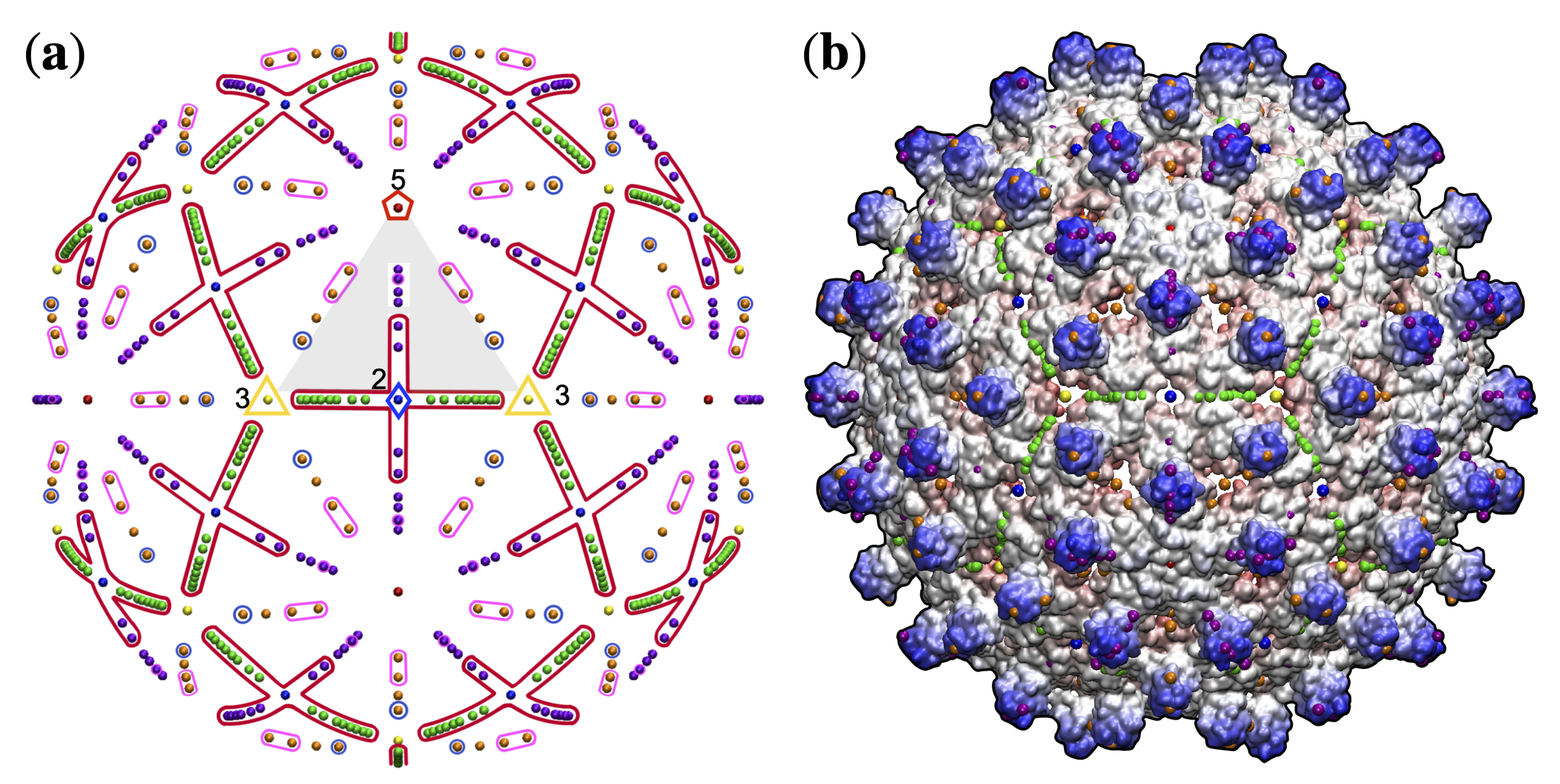
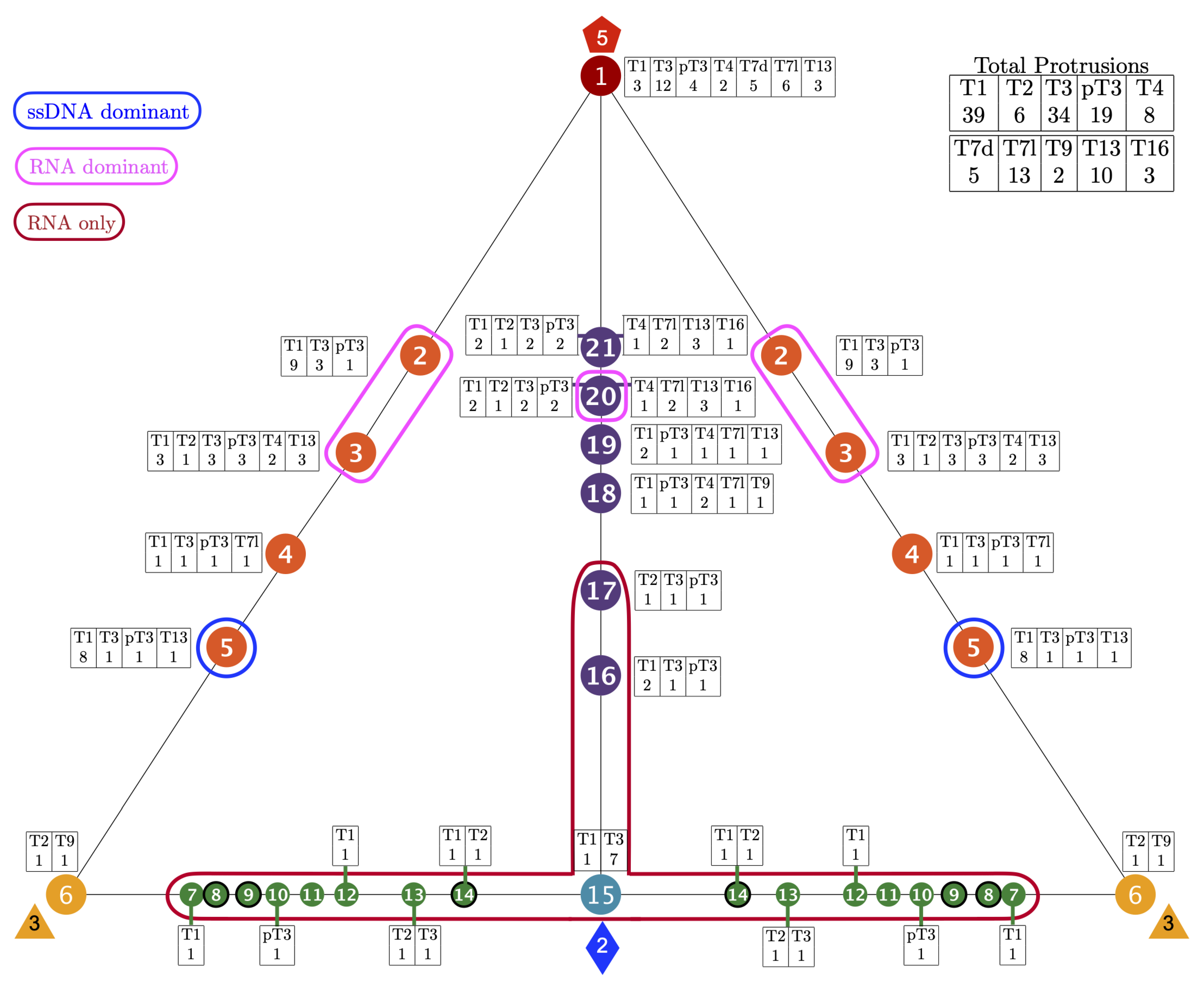
3.3. Gauge Points 1 to 6
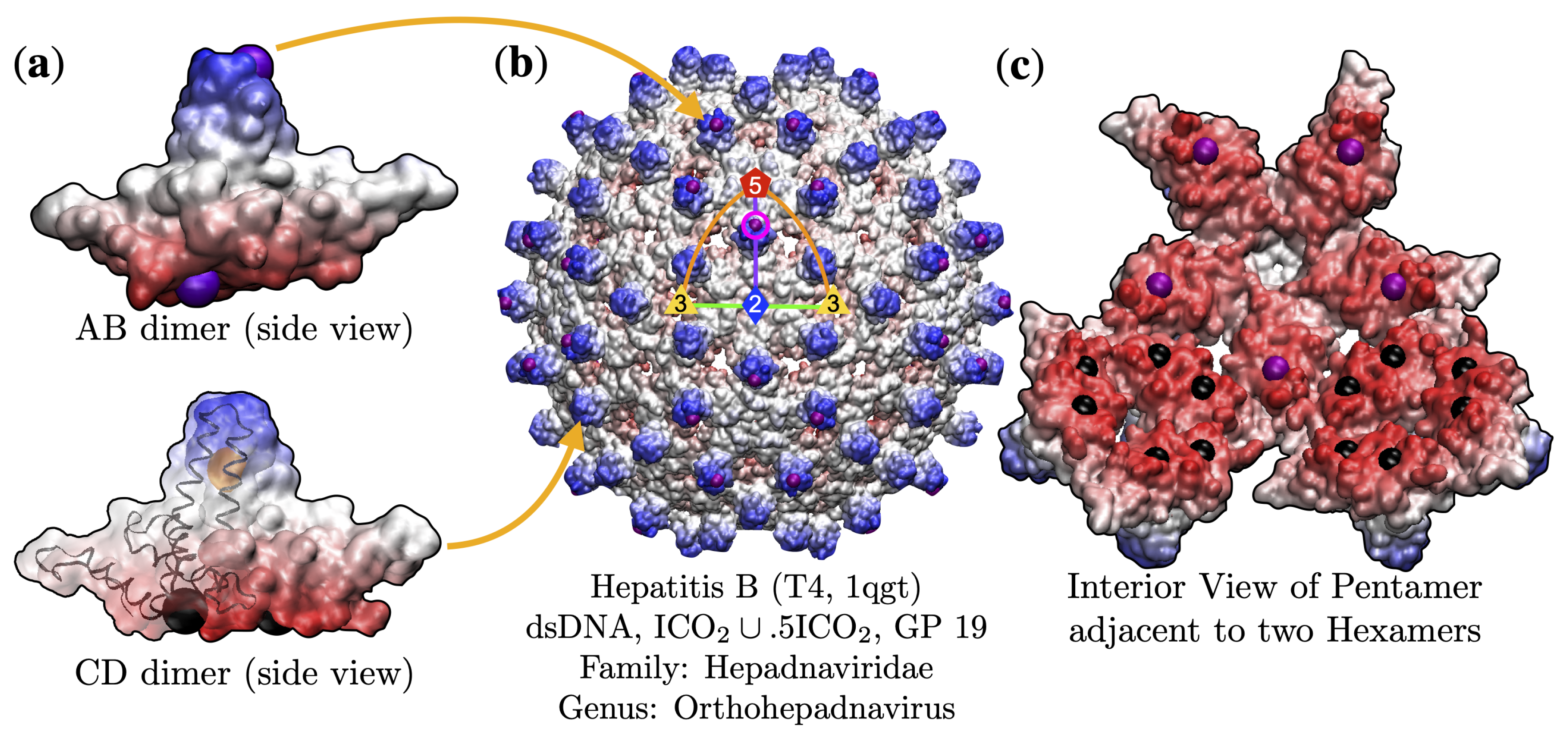
3.3.1. T7d Viral Capsids
3.3.2. Parvoviradae Family
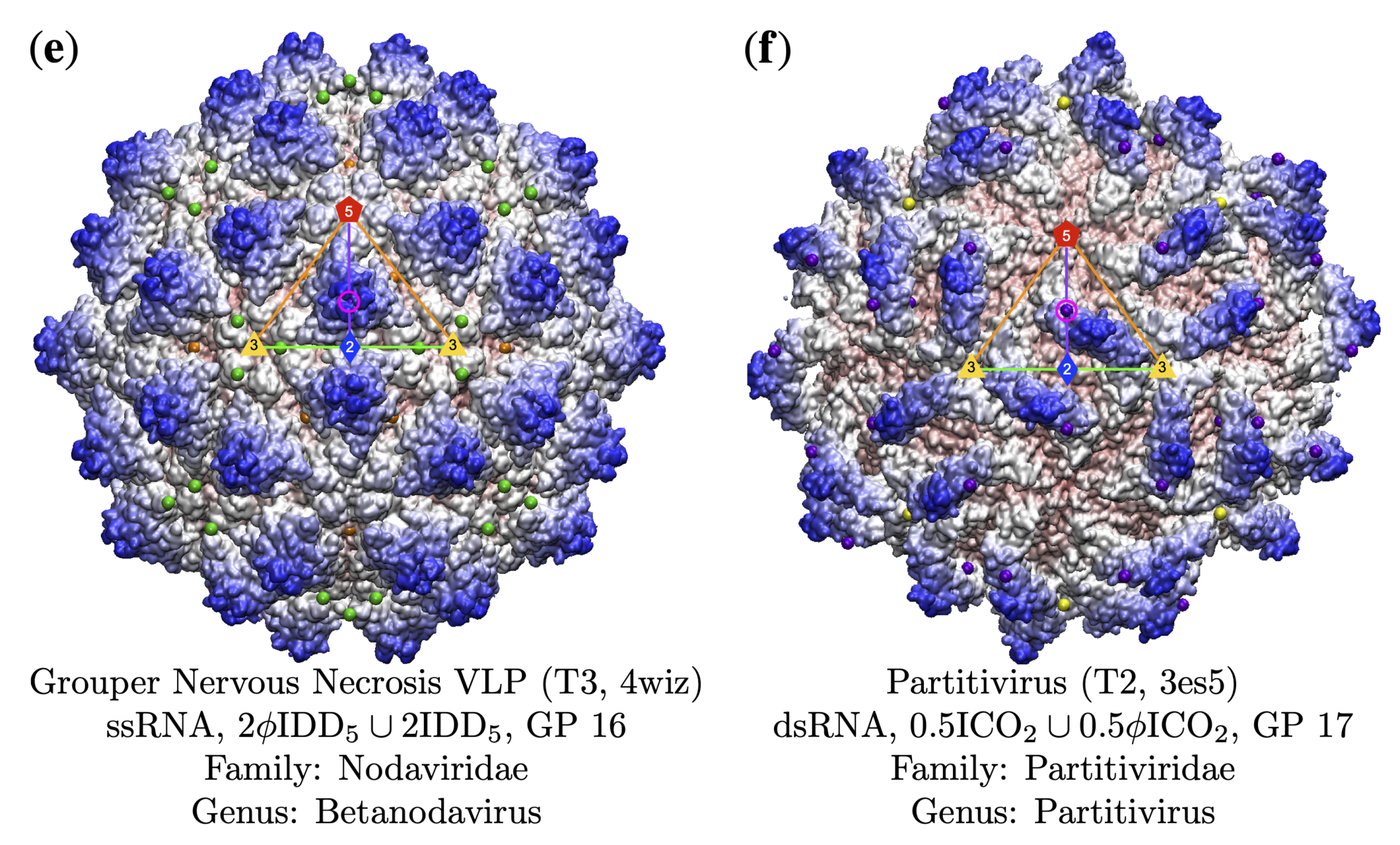
3.4. Gauge Points 7 to 17: RNA Viruses Only
3.5. Gauge Points 18 to 21
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AU | Asymmetric Unit |
| BC | Baltimore Classification |
| GP | Gauge Point |
| PA | Point Array |
| TX | Triangulation number X, e.g., T3 or T7. |
Appendix A. Data Set
| Family | Genus | T# | GP | pdb |
|---|---|---|---|---|
| Adenoviridae | Mastadenovirus | 1 | 19 | 4aqq |
| Mastadenovirus | pT25 | 21 | 6b1t | |
| Bacteria | Haliangium | 9 | 6 | 6mzx |
| Birnaviridae | Aquabirnavirus | 1 | 7 | 3ide |
| Avibirnavirus | 1 | 12 | 2df7 | |
| Avibirnavirus | 13 | 3 or 20 | 1wce | |
| Bromoviridae | Alfamovirus | 1 | 3 | amv |
| Bromovirus | 1 | 21 | 1yc6 | |
| Bromovirus | 3 | 5 or 20 | 1za7 | |
| Cucumovirus | 3 | 20 | 1f15 | |
| Caliciviridae | Lagovirus | 3 | 15 | 3j1p |
| Norovirus | 1 | 16 | 6ouc | |
| Norovirus | 3 | 15 | 6p4j | |
| Norovirus | 3 | 1 | 6p4l | |
| Norovirus | 4 | 18 | 6ouu | |
| Vesivirus | 1 | 14 | 4pb6 | |
| Vesivirus | 3 | 15 | 2gh8 | |
| Chrysoviridiae | Chrysovirus | 1 | 19 or 21 | 3j3i |
| Circoviridae | Circovirus | 1 | 20 | 5j37 |
| Corticoviridae | Corticovirus | pT21 | 1 | 2w0c |
| Cystoviridae | Cystovirus | 2 | 13 | 4btg |
| Dicistroviridae | Aparavirus | pT3 | 3 | 5lwg |
| Cripavirus | pT3 | 20 | 1b35 | |
| Triatovirus | pT3 | 3 | 5mqc | |
| Flaviviridae | Flavivirus | 3 | 21 | 6co8 |
| Hepadnaviridae | Orthohepadnavirus | 3 | 3 or 15 | 6bvn |
| Orthohepadnavirus | 4 | 18 | 6hu4 | |
| Hepeviridae | Hepevirus | 1 | 15 | 3hag |
| Herpesviridae | Alphaherpesvirinae | 16 | 19 | 5zap |
| Muromegalovirus | 16 | 21 | 6nhj | |
| Rhadinovirus | 16 | 20 | 6b43 | |
| Iflaviridae | Iflavirus | pT3 | 17 | 5lsf |
| Lavidaviridae | Sputnikvirus | pT27 | 1 | 3j26 |
| Leviviridae | Allolevivirus | 3 | 3 | 5vly |
| Levivirus | 1 | 16 | 4zor | |
| Levivirus | 3 | 2 | 1e6t | |
| Levivirus | 3 | 2 | 2bu1 | |
| Unclassified | 3 | 4 or 13 | 2vf9 | |
| Microviridae | Microvirus | 1 | 1 | 1gff |
| Microvirus | 1 | 1 | 2bpa | |
| Myoviridae | T4virus | 13 | 1 | 5vf3 |
| Nodaviridae | Alphanodavirus | 3 | 1 | 4ftb |
| Betanodavirus | 1 | 2 | 4rft | |
| Betanodavirus | 3 | 16 | 4wiz | |
| Unclassified | 1 | 20 or 2 | 5yl1 | |
| Unclassified | 3 | 17 | 4nwv | |
| Unclassified Nodaviridae | 3 | 1 | 6jjc | |
| Papillomaviridae | Alphapapillomavirus | 1 | 21 | 1dzl |
| Alphapapillomavirus | 7d | 1 | 5kep | |
| Alphapapillomavirus | 7d | 1 | 5keq | |
| Deltapapillomavirus | 7d | 1 | 3iyj | |
| Partitiviridae | Partitivirus | 2 | 17 | 3es5 |
| Parvoviridae | Ambidensovirus | 1 | 5 | 4mgu |
| Bocaparvovirus | 1 | 5 | 5us7 | |
| Densovirus | 1 | 5 | 3p0s | |
| Dependoparvovirus | 1 | 5 | 6e9d | |
| Dependoparvovirus | 1 | 5 | 6nz0 | |
| Erythroparvovirus | 1 | 2 or 3 | 6nn3 | |
| Parvovirus | 1 | 5 | 4g0r | |
| Penstyldensovirus | 1 | 1 | 3n7x | |
| Protoparvovirus | 1 | 5 | 6bwx | |
| Virus-Like Particle | 1 | 5 | 6nf9 | |
| Phycodnaviridae | Chlorovirus | 169 | 21 | 6ncl |
| Chlorovirus | pT169 | 1 | 1m4x | |
| Picobirnaviridae | Picobirnavirus | 2 | 14 | 2vf1 |
| Picornaviridae | Apthovirus | pT3 | 3 or 4 | 1qqp |
| Cardiovirus | pT3 | 19 | 5cfc | |
| Cardiovirus | pT3 | 2 | 5cfd | |
| Enterovirus | pT3 | 1 | 4q4w | |
| Enterovirus A | pT3 | 21 | 6smg | |
| Enterovirus F | pT3 | 5 or 21 | 6t40 | |
| Heptaovirus | 3 | 1 | 4qpi | |
| Heptaovirus | pT3 | 10 | 6jhs | |
| Kobuvirus | pT3 | 1 | 5aoo | |
| Parechovirus | pT3 | 16 | 6gv4 | |
| Rhinovirus | pT3 | 1 | 1aym | |
| Senecavirus | pT3 | 18 | 3cji | |
| Podoviridae | Bpp1virus | 7l | 1 | 3j4u |
| Epsilon15-like | 7l | 20 | 3j40 | |
| P22-like | 7l | 20 or 18 | 2xyy | |
| P22virus | 7l | 1 | 5l35 | |
| Phi29virus | 3 | 2 | 1yxn | |
| T7virus | 7l | 1 | 3j7w | |
| Unassigned Autographivirinae | 7l | 1 | 2xd8 | |
| Polyomaviridae | Betapolyomavirus | 7d | 1 | 6gg0 |
| Polyomavirus | 7d | 1 | 1sva | |
| Protogloboviridae | Alphaprotoglobovirus | 43 | 1 | 6oj0 |
| Reoviridae | Aquareovirus | 1 | 3 | 5zvt |
| Aquareovirus | 2 | 3 or 6 | 3iyl | |
| Cypovirus | 1 | 2 | 3jay | |
| Cypovirus | 2 | 20 | 3izx | |
| Dinovernavirus | 1 | 2 | 6djy | |
| Orbivirus | 13 | 5 or 20 | 2btv | |
| Orthoreovirus | 13 | 3 | 2cse | |
| Phytoreovirus | 13 | 20 | 1uf2 | |
| Rotavirus | 13 | 3 | 3iyu | |
| Retroviridae | Unclassified | 1 | 2 | 6ssj |
| Unclassified | 3 | 21 | 6ssm | |
| Saccharomycetals | Saccharomyces | 9 | 18 | 6r24 |
| Sarthroviridae | Macronovirus | 1 | 2 | 6jja |
| Satellites | Papanivirus | 1 | 18 | 5cvz |
| Secoviridae | Comovirus | pT3 | 1 | 5fmo |
| Nepovirus | pT3 | 20 | 2y26 | |
| Siphoviridae | Cyanophage Mic1 | 13 | 1 | 6j3q |
| Lambdavirus | 7l | 1 | 1ohg | |
| Oshimavirus | 7l | 21 | 6o3h | |
| P23 Virus | 7l | 19 or 21 | 6i9e | |
| Phietavirus | 4 | 1 | 6b23 | |
| Phietavirus | 7l | 4 | 6b0x | |
| Tequintavirus | 13 | 1 | 6omc | |
| Unclassified Siphovirus | 7l | 1 | 6r3a | |
| Sobemovirus | Sobemovirus | 1 | 2 | 1x36 |
| Sobemovirus | 3 | 1 | 1ng0 | |
| Sphaerolipoviridae | Alphasphaerolipovirus | 28d | 21 | 6qt9 |
| Tectiviridae | Tectivirus | pT25 | 1 | 1w8x |
| Betatetravirus | 4 | 3 | 2qqp | |
| Omegatetravirus | 4 | 19 or 3 | 3s6p | |
| Thermococcales | Pyrococcus | 3 | 1 | 2e0z |
| Togaviridae | Alphavirus | 4 | 20 | 6imm |
| Tombusviridae | Aureusvirus | 3 | 15 | 6mrl |
| Carmovirus | 3 | 15 | 2zah | |
| Dianthovirus | 3 | 15 | 6mrm | |
| Machlomovirus | 3 | 1 | 3jb8 | |
| Necrovirus | 3 | 1 | 1c8n | |
| Panicovirus | 3 | 1 | 4v99 | |
| Tombusvirus | 3 | 3 | 4llf | |
| Totiviridae | Totivirus | 1 | 4 | 1m1c |
| Turriviridae | Alphaturrivirus | pT31 | 1 | 3j31 |
| Tymoviridae | Tymovirus | 3 | 1 | 1ddl |
| Unclassified | Unclassified | 3 | 1 | 6izl |
| Unclassified | Unclassified | 4 | 1 | 6tap |
| Unknown | Unknown | pT21 | 21 | 5oac |
| Virtovirus | Tobacco virtovirus 1 | 1 | 2 | 4oq9 |
| Virus-Like Particle | Virus-Like Particle | 1 | 21 | 6i9g |
| Virus-Like Particle | Virus-Like Particle | 3 | 1 | 4pt2 |
References
- Montiel-Garcia, D.; Santoyo-Rivera, N.; Ho, P.; Carrillo-Tripp, M.; Brooks, C.L.; Johnson, J.E.; Reddy, V.S. VIPERdb v3.0: A structure-based data analytics platform for viral capsids. Nucleic Acids Res. 2021, 49, D809–D816. [Google Scholar] [CrossRef]
- Wilson, D.P. Protruding Features of Viral Capsids are Clustered on Icosahedral Great Circles. PLoS ONE 2016, 11, e0152319. [Google Scholar] [CrossRef][Green Version]
- Wilson, D.P. Unveiling the hidden rules of spherical viruses using point arrays. Viruses 2020, 12, 467. [Google Scholar] [CrossRef]
- Keef, T.; Twarock, R. Affine Extensions of the Icosahedral Group with Applications to the Three-dimensional Organisation of Simple Viruses. J. Math. Biol. 2009, 59, 287–313. [Google Scholar] [CrossRef]
- Keef, T.; Wardman, J.P.; Ranson, N.A.; Stockley, P.G.; Twarock, R. Structural constraints on the three-dimensional geometry of simple viruses: Case studies of a new predictive tool. Acta Crystallogr. Sect. Found. Crystallogr. 2013, 69, 140–150. [Google Scholar] [CrossRef] [PubMed]
- Janner, A. Strongly correlated structure of axial-symmetric proteins. II. Pentagonal, heptagonal, octagonal, nonagonal and ondecagonal symmetries. Acta Crystallogr. Biol. Crystallogr. 2005, 61, 256–268. [Google Scholar] [CrossRef] [PubMed]
- Janner, A. Crystallographic structural organization of human rhinovirus serotype 16, 14, 3, 2 and 1A. Acta Crystallogr. A 2006, 62, 270–286. [Google Scholar] [CrossRef] [PubMed]
- Janner, A. Form, Symmetry and Packing of Biomacro-molecules. I. Concepts and Tutorial Examples. Acta Crystallogr. Sect. Found. Crystallogr. 2010, 66, 301–311. [Google Scholar] [CrossRef] [PubMed]
- Janner, A. Form, symmetry and packing of biomacromolecules. II. Serotypes of human rhinovirus. Acta Crystallogr. Sect. Found. Crystallogr. 2010, 66, 312–326. [Google Scholar] [CrossRef]
- Janner, A. Form, Symmetry and Packing of Biomacromolecules. III. Antigenic, Receptor and Contact Binding Sites in Picornaviruses. Acta Crystallogr. Sect. Found. Crystallogr. 2011, 67, 174–189. [Google Scholar] [CrossRef]
- Janner, A. Form, Symmetry and Packing of Biomacromolecules. IV. Filled Capsids of Cowpea, Tobacco, MS2 and Pariacoto RNA Viruses. Acta Crystallogr. Sect. Found. Crystallogr. 2011, 67, 517–520. [Google Scholar] [CrossRef] [PubMed]
- Janner, A. Form, Symmetry and Packing of Biomacromolecules. V. Shells with Boundaries at anti-nodes of Resonant Vibrations in Icosahedral RNA Viruses. Acta Crystallogr. Sect. Found. Crystallogr. 2011, 67, 521–532. [Google Scholar] [CrossRef] [PubMed]
- Zappa, E.; Dykeman, E.C.; Twarock, R. On the Subgroup Structure of the Hyperoctahedral Group in Six Dimensions. Acta Crystallogr. Sect. Found. Adv. 2014, 70, 417–428. [Google Scholar] [CrossRef]
- Zappa, E.; Dykeman, E.C.; Geraets, J.A.; Twarock, R. A Group Theoretical Approach to Structural Transitions of Icosahedral Quasicrystal s and Point Arrays. J. Phys. Math. Theor. 2016, 49, 175–203. [Google Scholar] [CrossRef]
- Caspar, D.L.; Klug, A. Physical Principles in the Construction of Regular Viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Waltmann, C.; Asor, R.; Raviv, U.; Olvera de la Cruz, M. Assembly and Stability of Simian Virus 40 Polymorphs. ACS Nano 2020, 14, 4430–4443. [Google Scholar] [CrossRef]
- Prasad, B.V.V.; Schmid, M.F. Principles of Virus Structural Organization; Springer Science: Berlin, Germany, 2012; pp. 17–47. [Google Scholar] [CrossRef]
- Louten, J. Virus Structure and Classification; Academic Press: Cambridge, MA, USA, 2016; pp. 19–29. [Google Scholar]
- Baltimore, D. Expression of animal virus genomes. Bacteriol. Rev. 1971, 35, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Hartman, E.C.; Jakobson, C.M.; Favor, A.H.; Lobba, M.J.; Álvarez-Benedicto, E.; Francis, M.B.; Tullman-Ercek, D. Quantitative Characterization of All Single Amino Acid Variants of a Viral Capsid-Based Drug Delivery Vehicle. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Hartman, E.C.; Lobba, M.J.; Favor, A.H.; Robinson, S.A.; Francis, M.B.; Tullman-Ercek, D. Experimental Evaluation of Coevolution in a Self-Assembling Particle. Biochemistry 2019, 58, 1527–1538. [Google Scholar] [CrossRef]
- Wang, Q.; Kaltgrad, E.; Lin, T.; Johnson, J.E.; Finn, M.G. Natural Supramolecular Building Blocks: Wild-type Cowpea Mosaic Virus. Chem. Biol. 2002, 9, 805–811. [Google Scholar] [CrossRef]
- Chatterji, A.; Ochoa, W.F.; Paine, M.; Ratna, B.R.; Johnson, J.E.; Lin, T. New Addresses on an Addressable Virus Nanoblock: Uniquely Reactive Lys Residues on Cowpea Mosaic Virus. Chem. Biol. 2004, 11, 855–863. [Google Scholar] [CrossRef]
- Hadden, J.A.; Perilla, J.R.; Schlicksup, C.J.; Venkatakrishnan, B.; Zlotnick, A.; Schulten, K. All-atom molecular dynamics of the HBV capsid reveals insights into biological function and cryo-EM resolution limits. eLife 2018, 7, 1–27. [Google Scholar] [CrossRef]
- Mannige, R.V.; Brooks, C.L., III. Periodic table of virus capsids: Implications for natural selection and design. PLoS ONE 2010, 5, e0009423. [Google Scholar] [CrossRef]
- Wynne, S.A.; Crowther, R.A.; Leslie, A.G.W. The Crystal Structure of the Human Hepatitis B Virus Capsid. Mol. Cell 1999, 3, 771–780. [Google Scholar] [CrossRef]
- Erdemci-Tandogan, G.; Wagner, J.; Van Der Schoot, P.; Podgornik, R.; Zandi, R. Effects of RNA branching on the electrostatic stabilization of viruses. Phys. Rev. E 2016, 94, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Erdemci-Tandogan, G.; Wagner, J.; Van Der Schoot, P.; Zandi, R. Impact of a nonuniform charge distribution on virus assembly. Phys. Rev. E 2017, 96, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Panahandeh, S.; Li, S.; Marichal, L.; Leite Rubim, R.; Tresset, G.; Zandi, R. How a Virus Circumvents Energy Barriers to Form Symmetric Shells. ACS Nano 2020, 14, 3170–3180. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Ochoa, W.F.; Sinkovits, R.S.; Poulos, B.T.; Ghabrial, S.A.; Lightner, D.V.; Baker, T.S.; Nibert, M.L. Infectious myonecrosis virus has a totivirus-like, 120-subunit capsid, but with fiber complexes at the fivefold axes. Proc. Natl. Acad. Sci. USA 2008, 105, 17526–17531. [Google Scholar] [CrossRef]
- Hoppe, S.; Schelhaas, M.; Jaeger, V.; Liebig, T.; Petermann, P.; Knebel-Mö rsdorf, D. Early herpes simplex virus type 1 infection is dependent on regulated Rac1/Cdc42 signalling in epithelial MDCKII cells. J. Gen. Virol. 2006, 87, 3483–3494. [Google Scholar] [CrossRef] [PubMed]
- Venkatakrishnan, B.; Zlotnick, A. The Structural Biology of Hepatitis B Virus: Form and Function. Annu. Rev. Virol. 2016, 3, 429–451. [Google Scholar] [CrossRef]
- Nair, S.; Zlotnick, A. Asymmetric Modification of Hepatitis B Virus (HBV) Genomes by an Endogenous Cytidine Deaminase inside HBV Cores Informs a Model of Reverse Transcription. J. Virol. 2018, 92, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Greber, B.J.; Sutter, M.; Kerfeld, C.A. The plasticity of molecular interactions governs bacterial microcompartment shell assembly. Structure 2019, 27, 749–763. [Google Scholar] [CrossRef]
- El Omari, K.; Sutton, G.; Ravantti, J.J.; Zhang, H.; Walter, T.S.; Grimes, J.M.; Bamford, D.H.; Stuart, D.I.; Mancini, E.J. Plate tectonics of virus shell assembly and reorganization in phage ϕ8, a distant relative of mammalian reoviruses. Structure 2013, 21, 1384–1395. [Google Scholar] [CrossRef] [PubMed]
- Hadfield, A.T.; Lee, W.M.; Zhao, R.; Oliveira, M.A.; Minor, I.; Rueckert, R.R.; Rossmann, M.G. The refined structure of human rhinovirus 16 at 2.15 Å resolution: Implications for the viral life cycle. Structure 1997, 5, 427–441. [Google Scholar] [CrossRef]
- McKenna, R.; Bowman, B.R.; Ilag, L.L.; Rossmann, M.G.; Fane, B.A. Atomic structure of the degraded procapsid particle of the bacteriophage G4: Induced structural changes in the presence of calcium ions and functional implications. J. Mol. Biol. 1996, 256, 736–750. [Google Scholar] [CrossRef]
- Golmohammadi, R.; Valegard, K.; Fridborg, K.; Liljas, L. The Refined Structure of Bacteriophage MS2 at 2·8 Å Resolution. J. Mol. Biol. 1993, 234, 620–639. [Google Scholar] [CrossRef] [PubMed]
- Erickson, J.W.; Silva, A.M.; Murthy, M.R.; Fita, I.; Rossmann, M.G. The structure of a T = 1 icosahedral empty particle from southern bean mosaic virus. Science 1985, 229, 625–629. [Google Scholar] [CrossRef] [PubMed]
- Sangita, V.; Satheshkumar, P.S.; Savithri, H.S.; Murthy, M.R.N. Structure of a mutant ∖it T = 1 capsid of Sesbania mosaic virus: Role of water molecules in capsid architecture and integrity. Acta Crystallogr. Sect. D 2005, 61, 1406–1412. [Google Scholar] [CrossRef]
- Acton, O.; Grant, T.; Nicastro, G.; Ball, N.J.; Goldstone, D.C.; Robertson, L.E.; Sader, K.; Nans, A.; Ramos, A.; Stoye, J.P.; et al. Structural basis for Fullerene geometry in a human endogenous retrovirus capsid. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef]
- Ilyas, M.; Mietzsch, M.; Kailasan, S.; Väisänen, E.; Luo, M.; Chipman, P.; Smith, J.K.; Kurian, J.; Sousa, D.; McKenna, R.; et al. Atomic resolution structures of human bufaviruses determined by cryo-electron microscopy. Viruses 2018, 10, 22. [Google Scholar] [CrossRef]
- Guan, J.; Bywaters, S.M.; Brendle, S.A.; Ashley, R.E.; Makhov, A.M.; Conway, J.F.; Christensen, N.D.; Hafenstein, S. Cryoelectron Microscopy Maps of Human Papillomavirus 16 Reveal L2 Densities and Heparin Binding Site. Structure 2017, 25, 253–263. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.; Garcea, R.L.; Grigorieff, N.; Harrison, S.C. Subunit interactions in bovine papillomavirus. Proc. Natl. Acad. Sci. USA 2010, 107, 6298–6303. [Google Scholar] [CrossRef] [PubMed]
- Stehle, T.; Gamblin, S.J.; Yan, Y.; Harrison, S.C. The structure of simian virus 40 refined at 3.1 Å resolution. Structure 1996, 4, 165–182. [Google Scholar] [CrossRef]
- Lindner, J.M.; Cornacchione, V.; Sathe, A.; Be, C.; Srinivas, H.; Riquet, E.; Leber, X.C.; Hein, A.; Wrobel, M.B.; Scharenberg, M.; et al. Human Memory B Cells Harbor Diverse Cross-Neutralizing Antibodies against BK and JC Polyomaviruses. Immunity 2019, 50, 668–676.e5. [Google Scholar] [CrossRef]
- Yadav, R.; Zhai, L.; Tumban, E. Virus-like Particle-Based L2 Vaccines against HPVs: Where Are We Today? Viruses 2020, 12, 18. [Google Scholar] [CrossRef]
- Mietzsch, M.; Pénzes, J.J.; Agbandje-Mckenna, M. Twenty-five years of structural parvovirology. Viruses 2019, 11, 362. [Google Scholar] [CrossRef]
- Callaway, H.M.; Subramanian, S.; Urbina, C.A.; Barnard, K.N.; Dick, R.A.; Bator, C.M.; Hafenstein, S.L.; Gifford, R.J.; Parrish, C.R. Examination and Reconstruction of Three Ancient Endogenous Parvovirus Capsid Protein Gene Remnants Found in Rodent Genomes. J. Virol. 2019, 93, 1–14. [Google Scholar] [CrossRef]
- Halder, S.; Nam, H.J.; Govindasamy, L.; Vogel, M.; Dinsart, C.; Salome, N.; McKenna, R.; Agbandje-McKenna, M. Structural Characterization of H-1 Parvovirus: Comparison of Infectious Virions to Empty Capsids. J. Virol. 2013, 87, 5128–5140. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.Z.; Aiyer, S.; Mietzsch, M.; Hull, J.A.; McKenna, R.; Grieger, J.; Samulski, R.J.; Baker, T.S.; Agbandje-McKenna, M.; Lyumkis, D. Sub-2 Å Ewald curvature corrected structure of an AAV2 capsid variant. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Meyer, N.L.; Hu, G.; Davulcu, O.; Xie, Q.; Noble, A.J.; Yoshioka, C.; Gingerich, D.S.; Trzynka, A.; David, L.; Stagg, S.M.; et al. Structure of the gene therapy vector, adeno-associated virus with its cell receptor, aavr. eLife 2019, 8, 1–24. [Google Scholar] [CrossRef]
- Burmeister, W.P.; Buisson, M.; Estrozi, L.F.; Schoehn, G.; Billet, O.; Hannas, Z.; Sigoillot, C.; Poulet, H. Structure determination of feline calicivirus virus-like particles in the context of a pseudo-octahedral arrangement. PLoS ONE 2015, 10, e0119289. [Google Scholar] [CrossRef]
- Duquerroy, S.; Da Costa, B.; Henry, C.; Vigouroux, A.; Libersou, S.; Lepault, J.; Navaza, J.; Delmas, B.; Rey, F.A. The picobirnavirus crystal structure provides functional insights into virion assembly and cell entry. EMBO J. 2009, 28, 1655–1665. [Google Scholar] [CrossRef]
- Wada, Y.; Tanaka, H.; Yamashita, E.; Kubo, C.; Ichiki-Uehara, T.; Nakazono-Nagaoka, E.; Omura, T.; Tsukihara, T. The structure of melon necrotic spot virus determined at 2.8 Å resolution. Acta Crystallogr. Sect. Struct. Biol. Cryst. Commun. 2008, 64, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Guu, T.S.Y.; Liu, Z.; Ye, Q.; Mata, D.A.; Li, K.; Yin, C.; Zhang, J.; Tao, Y.J. Structure of the hepatitis E virus-like particle suggests mechanisms for virus assembly and receptor binding. Proc. Natl. Acad. Sci. USA 2009, 106, 12992–12997. [Google Scholar] [CrossRef]
- Chen, N.C.; Yoshimura, M.; Guan, H.H.; Wang, T.Y.; Misumi, Y.; Lin, C.C.; Chuankhayan, P.; Nakagawa, A.; Chan, S.I.; Tsukihara, T.; et al. Crystal Structures of a Piscine Betanodavirus: Mechanisms of Capsid Assembly and Viral Infection. PLoS Pathog. 2015, 11, e1005203. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Dong, L.; Lin, L.; Ochoa, W.F.; Sinkovits, R.S.; Havens, W.M.; Nibert, M.L.; Baker, T.S.; Ghabrial, S.A.; Tao, Y.J. Atomic structure reveals the unique capsid organization of a dsRNA virus. Proc. Natl. Acad. Sci. USA 2009, 106, 4225–4230. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.; Grant, T.; Thomas, D.R.; Diehnelt, C.W.; Grigorieff, N.; Joshua-Tor, L. High-resolution cryo-EM structures of outbreak strain human norovirus shells reveal size variations. Proc. Natl. Acad. Sci. USA 2019, 116, 12828–12832. [Google Scholar] [CrossRef] [PubMed]
- Madhumati, S.; Long, F.; Miller, A.; Klose, T.; Buda, G.; Sun, L.; Kuhn, R.; Rossmann, M.G. Refinement and Analysis of the Mature Zika Virus Cryo-EM Structure at 3.1 Å Resolution. Physiol. Behav. 2018, 26, 1169–1177. [Google Scholar] [CrossRef]
- Wolf, Y.I.; Kazlauskas, D.; Iranzo, J.; Lucía-Sanz, A.; Kuhn, J.H.; Krupovic, M.; Dolja, V.V.; Koonin, E.V. Origins and evolution of the global RNA virome. mBio 2018, 9, 1–31. [Google Scholar] [CrossRef] [PubMed]

| Genome | T1 | T2 | T3 | pT3 | T4 | T7d | T7l | T9 | T13 | T16 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|
| dsDNA | 2 | 1 | 2 | 0 | 2 | 5 | 11 | 0 | 2 | 3 | 28 |
| ssDNA | 13 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 15 |
| dsRNA | 7 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 5 | 0 | 17 |
| ssRNA | 13 | 0 | 27 | 16 | 4 | 0 | 0 | 1 | 0 | 0 | 61 |
| None | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 4 |
| Totals | 36 | 5 | 31 | 17 | 7 | 5 | 11 | 2 | 8 | 3 | 125 |
| GP | Loc. | Arrays per GP | Radial Levels |
|---|---|---|---|
| 1 | ICO | 3 | 5 |
| 2–5 | 3–5 | 2 * | 5 |
| 6 | DOD | 4 | 7 or 8 |
| 7–14 | 2–3 | 2 * | 7–11 |
| 15 | IDD | 11 | 9–16 |
| 16–21 | 5–2 | 2 * | 5–7 |
| GP | T1 | T2 | T3 | pT3 | T4 | T7d | T7l | T9 | T13 | T16 | Totals |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1(5-fold) | 3 | 12 | 4 | 2 | 5 | 6 | 3 | 35 (25.2%) | |||
| 2 | 9 | 3 | 1 | 13 (9.4%) | |||||||
| 3 | 3 | 1 | 3 | 3 | 2 | 3 | 15 (10.8%) | ||||
| 4 | 1 | 1 | 1 | 1 | 4 (2.9%) | ||||||
| 5 | 8 | 1 | 1 | 1 | 11 (7.9%) | ||||||
| 6 (3-fold) | 1 | 1 | 2 (1.4%) | ||||||||
| 7 | 1 | 1 (0.7%) | |||||||||
| 8 | 0 (0.0%) | ||||||||||
| 9 | 0 (0.0%) | ||||||||||
| 10 | 1 | 1 (0.7%) | |||||||||
| 11 | 0 (0.0%) | ||||||||||
| 12 | 1 | 1 (0.7%) | |||||||||
| 13 | 1 | 1 | 2 (1.4%) | ||||||||
| 14 | 1 | 1 | 2 (1.4%) | ||||||||
| 15 (2-fold) | 1 | 7 | 8 (5.8%) | ||||||||
| 16 | 2 | 1 | 1 | 4 (2.9%) | |||||||
| 17 | 1 | 1 | 1 | 3 (2.2%) | |||||||
| 18 | 1 | 1 | 2 | 1 | 1 | 6 (4.3%) | |||||
| 19 | 2 | 1 | 1 | 1 | 1 | 6 (4.3%) | |||||
| 20 | 2 | 1 | 2 | 2 | 1 | 2 | 3 | 1 | 14 (10.1%) | ||
| 21 | 4 | 2 | 2 | 2 | 1 | 11 (7.9%) | |||||
| Total | 39 | 6 | 34 | 19 | 8 | 5 | 13 | 2 | 10 | 3 | 139 |
| GP | dsDNA | ssDNA | dsRNA | ssRNA | None | Totals |
|---|---|---|---|---|---|---|
| 1 (5-fold) | 20 | 5 | 1 | 13 | 2 | 41 |
| 2 | 1 | 1 | 2 | 9 | 13 | |
| 3 | 2 | 1 | 4 | 8 | 15 | |
| 4 | 1 | 1 | 2 | 4 | ||
| 5 | 8 | 1 | 2 | 11 | ||
| 6 (3-fold) | 1 | 1 | 2 | |||
| 7 | 1 | 1 | ||||
| 8 | 0 | |||||
| 9 | 0 | |||||
| 10 | 1 | 1 | ||||
| 11 | 0 | |||||
| 12 | 1 | 1 | ||||
| 13 | 1 | 1 | 2 | |||
| 14 | 1 | 1 | 2 | |||
| 15 (2-fold) | 1 * | 7 | 8 | |||
| 16 | 4 | 4 | ||||
| 17 | 1 | 2 | 3 | |||
| 18 | 2 | 4 | 6 | |||
| 19 | 3 | 1 | 2 | 6 | ||
| 20 | 3 | 1 | 4 | 6 | 14 | |
| 21 | 8 | 1 | 5 | 1 | 15 | |
| Totals | 42 | 16 | 20 | 67 | 4 | 149 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, D.P.; Roof, D.A. Viral Phrenology. Viruses 2021, 13, 2191. https://doi.org/10.3390/v13112191
Wilson DP, Roof DA. Viral Phrenology. Viruses. 2021; 13(11):2191. https://doi.org/10.3390/v13112191
Chicago/Turabian StyleWilson, David P., and Danielle A. Roof. 2021. "Viral Phrenology" Viruses 13, no. 11: 2191. https://doi.org/10.3390/v13112191
APA StyleWilson, D. P., & Roof, D. A. (2021). Viral Phrenology. Viruses, 13(11), 2191. https://doi.org/10.3390/v13112191






