Modeling Within-Host Dynamics of SARS-CoV-2 Infection: A Case Study in Ferrets
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data
2.2. Mathematical Model
2.3. Parameters and Data Fitting
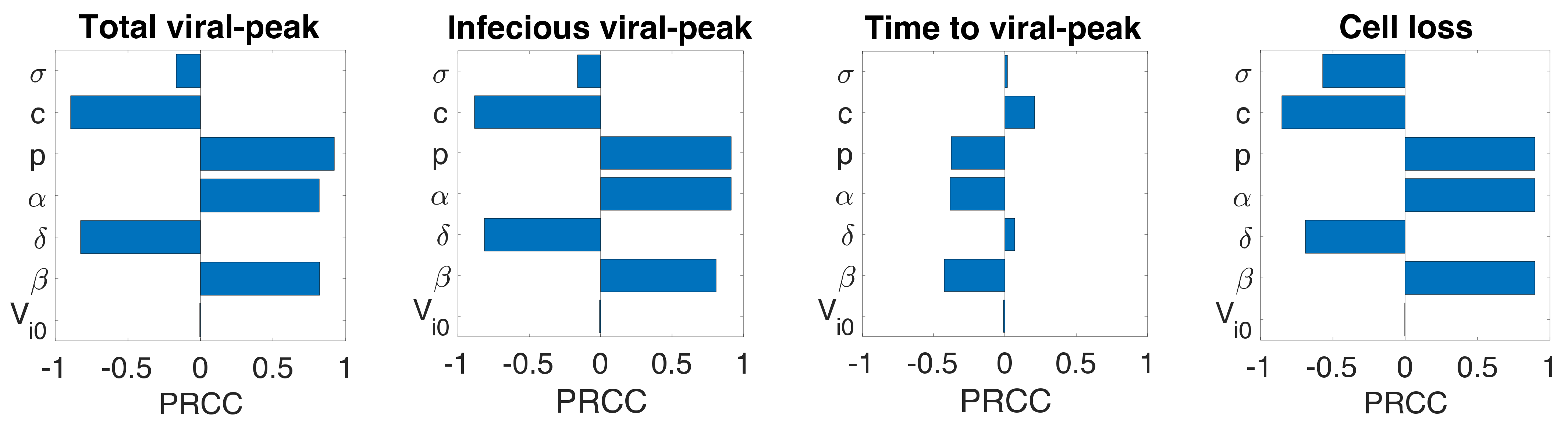
2.4. Sensitivity Analysis
3. Results
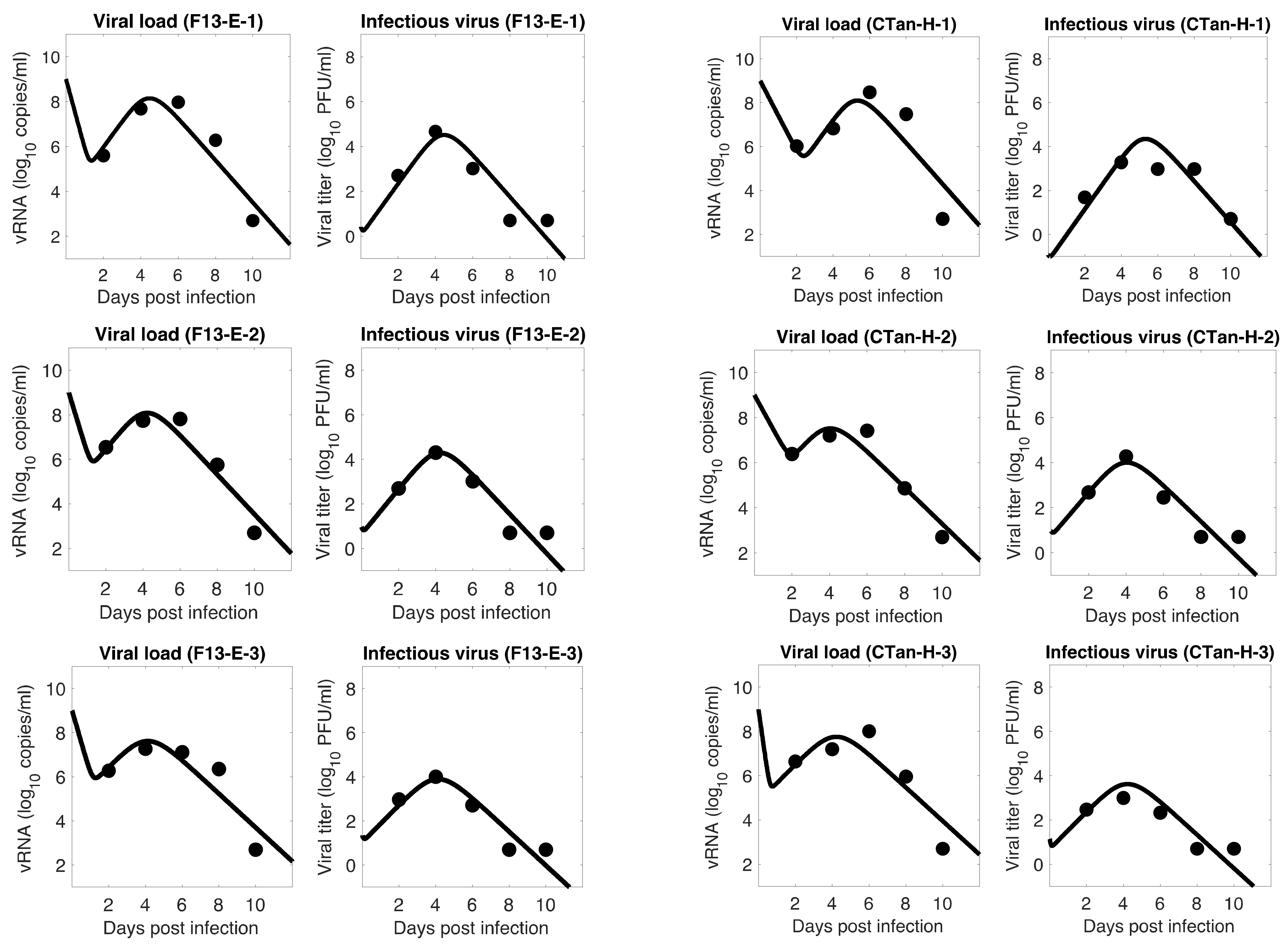
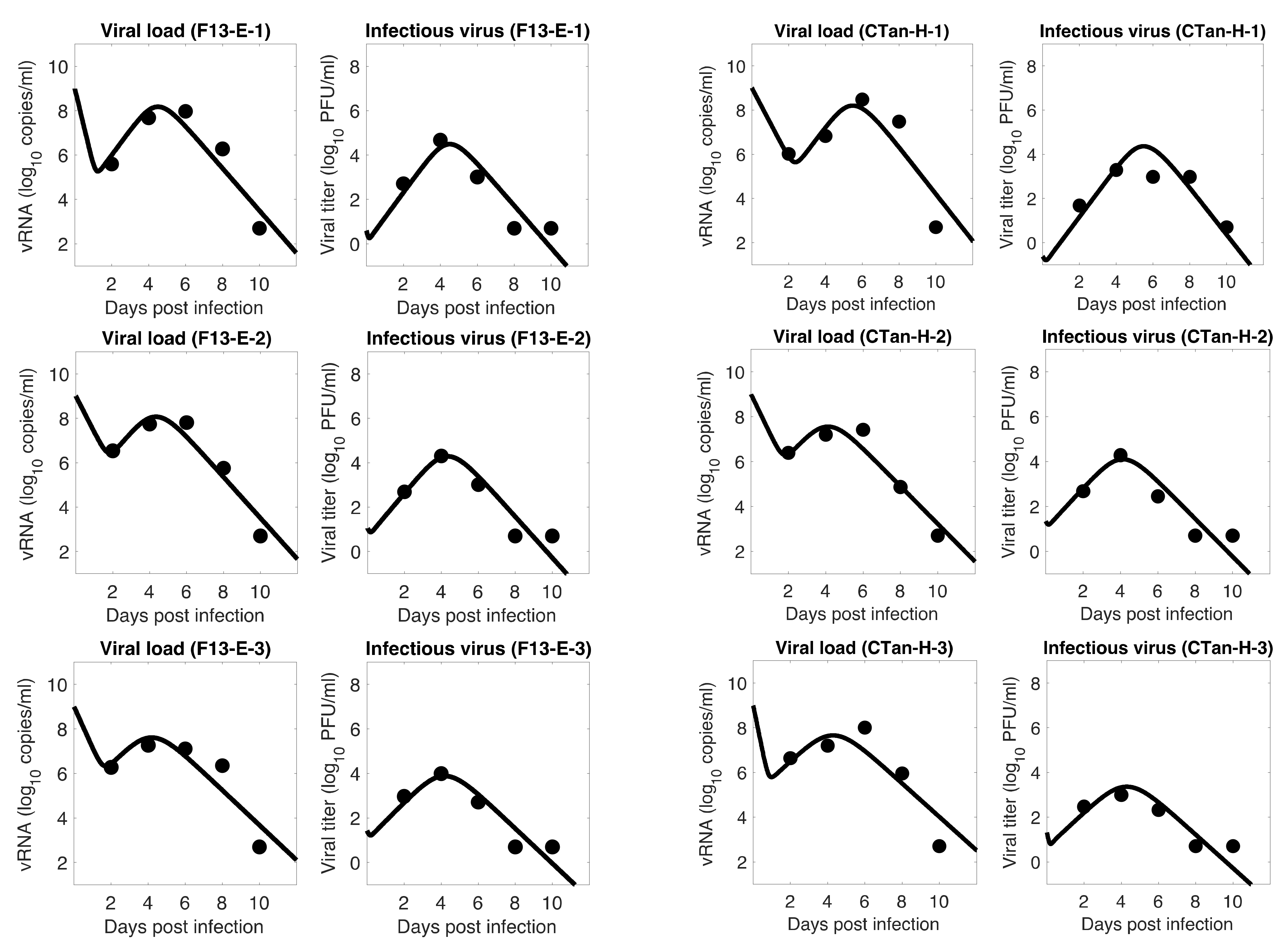
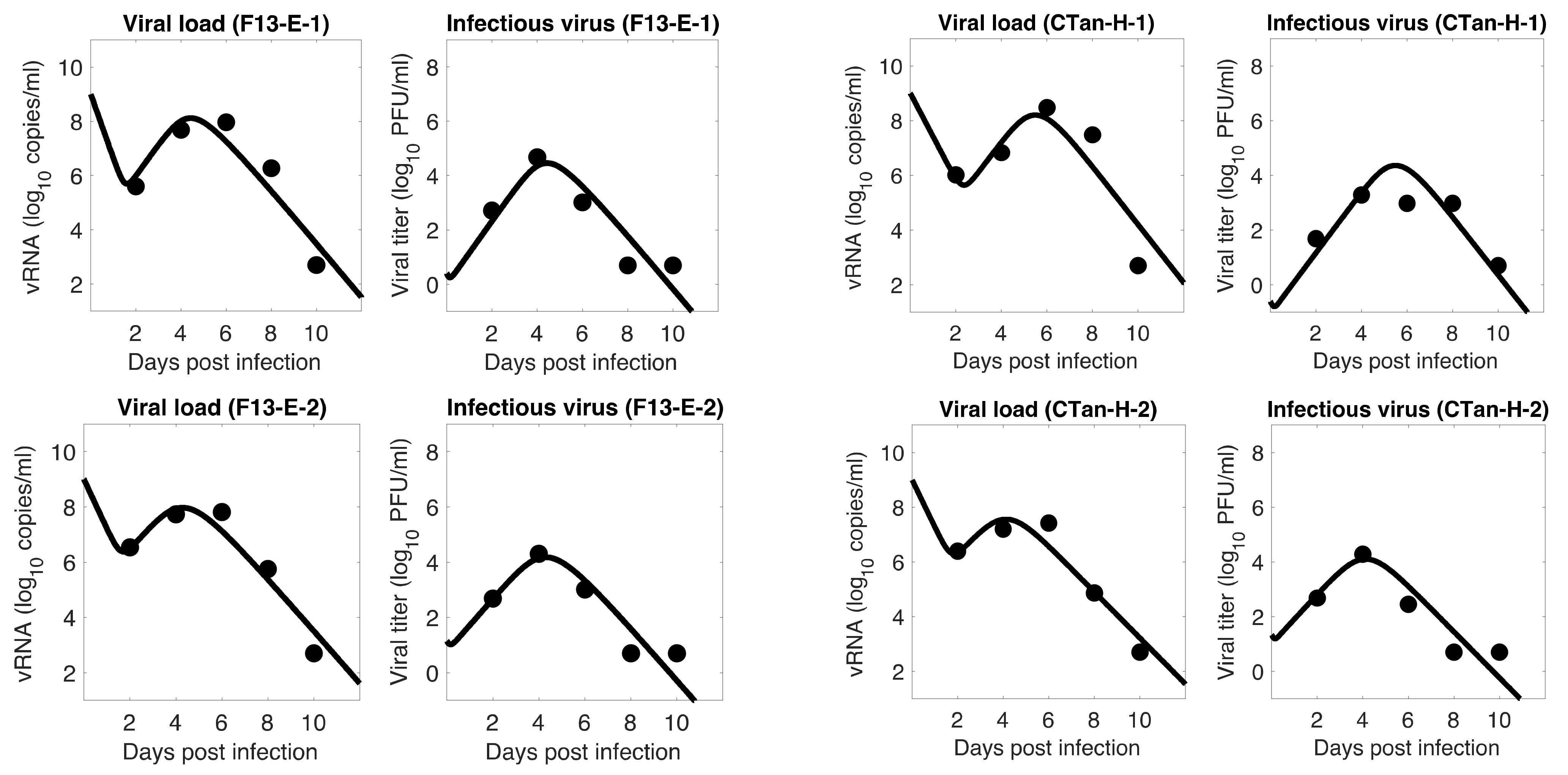
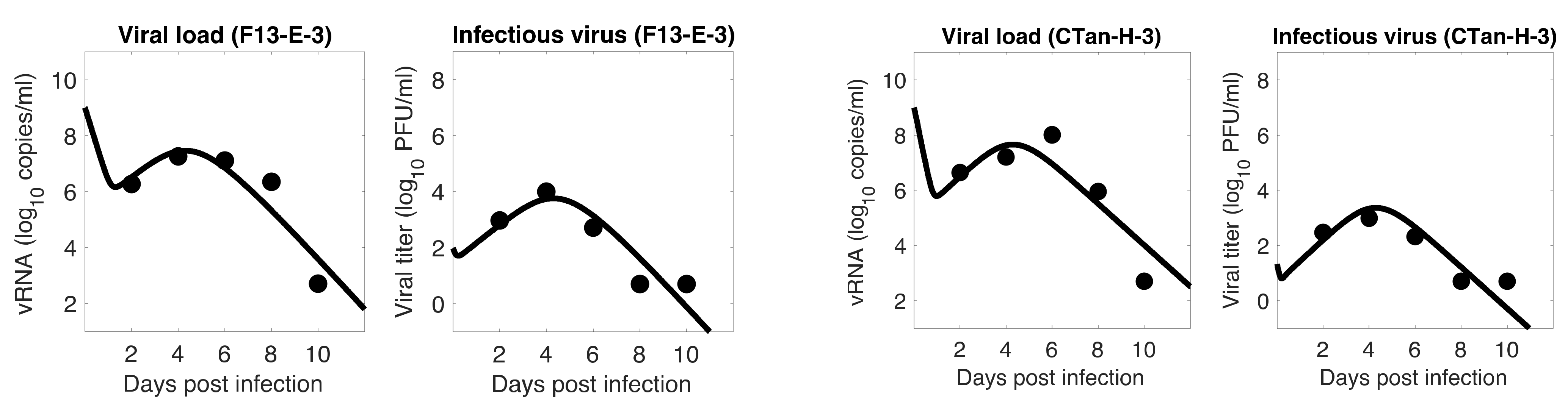
3.1. Data Fitting to Three Viral Dynamics Models and Comparison
3.2. Important Viral Dynamics Parameters
3.3. Basic Reproduction Number
3.4. Viral Kinetic Properties
3.5. Comparison between F13-E and CTan-H Viruses
3.6. Sensitivity Analysis
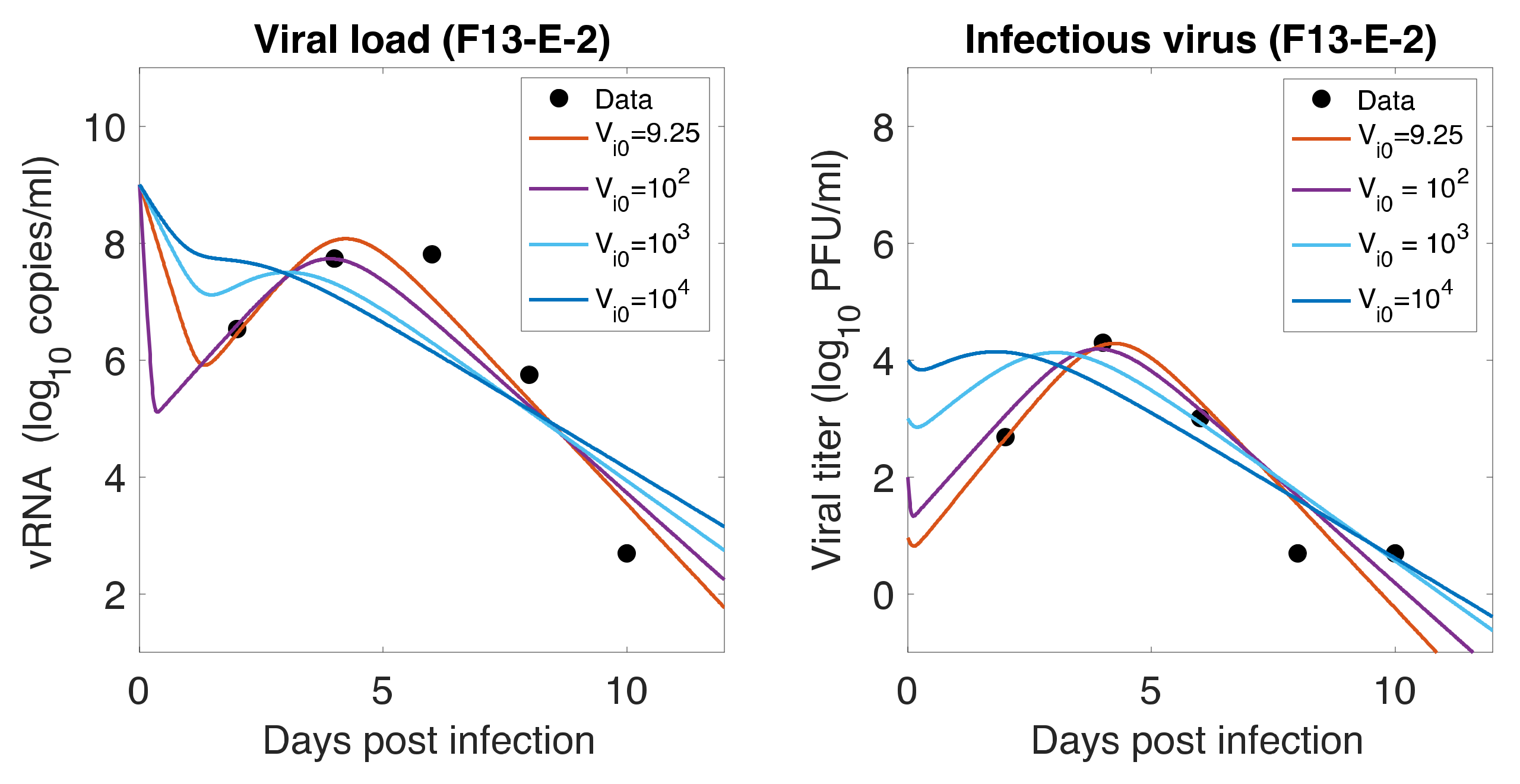
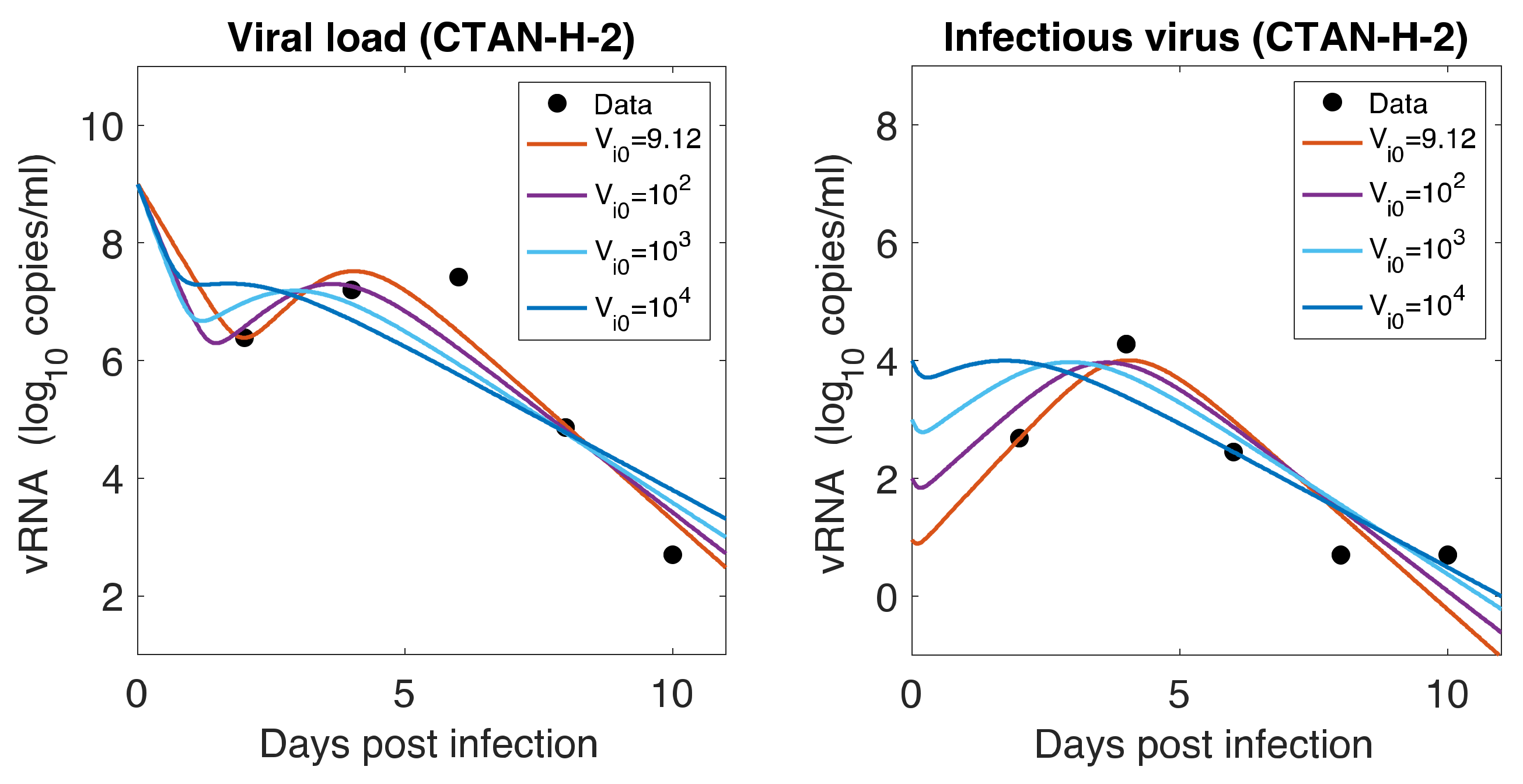
3.7. Initial Infectious Virus
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shi, J.; Wen, Z.; Zhong, G.; Yang, H.; Wang, C.; Huang, B.; Liu, R.; He, X.; Shuai, L.; Sun, Z.; et al. Susceptibility of ferrets, cats, dogs, and other domesticated animals to SARS-coronavirus 2. Science 2020, 368, 1016–1020. [Google Scholar] [CrossRef]
- Wu, F.; Zhao, S.; Yu, B.; Chen, Y.M.; Wang, W.; Song, Z.G.; Hu, Y.; Tao, Z.W.; Tian, J.H.; Pei, Y.Y.; et al. A new coronavirus associated with human respiratory disease in China. Nature 2020, 579, 265–269. [Google Scholar] [CrossRef]
- Chan, J.F.; Kok, K.H.; Zhu, Z.; Chu, H.; To, K.K.; Yuan, S.; Yuen, K.Y. Genomic characterization of the 2019 novel human-pathogenic coronavirus isolated from a patient with atypical pneumonia after visiting Wuhan. Emerg. Microbes Infect. 2020, 9, 221–236. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Ruan, F.; Huang, M.; Liang, L.; Huang, H.; Hong, Z.; Yu, J.; Kang, M.; Song, Y.; Xia, J.; et al. SARS-CoV-2 Viral Load in Upper Respiratory Specimens of Infected Patients. N. Engl. J. Med. 2020, 382, 1177–1179. [Google Scholar] [CrossRef]
- WHO. WHO Coronavirus (COVID-19) Dashboard; WHO: Geneva, Switzerland, 2021. [Google Scholar]
- Baric, R.S. Emergence of a Highly Fit SARS-CoV-2 Variant. N. Engl. J. Med. 2020, 383, 2684–2686. [Google Scholar] [CrossRef] [PubMed]
- Lauring, A.S.; Hodcroft, E.B. Genetic Variants of SARS-CoV-2-What Do They Mean? JAMA 2021, 325, 529–531. [Google Scholar] [CrossRef] [PubMed]
- Goyal, A.; Cardozo-Ojeda, E.F.; Schiffer, J.T. Potency and timing of antiviral therapy as determinants of duration of SARS-CoV-2 shedding and intensity of inflammatory response. Sci. Adv. 2020, 6, eabc7112. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Jerome, K.R.; Greninger, A.L.; Schiffer, J.T.; Goyal, A. Endogenously Produced SARS-CoV-2 Specific IgG Antibodies May Have a Limited Impact on Clearing Nasal Shedding of Virus during Primary Infection in Humans. Viruses 2021, 13, 516. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Ko, J.H.; Kim, Y.; Kim, Y.J.; Kim, J.M.; Chung, Y.S.; Kim, H.M.; Han, M.G.; Kim, S.Y.; Chin, B.S. Viral Load Kinetics of SARS-CoV-2 Infection in First Two Patients in Korea. J. Korean Med. Sci. 2020, 35, e86. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.M.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [PubMed]
- Berggren, K.A.; Suzuki, S.; Ploss, A. Animal Models Used in Hepatitis C Virus Research. Int. J. Mol. Sci. 2020, 21, 3869. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.M.; Stone, M.; Piatak, M.; Schweighardt, B.; Haigwood, N.L.; Montefiori, D.; Lifson, J.D.; Busch, M.P.; Miller, C.J. High specific infectivity of plasma virus from the pre-ramp-up and ramp-up stages of acute simian immunodeficiency virus infection. J. Virol. 2009, 83, 3288–3297. [Google Scholar] [CrossRef]
- Asabe, S.; Wieland, S.F.; Chattopadhyay, P.K.; Roederer, M.; Engle, R.E.; Purcell, R.H.; Chisari, F.V. The size of the viral inoculum contributes to the outcome of hepatitis B virus infection. J. Virol. 2009, 83, 9652–9662. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Orsoni, S.; Norman, L.; Verma, A.S.; Tirado, G.; Giavedoni, L.D.; Staprans, S.; Miller, G.M.; Buch, S.J.; Kumar, A. Chronic morphine exposure causes pronounced virus replication in cerebral compartment and accelerated onset of AIDS in SIV/SHIV-infected Indian rhesus macaques. Virology 2006, 354, 192–206. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kumar, R.; Torres, C.; Yamamura, Y.; Rodriguez, I.; Martinez, M.; Staprans, S.; Donahoe, R.M.; Kraiselburd, E.; Stephens, E.B.; Kumar, A. Modulation by morphine of viral set point in rhesus macaques infected with simian immunodeficiency virus and simian-human immunodeficiency virus. J. Virol. 2004, 78, 11425–11428. [Google Scholar] [CrossRef][Green Version]
- Maher, J.A.; DeStefano, J. The ferret: An animal model to study influenza virus. Lab. Anim. 2004, 33, 50–53. [Google Scholar] [CrossRef]
- Shi, J.; Deng, G.; Kong, H.; Gu, C.; Ma, S.; Yin, X.; Zeng, X.; Cui, P.; Chen, Y.; Yang, H.; et al. H7N9 virulent mutants detected in chickens in China pose an increased threat to humans. Cell Res. 2017, 27, 1409–1421. [Google Scholar] [CrossRef]
- Stittelaar, K.J.; de Waal, L.; van Amerongen, G.; Veldhuis Kroeze, E.J.; Fraaij, P.L.; van Baalen, C.A.; van Kampen, J.J.; van der Vries, E.; Osterhaus, A.D.; de Swart, R.L. Ferrets as a Novel Animal Model for Studying Human Respiratory Syncytial Virus Infections in Immunocompetent and Immunocompromised Hosts. Viruses 2016, 8, 168. [Google Scholar] [CrossRef]
- Zhang, Q.; Shi, J.; Deng, G.; Guo, J.; Zeng, X.; He, X.; Kong, H.; Gu, C.; Li, X.; Liu, J.; et al. H7N9 influenza viruses are transmissible in ferrets by respiratory droplet. Science 2013, 341, 410–414. [Google Scholar] [CrossRef]
- Imai, M.; Watanabe, T.; Hatta, M.; Das, S.C.; Ozawa, M.; Shinya, K.; Zhong, G.; Hanson, A.; Katsura, H.; Watanabe, S.; et al. Experimental adaptation of an influenza H5 HA confers respiratory droplet transmission to a reassortant H5 HA/H1N1 virus in ferrets. Nature 2012, 486, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Herfst, S.; Schrauwen, E.J.; Linster, M.; Chutinimitkul, S.; de Wit, E.; Munster, V.J.; Sorrell, E.M.; Bestebroer, T.M.; Burke, D.F.; Smith, D.J.; et al. Airborne transmission of influenza A/H5N1 virus between ferrets. Science 2012, 336, 1534–1541. [Google Scholar] [CrossRef] [PubMed]
- Herfst, S.; Mok, C.K.P.; van den Brand, J.M.A.; van der Vliet, S.; Rosu, M.E.; Spronken, M.I.; Yang, Z.; de Meulder, D.; Lexmond, P.; Bestebroer, T.M.; et al. Human Clade 2.3.4.4 A/H5N6 Influenza Virus Lacks Mammalian Adaptation Markers and Does Not Transmit via the Airborne Route between Ferrets. mSphere 2018, 3, e00405–e00417. [Google Scholar] [CrossRef] [PubMed]
- Van den Brand, J.M.; Haagmans, B.L.; Leijten, L.; van Riel, D.; Martina, B.E.; Osterhaus, A.D.; Kuiken, T. Pathology of experimental SARS coronavirus infection in cats and ferrets. Vet. Pathol. 2008, 45, 551–562. [Google Scholar] [CrossRef]
- Martina, B.E.; Haagmans, B.L.; Kuiken, T.; Fouchier, R.A.; Rimmelzwaan, G.F.; Van Amerongen, G.; Peiris, J.S.; Lim, W.; Osterhaus, A.D. Virology: SARS virus infection of cats and ferrets. Nature 2003, 425, 915. [Google Scholar] [CrossRef]
- Francis, M.E.; Richardson, B.; McNeil, M.; Rioux, M.; Foley, M.K.; Ge, A.; Pechous, R.D.; Kindrachuk, J.; Cameron, C.M.; Richardson, C.; et al. Male sex and age biases viral burden, viral shedding, and type 1 and 2 interferon responses during SARS-CoV-2 infection in ferrets. bioRxiv 2021. [Google Scholar] [CrossRef]
- Proud, P.C.; Tsitoura, D.; Watson, R.J.; Chua, B.Y.; Aram, M.J.; Bewley, K.R.; Cavell, B.E.; Cobb, R.; Dowall, S.; Fotheringham, S.A.; et al. Prophylactic intranasal administration of a TLR2/6 agonist reduces upper respiratory tract viral shedding in a SARS-CoV-2 challenge ferret model. EBioMedicine 2021, 63, 103153. [Google Scholar] [CrossRef]
- Ryan, K.A.; Bewley, K.R.; Fotheringham, S.A.; Slack, G.S.; Brown, P.; Hall, Y.; Wand, N.I.; Marriott, A.C.; Cavell, B.E.; Tree, J.A.; et al. Dose-dependent response to infection with SARS-CoV-2 in the ferret model and evidence of protective immunity. Nat. Commun. 2021, 12, 81. [Google Scholar] [CrossRef]
- Ryu, D.K.; Song, R.; Kim, M.; Kim, Y.I.; Kim, C.; Kim, J.I.; Kwon, K.S.; Tijsma, A.S.; Nuijten, P.M.; van Baalen, C.A.; et al. Therapeutic effect of CT-P59 against SARS-CoV-2 South African variant. Biochem. Biophys. Res. Commun. 2021, 566, 135–140. [Google Scholar] [CrossRef]
- Sourimant, J.; Lieber, C.M.; Aggarwal, M.; Cox, R.M.; Wolf, J.D.; Yoon, J.J.; Toots, M.; Ye, C.; Sticher, Z.; Kolykhalov, A.A.; et al. 4’-Fluorouridine is a broad-spectrum orally efficacious antiviral blocking respiratory syncytial virus and SARS-CoV-2 replication. bioRxiv 2021. [Google Scholar] [CrossRef]
- Vaidya, N.K.; Ribeiro, R.M.; Miller, C.J.; Perelson, A.S. Viral dynamics during primary simian immunodeficiency virus infection: Effect of time-dependent virus infectivity. J. Virol. 2010, 84, 4302–4310. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, N.K.; Ribeiro, R.M.; Perelson, A.S.; Kumar, A. Modeling the Effects of Morphine on Simian Immunodeficiency Virus Dynamics. PLoS Comput. Biol. 2016, 12, e1005127. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, N.K.; Ribeiro, R.M.; Liu, P.; Haynes, B.F.; Tomaras, G.D.; Perelson, A.S. Correlation Between Anti-gp41 Antibodies and Virus Infectivity Decay During Primary HIV-1 Infection. Front. Microbiol. 2018, 9, 1326. [Google Scholar] [CrossRef] [PubMed]
- Mutua, J.M.; Perelson, A.S.; Kumar, A.; Vaidya, N.K. Modeling the effects of morphine-altered virus specific antibody responses on HIV/SIV dynamics. Sci. Rep. 2019, 9, 5423. [Google Scholar] [CrossRef]
- Pawelek, K.A.; Huynh, G.T.; Quinlivan, M.; Cullinane, A.; Rong, L.; Perelson, A.S. Modeling within-host dynamics of influenza virus infection including immune responses. PLoS Comput. Biol. 2012, 8, e1002588. [Google Scholar] [CrossRef]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Dusheiko, G.; Perelson, A.S. The role of cells refractory to productive infection in acute hepatitis B viral dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 5050–5055. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, E.J.; Vaidya, N.K.; Dorman, K.S.; Carpenter, S.; Mealey, R.H. Dynamics of lentiviral infection in vivo in the absence of adaptive immune responses. Virology 2018, 513, 108–113. [Google Scholar] [CrossRef]
- Ciupe, S.M.; Vaidya, N.K.; Forde, J.E. Early events in hepatitis B infection: The role of inoculum dose. Proc. R. Soc. B 2021, 288, 20202715. [Google Scholar] [CrossRef]
- Wang, S.; Pan, Y.; Wang, Q.; Miao, H.; Brown, A.N.; Rong, L. Modeling the viral dynamics of SARS-CoV-2 infection. Math. Biosci. 2020, 328, 108438. [Google Scholar] [CrossRef]
- Gonçalves, A.; Bertrand, J.; Ke, R.; Comets, E.; de Lamballerie, X.; Malvy, D.; Pizzorno, A.; Terrier, O.; Rosa Calatrava, M.; Mentré, F.; et al. Timing of Antiviral Treatment Initiation is Critical to Reduce SARS-CoV-2 Viral Load. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 509–514. [Google Scholar] [CrossRef]
- Néant, N.; Lingas, G.; Le Hingrat, Q.; Ghosn, J.; Engelmann, I.; Lepiller, Q.; Gaymard, A.; Ferré, V.; Hartard, C.; Plantier, J.C.; et al. Modeling SARS-CoV-2 viral kinetics and association with mortality in hospitalized patients from the French COVID cohort. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef] [PubMed]
- Gonçalves, A.; Maisonnasse, P.; Donati, F.; Albert, M.; Behillil, S.; Contreras, V.; Naninck, T.; Marlin, R.; Solas, C.; Pizzorno, A.; et al. SARS-CoV-2 viral dynamics in non-human primates. PLoS Comput. Biol. 2021, 17, e1008785. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.S.; Ejima, K.; Iwanami, S.; Fujita, Y.; Ohashi, H.; Koizumi, Y.; Asai, Y.; Nakaoka, S.; Watashi, K.; Aihara, K.; et al. A quantitative model used to compare within-host SARS-CoV-2, MERS-CoV, and SARS-CoV dynamics provides insights into the pathogenesis and treatment of SARS-CoV-2. PLoS Biol. 2021, 19, e3001128. [Google Scholar] [CrossRef] [PubMed]
- Dogra, P.; Ruiz-Ramírez, J.; Sinha, K.; Butner, J.D.; Peláez, M.J.; Rawat, M.; Yellepeddi, V.K.; Pasqualini, R.; Arap, W.; Sostman, H.D.; et al. Innate Immunity Plays a Key Role in Controlling Viral Load in COVID-19: Mechanistic Insights from a Whole-Body Infection Dynamics Model. ACS Pharmacol. Transl. Sci. 2021, 4, 248–265. [Google Scholar] [CrossRef]
- Perelson, A.S.; Ke, R. Mechanistic Modeling of SARS-CoV-2 and Other Infectious Diseases and the Effects of Therapeutics. Clin. Pharmacol. Ther. 2021, 109, 829–840. [Google Scholar] [CrossRef]
- Iwanami, S.; Ejima, K.; Kim, K.S.; Noshita, K.; Fujita, Y.; Miyazaki, Y.; Kohno, S.; Miyazaki, K.; Morimoto, S.; Nakaoka, S.; et al. Detection of significant antiviral drug effects on COVID-19 with reasonable sample sizes in randomized controlled trials: A modeling study combined with clinical data. PLoS Med. 2021, 18, e1003660. [Google Scholar] [CrossRef] [PubMed]
- Czuppon, P.; Débarre, F.; Gonçalves, A.; Tenaillon, O.; Perelson, A.S.; Guedj, J.; Blanquart, F. Success of prophylactic antiviral therapy for SARS-CoV-2: Predicted critical efficacies and impact of different drug-specific mechanisms of action. PLoS Comput. Biol. 2021, 17, e1008752. [Google Scholar] [CrossRef]
- Baccam, P.; Beauchemin, C.; Macken, C.A.; Hayden, F.G.; Perelson, A.S. Kinetics of influenza A virus infection in humans. J. Virol. 2006, 80, 7590–7599. [Google Scholar] [CrossRef] [PubMed]
- Maines, T.R.; Szretter, K.J.; Perrone, L.; Belser, J.A.; Bright, R.A.; Zeng, H.; Tumpey, T.M.; Katz, J.M. Pathogenesis of emerging avian influenza viruses in mammals and the host innate immune response. Immunol. Rev. 2008, 225, 68–84. [Google Scholar] [CrossRef]
- Sungnak, W.; Huang, N.; Bécavin, C.; Berg, M.; Queen, R.; Litvinukova, M.; Talavera-López, C.; Maatz, H.; Reichart, D.; Sampaziotis, F.; et al. SARS-CoV-2 entry factors are highly expressed in nasal epithelial cells together with innate immune genes. Nat. Med. 2020, 26, 681–687. [Google Scholar] [CrossRef]
- Hou, Y.J.; Okuda, K.; Edwards, C.E.; Martinez, D.R.; Asakura, T.; Dinnon, K.H.; Kato, T.; Lee, R.E.; Yount, B.L.; Mascenik, T.M.; et al. SARS-CoV-2 Reverse Genetics Reveals a Variable Infection Gradient in the Respiratory Tract. Cell 2020, 182, 429.e414–446.e414. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman & Hall/CRC: New York, NY, USA, 1998. [Google Scholar]
- Bates, D.M.; Watts, D.G. Nonlinear Regression Analysis: Its Applications; Wiley: New York, NY, USA, 1988. [Google Scholar]
- Miao, H.; Xia, X.; Perelson, A.S.; Wu, H. On Identifiability of Nonlinear Ode Models and Applications in Viral Dynamics. SIAM Rev. Soc. Ind. Appl. Math. 2011, 53, 3–39. [Google Scholar] [CrossRef]
- Sender, R.; Bar-On, Y.M.; Gleizer, S.; Bernshtein, B.; Flamholz, A.; Phillips, R.; Milo, R. The total number and mass of SARS-CoV-2 virions. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef]
- Ho, D.D.; Huang, Y. The HIV-1 vaccine race. Cell 2002, 110, 135–138. [Google Scholar] [CrossRef][Green Version]
- Bonhoeffer, S.; May, R.M.; Shaw, G.M.; Nowak, M.A. Virus dynamics and drug therapy. Proc. Natl. Acad. Sci. USA 1997, 94, 6971–6976. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, R.M.; Dixit, N.M.; Perelson, A.S. Modelling the in vivo growth rate of HIV: Implications for vaccination. In Multidisciplinary Approaches to Theory in Medicine; Paton, R., McNamara, L.A., Eds.; Elsevier: Amsterdam, The Netherland, 2006. [Google Scholar]
- Desmyter, J.; Melnick, J.L.; Rawls, W.E. Defectiveness of interferon production and of rubella virus interference in a line of African green monkey kidney cells (Vero). J. Virol. 1968, 2, 955–961. [Google Scholar] [CrossRef] [PubMed]
- Mosca, J.D.; Pitha, P.M. Transcriptional and posttranscriptional regulation of exogenous human beta interferon gene in simian cells defective in interferon synthesis. Mol. Cell. Biol. 1986, 6, 2279–2283. [Google Scholar] [CrossRef]
- Klimstra, W.B.; Tilston-Lunel, N.L.; Nambulli, S.; Boslett, J.; McMillen, C.M.; Gilliland, T.; Dunn, M.D.; Sun, C.; Wheeler, S.E.; Wells, A.; et al. SARS-CoV-2 growth, furin-cleavage-site adaptation and neutralization using serum from acutely infected hospitalized COVID-19 patients. J. Gen. Virol. 2020, 101, 1156–1169. [Google Scholar] [CrossRef] [PubMed]
- Karimzadeh, S.; Bhopal, R.; Nguyen Tien, H. Review of infective dose, routes of transmission and outcome of COVID-19 caused by the SARS-COV-2: Comparison with other respiratory viruses. Epidemiol. Infect. 2021, 149, e96. [Google Scholar] [CrossRef]
- Monchatre-Leroy, E.; Lesellier, S.; Wasniewski, M.; Picard-Meyer, E.; Richomme, C.; Boué, F.; Lacôte, S.; Murri, S.; Pulido, C.; Vulin, J.; et al. Hamster and ferret experimental infection with intranasal low dose of a single strain of SARS-CoV-2. J. Gen. Virol. 2021, 102. [Google Scholar] [CrossRef]

| Ferret | (PFU/mL) | (PFU/mL) | (/Day) | (/Cell/Day) | (/Day) | |
|---|---|---|---|---|---|---|
| F13-E SARS-CoV-2 virus | ||||||
| F13-E-1 | ||||||
| F13-E-2 | ||||||
| F13-E-3 | ||||||
| G. Ave. (F13-E) | ||||||
| CTan-H SARS-CoV-2 virus | ||||||
| CTan-H-1 | ||||||
| CTan-H-2 | ||||||
| CTan-H-3 | ||||||
| G. Ave. (CTan-H) | ||||||
| Overall G. Ave. | ||||||
| p-value | ≥0.05 | ≥0.05 | ≥0.05 | ≥0.05 | ≥0.05 | ≥0.05 |
| Ferret | (PFU/mL) | (PFU/mL) | (/Day) | (/Cell/Day) | (/Day) | (/Day) | |
|---|---|---|---|---|---|---|---|
| F13-E SARS-CoV-2 virus | |||||||
| F13-E-1 | |||||||
| F13-E-2 | |||||||
| F13-E-3 | |||||||
| G. Ave. (F13-E) | |||||||
| CTan-H SARS-CoV-2 virus | |||||||
| CTan-H-1 | |||||||
| CTan-H-2 | |||||||
| CTan-H-3 | |||||||
| G. Ave. (CTan-H) | |||||||
| Overall G. Ave. | |||||||
| p-value | |||||||
| Ferret | (PFU/mL) | (PFU/mL) | (/Day) | (/Cell/Day) | (/Day) | (/IFN/Day) | |
|---|---|---|---|---|---|---|---|
| F13-E SARS-CoV-2 virus | |||||||
| F13-E-1 | |||||||
| F13-E-2 | |||||||
| F13-E-3 | |||||||
| G. Ave. (F13-E) | |||||||
| CTan-H SARS-CoV-2 virus | |||||||
| CTan-H-1 | |||||||
| CTan-H-2 | |||||||
| CTan-H-3 | |||||||
| G. Ave. (CTan-H) | |||||||
| Overall G. Ave. | |||||||
| p-value | |||||||
| Ferret | Cell Loss (%) | |||||
|---|---|---|---|---|---|---|
| F13-E SARS-CoV-2 virus | ||||||
| F13-E-1 | 2.27 | 2.66 | 2.17 | 6.26 | 7.68 | 85.76 |
| F13-E-2 | 2.01 | 2.34 | 2.04 | 7.10 | 8.14 | 79.98 |
| F13-E-3 | 1.72 | 1.95 | 1.77 | 8.52 | 9.38 | 69.95 |
| G. Ave. (F13) | 1.99 | 2.30 | 1.99 | 7.24 | 8.37 | 78.28 |
| CTan-H SARS-CoV-2 virus | ||||||
| CTan-H-1 | 2.69 | 2.70 | 2.16 | 6.16 | 7.69 | 91.48 |
| CTan-H-2 | 2.32 | 2.26 | 1.85 | 7.37 | 8.99 | 86.48 |
| CTan-H-3 | 1.52 | 1.94 | 1.74 | 8.55 | 9.54 | 59.35 |
| G. Ave. (CTan-H) | 2.12 | 2.28 | 1.91 | 7.29 | 8.71 | 77.72 |
| Overall G. Ave. | 2.05 | 2.29 | 1.95 | 7.27 | 8.54 | 78.00 |
| p-value | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaidya, N.K.; Bloomquist, A.; Perelson, A.S. Modeling Within-Host Dynamics of SARS-CoV-2 Infection: A Case Study in Ferrets. Viruses 2021, 13, 1635. https://doi.org/10.3390/v13081635
Vaidya NK, Bloomquist A, Perelson AS. Modeling Within-Host Dynamics of SARS-CoV-2 Infection: A Case Study in Ferrets. Viruses. 2021; 13(8):1635. https://doi.org/10.3390/v13081635
Chicago/Turabian StyleVaidya, Naveen K., Angelica Bloomquist, and Alan S. Perelson. 2021. "Modeling Within-Host Dynamics of SARS-CoV-2 Infection: A Case Study in Ferrets" Viruses 13, no. 8: 1635. https://doi.org/10.3390/v13081635
APA StyleVaidya, N. K., Bloomquist, A., & Perelson, A. S. (2021). Modeling Within-Host Dynamics of SARS-CoV-2 Infection: A Case Study in Ferrets. Viruses, 13(8), 1635. https://doi.org/10.3390/v13081635







