On the Parametrization of Epidemiologic Models—Lessons from Modelling COVID-19 Epidemic
Abstract
:1. Introduction
2. Materials and Methods
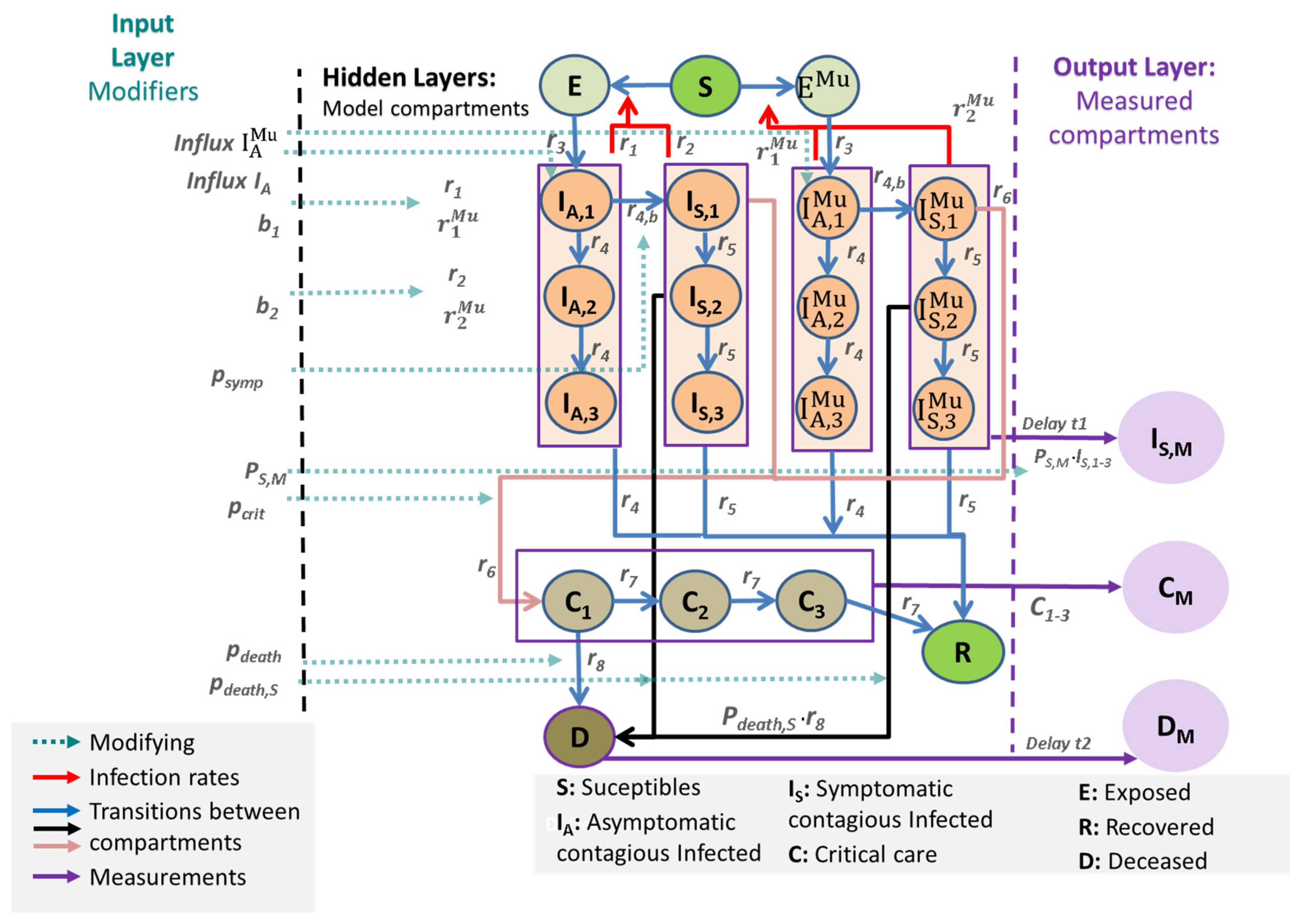
2.1. General Approach
- The input layer consists of external modifiers influencing (1) reporting policy (e.g., changing testing policy), (2) rates of infections (affected by non-pharmaceutical interventions, age structure, influx of cases), and (3) risks of severe disease conditions such as IC requirements and deaths, also depending on the changing age structure of infected subjects.
- The output layer of observable data is linked to the hidden layers of the core model by specific data models (see later).
- Susceptible, non-infected people (Sc): We assume that 100% of the population is susceptible to infection at the beginning of the epidemic.
- The latent state E comprises infected but non-infectious people.
- The asymptomatic infected state IA has three sub-compartments (I_(A,1), I_(A,2) and I_(A,3)). From I_(A,1), transitions to the symptomatic state or the second asymptomatic state are possible. From I_(A,2), only transitions to I_(A,3) and then to the recovered state R are assumed.
- The symptomatic infected state IS is also divided into three compartments (I_(S,1), I_(S,2), and I_(S,3)). The sub-compartment I_(S,1) comprises an efflux toward the sub-compartment C_1 representing deteriorations toward critical disease states. Otherwise, the patient transits to I_(S,2). From I_(S,2), a patient can either die representing deaths without prior intensive care or transit to I_(S,3). Finally, the efflux of I_(S,3) flows into R representing resolved disease courses.
- Both cases I_A and I_S contribute to new infections but with different rates to account for differences in infectivity and quarantine probabilities.
- The compartment C represents critical disease states requiring intensive care. We assume that these patients are not infectious due to isolation. Again, the compartment is divided into three sub-compartments, C_1, C_2, and C_3. In C_1, a patient can either die or transit to C_2, C_3, and finally, R.
- Patients on the recovered stage R are assumed to be immune against re-infections.
- We duplicate the compartments E, I_(A,1),…, I_(A,3), I_(S,1),…, I_(S,3) to account for two concurrent virus variants. We assume different infectivities for the two variants. All other parameters are assumed equal. No co-infections are assumed.
2.2. Input Layer
2.3. Output Layer and Data
2.4. Parametrization
2.5. Implementation
3. Results
3.1. Explanation of Epidemiologic Dynamics
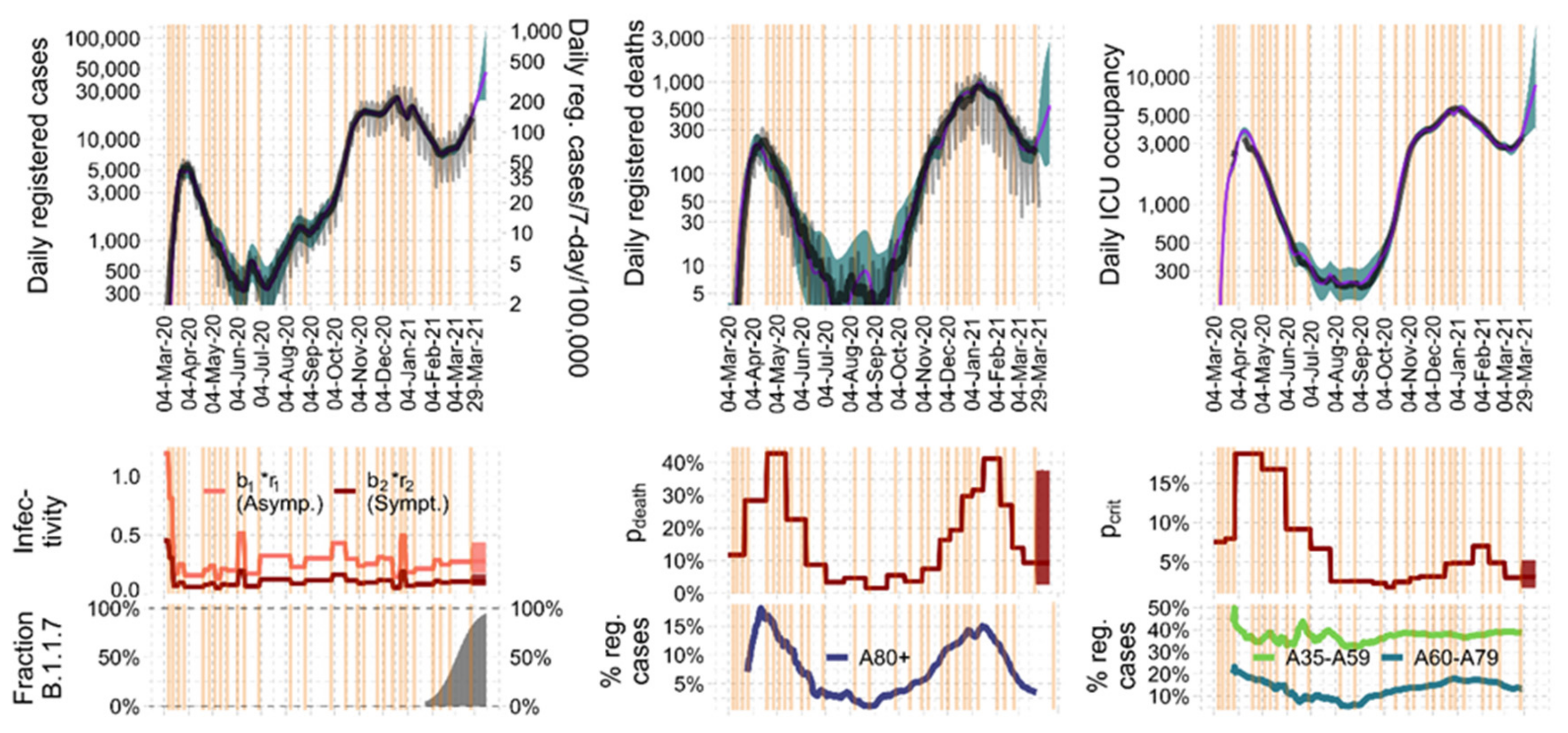
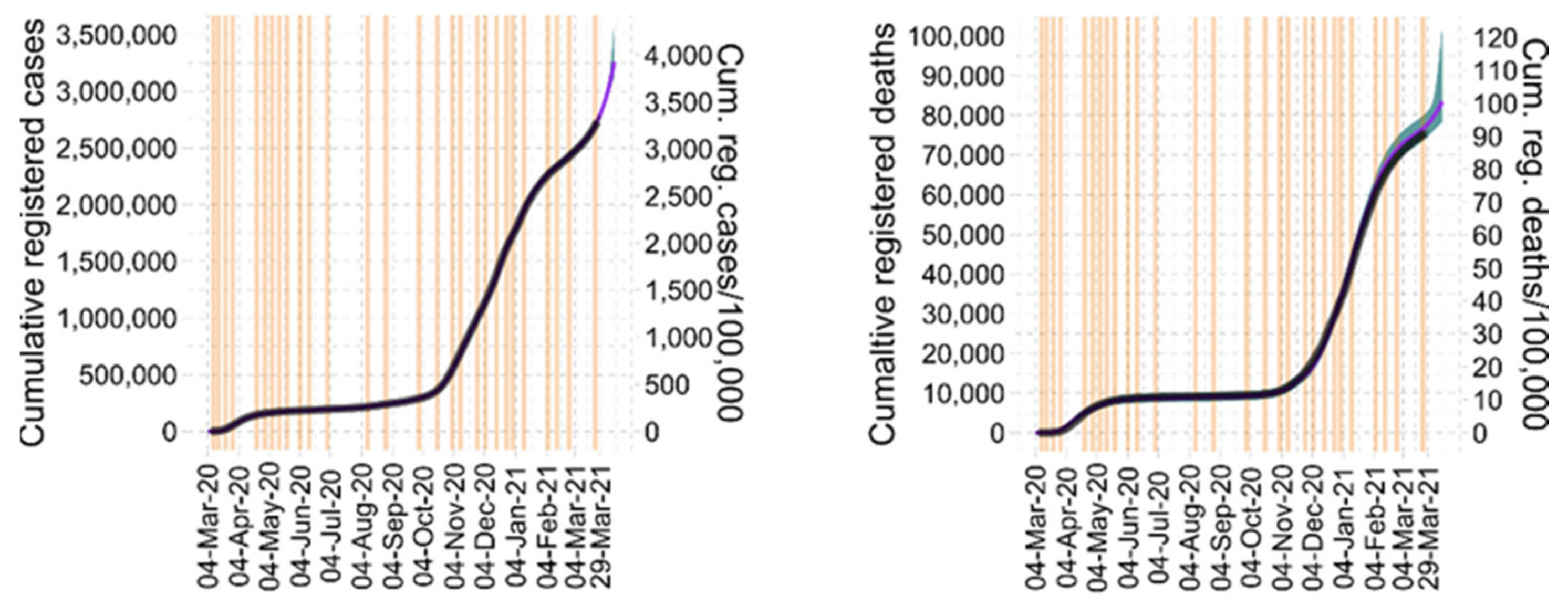
3.2. Parameter Estimates and Identifiability
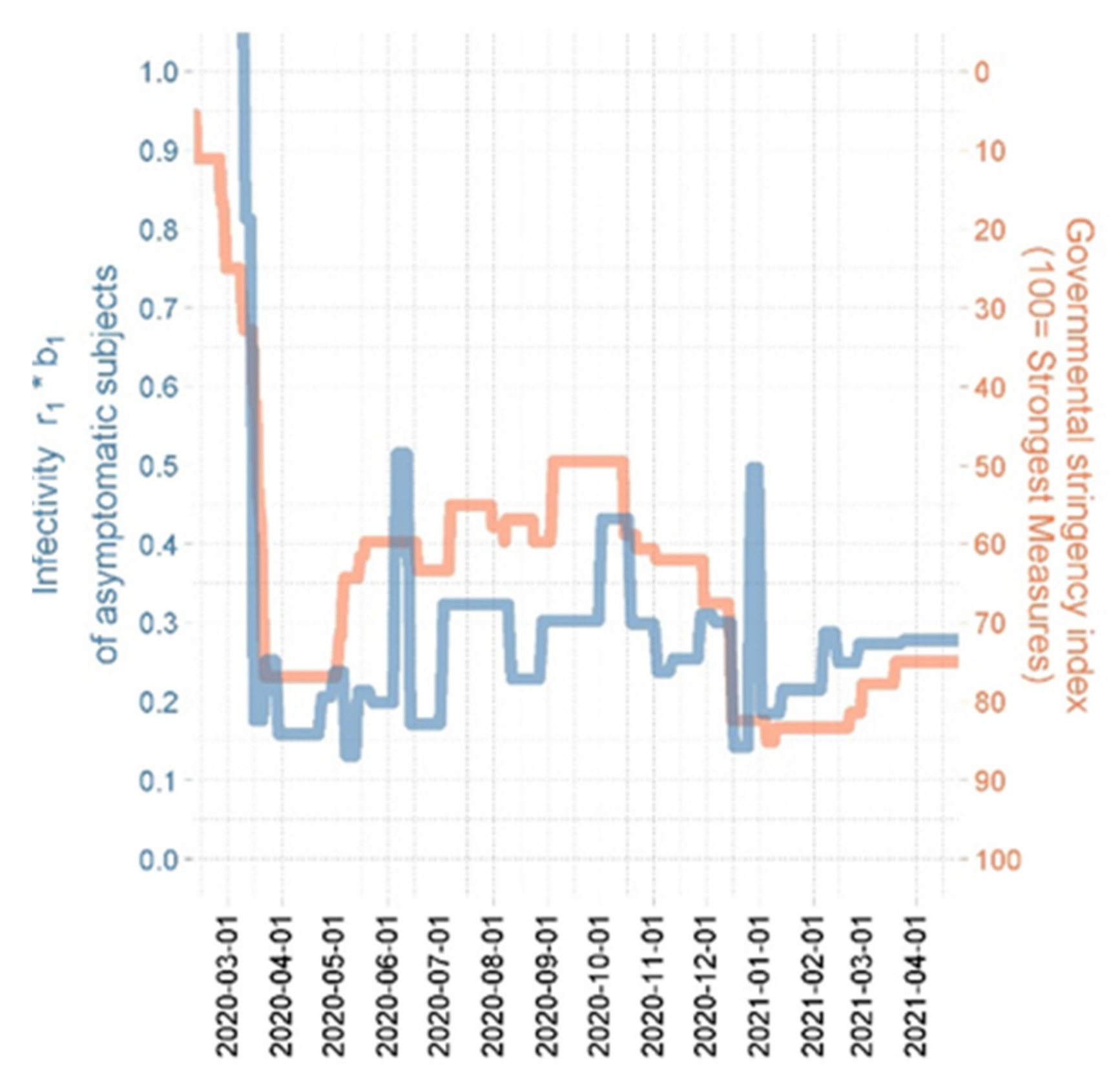
3.3. Plausibilization of Estimated Step Functions of Infectivity
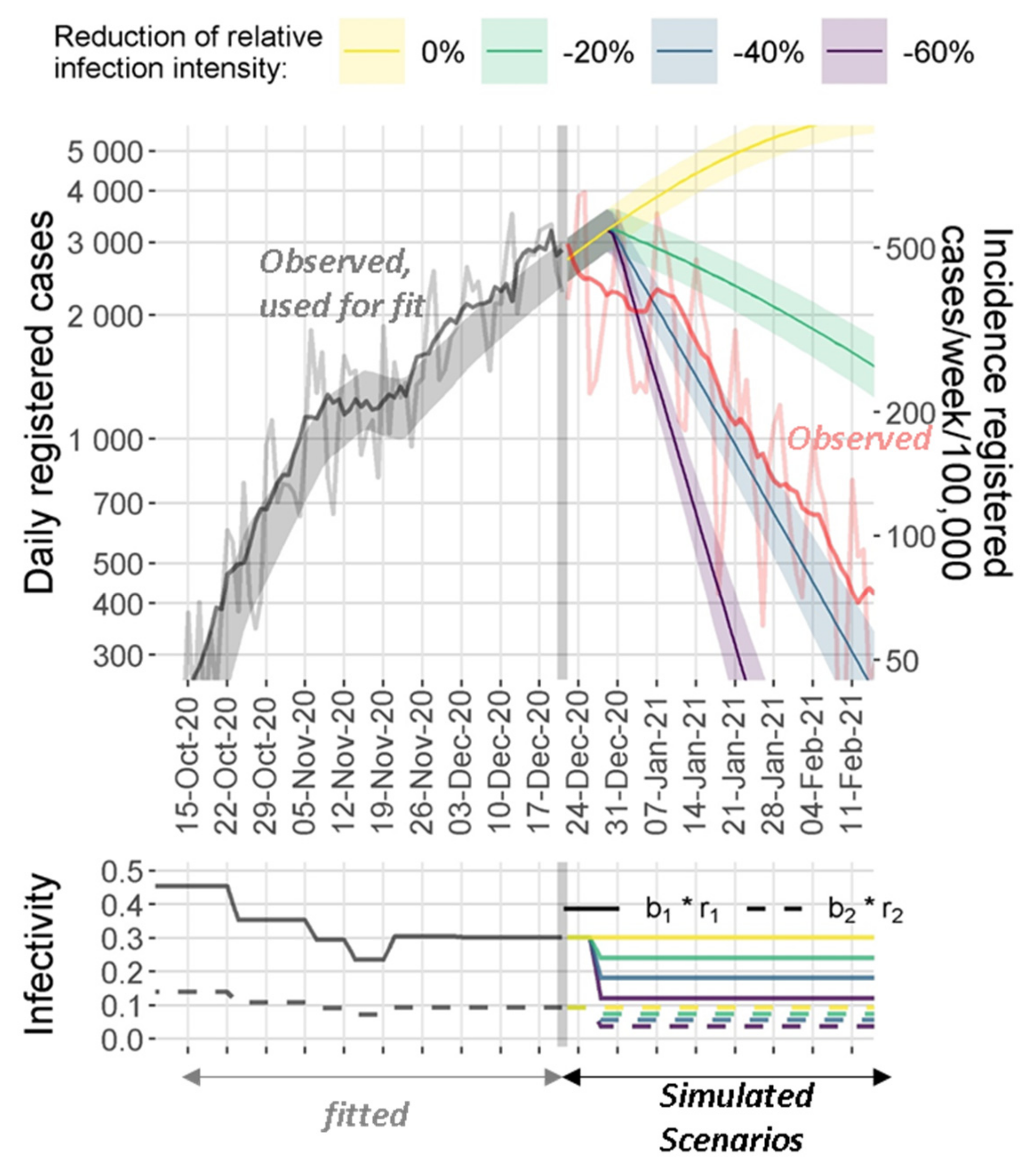
3.4. Model Predictions
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Equations of the SECIR Model
Appendix B. Input Layer
Appendix C. Output Layer

Appendix D. Parameter Estimation
Appendix E. Algorithm for Parameter Estimations and Prediction Sampling
- Simulation step: draw realizations of from the conditional distribution using MCMC algorithm.
- Stochastic approximation: updatewhere is a decreasing sequence of positive numbers.
- Maximization-step (correspondingly, minimization for negative log-likelihood): update according to
- Our stochastic approximation step is an improved version of the stochastic approximation of the integration of marginal distribution on the multidimensional domain of possible parameter values:
- In analogy to Monolix software, we selected as follows:We choose equal to 4 and run the algorithm until convergence with a tolerance 0.1% of estimates of population parameters (see below).
- We performed MCMC sampling 4000 times at each stage with a burn-in phase of 1000 steps. Thus, .
Appendix F. MCMC Algorithm for the Expectation Step
- The Mahalanobis distance of to the cluster from which it was generated is less than 0.025 or larger than 0.975. That is diverges significantly from the current multivariate normal distribution of the r-th cluster
- is significantly larger than π of the current cluster center. That is does not correspond to the local maximum of π in the neighbourhood of the r-th cluster.
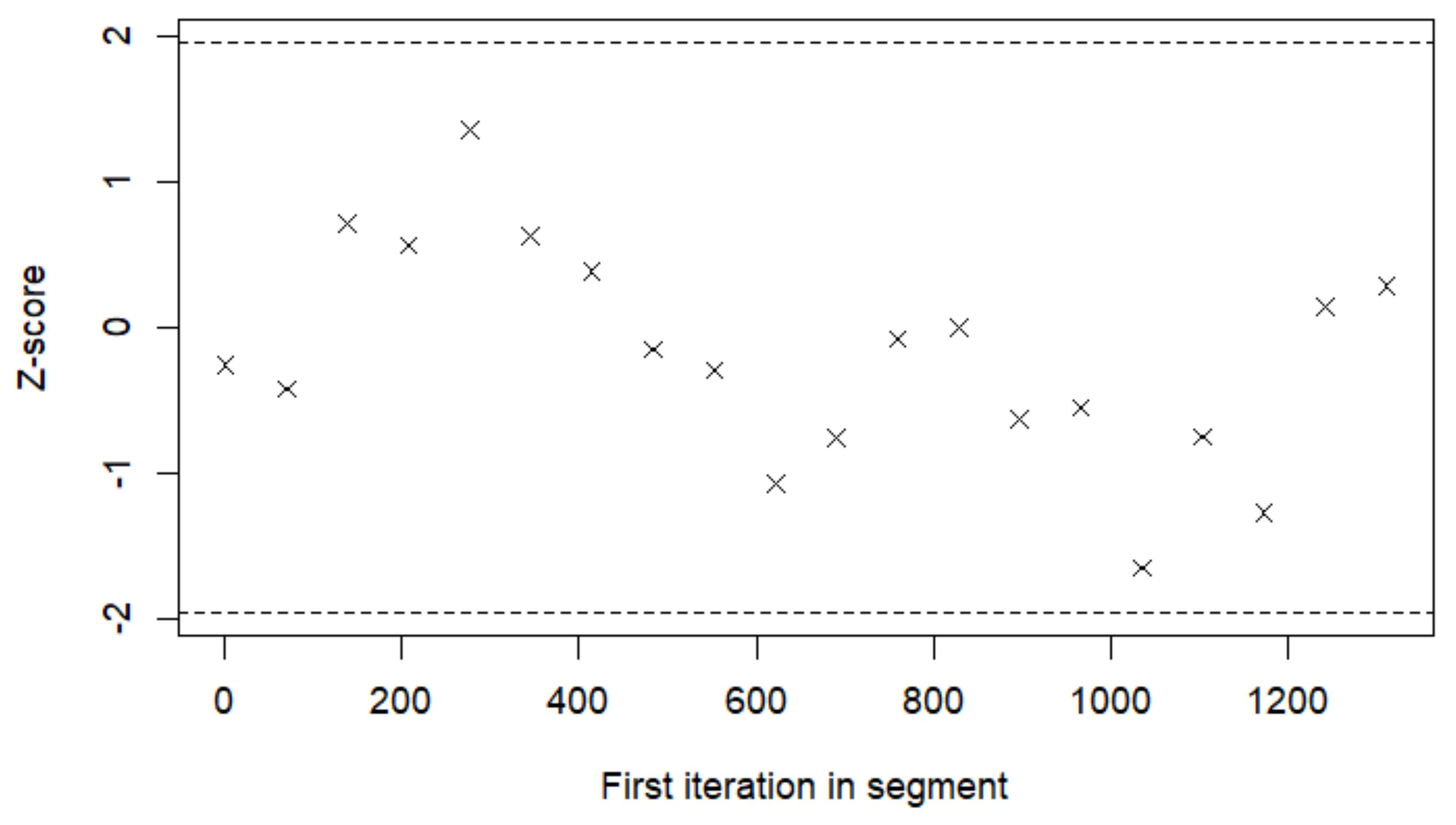
Appendix G. MCMC Simulation for Prediction and Controlling Goodness of Fit
Appendix H. Justification of Prior Parameters and Ranges
Appendix I. Parameter Values for Germany
| Number | Type of NPI/Contact Behaviour Change | Estimated New Infectivity | Relative Standard Error, % | Date | Source of Time Point | Standard Error (Days) |
|---|---|---|---|---|---|---|
| 1 | Intensification | 0.676 | 0.738 | 10 March 2020 | Fixed | - |
| 2 | Intensification | 0.150 | 3.99 | 15 March 2020 | Fixed | - |
| 3 | Relaxation | 0.214 | 0.711 | 22 March 2020 | Fixed | - |
| 4 | Intensification | 0.131 | 2.79 | 29 March 2020 | Estimated | 0.280 |
| 5 | Relaxation | 0.172 | 2.78 | 23 April 2020 | Estimated | 0.164 |
| 6 | Relaxation | 0.200 | 0.462 | 30 April 2020 | Fixed | - |
| 7 | Intensification | 0.109 | 5.78 | 7 May 2020 | Fixed | - |
| 8 | Relaxation | 0.177 | 5.13 | 14 May 2020 | Fixed | - |
| 9 | Intensification | 0.163 | 0.278 | 22 May 2020 | Estimated | 0.322 |
| 10 | Relaxation | 0.434 | 0.644 | 5 June 2020 | Estimated | 0.387 |
| 11 | Intensification | 0.142 | 3.67 | 13 June 2020 | Estimated | 0.360 |
| 12 | Relaxation | 0.270 | 2.80 | 1 July 2020 | Estimated | 0.251 |
| 13 | Intensification | 0.193 | 1.06 | 11 August 2020 | Estimated | 0.244 |
| 14 | Relaxation | 0.256 | 1.01 | 28 August 2020 | Estimated | 0.264 |
| 15 | Relaxation | 0.357 | 1.06 | 1 October 2020 | Estimated | 0.119 |
| 16 | Intensification | 0.246 | 0.967 | 19 October 2020 | Estimated | 0.334 |
| 17 | Intensification | 0.198 | 3.98 | 2 November 2020 | Fixed | - |
| 18 | Relaxation | 0.213 | 0.991 | 11 November 2020 | Estimated | 1.08 |
| 19 | Relaxation | 0.256 | 0.550 | 24 November 2020 | Estimated | 0.262 |
| 20 | Intensification | 0.248 | 1.61 | 1 December 2020 | Estimated | 0.303 |
| 21 | Intensification | 0.118 | 2.18 | 16 December 2020 | Fixed | - |
| 22 | Relaxation | 0.421 | 1.40 | 26 December 2020 | Estimated | 0.238 |
| 23 | Intensification | 0.154 | 3.48 | 1 January 2021 | Estimated | 0.118 |
| 24 | Relaxation | 0.182 | 11.0 | 12 January 2021 | Estimated | - |
| 25 | Relaxation | 0.237 | 3.09 | 6 February 2021 | Estimated | - |
| 26 | Intensification | 0.211 | 4.08 | 15 February 2021 | Estimated | - |
| 27 | Relaxation | 0.233 | 2.98 | 25 February 2021 | Estimated | - |
| 28 | Relaxation | 0.228 | 23.2 | 18 March 2021 | Fixed | - |
| nLL | BIC | |||
|---|---|---|---|---|
| 18 | 19 | 134 | 2620 | 6238 |
| 17 | 17 | 132 | 2661 | 6298 |
| 17 | 19 | 133 | 2645 | 6280 |
| 18 | 18 | 133 | 2633 | 6256 |
| 19 | 20 | 136 | 2616 | 6245 |
| 19 | 19 | 135 | 2618 | 6241 |
| Parameter | Description | Estimate | Relative Standard Error. % | Date Respective Controls | Standard Error (Days) |
|---|---|---|---|---|---|
| Relative values of starting at the respective date | 1.05 | 0.317 | 20 March 2020 | 0.0844 | |
| 2.48 | 3.18 | 1 April 2020 | 0.14 | ||
| 2.24 | 3.46 | 6 May 2020 | 1.06 | ||
| 1.22 | 3.20 | 4 June 2020 | 2.03 | ||
| 0.884 | 0.626 | 6 July 2020 | 3.75 | ||
| 0.344 | 2.07 | 30 July 2020 | 1.14 | ||
| 0.340 | 0.381 | 24 August 2020 | 6.94 | ||
| 0.301 | 4.25 | 20 September 2020 | 0.705 | ||
| 0.238 | 1.15 | 6 October 2020 | 1.52 | ||
| 0.330 | 1.03 | 23 October 2020 | 1.42 | ||
| 0.382 | 0.801 | 8 November 2020 | 0.870 | ||
| 0.419 | 1.70 | 20 November 2020 | 6.20 | ||
| 0.633 | 1.53 | 23 December 2020 | 1.43 | ||
| 0.651 | 1.51 | 1 January 2021 | 0.506 | ||
| 0.929 | 1.12 | 22 January 2021 | 3.43 | ||
| 0.647 | 3.41 | 13 February 2021 | 3.08 | ||
| 0.394 | 0.972 | 5 March 2021 | 6.15 | ||
| 0.441 | 62.8 | 18 March 2021 | - | ||
| Relative values of starting at the respective date | 2.39 | 1.88 | 26 March 2020 | 0.164 | |
| 3.58 | 1.17 | 23 April 2020 | 0.283 | ||
| 1.94 | 4.55 | 19 May 2020 | 1.45 | ||
| 0.743 | 1.19 | 10 June 2020 | 0.393 | ||
| 0.296 | 3.25 | 5 July 2020 | 5.72 | ||
| 0.401 | 0.635 | 27 July 2020 | 6.15 | ||
| 0.142 | 1.22 | 25 August 2020 | 4.51 | ||
| 0.473 | 7.46 | 17 September 2020 | 1.20 | ||
| 0.314 | 6.39 | 8 October 2020 | 1.56 | ||
| 0.638 | 0.966 | 1 November 2020 | 2.18 | ||
| 1.41 | 0.748 | 22 November 2020 | 1.17 | ||
| 1.64 | 2.53 | 11 December 2020 | 1.89 | ||
| 2.54 | 1.35 | 29 December 2020 | 0.499 | ||
| 2.66 | 3.01 | 7 January 2021 | 6.02 | ||
| 3.48 | 6.42 | 18 January 2021 | 1.43 | ||
| 2.31 | 4.80 | 5 February 2021 | 0.794 | ||
| 1.22 | 3.15 | 27 February 2021 | 2.315 | ||
| 0.807 | 2.15 | 09 March 2021 | 3.75 | ||
| 1.09 | 69.1 | 19 March 2021 | - |
| Parameter | Value for Germany | Value for Saxony |
|---|---|---|
| 3.62 | 0.921 | |
| 5.69 | 1.03 | |
| 1.19 | 0.442 | |
| 3.04 | 0.377 | |
| 0.99 | 1.14 |
| Parameter | Description | Posterior Estimate | Relative Standard Error, % | Prior Value | p-Value |
|---|---|---|---|---|---|
| influx | Initial influx of infections into compartment E until first interventions | 3171 | 3.12 | - | - |
| Infection rate through asymptomatic subjects | 1.19 | 0.582 | - | - | |
| Transit rate for compartment E (latent time) | 0.272 | 0.0571 | 1/3 | 0.213 | |
| Transit rate for asymptomatic sub-compartments | 0.636 | 0.734 | 3/5 | 0.429 | |
| Rate of development of symptoms after infection | 0.456 | 2.17 | 1/2.5 | 0.346 | |
| Transit rate for symptomatic sub-compartments | 0.946 | 2.33 | 3/2.5 | 0.499 | |
| Rate of development of critical state after being symptomatic | 0.186 | 0.405 | 1/5 | 0.457 | |
| Transit rate for critical state sub-compartment | 0.159 | 0.336 | 3/17 | 0.402 | |
| Death rate of patients in critical sub-compartment 1 | 0.104 | 0.409 | 1/8 | 0.441 | |
| Proportionality coefficient of inten-sifications/relaxations between and | 0.379 | 9.18 | - | - | |
| PS,M | Fraction of reported cases | 0.499 | 0.102 | 1/2 | |
| Probability of becoming critical after developing symptoms (initial value) | 0.0765 | 0.706 | - | - | |
| ) | Probability of death after becoming critical (initial value) | 0.119 | 1.24 | - | - |
| Proportionality coefficient for evaluating probability of death after developing symptoms without becoming critical, see (A6) | 0.587 | 8.04 | - | - |
Appendix J. Parameter Values for Saxony
| Numbers | Type of NPI/Behavior Change | Estimated New Infectivity | Relative Standard Error, % | Date | Source | Standard Error (Days) |
|---|---|---|---|---|---|---|
| 1 | Intensification | 0.606 | 0.877 | 10 March 2020 | Fixed | - |
| 2 | Intensification | 0.120 | 5.41 | 15 March 2020 | Fixed | - |
| 3 | Intensification | 0.0904 | 1.15 | 22 March 2020 | Fixed | - |
| 4 | Relaxation | 0.103 | 1.98 | 2 April 2020 | Estimated | 0.541 |
| 5 | Intensification | 0.0907 | 3.12 | 14 April 2020 | Estimated | 0.237 |
| 6 | Relaxation | 0.302 | 0.965 | 30 April 2020 | Fixed | - |
| 7 | Intensification | 0.0606 | 6.08 | 7 May 2020 | Fixed | - |
| 8 | Intensification | 0.0385 | 4.21 | 14 May 2020 | Fixed | - |
| 9 | Relaxation | 0.0601 | 0.199 | 19 May 2020 | Estimated | 0.487 |
| 10 | Relaxation | 0.817 | 0.505 | 4 June 2020 | Estimated | 0.603 |
| 11 | Intensification | 0.0344 | 4.18 | 11 June 2020 | Estimated | 0.456 |
| 12 | Relaxation | 0.219 | 3.23 | 30 June 2020 | Estimated | 0.298 |
| 13 | Intensification | 0.149 | 1.13 | 16 August 2020 | Estimated | 0.312 |
| 14 | Relaxation | 0.213 | 2.29 | 26 August 2020 | Estimated | 0.578 |
| 15 | Relaxation | 0.297 | 0.78 | 4 October 2020 | Estimated | 0.209 |
| 16 | Intensification | 0.185 | 1.26 | 21 October 2020 | Estimated | 0.352 |
| 17 | Intensification | 0.152 | 5.93 | 30 October 2020 | Fixed | - |
| 18 | Relaxation | 0.201 | 0.826 | 11 November 2020 | Estimated | 1.21 |
| 19 | Relaxation | 0.207 | 0.652 | 19 November 2020 | Estimated | 0.318 |
| 20 | Intensification | 0.201 | 2.13 | 22 November 2020 | Estimated | 0.554 |
| 21 | Intensification | 0.0672 | 1.87 | 10 December 2020 | Fixed | - |
| 22 | Relaxation | 0.228 | 1.36 | 18 December 2020 | Estimated | 0.426 |
| 23 | Intensification | 0.0937 | 5.09 | 1 January 2021 | Estimated | 0.141 |
| 24 | Relaxation | 0.120 | 9.78 | 14 January 2021 | Estimated | - |
| 25 | Relaxation | 0.229 | 10.1 | 5 February 2021 | Estimated | - |
| 26 | Intensification | 0.150 | 11.5 | 15 February 2021 | Estimated | - |
| 27 | Relaxation | 0.199 | 0.95 | 26 February 2021 | Estimated | - |
| 28 | Relaxation | 0.210 | 25.7 | 18 March 2021 | Fixed | - |
| Parameter | Description | Estimate | Relative Standard Error, % | Date Respective Controls | Standard Error (Days) |
|---|---|---|---|---|---|
| Relative values of starting at the respective date | 2.15 | 0.98 | 24 March 2020 | 0.34 | |
| 1.99 | 4.22 | 10 April 2020 | 0.672 | ||
| 1.01 | 3.54 | 11 May 2020 | 1.25 | ||
| 2.54 | 2.49 | 5 June 2020 | 3.73 | ||
| 1.50 | 1.26 | 2 July 2020 | 4.36 | ||
| 1.19 | 3.41 | 27 July 2020 | 0.75 | ||
| 0.764 | 0.478 | 29 August 2020 | 4.93 | ||
| 0.398 | 5.12 | 18 September 2020 | 2.96 | ||
| 0.300 | 2.09 | 25 September 2020 | 2.12 | ||
| 0.528 | 2.16 | 13 October 2020 | 0.49 | ||
| 0.908 | 3.72 | 26 October 2020 | 1.15 | ||
| 0.999 | 2.43 | 1 December 2020 | 5.31 | ||
| 1.76 | 1.91 | 26 December 2020 | 2.06 | ||
| 2.01 | 1.56 | 10 January 2021 | 0.67 | ||
| 2.99 | 0.98 | 25 January 2021 | 2.15 | ||
| 2.68 | 5.77 | 13 February 2021 | 4.12 | ||
| 1.11 | 1.33 | 5 March 2021 | 5.11 | ||
| 0.700 | 79.2 | 4 March 2021 | - | ||
| Relative values of starting at the respective date | 0.655 | 2.26 | 4 April 2020 | 0.241 | |
| 3.58 | 6.81 | 24 April 2020 | 0.335 | ||
| 1.94 | 5.32 | 17 May 2020 | 1.01 | ||
| 0.743 | 1.07 | 8 June 2020 | 0.619 | ||
| 0.296 | 4.32 | 7 July 2020 | 5.60 | ||
| 0.401 | 1.56 | 4 August 2020 | 6.13 | ||
| 0.142 | 6.77 | 26 August 2020 | 4.43 | ||
| 0.473 | 9.05 | 27 September 2020 | 0.95 | ||
| 0.314 | 1.42 | 3 October 2020 | 1.27 | ||
| 0.638 | 0.84 | 2 November 2020 | 3.62 | ||
| 1.41 | 0.9 | 16 November 2020 | 1.19 | ||
| 1.64 | 2.31 | 1 December 2020 | 1.63 | ||
| 2.54 | 1.555 | 20 December 2020 | 0.903 | ||
| 2.66 | 3.89 | 8 January 2021 | 5.52 | ||
| 3.48 | 5.53 | 19 January 2021 | 1.08 | ||
| 2.31 | 4.9 | 09 February 2021 | 0.383 | ||
| 1.22 | 2.76 | 26 February 2021 | 2.06 | ||
| 0.807 | 4.03 | 7 March 2021 | 5.34 | ||
| 1.09 | 70.1 | 11 March 2021 | - |
| Parameter | Description | Posterior Estimate | Relative Standard Error, % | Prior Value | p-Value |
|---|---|---|---|---|---|
| influx | Initial influx of infections into compartment E until first interventions | 68.1 | 6.17 | - | - |
| Infection rate through asymptomatic subjects | 1.61 | 1.32 | - | - | |
| Transit rate for compartment E (latent time) | 0.270 | 0.234 | 1/3 | 0.221 | |
| Transit rate for asymptomatic sub-compartments | 0.697 | 0.691 | 3/5 | 0.357 | |
| Rate of development of symptoms after infection | 0.294 | 3.27 | 1/2.5 | 0.489 | |
| Transit rate for symptomatic sub-compartments | 1.11 | 2.13 | 3/2.5 | 0.236 | |
| Rate of development of critical state after being symptomatic | 0.170 | 1.46 | 1/5 | 0.495 | |
| Transit rate for critical state sub-compartment | 0.198 | 0.659 | 3/17 | 0.372 | |
| Death rate of patients in critical sub-compartment 1 | 0.140 | 1.33 | 1/8 | 0.393 | |
| Proportional coefficient of intensifications/relaxations between and | 0.248 | 15.5 | - | - | |
| PS,M | Fraction of reported cases | 0.509 | 5.37 | 1/2 | |
| ( | Probability of becoming critical after developing symptoms (initial value) | 0.0794 | 1.76 | - | - |
| () | Probability of death after becoming critical (initial value) | 0.137 | 0.957 | - | - |
| Proportionality coefficient for evaluating probability of death after developing symptoms without becoming critical, see (A6) | 0.719 | 7.3 | - | - |
References
- Adiga, A.; Dubhashi, D.; Lewis, B.; Marathe, M.; Venkatramanan, S.; Vullikanti, A. Mathematical Models for COVID-19 Pandemic: A Comparative Analysis. J. Indian Inst. Sci. 2020, 100, 793–807. [Google Scholar] [CrossRef]
- Tang, J.; Vinayavekhin, S.; Weeramongkolkul, M.; Suksanon, C.; Pattarapremcharoen, K.; Thiwathittayanuphap, S.; Leelawat, N. Agent-Based Simulation and Modeling of COVID-19 Pandemic: A Bibliometric Analysis. J. Disaster Res. 2022, 17, 93–102. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Klepac, P.; Conlan, A.J.K.; Kissler, S.M.; Tang, M.L.; Fry, H.; Gog, J.R.; Edmunds, W.J.; Emery, J.C.; Medley, G.; et al. Effectiveness of isolation, testing, contact tracing, and physical distancing on reducing transmission of SARS-CoV-2 in different settings: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1151–1160. [Google Scholar] [CrossRef]
- Quilty, B.J.; Clifford, S.; Hellewell, J.; Russell, T.W.; Kucharski, A.J.; Flasche, S.; Edmunds, W.J.; E Atkins, K.; Foss, A.M.; Waterlow, N.R.; et al. Quarantine and testing strategies in contact tracing for SARS-CoV-2: A modelling study. Lancet Public Health 2021, 6, e175–e183. [Google Scholar] [CrossRef]
- Rahimi, I.; Chen, F.; Gandomi, A.H. A review on COVID-19 forecasting models. Neural Comput. Appl. 2021. [Google Scholar] [CrossRef]
- Flaxman, S.; Mishra, S.; Gandy, A.; Unwin, H.J.T.; Mellan, T.A.; Coupland, H.; Whittaker, C.; Zhu, H.; Berah, T.; Eaton, J.W.; et al. Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 2020, 584, 257–261. [Google Scholar] [CrossRef]
- Bo, Y.; Guo, C.; Lin, C.; Zeng, Y.; Li, H.B.; Zhang, Y.; Hossain, S.; Chan, J.W.; Yeung, D.W.; Kwok, K.O.; et al. Effectiveness of non-pharmaceutical interventions on COVID-19 transmission in 190 countries from 23 January to 13 April 2020. Int. J. Infect. Dis. 2020, 102, 247–253. [Google Scholar] [CrossRef]
- Khailaie, S.; Mitra, T.; Bandyophadhyay, A.; Schips, M.; Mascheroni, P.; Vanella, P.; Lange, B.; Binder, S.C.; Meyer-Hermann, M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. BMC Med. 2020, 19, 32. [Google Scholar] [CrossRef]
- Barbarossa, M.V.; Fuhrmann, J.; Meinke, J.H.; Krieg, S.; Varma, H.V.; Castelletti, N.; Lippert, T. Modeling the spread of COVID-19 in Germany: Early assessment and possible scenarios. PLoS ONE 2020, 15, e0238559. [Google Scholar] [CrossRef]
- der Heiden, M.; an Buchholz, U. Modellierung von Beispielszenarien der SARS-CoV-2-Epidemie 2020 in Deutschland; Robert Koch-Institut: Berlin, Germany, 2020. [Google Scholar]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef]
- Harris, J.E. Overcoming Reporting Delays Is Critical to Timely Epidemic Monitoring: The Case of COVID-19 in New York City. MedRxiv 2020. [Google Scholar] [CrossRef]
- Böttcher, S.; Oh, D.-Y.; Staat, D.; Stern, D.; Albrecht, S.; Wilrich, N.; Zacher, B.; Mielke, M.; Rexroth, U.; Hamouda, O. Erfassung der SARS-CoV-2-Testzahlen in Deutschland (Stand 2.12.2020); Robert Koch-Institut: Berlin, Germany, 2020. [Google Scholar]
- McCulloh, I.; Kiernan, K.; Kent, T. Improved Estimation of Daily COVID-19 Rate from Incomplete Data. In Proceedings of the 2020 Fourth International Conference on Multimedia Computing, Networking and Applications (MCNA), Valencia, Spain, 19–22 October 2020; pp. 153–158. [Google Scholar]
- Ram, V.; Schaposnik, L.P. A modified age-structured SIR model for COVID-19 type viruses. Sci. Rep. 2021, 11, 15194. [Google Scholar] [CrossRef] [PubMed]
- Cooper, I.; Mondal, A.; Antonopoulos, C.G. A SIR model assumption for the spread of COVID-19 in different communities. Chaos Solitons Fractals 2020, 139, 110057. [Google Scholar] [CrossRef] [PubMed]
- Georgatzis, K.; Williams, C.K.I.; Hawthorne, C. Input-Output Non-Linear Dynamical Systems applied to Physiological Condition Monitoring. In Proceedings of the 1st Machine Learning for Healthcare Conference 2016: PMLR, Los Angeles, CA, USA, 19–20 August 2016. [Google Scholar]
- Nishiura, H.; Linton, N.M.; Akhmetzhanov, A.R. Serial interval of novel coronavirus (COVID-19) infections. Int. J. Infect. Dis. 2020, 93, 284–286. [Google Scholar] [CrossRef]
- Tindale, L.C.; E Stockdale, J.; Coombe, M.; Garlock, E.S.; Lau, W.Y.V.; Saraswat, M.; Zhang, L.; Chen, D.; Wallinga, J.; Colijn, C. Evidence for transmission of COVID-19 prior to symptom onset. eLife 2020, 9, e57149. [Google Scholar] [CrossRef]
- Böhmer, M.M.; Buchholz, U.; Corman, V.M.; Hoch, M.; Katz, K.; Marosevic, D.V.; Böhm, S.; Woudenberg, T.; Ackermann, N.; Konrad, R.; et al. Investigation of a COVID-19 outbreak in Germany resulting from a single travel-associated primary case: A case series. Lancet Infect. Dis. 2020, 20, 920–928. [Google Scholar] [CrossRef]
- Ganyani, T.; Kremer, C.; Chen, D.; Torneri, A.; Faes, C.; Wallinga, J.; Hens, N. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Eurosurveillance 2020, 25, 2000257. [Google Scholar] [CrossRef]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [Green Version]
- Hu, Z.; Song, C.; Xu, C.; Jin, G.; Chen, Y.; Xu, X.; Ma, H.; Chen, W.; Lin, Y.; Zheng, Y.; et al. Clinical characteristics of 24 asymptomatic infections with COVID-19 screened among close contacts in Nanjing, China. Sci. China Life Sci. 2020, 63, 706–711. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Pei, S.; Chen, B.; Song, Y.; Zhang, T.; Yang, W.; Shaman, J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 2020, 368, 489–493. [Google Scholar] [CrossRef] [Green Version]
- Stebegg, M.; Kumar, S.D.; Silva-Cayetano, A.; Fonseca, V.R.; Linterman, M.A.; Graca, L. Regulation of the Germinal Center Response. Front. Immunol. 2018, 9, 2469. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hao, X.; Cheng, S.; Wu, D.; Wu, T.; Lin, X.; Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020, 584, 420–424. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Lau, E.H.Y.; Wu, P.; Deng, X.; Wang, J.; Hao, X.; Lau, Y.C.; Wong, J.Y.; Guan, Y.; Tan, X.; et al. Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 2020, 26, 672–675. [Google Scholar] [CrossRef] [Green Version]
- Epidemiologischer Steckbrief zu SARS-CoV-2 und COVID-19. RKI 2021. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Steckbrief.html;jses- (accessed on 26 November 2021).
- Zhou, F.; Yu, T.; Du, R.; Fan, G.; Liu, Y.; Liu, Z.; Xiang, J.; Wang, Y.; Song, B.; Gu, X.; et al. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: A retrospective cohort study. Lancet 2020, 395, 1054–1062. [Google Scholar] [CrossRef]
- Sanche, S.; Lin, Y.T.; Xu, C.; Romero-Severson, E.; Hengartner, N.; Ke, R. High Contagiousness and Rapid Spread of Severe Acute Respiratory Syndrome Coronavirus 2. Emerg. Infect. Dis. 2020, 26, 1470–1477. [Google Scholar] [CrossRef]
- COVID-19 National Emergency Response Center. Coronavirus Disease-19: The First 7755 Cases in the Republic of Korea. Osong Public Health Res. Perspect 2020, 11, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Schuppert, A.; Theisen, S.; Fränkel, P.; Weber-Carstens, S.; Karagiannidis, C. Bundesweites Belastungsmodell für Intensivstationen durch COVID-19. Med. Klin.-Intensivmed. Und Notf. 2022, 117, 218–226. [Google Scholar] [CrossRef]
- Tolksdorf, K.; Buda, S.; Schuler, E.; Wieler, L.H.; Haas, W. Eine höhere Letalität und lange Beatmungsdauer unterscheiden COVID-19 von schwer verlaufenden Atemwegsinfektionen in Grippewellen. Epidemiol. Bull. 2020, 41. [Google Scholar] [CrossRef]
- Karagiannidis, C.; Mostert, C.; Hentschker, C.; Voshaar, T.; Malzahn, J.; Schillinger, G.; Klauber, J.; Janssens, U.; Marx, G.; Weber-Carstens, S.; et al. Case characteristics, resource use, and outcomes of 10,021 patients with COVID-19 admitted to 920 German hospitals: An observational study. Lancet Respir. Med. 2020, 8, 853–862. [Google Scholar] [CrossRef]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Guomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infectious Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Linton, N.; Kobayashi, T.; Yang, Y.; Hayashi, K.; Akhmetzhanov, A.; Jung, S.-M.; Yuan, B.; Kinoshita, R.; Nishiura, H. Incubation Period and Other Epidemiological Characteristics of 2019 Novel Coronavirus Infections with Right Truncation: A Statistical Analysis of Publicly Available Case Data. J. Clin. Med. 2020, 9, 538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Byambasuren, O.; Cardona, M.; Bell, K.; Clark, J.; McLaws, M.-L.; Glasziou, P. Estimating the extent of asymptomatic COVID-19 and its potential for community transmission: Systematic review and meta-analysis. J. Assoc. Med. Microbiol. Infect. Dis. 2020, 5, 223–234. [Google Scholar] [CrossRef]
- Oran, D.P.; Topol, E.J. Prevalence of Asymptomatic SARS-CoV-2 Infection: A Narrative Review. Ann. Intern. Med. 2020, 173, 362–367. [Google Scholar] [CrossRef] [PubMed]
- Buitrago-Garcia, D.; Egli-Gany, D.; Counotte, M.J.; Hossmann, S.; Imeri, H.; Ipekci, A.M.; Salanti, G.; Low, N. Occurrence and transmission potential of asymptomatic and presymptomatic SARS-CoV-2 infections: A living systematic review and meta-analysis. PLoS Med. 2020, 17, e1003346. [Google Scholar] [CrossRef]
- Neuhauser, H.; Thamm, R.; Buttmann-Schweiger, N.; Fiebig, J.; Offergeld, R.; Poethko-Müller, C.; Prütz, F.; Santos-Hövener, C.; Sarganas, G.; Angelika, S.R.; et al. Ergebnisse seroepidemiologischer Studien zu SARS-CoV-2 in Stichproben der Allgemeinbevölkerung und bei Blutspenderinnen und Blutspendern in Deutschland (Stand 03.12.2020). Epidemiol. Bull. 2020, 50. [Google Scholar] [CrossRef]
- Gornyk, D.; Harries, M.; Glöckner, S.; Strengert, M.; Kerrinnes, T.; Bojara, G.; Krause, G. SARS-CoV-2 seroprevalence in Germany—A population based sequential study in five regions. medRxiv 2021. [Google Scholar] [CrossRef]
- Bock, W.; Jayathunga, Y.; Götz, T.; Rockenfeller, R. Are the upper bounds for new SARS-CoV-2 infections in Germany useful. Comput. Math. Biophys. 2021, 9, 242–260. [Google Scholar] [CrossRef]
- COVID-19-Fälle nach Meldewoche und Geschlecht sowie Anteile mit für COVID-19 relevanten Symptomen, Anteile Hospitalisierter/Verstorbener und Altersmittelwert/-median (Tabelle wird jeden Donnerstag aktualisiert). RKI 2020. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/Daten/Klinische_Aspekte.html (accessed on 26 June 2022).
- Tagesreport-Archiv. DIVI 2020. Available online: https://www.divi.de/divi-intensivregister-tagesreport- (accessed on 26 June 2022).
- Delgado, G.; Safranek, J.; Goyette, B.; Spady, R. Reported versus Actual Date of Death. “Reported” versus “Actual”: Two Different Things. Available online: https://covidplanningtools.com/reported-versus-actual-date-of-death/ (accessed on 26 June 2022).
- Robert Koch Institute. Bericht zu Virusvarianten von SARS-CoV-2 in Deutschland, insbesondere zur Variant of Concern (VOC) B.1.1.7. Available online: https://www.rki.de/DE/Content/InfAZ/N/Neuartiges_Coronavirus/DESH/Bericht_VOC_2021-03-03.pdf?__blob=publicationFile (accessed on 3 March 2021).
- Kheifetz, Y.; Scholz, M. Modeling individual time courses of thrombopoiesis during multi-cyclic chemotherapy. PLoS Comput. Biol. 2019, 15, e1006775. [Google Scholar] [CrossRef]
- Kuhn, E.; Lavielle, M. Coupling a stochastic approximation version of EM with an MCMC procedure. ESAIM Probab. Stat. 2004, 8, 115–131. [Google Scholar] [CrossRef] [Green Version]
- Meineke, F.A.; Löbe, M.; Stäubert, S. Introducing Technical Aspects of Research Data Management in the Leipzig Health Atlas. Stud. Health Technol. Inform. 2018, 247, 426–430. [Google Scholar]
- Hale, T.; Angrist, N.; Goldszmidt, R.; Kira, B.; Petherick, A.; Phillips, T.; Webster, S.; Cameron-Blake, E.; Hallas, L.; Majumdar, S.; et al. A global panel database of pandemic policies (Oxford COVID-19 Government Response Tracker). Nat. Hum. Behav. 2021, 5, 529–538. [Google Scholar] [CrossRef] [PubMed]
- COVID-19 Government Response Tracker; University of Oxford: Oxford, UK. 2020. Available online: https://www.bsg.ox.ac.uk/research/research-projects/covid-19-government-response-tracker (accessed on 3 March 2022).
- Mullen, J.L.; Tsueng, G.; Latif, A.A.; Alkuzweny, M.; Cano, M.; Haag, E.; Zhou, J.; Zeller, M.; Hufbauer, E.; Matteson, N. Outbreak.info. A Standardized, Open-Source Database of COVID-19 Resources and Epidemiology Data. Available online: https://outbreak.info (accessed on 18 July 2021).
- Aktuelle Entwicklung der COVID-19 Epidemie in Leipzig und Sachsen. Bulletin 14 vom 20.02.2021. Available online: https://www.imise.uni-leipzig.de/sites/www.imise.uni-leipzig.de/files/files/uploads/Medien/bulletin_n14_covid19_sachsen__2021_02_22_v11.pdf (accessed on 26 June 2022).
- Scholz, S.; Waize, M.; Weidemann, F.; Treskova-Schwarzbach, M.; Haas, L.; Harder, T.; Karch, A.; Lange, B.; Kuhlmann, A.; Jäger, V.; et al. Einfluss von Impfungen und Kontaktreduktionen auf die dritte Welle der SARS-CoV-2-Pandemie und perspektivische Rückkehr zu prä-pandemischem Kontaktverhalten. 2021. Available online: https://edoc.rki.de/handle/176904/8023?show=full (accessed on 26 June 2022).
- Friberg, L.E.; Henningsson, A.; Maas, H.; Nguyen, L.; Karlsson, M.O. Model of chemotherapy-induced myelosuppression with parameter consistency across drugs. J. Clin. Oncol. 2002, 20, 4713–4721. [Google Scholar] [CrossRef] [PubMed]
- Maire, F.; Friel, N.; Mira, A.; Raftery, A.E. Adaptive Incremental Mixture Markov Chain Monte Carlo. J. Comput. Graph. Stat. 2019, 28, 790–805. [Google Scholar] [CrossRef] [Green Version]
- Bracher, J.; Wolffram, D.; Deuschel, J.; Görgen, K.; Ketterer, J.L.; Ullrich, A.; Abbott, S.; Barbarossa, M.V.; Bertsimas, D.; Bhatia, S.; et al. A pre-registered short-term forecasting study of COVID-19 in Germany and Poland during the second wave. Nat. Commun. 2021, 12, 5173. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data Via the EM Algorithm. J. R. Stat. Soc. Ser. B Methodol. 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Tierney, L. Markov Chains for Exploring Posterior Distributions. Ann. Stat. 1994, 22, 1701–1728. [Google Scholar] [CrossRef]
- Haario, H.; Saksman, E.; Tamminen, J. An Adaptive Metropolis Algorithm. Bernoulli 2001, 7, 223. [Google Scholar] [CrossRef] [Green Version]
- Geweke, J.F. Evaluating the Accuracy of Sampling-Based Approaches to the Calculation of Posterior Moments. In Bayesian Statistics; Bernado, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Clarendon Press: Oxford, UK, 1992; p. 4. [Google Scholar]
- Wu, Z.; McGoogan, J.M. Characteristics of and Important Lessons From the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72 314 Cases From the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef]


| Compartment Name | Sub-Compartments | Description |
|---|---|---|
| Susceptible | ||
| E | Latent stage (not infectious) | |
| Asymptomatic infected state 1, can either develop symptoms, i.e., transit to with probability and rate r4b or stays asymptomatic with probability and transits to with rate r4 | ||
| Asymptomatic infected state 2, transits to with rate r4 | ||
| Asymptomatic infected stage 3 transits to R with rate r4 | ||
| Symptomatic infected state 1. Can either become critical, i.e., transits to with probability and rate r6 or stays sub-critical with probability and transits to with rate r5 | ||
| Symptomatic infected state 2, can either die, i.e., transits to D with probability or transits to with probability and rate r5 | ||
| Symptomatic infected state 3, transits to R with rate r5 | ||
| C | Critical state 1, not infectious. Can either die, i.e., transits to D with probability and transit rate r8 or stays critical with probability and transits to with rate r7 | |
| Critical state 2, transits to C3 with rate r7 | ||
| Critical state 3, transits to R with rate r7 | ||
| R | Recovered (absorbing state) | |
| D | Dead (absorbing state) |
| Parameter | Unit | Description | Source | Reference | Value | Prior Mean | Min | Max |
|---|---|---|---|---|---|---|---|---|
| influx | Subjects per day | Initial influx of infections into compartment E until first interventions | Estimated | § | 3171 | - | - | - |
| Day−1 | Infection rate through asymptomatic subjects | Estimated | § | 1.19 | - | - | - | |
| Day−1 | Infection rate through symptomatic subjects | (parsimony) | § | 0.451 | - | - | - | |
| - | Proportion of infection rate symptomatics/asymptomatics r1/r2 | Estimated | § | 0.379 | - | 0 | - | |
| Day−1 | Transit rate for compartment E (latent time) | prior constraint | §, [10,18,19,20,21] | 0.272 | 1/3 | 1/4 | 1/2 | |
| Day−1 | Transit rate for asymptomatic sub-compartments | prior constraint | §,[22,23,24,25] | 0.636 | 3/5 | 3/10 | 3/4 | |
| Day−1 | Rate of development of symptoms after infection | prior constraint | §, [10,18,19,20,21,26,27,28] | 0.456 | 2/55 | 1/5 | 1 | |
| Day−1 | Transit rate for symptomatic sub-compartments | prior constraint | § | 0.946 | 6/5 | 6/15 | 6/3 | |
| Day−1 | Rate of development of critical state after being symptomatic | prior constraint | §, [10,29,30,31] | 0.186 | 1/5 | 1/7 | 1/4 | |
| Day−1 | Transit rate for critical state sub-compartment | prior constraint | §,[10,32,33,34] | 0.159 | 3/17 | 3/35 | 3/8 | |
| Day−1 | Death rate of patients in critical sub-compartment 1 | prior constraint | §, [29,35,36] | 0.104 | 1/8 | 1/14 | 2/13 | |
| - | Probability of symptoms development after being infected | Set or prior constrained (overfitted if estimated unconstrained) | §,[37,38,39] | 0.5 | - | 0.3 | 0.8 | |
| - | Initial value of step function , the probability of becoming critical after developing symptoms | Estimated | §, [9,27] | 0.0765 | - | 0 | 1 | |
| () | - | Initial value of step function , the probability of dying after becoming critical | Estimated | §, [32] | 0.119 | - | 0 | 1 |
| - | Probability of death after developing symptoms without becoming critical | Set equal to (parsimony) | §, [32] | - | - | 0 | 1 | |
| Proportionality factor for probability of death after developing symptoms without becoming critical | Estimated | § | 0.587 | |||||
| - | Fraction of unreported cases | prior constraint | §, [40,41] | 0.499 | 0.5 | 0.1 | 0.90 | |
| mur | Ratio of r1Mu/r1 = r2Mu/r2 reflecting higher infectivity of B.1.1.7 variant | Set | § | 1.65 | - | - | - |
| Parameter | Unit | Description | Source | Remarks |
|---|---|---|---|---|
| - | Number of time points of changes of NPI/contact behavior | Empirically defined | 13 intensifications, 15 relaxations identified (determined by information criterion) | |
| , j = 1,…, | - | Relative infectivity of subjects in the time interval [tr, tr + 1] | Estimated | assumed to be the same for symptomatic and asymptomatic patients |
| , j = 1,…, | Days | Time points of NPI/contact behavior changes | Estimated or fixed | Strictly monotone sequence |
| - | Number of time steps of | Empirically defined | 18 (determined by information criterion) | |
| , j = 1,…, | - | Value of between two time steps | Estimated | Within the interval [0, 1] |
| , j = 1,…, | Days | Time points of changes of | Estimated | Strictly monotone sequence |
| - | Number of time steps of | Empirically defined | 19 (determined by information criterion) | |
| , j = 1,…, | - | Value of between two time steps | Estimated | Within the interval [0, 1] |
| , j = 1,…, | Days | Time points of changes of | Estimated | Strictly monotone sequence |
| Days | Delay of activation of NPI | Fixed | 2 days |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kheifetz, Y.; Kirsten, H.; Scholz, M. On the Parametrization of Epidemiologic Models—Lessons from Modelling COVID-19 Epidemic. Viruses 2022, 14, 1468. https://doi.org/10.3390/v14071468
Kheifetz Y, Kirsten H, Scholz M. On the Parametrization of Epidemiologic Models—Lessons from Modelling COVID-19 Epidemic. Viruses. 2022; 14(7):1468. https://doi.org/10.3390/v14071468
Chicago/Turabian StyleKheifetz, Yuri, Holger Kirsten, and Markus Scholz. 2022. "On the Parametrization of Epidemiologic Models—Lessons from Modelling COVID-19 Epidemic" Viruses 14, no. 7: 1468. https://doi.org/10.3390/v14071468
APA StyleKheifetz, Y., Kirsten, H., & Scholz, M. (2022). On the Parametrization of Epidemiologic Models—Lessons from Modelling COVID-19 Epidemic. Viruses, 14(7), 1468. https://doi.org/10.3390/v14071468






