Robust Approaches to the Quantitative Analysis of Genome Formula Variation in Multipartite and Segmented Viruses
Abstract
1. Introduction
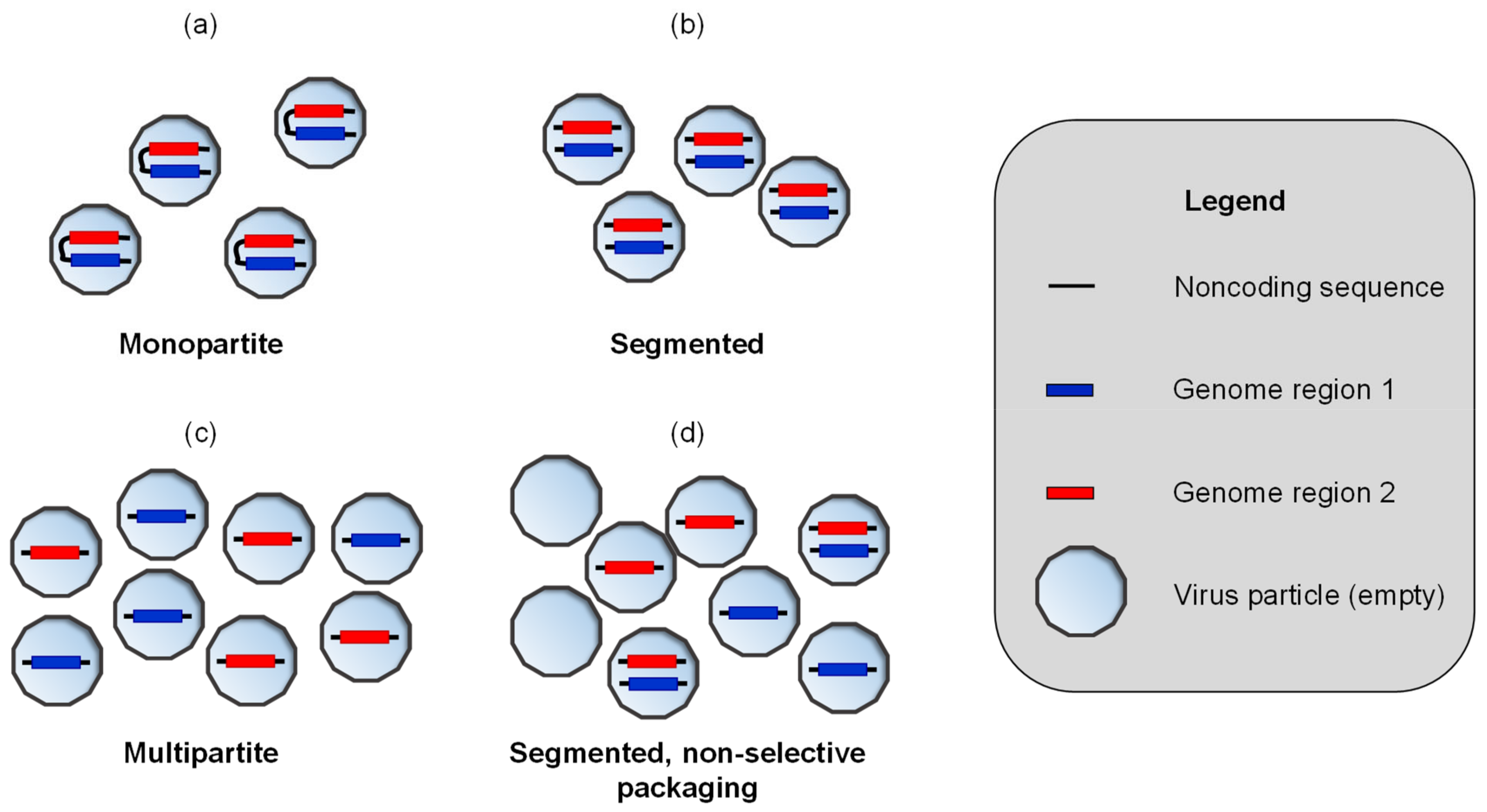
2. Methods
3. Results
3.1. The Genome Formula Distance Metric
3.1.1. The Genome Formula Distance Metric
3.1.2. Minimum and Maximum Values of the Genome Formula Distance Metric
3.1.3. Distance Metric for Random Genome Formula Variation
3.1.4. Distance Metric for Maximum Genome Formula Drift
3.2. Applications of the Genome Formula Distance Metric
3.2.1. Comparison of the Genome Formula to Theoretical Values
3.2.2. Comparison of the Genome Formula for Different Groups
3.2.3. Comparison of the Genome Formula to Reference
4. Discussion
4.1. Alternative Metrics for Analyzing Genome Formula Data
4.2. Caveats
4.3. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Results for the Comparison of the Genome Formula for Different Groups
| PERMANOVA | PERMDISP2 | |||
|---|---|---|---|---|
| Data Included in Analysis | F (d.f.) | P | F (d.f.) | P |
| C. quinoa, all methods | 9.523 (1,14) | 0.007 ** | 2.293 (3,12) | 0.069 |
| N. tabacum, all methods | 3.105 (1,14) | 0.072 | 2.144 (3,12) | 0.148 |
| N. benthamiana, all methods | 2.342 (1,14) | 0.126 | 0.622 (3,12) | 0.598 |
| RT-qPCR, all host species | 1.723 (1,10) | 0.208 | 1.900 (2,9) | 0.205 |
| RT-dPCR, all host species | 7.187 (1,10) | 0.007 ** | 0.671 (2,9) | 0.538 |
| Illumina, all host species | 3.242 (1,10) | 0.101 | 12.65 (2,9) | <0.001 *** |
| Nanopore, all host species | 3.632 (1,10) | 0.072 | 2.988 (2,9) | 0.105 |
| Experiment | ||||||
|---|---|---|---|---|---|---|
| V. faba 1 | V. faba 2 | V. faba 3 | M. truncatula 1 | M. truncatula 2 | ||
| Experiment | V. faba 1 | F1,14 = 0.593 p = 0.483 | F1,40 = 3.525 p = 0.062 | F1,21 = 0.185 p = 0.679 | F1,X = 0.260 p = 0.712 | |
| V. faba 2 | F1,14 = 4.397 p = 0.011 | F1,36 = 1.124 p = 0.297 | F1,16 = 2.130 p = 0.170 | F1,17 < 0.001 p = 0.985 | ||
| V. faba 3 | F1,40 = 1.659 p = 0.164 | F1,36 = 3.735 p = 0.013 | F1,42 = 5.631 p = 0.021 | F1,43 = 1.558 p = 0.227 | ||
| M. truncatula 1 | F1,21 = 73.68 p < 0.0001 * | F1,16 = 52.959 p < 0.0001 * | F1,42 = 44.458 p < 0.0001 * | F1,24 = 0.679 p = 0.518 | ||
| M. truncatula 2 | F1,X = 40.926 p < 0.0001 * | F1,17 = 28.968 p = 0.0001 * | F1,43 = 35.289 p < 0.0001 * | F1,24 = 2.006 p = 0.116 | ||
Appendix B. Results for the Comparison of the Genome Formula to A Reference
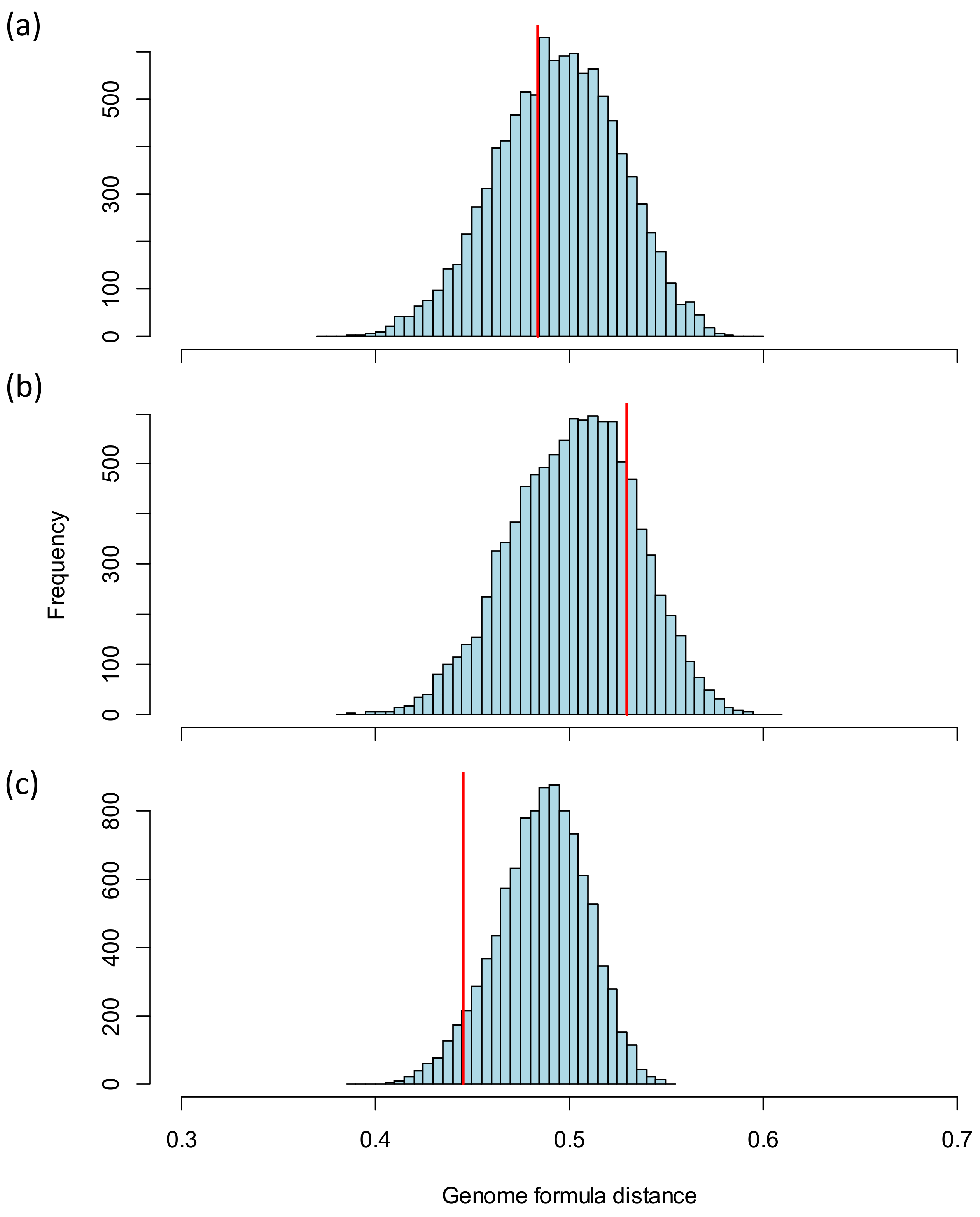
Appendix C. Predicted Properties of the ΔGF Metric
| Number of Genome Segments | λ1 | ||
|---|---|---|---|
| 2 | 0.2726 | 0.2034 | 5.37 |
| 3 | 0.3046 | 0.1981 | 7.08 |
| 4 | 0.3157 | 0.1850 | 9.33 |
| 5 | 0.3211 | 0.1742 | 10.96 |
| 6 | 0.3241 | 0.1585 | 13.49 |
| 7 | 0.3260 | 0.1493 | 15.14 |
| 8 | 0.3274 | 0.1411 | 16.98 |
| 9 | 0.3285 | 0.1324 | 19.05 |
| 10 | 0.3291 | 0.1236 | 21.88 |
References
- Sicard, A.; Michalakis, Y.; Gutiérrez, S.; Blanc, S. The strange lifestyle of multipartite viruses. PLoS Pathog. 2016, 12, e1005819. [Google Scholar] [CrossRef]
- Michalakis, Y.; Blanc, S. The curious strategy of multipartite viruses. Annu. Rev. Virol. 2020, 7, 203–218. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Navarro, J.A.; Zwart, M.P.; Elena, S.F. Effects of the number of genome segments on primary and systemic infections with a multipartite plant RNA virus. J. Virol. 2013, 87, 10805–10815. [Google Scholar] [CrossRef][Green Version]
- Fulton, R.W. The effect of dilution on Necrotic ringspot virus infectivity and the enhancement of infectivity by noninfective virus. Virology 1962, 18, 477–485. [Google Scholar] [CrossRef] [PubMed]
- Wichgers Schreur, P.J.; Kortekaas, J. Single-molecule FISH reveals non-selective packaging of Rift Valley fever virus genome segments. PLoS Pathog. 2016, 12, e1005800. [Google Scholar] [CrossRef] [PubMed]
- Yvon, M.; German, T.; Ullman, D.; Dasgupta, R.; Parker, M.; Ben- Mahmoud, S.; Verdin, E.; Gognalons, P.; Ancelin, A.; Him, J.; et al. The genome of a bunyavirus cannot be defined at the level of the viral particle but only at the scale of the viral population. Proc. Natl. Acad. Sci. USA 2023, 120, e2309412120. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, N.T.; Onuoha, N.O.; Antia, A.; Steel, J.; Antia, R.; Lowen, A.C. Incomplete influenza A virus genomes occur frequently but are readily complemented during localized viral spread. Nat. Commun. 2019, 10, 3526. [Google Scholar] [CrossRef] [PubMed]
- Diefenbacher, M.; Sun, J.; Brooke, C. The parts are greater than the whole: The role of semi-infectious particles in influenza A virus biology. Curr. Opin. Virol. 2018, 33, 42–46. [Google Scholar] [CrossRef] [PubMed]
- Bermúdez-Méndez, E.; Bronsvoort, K.F.; Zwart, M.P.; van de Water, S.; Cárdenas-Rey, I.; Vloet, R.P.M.; Koenraadt, C.J.M.; Pijlman, G.P.; Kortekaas, J.; Wichgers Schreur, P.J. Incomplete bunyavirus particles can cooperatively support virus infection and spread. PLOS Biol. 2022, 20, e3001870. [Google Scholar] [CrossRef]
- Lucía-Sanz, A.; Manrubia, S. Multipartite viruses: Adaptive trick or evolutionary treat? NPJ Syst. Biol. Appl. 2017, 3, 34. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, X.; Liu, W.; Zhou, Q.; Zhang, Q.; Li, G.; Yao, Q. Genome segments accumulate with different frequencies in Bombyx mori bidensovirus. J. Basic Microbiol. 2016, 56, 1338–1343. [Google Scholar] [CrossRef] [PubMed]
- Ladner, J.T.; Wiley, M.R.; Beitzel, B.; Kramer, L.D.; Tesh, R.B.; Palacios, G.; Auguste, A.J.; Dupuis Ii, A.P.; Lindquist, M.E.; Sibley, S.D.; et al. A multicomponent animal virus isolated from mosquitoes. Cell Host Microbe 2016, 20, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Sicard, A.; Yvon, M.; Timchenko, T.; Gronenborn, B.; Michalakis, Y.; Gutierrez, S.; Blanc, S. Gene copy number is differentially regulated in a multipartite virus. Nat. Commun. 2013, 4, 2248. [Google Scholar] [CrossRef] [PubMed]
- Wu, B.; Zwart, M.P.; Sánchez-Navarro, J.A.; Elena, S.F. Within-host evolution of segments ratio for the tripartite genome of alfalfa mosaic virus. Sci. Rep. 2017, 7, 5004. [Google Scholar] [CrossRef] [PubMed]
- Boezen, D.; Vermeulen, M.; Johnson, M.L.; van der Vlugt, R.A.A.; Malmstrom, C.M.; Zwart, M.P. Mixed viral infection constrains the genome formula of multipartite cucumber mosaic virus. Front. Virol. 2023, 3, 1225818. [Google Scholar] [CrossRef]
- Moreau, Y.; Gil, P.; Exbrayat, A.; Rakotoarivony, I.; Bréard, E.; Sailleau, C.; Viarouge, C.; Zientara, S.; Savini, G.; Goffredo, M.; et al. The genome segments of bluetongue virus differ in copy number in a host-specific manner. J. Virol. 2020, 95, 10–1128. [Google Scholar] [CrossRef]
- Hajimorad, M.R.; Kurath, G.; Randles, J.W.; Francki, R.I.B. Change in phenotype and encapsidated RNA segments of an isolate of alfalfa mosaic virus: An influence of host passage. J. Gen. Virol. 1991, 72, 2885–2893. [Google Scholar] [CrossRef]
- Kormelink, R.; De Haan, P.; Peters, D.; Goldbach, R. Viral RNA synthesis in tomato spotted wilt virus-infected Nicotiana rustica plants. J. Gen. Virol. 1992, 73, 687–693. [Google Scholar] [CrossRef]
- Wichgers Schreur, P.J.; Kormelink, R.; Kortekaas, J. Genome packaging of the Bunyavirales. Curr. Opin. Virol. 2018, 33, 151–155. [Google Scholar] [CrossRef]
- Boezen, D.; Johnson, M.L.; Grum-Grzhimaylo, A.A.; van der Vlugt, R.A.; Zwart, M.P. Evaluation of sequencing and PCR-based methods for the quantification of the viral genome formula. Virus Res. 2023, 326, 199064. [Google Scholar] [CrossRef]
- Roossinck, M.J. Cucumber mosaic virus, a model for RNA virus evolution. Mol. Plant Pathol. 2001, 2, 59–63. [Google Scholar] [CrossRef]
- Mansourpour, M.; Gallet, R.; Abbasi, A.; Blanc, S.; Dizadji, A.; Zeddam, J.-L. Effects of an alphasatellite on the life cycle of the nanovirus faba bean necrotic yellows virus. J. Virol. 2022, 96, e01388-21. [Google Scholar] [CrossRef] [PubMed]
- Obrępalska-Stęplowska, A.; Renaut, J.; Planchon, S.; Przybylska, A.; Wieczorek, P.; Barylski, J.; Palukaitis, P. Effect of temperature on the pathogenesis, accumulation of viral and satellite RNAs and on plant proteome in peanut stunt virus and satellite RNA-infected plants. Front. Plant Sci. 2015, 6, 903. [Google Scholar] [CrossRef] [PubMed]
- Gutiérrez, S.; Zwart, M.P. Population bottlenecks in multicomponent viruses: First forays into the uncharted territory of genome-formula drift. Curr. Opin. Virol. 2018, 33, 184–190. [Google Scholar] [CrossRef] [PubMed]
- Zwart, M.P.; Elena, S.F. Modeling multipartite virus evolution: The genome formula facilitates rapid adaptation to heterogeneous environments. Virus Evol. 2020, 6, veaa022. [Google Scholar] [CrossRef] [PubMed]
- Rybicki, E.P. A Top Ten list for economically important plant viruses. Arch. Virol. 2015, 160, 17–20. [Google Scholar] [CrossRef]
- Lamy-Besnier, Q.; Brancotte, B.; Ménager, H.; Debarbieux, L. Viral Host Range database, an online tool for recording, analyzing and disseminating virus-host interactions. Bioinformatics 2021, 37, 2798–2801. [Google Scholar] [CrossRef] [PubMed]
- Moury, B.; Fabre, F.; Hébrard, E.; Froissart, R. Determinants of host species range in plant viruses. J. Gen. Virol. 2017, 98, 862–873. [Google Scholar] [CrossRef]
- Valdano, E.; Manrubia, S.; Gómez, S.; Arenas, A. Endemicity and prevalence of multipartite viruses under heterogeneous between-host transmission. PLoS Comput. Biol. 2019, 15, e1006876. [Google Scholar] [CrossRef]
- Gallet, R.; Fabre, F.; Michalakis, Y.; Blanc, S. The number of target molecules of the amplification step limits accuracy and sensitivity in ultradeep-sequencing viral population studies. J. Virol. 2017, 91, 10–1128. [Google Scholar] [CrossRef]
- Kennedy, G.G.; Sharpee, W.; Jacobson, A.L.; Wambugu, M.; Mware, B.; Hanley-Bowdoin, L. Genome segment ratios change during whitefly transmission of two bipartite cassava mosaic begomoviruses. Sci. Rep. 2023, 13, 10059. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing, version 4.3; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Oksanen, J.; Simpson, G.; Blanchet, F.; Kindt, R.; Legendre, P.M.P.; O’Hara, R.; Solymos, P.; Stevens, M.; Szoecs, E.; Wagner, H.B.M.; et al. Vegan: Community Ecology Package, version 2.6-4; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Anderson, M.J. Permutational multivariate analysis of variance (PERMANOVA). Wiley StatsRef Stat. Ref. Online 2017, 1–15. [Google Scholar] [CrossRef]
- Anderson, M.J. A new method for non-parametric multivariate analysis of variance. Austral Ecol. 2001, 26, 32–46. [Google Scholar] [CrossRef]
- Di Mattia, J.; Torralba, B.; Yvon, M.; Zeddam, J.L.; Blanc, S.; Michalakis, Y. Nonconcomitant host-to-host transmission of multipartite virus genome segments may lead to complete genome reconstitution. Proc. Natl. Acad. Sci. USA 2022, 119, e2201453119. [Google Scholar] [CrossRef]
- Zwart, M.P.; Blanc, S.; Johnson, M.; Manrubia, S.; Michalakis, Y.; Sofonea, M.T. Unresolved advantages of multipartitism in spatially structured environments. Virus Evol. 2021, 7, veab004. [Google Scholar] [CrossRef]
- Leeks, A.; Young, P.G.; Turner, P.E.; Wild, G.; West, S.A. Cheating leads to the evolution of multipartite viruses. PLoS Biol. 2023, 21, e3002092. [Google Scholar] [CrossRef]
- Warton, D.I.; Blanchet, F.G.; O’Hara, R.B.; Ovaskainen, O.; Taskinen, S.; Walker, S.C.; Hui, F.K.C. So many variables: Joint modeling in community ecology. Trends Ecol. Evol. 2015, 30, 766–779. [Google Scholar] [CrossRef] [PubMed]
- Pichler, M.; Hartig, F. Machine learning and deep learning—A review for ecologists. Methods Ecol. Evol. 2023, 14, 994–1016. [Google Scholar] [CrossRef]

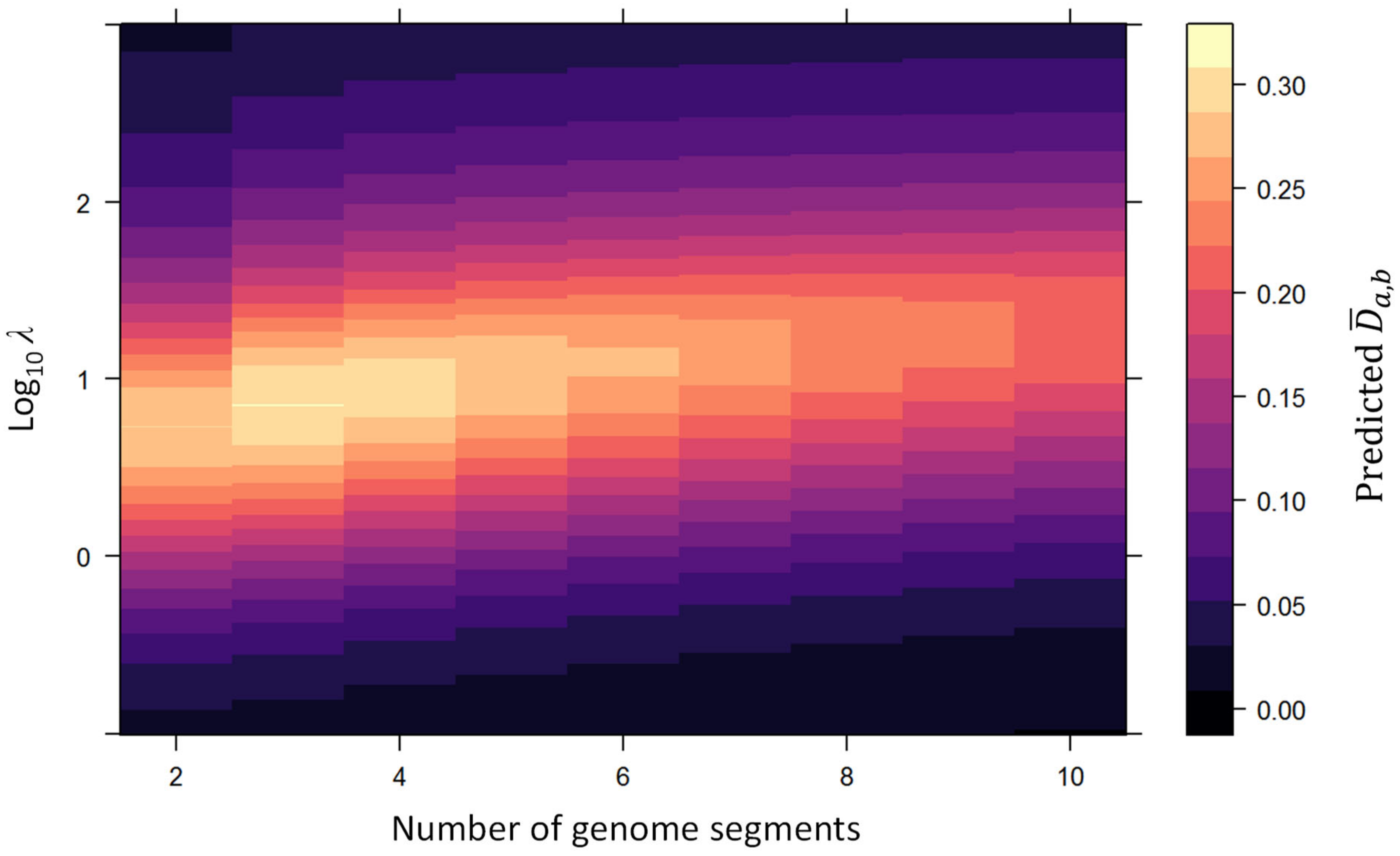
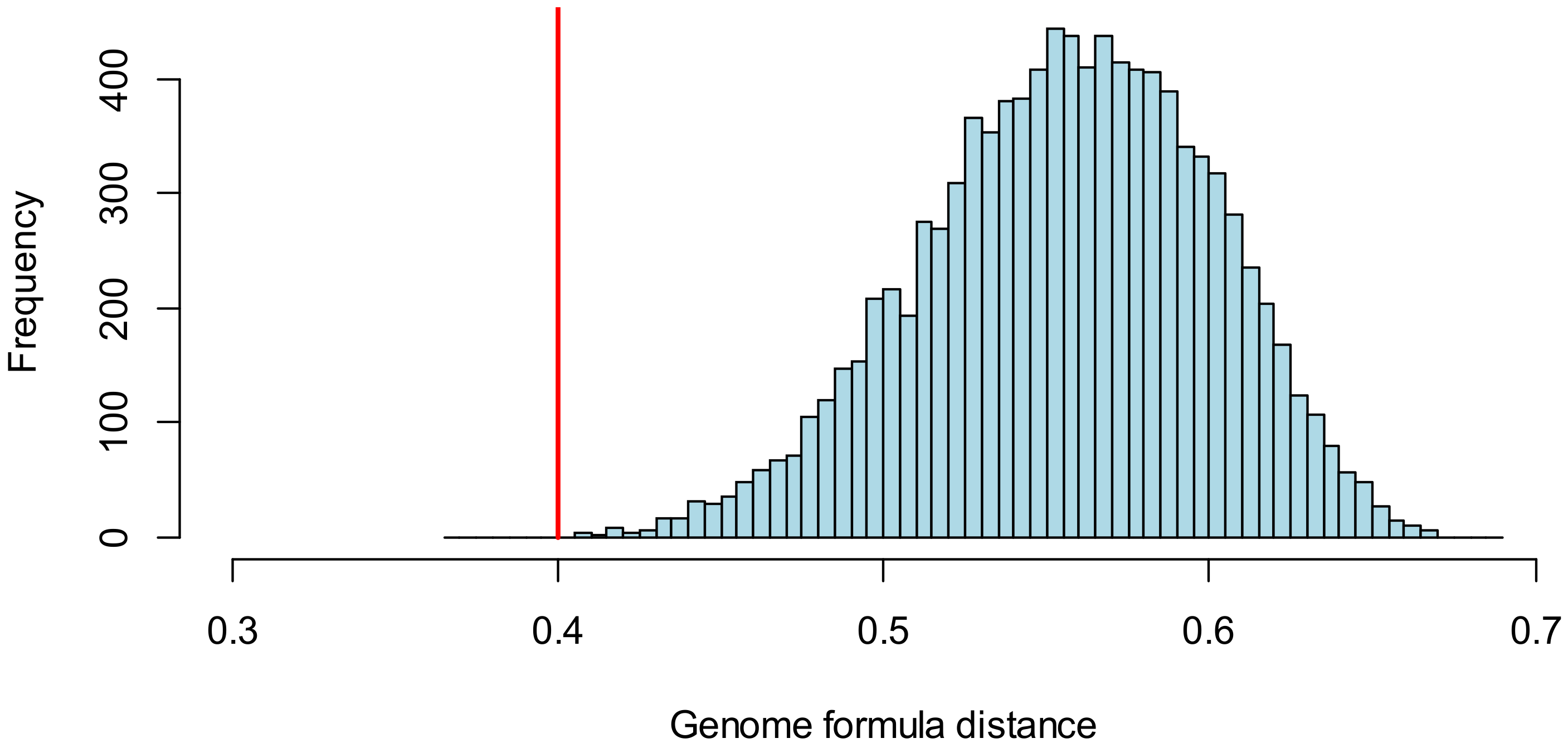
| Approach | Strengths | Weaknesses | Ref. |
|---|---|---|---|
| Analysis of variance (ANOVA) on the relative frequencies of individual genome segments | (i) Parsimony of the analysis | (i) Limited to the analysis of individual segments (ii) Model assumptions 1 | [13] |
| Multivariate analysis of variance (MANOVA) on the relative frequency of all genome segments | (i) Single analysis of all segments (ii) Technical error included in the analysis | (i) Dependence between relative frequencies (ii) Model assumptions 1,2 | [14] |
| Model selection based on the ΔGF metric 3 for all genome segments | (i) Single analysis of all segments | (i) Assumptions for estimating the likelihoods and weighing of model parameters for model selection 4 | [20] |
| T-tests on ratio of the log-tranformed RNA1:RNA2 | (i) Parsimony (ii) Model assumptions met | (i) Only applicable to bipartite viruses (ii) Consider effects of a single factor | [31] |
| PERMANOVA on the genome formula distance metric 5 | (i) Parsimony (ii) Single analysis of all segments (iii) Model assumptions met | (i) If there are differences in spread, differences in centroid cannot be assessed | [15] |
| Number of Genome Segments | λ1 | ||
|---|---|---|---|
| 2 | 0.3855 | 0.2877 | 5.37 |
| 3 | 0.3905 | 0.2801 | 7.08 |
| 4 | 0.3638 | 0.2629 | 9.12 |
| 5 | 0.3367 | 0.2494 | 10.47 |
| 6 | 0.3132 | 0.2341 | 12.30 |
| 7 | 0.2934 | 0.2189 | 14.12 |
| 8 | 0.2767 | 0.2060 | 15.85 |
| 9 | 0.2625 | 0.1929 | 18.20 |
| 10 | 0.2501 | 0.1847 | 19.50 |
| Genome Segments | Model Predictions 1 | |||||
|---|---|---|---|---|---|---|
| Ref | Experiment | n | ± SD | |||
| 3 | 0.391 | 0.280 | [14] | AMV in N. benthamiana, inoculated | 6 | 0.077 ± 0.015 |
| AMV in N. benthamiana, lower leaf | 6 | 0.195 ± 0.029 | ||||
| AMV in N. benthamiana, upper leaf | 6 | 0.197 ± 0.124 | ||||
| [15] | CMV in N. tabacum, whole plant | 9 | 0.207 ± 0.069 | |||
| 8 | 0.277 | 0.206 | [13] | FBNSV in V. faba, leaf level 1 | 9 | 0.352 ± 0.097 |
| FBNSV in V. faba, leaf level 2 | 8 | 0.275 ± 0.062 | ||||
| FBNSV in V. faba, leaf level 3 | 13 | 0.198 ± 0.045 | ||||
| FBNSV in V. faba, leaf level 4 | 15 | 0.175 ± 0.050 | ||||
| FBNSV in V. faba, leaf level 5 | 16 | 0.198 ± 0.063 | ||||
| FBNSV in V. faba, leaf level 6 | 16 | 0.178 ± 0.031 | ||||
| Genome Formula Distance to Inoculum | |||
|---|---|---|---|
| Tissue | Observed 1 | Predicted 2 | Ranking 3 |
| Inoculated leaf | 0.400 ± 0.242 | 0.556 [0.434–0.652] | 5 |
| Middle leaf | 0.484 ± 0.261 | 0.494 [0.410–0.568] | 3683 |
| Upper leaf | 0.530 ± 0.237 | 0.503 [0.418–0.576] | 7919 |
| Rest of plant | 0.445 ± 0.245 | 0.486 [0.421–0.538] | 533 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, M.L.; Zwart, M.P. Robust Approaches to the Quantitative Analysis of Genome Formula Variation in Multipartite and Segmented Viruses. Viruses 2024, 16, 270. https://doi.org/10.3390/v16020270
Johnson ML, Zwart MP. Robust Approaches to the Quantitative Analysis of Genome Formula Variation in Multipartite and Segmented Viruses. Viruses. 2024; 16(2):270. https://doi.org/10.3390/v16020270
Chicago/Turabian StyleJohnson, Marcelle L., and Mark P. Zwart. 2024. "Robust Approaches to the Quantitative Analysis of Genome Formula Variation in Multipartite and Segmented Viruses" Viruses 16, no. 2: 270. https://doi.org/10.3390/v16020270
APA StyleJohnson, M. L., & Zwart, M. P. (2024). Robust Approaches to the Quantitative Analysis of Genome Formula Variation in Multipartite and Segmented Viruses. Viruses, 16(2), 270. https://doi.org/10.3390/v16020270






