The Anthrax Toxin Lethal Factor in Solution Does Not Have the Protein’s Crystallized Structure
Abstract
1. Introduction
2. Results
2.1. Analysis of the SANS Scattering Curve
2.2. The Molecular Properties Found by SANS Compared with Known LF
3. Discussion
3.1. The Crystal Structure and Solution Structure Compared
3.2. Perspective on the Lethal Factor’s Properties
4. Conclusions
5. Materials and Methods
5.1. Lethal Factor Solution
5.2. Small-Angle Neutron Scattering (SANS) Data Collection
5.3. Scattering Curve Fitting
5.4. Calculating the SANS Scattering Equivalent to the Crystal Structure
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fee, E.; Brown, T.M. John Henry Bell: Occupational anthrax pioneer. Am. J. Public Health 2002, 92, 756–757. [Google Scholar]
- Ashique, S.; Biswas, A.; Mohanto, S.; Srivastava, S.; Hussain, M.S.; Ahmed, M.G.; Subamaniyan, V. Anthrax: A narrative review. New Microbes New Infect. 2024, 62, 101501. [Google Scholar]
- Peters, C.; Hartley, D. Anthrax inhalation and lethal human infection. Lancet 2002, 359, 710–711. [Google Scholar] [PubMed]
- Liu, H.; Bergman, N.H.; Thomason, B.; Shallom, S.; Hazen, A.; Crossno, J.; Rasko, D.A.; Ravel, J.; Read, T.D.; Peterson, S.N.; et al. Formation and composition of the Bacillus anthracis endospore. J. Bacteriol. 2004, 186, 164–178. [Google Scholar]
- Riedel, S. Anthrax: A continuing concern in the era of bioterrorism. Bayl. Univ. Med. Cent. Proc. 2005, 18, 234–243. [Google Scholar]
- Sweeney, D.A.; Hicks, C.W.; Cui, X.; Li, Y.; Eichacker, P.Q. Anthrax infection. Am. J. Respir. Crit. Care Med. 2011, 184, 1333–1341. [Google Scholar]
- Collier, R.J.; Young, J.A.T. Anthrax toxin. Annu. Rev. Cell Dev. Biol. 2003, 19, 45–70. [Google Scholar]
- Antoni, C.; Quentin, D.; Lang, A.E.; Aktories, K.; Gatsogiannis, C.; Raunser, S. Cryo-EM structure of the fully-loaded asymmetric anthrax lethal toxin in its heptameric pre-pore state. PLoS Pathog. 2020, 16, e1008530. [Google Scholar]
- Duesbery, N.S.; Webb, C.P.; Leppla, S.H.; Gordon, V.M.; Klimpel, K.R.; Copeland, T.D.; Ahn, N.G.; Oskarsson, M.K.; Fukasawa, K.; Paull, K.D.; et al. Proteolytic inactivation of MAP-kinase-kinase by anthrax Lethal Factor. Science 1998, 280, 734–737. [Google Scholar]
- Gwaltney-Brant, S.M. Renal System. In Handbook of Toxicology of Chemical Warfare Agents, 3rd ed.; Gupta, R.C., Ed.; AP: London, UK, 2020; pp. 673–684. [Google Scholar]
- Zaccai, G.; Jacrot, B. Small Angle Neutron Scattering. Ann. Rev. Biophys. Bioeng. 1983, 12, 139–157. [Google Scholar]
- Wong, P.-z.; Bray, A.J. Porod scattering from fractal surfaces. Phys. Rev. Lett. 1988, 60, 1344. [Google Scholar] [CrossRef]
- Teixeira, J. Small-angle scattering by fractal systems. J. Appl. Cryst. 1988, 21, 781–785. [Google Scholar] [CrossRef]
- Hammouda, B. Probing nanoscale structures--The SANS Toolbox. 2009. Available online: https://www.nist.gov/document/sans-toolbox-probing-nanostructured-materials (accessed on 8 March 2025).
- Fischer, H.; Polikarpov, I.; Craievich, A.F. Average protein density is a molecular-weight-dependent function. Prot. Sci. 2004, 13, 2825–2828. [Google Scholar] [CrossRef] [PubMed]
- Bragg, T.S.; Robertson, D.L. Nucleotide sequence and analysis of the lethal factor gene (lef) from Bacillus anthracis. Gene 1989, 81, 45–54. [Google Scholar] [CrossRef]
- Kalakoti, Y.; Wallner, B. AFsample2: Predicting multiple conformations and ensembles with AlphaFold2. bioRxiv 2024, 2024.05.28.59615. [Google Scholar]
- Wayment-Steele, H.K.; Ojoawo, A.; Otten, R.; Apitz, J.M.; Pitsawong, W.; Hömberger, M.; Ovchinnikov, S.; Colwell, L.; Kern, D. Predicting multiple conformations via sequence clustering and AlphaFold2. Nature 2024, 625, 832. [Google Scholar]
- Zhou, K.; Liu, S.; Hardenbrook, N.J.; Cui, Y.; Krantz, B.A.; Zhou, Z.H. Atomic structures of anthrax prechannel bound with full-length lethal and edema factors. Structure 2020, 28, 879–887. [Google Scholar]
- Dalkas, G.A.; Chasapis, C.T.; Gkazonis, P.V.; Bentrop, D.; Spyroulias, G.A. Conformational dynamics of the anthrax Lethal Factor catalytic center. Biochem. 2010, 49, 10767–10769. [Google Scholar]
- Baker, C.A.; Schudel, B.; Chaudhari, M.I.; Wu, K.; Dunford, D.; Singh, A.K.; Rempe, S.B.; Hatch, A.V. Nanoporous hydrogels for the observation of anthrax exotoxin translocation dynamics. ACS App. Mat. Interface. 2018, 10, 1342–13349. [Google Scholar] [CrossRef]
- Liu, W.; Nestorovich, E.M. Anthrax toxin channel: What we know based on over 30 years of research. BBA-Biomemb. 2021, 1863, 183715. [Google Scholar] [CrossRef]
- Nablo, B.J.; Halverson, K.M.; Robertson, J.W.F.; Nguyen, T.L.; Panchal, R.G.; Gussio, R.; Bavari, S.; Krasilnikov, O.V.; Kasianowicz, J.J. Sizing the Bacillus anthracis PA63 channel with nonelectrolyte poly(ethylene glycols). Biophys. J. 2008, 95, 1157–1164. [Google Scholar] [CrossRef] [PubMed]
- Nablo, B.; Panchal, R.G.; Bavari, S.; Nguen, T.L.; Gussio, R.; Ribot, W.; Friedlander, A.; Chablt, D.; Reiner, J.E.; Robertson, J.W.F.; et al. Anthrax toxin-induced rupture of artificial lipid bilayer membranes. J. Chem. Phys. 2013, 139, 065101. [Google Scholar] [PubMed]
- Glinka, C.J.; Barker, J.G.; Hammouda, B.; Krueger, S.; Mover, J.J.; Orts, W.J. The 30 m Small-Angle Neutron Scattering instruments at the National Institute of Standards and Technology. J. Appl. Cryst. 1998, 31, 430–445. [Google Scholar]
- Kline, S.R. Reduction and analysis of SANS and USANS data using IGOR Pro. J. Appl. Cryst. 2006, 39, 895–900. [Google Scholar]
- Jacrot, B. The study of biological structures by neutron scattering from solution. Rep. Prog. Phys. 1976, 39, 911–953. [Google Scholar]
- Heidorn, D.B.; Trewhella, J. Comparison of the crystal and solution structures of calmodulin and troponin C. Biochem. 1988, 27, 909–915. [Google Scholar]
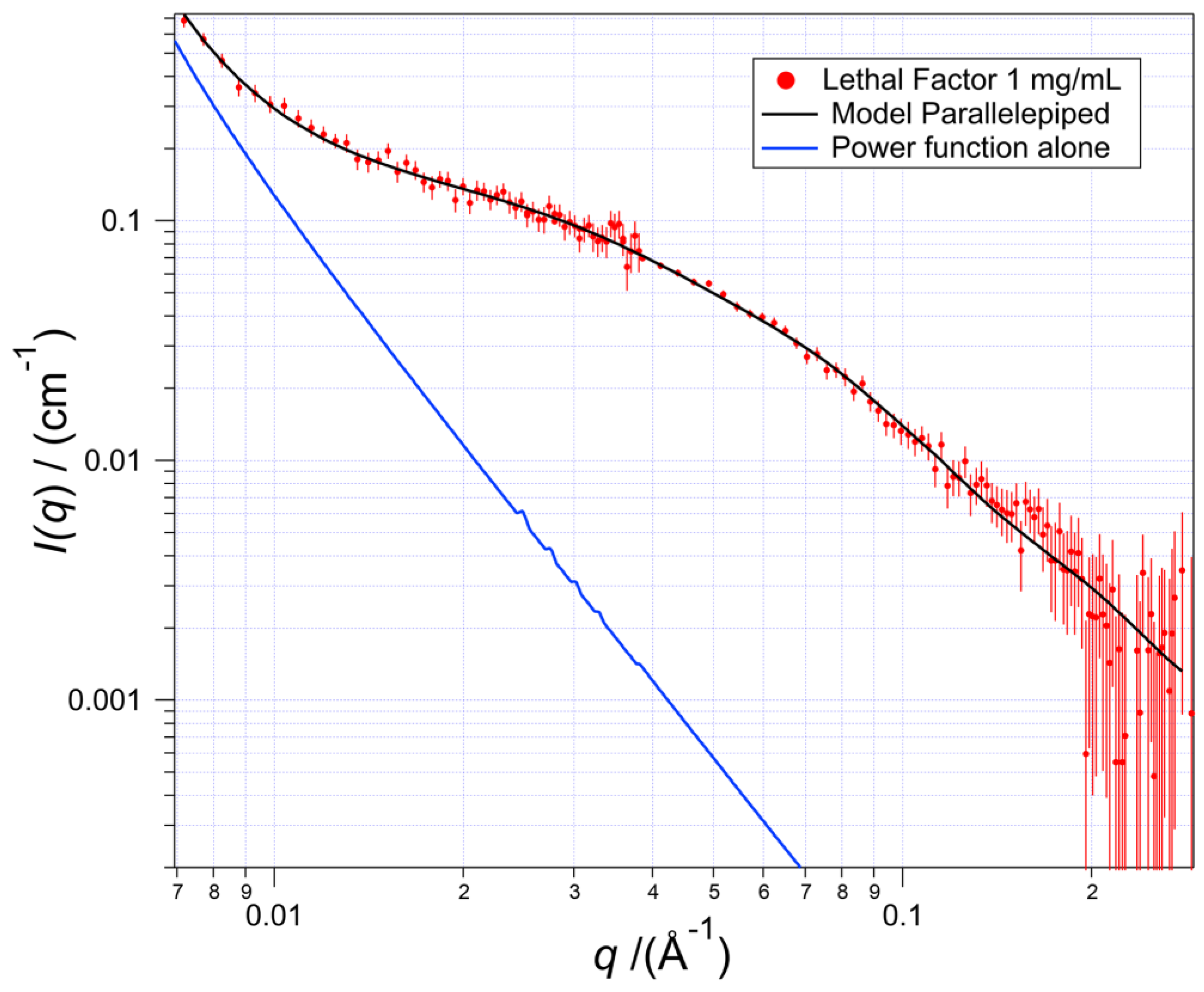
| Parallelepiped Model | Shortest/Å | Middle/Å | Longest/Å | Volume/Å3 | MW for ρ = 1.4 | (Rg/Å) b |
|---|---|---|---|---|---|---|
| SANS data | 12(+4.5,−1) | 49 ± 1 | 129 ± 6 | 76(+35,−11) × 103 | 65(+29,−10) kDa | 42 ± 2 |
| 1pwu | ≈30 | ≈48 | ≈104 | ≈150 × 103 | 124 kDa | 34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubinson, K.A.; Kasianowicz, J.J. The Anthrax Toxin Lethal Factor in Solution Does Not Have the Protein’s Crystallized Structure. Toxins 2025, 17, 157. https://doi.org/10.3390/toxins17040157
Rubinson KA, Kasianowicz JJ. The Anthrax Toxin Lethal Factor in Solution Does Not Have the Protein’s Crystallized Structure. Toxins. 2025; 17(4):157. https://doi.org/10.3390/toxins17040157
Chicago/Turabian StyleRubinson, Kenneth A., and John J. Kasianowicz. 2025. "The Anthrax Toxin Lethal Factor in Solution Does Not Have the Protein’s Crystallized Structure" Toxins 17, no. 4: 157. https://doi.org/10.3390/toxins17040157
APA StyleRubinson, K. A., & Kasianowicz, J. J. (2025). The Anthrax Toxin Lethal Factor in Solution Does Not Have the Protein’s Crystallized Structure. Toxins, 17(4), 157. https://doi.org/10.3390/toxins17040157






