A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion
Abstract
:1. Introduction
2. Design and Modeling
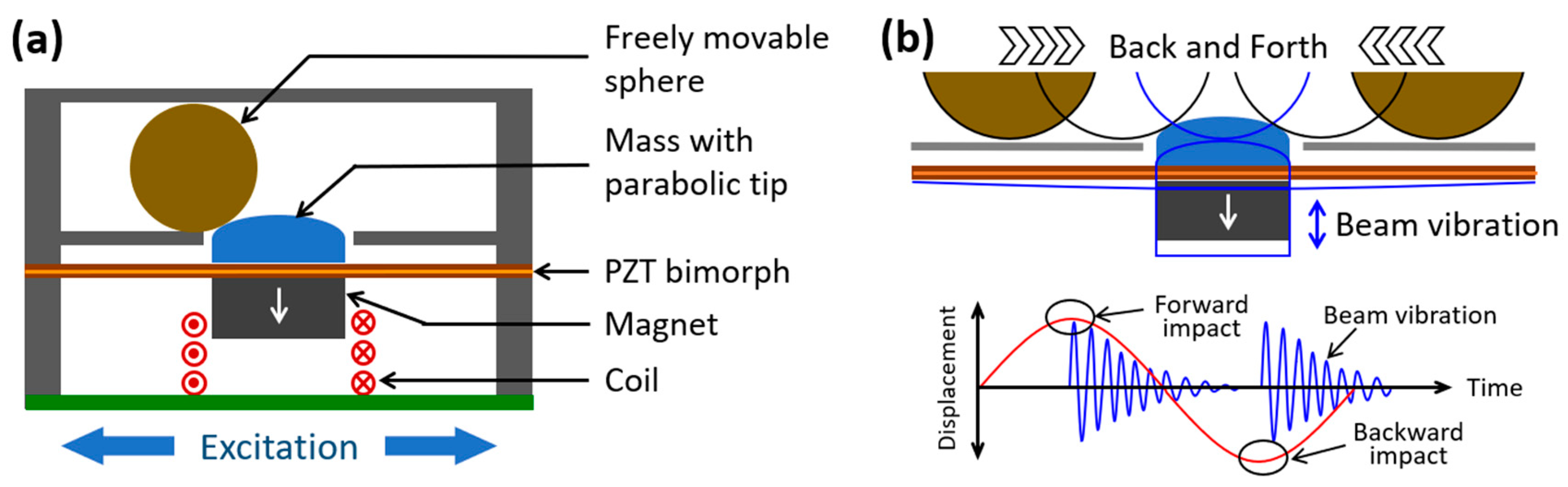
2.1. Harvester Structure and Its Operation
2.2. Electromechanical Modeling
2.3. Simulation
3. Prototype and Test Setup
3.1. Prototype Fabrication
3.2. Human-Limb Motion Test Setup
4. Experimental Results and Discussion
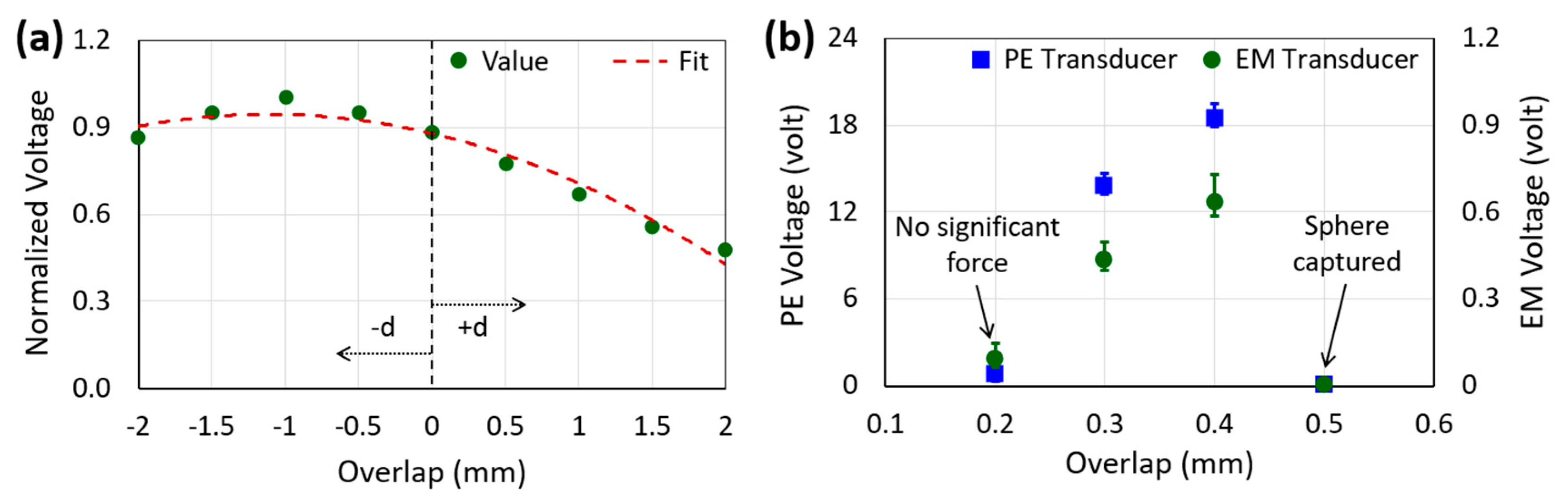
4.1. Optimal Overlap and Damping Measurements
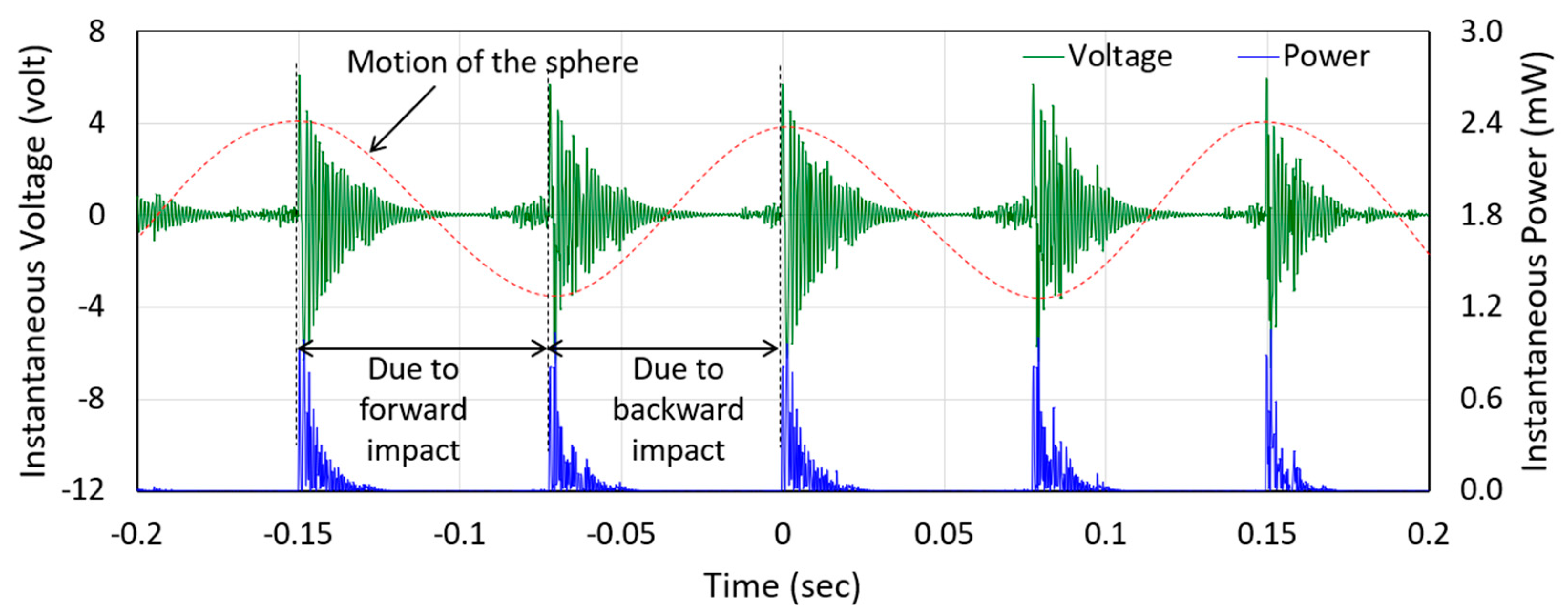
4.2. Transducer Outputs
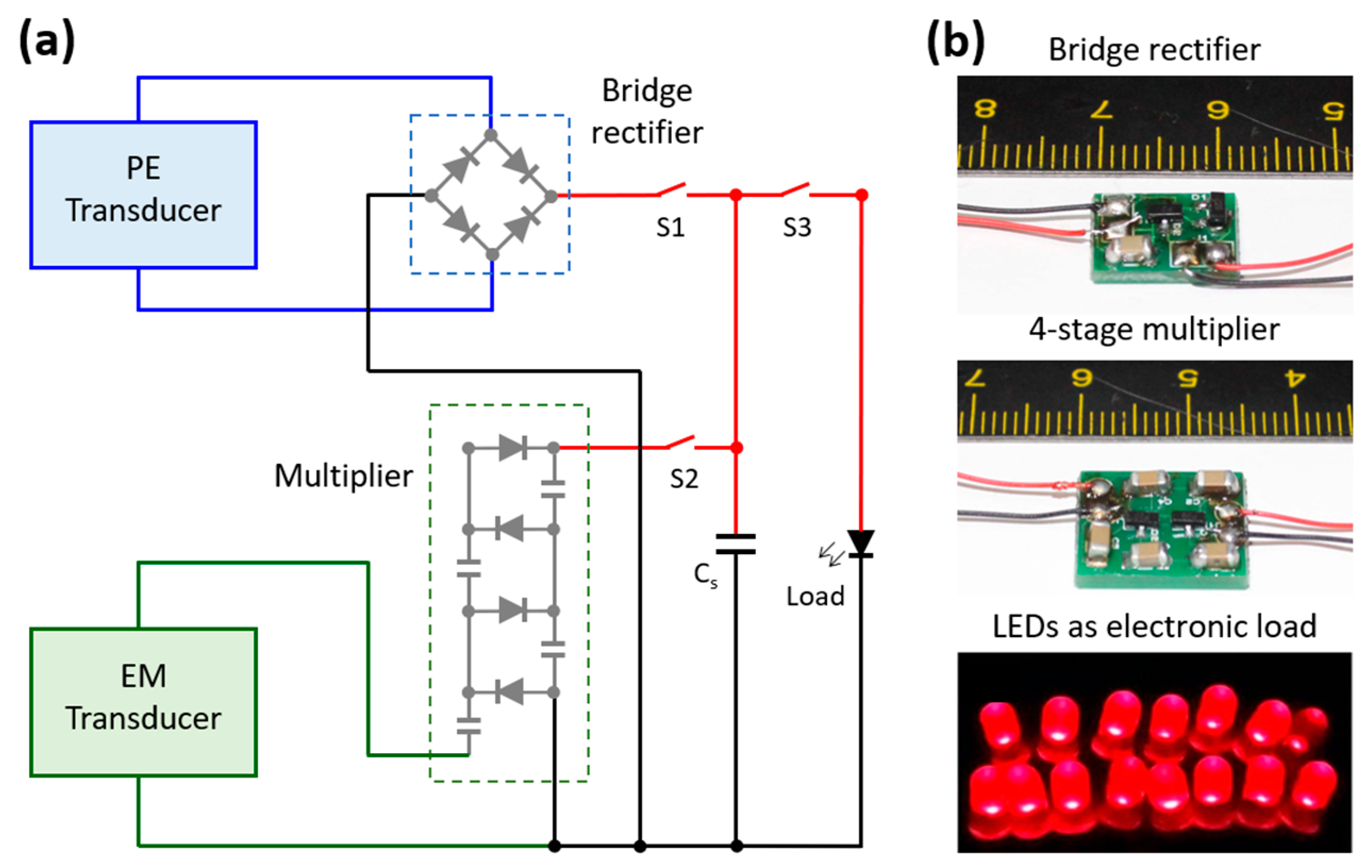
4.3. AC–DC Conversion
5. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Prauzek, M.; Konecny, J.; Borova, M.; Janosova, K.; Hlavica, J.; Musilek, P. Energy harvesting sources, storage devices and system topologies for environmental wireless sensor networks: A review. Sensors 2018, 18, 2446. [Google Scholar] [CrossRef] [PubMed]
- Cook-Chennault, K.A.; Thambi, N.; Sastry, A. Powering MEMS portable devices—A review of non-regenerative and regenerative power supply system with special emphasis on piezoelectric energy harvesting systems. Smart Mater. Struct. 2008, 17, 043001. [Google Scholar] [CrossRef]
- Ahmed, R.; Mir, F.; Banerjee, S. A review on energy harvesting approaches for renewable energies from ambient vibrations and acoustic waves using piezoelectricity. Smart Mater. Struct. 2017, 26, 085031. [Google Scholar] [CrossRef]
- Beeby, S.P.; Tudor, M.J.; White, N.M. Energy harvesting vibration sources for microsystems applications. Meas. Sci. Technol. 2006, 17, R175–R195. [Google Scholar] [CrossRef]
- Mitcheson, P.D.; Yeatman, E.M.; Rao, G.K.; Holmes, A.S.; Green, T.C. Energy harvesting from human and machine motion for wireless electronic devices. Proc. IEEE 2008, 96, 1457–1486. [Google Scholar] [CrossRef]
- Wang, D.-A.; Ko, H.H. Piezoelectric energy harvesting from flow-induced vibration. J. Micromech. Microeng. 2010, 20, 025019. [Google Scholar] [CrossRef]
- Khameneifar, F.; Moallem, M.; Arzanpour, S. Modeling and analysis of a piezoelectric energy scavenger for rotary motion applications. J. Vib. Acoust. 2011, 133, 011005. [Google Scholar] [CrossRef]
- Priya, S.; Song, H.-C.; Zhou, Y.; Varghese, R.; Chopra, A.; Kim, S.-G.; Kanno, I.; Wu, L.; Ha, D.S.; Ryu, J.; et al. A review on piezoelectric energy harvesting: materials, methods, and circuits. Energy Harvest. Syst. 2017, 4, 1–37. [Google Scholar] [CrossRef]
- Tan, Y.; Dong, Y.; Wang, X. Review of MEMS electromagnetic vibration energy harvester. J. Microelectromech. Syst. 2017, 26, 1–16. [Google Scholar] [CrossRef]
- Khan, F.U.; Qadir, M.U. State-of-the-art in vibration-based electrostatic energy harvesting. J. Micromech. Microeng. 2016, 26, 103001. [Google Scholar] [CrossRef]
- Deng, Z.; Dapino, M.J. Review of magnetostrictive vibration energy harvesters. Smart Mater. Struct. 2017, 26, 103001. [Google Scholar] [CrossRef]
- Wang, Z.L.; Chen, J.; Lin, L. Progress in triboelectric nanogenerators as a new energy technology and self-powered sensors. Energy Environ. Sci. 2015, 8, 2250–2282. [Google Scholar] [CrossRef]
- Williams, C.B.; Yates, R.B. Analysis of a micro-electric generator for microsystems. Sens. Actuators A Phys. 1996, 52, 8–11. [Google Scholar] [CrossRef]
- Ju, S.; Chae, S.H.; Choi, Y.; Lee, S.; Lee, H.W.; Ji, C.-H. A low frequency vibration energy harvester using magnetoelectric laminate composite. Smart Mater. Struct. 2013, 22, 115037. [Google Scholar] [CrossRef]
- Gogurla, N.; Roy, B.; Park, J.-Y.; Kim, S. Skin-contact actuated single-electrode protein triboelectric nanogenerator and strain sensor for biomechanical energy harvesting and motion sensing. Nano Energy 2019, 62, 674–681. [Google Scholar] [CrossRef]
- Lee, S.; Ko, W.; Oh, Y.; Lee, J.; Baek, G.; Lee, Y.; Sohn, J.; Cha, S.; Kim, J.; Park, J.; et al. Triboelectric energy harvester based on wearable textile platforms employing various surface morphologies. Nano Energy 2015, 12, 410–418. [Google Scholar] [CrossRef]
- Alluri, N.R.; Vivekananthan, V.; Chandrasekhar, A.; Kim, S.-J. Adaptable piezoelectric hemispherical composite strips using a scalable groove technique for a self-powered muscle monitoring system. Nanoscale 2018, 10, 907–913. [Google Scholar] [CrossRef]
- Wu, Y.; Qu, J.; Daoud, W.A.; Wang, L.; Qi, T. Flexible composite-nanofiber based piezo-triboelectric nanogenerators for wearable electronics. J. Mater. Chem. A 2019, 7, 13347–13355. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. Theoretical modeling and analysis of mechanical impact driven and frequency up-converted piezoelectric energy harvester for low-frequency and wide-bandwidth operation. Sens. Actuators A Phys. 2014, 208, 56–65. [Google Scholar] [CrossRef]
- Renaud, M.; Fiorini, P.; van Schaijk, R.; van Hoof, C. Harvesting energy from the motion of human limbs: the design and analysis of an impact-based piezoelectric generator. Smart Mater. Struct. 2009, 18, 035001. [Google Scholar] [CrossRef]
- Halim, M.A.; Cho, H.; Salauddin, M.; Park, J.Y. A miniaturized electromagnetic vibration energy harvester using flux-guided magnet stacks for human-body-induced motion. Sens. Actuators A Phys. 2016, 249, 23–31. [Google Scholar] [CrossRef]
- Pozzi, M.; Zhu, M. Characterization of a rotary piezoelectric energy harvester based on plucking excitation for knee-joint wearable applications. Smart Mater. Struct. 2012, 21, 055004. [Google Scholar] [CrossRef]
- Xue, T.; Yeo, H.G.; Trolier-McKinstry, S.; Roundy, S. Wearable inertial energy harvester with sputtered bimorph lead zirconate titanate (PZT) thin-film beams. Smart Mater. Struct. 2018, 27, 085026. [Google Scholar] [CrossRef] [Green Version]
- Halim, M.A.; Park, J.Y. Modeling and experiment of a handy motion driven, frequency up-converting electromagnetic energy harvester using transverse impact by spherical ball. Sens. Actuators A Phys. 2015, 229, 50–58. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. A non-resonant, frequency up-converted electromagnetic energy harvester from human-body-induced vibration for hand-held smart system applications. J. Appl. Phys. 2014, 115, 094901. [Google Scholar] [CrossRef]
- Fan, K.; Liu, S.; Liu, Y.; Zhu, Y.; Wang, W.; Zhang, D. Scavenging energy from ultra-low frequency mechanical excitations through a bi-directional hybrid energy harvester. Appl. Energy 2018, 216, 8–20. [Google Scholar] [CrossRef]
- Salauddin, M.; Toyabur, R.M.; Maharjan, P.; Rasel, M.S.; Kim, J.W.; Cho, H.; Park, J.Y. Miniaturized springless hybrid nanogenerator for powering portable and wearable electronic devices from human-body-induced vibration. Nano Energy 2018, 51, 61–72. [Google Scholar] [CrossRef]
- Wang, X.; Yang, B.; Liu, J.; Zhu, Y.; Yang, C.; He, Q. A flexible triboelectric-piezoelectric hybrid nanogenerator based on P(VDF-TrFE) nanofibers and PDMS/MWCNT for wearable devices. Sci. Rep. 2016, 6, 36409. [Google Scholar] [CrossRef] [Green Version]
- Erturk, A. Electromechanical Modeling of Piezoelectric Energy Harvesters. Ph.D Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2009. [Google Scholar]
- Gu, L. Low-frequency piezoelectric energy harvesting prototype suitable for the MEMS implementation. Microelectron. J. 2011, 42, 277–282. [Google Scholar] [CrossRef]
- Budynas, R.G.; Nisbett, J.K. Shigley’s Mechanical Engineering Design, 8th ed.; McGraw-Hill: New York, NY, USA, 2006; ISBN 0-390-76487-6. [Google Scholar]
- Wang, Q.-M.; Cross, L.E. Performance analysis of piezoelectric cantilever bending actuators. Ferroelectrics 1998, 215, 187–213. [Google Scholar] [CrossRef]
- Mizuno, M.; Chetwynd, D.G. Investigation of a resonance micro generator. J. Micromech. Microeng. 2003, 13, 209–216. [Google Scholar] [CrossRef]
- Halim, M.A.; Park, J.Y. Piezoelectric energy harvester using impact-driven flexible side-walls for human-limb motion. Microsyst. Technol. 2018, 24, 2099–2107. [Google Scholar] [CrossRef]
- Lui, H.; Ji, Z.; Chen, T.; Sun, L.; Menon, S.C.; Lee, C. An intermittent self-powered energy harvesting system from low-frequency hand shaking. IEEE Sens. J. 2015, 15, 4782–4790. [Google Scholar]






| Parameter | Value |
|---|---|
| Dimension of the Piezoelectric bimorph | 40 × 6 × 0.5 mm3 |
| Thickness of each piezoelectric (PZT) layer | 0.2 mm |
| Thickness of middle shim (copper) layer | 0.1 mm |
| Young’s modulus of PZT | 72 GPa |
| Dimension of the cylinder magnet | Ø6 × 5 mm2 |
| Remnant flux density of the magnet | 1.18 T |
| Mass of the magnet | 1 g |
| Mass of the attached proof-mass | 1.73 g |
| Diameter of the sphere | 10.3 mm |
| Mass of the sphere | 4.36 gm |
| Length of the channel | 30 mm |
| Inner diameter of the coil | 8 mm |
| Outer diameter of the coil | 10 mm |
| Number of coil turns | 1000 |
| Height of the coil | 5 mm |
| Resistance of the coil | 84 Ω |
| Dimension of the fabricated prototype | 40 × 30 × 16 mm3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halim, M.A.; Kabir, M.H.; Cho, H.; Park, J.Y. A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion. Micromachines 2019, 10, 701. https://doi.org/10.3390/mi10100701
Halim MA, Kabir MH, Cho H, Park JY. A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion. Micromachines. 2019; 10(10):701. https://doi.org/10.3390/mi10100701
Chicago/Turabian StyleHalim, Miah Abdul, M. Humayun Kabir, Hyunok Cho, and Jae Yeong Park. 2019. "A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion" Micromachines 10, no. 10: 701. https://doi.org/10.3390/mi10100701
APA StyleHalim, M. A., Kabir, M. H., Cho, H., & Park, J. Y. (2019). A Frequency Up-Converted Hybrid Energy Harvester Using Transverse Impact-Driven Piezoelectric Bimorph for Human-Limb Motion. Micromachines, 10(10), 701. https://doi.org/10.3390/mi10100701





