Research on an Artificial Lateral Line System Based on a Bionic Hair Sensor with Resonant Readout
Abstract
:1. Introduction
2. Structure Design and Simulation
2.1. Structure Design
2.2. Artificial Lateral Line System
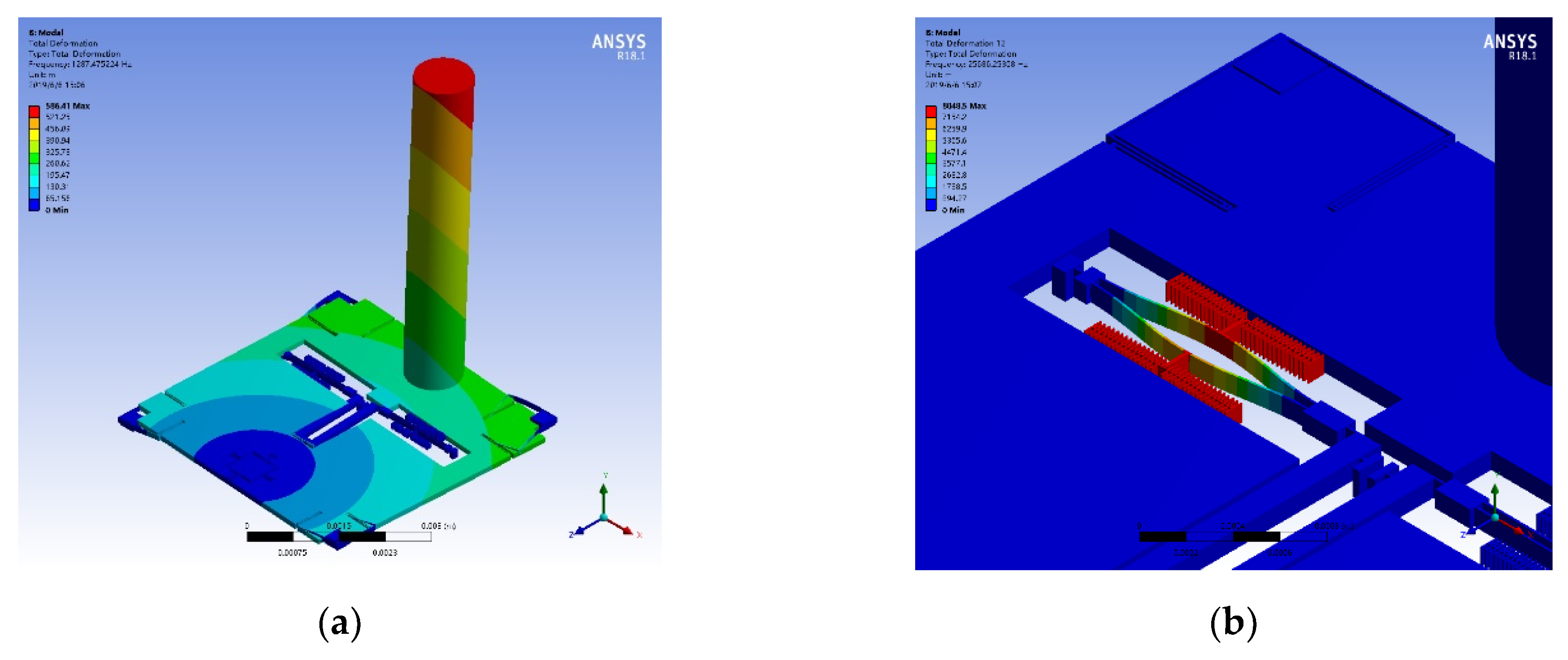
2.3. Simulation
3. Measurement Circuit and Demodulation Algorithm
3.1. Measurement Circuit
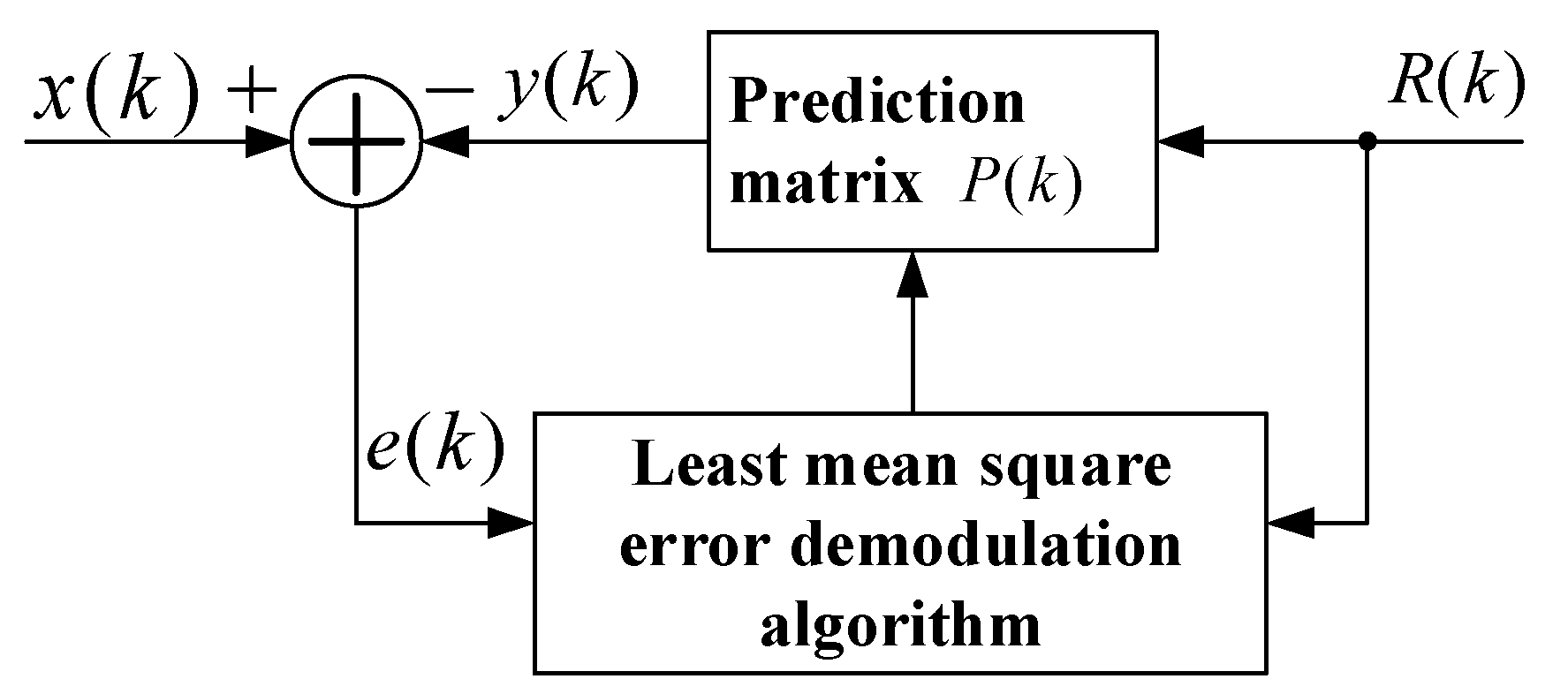
3.2. Demodulation Algorithm
4. Experiments
4.1. Excitation of Constant Flow Velocity for the Artificial Lateral Line System
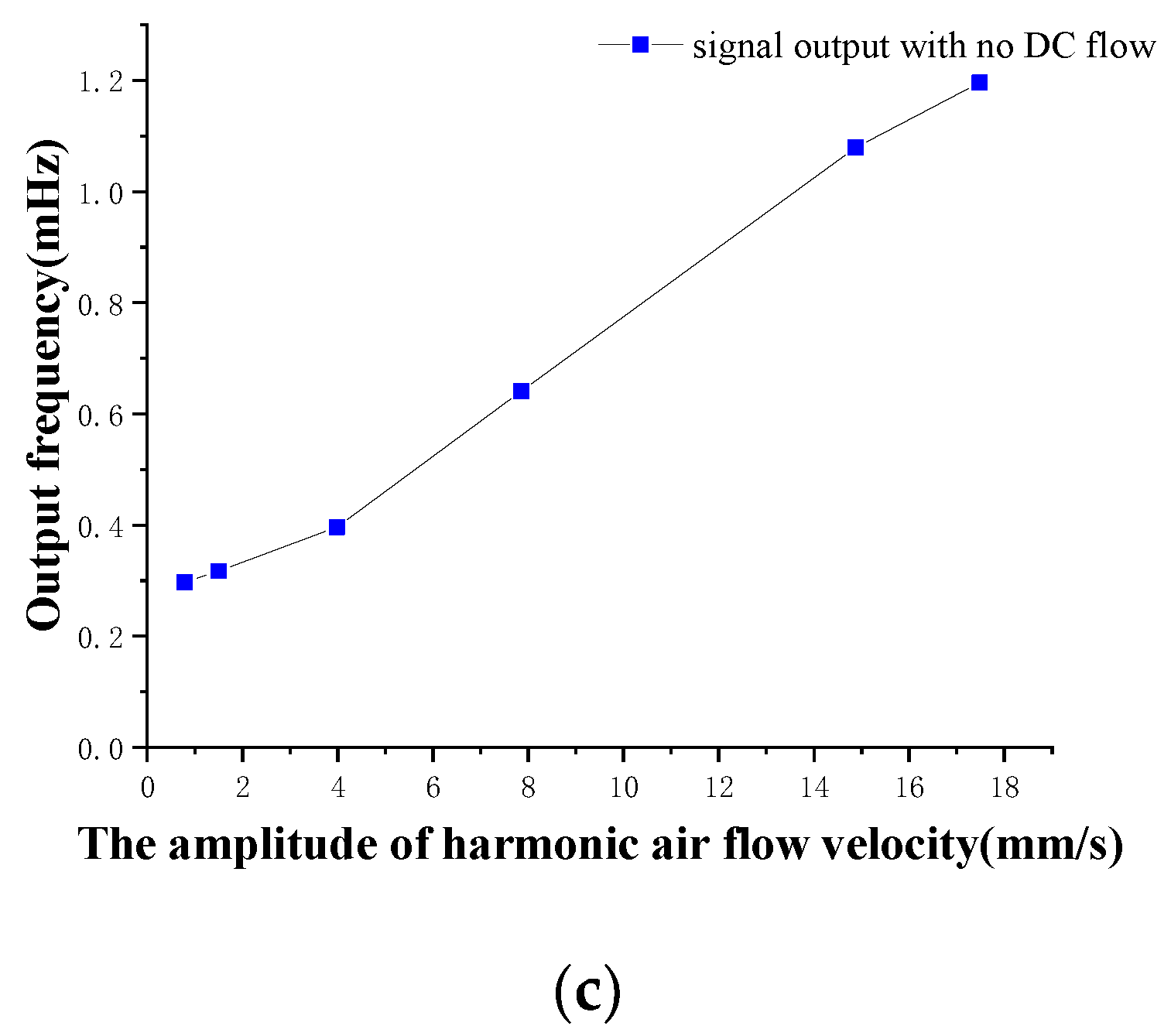
4.2. Excitation of the Oscillatory Flow Velocity for an Artificial Lateral Line System
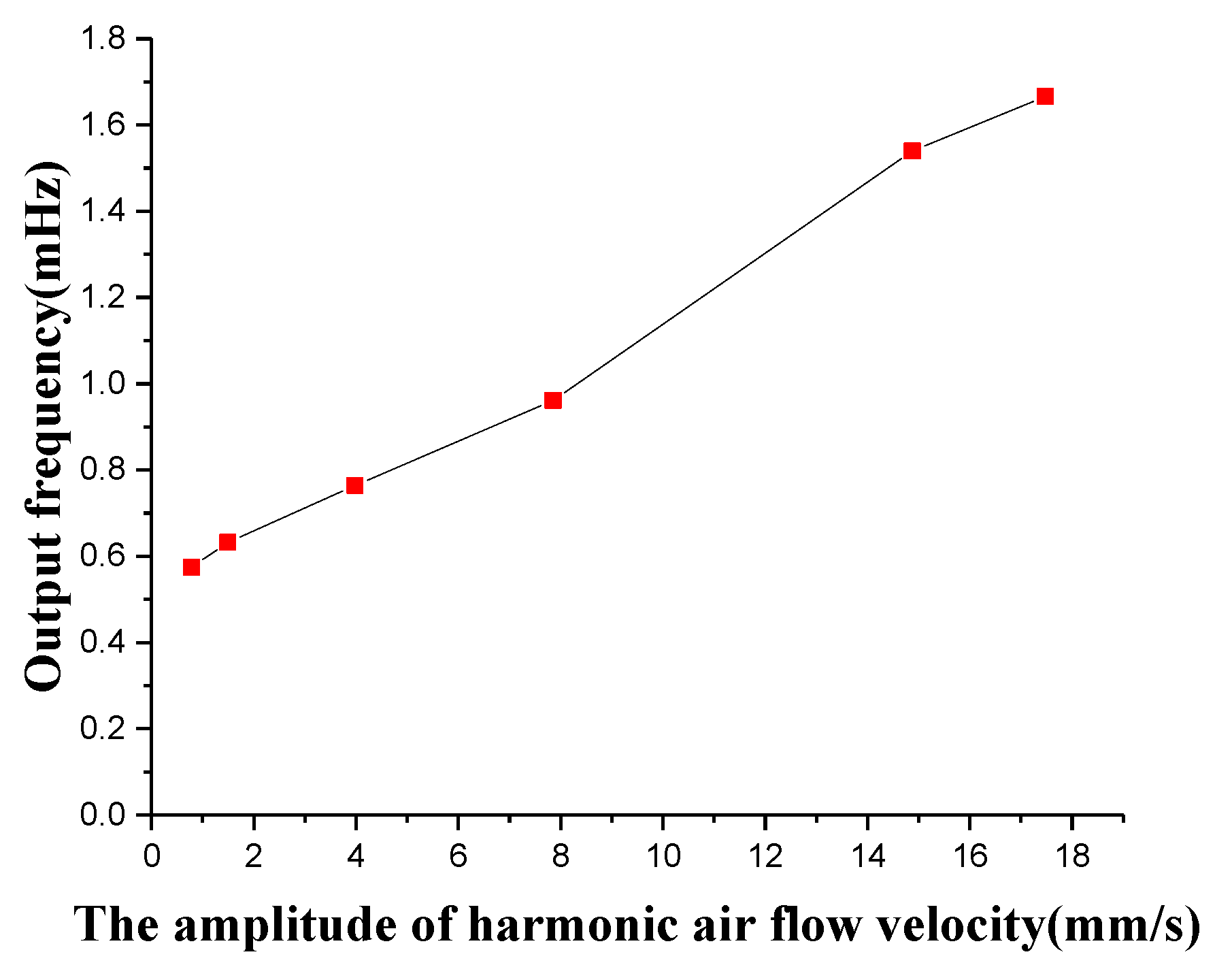
4.3. Excitation of Superimposed Constant and Oscillatory Air Flow Velocity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bora, M.; Kottapalli, A.G.P.; Miao, J.M.; Triantafyllou, M.S. Fish-inspired self-powered microelectromechanical flow sensor with biomimetic hydrogel cupula. APL Mater. 2017, 5, 104902. [Google Scholar] [CrossRef] [Green Version]
- Asadnia, M.; Kottapalli, A.G.P.; Miao, J.; Warkiani, M.E.; Triantafyllou, M.S. Artificial fish skin of self-powered micro-electromechanical systems hair cells for sensing hydrodynamic flow phenomena. J. R. Soc. Interface 2015, 12, 20150322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dagamseh, A.M.K.; Wiegerink, R.J.; Lammerink, T.S.J.; Krijnen, G.J.M. Towards a high-resolution flow camera using artificial hair sensor arrays for flow pattern observations. Bioinspiration Biomimetics 2012, 7, 046009. [Google Scholar] [CrossRef] [PubMed]
- Dagamseh, A.; Wiegerink, R.; Lammerink, T.; Krijnen, G. Imaging dipole flow sources using an artificial lateral-line system made of biomimetic hair flow sensors. J. R. Soc. Interface 2013, 10, 20130162. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, M.M.; Peterson, R.L.; Najafi, K. A 2-D directional air flow sensor array made using stereolithography and MEMS micro-hydraulic structures. In Proceedings of the 2013 Transducers & Eurosensors XXVII: The 17th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS & EUROSENSORS XXVII), Barcelona, Spain, 16–20 June 2013; pp. 722–725. [Google Scholar]
- Tucker, C.; Chen, N.; Engel, J.; Yang, Y.-C.; Pandya, S.; Liu, C. High-sensitivity bi-directional flow sensor based on biological inspiration of animal haircell sensors. In Proceedings of the SENSORS, 2006 IEEE, Daegu, Korea, 22–25 October 2006; pp. 1440–1442. [Google Scholar]
- Chen, N. Artificial lateral line canal system for underwater disturbance sensing. Ph.D. Thesis, University of Illinois at Urbana-Champaign, Champaign, IL, USA, 2008. [Google Scholar]
- Kottapalli, A.G.P.; Asadnia, M.; Miao, J.; Triantafyllou, M. Touch at a distance sensing: Lateral-line inspired MEMS flow sensors. Bioinspiration Biomimetics 2014, 9, 046011. [Google Scholar] [CrossRef] [PubMed]
- Bora, M.; Kottapalli, A.G.P.; Miao, J.M.; Asadnia, M.; Triantafyllou, M.S. Biomimetic hydrogel cupula for canal neuromasts inspired sensors. In Proceedings of the 2016 IEEE SENSORS, Orlando, FL, USA, 9 January 2017; pp. 1–3. [Google Scholar]
- Herzog, H.; Klein, A.; Bleckmann, H.; Holik, P.; Schmitz, S.; Siebke, G.; Tätzner, S.; Lacher, M.; Steltenkamp, S. μ-Biomimetic flow-sensors--introducing light-guiding PDMS structures into MEMS. Bioinspiration Biomimetics 2015, 10, 036001. [Google Scholar] [CrossRef] [PubMed]
- Herzog, H.; Steltenkamp, S.; Klein, A.; Tätzner, S.; Schulze, E.; Bleckmann, H. Micro-Machined Flow Sensors Mimicking Lateral Line Canal Neuromasts. Micromachines 2015, 6, 1189–1212. [Google Scholar] [CrossRef] [Green Version]
- Kaldenbach, F.; Klein, A.; Bleckmann, H. Form-function relationship in artificial lateral lines. Bioinspiration Biomimetics 2019, 14, 026001. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Guo, X.; Wang, Q.-H.; Lu, C.F.; Hu, D. A novel flow sensor based on resonant sensing with two-stage microleverage mechanism. Rev. Sci. Instrum. 2018, 89, 045002. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Zhao, H.; Dai, B.; Liu, X.J. A new silicon biaxial decoupled resonant micro-accelerometer. Microsyst. Technol. 2015, 21, 109–115. [Google Scholar] [CrossRef]
- Bathellier, B.; Steinmann, T.; Barth, F.G.; Casas, J. Air motion sensing hairs of arthropods detect high frequencies at near-maximal mechanical efficiency. J. R. Soc. Interface 2012, 9, 1131–1143. [Google Scholar] [CrossRef] [PubMed]
- Shimozawa, T.; Kumagai, T.; Baba, Y. Structural scaling and functional design of the cercal wind-receptor hairs of cricket. J Comp. Physiol. A 1998, 183, 171–186. [Google Scholar] [CrossRef]
- Du, G.H.; Zhu, Z.M.; Gong, X.F. Fundamentals of Acoustics (in Chinese), 2nd ed.; Nanjing University Press: Nanjing, China, 2001; pp. 182–184. ISBN 7-305-03631-5. [Google Scholar]
- Klein, A.; Bleckmann, H. Function of lateral line canal morphology. Integr. Zool. 2015, 10, 111–121. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Wang, X.J.; Dai, B.; Liu, X.J. A New Z-axis Resonant Micro-Accelerometer Based on Electrostatic Stiffness. Sensors 2015, 15, 687–702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, B.; Wu, L.; Wang, B.L.; Wang, Q.H. Digital Closed-Loop Driving Technique Using the PFD-Based CORDIC Algorithm for a Biaxial Resonant Microaccelerometer. J. Sens. 2017, 2017, 7861025. [Google Scholar] [CrossRef]

















| Parameter (Unit) | Value |
|---|---|
| Hair height LH (µm) | 3000/6000/9000 |
| Hair diameter R (µm) | 1000 |
| Hair density ρ (g/cm3) | 1.05 |
| Natural frequency of resonant beam f0 (kHz) | 20 |
| Drag coefficient CD | 0.62 |
| Coefficient related to the resonator λ | 0.14 |
| Magnification time A | 7.06 |
| Attenuation coefficient η | 0.81 |
| Resonator beam length L (µm) | 1300 |
| Resonant beam width w (µm) | 10 |
| Resonant beam thickness h (µm) | 100 |
| Parameter (Unit) | Value |
|---|---|
| Natural frequency of resonator ωd (rad/s) | 22000 × 2π |
| Quality factor of resonator Q | 42 |
| Damping ratio of resonator ξ | 0.0119 |
| Proof mass of resonator m (kg) | 8 × 10−9 |
| Damping coefficient of resonator c (Ns/m) | 2.63 × 10−5 |
| Stiffness coefficient of resonator k (N/m) | 152.86 |
| The cutoff frequency of low pass filter fc (Hz) | 75 |
| System sampling time Ts (s) | 1 × 10−6 |
| Proportion factor of PI(1) in amplitude closed loop Kp1 | 0.1 |
| Integral factor of PI(1) in amplitude closed loop Ki1 | 2.2 × 10−4 |
| Loop filter coefficient C1 | 0.01 |
| Loop filter coefficient C2 | 0.001 |
| VCO sensitivity (Hz/V) | 50 |
| Initial frequency of VCO (Hz) | 21860 |
| Torque coefficient of Fd in the module ‘Fcn’ | 5.664 × 10−9 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Zhang, T.; Liang, Z.; Lu, C. Research on an Artificial Lateral Line System Based on a Bionic Hair Sensor with Resonant Readout. Micromachines 2019, 10, 736. https://doi.org/10.3390/mi10110736
Yang B, Zhang T, Liang Z, Lu C. Research on an Artificial Lateral Line System Based on a Bionic Hair Sensor with Resonant Readout. Micromachines. 2019; 10(11):736. https://doi.org/10.3390/mi10110736
Chicago/Turabian StyleYang, Bo, Ting Zhang, Zhuoyue Liang, and Chengfu Lu. 2019. "Research on an Artificial Lateral Line System Based on a Bionic Hair Sensor with Resonant Readout" Micromachines 10, no. 11: 736. https://doi.org/10.3390/mi10110736
APA StyleYang, B., Zhang, T., Liang, Z., & Lu, C. (2019). Research on an Artificial Lateral Line System Based on a Bionic Hair Sensor with Resonant Readout. Micromachines, 10(11), 736. https://doi.org/10.3390/mi10110736




