AC Electrothermal Effect in Microfluidics: A Review
Abstract
:1. Introduction
2. AC Electrokinetics
2.1. Dielectrophoresis
2.2. AC Electroosmosis
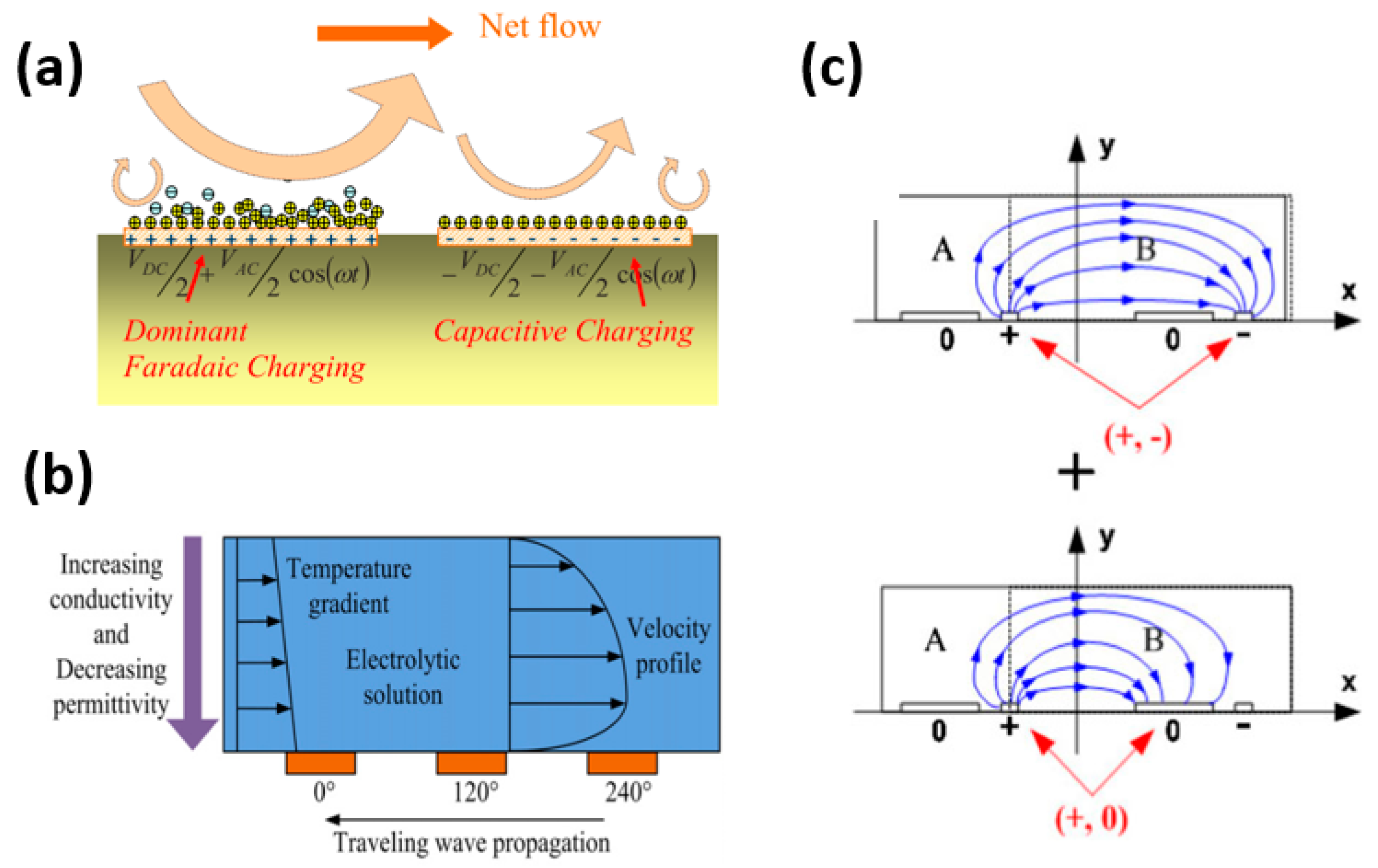
2.3. AC Electrothermal
3. Theory
4. Electric Field
4.1. Introducing Asymmetry to Geometry
4.2. Introducing Asymmetry in Electric Potential
4.2.1. DC Biased
4.2.2. Travelling Wave (TW)
4.2.3. Two-Phase Actuation
5. Temperature Field
Internal and External Heating
6. Fluid Flow Regime
6.1. Flow Velocity
6.2. Direction of AC Electrothermal (ACET) Flow
6.3. Flow Reversal
7. Application
8. Substrate Material
9. Channel Height
10. Numerical and Experimental Settings
10.1. Numerical Simulation
- Since the wavelength of the electric field is typically larger than the dimensions of the microchannel, electrostatic assumptions can be made [41].
- In typical ACET devices, the ratio of buoyancy force to electrothermal force, i.e., , is estimated to be in the range of [41,85]. When buoyancy is included in the simulations, only a 0.1–0.8% decrease in flow velocity is obtained [41]. Therefore, the buoyancy effect can be neglected in simulations. However, at large length scales and low voltages, it becomes important [41].
- ACEO effect can be neglected at high frequencies and high conductivities [41].
- While in most studies electric and thermal fields are considered independent, using the results of Loire et al. [86], Williams [74] conducted numerical simulations with coupled electrical and thermal fields as , where , instead of the conventional sequential method i.e., . It was shown that when the temperature rise in a system is >5 K, the two fields can no longer be considered independent [86].
10.2. Experimental Setup
- The lighting on the microscope, on which the ACET device is mounted, can play as an external heat source and interfere with the experiments, and thus cause unreliable results. In order to reduce the effects of microscope light, either it needs to be set at its lowest power [13] or a heat absorbing filter between the device and the objective lens needs to be used [62]. Otherwise, illumination effects must be taken into account as an external heat source.
- To reduce the effect of Brownian motion, the average of at least four velocity readings at each voltage setting is recommended to be taken [13].
- If the work involves study of temperature on DEP effect, a non-invasive method (i.e., with no particles involved) must be used to measure temperature in the device. Laser-induced fluorescence (LIF) thermometry, in which a dye is used to measure temperature, is recommended for this purpose [80].
- For generating effective electric field at the electrode surface, electrodes should be fabricated relatively thin, e.g., 50–100 nm [32].
11. Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Article | Application | Achievement | Specific Observations |
|---|---|---|---|
| [71] | Mixing | Experimental study of illumination-induced electrothermal | The direction of force at high frequencies is form hot regions to cold regions while at low frequencies the opposite is true. |
| [14,61] | Mixing | Increasing the binding rate and significantly decreasing the incubation time to minutes | Binding rate increased by a factor of nine compared to diffusion-limited reaction |
| [4] | Pumping | Study of pumping for two electrode configurations of planar asymmetric and orthogonal | Orthogonal configuration yields higher velocities |
| [13] | Particle manipulation and pumping | Manipulation of particles and fluids of high conductivity at low voltages using a parallel plate and a planar asymmetric electrode configuration | Velocity of 162 µm·s−1 |
| [93] | Pumping | Numerical and experimental investigation of flow reversal in orthogonal electrodes | Change of flow patterns is a result of change from alternating current electrothermal (ACET) effects to alternating current electroosmosis (ACEO) phenomenon |
| [6] | Pumping | Applying asymmetry in electric potentials in conjunction with spatial asymmetry | Velocity of 2500 µm·s−1 |
| [62] | Mixing | Introducing meandering electrode configuration with electrothermal effect in a Y-shaped channel | Fivefold reduction of the mixing time of high salt content fluids compared to diffusion-limited methods |
| [97,85] | Pumping | Introducing microgrooved electrode configuration | Five times increase in pumping rate compared to conventional planar configurations |
| [69] | Pumping | Introducing two-phase AC signal configuration | 25–50% faster flow rates in two-phase configuration compared to the conventional single-phase configuration |
| [60] | Mixing | Introducing concentric electrode design | Velocity of 70 µm·s−1 |
| [11] | Mixing | Using asymmetric electrodes for immunoassay | Ten times acceleration in binding rate compared to diffusion-limited method (30 min vs. 3 min) |
| [1] | Pumping | Thermally biased ACET pumping using symmetric and asymmetric electrodes | Velocity of 750 µm·s−1 |
| [75] | Particle manipulation | Using parallel plate (opposing) electrodes in conjunction with thin film resistive heaters | Sorting between 1 µm and 2 µm particles |
| [92] | Pumping | Study on the effect of the number of electrode pairs over channel length; asymmetric planar electrodes | Increasing the number of electrode pairs helps increase the pumping efficiency |
| [105] | Pumping | Introducing electrodes both on top and bottom of the microchannel; asymmetric planar electrodes | Opposing electrodes increase the flow rate by 105% |
| [76] | Pumping | Multiple Array Electrothermal Micropump (MAET) with different actuation patterns and cross sections | Flow rate of 16 × 106 µm3·s−1 |
| [96] | Pumping | 3D circular electrodes | Flow rate of 15 × 106 µm3·s−1 |
| [104] | Mixing and pumping | Numerical investigation of simultaneous pumping and mixing by introducing microelectrodes on side walls of the microchannel | Mixing efficiency of 80% in ˂3 min and over a length of ˂600 µm |
| [135] | Pumping | Numerical study of multiple array ACET channel | Flow rate of 16 × 106 µm3·s−1 |
| [74,108] | Pumping | Study of using thin film heaters for pumping | 2.5 times faster flow rate with thin film heaters compared to Joule heating alone |
| [63] | Pumping | Application of ACET pumping to cell culture on chip | Flow rate of 44.82 µL·h−1 |
| [139] | Particle manipulation | Combining ACET and dielectrophoresis (DEP) for detection of circulating cell-free DNA (cfDNA) | Detection of cfDNA in 10 min in concentrations as low as 43 ng·mL−1 |
| [140] | Pumping | Numerical and experimental study of the effects of conductivity and channel height on ACET flow | A critical conductivity exists below which there is no net flow and there exists only microvortices |
| [119] | Mixing | Quantum dot-linked immunodiagnostic assay coupled with ACET mixing | Reduction of detection time from 3.5 h to 30 min using a volume of 2 µL |
| [59] | Particle manipulation | Development of a mathematical model for rapid electrokinetic patterning (REP) REP based on ACET and DEP | Increasing particle size results in an increase in ratio of ACET to DEP velocity and therefore results in a lower focusing performance |
| [73] | Mixing | Experimental study of light actuated ACET flow | When AC frequency is above liquid charge relaxation frequency, natural convection is above 35% of the ET flow. |
| [123] | Mixing | Numerical and experimental comparison of immunoassay performance when using symmetric or asymmetric electrodes | Symmetric and asymmetric geometries render different performance efficiencies only at high electric fields |
| [102] | Particle manipulation | Numerical and experimental study of electrode material in REP | Titanium electrodes are more efficient than conventionally used indium tin oxide (ITO) electrodes |
| [141] | Mixing | Numerical and experimental study of AC biased concentric electrodes in biosensors | Faster sensing speed compared to diffusion-limited conditions |
| [142] | Mixing | Numerical and experimental study of rotating asymmetric electrode pair; Supplying controlled drug concentration to tumor cells | Mixing efficiency 89.12% |
| [70] | Mixing | Numerical and experimental study of long-range fluid motion induced by ACET microvortices | Centimeter scale ACET vortices are observed |
| [124] | Mixing | Numerical study of the effect of temperature on binding efficiency in immunoassays | Keeping external surfaces of the microchannel at a constant temperature improves the binding efficiency |
| [143] | Mixing | Numerical and experimental-3D electrodes embedded inside walls of the channel | Mixing efficiency of 90% |
| [113] | Pumping | Numerical and experimental study of bi-directional micropump using asymmetric planar electrodes | 1500 µm·s−1 fluid velocity |
| [121] | Mixing | Numerical study of electrothermal effect in immunoassays | Placement of electrodes on the same wall as the reaction surface renders the best performance of the biosensor |
| [126] | Mixing | Study of pulsed ACET flow for detection of dilute samples of small molecules | 83% mixing efficiency over a length of 400 µm |
| [125] | Mixing | Numerical investigation of amplitude modulated (AM) sinewave | 100% mixing efficiency with maximum 5.5 K temperature rise |
| [144] | Mixing | Numerical investigation of the effect of ionic strength on mixing | Mixing efficiency 90% |
| [134] | Pumping | Experimental study of an immunoassay chip featuring an ACET micropump | Reducing incubation time to 1 min vs. hours in conventional methods |
| [99] | Simultaneous pumping and mixing | Numerical study of high throughput mixing using opposing asymmetric microgrooved electrodes and symmetric electrode pair | Mixing efficiency of 97.25% |
| [114] | Simultaneous pumping and mixing | Numerical study of bi-directional pumping and mixing by switching electric potential on planar electrodes | Mixing efficiency of 90% Pumping velocity 90 µm·s−1 |
| [90] | pumping | Numerical investigation of pumping non-Newtonian blood flow | Velocity of 0.02 m·s−1 |
| [89] | Mixing | Numerical investigation of the effect of shear dependent viscosity on mixing efficiency and flow rate using opposing asymmetric microgrooved electrodes and symmetric electrode pair | In similar configurations, dilatant fluids show better mixing efficiency compared to pseudoplastic fluids |
| [101] | Mixing | Study of arc electrodes in ring-shaped microchamber | 100% mixing efficiency at 8 V |
| [127] | Trapping | Using ACET and DEP to preconcentrate and detect E. Coli | Method can detect concentrations two orders of magnitude smaller than what is possible with diffusion limited methods |
| [133] | Pumping | Using laser etching on ITO glass to pattern electrodes for pumping cell culture medium in a 3D biomimetic liver lobule model | 2 µm·s−1 at 5.5 V |
| [100] | Pumping | Using castellated electrodes; combined DEP and ACET EHD for bioparticle delivery | Negative DEP prevents particles from colliding with channel surfaces; castellated electrodes eliminate ACET vortices |
| [138] | Pumping | Combining ACET and negative DEP for long range cell transport and suspension in high conductivity medium | DEP is essential for cell suspension under ACET effect |
| [95] | Simultaneous pumping and mixing | Numerical investigation of 3D asymmetric spiral microelectrode pair | Flow rate 440 µm·s−1 |
| [91] | Pumping | Numerical investigation of the effect of electrode configuration on pumping mechanism of non-Newtonian blood flow | Ring shaped electrodes are the optimal configuration for blood flow pumping |
| [88] | Pumping, mixing, and trapping | Study of 3D particle-fluid flow under simultaneous effects of ACET, thermal buoyancy (TB), and DEP using multi-layered electrodes | Long range vortices induced by ACET and short-range circulations induced by TB |
| [77] | Simultaneous pumping and mixing | Introducing two opposing microelectrode arrays placed at an angle relative to channel length | Mixing time reduced by 95% compared to diffusion-limited methods |
| [72] | Mixing | Study of light induced ACET flow over electrodes of different materials using opposing electrodes | Electrodes with high optical absorption rate and low thermal conductivity are best for effective light-induced heating |
| [58] | Comprehensive particle and droplet manipulation | Combining ACET and DEP | Particle transit time between multiple branches 0.008 s; droplet sorting purity 90%; particle sorting purity 93% |
References
- Yuan, Q.; Wu, J. Thermally biased AC electrokinetic pumping effect for lab-on-a-chip based delivery of biofluids. Biomed. Microdevices 2013, 15, 125–133. [Google Scholar] [CrossRef] [PubMed]
- Nisar, A.; Afzulpurkar, N.; Mahaisavariya, B.; Tuantranont, A. MEMS-based micropumps in drug delivery and biomedical applications. Sens. Actuator B Chem. 2008, 130, 917–942. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, C. Advances in electrokinetics and their applications in micro/nano fluidics. Microfluid. Nanofluid. 2012, 13, 179–203. [Google Scholar] [CrossRef]
- Wu, J.; Lian, M.; Yang, K. Micropumping of biofluids by alternating current electrothermal effects. Appl. Phys. Lett. 2007, 90, 234103. [Google Scholar] [CrossRef]
- Gagnon, Z.R.; Chang, H.-C. Electrothermal ac electro-osmosis. Appl. Phys. Lett. 2009, 94, 024101. [Google Scholar] [CrossRef]
- Lian, M.; Wu, J. Ultrafast micropumping by biased alternating current electrokinetics. Appl. Phys. Lett. 2009, 94, 064101. [Google Scholar] [CrossRef]
- Fuhr, G.; Hagedorn, R.; Muller, T.; Benecke, W.; Wagne, Z. Microfabricated electrohydrodynamic (EHD) pumps for liquids of higher conductivity. J. Microelectromech. Syst. 1992, 1, 141–146. [Google Scholar] [CrossRef]
- Moroney, R.M.; White, R.M.; Howe, R.T. Ultrasonically induced microtransport. In Proceedings of the IEEE Micro Electro Mechanical Systems, Nara, Japan, 30 January 1991; pp. 277–282. [Google Scholar]
- Richter, A.; Sandmaier, H. An electrohydrodynamic micropump. In IEEE MEMS; IEEE: Napa Valley, CA, USA, 1990; pp. 99–104. [Google Scholar]
- Bart, S.F.; Tavrow, L.S.; Mehregany, M.; Lang, J.H. Microfabricated electrohydrodynamic pumps. Sens. Actuator A Phys. 1990, 21, 193–197. [Google Scholar] [CrossRef]
- Liu, X.; Yang, K.; Wadhwa, A.; Eda, S.; Li, S.; Wu, J. Development of an AC electrokinetics-based immunoassay system for on-site serodiagnosis of infectious diseases. Sens. Actuator A Phys. 2011, 171, 406–413. [Google Scholar] [CrossRef]
- Li, D. Electrokinetics in Microfluidics; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- Lian, M.; Islam, N.; Wu, J. AC electrothermal manipulation of conductive fluids and particles for lab-chip applications. IET Nanobiotechnol. 2007, 1, 36–43. [Google Scholar] [CrossRef] [PubMed]
- Sigurdson, M.; Wang, D.; Meinhart, C.D. Electrothermal stirring for heterogeneous immunoassays. Lab Chip 2005, 5, 1366–1373. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. AC electrokinetics: A review of forces in microelectrode structures. J. Phys. D Appl. Phys. 1998, 31, 2338–2353. [Google Scholar] [CrossRef]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35–R64. [Google Scholar] [CrossRef]
- Hossan, M.R.; Dutta, D.; Islam, N.; Dutta, P. Review: Electric field driven pumping in microfluidic device. Electrophoresis 2018, 39, 702–731. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Cheng, P.; Hong, F. Applications of electrohydrodynamics and Joule heating effects in microfluidic chips: A review. Sci. China Ser. E 2009, 52, 3477–3490. [Google Scholar] [CrossRef]
- Lu, Y.; Liu, T.; Lamanda, A.C.; Sin, M.L.Y.; Gau, V.; Liao, J.C.; Wong, P.K. AC electrokinetics of physiological fluids for biomedical applications. J. Lab. Autom. 2015, 20, 611–620. [Google Scholar] [CrossRef] [PubMed]
- Salari, A.; Thompson, M. Recent advances in AC electrokinetic sample enrichment techniques for biosensor development. Sens. Actuators B Chem. 2018, 255, 3601–3615. [Google Scholar] [CrossRef]
- Ashraf, M.W.; Tayyaba, S.; Afzulpurkar, N. Micro electromechanical systems (MEMS) based microfluidic devices for biomedical applications. Int. J. Mol. Sci. 2011, 12, 3648–3704. [Google Scholar] [CrossRef] [PubMed]
- Xuan, X.; Xu, B.; Li, D. Electroosmotic flow with Joule heating effects. Lab Chip 2004, 4, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Pohl, H.A. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1978. [Google Scholar]
- Chakraborty, S. Microfluidics and Microfabrication; Springer: Berlin, Germany, 2010. [Google Scholar]
- Yang, J.; Huang, Y.; Wang, X.B.; Becker, F.F.; Gascoyne, P.R. Differential analysis of human leukocytes by dielectrophoretic field-flow-fractionation. Biophys. J. 2000, 78, 2680–2689. [Google Scholar] [CrossRef]
- Huang, Y.; Ynag, J.; Wang, X.B.; Frederick, F.B.; Gascoyne, P.R.C. The removal of human breast cancer cells from hematopoietic CD34+ stem cells by dielectrophoretic field-flow-fractionation. J. Hematother. Stem Cells Res. 1999, 8, 481–490. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Bessette, P.H.; Qian, J.; Meinhart, C.D.; Daugherty, P.S.; Soh, H.T. Marker-specific sorting of rare cells using dielectrophoresis. Proc. Natl. Acad. Sci. USA 2005, 102, 15757–15761. [Google Scholar] [CrossRef] [PubMed]
- Müller, T.; Fiedler, S.; Schnelle, T.; Ludwig, K.; Jung, H.; Fuhr, G. High frequency electric fields for trapping of viruses. Biotechnol. Technol. 1996, 10, 221–226. [Google Scholar] [CrossRef]
- Morgan, H.; Hughes, M.P.; Green, N.G. Separation of submicron bioparticles by dielectrophoresis. Biophys. J. 1999, 77, 516–525. [Google Scholar] [CrossRef]
- Bhatt, K.H.; Grego, S.; Velev, O.D. An AC electrokinetic technique for collection and concentration of particles and cells on patterned electrodes. Langmuir 2005, 21, 6603–6612. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Sin, M.L.Y.; Liu, T.; Gau, V.; Liao, J.C.; Wong, P.K. Hybrid electrokinetic manipulation in high-conductivity media. Lab Chip 2011, 11, 1770–1775. [Google Scholar] [CrossRef] [PubMed]
- Wu, J. Biased AC electro-osmosis for on-chip bioparticle processing. IEEE Trans. Nanotechnol. 2006, 5, 84–88. [Google Scholar]
- Pethig, R. Review Article—Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics 2010, 4, 039901. [Google Scholar] [CrossRef]
- Pethig, R. Review—Where is dielectrophoresis (DEP) going? J. Electrochem. Soc. 2017, 164, B3049–B3055. [Google Scholar] [CrossRef]
- Green, N.; Ramos, A.; Gonzalez, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. I. experimental measurements. Phys. Rev. E 2000, 61, 4011–4018. [Google Scholar] [CrossRef] [PubMed]
- Green, N.G.; Ramos, A.; González, A.; Morgan, H.; Castellanos, A. Fluid flow induced by nonuniform ac electric fields in electrolytes on microelectrodes. III. observation of streamlines and numerical simulation. Phys. Rev. E 2002, 66, 026305. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; González, A.; Castellanos, A.; Green, N.; Morgan, H. Pumping of liquids with ac voltages applied to asymmetric pairs of microelectrodes. Phys. Rev. E 2003, 67, 056302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hunter, R.J. Zeta Potential in Colloid Science: Principles; Applications; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Stubbe, M.; Gimsa, J. A short review on AC electro-thermal micropumps based on smeared structural polarizations in the presence of a temperature gradient. Colloids Surf. A 2011, 376, 97–101. [Google Scholar] [CrossRef]
- Studer, V.; Pepin, A.; Chen, Y.; Ajdari, A. An integrated AC electrokinetic pump in a microfluidic loop for fast and tunable flow control. Analyst 2004, 129, 944–949. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Q.; Yang, K.; Wu, J. Optimization of planar interdigitated microelectrode array for biofluid transport by AC electrothermal effect. Microfluid. Nanofluid. 2014, 16, 167–178. [Google Scholar] [CrossRef]
- Wu, J. AC electro-osmotic micropump by asymmetric electrode polarization. J. Appl. Phys. 2008, 103, 024907. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Ben, Y. Theoretical prediction of fast 3D AC electro-osmotic pumps. Lab Chip 2006, 6, 1455–1461. [Google Scholar] [CrossRef] [PubMed]
- Urbanski, J.P.; Thorsen, T.; Levitan, J.A.; Bazant, M.Z. Fast AC electro-osmotic micropumps with nonplanar electrodes. Appl. Phys. Lett. 2006, 89, 143508. [Google Scholar] [CrossRef]
- Ramos, A.; Morgan, H.; Green, N.G.; González, A.; Castellanos, A. Pumping of liquids with traveling-wave electroosmosis. J. Appl. Phys. 2005, 97, 084906. [Google Scholar] [CrossRef] [Green Version]
- Hoettges, K.F.; McDonnell, M.B.; Hughes, M.P. Use of combined dielectrophoretic/electrohydrodynamic forces for biosensor enhancement. J. Phys. D Appl. Phys. 2003, 36, L101–L104. [Google Scholar] [CrossRef]
- Wu, J.; Ben, Y.; Battigelli, D.; Chang, H.C. Long-range AC electroosmotic trapping and detection of bioparticles. Ind. Eng. Chem. Res. 2005, 44, 2815–2822. [Google Scholar] [CrossRef]
- Debesset, S.; Hayden, C.J.; Dalton, C.; Eijkel, J.C.T.; Manz, A. An AC electroosmotic micropump for circular chromatographic applications. Lab Chip 2004, 4, 396. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electroosmotic pumps and their applications in microfluidic systems. Microfluid. Nanofluid. 2009, 6, 145–162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lastochkin, D.; Zhou, R.; Wang, P.; Ben, Y.; Chang, H.-C. Electrokinetic micropump and micromixer design based on ac faradaic polarization. J. Appl. Phys. 2004, 96, 1730. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.C.; Chen, H.P.; Chang, H.C. Ac Electroosmotic Pumping Induced By Noncontact External. Electrodes. Biomicrofluidics 2007, 1, 034106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eckstein, Y.; Yossifon, G.; Seifert, A.; Miloh, T. Nonlinear electrokinetic phenomena around nearly insulated sharp tips in microflows. J. Colloid Interface Sci. 2009, 338, 243–249. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.C.; Lai, Y.W.; Ben, Y.; Chang, H.C. Microfluidic mixing by dc and ac nonlinear electrokinetic vortex flows. Ind. Eng. Chem. Res. 2004, 43, 2902–2911. [Google Scholar] [CrossRef]
- Chang, H.-C.; Yeo, L.Y. Electrokinetically-Driven Microfluidics; Nanofluidics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Morgan, H.; Green, N.G. AC Electrokinetics: Colloids and Nanoparticles; Research Studies Press: Boston, MA, USA, 2003. [Google Scholar]
- Siva Kumar Gunda, N.; Bhattacharjee, S.; Mitra, S.S.K. Study on the use of dielectrophoresis and electrothermal forces to produce on-chip micromixers and microconcentrators. Biomicrofluidics 2012, 034118, 1–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, D.F.; Du, H. Simulation studies on electrothermal fluid flow induced in a dielectrophoretic microelectrode system. J. Micromech. Microeng. 2006, 16, 2411–2419. [Google Scholar] [CrossRef]
- Sun, H.; Ren, Y.; Hou, L.; Tao, Y.; Liu, W.; Jiang, T.; Jiang, H. Continuous particle trapping, switching, and sorting utilizing a combination of dielectrophoresis and alternating current electrothermal flow. Anal. Chem. 2019, 91, 5729–5738. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Shim, J.; Chuang, H.; Kim, K.C. Numerical simulation on the opto-electro-kinetic patterning for rapid concentration of particles in a microchannel. Biomicrofluidics 2015, 9, 034102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sin, M.L.Y.; Gau, V.; Liao, J.C.; Wong, P.K. Electrothermal fluid manipulation of high-conductivity samples for laboratory automation applications. JALA 2010, 15, 426–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feldman, H.C.; Sigurdson, M.; Meinhart, C.D. AC electrothermal enhancement of heterogeneous assays in microfluidics. Lab Chip 2007, 7, 1553–1559. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, N.; Kitamori, T.; Kim, H.-B. Fluid mixing using AC electrothermal flow on meandering electrodes in a microchannel. Electrophoresis 2012, 33, 2668–2673. [Google Scholar] [CrossRef] [PubMed]
- Lang, Q.; Wu, Y.; Ren, Y.; Tao, Y.; Lei, L.; Jiang, H. AC electrothermal circulatory pumping chip for cell culture. ACS Appl. Mater. Interfaces 2015, 7, 26792–26801. [Google Scholar] [CrossRef] [PubMed]
- Melcher, J.R. Traveling-wave induced electroconvection. Phys. Fluids 1966, 9, 1548. [Google Scholar] [CrossRef]
- Melcher, J.R. Traveling-wave bulk electroconvection induced across a temperature gradient. Phys. Fluids 1967, 10, 1178. [Google Scholar] [CrossRef]
- Fuhr, G.; Schnellet, T.; Wagnert, B. Travelling wave-d riven microfabricated electrohydrodynamic pumps for liquids. J. Micromech. Microeng. 1994, 4, 217–226. [Google Scholar] [CrossRef]
- Castellanos, A.; Ramos, A.; González, A.; Green, N.G.; Morgan, H. Electrohydrodynamics and dielectrophoresis in microsystems: Scaling laws. J. Phys. D Appl. Phys. 2003, 36, 2584–2597. [Google Scholar] [CrossRef]
- Liu, W.; Ren, Y.; Shao, J.; Jiang, H.; Ding, Y. A theoretical and numerical investigation of travelling wave induction microfluidic pumping in a temperature gradient. J. Phys. D Appl. Phys. 2014, 47, 075501. [Google Scholar] [CrossRef]
- Zhang, R.; Dalton, C.; Jullien, G.A. Two-phase AC electrothermal fluidic pumping in a coplanar asymmetric electrode array. Microfluid. Nanofluid. 2011, 10, 521–529. [Google Scholar] [CrossRef]
- Lu, Y.; Ren, Q.; Liu, T.; Leung, S.L.; Gau, V.; Liao, J.C.; Chan, C.L.; Wong, P.K. Long-range electrothermal fluid motion in microfluidic systems. Int. J. Heat Mass Transf. 2016, 98, 341–349. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electric field induced fluid flow on microelectrodes: The effect of illumination. J. Phys. D Appl. Phys. 1999, 33, L13–L17. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Kim, J.; Wereley, S.T.; Kwon, J. Light-actuated electrothermal microfluidic flow for micro-mixing. J. Micromech. Microeng. 2019, 29, 017003. [Google Scholar] [CrossRef]
- Kwon, J.S.; Wereley, S.T. Light-actuated electrothermal microfluidic motion: Experimental investigation and physical interpretation. Microfluid. Nanofluid. 2015, 19, 609–619. [Google Scholar] [CrossRef]
- Williams, S.J. Enhanced electrothermal pumping with thin film resistive heaters. Electrophoresis 2013, 34, 1400–1406. [Google Scholar] [CrossRef] [PubMed]
- Velasco, V.; Williams, S.J. Electrokinetic concentration, patterning, and sorting of colloids with thin film heaters. J. Coll. Interf. Sci. 2013, 394, 598–603. [Google Scholar] [CrossRef] [PubMed]
- Salari, A.; Navi, M.; Dalton, C. A novel AC multiple array electrothermal micropump for lab-on-a-chip applications. Biomicrofluidics 2015, 9, 014113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salari, A.; Dalton, C. Simultaneous pumping and mixing of biological fluids in a double-array electrothermal microfluidic device. Micromachines 2019, 10, 1–11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cao, J.; Cheng, P.; Hong, F.J. A numerical study of an electrothermal vortex enhanced micromixer. Microfluid. Nanofluid. 2008, 5, 13–21. [Google Scholar] [CrossRef]
- Lijnse, T.; Cenaiko, S.; Dalton, C. Prevention of electrode degradation in ACET micropumps for biomedical devices. Alta. BME 2019, 1, 40. [Google Scholar]
- Williams, S.J.; Chamarthy, P.; Wereley, S.T. Comparison of experiments and simulation of Joule heating in AC electrokinetic chips. J. Fluid Eng. T ASME 2010, 132, 021103. [Google Scholar] [CrossRef]
- Sridharan, S.; Zhu, J.; Hu, G.; Xuan, X. Joule heating effects on electroosmotic flow in insulator-based dielectrophoresis. Electrophoresis 2011, 32, 2274–2281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hong, F.; Bai, F.; Cheng, P. A parametric study of electrothermal flow inside an AC EWOD droplet. Int. Commun. Heat Mass Transf. 2014, 55, 63–70. [Google Scholar] [CrossRef]
- Green, N.G.; Ramos, A.; González, A.; Castellanos, A.; Morgan, H. Electrothermally induced fluid flow on microelectrodes. J. Electrost. 2001, 53, 71–87. [Google Scholar] [CrossRef] [Green Version]
- Lide, D.R. CRC Handbook of Chemistry, Physics, 93rd ed.; Haynes, W.M., Ed.; CRC Press: New York, NY, USA, 2012. [Google Scholar]
- Du, E.; Manoochehri, S. Microfluidic pumping optimization in microgrooved channels with AC electrothermal actuations. Appl. Phys. Lett. 2010, 96, 034102. [Google Scholar] [CrossRef]
- Loire, S.; Kauffmann, P.; Mezić, I.; Meinhart, C.D. A theoretical and experimental study of AC electrothermal flows. J. Phys. D Appl. Phys. 2012, 45, 185301. [Google Scholar] [CrossRef]
- Hong, F.J.; Bai, F.; Cheng, P. Numerical simulation of AC electrothermal micropump using a fully coupled model. Microfluid. Nanofluid. 2012, 13, 411–420. [Google Scholar] [CrossRef]
- Sato, N.; Yao, J.; Sugawara, M.; Takei, M. Numerical study of particle-fluid flow under AC electrokinetics in electrode-multilayered microfluidic device. IEEE Trans. Biomed. Eng. 2019, 66, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Kunti, G.; Bhattacharya, A.; Chakraborty, S. Analysis of micromixing of non-Newtonian fluids driven by alternating current electrothermal flow. J. Nonnewton. Fluid Mech. 2017, 247, 123–131. [Google Scholar] [CrossRef]
- Ren, Q. Investigation of pumping mechanism for non-Newtonian blood flow with AC electrothermal forces in a microchannel by hybrid boundary element method and immersed boundary-lattice Boltzmann method. Electrophoresis 2018, 39, 1329–1338. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q.; Wang, Y.; Lin, X.; Chan, C.L. AC electrokinetic induced non-Newtonian electrothermal blood flow in 3D microfluidic biosensor with ring electrodes for point-of-care diagnostics AC electrokinetic induced non-Newtonian electrothermal blood flow in 3D micro fl uidic biosensor with ring. J. Appl. Phys. 2019, 126, 084501. [Google Scholar]
- Salari, A.; Navi, M.; Dalton, C. AC electrothermal micropump for biofluidic applications using numerous microelectrode pairs. In IEEE CEIDP; IEEE: Des Moines, IA, USA, 2014; pp. 1–4. [Google Scholar]
- Yang, K.; Wu, J. Investigation of microflow reversal by ac electrokinetics in orthogonal electrodes for micropump design. Biomicrofluidics 2008, 2, 024101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ajdari, A. Pumping liquids using asymmetric electrode arrays. Phys. Rev. E 2000, 61, 45–48. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Li, Y. Biofluid pumping and mixing by an AC electrothermal micropump embedded with a spiral microelectrode pair in a cylindrical microchannel. Electrophoresis 2018, 39, 3156–3170. [Google Scholar] [CrossRef] [PubMed]
- Salari, A.; Dalton, C.A.; Dalton, C. A novel AC electrothermal micropump for biofluid transport using circular interdigitated microelectrode array. In SPIE BiOS; Gray, B.L., Becker, H., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9320, p. 932016. [Google Scholar]
- Du, E.; Manoochehri, S. Enhanced AC electrothermal fluidic pumping in microgrooved channels. J. Appl. Phys. 2008, 104, 064902. [Google Scholar] [CrossRef] [Green Version]
- Shojaei, A.; Ramiar, A.; Ghasemi, A.H. Numerical investigation of the effect of the electrodes bed on the electrothermally induced fluid flow velocity inside a microchannel. Int. J. Mech. Sci. 2019, 157, 415–427. [Google Scholar] [CrossRef]
- Kunti, G.; Bhattacharya, A.; Chakraborty, S. Rapid mixing with high-throughput in a semi-active semi-passive micromixer. Electrophoresis 2017, 38, 1310–1317. [Google Scholar] [CrossRef] [PubMed]
- Ren, Q. Bioparticle delivery in physiological conductivity solution using AC electrokinetic micropump with castellated electrodes. J. Phys. D. Appl. Phys. 2018, 51, aae233. [Google Scholar] [CrossRef]
- Meng, J.; Li, S.; Li, J.; Yu, C.; Wei, C.; Dai, S. AC electrothermal mixing for high conductive biofluids by arc-electrodes. J. Micromech. Microeng. 2018, 28, 065004. [Google Scholar] [CrossRef]
- Mishra, A.; Khor, J.; Clayton, K.N.; Williams, S.J.; Pan, X.; Kinzer-ursem, T.; Wereley, S. Optoelectric patterning: Effect of electrode material and thickness on laser-induced AC electrothermal flow. Electrophoresis 2016, 37, 658–665. [Google Scholar] [CrossRef] [PubMed]
- Work, A.H.; Williams, S.J. Characterization of 2D colloids assembled by optically-induced electrohydrodynamics. Soft Matter 2015, 11, 4266–4272. [Google Scholar] [CrossRef] [PubMed]
- Salari, A.; Dalton, C. A novel AC electrothermal micropump consisting of two opposing parallel coplanar asymmetric microelectrode arrays. In Proceedings of the 18th International Conference on Miniaturized Systems for Chemistry and Life Sciences, San Antonio, TX, USA, 26–30 October 2014. [Google Scholar]
- Salari, A.; Dalton, C. High efficient biofuid micromixing using ultra-fast AC electrothermal flow. In SPIE BiOS; Gray, B.L., Becker, H., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9320, p. 93201C. [Google Scholar]
- González, A.; Ramos, A.; Morgan, H.; Green, N.G.; Castellanos, A. Electrothermal flows generated by alternating and rotating electric fields in microsystems. J. Fluid Mech. 2006, 564, 415. [Google Scholar] [CrossRef] [Green Version]
- Perch-Nielsen, I.R.; Green, N.G.; Wolff, A. Numerical simulation of travelling wave induced electrothermal fluid flow. J. Phys. D Appl. Phys. 2004, 37, 2323–2330. [Google Scholar] [CrossRef]
- Williams, S.J.; Green, N.G. Electrothermal pumping with interdigitated electrodes and resistive heaters. Electrophoresis 2015, 36, 1681–1689. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Dingari, N.N.; Buie, C.R. Nonlinear electrokinetic effects in insulator-based dielectrophoretic systems. Electrophoresis 2017, 38, 2576–2586. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Sigurdson, M.; Meinhart, C.D. Experimental analysis of particle and fluid motion in ac electrokinetics. Exp. Fluids 2005, 38, 1–10. [Google Scholar] [CrossRef]
- Santiago, J.G.; Wereley, S.T.; Meinhart, C.D.; Beebe, D.J.; Adrian, R.J. A particle image velocimetry system for microfluidics. Exp. Fluids 1998, 25, 316–319. [Google Scholar] [CrossRef]
- Meinhart, C.D.; Wereley, S.T.; Santiago, J.G. PIV measurements of a microchannel flow. Exp. Fluids 1999, 27, 414–419. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Ghavifekr, H.B.; Van Lintel, H.; Brugger, J.; Renaud, P. Bi-directional ACET micropump for on-chip biological applications. Electrophoresis 2016, 37, 719–726. [Google Scholar] [CrossRef] [PubMed]
- Hadjiaghaie, R.; Habib, V.; Ghavifekr, B. Configurable ACET micro—Manipulator for high conductive mediums by using a novel electrode engineering. Microsyst. Technol. 2017, 23, 1393–1403. [Google Scholar]
- Lian, M.; Wu, J. Microfluidic flow reversal at low frequency by AC electrothermal effect. Microfluid. Nanofluid. 2009, 7, 757–765. [Google Scholar] [CrossRef]
- Wu, J.; Ben, Y.; Chang, H.C. Particle detection by electrical impedance spectroscopy with asymmetric-polarization AC electroosmotic trapping. Microfluid. Nanofluid. 2005, 1, 161–167. [Google Scholar] [CrossRef]
- Storey, B.D.; Edwards, L.R.; Kilic, M.S.; Bazant, M.Z. Steric effects on ac electro-osmosis in dilute electrolytes. Phys. Rev. E 2008, 77, 036317. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. I. Double-layer charging. Phys. Rev. E 2007, 75, 021502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, C.; Kim, G.-B.; Clark, P.M.; Zubkov, L.; Papazoglou, E.S.; Noh, M.A. microfabricated quantum dot-linked immuno-diagnostic assay (μQLIDA) with an electrohydrodynamic mixing element. Sens. Actuators B Chem. 2015, 209, 722–728. [Google Scholar] [CrossRef]
- Porter, J.M.; Modares, P.; Castiello, F.; Tabrizian, M. Capacitive detection of insulin antibody enhanced by AC electrothermal mixing. In Proceedings of the 2019 IEEE 6th Portuguese Meeting on Bioengineering (ENBENG), Lisbon, Portugal, 22–23 February 2019; pp. 1–4. [Google Scholar]
- Selmi, M.; Gazzah, M.H.; Belmabrouk, H. Numerical study of the electrothermal effect on the kinetic reaction of immunoassays for a microfluidic biosensor. Langmuir 2016, 32, 13305–13312. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.-R.; Chang, J.-S.; Chao, S.D.; Wu, K.-C.; Yang, C.-K.; Lai, C.-Y.; Chen, S.-H. Simulation on binding efficiency of immunoassay for a biosensor with applying electrothermal effect. J. Appl. Phys. 2008, 104, 064702. [Google Scholar] [CrossRef]
- Li, S.; Ren, Y.; Cui, H.; Yuan, Q.; Wu, J.; Eda, S.; Jiang, H. Alternating current electrokinetics enhanced in situ capacitive immunoassay. Electrophoresis 2015, 36, 471–474. [Google Scholar] [CrossRef] [PubMed]
- Selmi, M.; Khemiri, R.; Echouchene, F.; Belmabrouk, H. Electrothermal effect on the immunoassay in a microchannel of a biosensor with asymmetrical interdigitated electrodes. Appl. Eng. 2016, 105, 77–84. [Google Scholar] [CrossRef]
- Ghandchi, M.; Hadjiaghaie Vafaie, R. AC electrothermal actuation mechanism for on-chip mixing of high ionic strength fluids. Microsyst. Technol. 2017, 23, 1495–1507. [Google Scholar] [CrossRef]
- Hadjiaghaie Vafaie, R. A high-efficiency micromixing effect by pulsed AC electrothermal flow. Compel 2018, 37, 418–431. [Google Scholar] [CrossRef]
- Frkonja-kuczin, A.; Ray, L.; Zhao, Z.; Konopka, M.C.; Boika, A. Electrokinetic preconcentration and electrochemical detection of Escherichia coli at a microelectrode. Electrochim. Acta 2018, 280, 191–196. [Google Scholar] [CrossRef]
- Kale, A.; Song, L.; Lu, X.; Yu, L.; Hu, G.; Xuan, X. Electrothermal enrichment of submicron particles in an insulator-based dielectrophoretic microdevice. Electrophoresis 2018, 39, 887–896. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dies, H.; Raveendran, J.; Escobedo, C.; Docoslis, A. In situ assembly of active surface-enhanced Raman scattering substrates via electric field-guided growth of dendritic nanoparticle structures. Nanoscale 2017, 9, 7847–7857. [Google Scholar] [CrossRef] [PubMed]
- Ramos, A.; García-Sánchez, P.; Morgan, H. AC electrokinetics of conducting microparticles: A review. Curr. Opin. Coll. Interface Sci. 2016, 24, 79–90. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Wang, J.; Wu, J.; Qi, H.; Wang, C.; Fang, X.; Cheng, C.; Yang, W. Rapid detection of ultra-trace nanoparticles based on ACEK enrichment for semiconductor manufacturing quality control. Microfluid. Nanofluid. 2019, 23, 1–11. [Google Scholar] [CrossRef]
- Bottausci, F.; Neumann, T.; Mader, M.A.; Mezic, I.; Jaeger, L.; Tirrell, M. DNA Hybridization Enhancement in Microarrays Using AC-Electrothermal Flow; Volume 2: Fora; ASME: Jacksonville, FL, USA, 2008; pp. 629–636. [Google Scholar]
- Mi, S.; Li, B.; Yi, X.; Xu, Y.; Du, Z.; Yang, S.; Li, W.; Sun, W. An AC electrothermal self-circulating system with a minimalist process to construct a biomimetic liver lobule model for drug testing. RSC Adv. 2018, 8, 36987–36998. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Islam, N.; Eda, S.; Wu, J. Optimization of an AC electrokinetics immunoassay lab - chip for biomedical diagnostics. Microfluid. Nanofluid. 2017, 21, 1–11. [Google Scholar] [CrossRef]
- Salari, A.; Dalton, C. Fluid flow study of an AC electrothermal micropump consisting of multiple arrays of microelectrodes for biofluidic applications. In SPIE BiOS; Gray, B.L., Becker, H., Eds.; International Society for Optics and Photonics: Bellingham, DC, USA, 2015; Volume 9320, p. 93200G. [Google Scholar]
- Zhang, R.; Jullien, G.A.; Dalton, C. Study on an alternating current electrothermal micropump for microneedle-based fluid delivery systems. J. Appl. Phys. 2013, 114, 024701. [Google Scholar] [CrossRef]
- Ren, Q.; Chan, C.L. Numerical simulation of a 2D electrothermal pump by lattice Boltzmann method on GPU. Numer. Heat Transf. Part A Appl. 2016, 69, 677–693. [Google Scholar] [CrossRef]
- Ren, Q.; Meng, F.; Lik, C. Cell transport and suspension in high conductivity electrothermal flow with negative dielectrophoresis by immersed boundary-lattice Boltzmann method. Int. J. Heat Mass Transf. 2019, 128, 1229–1244. [Google Scholar] [CrossRef]
- Lamanda, A.; Lu, Y.; Gill, N.; Wong, P.K. An electrokinetic microdevice for isolation and quantification of circulating cell-free DNA from physiological samples. In IEEE Transducers; IEEE: Anchorage, AK, USA, 2015; pp. 544–547. [Google Scholar]
- Tansel, O.; Oksuzoglu, H.; Koklu, A.; Sabuncu, A.C. Electrothermal flow on electrodes arrays at physiological conductivities. IET Nanobiotechnol. 2016, 10, 54–61. [Google Scholar]
- Lee, W.C.; Lee, H.; Lim, J.; Park, Y.J. An effective electrical sensing scheme using AC electrothermal flow on a biosensor platform based on a carbon nanotube network. Appl. Phys. Lett. 2016, 109, 223701. [Google Scholar] [CrossRef]
- Lang, Q.; Ren, Y.; Hobson, D.; Tao, Y.; Hou, L.; Jia, Y.; Hu, Q.; Liu, J.; Zhao, X.; Jiang, H. In-plane microvortices micromixer-based AC electrothermal for testing drug induced death of tumor cells. Biomicrofluidics 2016, 10, 064102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Ren, Y.; Jiang, H. Enhanced model-based design of a high-throughput three dimensional micromixer driven by alternating-current electrothermal flow. Electrophoresis 2017, 38, 258–269. [Google Scholar] [CrossRef] [PubMed]
- Vafaie, R.H.; Madanpasandi, A. In-situ AC electroosmotic and thermal perturbation effects for wide range of ionic strength. Aims Biophys. 2017, 4, 451–464. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salari, A.; Navi, M.; Lijnse, T.; Dalton, C. AC Electrothermal Effect in Microfluidics: A Review. Micromachines 2019, 10, 762. https://doi.org/10.3390/mi10110762
Salari A, Navi M, Lijnse T, Dalton C. AC Electrothermal Effect in Microfluidics: A Review. Micromachines. 2019; 10(11):762. https://doi.org/10.3390/mi10110762
Chicago/Turabian StyleSalari, Alinaghi, Maryam Navi, Thomas Lijnse, and Colin Dalton. 2019. "AC Electrothermal Effect in Microfluidics: A Review" Micromachines 10, no. 11: 762. https://doi.org/10.3390/mi10110762
APA StyleSalari, A., Navi, M., Lijnse, T., & Dalton, C. (2019). AC Electrothermal Effect in Microfluidics: A Review. Micromachines, 10(11), 762. https://doi.org/10.3390/mi10110762






