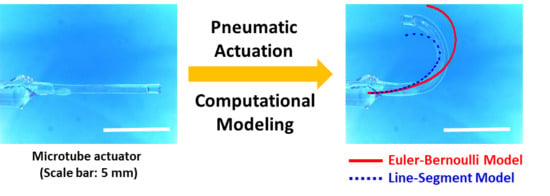
Rapid Design and Analysis of Microtube Pneumatic Actuators Using Line-Segment and Multi-Segment Euler–Bernoulli Beam Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microtube Actuator Fabrication
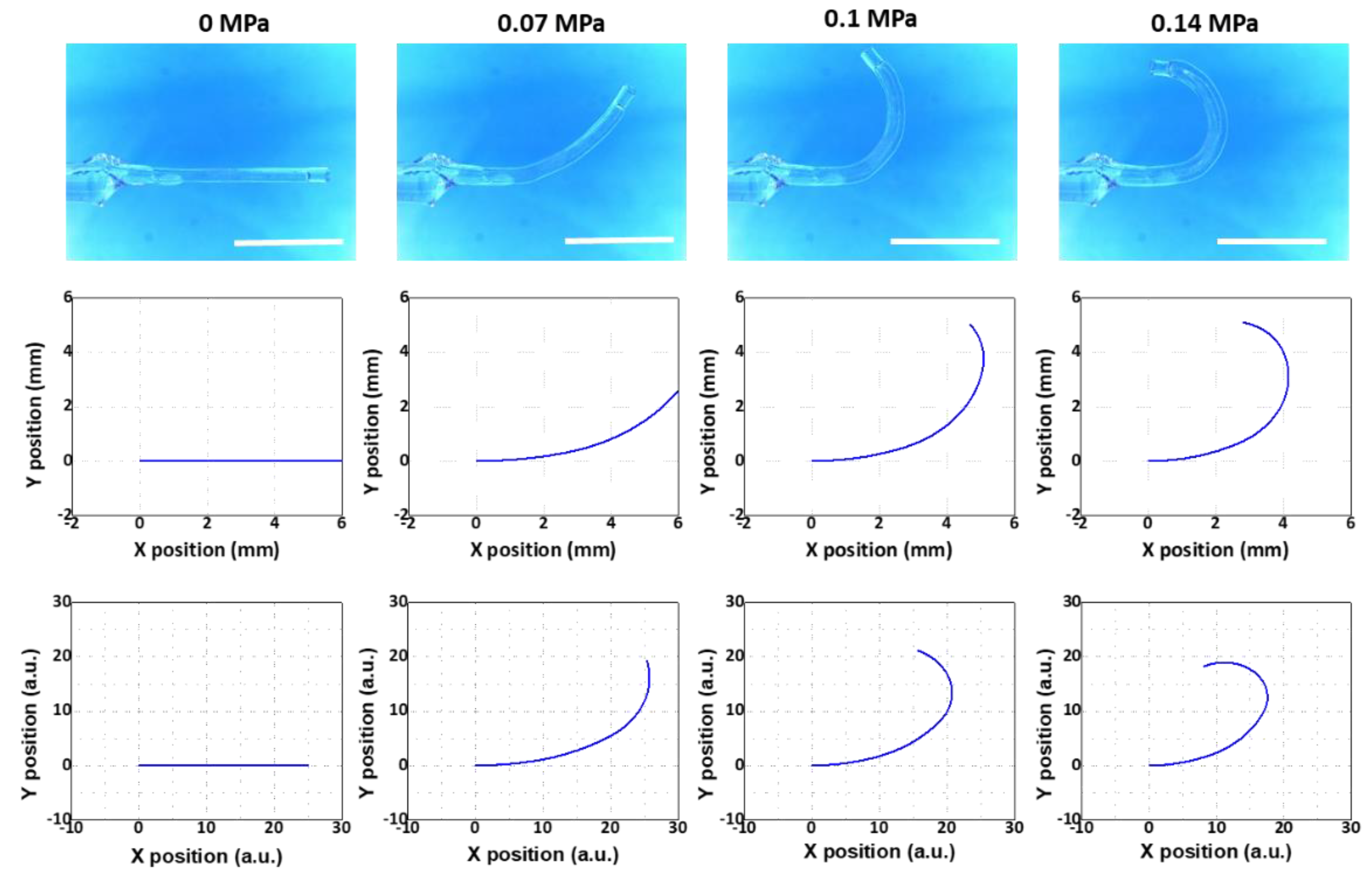
2.2. Pneumatic Actuation and Characterization
2.3. Multi-Segment Euler–Bernoulli’s Beam Model
2.4. Line-Segment Model
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| List of Symbols | |
| Symbol | Explanation |
| Cross-sectional area of pneumatic actuator | |
| Fractional section lengths (a, b, c | |
| Distance between the neutral axis and the void center | |
| Young’s modulus | |
| Tensile force | |
| Second moment of area | |
| Length of each section | |
| Length of top & bottom side | |
| Total length of PDMS microtube | |
| Bending moment of each section | |
| Pneumatic pressure | |
| Current applied pneumatic pressure | |
| Maximum applied pneumatic pressure | |
| Cylindrical template radius | |
| The original axial coordinate of the undeformed pneumatic actuator | |
| Top wall thickness of each segment | |
| Bottom wall thickness of each segment | |
| Deviation angle | |
| x, y-axis deformed coordinate | |
| x, y coordinate (in line-segment model) | |
| Engineering strain | |
| Top and bottom wall strain | |
| Engineering stress | |
| Final tilt angle (in line-segment model) | |
References
- Majidi, C. Soft robotics: A perspective—current trends and prospects for the future. Soft Robot. 2014, 1, 5–11. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.J. Microscale Soft Robotics: Motivations, Progress, and Outlook; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783319502854. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.Y.; Zhu, J.; Zhu, L.M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspir. Biomim. 2017, 12, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Rich, S.I.; Wood, R.J.; Majidi, C. Untethered soft robotics. Nat. Electron. 2018, 1, 102–112. [Google Scholar] [CrossRef]
- Do, T.N.; Phan, H.; Nguyen, T.Q.; Visell, Y. Miniature soft electromagnetic actuators for robotic applications. Adv. Funct. Mater. 2018, 28, 1–11. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Guo, J.; Sun, Y.; Liang, X.; Low, J.H.; Wong, Y.R.; Tay, V.S.C.; Yeow, C.H. Design and fabrication of a pneumatic soft robotic gripper for delicate surgical manipulation. In Proceedings of the 2017 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 6–9 August 2017; pp. 1069–1074. [Google Scholar] [CrossRef]
- Johnston, I.D.; McCluskey, D.K.; Tan, C.K.L.; Tracey, M.C. Mechanical characterization of bulk Sylgard 184 for microfluidics and microengineering. J. Micromech. Microeng. 2014, 24. [Google Scholar] [CrossRef]
- Liu, M.; Sun, J.; Sun, Y.; Bock, C.; Chen, Q. Thickness-dependent mechanical properties of polydimethylsiloxane membranes. J. Micromech. Microeng. 2009, 19, 3. [Google Scholar] [CrossRef]
- Hwang, Y.; Paydar, O.H.; Candler, R.N. Pneumatic microfinger with balloon fins for linear motion using 3D printed molds. Sens. Actuators Phys. 2015, 234, 65–71. [Google Scholar] [CrossRef]
- Liang, X.; Sun, Y.; Ren, H. A flexible fabrication approach toward the shape engineering of microscale soft pneumatic actuators. IEEE Robot. Autom. Lett. 2017, 2, 165–170. [Google Scholar] [CrossRef]
- Sinatra, N.R.; Ranzani, T.; Vlassak, J.J.; Parker, K.K.; Wood, R.J. Nanofiber-reinforced soft fluidic micro-actuators. J. Micromech. Microeng. 2018, 28, 8. [Google Scholar] [CrossRef]
- Jang, S.H.; Na, S.H.; Park, Y.L. Magnetically assisted bilayer composites for soft bending actuators. Materials 2017, 10, 646. [Google Scholar] [CrossRef] [PubMed]
- Amiri Moghadam, A.A.; Alaie, S.; Deb Nath, S.; Aghasizade Shaarbaf, M.; Min, J.K.; Dunham, S.; Mosadegh, B. Laser cutting as a rapid method for fabricating thin soft pneumatic actuators and robots. Soft Robot. 2018, 5, 443–451. [Google Scholar] [CrossRef] [PubMed]
- Suzumori, K.; Iikura, S.; Tanaka, H. Development of flexible microactuator and its applications to robotic mechanisms. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; Volume 2, pp. 1622–1627. [Google Scholar]
- Rodrigue, H.; Wang, W.; Kim, D.R.; Ahn, S.H. Curved shape memory alloy-based soft actuators and application to soft gripper. Compos. Struct. 2017, 176, 398–406. [Google Scholar] [CrossRef]
- Lum, G.Z.; Ye, Z.; Dong, X.; Marvi, H.; Erin, O.; Hu, W.; Sitti, M. Shape-programmable magnetic soft matter. Proc. Natl. Acad. Sci. USA 2016, 113, E6007–E6015. [Google Scholar] [CrossRef]
- Li, L.; Meng, J.; Hou, C.; Zhang, Q.; Li, Y.; Yu, H.; Wang, H. Dual-mechanism and multimotion soft actuators based on commercial plastic film. ACS Appl. Mater. Interfaces 2018, 10, 15122–15128. [Google Scholar] [CrossRef]
- Oscurato, S.L.; Salvatore, M.; Maddalena, P.; Ambrosio, A. From nanoscopic to macroscopic photo-driven motion in azobenzene-containing materials. Nanophotonics 2018, 7, 1387–1422. [Google Scholar] [CrossRef]
- Mauro, M. Gel-based soft actuators driven by light. J. Mater. Chem. B 2019, 7, 4234–4242. [Google Scholar] [CrossRef]
- Ryabchun, A.; Li, Q.; Lancia, F.; Aprahamian, I.; Katsonis, N. Shape-persistent actuators from hydrazone photoswitches. J. Am. Chem. Soc. 2019, 141, 1196–1200. [Google Scholar] [CrossRef]
- Paek, J.; Cho, I.; Kim, J. Microrobotic tentacles with spiral bending capability based on shape-engineered elastomeric microtubes. Sci. Rep. 2015, 5, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Sadati, S.M.H.; Naghibi, S.E.; Shiva, A.; Walker, I.D.; Althoefer, K.; Nanayakkara, T. Mechanics of Continuum Manipulators, a Comparative Study of Five Methods with Experiments. In Towards Autonomous Robotic Systems; Gao, Y., Fallah, S., Jin, Y., Lekakou, C., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 686–702. [Google Scholar] [CrossRef]
- Moseley, P.; Florez, J.M.; Sonar, H.A.; Agarwal, G.; Curtin, W.; Paik, J. Modeling, design, and development of soft pneumatic actuators with finite element method. Adv. Eng. Mater. 2016, 18, 978–988. [Google Scholar] [CrossRef]
- Pozzi, M.; Miguel, E.; Deimel, R.; Malvezzi, M.; Bickel, B.; Brock, O.; Prattichizzo, D. Efficient FEM-Based simulation of soft robots modeled as kinematic chains. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 4206–4213. [Google Scholar] [CrossRef]
- Gorissen, B.; Vincentie, W.; Al-Bender, F.; Reynaerts, D.; De Volder, M. Modeling and bonding-free fabrication of flexible fluidic microactuators with a bending motion. J. Micromech. Microeng. 2013, 23, 4. [Google Scholar] [CrossRef]
- Gorissen, B.; De Volder, M.; De Greef, A.; Reynaerts, D. Theoretical and experimental analysis of pneumatic balloon microactuators. Sens. Actuators Phys. 2011, 168, 58–65. [Google Scholar] [CrossRef]
- Popov, E.P. Introduction to Mechanics of Solids; Prentice-Hall Civil Engineering and Engineering Mechanics Series; Prentice-Hall: Sadr River, NJ, USA, 1968. [Google Scholar]
- Shao, T.; Zhang, L.; Bao, G.; Luo, X.; Yang, Q. Basic characteristics of a new flexible pneumatic bending joint. Chin. J. Mech. Eng. (Engl. Ed.) 2014, 27, 1143–1149. [Google Scholar] [CrossRef]
- Shapiro, Y.; Gabor, K.; Wolf, A. Modeling a hyperflexible planar bending actuator as an inextensible euler-bernoulli beam for use in flexible robots. Soft Robot. 2015, 2, 71–79. [Google Scholar] [CrossRef]
- Shapiro, Y.; Wolf, A.; Gabor, K. Bi-bellows: Pneumatic bending actuator. Sens. Actuators Phys. 2011, 167, 484–494. [Google Scholar] [CrossRef]
- Wang, Z.; Hirai, S. Soft gripper dynamics using a line-segment model with an optimization-based parameter identification method. IEEE Robot. Autom. Lett. 2017, 2, 624–631. [Google Scholar] [CrossRef]
- Grilli, S.; Coppola, S.; Vespini, V.; Merola, F.; Finizio, A.; Ferraro, P. 3D lithography by rapid curing of the liquid instabilities at nanoscale. Proc. Natl. Acad. Sci. USA 2011, 108, 15106–15111. [Google Scholar] [CrossRef] [Green Version]
- Paek, J.; Kim, J. Microsphere-assisted fabrication of high aspect-ratio elastomeric micropillars and waveguides. Nat. Commun. 2014, 5, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Dhakal, R.; Kim, J. Microdroplet-based on-demand drawing of high aspect-ratio elastomeric micropillar and its contact sensing application. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Udofia, E.N.; Zhou, W. A guiding framework for microextrusion additive manufacturing. J. Manuf. Sci. Eng. Trans. ASME 2019, 141. [Google Scholar] [CrossRef]








| Sample | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Template Diameter (μm) | 470 | 250 | ||||||||
| (mm) | 12.29 | 8.38 | 8.78 | 12.06 | 9.17 | 9.57 | 8.88 | 8.80 | ||
| Fractional Section Length () | 0 | 0.43 | 0.33 | 0.61 | 0.17 | 0.60 | 0.17 | 0.75 | 1.00 | |
| 1 | 0.24 | 0.36 | 0.39 | 0.41 | 0.30 | 0.83 | 0.13 | - | ||
| 2 | 0.23 | 0.31 | - | 0.42 | 0.10 | - | 0.12 | - | ||
| 3 | 0.10 | - | - | - | - | - | - | - | ||
| Wall Thickness (μm) | 0 | 134 | 200 | 129 | 164 | 126 | 101 | 92 | 63 | |
| 67 | 140 | 72 | 72 | 100 | 38 | 51 | 42 | |||
| 1 | 166 | 113 | 113 | 250 | 142 | 167 | 123 | - | ||
| 72 | 67 | 62 | 72 | 59 | 38 | 82 | - | |||
| 2 | 211 | 185 | - | 123 | 80 | - | 82 | - | ||
| 67 | 62 | - | 72 | 67 | - | 51 | - | |||
| 3 | 139 | - | - | - | - | - | - | - | ||
| 67 | - | - | - | - | - | - | - | |||
| Sample | #1 | #2 | #3 |
|---|---|---|---|
| Experiment | 306.4° | 175.7° | 273.2° |
| Multi-segment Euler–Bernoulli’s beam model | 332.7° | 180.8° | 243.8° |
| Line-segment model | 292.7° | 198.2° | 283.1° |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, M.; Li, Q.; Cho, I.H.; Kim, J. Rapid Design and Analysis of Microtube Pneumatic Actuators Using Line-Segment and Multi-Segment Euler–Bernoulli Beam Models. Micromachines 2019, 10, 780. https://doi.org/10.3390/mi10110780
Ji M, Li Q, Cho IH, Kim J. Rapid Design and Analysis of Microtube Pneumatic Actuators Using Line-Segment and Multi-Segment Euler–Bernoulli Beam Models. Micromachines. 2019; 10(11):780. https://doi.org/10.3390/mi10110780
Chicago/Turabian StyleJi, Myunggi, Qiang Li, In Ho Cho, and Jaeyoun Kim. 2019. "Rapid Design and Analysis of Microtube Pneumatic Actuators Using Line-Segment and Multi-Segment Euler–Bernoulli Beam Models" Micromachines 10, no. 11: 780. https://doi.org/10.3390/mi10110780
APA StyleJi, M., Li, Q., Cho, I. H., & Kim, J. (2019). Rapid Design and Analysis of Microtube Pneumatic Actuators Using Line-Segment and Multi-Segment Euler–Bernoulli Beam Models. Micromachines, 10(11), 780. https://doi.org/10.3390/mi10110780