Modeling and Analysis of the Noise Performance of the Capacitive Sensing Circuit with a Differential Transformer
Abstract
:1. Introduction
2. Front-End Circuit Analysis
2.1. Sensing Function
2.2. Noise Analysis
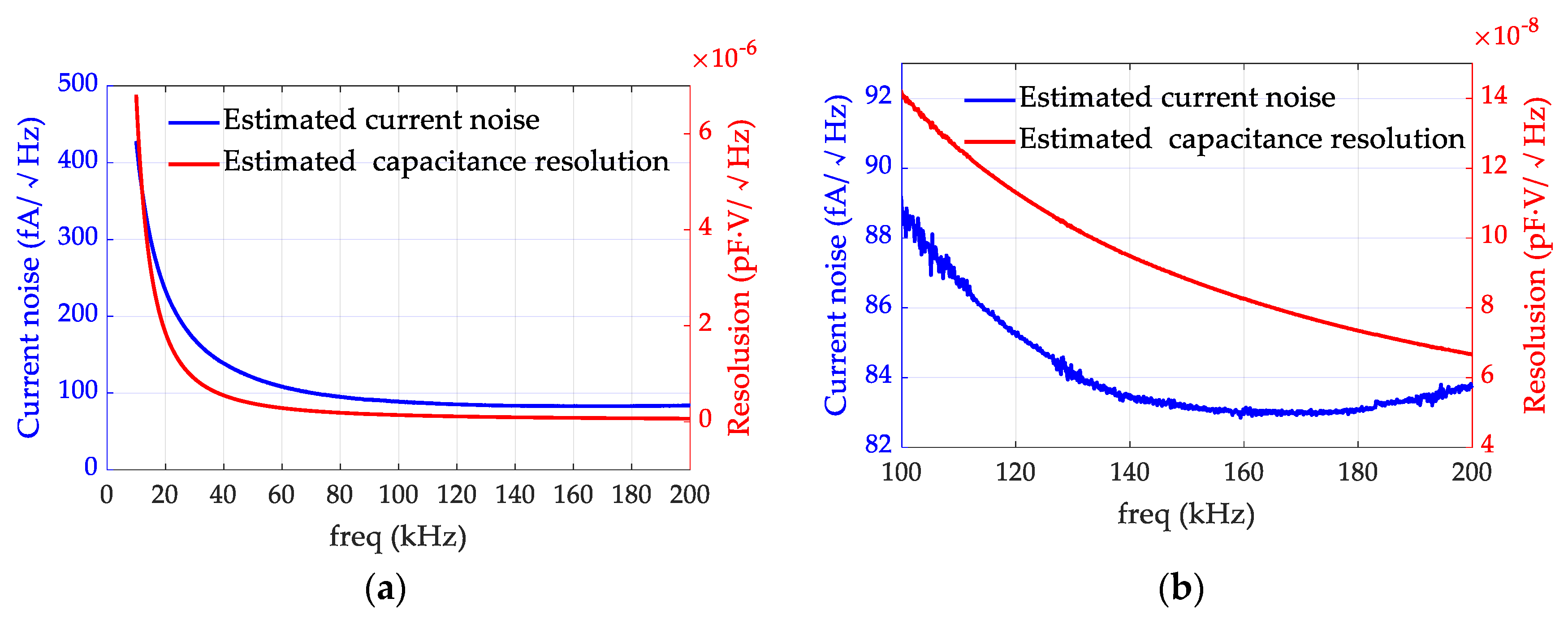
2.2.1. The Equivalent Input Current Noise
2.2.2. Capacitance Resolution
3. Experiment Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, X.; Cheng, S.; Liu, H.; Hu, S.; Zhang, D.; Ning, H. A Survey on Gas Sensing Technology. Sensors 2012, 12, 9635–9665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salim, A.; Lim, S. Review of Recent Inkjet-Printed Capacitive Tactile Sensors. Sensors 2017, 17, 2593. [Google Scholar] [CrossRef] [PubMed]
- Pike, W.T.; Calcutt, S.; Standley, I.M.; Mukherjee, A.G.; Temple, J.; Warren, T.; Charalambous, C.; Liu, H.; Stott, A.; McClean, J.B. A Silicon Seismic Package (SSP) for Planetary Geophysics. In Proceedings of the 47th Lunar and Planetary Science Conference, Woodlands, TX, USA, 21–25 March 2016; p. 2081. [Google Scholar]
- Balmino, G.; Perosanz, F.; Rummel, R.; Sneeuw, N.; Sunkel, H. GRACE and GOCE: Mission Concepts and Simulations. Bollettino di Geofisica Teorica ed Applicata 1999, 40, 309–319. [Google Scholar]
- Touboul, P.; Foulon, B.; Christophe, B.; Marque, J.P. CHAMP, GRACE, GOCE Instruments and Beyond. In Proceedings of the Geodesy for Planet Earth; Kenyon, S., Pacino, M.C., Marti, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 215–221. [Google Scholar]
- Touboul, P.; Métris, G.; Rodrigues, M.; André, Y.; Baghi, Q.; Bergé, J.; Boulanger, D.; Bremer, S.; Carle, P.; Chhun, R.; et al. MICROSCOPE Mission: First Results of a Space Test of the Equivalence Principle. Phys. Rev. Lett. 2017, 119, 231101. [Google Scholar] [CrossRef] [PubMed]
- Danzmann, K.; Rüdiger, A.R. LISA technology concept, status, prospects. Class. Quantum Grav. 2003, 20, S1–S9. [Google Scholar] [CrossRef] [Green Version]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Jones, R.V.; Richards, J.C.S. The design and some applications of sensitive capacitance micrometers. J. Phys. E Sci. Instrum. 1973, 6, 589–600. [Google Scholar] [CrossRef]
- Josselin, V.; Touboul, P.; Kielbasa, R. Capacitive detection scheme for space accelerometers applications. Sens. Actuators A Phys. 1999, 78, 92–98. [Google Scholar] [CrossRef]
- Cavalleri, A.; Dolesi, R.; Fontana, G.; Hueller, M.; Turneaure, J.; Vitale, S.; Weber, W. Progress in the development of a position sensor for LISA drag-free control. Class. Quantum Grav. 2001, 18, 4133–4144. [Google Scholar] [CrossRef]
- Li, Z.; Wu, W.J.; Zheng, P.P.; Liu, J.Q.; Fan, J.; Tu, L.C. Novel Capacitive Sensing System Design of a Microelectromechanical Systems Accelerometer for Gravity Measurement Applications. Micromachines 2016, 7, 167. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Xie, Y.; Zhang, M.; Deng, Z.; Tu, L. A Subnano-g Electrostatic Force-Rebalanced Flexure Accelerometer for Gravity Gradient Instruments. Sensors 2017, 17, 2669. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Bai, Y.Z.; Zhou, Z.B.; Li, Z.X.; Luo, J. Resonant frequency detection and adjustment method for a capacitive transducer with differential transformer bridge. Rev. Sci. Instrum. 2014, 85, 055001. [Google Scholar] [CrossRef] [PubMed]
- Weber, W.J.; Cavalleri, A.; Dolesi, R.; Fontana, G.; Hueller, M.; Vitale, S. Position sensors for LISA drag-free control. Class. Quantum Grav. 2002, 19, 1751–1756. [Google Scholar] [CrossRef]
- LISA Pathfinder Collaboration; Armano, M.; Audley, H.; Auger, G.; Baird, J.; Bassan, M.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; et al. Capacitive sensing of test mass motion with nanometer precision over millimeter-wide sensing gaps for space-borne gravitational reference sensors. Phys. Rev. D 2017, 96, 062004. [Google Scholar] [CrossRef] [Green Version]
- Amaro-Seoane, P.; Aoudia, S.; Babak, S.; Binétruy, P.; Berti, E.; Bohé, A.; Caprini, C.; Colpi, M.; Cornish, N.J.; Danzmann, K.; et al. Low-frequency gravitational-wave science with eLISA/NGO. Class. Quantum Grav. 2012, 29, 124016. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-M.; Nester, J.M.; Ni, W.-T. A brief history of gravitational wave research. Chin. J. Phys. 2017, 55, 142–169. [Google Scholar] [CrossRef] [Green Version]
- Luo, J.; Chen, L.-S.; Duan, H.-Z.; Gong, Y.-G.; Hu, S.; Ji, J.; Liu, Q.; Mei, J.; Milyukov, V.; Sazhin, M.; et al. TianQin: A space-borne gravitational wave detector. Class. Quantum Grav. 2016, 33, 035010. [Google Scholar] [CrossRef]
- Cai, R.; Cao, Z.; Guo, Z.; Wang, S.; Yang, T. The Gravitational-Wave Physics. Natl. Sci. Rev. 2017, 4, 687–706. [Google Scholar] [CrossRef]
- Larson, S.L.; Hiscock, W.A.; Hellings, R.W. Sensitivity curves for spaceborne gravitational wave interferometers. Phys. Rev. D 2000, 62, 062001. [Google Scholar] [CrossRef]
- Kokkotas, K.D. Gravitational Wave Physics. In Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 67–85. ISBN 978-0-12-227410-7. [Google Scholar]
- Speake, C.C.; Andrews, P.L. Capacitive sensing for drag-free satellites. Class. Quantum Grav. 1997, 14, 1557. [Google Scholar] [CrossRef]
- Weber, W.J.; Bortoluzzi, D.; Cavalleri, A.; Carbone, L.; Lio, M.D.; Dolesi, R.; Fontana, G.; Hoyle, C.D.; Hueller, M.; Vitale, S. Position sensors for flight testing of LISA drag-free control. Proc. SPIE 2003, 4856. [Google Scholar] [CrossRef]
- Mance, D. Development of Electronic System for Sensing and Actuation of Test Mass of the Inertial Sensor LISA. Ph.D. Thesis, University of Split, Split, Croatia, 2012. [Google Scholar]
- Gan, L.; Mance, D.; Zweifel, P. Actuation to sensing crosstalk investigation in the inertial sensor front-end electronics of the laser interferometer space antenna pathfinder satellite. Sens. Actuators A Phys. 2011, 167, 574–580. [Google Scholar] [CrossRef]
- Alexander, C.; Sadiku, M. Fundamentals of Electric Circuits; McGraw-Hill Companies, Incorporated: New York, NY, USA, 2008; ISBN 978-0-07-726319-5. [Google Scholar]
- Touboul, P.; Foulon, B.; Rodrigues, M.; Marque, J.P. In orbit nano-g measurements, lessons for future space missions. Aerosp. Sci. Technol. 2004, 8, 431–441. [Google Scholar] [CrossRef]
- Marque, J.P.; Christophe, B.; Foulon, B.; Touboul, P. The Ultra Sensitive GOCE Accelerometers and Their Future Developments; Towards a Roadmap for Future Satellite Gravity Missions; IGCP: Graz, Austria, 2009. [Google Scholar]




| Items | LISA | TianQin |
|---|---|---|
| Orbit center | Sun | Earth |
| Arm length | 2.5 × 106 km | 1.7 × 105 km |
| Number of spacecrafts | 3 | 3 |
| Residual acceleration | 3 × 10−15 ms−2/Hz1/2 @1 mHz | 10−15 ms−2/Hz1/2 @6 mHz |
| Cubic test mass | 46 × 46 × 46 mm3 | 50 × 50 × 50 mm3 |
| Weight of test mass | 2 kg | 2.5 kg |
| Electrode gap for x-axis | 4 mm | 5 mm |
| Capacitance of single frame electrode for x-axis | 1.15 pF | 1.4 pF |
| Amplitude of injection voltage | 0.6 V | 1.4 V |
| Capacitance resolution | 1 aF/Hz1/2 | ≤0.69 aF/Hz1/2 |
| Position sensing accuracy | 1.8 nm/Hz1/2 | ≤1.7 nm/Hz1/2 |
| Electrostatic stiffness | 0.25 × 10−7/s2 | 0.92 × 10−7/s2 |
| Parameter | Typical Value |
|---|---|
| Transformer inductance | 8.2 mH |
| Self-resonant frequency | 463 kHz |
| Stray capacitance | 14 pF |
| DC resistance | 1.8 Ω |
| Coupling factor | 0.98 |
| Frequency (kHz) | LQ (H) | Estimated Current Noise (fA/Hz1/2) | Estimated Capacitance Resolution (aF·V/Hz1/2) |
|---|---|---|---|
| 50 | 3.64 | 120.3 | 0.38 |
| 65 | 3.82 | 103.0 | 0.25 |
| 100 | 3.36 | 88.6 | 0.14 |
| 160 | 2.38 | 82.7 | 0.082 |
| 200 | 1.88 | 83.7 | 0.067 |
| Existing Work | Resonant Frequency (kHz) | Amplitude of Injection Voltage (V) | Capacitance Resolution (aF/Hz1/2) |
|---|---|---|---|
| P. Touboul et al. [28] | 100 | 7.1 | 0.1 |
| J.P. Marque et al. [29] | 100 | 7.6 | 0.2 |
| M. Armano et al. [16] | 100 | 0.6 | 0.7 |
| M. Hu et al. [14] | 50 | 8.5 | 0.14 |
| This work | 200 | 0.6 | 0.11 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Fan, J.; Zhao, C.; Yan, S.; Hu, C.; Tu, L. Modeling and Analysis of the Noise Performance of the Capacitive Sensing Circuit with a Differential Transformer. Micromachines 2019, 10, 325. https://doi.org/10.3390/mi10050325
Xie Y, Fan J, Zhao C, Yan S, Hu C, Tu L. Modeling and Analysis of the Noise Performance of the Capacitive Sensing Circuit with a Differential Transformer. Micromachines. 2019; 10(5):325. https://doi.org/10.3390/mi10050325
Chicago/Turabian StyleXie, Yafei, Ji Fan, Chun Zhao, Shitao Yan, Chenyuan Hu, and Liangcheng Tu. 2019. "Modeling and Analysis of the Noise Performance of the Capacitive Sensing Circuit with a Differential Transformer" Micromachines 10, no. 5: 325. https://doi.org/10.3390/mi10050325
APA StyleXie, Y., Fan, J., Zhao, C., Yan, S., Hu, C., & Tu, L. (2019). Modeling and Analysis of the Noise Performance of the Capacitive Sensing Circuit with a Differential Transformer. Micromachines, 10(5), 325. https://doi.org/10.3390/mi10050325






