A Shear-Mode Piezoelectric Heterostructure for Electric Current Sensing in Electric Power Grids
Abstract
:1. Introduction
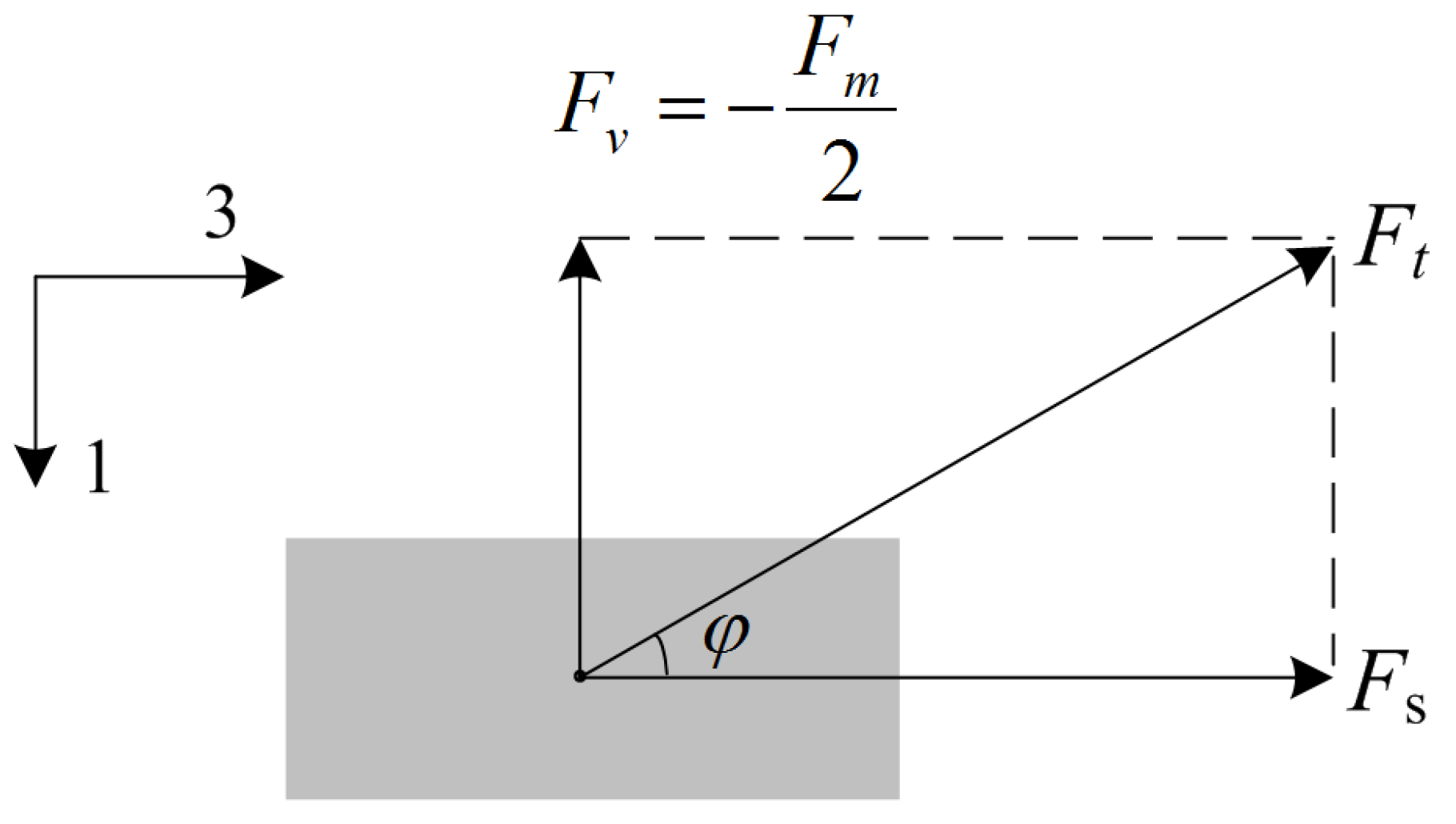
2. Structure and Analysis
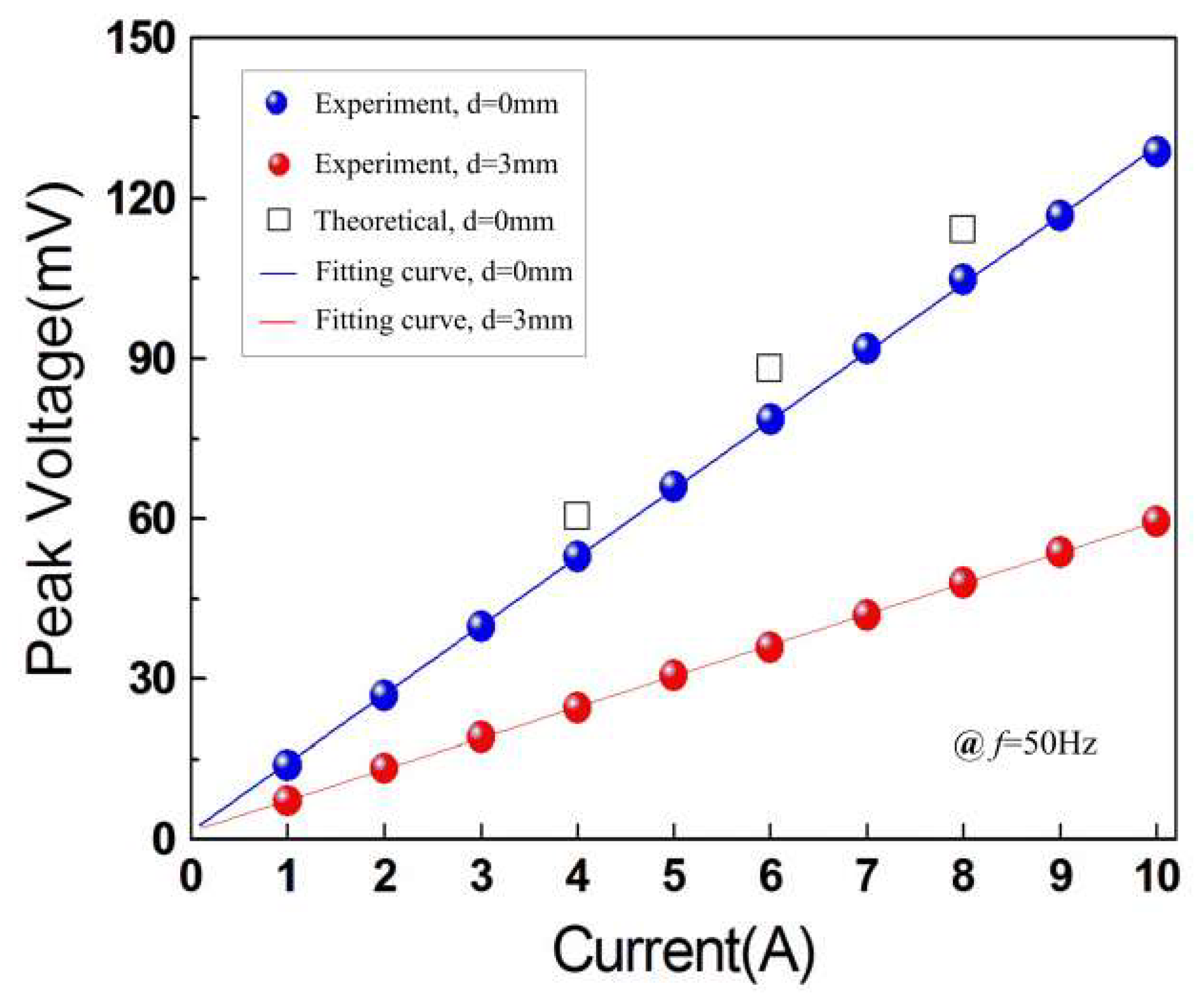
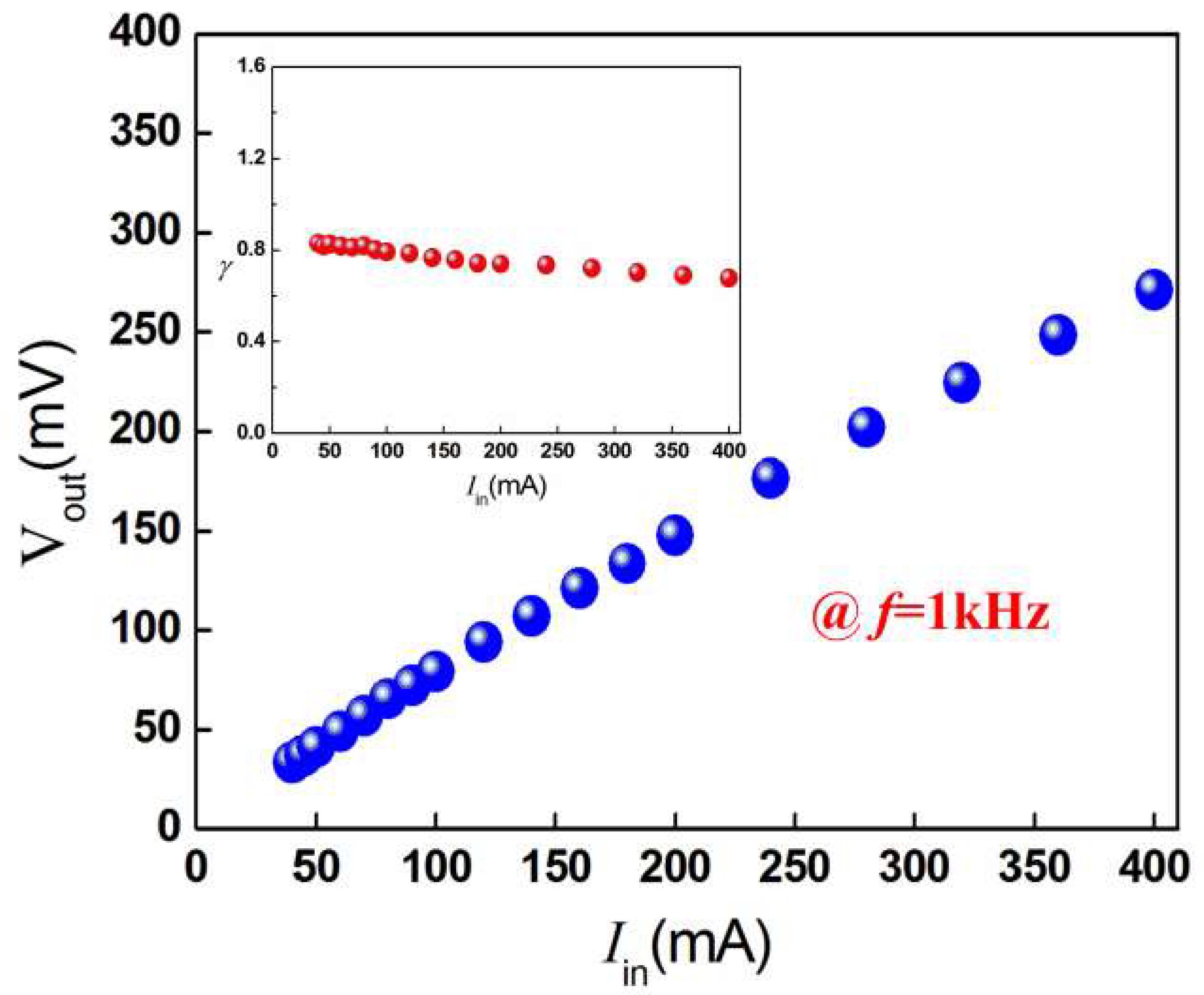
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cataliotti, A.; Di Cara, D.; Emanuel, A.E.; Nuccio, S. Improvement of Hall effect current transducer metrological performances in the presence of harmonic distortion. IEEE Trans. Instrum. Meas. 2010, 59, 1091–1097. [Google Scholar] [CrossRef]
- Mlejnek, P.; Vopálenský, M.; Ripka, P. AMR current measurement device. Sens. Actuators A 2008, 141, 649–653. [Google Scholar] [CrossRef]
- Jedlicska, I.; Weiss, R.; Weigel, R. Linearizing the output characteristic of GMR current sensors through hysteresis modeling. IEEE Trans. Ind. Electron. 2009, 57, 1728–1734. [Google Scholar] [CrossRef]
- Salach, J.; Hasse, L.; Szewczyk, R.; Smulko, J.; Bienkowski, A.; Frydrych, P.; Kolano-Burian, A. Low current transformer utilizing Co-based amorphous alloys. IEEE Trans. Magn. 2012, 48, 1493–1496. [Google Scholar] [CrossRef]
- Dong, S.; Li, J.F.; Viehland, D. Circumferentially magnetized and circumferentially polarized magnetostrictive/piezoelectric laminated rings. J. Appl. Phys. 2004, 96, 3382–3387. [Google Scholar] [CrossRef]
- Leung, C.M.; Or, S.W.; Zhang, S.; Ho, S.L. Ring-type electric current sensor based on ring-shaped magnetoelectric laminate of epoxy-bonded Tb0.3Dy0.7Fe1.92 short-fiber/NdFeB magnet magnetostrictive composite and Pb (Zr, Ti) O3 piezoelectric ceramic. J. Appl. Phys. 2010, 107, 09D918. [Google Scholar]
- Zhang, J.; Li, P.; Wen, Y.; He, W.; Yang, A.; Lu, C.; Qiu, J.; Wen, J.; Yang, J.; Zhu, Y.; et al. High-resolution current sensor utilizing nanocrystalline alloy and magnetoelectric laminate composite. Rev. Sci. Instrum. 2012, 83, 115001. [Google Scholar] [CrossRef]
- Zhang, J.; He, W.; Zhang, M.; Zhao, H.; Yang, Q.; Guo, S.; Wang, X.; Zheng, X.; Cao, L. Broadband high-sensitivity current-sensing device utilizing nonlinear magnetoelectric medium and nanocrystalline flux concentrator. Rev. Sci. Instrum. 2015, 86, 095005. [Google Scholar] [CrossRef]
- Leland, E.S.; Wright, P.K.; White, R.M. Design of a MEMS passive, proximity-based AC electric current sensor for residential and commercial loads. Proc. PowerMEMS 2007, 77–80. [Google Scholar]
- Leland, E.S.; Wright, P.K.; White, R.M. A MEMS AC current sensor for residential and commercial electricity end-use monitoring. J. Micromech. Microeng. 2009, 19, 094018. [Google Scholar] [CrossRef]
- Lu, C.; Li, P.; Wen, Y.; Yang, A.; Yang, C.; Wang, D.; He, W.; Zhang, J. Zero-biased magnetoelectric composite Fe73.5Cu1Nb3Si13.5B9/Ni/Pb (Zr1−x, Tix)O3 for current sensing. J. Alloys Compd. 2014, 589, 498–501. [Google Scholar]
- Shen, D.; Park, J.H.; Noh, J.H.; Choe, S.Y.; Kim, S.H.; Wikle, H.C., III; Kim, D.J. Micromachined PZT cantilever based on SOI structure for low frequency vibration energy harvesting. Sens. Actuators A 2009, 154, 103–108. [Google Scholar]
- He, W.; Li, P.; Wen, Y.; Zhang, J.; Yang, A.; Lu, C. Note: A high-sensitivity current sensor based on piezoelectric ceramic Pb (Zr, Ti) O3 and ferromagnetic materials. Rev. Sci. Instrum. 2014, 85, 026110. [Google Scholar] [CrossRef]
- He, W.; Lu, Y.; Qu, C.; Peng, J. A non-invasive electric current sensor employing a modified shear-mode cymbal transducer. Sens. Actuators A 2016, 241, 120–123. [Google Scholar] [CrossRef]
- Ren, B.; Or, S.W.; Zhang, Y.; Zhang, Q.; Li, X.; Jiao, J.; Wang, W.; Liu, D.; Zhao, X.; Luo, H. Piezoelectric energy harvesting using shear mode 0.71Pb (Mg1/3Nb2/3)O3–0.29 PbTiO3 single crystal cantilever. Appl. Phys. Lett. 2010, 96, 083502. [Google Scholar]
- Carrera, E.; Valvano, S.; Kulikov, G.M. Multilayered plate elements with node-dependent kinematics for electro-mechanical problems. Int. J. Smart Nano Mater. 2018, 9, 279–317. [Google Scholar] [CrossRef]
- Carrera, E.; Valvano, S.; Kulikov, G.M. Electro-mechanical analysis of composite and sandwich multilayered structures by shell elements with node-dependent kinematics. Int. J. Smart Nano Mater. 2018, 9, 1–33. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, X.; Li, L.; Yu, Y.; Liu, X.; Chen, J. Evaluation of shear piezoelectric coefficient d15 of piezoelectric ceramics by using piezoelectric cantilever beam in dynamic resonance. Ferroelectrics 2017, 520, 202–211. [Google Scholar] [CrossRef]
- Gao, X.; Xin, X.; Wu, J.; Chu, Z.; Dong, S. A multilayered-cylindrical piezoelectric shear actuator operating in shear (d15) mode. Appl. Phys. Lett. 2018, 112, 152902. [Google Scholar] [CrossRef]
- Qin, L.; Jia, J.; Choi, M.; Uchino, K. Improvement of electromechanical coupling coefficient in shear-mode of piezoelectric ceramics. Ceram. Int. 2019, 45, 1496–1502. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, C.; Dong, S. Magnetoelectric effect in magnetostrictive/piezoelectric laminated composite operating in shear-shear mode. J. Appl. Phys. 2014, 116, 074104. [Google Scholar] [CrossRef]
- Zhai, J.; Xing, Z.; Dong, S.; Li, J.; Viehland, D. Magnetoelectric laminate composites: an overview. J. Am. Ceram. Soc. 2008, 91, 351–358. [Google Scholar] [CrossRef]
- Yao, Y.P.; Hou, Y.; Dong, S.N.; Li, X.G. Giant magnetodielectric effect in Terfenol-D/PZT magnetoelectric laminate composite. J. Appl. Phys. 2011, 110, 014508. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, G.; Xie, Y.; Lv, H.; Huang, C.; Chen, Y.; Tong, Z.; Shi, J.; Xiong, R. Magnetoelectric behaviors in BaTiO3/CoFe2O4/BaTiO3 laminated ceramic composites prepared by spark plasma sintering. Ceram. Int. 2018, 44, 9649–9655. [Google Scholar] [CrossRef]
- Xu, Y.; Jiang, Z.S.; Wang, Q.; Xu, X.; Sun, D.S.; Zhou, J.; Yang, G. Three dimensional magnetostatic field calculation using equivalent magnetic charge method. IEEE Trans. Magn. 1991, 27, 5010–5012. [Google Scholar] [CrossRef]
- Ikeda, T. Fundamentals of Piezoelectricity; Oxford University Press: Oxford, UK, 1990; pp. 38–39. [Google Scholar]
- Zeng, M.; Or, S.W.; Chan, H.L.W. Giant resonance frequency tunable magnetoelectric effect in a device of Pb(Zr0.52Ti0.48)O3 drum transducer, NdFeB magnet, and Fe-core solenoid. Appl. Phys. Lett. 2010, 96, 203502. [Google Scholar]
- Zeng, M.; Or, S.W.; Chan, H.L.W. Giant magnetoelectric effect in magnet-cymbal-solenoid current-to-voltage conversion device. J. Appl. Phys. 2010, 107, 074509. [Google Scholar] [CrossRef] [Green Version]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Yang, A. A Shear-Mode Piezoelectric Heterostructure for Electric Current Sensing in Electric Power Grids. Micromachines 2019, 10, 421. https://doi.org/10.3390/mi10060421
He W, Yang A. A Shear-Mode Piezoelectric Heterostructure for Electric Current Sensing in Electric Power Grids. Micromachines. 2019; 10(6):421. https://doi.org/10.3390/mi10060421
Chicago/Turabian StyleHe, Wei, and Aichao Yang. 2019. "A Shear-Mode Piezoelectric Heterostructure for Electric Current Sensing in Electric Power Grids" Micromachines 10, no. 6: 421. https://doi.org/10.3390/mi10060421
APA StyleHe, W., & Yang, A. (2019). A Shear-Mode Piezoelectric Heterostructure for Electric Current Sensing in Electric Power Grids. Micromachines, 10(6), 421. https://doi.org/10.3390/mi10060421




