Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules
Abstract
:1. Introduction
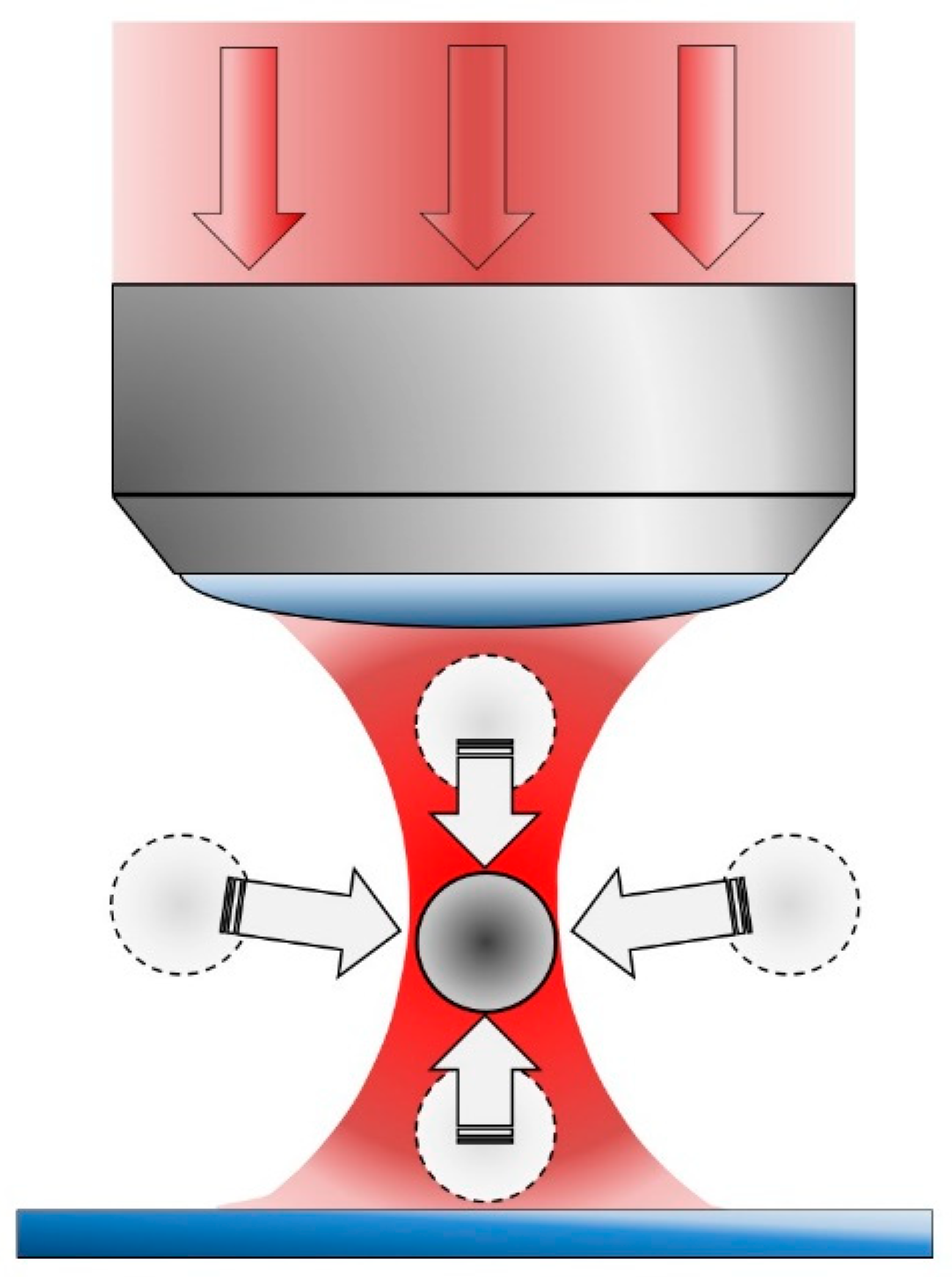
2. Photodamage in Optical Tweezers
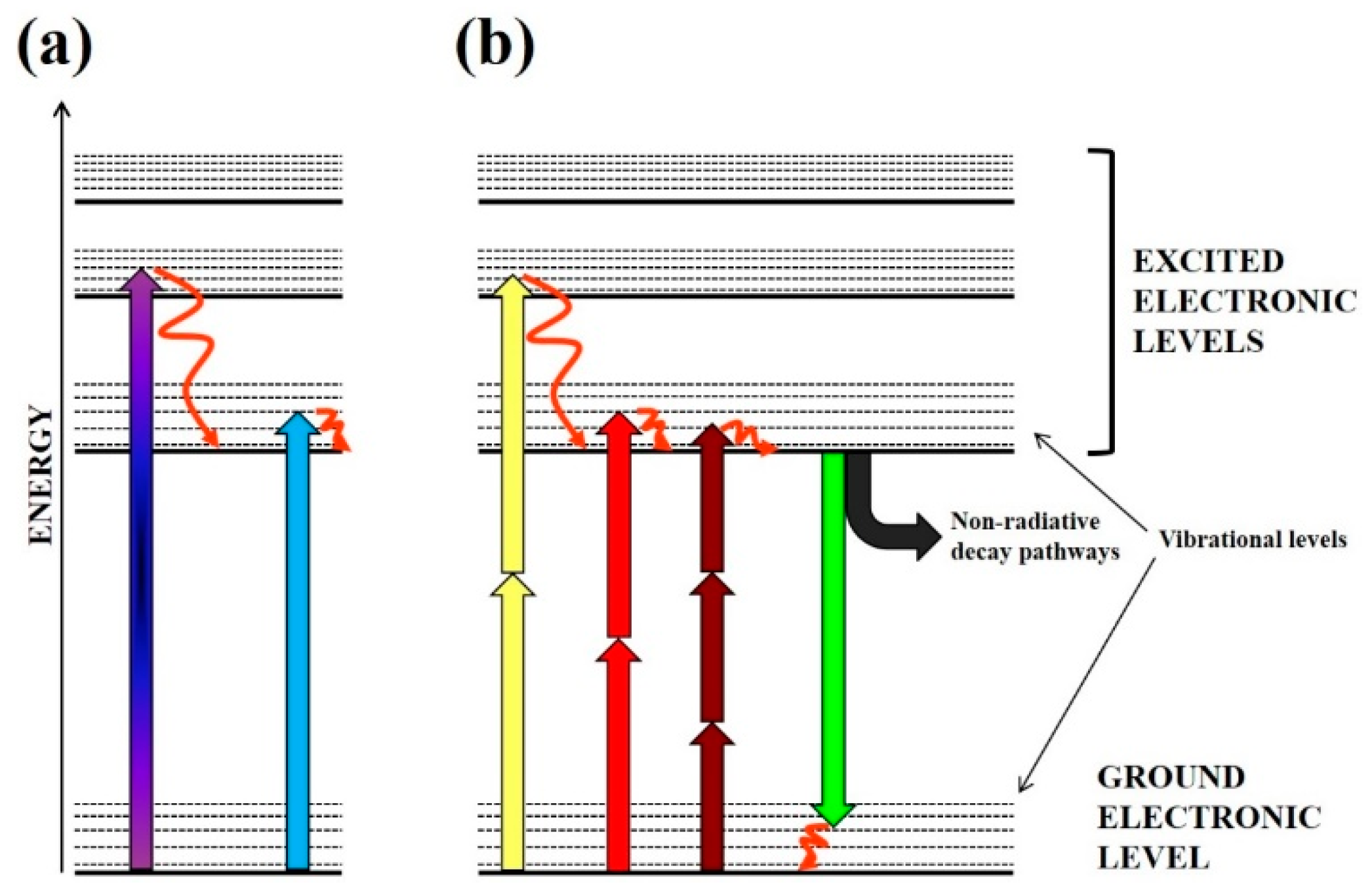
2.1. Linear Excitation Photodamage
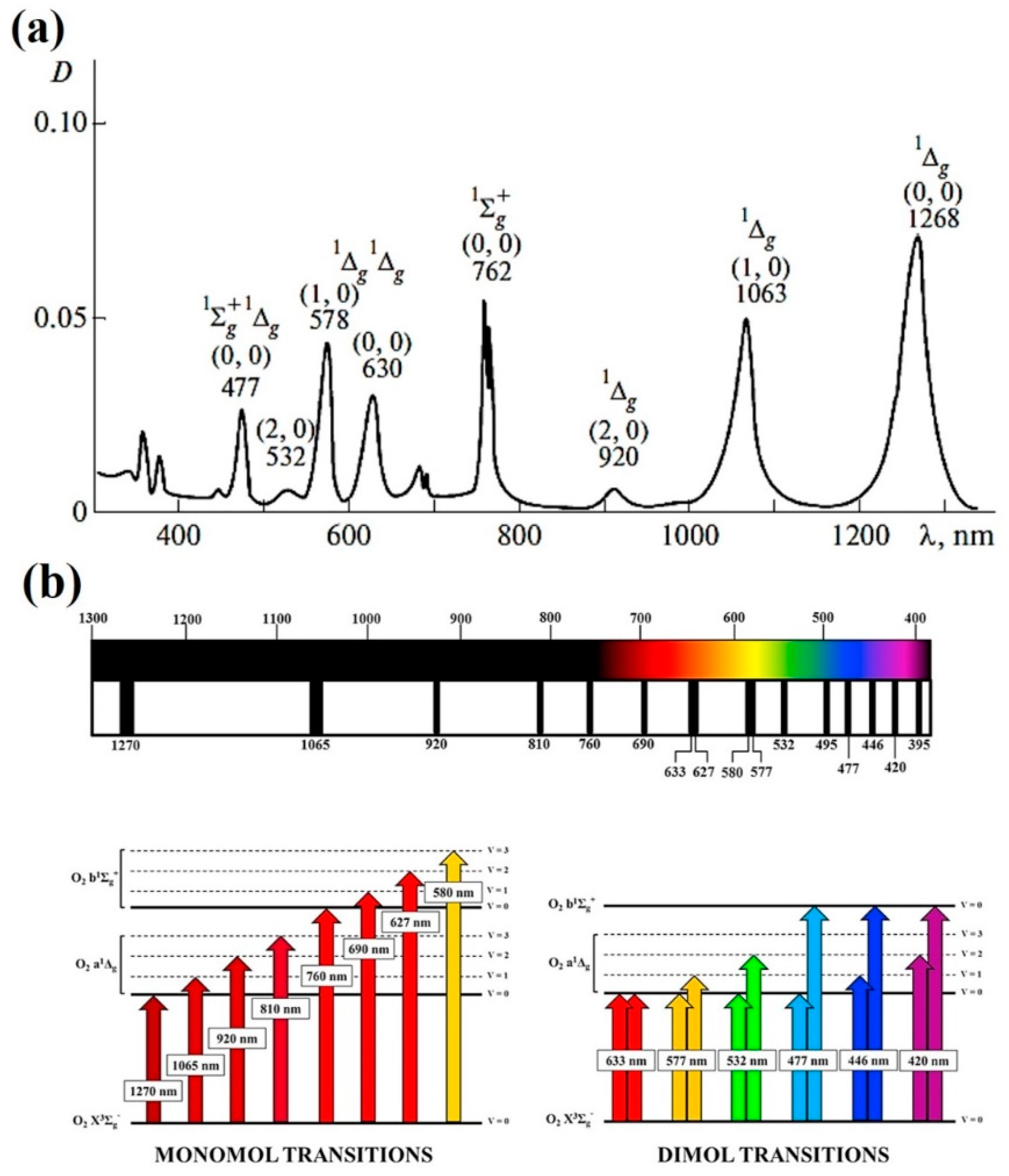
2.2. Direct 1O2 Light Excitation
2.3. Non-Linear Excitation Photodamage
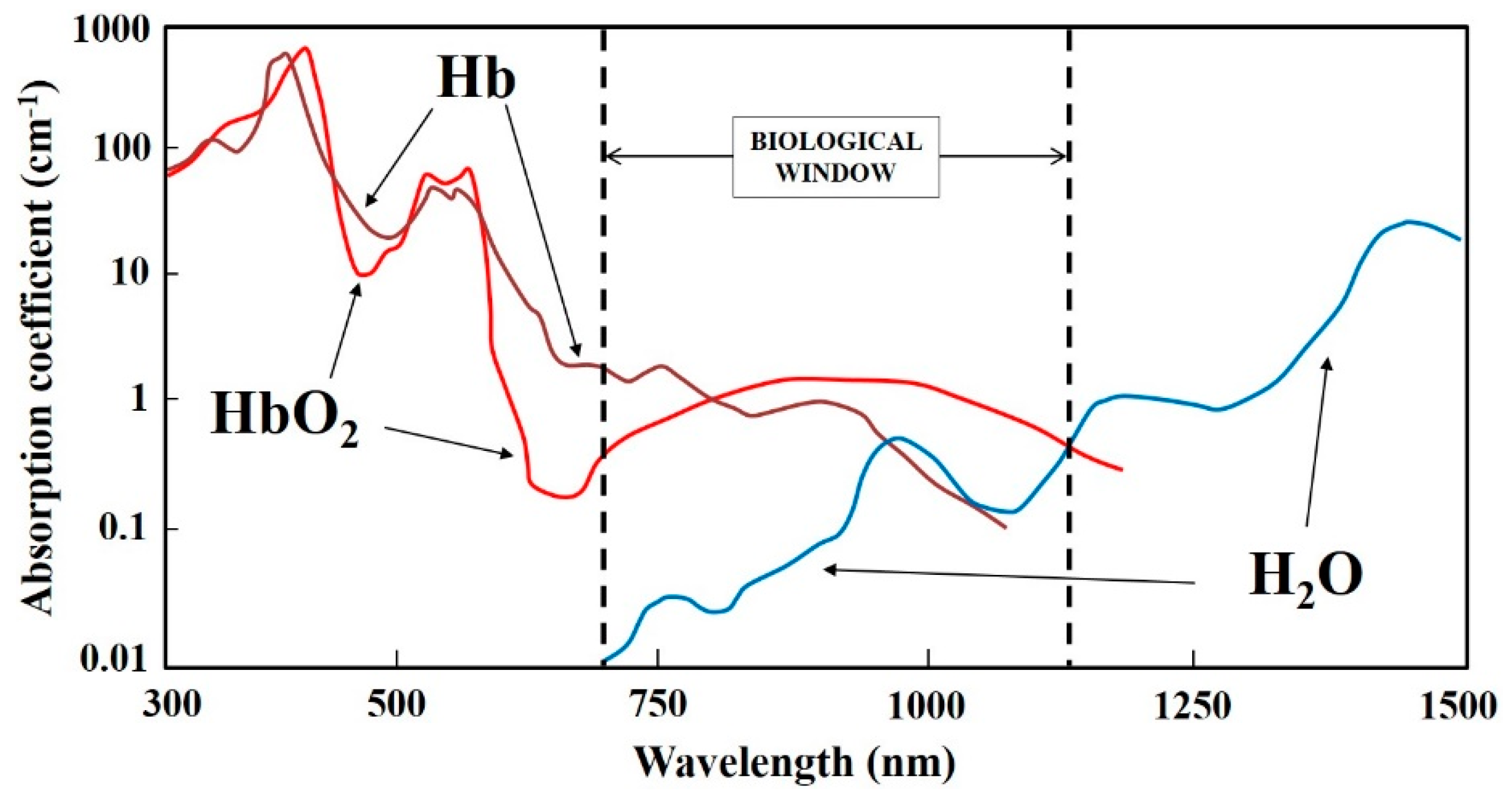
3. Thermal Damage and Stress in Optical Tweezers
4. Mechanical Damage in Optical Tweezers
5. Strategies to Avoid Damage in Optical Tweezers
6. Outlook and Perspectives
Funding
Conflicts of Interest
References
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156–159. [Google Scholar] [CrossRef]
- Dholakia, K.; Reece, P.; Gu, M. Optical micromanipulation. Chem. Soc. Rev. 2008, 37, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Bowman, R.W.; Padgett, M.J. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef] [PubMed]
- Dhakal, K.R.; Lakshminarayanan, V. Chapter one—Optical tweezers: Fundamentals and some biophysical applications. Prog. Opt. 2018, 63, 1–31. [Google Scholar]
- Ashkin, A.; Dziedzic, J.M. Optical trapping and manipulation of viruses and bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M. Internal cell manipulation using infrared laser traps. Proc. Natl. Acad. Sci. USA 1989, 86, 7914–7918. [Google Scholar] [CrossRef]
- Ashkin, A. The study of cells by optical trapping and manipulation of living cells using infrared laser beams. ASGSB Bull. 1991, 4, 133–146. [Google Scholar]
- Svoboda, K.; Block, S.M. Biological applications of optical forces. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 247–285. [Google Scholar] [CrossRef]
- Hormeño, S.; Arias-Gonzalez, J.R. Exploring mechanochemical processes in the cell with optical tweezers. Biol. Cell 2006, 98, 679–695. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, K.K. Optical tweezers for single cells. J. R. Soc. Interface 2008, 5, 671–690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greulich, K.O. Manipulation of cells with laser microbeam scissors and optical tweezers: A review. Rep. Prog. Phys. 2017, 80, 026601. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Shakoor, A.; Shen, Y.; Mills, J.K.; Sun, D. Out-of-plane rotation control of biological cells with a robot-tweezers manipulation system for orientation-based cell surgery. IEEE Tran. Biomed. Eng. 2019, 66, 199–207. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, Y. Optical Fiber Probe-based Manipulation of Cells. In Fiber Optics; IntechOpen: London, UK, 2018; pp. 1–14. [Google Scholar] [CrossRef]
- Keloth, A.; Anderson, O.; Risbridger, D.; Paterson, L. Single cell isolation using optical tweezers. Micromachines 2018, 9, 434. [Google Scholar] [CrossRef]
- Mirsaidov, U.; Scrimgeour, J.; Timp, W.; Beck, K.; Mir, M.; Matsudaira, P.; Timp, G. Live cell lithography: Using optical tweezers to create synthetic tissue. Lab Chip 2008, 8, 2174–2181. [Google Scholar] [CrossRef] [PubMed]
- Bezryadina, A.S.; Preece, D.C.; Chen, J.C.; Chen, Z. Optical disassembly of cellular clusters by tunable “tug-of-war” tweezers. Light Sci. Appl. 2016, 5, e16158. [Google Scholar] [CrossRef]
- Jing, P.; Liu, Y.; Keeler, E.G.; Cruz, N.M.; Freedman, B.S.; Lin, L.Y. Optical tweezers system for live stem cell organization at the single-cell level. Biomed. Opt. Express 2018, 9, 771–779. [Google Scholar] [CrossRef]
- Zhong, M.C.; Wei, X.B.; Zhou, J.H.; Wang, Z.Q.; Li, Y.M. Trapping red blood cells in living animals using optical tweezers. Nat. Commun. 2013, 4, 1768. [Google Scholar] [CrossRef] [Green Version]
- Johansen, P.L.; Fenaroli, F.; Evensen, L.; Griffiths, G.; Koster, G. Optical micromanipulation of nanoparticles and cells inside living zebrafish. Nat. Commun. 2016, 7, 10974. [Google Scholar] [CrossRef]
- Banerjee, A.G.; Chowdhury, S.; Losert, W.; Gupta, S.K. Survey on indirect optical manipulation of cells, nucleic acids, and motor proteins. J. Biomed. Opt. 2011, 16, 051302. [Google Scholar] [CrossRef]
- Norregaard, K.; Jauffred, L.; Berg-Sørensen, K.; Oddershede, L.B. Optical manipulation of single molecules in the living cell. Phys. Chem. Chem. Phys. 2014, 16, 12614–12624. [Google Scholar] [CrossRef] [PubMed]
- Heller, I.; Hoekstra, T.P.; King, G.A.; Peterman, E.J.G.; Wuite, G.J.L. Optical tweezers analysis of dna-protein complexes. Chem. Rev. 2014, 114, 3087–3119. [Google Scholar] [CrossRef] [PubMed]
- Snook, R.D.; Harvey, T.J.; Correia Faria, E.; Gardner, P. Raman tweezers and their application to the study of singly trapped eukaryotic cells. Integr. Biol. 2009, 1, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Redding, B.; Schwab, M.J.; Pan, Y. Raman spectroscopy of optically trapped single biological micro-particles. Sensors 2015, 15, 19021–19046. [Google Scholar] [CrossRef] [PubMed]
- Al Balushi, A.A.; Kotnala, A.; Wheaton, S.; Gelfand, R.M.; Rajashekara, T.; Gordon, R. Label-free free-solution nanoaperture optical tweezers for single molecule protein studies. Analyst 2015, 140, 4760–4778. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Ding, W.; Nieto-Vesperinas, M.; Ding, X.; Rahman, M.; Zhang, T.; Lim, C.; Qiu, C.W. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light Sci. Appl. 2017, 6, e17039. [Google Scholar] [CrossRef] [PubMed]
- Bradac, C. Nanoscale optical trapping: A review. Adv. Opt. Mater. 2018, 6, 1800005. [Google Scholar] [CrossRef]
- Jing, P.; Wu, J.; Liu, G.W.; Keeler, E.G.; Pun, S.H.; Lin, L.Y. Photonic crystal optical tweezers with high efficiency for live biological samples and viability characterization. Sci. Rep. 2016, 6, 19924. [Google Scholar] [CrossRef] [PubMed]
- Bhebhe, N.; Williams, P.A.C.; Rosales-Guzmán, C.; Rodriguez-Fajardo, V.; Forbes, A. A vector holographic optical trap. Sci. Rep. 2018, 8, 17387. [Google Scholar] [CrossRef]
- Choudhary, D.; Mossa, A.; Jadhav, M.; Cecconi, C. Bio-molecular applications of recent developments in optical tweezers. Biomolecules 2019, 9, 23. [Google Scholar] [CrossRef]
- Amy, R.L.; Storb, R. Selective Mitochondrial damage by a ruby laser microbeam: An electron microscopic study. Science 1965, 150, 756–758. [Google Scholar] [CrossRef] [PubMed]
- Berns, M.W.; Cheng, W.K.; Floyd, A.D.; Ohnuki, Y. Chromosome lesions produced with an argon laser microbeam without dye sensitization. Science 1971, 171, 903–905. [Google Scholar] [CrossRef] [PubMed]
- Berns, M.W. Directed chromosome loss by laser microirradiation. Science 1974, 186, 700–705. [Google Scholar] [CrossRef] [PubMed]
- Berns, M.W. A possible two-photon effect in vitro using a focused laser beam. Biophys. J. 1976, 16, 973–977. [Google Scholar] [CrossRef] [Green Version]
- Turro, N.J.; Ramamurthy, V.; Scaiano, J.C. Modern Molecular Photochemistry of Organic Molecules, 1st ed.; University Science Books: Sausalito, CA, USA, 2010. [Google Scholar]
- Stockert, J.C.; Blázquez-Castro, A. Fluorescence Microscopy in Life Sciences, 1st ed.; Bentham Science Publishers: Sharjah, UAE, 2017. [Google Scholar]
- Salet, C.; Moreno, G.; Vinzens, F. A study of beating frequency of a single myocardial cell: II. Ultraviolet micro-irradiation of the nucleus and of the cytoplasm. Exp. Cell Res. 1976, 100, 365–373. [Google Scholar] [CrossRef]
- Moreno, G. Partial nuclear and cytoplasmic (mitochondrial) irradiation of single living cells using ultraviolet and visible light. In Technical Advances in Biomedical Physics; NATO ASI Series (Series E: Applied Sciences); Dendy, P.P., Ernst, D.W., Şengün, A., Eds.; Springer: Dordrecht, The Netherlands, 1984; Volume 77, pp. 139–145. [Google Scholar]
- Splinter, J.; Jakob, B.; Lamg, M.; Yano, K.; Engelhardt, J.; Hell, S.W.; Chen, D.J.; Durante, M.; Taucher-Scholz, G. Biological dose estimation of UVA laser microirradiation utilizing charged particle-induced protein foci. Mutagenesis 2010, 25, 289–297. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De With, A.; Greulich, K.O. Wavelength dependence of laser-induced DNA damage in lymphocytes observed by single-cell gel electrophoresis. J. Photochem. Photobiol. B Biol. 1995, 30, 71–76. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Rapp, A.; Monajembashi, S.; Gupta, P.K.; Greulich, K.O. Comet assay measurements of dna damage in cells by laser microbeams and trapping with wavelengths spanning a range of 308 nm to 1064 nm. Rad. Res. 2002, 157, 378–385. [Google Scholar] [CrossRef]
- Walter, J.; Cremer, T.; Miyagawa, K.; Tashiro, S. A new system for laser-UVA-microirradiation of living cells. J. Microsc. 2003, 209, 71–75. [Google Scholar] [CrossRef]
- Kong, X.; Mohanty, S.K.; Stephens, J.; Heale, J.T.; Gomez-Godinez, V.; Shi, L.Z.; Kim, J.S.; Yokomori, K.; Berns, M.W. Comparative analysis of different laser systems to study cellular responses to DNA damage in mammalian cells. Nucleic Acids Res. 2009, 37, e68. [Google Scholar] [CrossRef]
- Grigaravičius, P.; Greulich, K.O.; Monajembashi, S. Laser Microbeams and optical tweezers in ageing research. Chem. Phys. Chem. 2009, 10, 79–85. [Google Scholar] [CrossRef]
- Drexler, G.A.; Ruiz-Gómez, M.J. Microirradiation techniques in radiobiological research. J. Biosci. 2015, 40, 629–643. [Google Scholar] [CrossRef]
- Gassman, N.R.; Wilson, S.H. Micro-irradiation tools to visualize base excision repair and single-strand break repair. DNA Repair 2015, 31, 52–63. [Google Scholar] [CrossRef] [Green Version]
- Gibhardt, C.S.; Roth, B.; Schroeder, I.; Fuck, S.; Becker, P.; Jakob, B.; Fournier, C.; Moroni, A.; Thiel, G. X-ray irradiation activates K+ channels via H2O2 signaling. Sci. Rep. 2015, 5, 13861. [Google Scholar] [CrossRef]
- Muster, B.; Rapp, A.; Cardoso, M.C. Systematic analysis of DNA damage induction and DNA repair pathway activation by continuous wave visible light laser micro-irradiation. AIMS Gen. 2017, 4, 47–68. [Google Scholar] [CrossRef]
- Wang, Y.; Lan, B.; He, H.; Hu, M.; Cao, Y.; Wang, C. Laser stimulation can activate autophagy in HeLa cells. Appl. Phys. Lett. 2014, 105, 173703. [Google Scholar] [CrossRef]
- Kobayashi, H.; Ogawa, M.; Alford, R.; Choyke, P.L.; Urano, Y. New Strategies for fluorescent probe design in medical diagnostic imaging. Chem. Rev. 2010, 110, 2620–2640. [Google Scholar] [CrossRef]
- Dasgupta, R.; Ahlawat, S.; Verma, R.S.; Uppal, A.; Gupta, P.K. Hemoglobin degradation in human erythrocytes with long-duration near-infrared laser exposure in Raman optical tweezers. J. Biomed. Opt. 2010, 15, 055009. [Google Scholar] [CrossRef]
- Schweitzer, C.; Schmidt, R. Physical mechanisms of generation and deactivation of singlet oxygen. Chem. Rev. 2003, 103, 1685–1757. [Google Scholar] [CrossRef]
- Cooper, P.D.; Johnson, R.E.; Quickenden, T.I. A review of possible optical absorption features of oxygen molecules in the icy surfaces of outer solar system bodies. Planet. Space Sci. 2003, 51, 183–192. [Google Scholar] [CrossRef]
- Bagrov, I.V.; Belousova, I.M.; Kiselev, V.M.; Kislyakov, I.M.; Sosnov, E.N. Observation of the luminescence of singlet oxygen at λ = 1270 nm under LED irradiation of CCl4. Opt. Spectrosc. 2012, 113, 57–62. [Google Scholar] [CrossRef]
- Jockusch, S.; Turro, N.J.; Thompson, E.K.; Gouterman, M.; Callis, J.B.; Khalil, G.E. Singlet molecular oxygen by direct excitation. Photochem. Photobiol. Sci. 2008, 7, 235–239. [Google Scholar] [CrossRef]
- Thalman, R.; Volkamer, R. Temperature dependent absorption cross-sections of O2-O2 collision pairs between 340 and 630 nm and at atmospherically relevant pressure. Phys. Chem. Chem. Phys. 2013, 15, 15371–15381. [Google Scholar] [CrossRef]
- Krasnovsky, A.A., Jr.; Kozlov, A.S.; Roumbal, Y.V. Photochemical investigation of the IR absorption bands of molecular oxygen in organic and aqueous environment. Photochem. Photobiol. Sci. 2012, 11, 988–997. [Google Scholar] [CrossRef]
- Krasnovsky, A.A., Jr.; Kozlov, A.S. New approach to measurement of ir absorption spectra of dissolved oxygen molecules based on photochemical activity of oxygen upon direct laser excitation. Biophysics 2014, 59, 199–205. [Google Scholar] [CrossRef]
- Krasnovsky, A.A., Jr.; Kozlov, A.S. Photonics of dissolved oxygen molecules. Comparison of the rates of direct and photosensitized excitation of oxygen and reevaluation of the oxygen absorption coefficients. J. Photochem. Photobiol. A Chem. 2016, 329, 167–174. [Google Scholar] [CrossRef]
- Bregnhøj, M.; Krægpøth, M.V.; Sørensen, R.J.; Westberg, M.; Ogilby, P.R. Solvent and heavy-atom effects on the O2(X3Σg−) → O2(b1Σg+) absorption transition. J. Phys. Chem. A 2016, 120, 8285–8296. [Google Scholar] [CrossRef]
- Blázquez-Castro, A. Direct 1O2 optical excitation: A tool for redox biology. Redox Biol. 2017, 13, 39–59. [Google Scholar] [CrossRef]
- Pryor, W.A.; Houk, K.N.; Foote, C.S.; Fukuto, J.M.; Ignarro, L.J.; Squadrito, G.L.; Davies, K.J.A. Free radical biology and medicine: It’s a gas, man! Am. J. Physiol. Regul. Integr. Comp. Physiol. 2006, 291, R491–R511. [Google Scholar] [CrossRef]
- Pibiri, I.; Buscemi, S.; Piccionello, A.P.; Pace, A. photochemically produced singlet oxygen: Applications and perspectives. Chem. Photochem. 2018, 2, 535–547. [Google Scholar] [CrossRef]
- Di Mascio, P.; Martinez, G.R.; Miyamoto, S.; Ronsein, G.E.; Medeiros, M.H.G.; Cadet, J. Singlet molecular oxygen reactions with nucleic acids, lipids, and proteins. Chem. Rev. 2019, 119, 2043–2086. [Google Scholar] [CrossRef]
- Blázquez-Castro, A.; Westberg, M.; Bregnhøj, M.; Breitenbach, T.; Mogensen, D.J.; Etzerodt, M.; Ogilby, P.R. Light-Initiated Oxidative Stress. In Oxidative Stress: Eustress and Distress. Role in Health and Disease Processes, 1st ed.; Sies, H., Ed.; Elsevier: Cambridge, MA, USA, 2019; Chapter 19. (in press) [Google Scholar]
- Anquez, F.; Yazidi-Belkoura, I.E.; Randoux, S.; Suret, P.; Courtade, E. Cancerous cell death from sensitizer free photoactivation of singlet oxygen. Photochem. Photobiol. 2012, 88, 167–174. [Google Scholar] [CrossRef]
- Sokolovski, S.G.; Zolotovskaya, S.A.; Goltsov, A.; Pourreyron, C.; South, A.P.; Rafailov, E.U. Infrared laser pulse triggers increased singlet oxygen production in tumour cells. Sci. Rep. 2013, 3, 3484. [Google Scholar] [CrossRef]
- Liang, H.; Wright, W.H.; He, W.; Berns, M.W. Micromanipulation of mitotic chromosomes in PTK2 cells using laser-induced optical forces (“Optical Tweezers”). Exp. Cell Res. 1991, 197, 21–35. [Google Scholar] [CrossRef]
- Liu, Y.; Sonek, G.J.; Berns, M.W.; Tromberg, B.J. Physiological monitoring of optically trapped cells: Assessing the effects of confinement by 1064-nm laser tweezers using microfluorimetry. Biophys. J. 1996, 71, 2158–2167. [Google Scholar] [CrossRef]
- Liang, H.; Vu, K.T.; Krishnan, P.; Trang, T.C.; Shin, D.; Kimel, S.; Berns, M.W. Wavelength dependence of cell cloning efficiency after optical trapping. Biophys. J. 1996, 70, 1529–1533. [Google Scholar] [CrossRef] [Green Version]
- Neuman, K.C.; Chadd, E.H.; Liou, G.F.; Bergman, K.; Block, S.M. Characterization of photodamage to Escherichia coli in optical traps. Biophys. J. 1999, 77, 2856–2863. [Google Scholar] [CrossRef]
- Pilát, Z.; Ježek, J.; Šerý, M.; Trtílek, M.; Nedbal, L.; Zemánek, P. Optical trapping of microalgae at 735–1064 nm: photodamage assessment. J. Photochem. Photobiol. B Biol. 2013, 121, 27–31. [Google Scholar] [CrossRef]
- Schneckenburger, H.; Hendinger, A.; Sailer, R.; Gschwend, M.H.; Strauss, W.S.L.; Bauer, M.; Schütze, K. Cell viability in optical tweezers: High power red laser diode versus Nd:YAG laser. J. Biomed. Opt. 2000, 5, 40–44. [Google Scholar] [CrossRef]
- Ayano, S.; Wakamoto, Y.; Yamashita, S.; Yasuda, K. Quantitative measurement of damage by 1064-nm wavelength optical trapping of Escherichia coli cells using on-chip single cell cultivation system. Biochem. Biophys. Res. Commun. 2006, 350, 678–684. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Sharma, M.; Gupta, P.K. Generation of ROS in cells on exposure to CW and pulsed near-infrared laser tweezers. Photochem. Photobiol. Sci. 2006, 5, 134–139. [Google Scholar] [CrossRef]
- Rasmussen, M.B.; Oddershede, L.B.; Siegumfeldt, H. optical tweezers cause physiological damage to escherichia coli and listeria bacteria. Appl. Environm. Microbiol. 2008, 74, 2441–2446. [Google Scholar] [CrossRef]
- Aabo, T.; Perch-Nielsen, I.R.; Dam, J.S.; Palima, D.Z.; Siegumfeldt, H.; Glückstad, J.; Arneborg, N. Inhibition of yeast growth during long term exposure to laser light around 1064 nm. Proc. SPIE 2009, 7227, 722706. [Google Scholar] [CrossRef]
- Landry, M.P.; McCall, P.M.; Qi, Z.; Chemla, Y.R. Characterization of photoactivated singlet oxygen damage in single-molecule optical trap experiments. Biophys. J. 2009, 97, 2128–2136. [Google Scholar] [CrossRef]
- Aabo, T.; Perch-Nielsen, I.R.; Dam, J.S.; Palima, D.Z.; Siegumfeldt, H.; Glückstad, J.; Arneborg, N. Effect of long- and short-term exposure to laser light at 1070 nm on growth of Saccharomyces cerevisiae. J. Biomed. Opt. 2010, 15, 041505. [Google Scholar]
- Barroso Peña, A.; Kemper, B.; Woerdemann, M.; Vollmer, A.; Ketelhut, S.; von Bally, G.; Denz, C. Optical tweezers induced photodamage in living cells quantified with digital holographic phase microscopy. Proc. SPIE 2012, 8427, 84270A. [Google Scholar] [CrossRef]
- Ahlawat, S.; Kumar, N.; Dasgupta, R.; Verma, R.S.; Uppal, A.; Gupta, P.K. Raman spectroscopic investigations on optical trap induced deoxygenation of red blood cells. Appl. Phys. Lett. 2013, 103, 183704. [Google Scholar] [CrossRef]
- De Oliveira, M.A.S.; Moura, D.S.; Fontes, A.; de Araujo, R.E. Damage induced in red blood cells by infrared optical trapping: An evaluation based on elasticity measurements. J. Biomed. Opt. 2016, 21, 075012. [Google Scholar] [CrossRef]
- Chow, K.W.; Preece, D.; Berns, M.W. Effect of red light on optically trapped spermatozoa. Biomed. Opt. Express 2017, 8, 4200–4205. [Google Scholar] [CrossRef] [Green Version]
- Pilát, Z.; Jonáš, A.; Ježek, J.; Zmánek, P. Effects of infrared optical trapping on saccharomyces cerevisiae in a microfluidic system. Sensors 2017, 17, 2640. [Google Scholar] [CrossRef]
- Vorobjev, I.A.; Liang, H.; Wright, W.H.; Berns, M.W. Optical trapping for chromosome manipulation: A wavelength dependence of induced chromosome bridges. Biophys. J. 1993, 64, 533–538. [Google Scholar] [CrossRef]
- Leitz, G.; Fällman, E.; Tuck, S.; Axner, O. Stress response in caenorhabditis elegans caused by optical tweezers: Wavelength, power, and time dependence. Biophys. J. 2002, 82, 2224–2231. [Google Scholar] [CrossRef]
- Bregnhøj, M.; Blázquez-Castro, A.; Westberg, M.; Breitenbach, T.; Ogilby, P.R. Direct 765 nm optical excitation of molecular oxygen in solution and in single mammalian cells. J. Phys. Chem. B 2015, 119, 5422–5429. [Google Scholar] [CrossRef]
- König, K.; Liang, H.; Berns, M.W.; Tromberg, B.J. Cell damage by near-IR microbeams. Nature 1995, 377, 20–21. [Google Scholar] [CrossRef]
- König, K.; Liang, H.; Berns, M.W.; Tromberg, B.J. Cell damage in near-infrared multimode optical traps as a result of multiphoton absorption. Opt. Lett. 1996, 21, 1090–1092. [Google Scholar] [Green Version]
- Liang, H.; Vu, K.T.; Trang, T.C.; Shin, D.; Lee, Y.E.; Nguyen, D.C.; Tromberg, B.; Berns, M.W. Giant cell formation in cells exposed to 740 nm and 760 nm optical traps. Lasers Surg. Med. 1997, 21, 159–165. [Google Scholar] [CrossRef]
- Mirsaidov, U.; Timp, W.; Timp, K.; Mir, M.; Matsudaira, P.; Timp, G. Optimal optical trap for bacterial viability. Phys. Rev. E 2008, 78, 021910. [Google Scholar] [CrossRef] [Green Version]
- Zakharov, S.D.; Thanh, N.C. Combined absorption of light in the process of photoactivation of biosystems. J. Russ. Laser Res. 2008, 29, 558–563. [Google Scholar] [CrossRef]
- Zakharov, S.; Thanh, N.C. Photogenerated singlet oxygen damages cells in optical traps. arXiv 2009, arXiv:0911.4651. [Google Scholar]
- Liu, Y.; Sonek, G.J.; Berns, M.W.; Konig, K.; Tromberg, B.J. Two-photon fluorescence excitation in continuous-wave infrared optical tweezers. Opt. Lett. 1995, 20, 2246–2248. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Sonek, G.J.; Wei, X.B.; Sun, C.; Berns, M.W.; Tromberg, B.J. Cell viability and DNA denaturation measurements by two-photon fluorescence excitation in CW Al: GaAs diode laser optical traps. J. Biomed. Opt. 1999, 4, 256–259. [Google Scholar] [CrossRef]
- König, K.; So, P.T.C.; Mantulin, W.W.; Gratton, E. Cellular response to near-infrared femtosecond laser pulses in two-photon microscopes. Opt. Lett. 1997, 22, 135–136. [Google Scholar] [CrossRef]
- Hopt, A.; Neher, E. Highly Nonlinear photodamage in two-photon fluorescence microscopy. Biophys. J. 2001, 80, 2029–2036. [Google Scholar] [CrossRef]
- Agate, B.; Brown, C.T.A.; Sibbett, W.; Dholakia, K. Femtosecond optical tweezers for in-situ control of two-photon fluorescence. Opt. Express 2004, 12, 3011–3017. [Google Scholar] [CrossRef]
- Vogel, A.; Venugopalan, V. Mechanisms of pulsed laser ablation of biological tissues. Chem. Rev. 2003, 103, 577–644. [Google Scholar] [CrossRef]
- Vogel, A.; Noack, J.; Hüttman, G.; Paltauf, G. Mechanisms of femtosecond laser nanosurgery of cells and tissues. Appl. Phys. B 2005, 81, 1015–1047. [Google Scholar] [CrossRef]
- Vogel, A.; Linz, N.; Freidank, S.; Paltauf, G. Femtosecond-laser-induced nanocavitation in water: Implications for optical breakdown threshold and cell surgery. Phys. Rev. Lett. 2008, 100, 038102. [Google Scholar] [CrossRef]
- Im, K.B.; Ju, S.B.; Han, S.; Park, H.; Kim, B.M.; Jin, D.; Kim, S.K. Trapping Efficiency of a femtosecond laser and damage thresholds for biological cells. J. Korean Phys. Soc. 2006, 48, 968–973. [Google Scholar]
- Ju, S.; Pyo, J.; Jang, J.; Lee, S.; Kim, B.M. Analysis of RBC damage using laser tweezers raman spectroscopy (LTRS) during femtosecond laser optical trapping. Proc. SPIE 2008, 6859, 68591R. [Google Scholar] [CrossRef]
- Ando, J.; Bautista, G.; Smith, N.; Fujita, K.; Daria, V.R. Optical trapping and surgery of living yeast cells using a single laser. Rev. Sci. Instrum. 2008, 79, 103705. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Cheng, D.K.; Sonek, G.J.; Berns, M.W.; Chapman, C.F.; Tromberg, B.J. Evidence for localized cell heating induced by infrared optical tweezers. Biophys. J. 1995, 68, 2137–2144. [Google Scholar] [CrossRef] [Green Version]
- Celliers, P.M.; Conia, J. Measurement of localized heating in the focus of an optical trap. Appl. Opt. 2000, 39, 3396–3407. [Google Scholar] [CrossRef]
- Peterman, E.J.G.; Gittes, F.; Schmidt, C.F. Laser-Induced Heating in Optical Traps. Biophys. J. 2003, 84, 1308–1316. [Google Scholar] [CrossRef] [Green Version]
- Català, F.; Marsà, F.; Montes-Usategui, M.; Farré, A.; Martín-Badosa, E. Influence of experimental parameters on the laser heating of an optical trap. Sci. Rep. 2017, 7, 16052. [Google Scholar] [CrossRef]
- Haro-González, P.; Ramsay, W.T.; Maestro, L.M.; del Rosal, B.; Santacruz-Gómez, K.; Iglesias-de la Cruz, M.C.; Sanz-Rodríguez, F.; Choo, J.Y.; Rodríguez-Sevilla, P.; Bettinelli, M.; et al. Quantum dot-based thermal spectroscopy and imaging of optically trapped microspheres and single cells. Small 2013, 9, 2162–2170. [Google Scholar]
- Wetzel, F.; Rönicke, S.; Müller, K.; Gyger, M.; Rose, D.; Zink, M.; Käs, J. Single cell viability and impact of heating by laser absorption. Eur. Biophys. J. 2011, 40, 1109–1114. [Google Scholar] [CrossRef]
- Csoboz, B.; Balogh, G.E.; Kusz, E.; Gombos, I.; Peter, M.; Crul, T.; Gungor, B.; Haracska, L.; Bogdanovics, G.; Torok, Z.; et al. Membrane fluidity matters: Hyperthermia from the aspects of lipids and membranes. Int. J. Hyperthermia 2013, 29, 491–499. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, A.; Waghmare, D.; Dasgupta, R.; Majumder, S.K. Red blood cell membrane damage by light-induced thermal gradient under optical trap. J. Biophot. 2018, 11, e201700222. [Google Scholar] [CrossRef]
- Krasnikov, I.; Seteikin, A.; Bernhardt, I. Thermal processes in red blood cells exposed to infrared laser tweezers (λ = 1064 nm). J. Biophot. 2011, 4, 206–212. [Google Scholar] [CrossRef]
- Garner, A.L.; Bogdan Neculaes, V.; Deminsky, M.; Dylov, D.V.; Joo, C.; Loghin, E.R.; Yazdanfar, S.; Conway, K.R. Plasma membrane temperature gradients and multiple cell permeabilization induced by low peak power density femtosecond lasers. Biochem. Biophys. Rep. 2016, 5, 168–174. [Google Scholar] [CrossRef]
- Song, J.; Garner, A.L.; Joshi, R.P. Effect of thermal gradients created by electromagnetic fields on cell-membrane electroporation probed by molecular-dynamics simulations. Phys. Rev. Appl. 2017, 7, 024003. [Google Scholar] [CrossRef]
- Duhr, S.; Braun, D. Why molecules move along a temperature gradient. Proc. Natl. Acad. Sci. USA 2006, 103, 19678–19682. [Google Scholar] [CrossRef] [Green Version]
- Reichl, M.; Herzog, M.; Götz, A.; Braun, D. Why charged molecules move across a temperature gradient: The role of electric fields. Phys. Rev. Lett. 2014, 112, 198101. [Google Scholar] [CrossRef]
- Jiang, H.R.; Wada, H.; Yoshinaga, N.; Sano, M. Manipulation of colloids by a nonequilibrium depletion force in a temperature gradient. Phys. Rev. Lett. 2009, 102, 208301. [Google Scholar] [CrossRef]
- Reichl, M.R.; Braun, D. Thermophoretic manipulation of molecules inside living cells. J. Am. Chem. Soc. 2014, 136, 15955–15960. [Google Scholar] [CrossRef]
- Majee, A.; Würger, A. Charging of heated colloidal particles using the electrolyte seebeck effect. Phys. Rev. Lett. 2012, 108, 118301. [Google Scholar] [CrossRef]
- Majee, A.; Würger, A. Thermocharge of a hot spot in an electrolyte solution. Soft Matter 2013, 9, 2145–2153. [Google Scholar] [CrossRef] [Green Version]
- Keil, L.M.R.; Möller, F.M.; Kieβ, M.; Kudella, P.W.; Mast, C.B. Proton gradients and pH oscillations emerge from heat flow at the microscale. Nat. Commun. 2017, 8, 1897. [Google Scholar] [CrossRef]
- Bresme, F.; Lervik, A.; Bedeaux, D.; Kjelstrup, S. Water polarization under thermal gradients. Phys. Rev. Lett. 2008, 101, 020602. [Google Scholar] [CrossRef]
- Muscatello, J.; Römer, F.; Sala, J.; Bresme, F. Water under temperature gradients: Polarization effects and microscopic mechanisms of heat transfer. Phys. Chem. Chem. Phys. 2011, 13, 19970–19978. [Google Scholar] [CrossRef]
- Iriarte-Carretero, I.; Gonzalez, M.A.; Armstrong, J.; Fernandez-Alonso, F.; Bresme, F. The rich phase behavior of the thermopolarization of water: From a reversal in the polarization, to enhancement near criticality conditions. Phys. Chem. Chem. Phys. 2016, 18, 19894–19901. [Google Scholar] [CrossRef]
- Il´ichev, N.N.; Kulevsky, L.A.; Pashinin, P.P. Photovoltaic effect in water induced by a 2.92 μm Cr3+:Yb3+:Ho3+:YSGG laser. Quant. Electron. 2005, 35, 959–961. [Google Scholar] [CrossRef]
- Andreev, S.N.; Kazantsev, S.Y.; Kononov, I.G.; Pashinin, P.P.; Firsov, K.N. Generation of an electric signal in the interaction of HF-laser radiation wit bottom surface of a water column. Quant. Electron. 2010, 40, 716–719. [Google Scholar] [CrossRef]
- Il´ichev, N.N.; Kulevskii, L.A.; Pashinin, P.P. Spatial separation and motion of electric charges arising due to the interaction of high-power IR laser radiation with water. Quant. Electron. 2013, 43, 47–54. [Google Scholar] [CrossRef]
- Antonova, O.Y.; Kochetkova, O.Y.; Shabarchina, L.I.; Zeeb, V.E. Local thermal activation of individual living cells and measurement of temperature gradients in microscopic volumes. Biophysics 2017, 62, 769–777. [Google Scholar] [CrossRef]
- Mondal, D.; Singhal, S.; Goswami, D. Femtosecond laser-induced photothermal effect for nanoscale viscometer and thermometer. In Selected Topics in Photonics; Pradhan, A., Krishnamurthy, P.K., Eds.; Springer Nature: Singapore, 2018; Character 2; pp. 13–17. [Google Scholar]
- Ng, K.S.; Zhou, Z.L.; Ngan, A.H.W. Frequency-dependent cell death by optical tweezers manipulation. J. Cell. Physiol. 2013, 228, 2037–2041. [Google Scholar] [CrossRef]
- Sun, X.X.; Zhou, Z.L.; Man, C.H.; Leung, A.Y.H.; Ngan, A.H.W. Cell-structure specific necrosis by optical-trap induced intracellular nuclear oscillation. J. Mech. Behav. Biomed. Mater. 2017, 66, 58–67. [Google Scholar] [CrossRef]
- Letfullin, R.R.; Szatkowsli, S.A. Laser-induced thermal ablation of cancerous cell organelles. Ther. Deliv. 2017, 8, 501–509. [Google Scholar] [CrossRef]
- Chan, C.J.; Li, W.; Cojoc, G.; Guck, J. Volume transitions of isolated cell nuclei induced by rapid temperature increase. Biophys. J. 2017, 112, 1063–1076. [Google Scholar] [CrossRef]
- Lele, T.P.; Dickinson, R.B.; Gundersen, G.G. Mechanical principles of nuclear shaping and positioning. J. Cell Biol. 2018, 217, 3330–3342. [Google Scholar] [CrossRef] [Green Version]
- Mathieu, S.; Manneville, J.B. Intracellular mechanics: Connecting rheology and mechanotransduction. Curr. Opin. Cell Biol. 2019, 56, 34–44. [Google Scholar]
- Zhou, Z.L.; Sun, X.X.; Ma, C.H.; Wong, A.S.T.; Leung, A.Y.; Ngan, A.H.W. Mechanical oscillations enhance gene delivery into suspended cells. Sci. Rep. 2016, 6, 22824. [Google Scholar] [CrossRef] [Green Version]
- Falleroni, F.; Torre, V.; Cojoc, D. Cell Mechanotransduction with piconewton forces applied by optical tweezers. Front. Cell. Neurosci. 2018, 12, 130. [Google Scholar] [CrossRef]
- Shneider, M.N.; Pekker, M. Initiation and blocking of the action potential in an axon in weak ultrasonic or microwave fields. Phys. Rev. E 2014, 89, 052713. [Google Scholar] [CrossRef] [Green Version]
- Plaksin, M.; Shapira, E.; Kimmel, E.; Shoham, S. Thermal transients excite neurons through universal intramembrane mechanoelectrical effects. Phys. Rev. X 2018, 8, 011043. [Google Scholar] [CrossRef]
- Plaksin, M.; Shoham, S.; Kimmel, E. Intramembrane cavitation as a predictive bio-piezoelectric mechanism for ultrasonic brain stimulation. Phys. Rev. X 2014, 4, 011004. [Google Scholar] [CrossRef]
- Mayama, H.; Nomura, S.M.; Oana, H.; Yoshikawa, K. Self-oscillating polymer chain. Chem. Phys. Lett. 2000, 330, 361–367. [Google Scholar] [CrossRef]
- Kitahata, H.; Mayama, H.; Yoshikawa, K. Spontaneous rhythmic motion of a polymer chain in a continuous-wave laser field. Phys. Rev. E 2004, 70, 021910. [Google Scholar] [CrossRef] [Green Version]
- Bunea, A.I.; Glückstad, J. Strategies for optical trapping in biological samples: Aiming at microrobotic surgeons. Laser Photonics Rev. 2019, 13, 1800227. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, L.; Zhang, Y.; Liu, C.; Wu, J.; Zhang, Y.; Yang, X.; Zhang, J.; Yang, J.; Yuan, L. Optical funnel for living cells trap. Opt. Commun. 2019, 431, 196–198. [Google Scholar] [CrossRef]
- Koss, B.; Chowdhury, S.; Aabo, T.; Gupta, S.K.; Losert, W. Indirect optical gripping with triplet traps. J. Opt. Soc. Am. B 2011, 28, 982–985. [Google Scholar] [CrossRef]
- Blázquez-Castro, A.; García-Cabañes, A.; Carrascosa, M. Biological applications of ferroelectric materials. Appl. Phys. Rev. 2018, 5, 041101. [Google Scholar] [CrossRef] [Green Version]
- Débarre, D.; Olivier, N.; Suppato, W.; Beaurepaire, E. Mitigating phototoxicity during multiphoton microscopy of live drosophila embryos in the 1.0–1.2 m wavelength range. PLoS ONE 2014, 9, e104250. [Google Scholar] [CrossRef] [PubMed]
- Macias-Romero, C.; Zubkovs, V.; Wang, S.; Roke, S. Wide-field medium-repetition-rate multiphoton microscopy reduces photodamage of living cells. Biomed. Opt. Express 2016, 7, 1458–1467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Westberg, M.; Bregnhøj, M.; Blázquez-Castro, A.; Breitenbach, T.; Etzerodt, M.; Ogilby, P.R. Control of singlet oxygen production in experiments performed on single mammalian cells. J. Photochem. Photobiol. A Chem. 2016, 321, 297–308. [Google Scholar] [CrossRef]
- Westberg, M.; Bregnhøj, M.; Banerjee, C.; Blázquez-Castro, A.; Breitenbach, T.; Ogilby, P.R. Exerting better control and specificity with singlet oxygen experiments in live mammalian cells. Methods 2016, 109, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Min, T.L.; Mears, P.J.; Chubiz, L.M.; Rao, C.V.; Golding, I.; Chemla, Y.R. High-resolution, long-term characterization of bacterial motility using optical tweezers. Nat. Methods 2009, 6, 831–835. [Google Scholar] [CrossRef] [PubMed]
- Swoboda, M.; Henig, J.; Cheng, H.M.; Brugger, D.; Haltrich, D.; Plumeré, N.; Schlierf, M. Enzymatic oxygen scavenging for photostability without pH drop in single-molecule experiments. ACS Nano 2012, 6, 6364–6369. [Google Scholar] [CrossRef] [PubMed]
- Takeda, H.; Nio, Y.; Omori, H.; Uegaki, K.; Hirahara, N.; Sasaki, S.; Tamura, K.; Ohtani, H. Mechanisms of cytotoxic effects of heavy water (deuterium oxide: D2O) on cancer cells. Anticancer Drugs 1998, 9, 715–725. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Sevilla, P.; Zhang, Y.; Haro-González, P.; Sanz-Rodríguez, F.; Jaque, F.; García Sole, J.; Liu, X.; Jaque, D. Avoiding induced heating in optical trap. Proc. SPIE 2017, 10347, 1034716. [Google Scholar] [CrossRef]
- Mao, H.; Arias-Gonzalez, J.R.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Temperature Control Methods in a Laser Tweezers System. Biophys. J. 2005, 89, 1308–1316. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Del Rosal, B.; Sun, C.; Yan, Y.; Mackenzie, M.D.; Lu, C.; Bettiol, A.A.; Kar, A.K.; Jaque, D. Flow effects in the laser-induced thermal loading of optical traps and optofluidic devices. Opt. Express 2014, 22, 23938–23954. [Google Scholar] [CrossRef] [PubMed]
- Sitnikov, D.S.; Ilina, I.V.; Khramova, Y.V.; Filatov, M.A.; Semenova, M.L. Femtosecond scalpel-optical tweezers: Efficient tool for assisted hatching and trophectoderm biopsy. J. Phys. Conf. Ser. 2016, 735, 012034. [Google Scholar] [CrossRef]
- Avila, R.; Medina-Villalobos, N.; Tamariz, E.; Chiu, R.; Lopez-Marín, L.M.; Acosta, A.; Castaño, V. Optical tweezers experiments for fibroblast cell growth stimulation. Proc. SPIE 2014, 9129, 91291U. [Google Scholar] [CrossRef]
- Oyama, K.; Arai, T.; Isaka, A.; Sekiguchi, T.; Itoh, H.; Seto, Y.; Miyazaki, M.; Itabashi, T.; Ohki, T.; Suzuki, M.; et al. Directional Bleb Formation in Spherical Cells under Temperature Gradient. Biophys. J. 2015, 109, 355–364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Black, B.; Vishwakarma, V.; Dhakal, K.; Bhattarai, S.; Pradhan, P.; Jain, A.; Kim, Y.; Mohanty, S. Spatial temperature gradients guide axonal outgrowth. Sci. Rep. 2016, 6, 29876. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Drobczyński, S.; Prorok, K.; Tamarov, K.; Duś-Szachniewicz, K.; Lehto, V.P.; Bednarkiewicz, A. Toward controlled photothermal treatment of single cell: Optically induced heating and remote temperature monitoring in vitro through double wavelength optical tweezers. ACS Phot. 2017, 4, 1993–2002. [Google Scholar]
- Charrunchon, S.; Limtrakul, J.; Chattam, N. Growth pattern of yeast cells studied under line optical tweezers. Int. J. Appl. Phys. Math. 2013, 3, 198–202. [Google Scholar] [CrossRef]
- Lin, L.; Hill, E.H.; Peng, X.; Zheng, Y. Optothermal manipulations of colloidal particles and living cells. Acc. Chem. Res. 2018, 51, 1465–1474. [Google Scholar] [CrossRef]
- Bahadori, A.; Oddershede, L.B.; Bendix, P.M. Hot-nanoparticle-mediated fusion of selected cells. Nano Res. 2017, 10, 2034–2045. [Google Scholar] [CrossRef]
- Bolognesi, G.; Friddin, M.S.; Salehi-Reyhani, A.; Barlow, N.E.; Brooks, N.J.; Ces, O.; Elani, Y. Sculpting and fusing biomimetic vesicle networks using optical tweezers. Nat. Commun. 2018, 9, 1882. [Google Scholar] [CrossRef] [PubMed]
- Sies, H. Oxidative Stress: Eustress and Distress. Role in Health and Disease Processes, 1st ed.; Elsevier: Cambridge, MA, USA, 2019. (in press) [Google Scholar]
- Blázquez-Castro, A.; Breitenbach, T.; Ogilby, P.R. Cell cycle modulation through subcellular spatially resolved production of singlet oxygen via direct 765 nm irradiation: Manipulating the onset of mitosis. Photochem. Photobiol. Sci. 2018, 17, 1310–1318. [Google Scholar] [CrossRef] [PubMed]
- Blázquez-Castro, A.; Breitenbach, T.; Ogilby, P.R. Singlet oxygen and ROS in a new light: Low-dose subcellular photodynamic treatment enhances proliferation at the single cell level. Photochem. Photobiol. Sci. 2014, 13, 1235–1240. [Google Scholar] [CrossRef] [PubMed]
- Blázquez-Castro, A.; Carrasco, E.; Calvo, M.I.; Jaén, P.; Stockert, J.C.; Juarranz, A.; Sánz-Rodríguez, F.; Espada, J. Protoporphyrin IX-dependent photodynamic production of endogenous ROS stimulates cell proliferation. Eur. J. Cell Biol. 2012, 91, 216–223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrasco, E.; Blázquez-Castro, A.; Calvo, M.I.; Juarranz, A.; Espada, J. Switching on a transient endogenous ROS production in mammalian cells and tissues. Methods 2016, 109, 180–189. [Google Scholar] [CrossRef] [PubMed]
- De Lorenzo, S.; Ribezzi-Crivellari, M.; Arias-Gonzalez, J.R.; Smith, S.B.; Ritort, F. A Temperature-Jump Optical Trap for Single-Molecule Manipulation. Biophys. J. 2015, 108, 2854–2864. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minamikawa, T.; Murakami, Y.; Matsumura, N.; Niioka, H.; Fukushima, S.; Araki, T.; Hashimoto, M. Photo-induced cell damage analysis for single- and multifocus coherent anti-stokes raman scattering microscopy. J. Spectros. 2017, 2017, 5725340. [Google Scholar] [CrossRef]
- Yuan, X.; Song, Y.; Song, Y.; Xu, J.; Wu, Y.; Glidle, A.; Cusack, M.; Ijaz, U.Z.; Cooper, J.M.; Huang, W.E.; et al. Effect of laser irradiation on cell function and its implications in raman spectroscopy. Appl. Environ Microbiol. 2018, 84, e02508-17. [Google Scholar] [CrossRef]


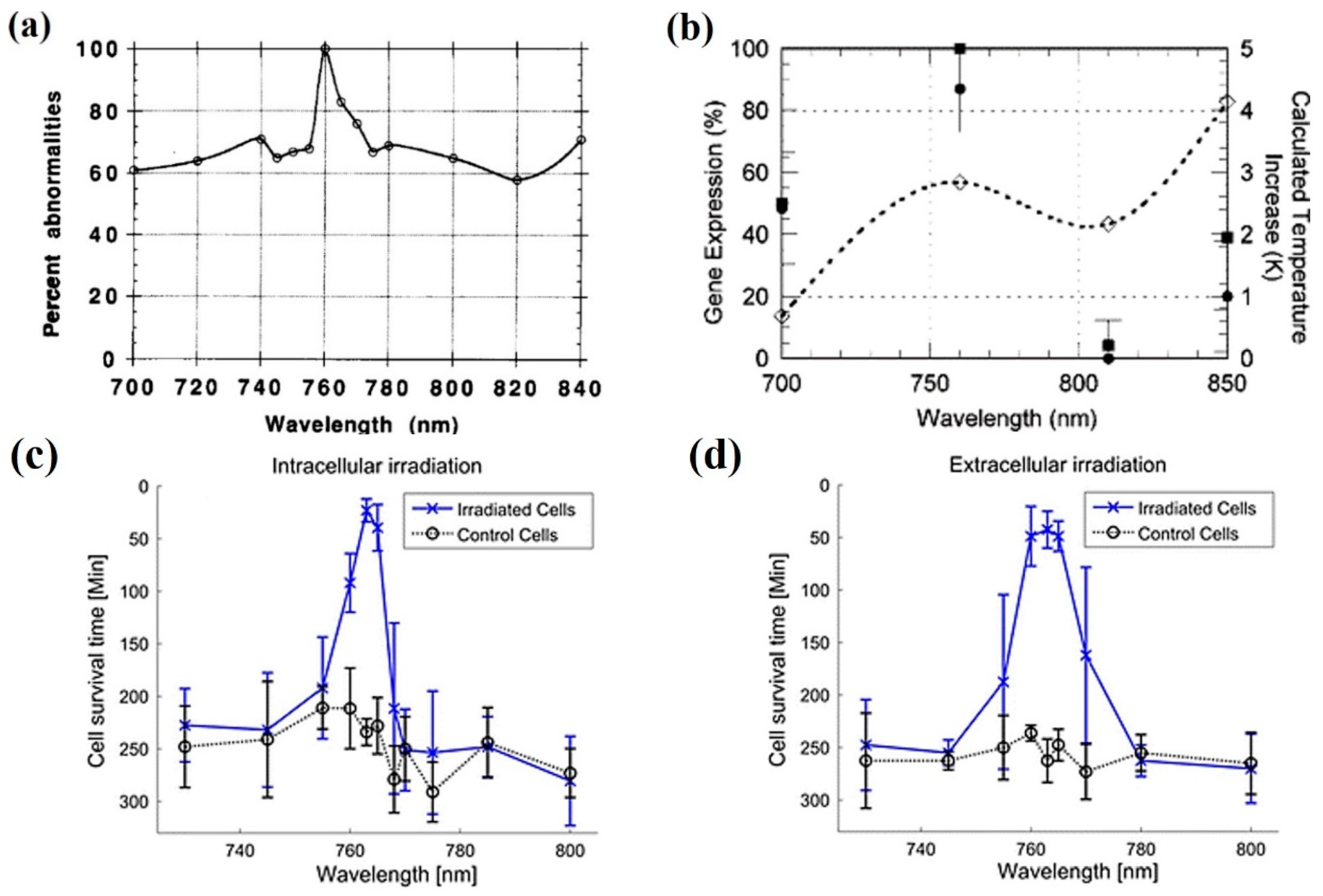


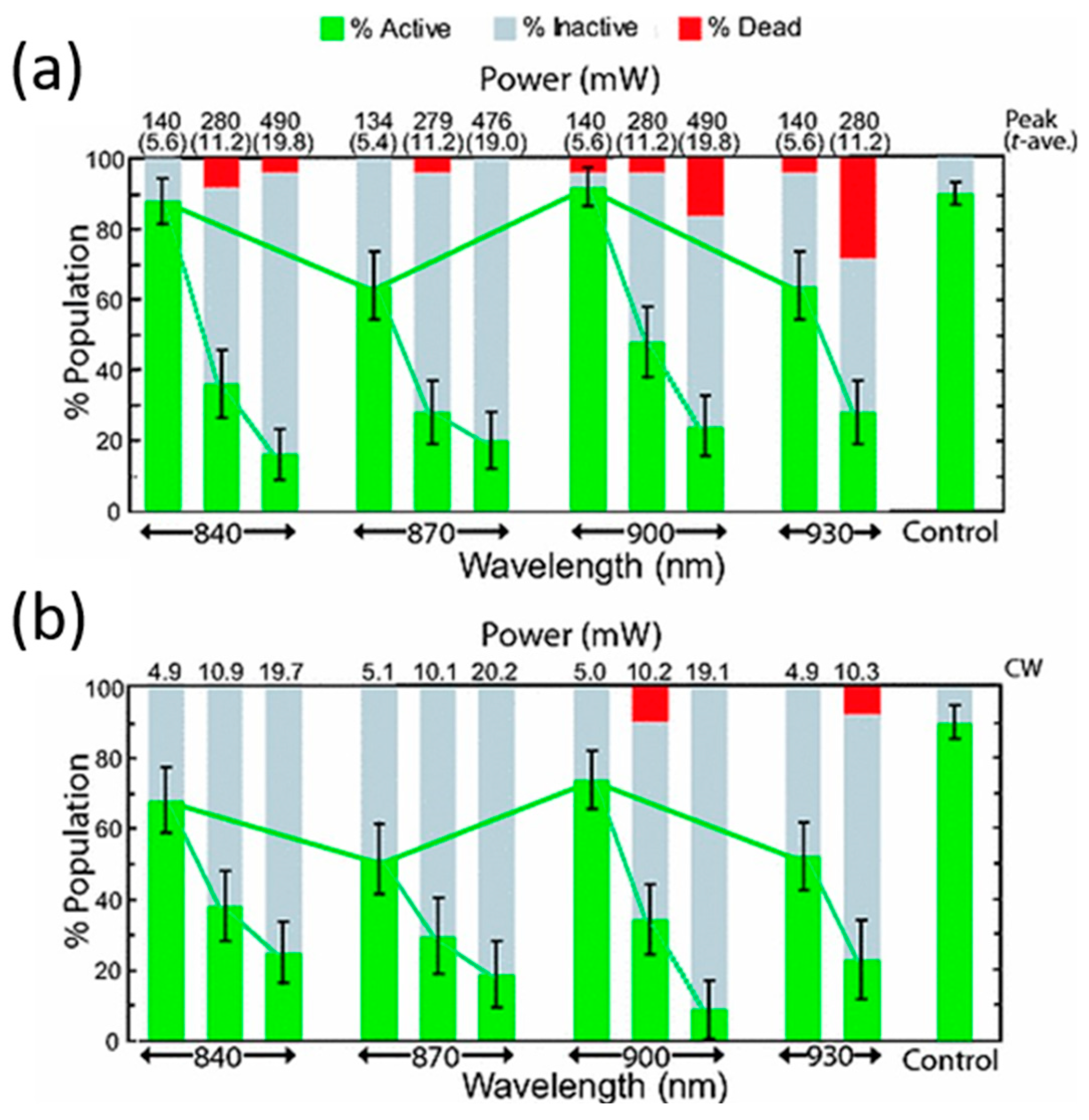
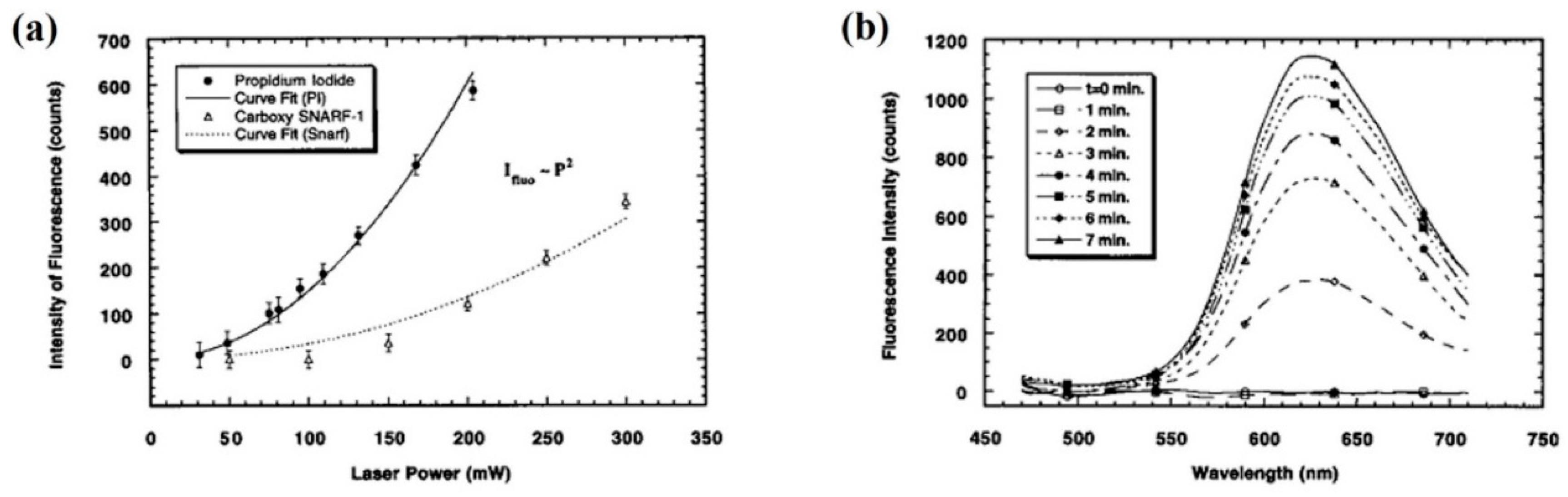
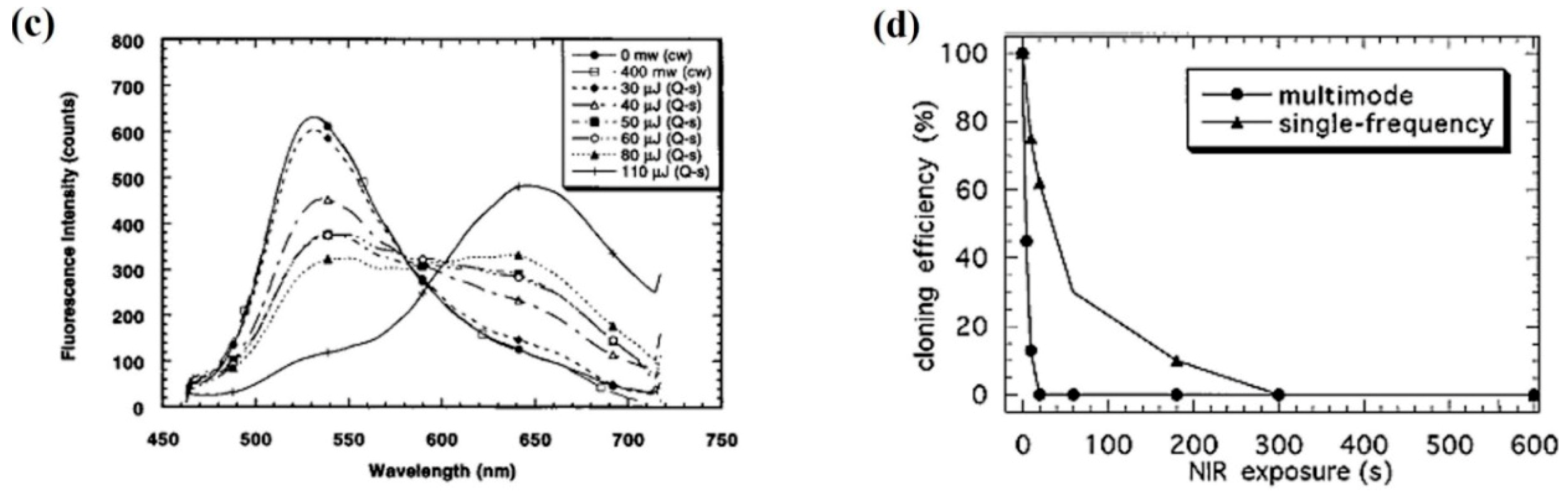

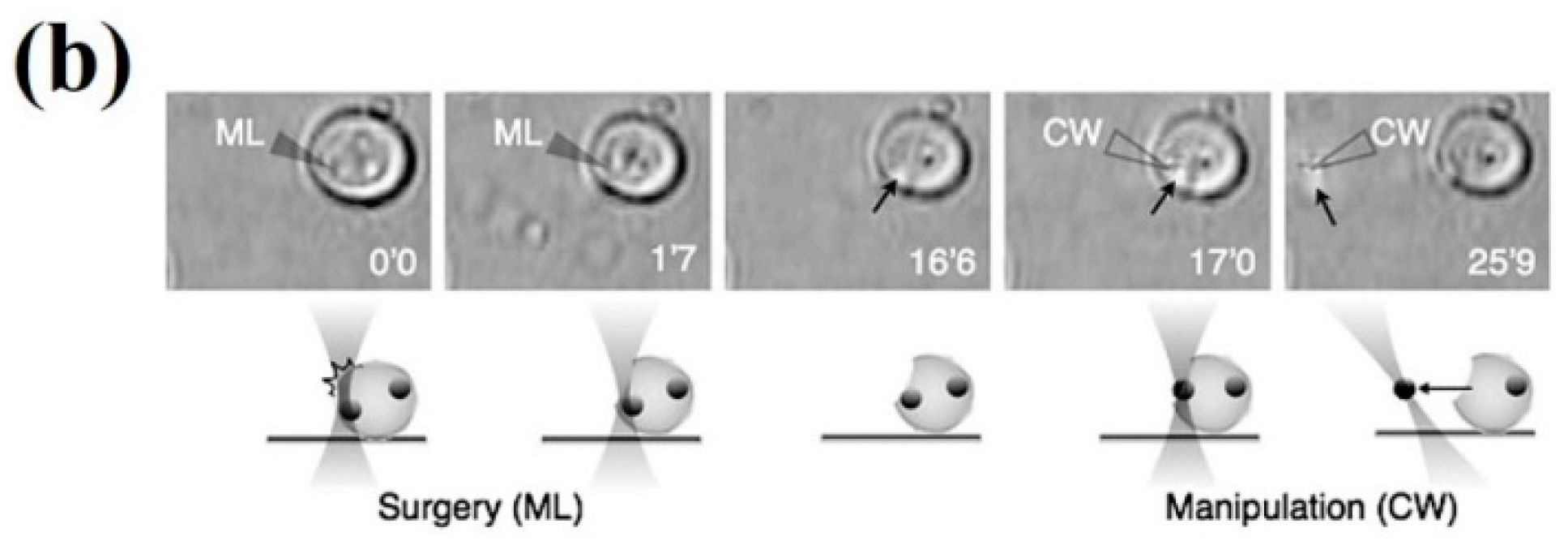

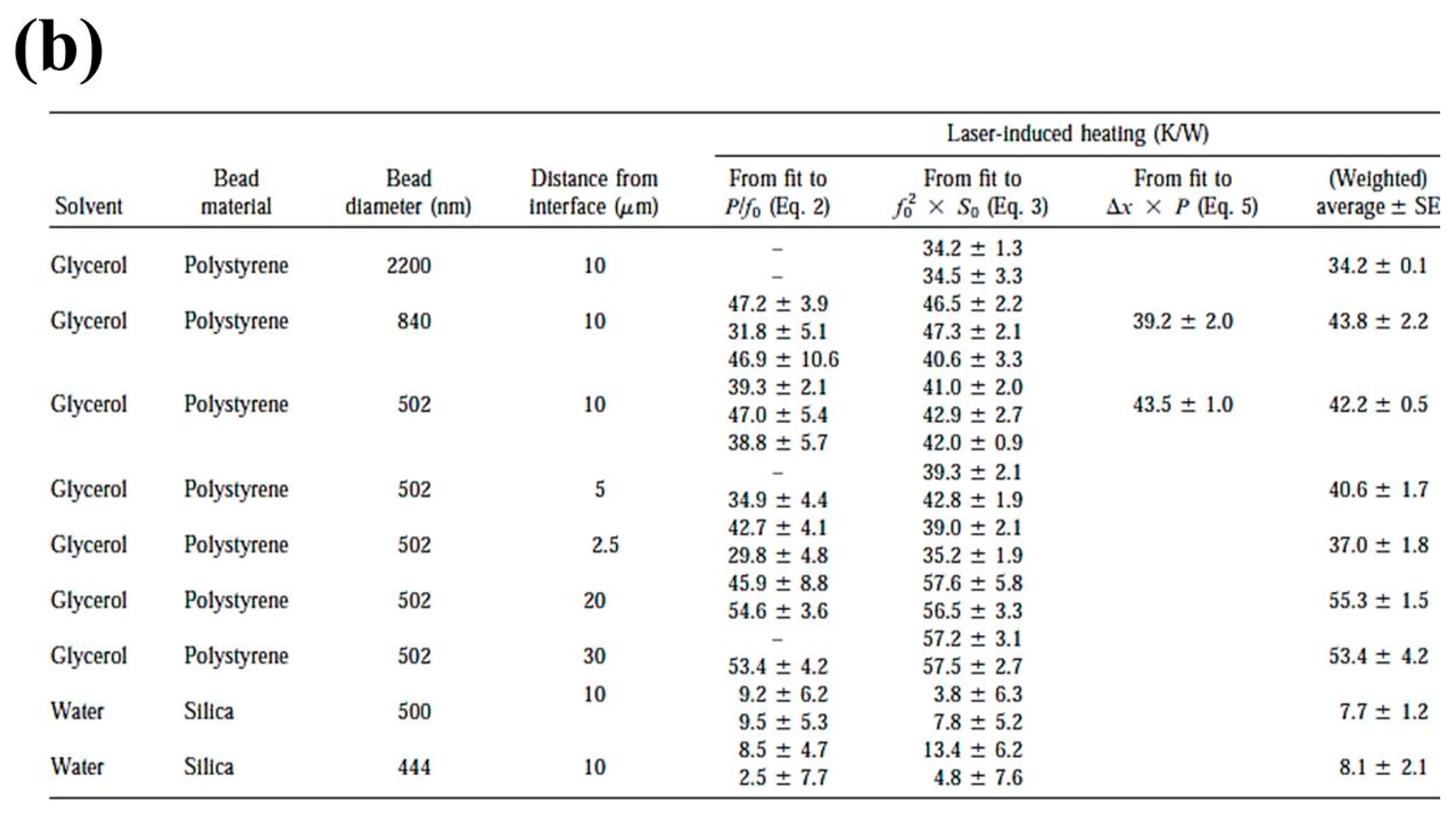
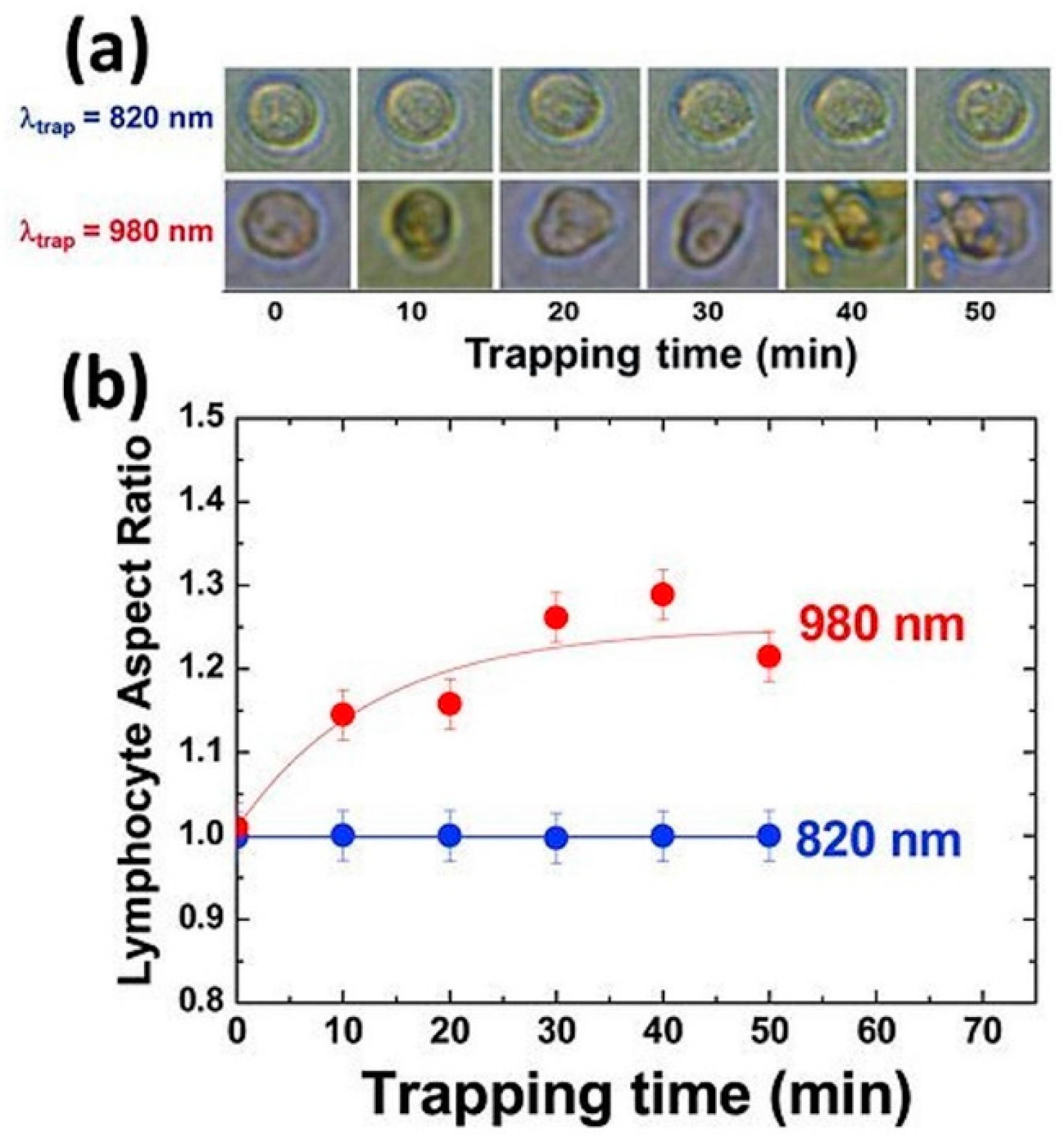
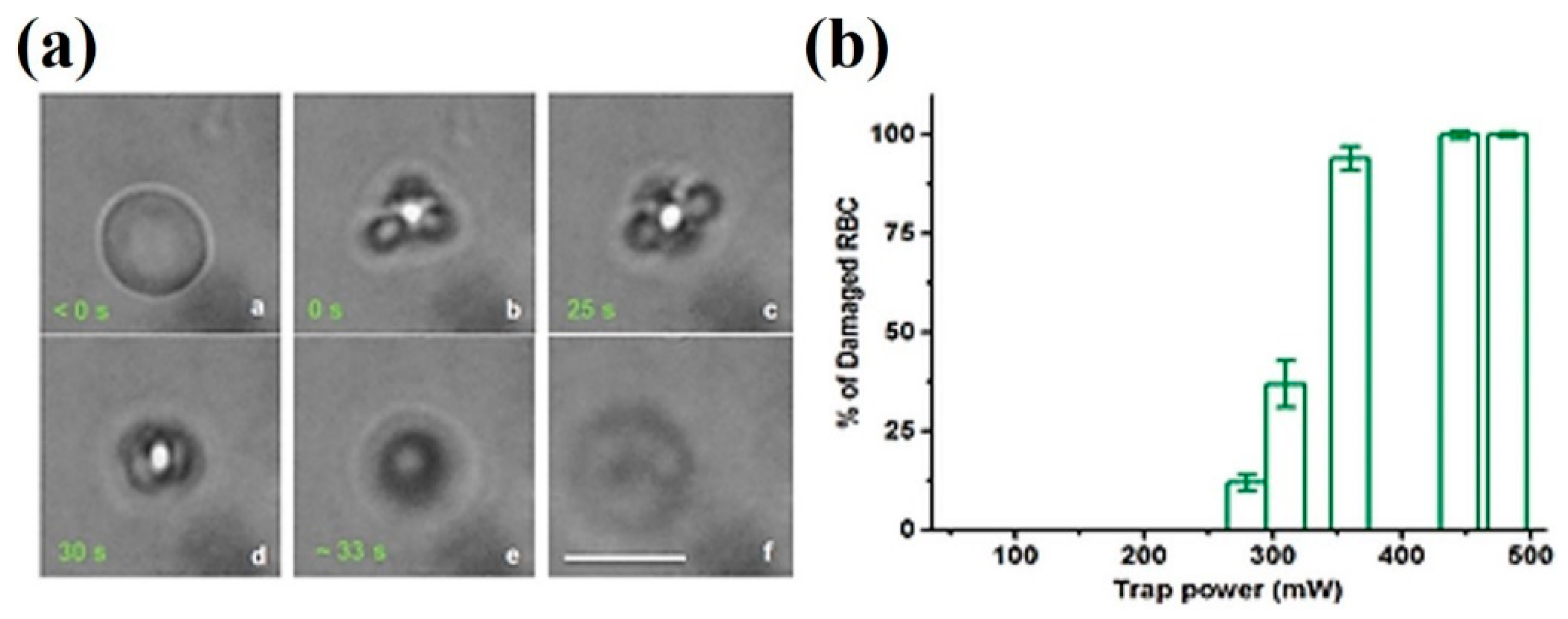

| Wavelength | Laser Source (all CW) | Power | Biological Model | Remarks | Reference |
|---|---|---|---|---|---|
| 514.5 nm | Ar ion | 10–100 mW | E. coli | Earliest report on biological damage | [5] |
| 405 nm | Diode | 75 nW/pixel | HeLa | Assessment of DNA damage response | [44] |
| 405 nm | Diode | 1–8 mW | HeLa; mouse fibroblasts; human fibroblasts | Analysis of DNA damage by visible wavelengths | [49] |
| 488 nm | Ar ion | ||||
| 561 nm | DPSS | ||||
| 633 nm | He-Ne | ||||
| 473 nm | Diode | 1 mW | HeLa | Autophagy photo-activation | [50] |
| 543 nm | |||||
| 650 nm | |||||
| 785 nm | Ti:sapphire | 3–9 mW | RBC | Kinetics of hemoglobin photo-degradation | [52] |
| Wavelength | Laser Source (all CW) | Power | Biological Model | Remarks | Reference |
|---|---|---|---|---|---|
| 750–850 nm | Ti:sapphire | 60–120 mW | NC-37 | Analysis of DNA damage by NIR wavelengths | [42] |
| 1064 nm | Nd:YAG | 60–240 mW | |||
| 1270 nm | Raman fiber | 100–400 mW | MCF-7 | Cell death induction | [67] |
| 1268 nm | Q-dot diode | 200–500 mW | HaCaT; primary keratinocytes; HeLa | Cell death induction | [68] |
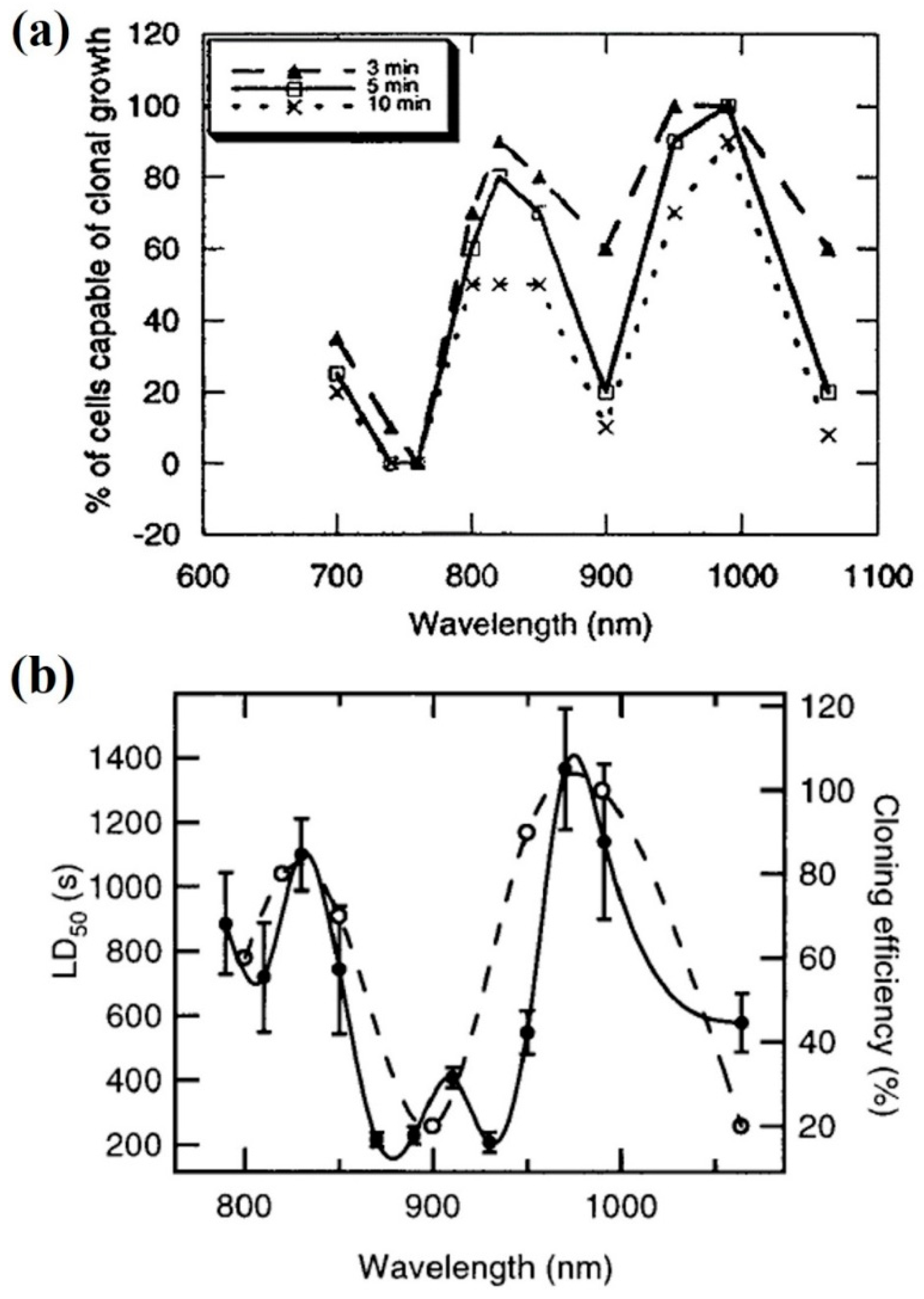
| 700–990 nm | Ti:sapphire | 88–176 mW | CHO | Assessment of cell cloning capacity | [71] |
| 1064 nm | Nd:YAG | 88–176 mW | |||
| 1064 nm | Nd:YAG | 3–30 mW | E. coli | Cell mobility and damage | [75] |
| 1064 nm | Nd:YAG | 30–230 mW | DNA molecules | Analysis of molecular structural damage | [79] |
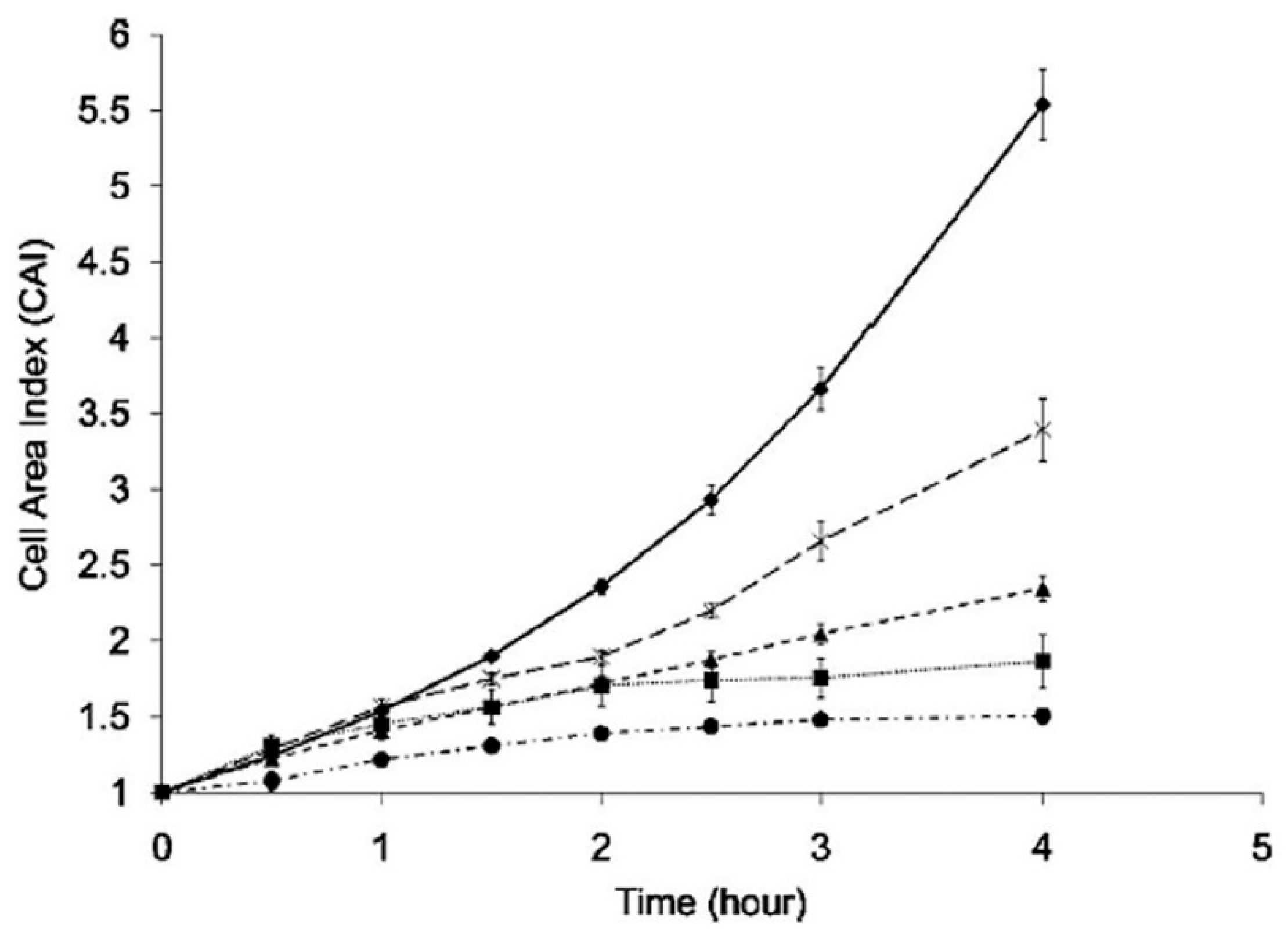
| 1070 nm | Yb fiber | 0.7–2.6 mW | S. cerevisiae | Study of cell growth and division | [80] |
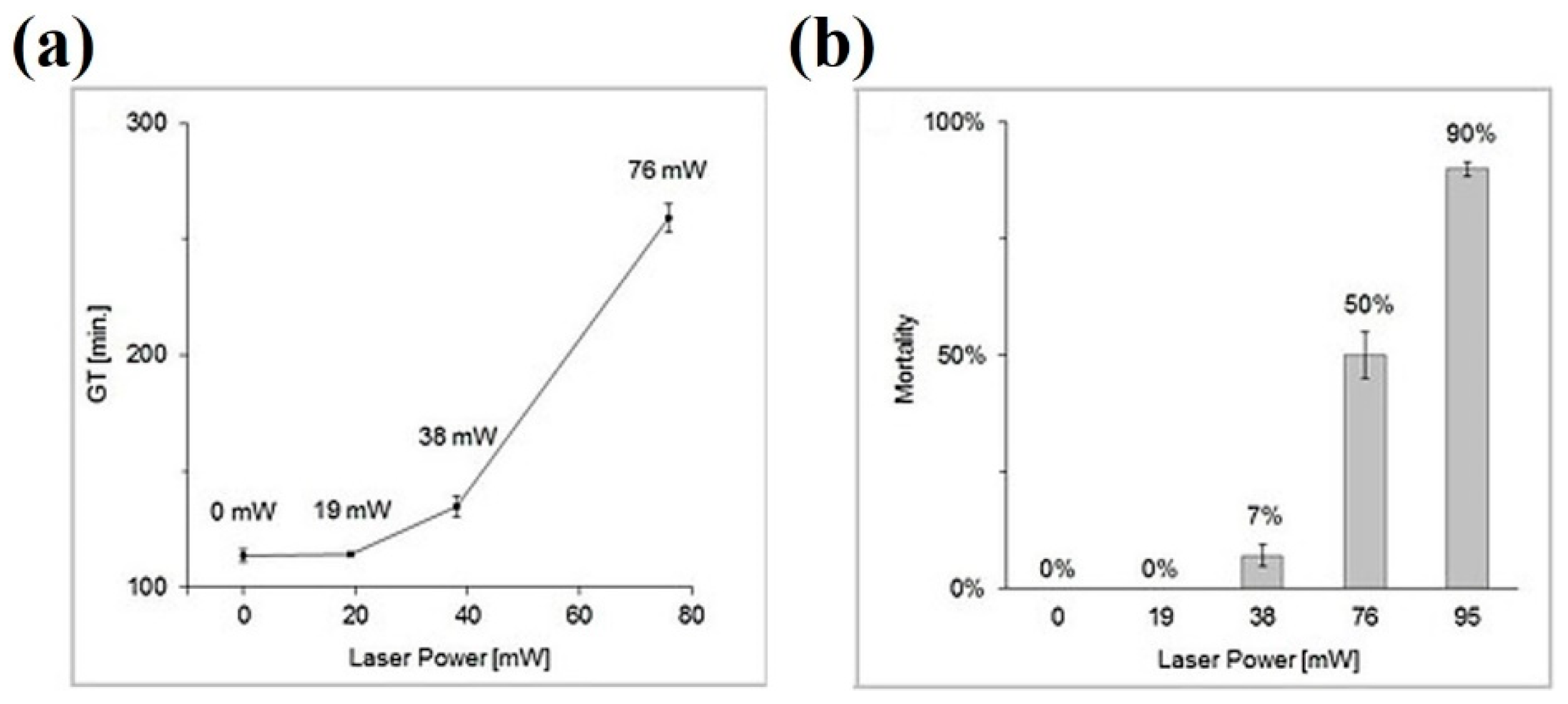
| 1064 nm | Nd:YAG | 19–95 mW | S. cerevisiae | Study of cell growth and division | [85] |
| 700–840 nm | Ti:sapphire | 130 mW | PtK2 | Assessment of chromosomal abnormalities | [86] |
| 700–850 nm | Ti:sapphire | 360 mW | C. elegans | Study of heat shock protein induction | [87] |
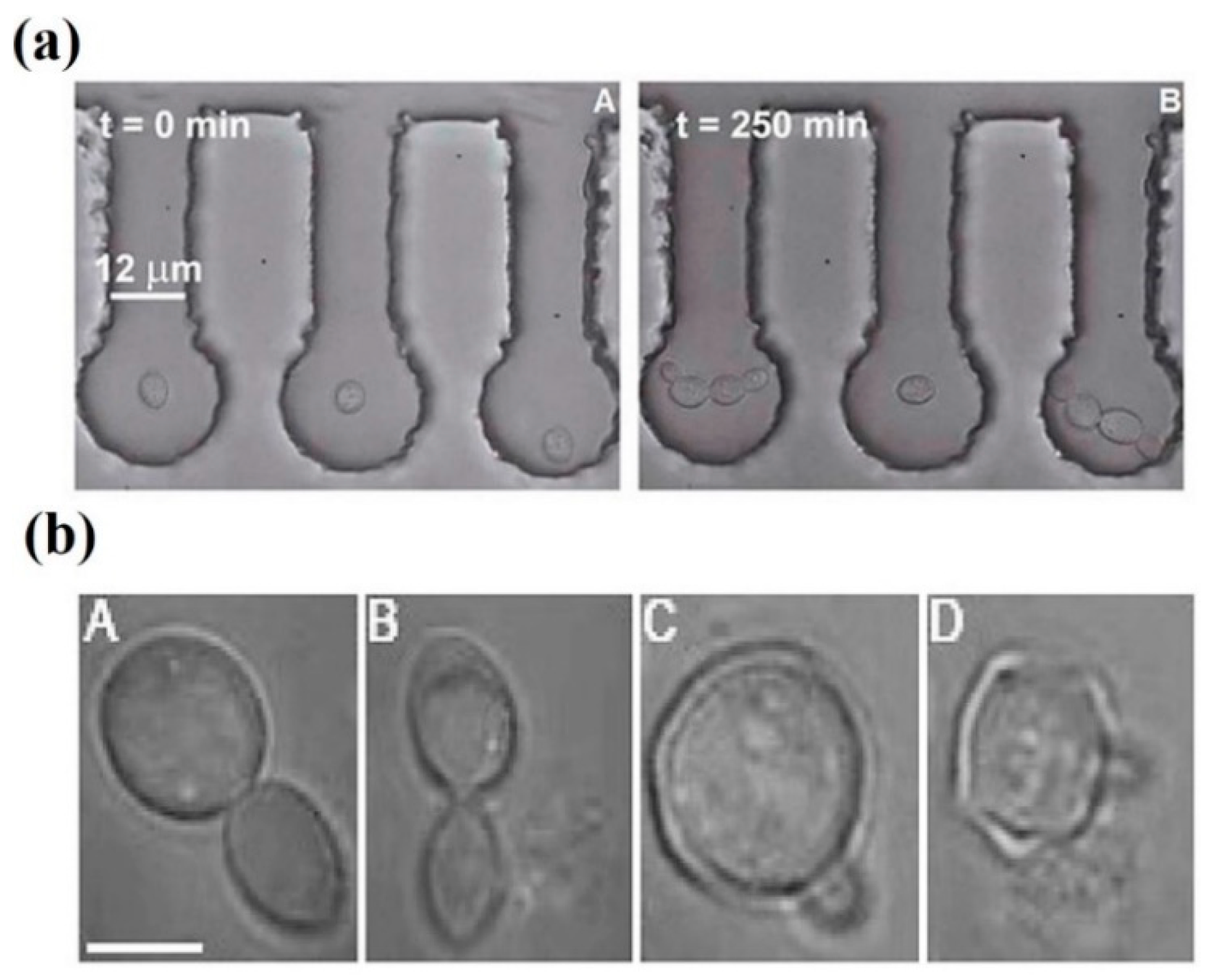
| 730–800 nm | Ti:sapphire (pulsed fs) | 91.5 mW (average power) | HeLa | Necrotic cell death induction | [88] |
| 740–760 nm | Ti:sapphire | 88–176 mW | CHO | Induction of “giant” cells | [91] |
| Wavelength | Laser Source (all pulsed) | Energy/Power | Biological Model | Remarks | Reference |
|---|---|---|---|---|---|
| 308 nm | XeCl excimer (ns) | 525 Jm−2 (flux/pulse) | Human lymphocytes | Analysis of DNA damage by UVA-VIS wavelengths | [41] |
| 312–318 nm | Doubled dye (ns) | 9 Jm−2 (flux/pulse) | |||
| 340–640 nm | Dye (ns) | 260–460 Jm−2 (flux/pulse) | |||
| 337 nm | Nitrogen (ns) | 4-40 nJ/pulse | HeLa | Analysis of DNA damage at several wavelengths | [44] |
| 532 nm | Nd:YAG (ns) | 31 nJ/pulse | |||
| 532 nm | Nd:YVO4 (ps) | 44 nJ/pulse | |||
| 800 nm | Ti:sapphire (fs) | 0.47 nJ/pulse | |||
| >750 nm | Ti:sapphire (fs) | 10–70 mW (average) | HeLa | Autophagy induction | [50] |
| 1064 nm | Nd:YAG (ns) | 0-500 μJ/pulse | CHO; human spermatozoa | Cell viability assessment | [70] |
| 750–800 nm | Ti:sapphire (fs) | 70–88 mW (average) | CHO; human spermatozoa | Cell viability assessment | [90] |
| 1064 nm | Nd:YAG (CW) | 20–400 mW | CHO; human spermatozoa | Cell viability assessment | [95] |
| 840 nm | Ti:sapphire (fs) | 7–75 mW (average) | Bovine adrenal chromaffin cells | Study Ca2+ uptake and degranulation reaction | [98] |
| 800 nm | Ti:sapphire (fs) | 1.8–20 mW (average) | RBC | Plasmatic membrane collapse | [103] |
| Wavelength | Laser Source (all CW) | Power | Biological Model | T Increase (°C/100 mW Optical Power) | Reference |
|---|---|---|---|---|---|
| 1064 nm | Nd:YAG | 4–160 mW | E. coli | “estimated to be several degrees Centigrade.” | [6] |
| S. cerevisiae | |||||
| RBC | |||||
| Spirogyra | |||||
| Protozoa | |||||
| 1064 nm | Nd:YAG | 45–255 mW | Liposomes | 1.45 ± 0.15 °C | [106] |
| CHO | 1.15 ± 0.25 °C | ||||
| 985 nm | Yb fiber | 55 mW | Water | 7.3 °C | [107] |
| 750/920 nm | Ti:sapphire | 15–200 mW | Jurkat | 0 °C/5 °C | [110] |
| 808/980 nm | Diode | 0 °C/9.9 °C | |||
| 1090 nm | Yb fiber | 4.9 °C | |||
| 1064 nm | Nd:YAG | 64–1150 mW | RBC | Unspecified | [113] |
| Strategy | Biological Model | Remarks | References | |
|---|---|---|---|---|
| NIR wavelengths | 810–860 nm | E. coli | Wavelengths in the biological window, avoiding molecular oxygen absorption bands. | [72,87,88,92,110] |
| HeLa | ||||
| 940–960 nm | C. elegans | |||
| Spatial light patterns | Optical beam patterning | - | Bessel beams, Airy beams, Laguerre-Gaussian beams. | [145] |
| Optical funnels | Yeast cell | Annular beams produces hollow trapping light cone | [146] | |
| Indirect particle trap | Yeast cell | Trapped inorganic particle acts upon biological sample | [147] | |
| Exposure management | Scanning beam | D. melanogaster | Reduce exciting beam dwelling time and/or introduce “pulsing” at 1–100 kHz to reduce photodamage | [149] |
| Pulsing exciting beam | HEK cells | [150] | ||
| ROS quenchers | NaN3 | DNA, HeLa, MCF-7 | Deactivates 1O2 | [76,79,88] |
| α-tocopherol | HaCaT, primary keratinocytes, HeLa | Deactivates 1O2, reacts with ROS | [68,88] | |
| BSA | MCF-7 | Reacts with ROS | [67] | |
| Ascorbic acid | DNA | Reacts with ROS | [79] | |
| Oxygen depletion | GODCAT | DNA, E. coli | Enzymatic mixture consumes local oxygen | [79,153] |
| POC | - | Consumes oxygen but does not affect pH | [154] | |
| Active thermal control | CW laser pulsing | Water | Sample is exposed to light for short periods | [156] |
| Heat sinks/NIR laser-driven convective flows | Water/heavy water | Active thermal sinks to dissipate heat; or NIR laser mildly heating to induce convection and cool fluid entrainment. | [157] | |
| Microfluidic chambers | Water/Jurkat cells | Micro-flows to increase heat dissipation. | [158] | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Castro, A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines 2019, 10, 507. https://doi.org/10.3390/mi10080507
Blázquez-Castro A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines. 2019; 10(8):507. https://doi.org/10.3390/mi10080507
Chicago/Turabian StyleBlázquez-Castro, Alfonso. 2019. "Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules" Micromachines 10, no. 8: 507. https://doi.org/10.3390/mi10080507
APA StyleBlázquez-Castro, A. (2019). Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines, 10(8), 507. https://doi.org/10.3390/mi10080507





