Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions
Abstract
:1. Introduction
2. Experimental
2.1. Microchannel and Materials
2.2. Microfluidics, Imaging, and Flow Characterization
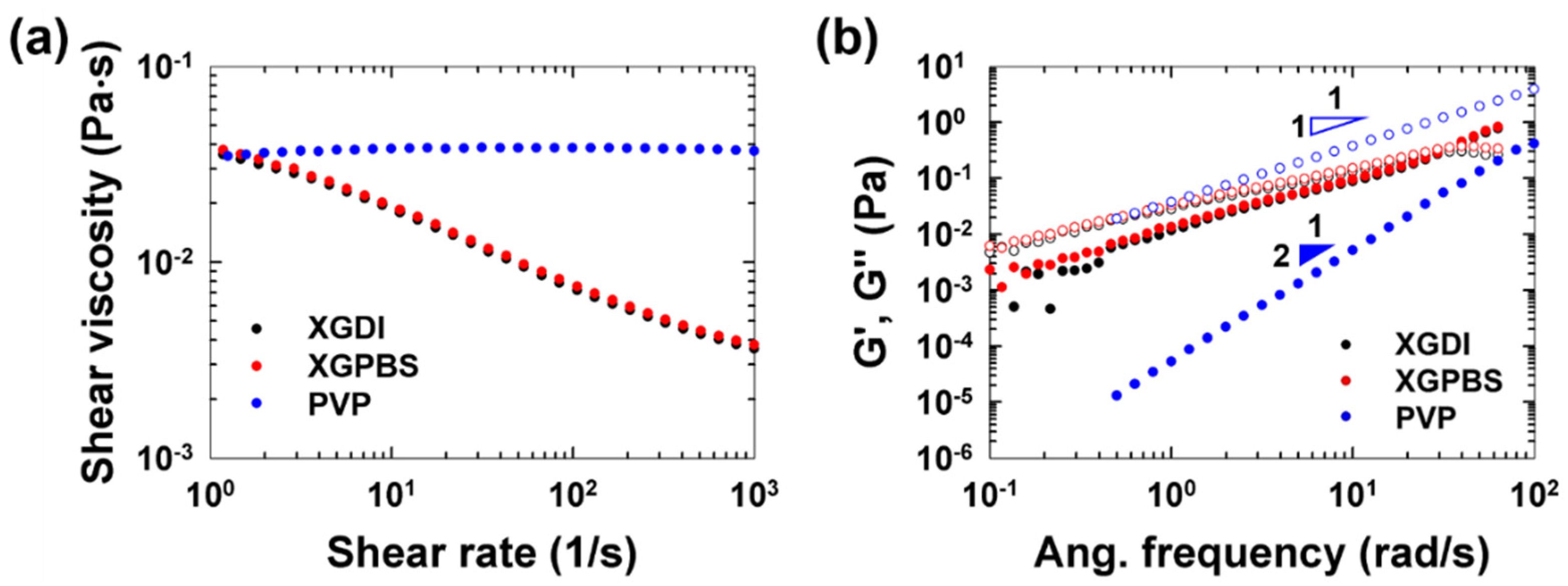
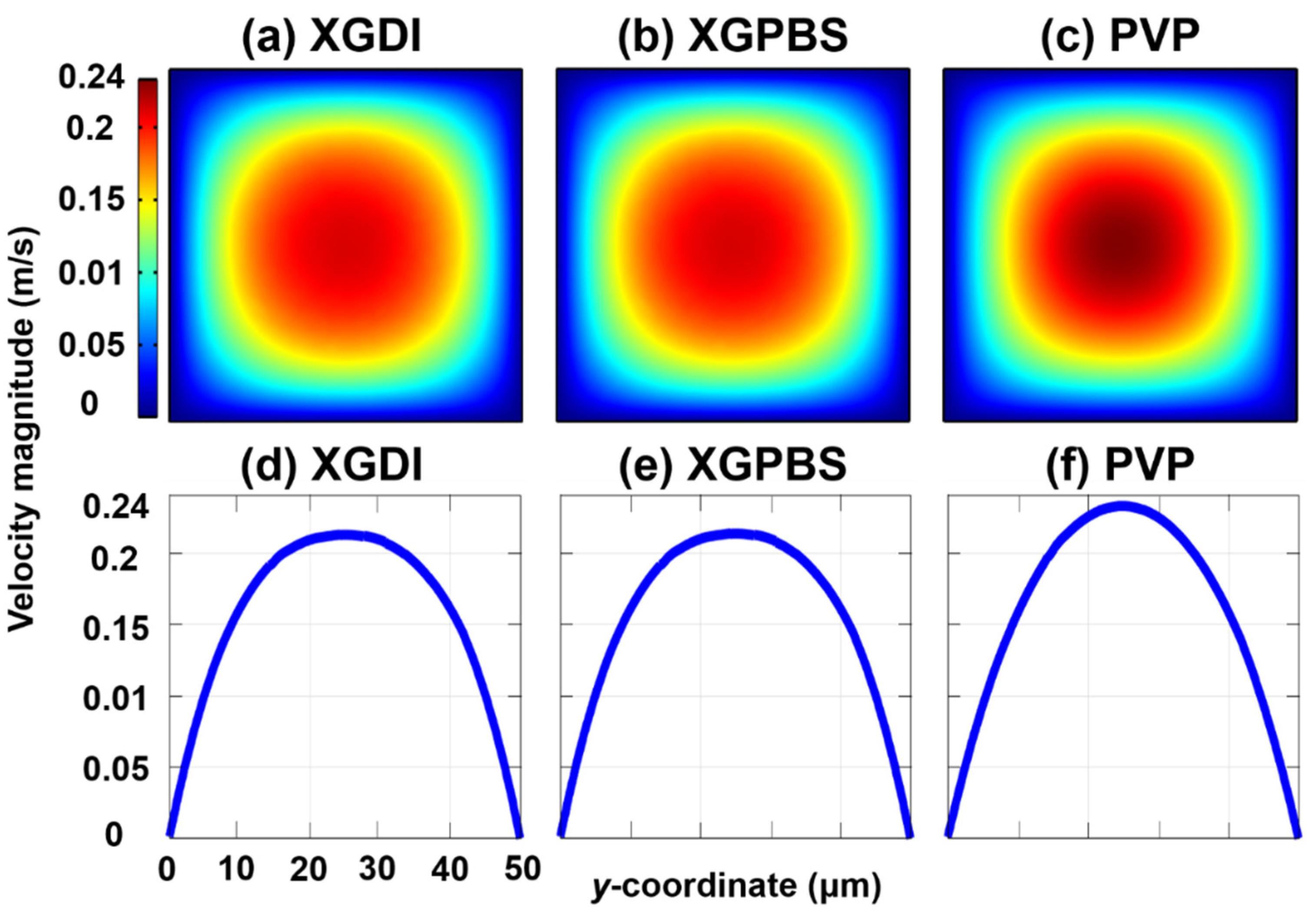
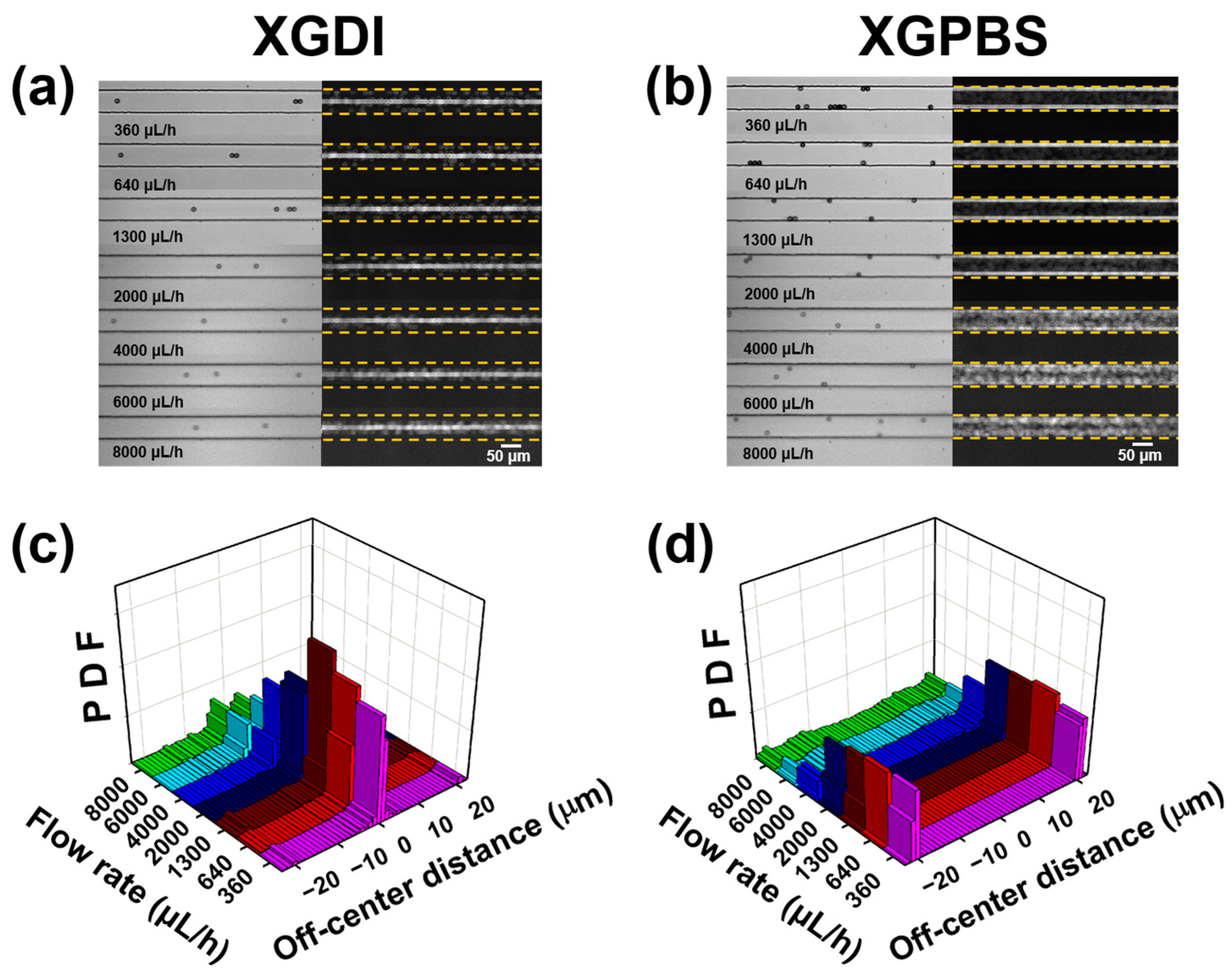
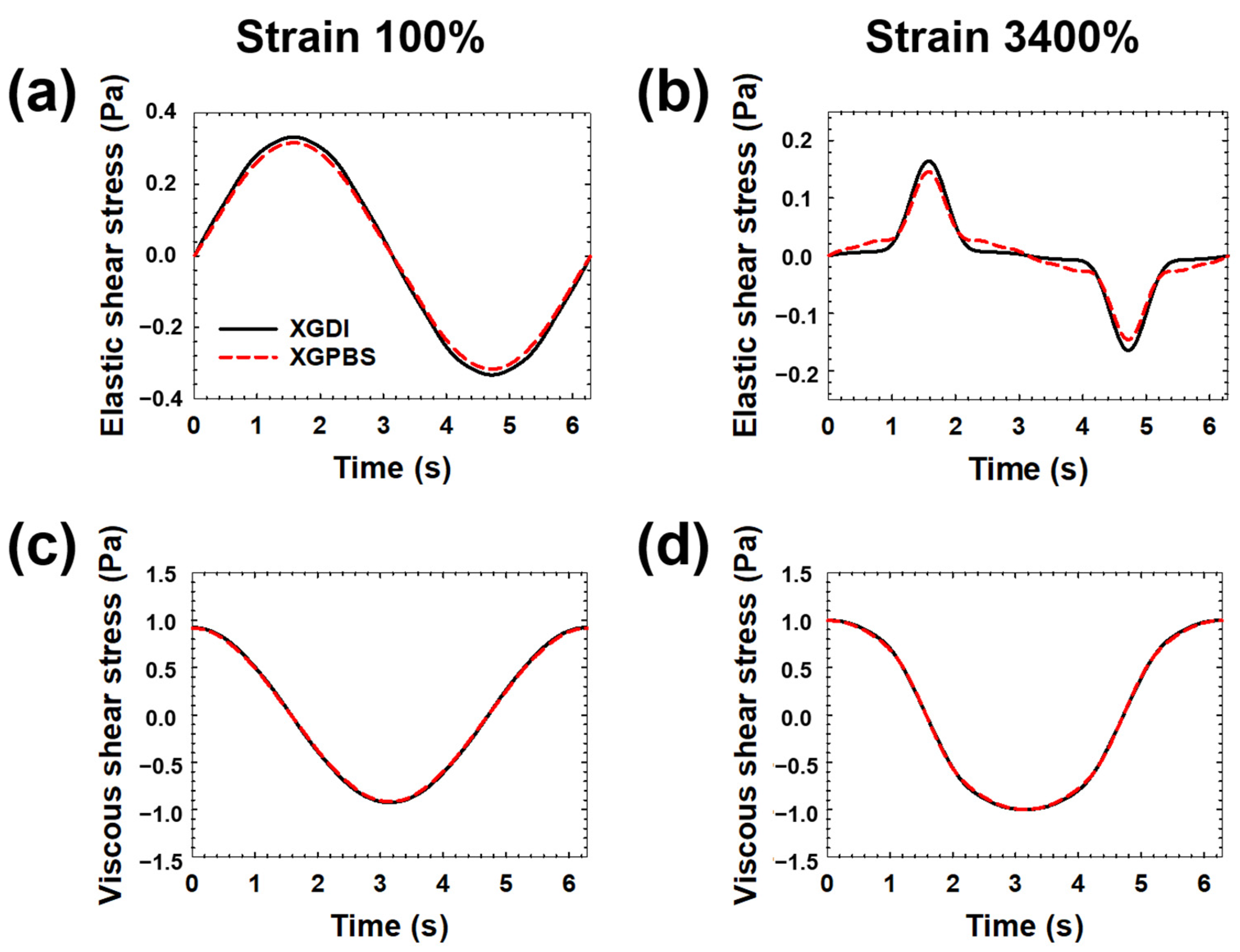
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tabeling, P. Introduction to Microfluidics; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Ligler, F.S.; Kim, J.S. The Microflow Cytometer; Pan Stanford Publishing: Danvers, MA, USA, 2010. [Google Scholar]
- Xuan, X.; Zhu, J.; Church, C. Particle focusing in microfluidic devices. Microfluid. Nanofluid. 2010, 9, 1–16. [Google Scholar] [CrossRef]
- Amini, H.; Lee, W.; Di Carlo, D. Inertial microfluidic physics. Lab Chip 2014, 14, 2739. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, D. Inertial microfluidics. Lab Chip 2009, 9, 3038. [Google Scholar] [CrossRef] [PubMed]
- D’Avino, G.; Greco, F.; Maffettone, P.L. Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Lu, X.; Liu, C.; Hu, G.; Xuan, X. Particle manipulations in non-Newtonian microfluidics: A review. J. Colloid Interface Sci. 2017, 500, 182–201. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, S.; Kim, J.Y.; Lee, S.J.; Lee, S.S.; Kim, J.M. Sheathless elasto-inertial particle focusing and continuous separation in a straight rectangular microchannel. Lab Chip 2011, 11, 266–273. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ahn, S.W.; Lee, S.S.; Kim, J.M. Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow. Lab Chip 2012, 12, 2807–2814. [Google Scholar] [PubMed]
- Kang, K.; Lee, S.S.; Hyun, K.; Lee, S.J.; Kim, J.M. DNA-based highly tunable particle focuser. Nat. Commun. 2013, 4, 2567. [Google Scholar] [CrossRef]
- Cha, S.; Shin, T.; Lee, S.S.; Shim, W.; Lee, G.; Lee, S.J.; Kim, Y.; Kim, J.M. Cell stretching measurement utilizing viscoelastic particle focusing. Anal. Chem. 2012, 84, 10471–10477. [Google Scholar] [CrossRef]
- D’Avino, G.; Romeo, G.; Villone, M.M.; Greco, F.; Netti, P.A.; Maffettone, P.L. Single line particle focusing induced by viscoelasticity of the suspending liquid: Theory, experiments and simulations to design a micropipe flow-focuser. Lab Chip 2012, 12, 1638. [Google Scholar] [CrossRef]
- Leshansky, A.M.; Bransky, A.; Korin, N.; Dinnar, U.; Leshansky, A. Tunable nonlinear viscoelastic “focusing” in a microfluidic device. Phys. Rev. Lett. 2007, 98, 234501. [Google Scholar] [CrossRef] [PubMed]
- Del Giudice, F.; Sathish, S.; D’Avino, G.; Shen, A.Q. “From the Edge to the Center”: Viscoelastic migration of particles and cells in a strongly shear-thinning liquid flowing in a microchannel. Anal. Chem. 2017, 89, 13146–13159. [Google Scholar] [CrossRef] [PubMed]
- Seo, K.W.; Kang, Y.J.; Lee, S.J. Lateral migration and focusing of microspheres in a microchannel flow of viscoelastic fluids. Phys. Fluids 2014, 26, 63301. [Google Scholar] [CrossRef] [Green Version]
- Gauthier, F.; Goldsmith, H.L.; Mason, S.G. Particle motions in non-Newtonian media. Rheol. Acta 1971, 10, 344–364. [Google Scholar] [CrossRef]
- Villone, M.; D’Avino, G.; Hulsen, M.; Greco, F.; Maffettone, P.L. Particle motion in square channel flow of a viscoelastic liquid: Migration vs. secondary flows. J. Non-Newton. Fluid Mech. 2013, 195, 1–8. [Google Scholar] [CrossRef]
- Huang, P.; Joseph, D. Effects of shear thinning on migration of neutrally buoyant particles in pressure driven flow of Newtonian and viscoelastic fluids. J. Non-Newton. Fluid Mech. 2000, 90, 159–185. [Google Scholar] [CrossRef]
- Li, D.; Xuan, X. The motion of rigid particles in the Poiseuille flow of pseudoplastic fluids through straight rectangular microchannels. Microfluid. Nanofluid. 2019, 23, 54. [Google Scholar] [CrossRef]
- Li, D.; Xuan, X. Fluid rheological effects on particle migration in a straight rectangular microchannel. Microfluid. Nanofluid. 2018, 22, 49. [Google Scholar] [CrossRef]
- Whitcomb, P.J.; Macosko, C.W. Rheology of xanthan gum. J. Rheol. 1978, 22, 493–505; [Google Scholar] [CrossRef]
- Song, K.W.; Kim, Y.S.; Chang, G.S. Rheology of concentrated xanthan gum solutions: Steady shear flow behavior. Fiber Polym. 2006, 7, 129–138. [Google Scholar] [CrossRef]
- Zirnsak, M.A.; Boger, D.V.; Tirtaatmadja, V. Steady shear and dynamic rheological properties of xanthan gum solutions in viscous solvents. J. Rheol. 1999, 43, 627–650. [Google Scholar] [CrossRef]
- Khagram, M. Extensional Flow of Xanthan Gum Solutions. J. Rheol. 1985, 29, 191–207. [Google Scholar] [CrossRef]
- Sousa, P.C.; Pinho, F.T.; Oliveira, M.S.N.; Alves, M.A. Extensional flow of blood analog solutions in microfluidic devices. Biomicrofluidics 2011, 5, 14108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calejo, J.; Pinho, D.; Galindo-Rosales, F.; Lima, R.; Campo-Deaño, L. Particulate blood analogues reproducing the erythrocytes cell-free layer in a microfluidic device containing a hyperbolic contraction. Micromachines 2016, 7, 4. [Google Scholar] [CrossRef] [PubMed]
- Pinho, D.; Campo-Deaño, L.; Lima, R.; Pinho, F.T. In vitro particulate analogue fluids for experimental studies of rheological and hemorheological behavior of glucose-rich RBC suspensions. Biomicrofluidics 2017, 11, 054105. [Google Scholar] [CrossRef] [PubMed]
- Campo-Deaño, L.; Dullens, R.P.A.; Aarts, D.G.A.L.; Pinho, F.T.; Oliveira, M.S.N. Viscoelasticity of blood and viscoelastic blood analogues for use in polydymethylsiloxane in vitro models of the circulatory system. Biomicrofluidics 2013, 7, 034102. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Norisuye, T.; Fujita, H. Double-stranded helix of xanthan in dilute solution: Evidence from light scattering. Polym. J. 1984, 16, 341–350. [Google Scholar] [CrossRef]
- Camesano, T.A.; Wilkinson, K.J. Single molecule study of xanthan conformation using atomic force microscopy. Biomacromolecules 2001, 2, 1184–1191. [Google Scholar] [CrossRef]
- Xia, Y.; Whitesides, G.M. Soft lithography. Angew. Chem. 1998, 37, 550–575. [Google Scholar] [CrossRef]
- Cho, K.S.; Hyun, K.; Ahn, K.H.; Lee, S.J. A geometrical interpretation of large amplitude oscillatory shear response. J. Rheol. 2005, 49, 747. [Google Scholar] [CrossRef]
- Bird, R.B.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Morris, C.J.; Forster, F.K. Oscillatory flow in microchannels. Exp. Fluids 2004, 36, 928–937. [Google Scholar] [CrossRef]
- Fuerstman, M.J.; Lai, A.; Thurlow, M.E.; Shevkoplyas, S.S.; Stone, H.A.; Whitesides, G.M. The pressure drop along rectangular microchannels containing bubbles. Lab Chip 2007, 7, 1479–1489. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Lee, S.S.; Ahn, S.W.; Kang, K.; Shim, W.; Lee, G.; Hyun, K.; Kim, J.M. Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity. Soft Matter 2012, 18, 5011. [Google Scholar] [CrossRef]
- Japper-Jaafar, A.; Escudier, M.; Poole, R. Laminar, transitional and turbulent annular flow of drag-reducing polymer solutions. J. Non-Newton. Fluid Mech. 2010, 165, 1357–1372. [Google Scholar] [CrossRef]
- Li, G.; McKinley, G.H.; Ardekani, A.M. Dynamics of particle migration in channel flow of viscoelastic fluids. J. Fluid Mech. 2015, 785, 486–505. [Google Scholar] [CrossRef] [Green Version]
- Ho, B.P.; Leal, L.G. Migration of rigid spheres in a 2-dimensional unidirectional shear-flow of a 2nd-order fluid. J. Fluid Mech. 1976, 76, 783–799. [Google Scholar] [CrossRef]
- Hyun, K.; Wilhelm, M.; Klein, C.O.; Cho, K.S.; Nam, J.G.; Ahn, K.H.; Lee, S.J.; Ewoldt, R.H.; McKinley, G.H. A review of nonlinear oscillatory shear tests: Analysis and application of large amplitude oscillatory shear (LAOS). Prog. Polym. Sci. 2011, 36, 1697–1753. [Google Scholar] [CrossRef]
- Jendrejack, R.M.; Schwartz, D.C.; De Pablo, J.J.; Graham, M. Shear-induced migration in flowing polymer solutions: Simulation of long-chain DNA in microchannels. J. Chem. Phys. 2004, 120, 2513–2529. [Google Scholar] [CrossRef] [Green Version]
- Jo, K.; Chen, Y.L.; De Pablo, J.J.; Schwartz, D.C. Elongation and migration of single DNA molecules in microchannels using oscillatory shear flows. Lab Chip 2009, 9, 2348–2355. [Google Scholar] [CrossRef] [Green Version]
- Losserand, S.; Coupier, G.; Podgorski, T. Migration velocity of red blood cells in microchannels. Microvasc. Res. 2019, 124, 30–36. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Graham, M. Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matter 2012, 8, 10536. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Gompper, G. White blood cell margination in microcirculation. Soft Matter 2014, 10, 2961–2970. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Del Giudice, F.; D’Avino, G.; Greco, F.; Netti, P.A.; Maffettone, P.L. Effect of fluid rheology on particle migration in a square-shaped microchannel. Microfluid. Nanofluid. 2015, 19, 95–104. [Google Scholar] [CrossRef] [Green Version]

| Property | XGDI | XGPBS | PVP | |
|---|---|---|---|---|
| Zero-shear viscosity (cP) | μ0 | 38.9 | 45.6 | 38.1 |
| Infinite-shear viscosity (cP) | μinf | 1.3 | 1.7 | |
| Power-law index | n | 0.56 | 0.58 | |
| Relaxation time (ms) | λ | 34.2 | 29.3 | 1.4 |
| Q (mL·h−1) | XGDI | XGPBS | PVP | |||
|---|---|---|---|---|---|---|
| Re | Wi | Re | Wi | Re | Wi | |
| 0.2 | - | - | 0.0292 | 1.2 | ||
| 0.36 | 0.0514 | 54.6 | 0.0439 | 46.9 | 0.0525 | 2.2 |
| 0.64 | 0.0914 | 97.1 | 0.0780 | 83.3 | 0.0933 | 3.9 |
| 1.3 | 0.1857 | 197.3 | 0.1584 | 169.2 | - | |
| 2 | 0.2856 | 303.6 | 0.2437 | 260.4 | ||
| 4 | 0.5713 | 607.1 | 0.4873 | 520.7 | ||
| 6 | 0.8569 | 910.7 | 0.7310 | 781.1 | ||
| 8 | 1.1425 | 1214.2 | 0.9747 | 1041.4 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cho, M.; Hong, S.O.; Lee, S.H.; Hyun, K.; Kim, J.M. Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines 2019, 10, 535. https://doi.org/10.3390/mi10080535
Cho M, Hong SO, Lee SH, Hyun K, Kim JM. Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines. 2019; 10(8):535. https://doi.org/10.3390/mi10080535
Chicago/Turabian StyleCho, Mira, Sun Ok Hong, Seung Hak Lee, Kyu Hyun, and Ju Min Kim. 2019. "Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions" Micromachines 10, no. 8: 535. https://doi.org/10.3390/mi10080535
APA StyleCho, M., Hong, S. O., Lee, S. H., Hyun, K., & Kim, J. M. (2019). Effects of Ionic Strength on Lateral Particle Migration in Shear-Thinning Xanthan Gum Solutions. Micromachines, 10(8), 535. https://doi.org/10.3390/mi10080535




