Mechanical Behavior Investigation of 4H-SiC Single Crystal at the Micro–Nano Scale
Abstract
:1. Introduction
2. Experimental Procedure and Methods
2.1. Materials and Preprocess
2.2. Experimental Design
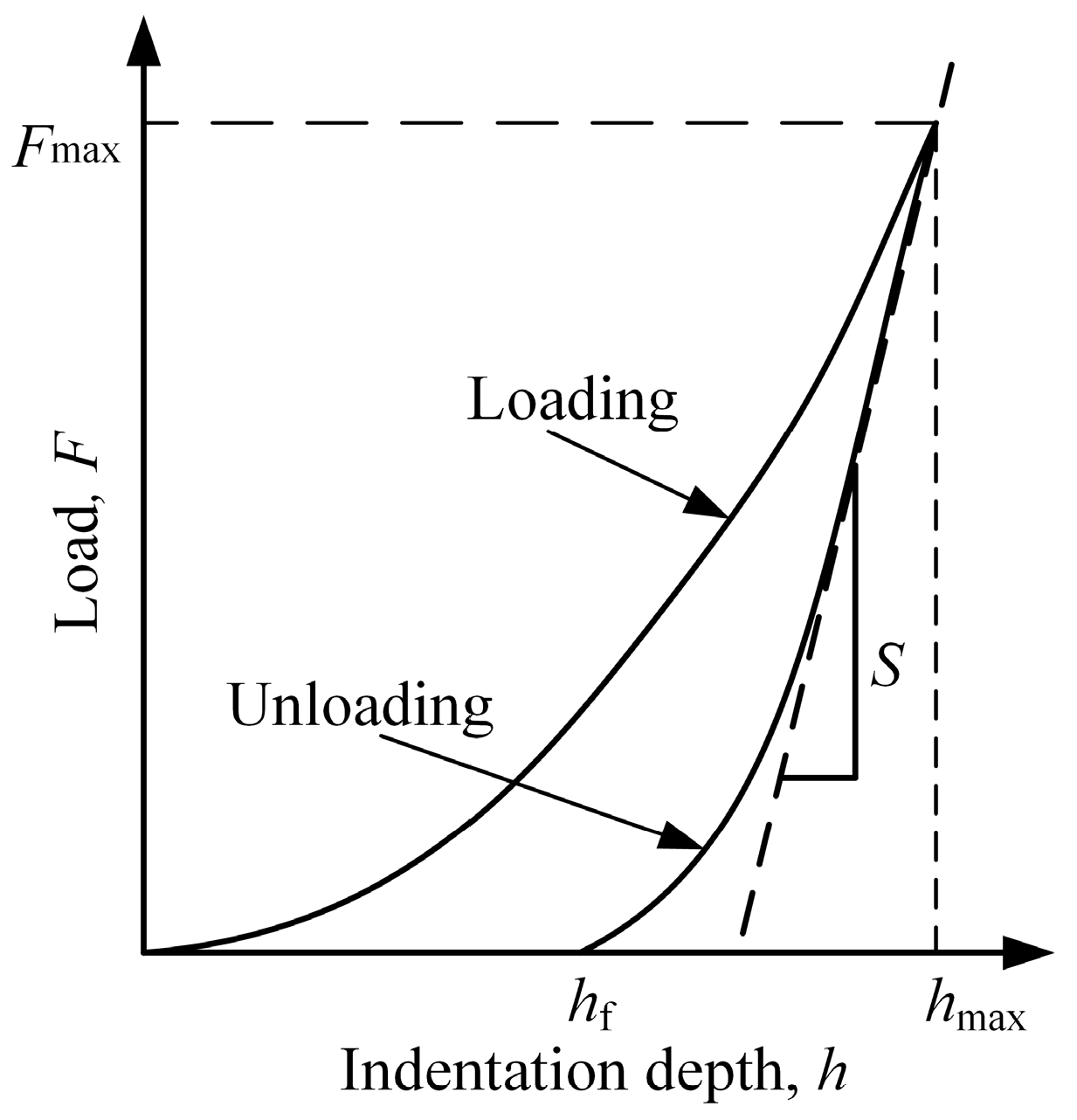
2.3. Determination of Hardness and Modulus
2.4. Determination of the Critical Indentation Depth for the Plastic–Brittle Transition
3. Results Analysis and Discussion
3.1. Elastic and Plastic Deformation of Nanoindentation
3.2. Critical Indentation Depth for the Plastic–Brittle Transition
3.3. The Influence of Cracks on the Modulus and Hardness
4. Conclusions
- The stages of brittle material deformation (elastic, plastic, and brittle) can be characterized by the load versus indentation depth curves through the nanoindentation test. The curve of the elastic deformation stage follows the Hertz contact theory, and the plastic deformation occurs in nanoindentation at an indentation depth of up to 10 nm.
- The crackling mechanism of 4H-SiC single crystal is discussed and the theoretical models of critical indentation depth and critical force for the plastic–brittle transition are proposed using cleavage strength theory and contact theory. The test results were obtained through the occurrence of the pop-in point, and the theoretical results show good agreement with the test results.
- Both the values of elastic modulus and hardness decrease as the crack length increases, because the crack extension increases the projected contact area Ap. In order to obtain more accurate mechanical property values in nanoindentation tests for brittle materials like SiC, an appropriate load for avoiding surface cracks should be adopted.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hussain, A.M. Extending Moore’s Law for Silicon CMOS Using More-Moore and More-than-Moore Technologies. Ph.D. Thesis, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 2016. [Google Scholar]
- Pushpakaran, B.N.; Subburaj, A.S.; Bayne, S.B.; Mookken, J. Impact of silicon carbide semiconductor technology in Photovoltaic Energy System. Renew. Sustain. Energy Rev. 2016, 55, 971–989. [Google Scholar] [CrossRef]
- Ando, T.; Fu, X.-A. Materials: Silicon and beyond. Sens. Actuators A Phys. 2019, 296, 340–351. [Google Scholar] [CrossRef]
- Phan, H.P.; Zhong, Y.; Nguyen, T.K.; Park, Y.; Dinh, T.; Song, E.; Vadivelu, R.K.; Masud, M.K.; Li, J.; Shiddiky, M.J.A.; et al. Long-Lived, Transferred Crystalline Silicon Carbide Nanomembranes for Implantable Flexible Electronics. ACS Nano 2019, 13, 11572–11581. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Dinh, T.; Foisal, A.R.M.; Phan, H.P.; Nguyen, T.K.; Nguyen, N.T.; Dao, D.V. Giant piezoresistive effect by optoelectronic coupling in a heterojunction. Nat. Commun. 2019, 10, 4139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, T.-K.; Phan, H.-P.; Dinh, T.; Dowling, K.M.; Foisal, A.R.M.; Senesky, D.G.; Nguyen, N.-T.; Dao, D.V. Highly sensitive 4H-SiC pressure sensor at cryogenic and elevated temperatures. Mater. Des. 2018, 156, 441–445. [Google Scholar] [CrossRef]
- Nagy, R.; Niethammer, M.; Widmann, M.; Chen, Y.C.; Udvarhelyi, P.; Bonato, C.; Hassan, J.U.; Karhu, R.; Ivanov, I.G.; Son, N.T.; et al. High-fidelity spin and optical control of single silicon-vacancy centres in silicon carbide. Nat. Commun. 2019, 10, 1954. [Google Scholar] [CrossRef]
- Neudeck, P.G. Silicon Carbide Electronic Devices, Encyclopedia of Materials: Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 2001. [Google Scholar] [CrossRef]
- Shcherban, N.D. Review on synthesis, structure, physical and chemical properties and functional characteristics of porous silicon carbide. J. Ind. Eng. Chem. 2017, 50, 15–28. [Google Scholar] [CrossRef]
- Goel, S. The current understanding on the diamond machining of silicon carbide. J. Phys. D Appl. Phys. 2014, 47, 243001. [Google Scholar] [CrossRef] [Green Version]
- Hui Zhang, L.M.T. Efficiency Impact of Silicon Carbide Power Electronics for Modern Wind Turbine Full Scale Frequency Converter. IEEE Trans. Ind. Electron. 2011, 58, 21–28. [Google Scholar] [CrossRef]
- Masumoto, K.; Kudou, C.; Tamura, K.; Nishio, J.; Ito, S.; Kojima, K.; Ohno, T.; Okumura, H. Growth of silicon carbide epitaxial layers on 150-mm-diameter wafers using a horizontal hot-wall chemical vapor deposition. J. Cryst. Growth 2013, 381, 139–143. [Google Scholar] [CrossRef]
- Kimoto, T. Bulk and epitaxial growth of silicon carbide. Prog. Cryst. Growth Charact. Mater. 2016, 62, 329–351. [Google Scholar] [CrossRef]
- Madar, R. Silicon carbide in contention. Nature 2004, 430, 974–975. [Google Scholar] [CrossRef] [PubMed]
- Fischer-Cripps, A.C. Critical review of analysis and interpretation of nanoindentation test data. Surf. Coat. Technol. 2006, 200, 4153–4165. [Google Scholar] [CrossRef]
- Hu, C.; Li, Z. A review on the mechanical properties of cement-based materials measured by nanoindentation. Constr. Build. Mater. 2015, 90, 80–90. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Lucca, D.A.; Herrmann, K.; Klopfstein, M.J. Nanoindentation: Measuring methods and applications. Cirp Ann. 2010, 59, 803–819. [Google Scholar] [CrossRef]
- Nawaz, A.; Mao, W.G.; Lu, C.; Shen, Y.G. Mechanical properties, stress distributions and nanoscale deformation mechanisms in single crystal 6H-SiC by nanoindentation. J. Alloys Compd. 2017, 708, 1046–1053. [Google Scholar] [CrossRef]
- Matsumoto, M.; Harada, H.; Kakimoto, K.; Yan, J.W. Study on Mechanical Properties of Single-Crystal Silicon Carbide by Nanoindentation. Adv. Mater. Res. 2016, 1136, 549–554. [Google Scholar] [CrossRef]
- Ma, X.G.; Komvopoulos, K.; Bogy, D.B. Nanoindentation of polycrystalline silicon-carbide thin films studied by acoustic emission. Appl. Phys. Lett. 2004, 85, 1695–1697. [Google Scholar] [CrossRef]
- Lu, J.; Luo, Q.; Xu, X.; Huang, H.; Jiang, F. Removal mechanism of 4H- and 6H-SiC substrates (0001 and 0001−) in mechanical planarization machining. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 233, 69–76. [Google Scholar] [CrossRef]
- Datye, A.; Schwarz, U.; Lin, H.-T. Fracture Toughness Evaluation and Plastic Behavior Law of a Single Crystal Silicon Carbide by Nanoindentation. Ceramics 2018, 1, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Pang, K.H.; Tymicki, E.; Roy, A. Indentation in single-crystal 6H silicon carbide: Experimental investigations and finite element analysis. Int. J. Mech. Sci. 2018, 144, 858–864. [Google Scholar] [CrossRef] [Green Version]
- Goel, S.; Yan, J.; Luo, X.; Agrawal, A. Incipient plasticity in 4H-SiC during quasistatic nanoindentation. J. Mech. Behav. Biomed. Mater. 2014, 34, 330–337. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goel, S.; Luo, X.; Comley, P.; Reuben, R.L.; Cox, A. Brittle–ductile transition during diamond turning of single crystal silicon carbide. Int. J. Mach. Tools Manuf. 2013, 65, 15–21. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.H. Analysis of ductile mode and brittle transition of AFM nanomachining of silicon. Int. J. Mach. Tools Manuf. 2012, 61, 71–79. [Google Scholar] [CrossRef]
- Goel, S.; Luo, X.; Agrawal, A.; Reuben, R.L. Diamond machining of silicon: A review of advances in molecular dynamics simulation. Int. J. Mach. Tools Manuf. 2015, 88, 131–164. [Google Scholar] [CrossRef] [Green Version]
- Antwi, E.K.; Liu, K.; Wang, H. A review on ductile mode cutting of brittle materials. Front. Mech. Eng. 2018, 13, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Lawn, B.R.; Swain, M.V. Microfracture beneath point indentations in brittle solids. J. Mater. Sci. 1975, 10, 113–122. [Google Scholar] [CrossRef]
- Op Het Veld, A.J.; Veldkamp, J.D.B. Mechanical and microscopical investigation of SiC whiskers. Fibre Sci. Technol. 1970, 2, 269–281. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar] [CrossRef]
- Cheng, Y.-T.; Cheng, C.-M. Scaling, dimensional analysis, and indentation measurements. Mater. Sci. Eng. R Rep. 2004, 44, 91–149. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, L. Mechanical behaviour characterisation of silicon and effect of loading rate on pop-in: A nanoindentation study under ultra-low loads. Mater. Sci. Eng. A 2009, 506, 125–129. [Google Scholar] [CrossRef]
- Chai, P.; Li, S.; Li, Y. Modeling and Experiment of the Critical Depth of Cut at the Ductile-Brittle Transition for a 4H-SiC Single Crystal. Micromachines 2019, 10, 382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, J.; Sun, J.; Xu, S.; Song, D.; Liu, H.; Han, Y.; Fang, L. Deformation mechanisms at multiple pop-ins under spherical nanoindentation of (1 1 1) Si. Comput. Mater. Sci. 2018, 143, 480–485. [Google Scholar] [CrossRef]
- Lawn, B. Fracture of Brittle Solids, 2nd ed.; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar] [CrossRef]
- Wells, G.H.; Hopf, T.; Vassilevski, K.V.; Escobedo-Cousin, E.; Wright, N.G.; Horsfall, A.B.; Goss, J.P.; O’Neill, A.G.; Hunt, M.R.C. Determination of the adhesion energy of graphene on SiC(0001) via measurement of pleat defects. Appl. Phys. Lett. 2014, 105, 193109. [Google Scholar] [CrossRef] [Green Version]
- Goel, S.; Stukowski, A.; Luo, X.; Agrawal, A.; Reuben, R.L. Anisotropy of single-crystal 3C–SiC during nanometric cutting. Model. Simul. Mater. Sci. Eng. 2013, 21, 065004. [Google Scholar] [CrossRef]
- Field, J.E.; Telling, R.H. The Young Modulus and Poisson Ratio of Diamond; Research Note; PCS Cavendish Laboratory, Department of Physics: Cambridge, UK, 1999. [Google Scholar]
- Díez-Pascual, A.M.; Gómez-Fatou, M.A.; Ania, F.; Flores, A. Nanoindentation in polymer nanocomposites. Prog. Mater. Sci. 2015, 67, 1–94. [Google Scholar] [CrossRef] [Green Version]
- Voyiadjis, G.; Yaghoobi, M. Review of Nanoindentation Size Effect: Experiments and Atomistic Simulation. Crystals 2017, 7, 321. [Google Scholar] [CrossRef] [Green Version]
- Peng, Z.; Gong, J.; Miao, H. On the description of indentation size effect in hardness testing for ceramics: Analysis of the nanoindentation data. J. Eur. Ceram. Soc. 2004, 24, 2193–2201. [Google Scholar] [CrossRef]
- Bull, S.J.; Page, T.F.; Yoffe, E.H. An explanation of the indentation size effect in ceramics. Philos. Mag. Lett. 1989, 59, 281–288. [Google Scholar] [CrossRef]
- Zhu, T.; Bushby, A.; Dunstan, D. Size effect in the initiation of plasticity for ceramics in nanoindentation. J. Mech. Phys. Solids 2008, 56, 1170–1185. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystallinematerials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Kitahara, H.; Noda, Y.; Yoshida, F.; Nakashima, H.; Shinohara, N.; Abe, H. Mechanical Behavior of Single Crystalline and Polycrystalline Silicon Carbides Evaluated by Vickers Indentation. J. Ceram. Soc. Jpn. 2001, 109, 602–606. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.-K.; Phan, H.-P.; Dinh, T.; Han, J.; Dimitrijev, S.; Tanner, P.; Md Foisal, A.R.; Zhu, Y.; Nguyen, N.-T.; Dao, D.V. Experimental Investigation of Piezoresistive Effect in p-Type 4H–SiC. IEEE Electron Device Lett. 2017, 38, 955–958. [Google Scholar] [CrossRef]
- Konstantinova, E.; Bell, M.J.V.; Anjos, V. Ab initio calculations of some electronic and elastic properties for SiC polytypes. Intermetallics 2008, 16, 1040–1042. [Google Scholar] [CrossRef]
- Islam, M.M.; Huang, C.F.; Zhao, F. Single-Crystal SiC Resonators by Photoelectrochemical Etching. Mater. Sci. Forum 2012, 717–720, 529–532. [Google Scholar] [CrossRef]




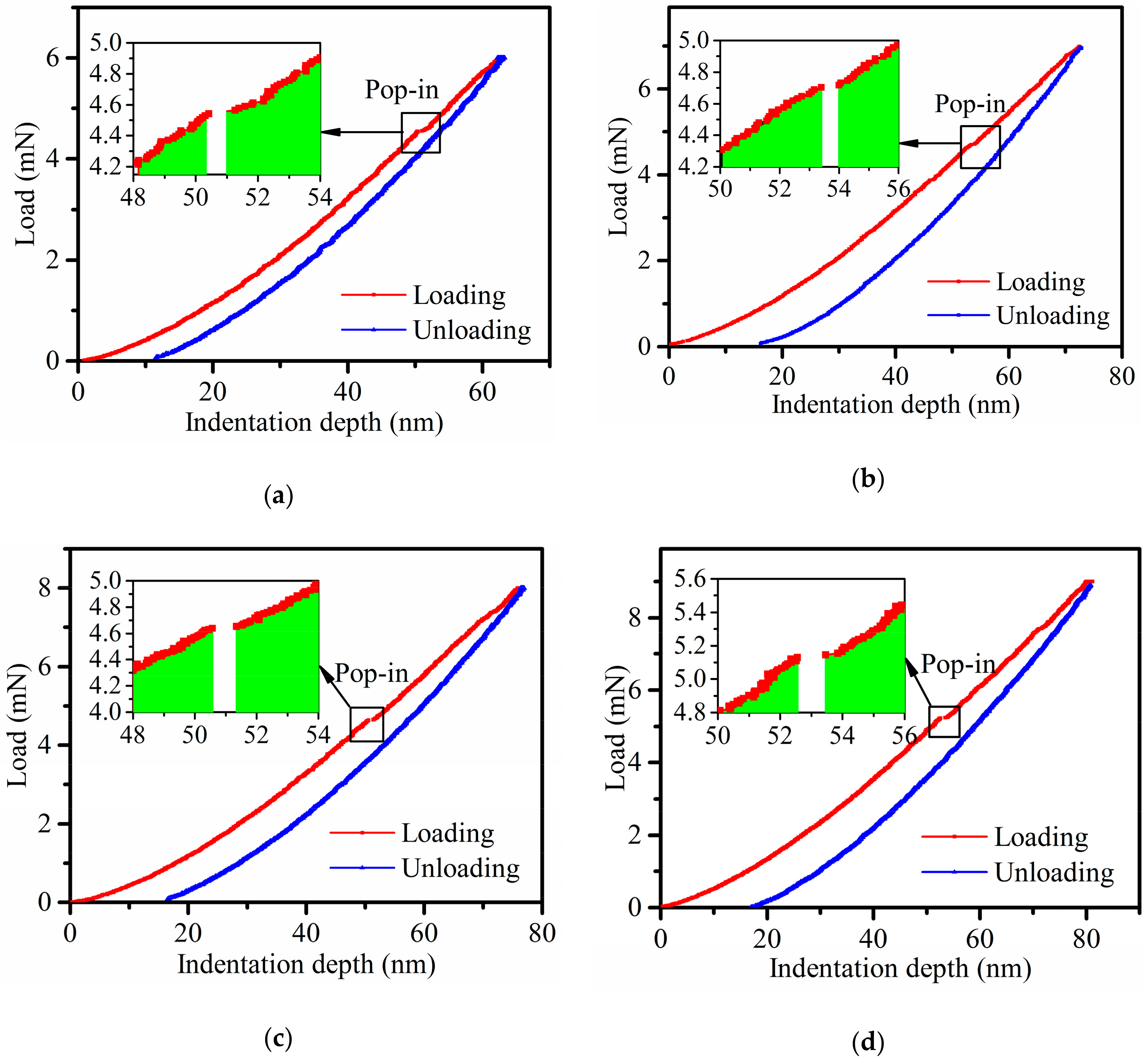



| Max Load (mN) | Indentation Depth (nm) | First Pop-in Depth (nm) | First Pop-in Load (mN) |
|---|---|---|---|
| 6 | 62 | 50.3 | 4.56 |
| 7 | 72 | 53.4 | 4.72 |
| 8 | 77 | 50.6 | 4.75 |
| 9 | 82 | 52.6 | 5.16 |
| Average | - | 51.7 | 4.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, P.; Li, S.; Li, Y.; Liang, L.; Yin, X. Mechanical Behavior Investigation of 4H-SiC Single Crystal at the Micro–Nano Scale. Micromachines 2020, 11, 102. https://doi.org/10.3390/mi11010102
Chai P, Li S, Li Y, Liang L, Yin X. Mechanical Behavior Investigation of 4H-SiC Single Crystal at the Micro–Nano Scale. Micromachines. 2020; 11(1):102. https://doi.org/10.3390/mi11010102
Chicago/Turabian StyleChai, Peng, Shujuan Li, Yan Li, Lie Liang, and Xincheng Yin. 2020. "Mechanical Behavior Investigation of 4H-SiC Single Crystal at the Micro–Nano Scale" Micromachines 11, no. 1: 102. https://doi.org/10.3390/mi11010102
APA StyleChai, P., Li, S., Li, Y., Liang, L., & Yin, X. (2020). Mechanical Behavior Investigation of 4H-SiC Single Crystal at the Micro–Nano Scale. Micromachines, 11(1), 102. https://doi.org/10.3390/mi11010102





