An Empirical Model for GaN Light Emitters with Dot-in-Wire Polar Nanostructures
Abstract
:1. Introduction
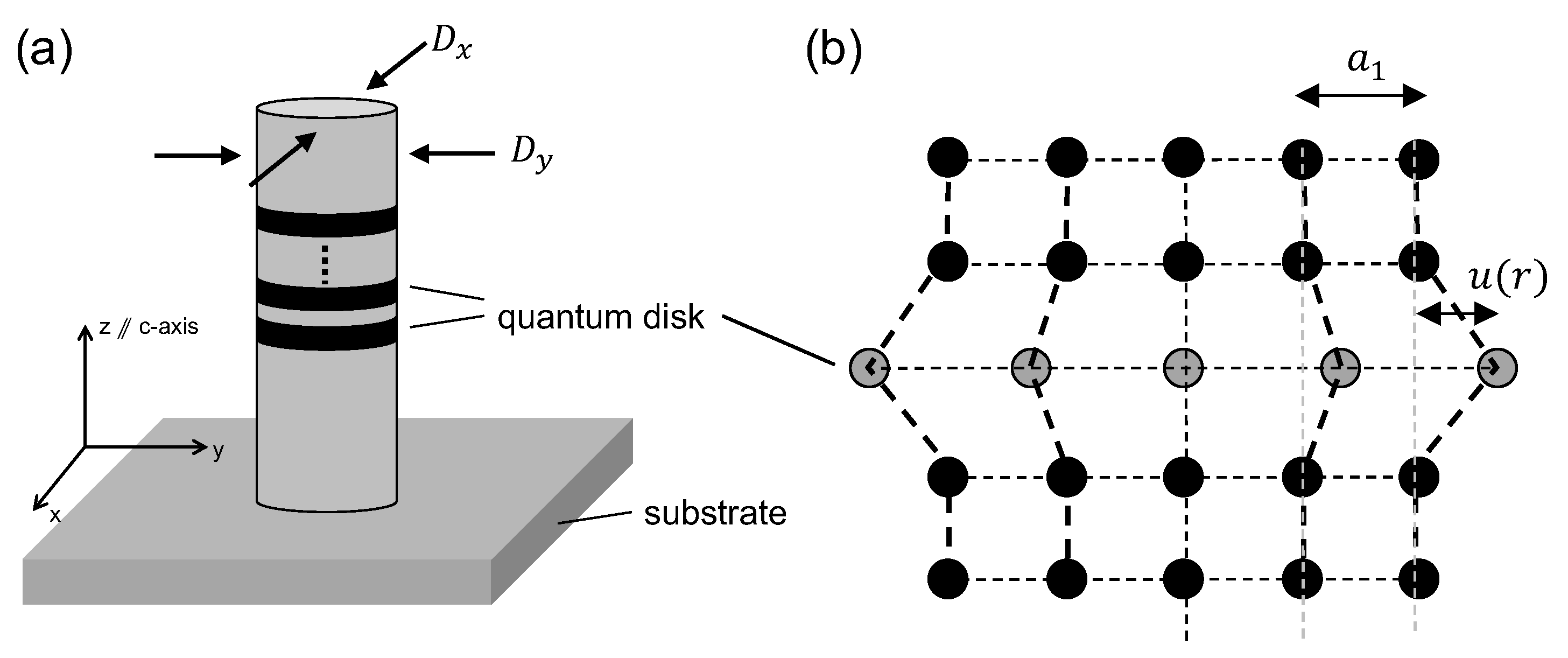
2. Methodology
2.1. Theoretical Model
2.2. Experimental Method
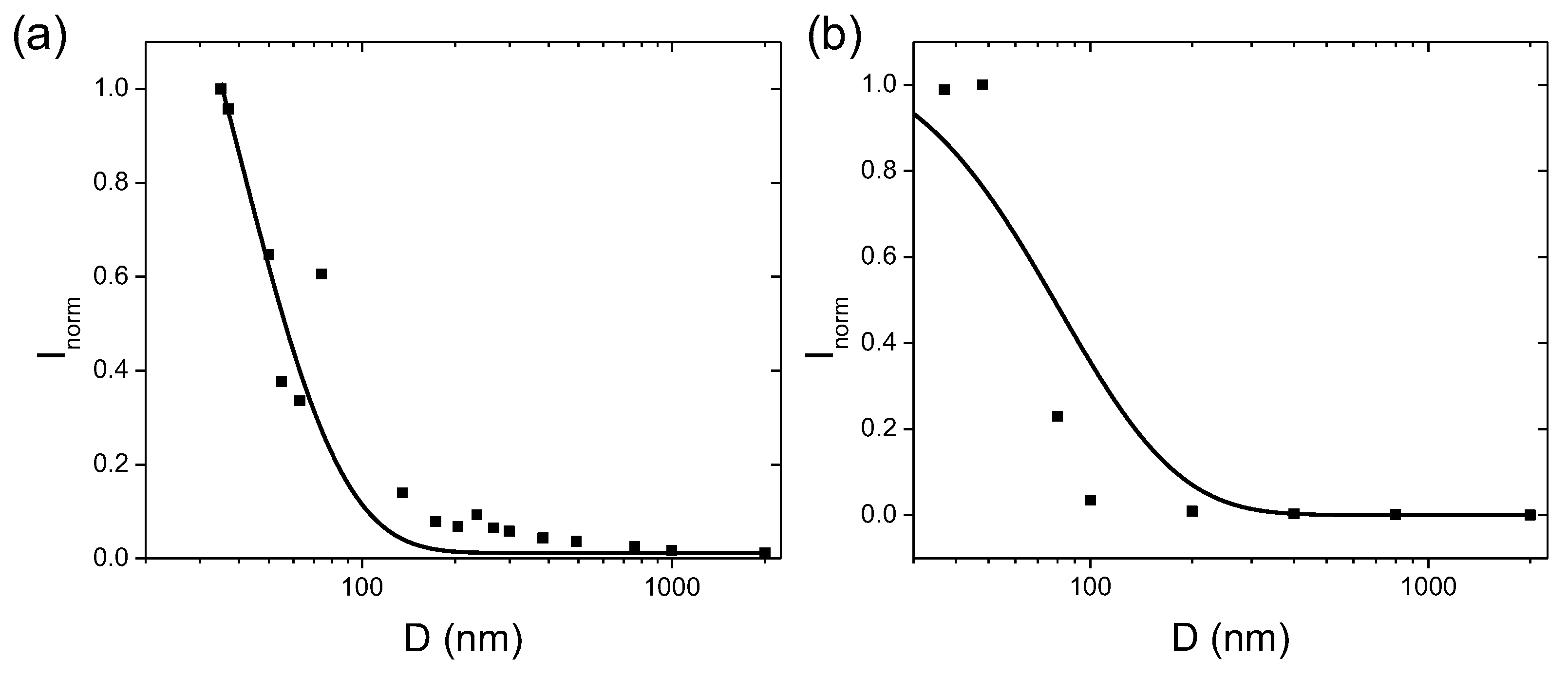
3. Results and Discussions
3.1. Emission Wavelength
3.2. Optical Intensity
3.3. Emission Polarization
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nakamura, S. Nobel Lecture: Background story of the invention of efficient blue InGaN light emitting diodes. Rev. Mod. Phys. 2015, 87, 1139–1151. [Google Scholar] [CrossRef]
- Weisbuch, C.; Piccardo, M.; Martinelli, L.; Iveland, J.; Peretti, J.; Speck, J.S. The efficiency challenge of nitride light-emitting diodes for lighting. Phys. Status Solidi (A) Appl. Mater. Sci. 2015, 212, 899–913. [Google Scholar] [CrossRef]
- Waag, A.; Wang, X.; Fündling, S.; Ledig, J.; Erenburg, M.; Neumann, R.; Al Suleiman, M.; Merzsch, S.; Wei, J.; Li, S.; et al. The nanorod approach: GaN NanoLEDs for solid state lighting. Phys. Status Solidi (C) 2011, 8, 2296–2301. [Google Scholar] [CrossRef]
- Wierer, J.J.; Tansu, N.; Fischer, A.J.; Tsao, J.Y. III-nitride quantum dots for ultra-efficient solid-state lighting. Laser Photonics Rev. 2016, 10, 612–622. [Google Scholar] [CrossRef]
- Chang, S.P.; Chen, Y.C.; Huang, J.K.; Cheng, Y.J.; Chang, J.R.; Sou, K.P.; Kang, Y.T.; Yang, H.C.; Hsu, T.C.; Kuo, H.C.; et al. Electrically driven nanopyramid green light emitting diode. Appl. Phys. Lett. 2012, 100, 061106. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Zhang, M.; Banerjee, A.; Bhattacharya, P. Catalyst-Free InGaN/GaN Nanowire Light Emitting Diodes Grown on (001) Silicon by Molecular Beam Epitaxy. Nano Lett. 2010, 10, 3355–3359. [Google Scholar] [CrossRef]
- Wang, A.; Li, P.; Zhang, J.; Zhang, J.; Li, L.; Wang, Y. 45 Gbps high-speed real-time physical random bit generator. Opt. Express 2013, 21, 20452. [Google Scholar] [CrossRef]
- Zhao, S.; Connie, A.T.; Dastjerdi, M.H.; Kong, X.H.; Wang, Q.; Djavid, M.; Sadaf, S.; Liu, X.D.; Shih, I.; Guo, H.; et al. Aluminum nitride nanowire light emitting diodes: Breaking the fundamental bottleneck of deep ultraviolet light sources. Sci. Rep. 2015, 5, 8332. [Google Scholar] [CrossRef]
- Chen, X.; Li, X.; Shao, J.; An, N.; Tian, H.; Wang, C.; Han, T.; Wang, L.; Lu, B. High-Performance Piezoelectric Nanogenerators with Imprinted P(VDF-TrFE)/BaTiO3 Nanocomposite Micropillars for Self-Powered Flexible Sensors. Small 2017, 13, 1–12. [Google Scholar] [CrossRef]
- Nguyen, H.P.T.; Zhang, S.; Cui, K.; Korinek, A.; Botton, G.A.; Mi, Z. High-efficiency InGaN/GaN dot-in-a-wire red light-emitting diodes. IEEE Photonics Technol. Lett. 2012, 24, 321–323. [Google Scholar] [CrossRef]
- Kishino, K.; Nagashima, K.; Yamano, K. Monolithic Integration of InGaN-Based Nanocolumn Light-Emitting Diodes with Different Emission Colors. Appl. Phys. Express 2013, 6, 12101. [Google Scholar] [CrossRef]
- Kawakami, Y.; Kaneta, A.; Su, L.; Zhu, Y.; Okamoto, K.; Funato, M.; Kikuchi, A.; Kishino, K. Optical properties of InGaN/GaN nanopillars fabricated by postgrowth chemically assisted ion beam etching. J. Appl. Phys. 2010, 107, 23522. [Google Scholar] [CrossRef] [Green Version]
- Keller, S.; Schaake, C.; Fichtenbaum, N.A.; Neufeld, C.J.; Wu, Y.; McGroddy, K.; David, A.; DenBaars, S.P.; Weisbuch, C.; Speck, J.S.; et al. Optical and structural properties of GaN nanopillar and nanostripe arrays with embedded InGaN/GaN multi-quantum wells. J. Appl. Phys. 2006, 100, 054314. [Google Scholar] [CrossRef]
- Li, C.K.; Piccardo, M.; Lu, L.S.; Mayboroda, S.; Martinelli, L.; Peretti, J.; Speck, J.S.; Weisbuch, C.; Filoche, M.; Wu, Y.R. Localization landscape theory of disorder in semiconductors. III. Application to carrier transport and recombination in light emitting diodes. Phys. Rev. B 2017, 95, 144206. [Google Scholar] [CrossRef] [Green Version]
- Chung, K.; Sui, J.; Demory, B.; Ku, P.C. Color mixing from monolithically integrated InGaN-based light-emitting diodes by local strain engineering. Appl. Phys. Lett. 2017, 111, 041101. [Google Scholar] [CrossRef]
- Teng, C.H.; Zhang, L.; Hill, T.A.; Demory, B.; Deng, H.; Ku, P.C. Elliptical quantum dots as on-demand single photons sources with deterministic polarization states. Appl. Phys. Lett. 2015, 107, 191105. [Google Scholar] [CrossRef]
- Nguyen, H.P.T.; Cui, K.; Zhang, S.; Fathololoumi, S.; Mi, Z. Full-color InGaN/GaN dot-in-a-wire light emitting diodes on silicon. Nanotechnology 2011, 22, 445202. [Google Scholar] [CrossRef]
- Wang, R.J.; Nguyen, H.P.T.; Connie, A.T.; Lee, J.; Shih, I.S.; Mi, Z.T. Color-tunable, phosphor-free InGaN nanowire light-emitting diode arrays monolithically integrated on silicon. Opt. Express 2014, 22, A1768–A1775. [Google Scholar] [CrossRef]
- Ra, Y.H.; Wang, R.; Woo, S.Y.; Djavid, M.; Sadaf, S.M.; Lee, J.; Botton, G.A.; Mi, Z. Full-Color Single Nanowire Pixels for Projection Displays. Nano Lett. 2016, 16, 4608–4615. [Google Scholar] [CrossRef]
- Sacconi, F.; Auf der Maur, M.; Di Carlo, A. Optoelectronic Properties of Nanocolumn InGaN/GaN LEDs. IEEE Trans. Electron Devices 2012, 59, 2979–2987. [Google Scholar] [CrossRef]
- Teng, C.H.; Zhang, L.; Deng, H.; Ku, P.C. Strain-induced red-green-blue wavelength tuning in InGaN quantum wells. Appl. Phys. Lett. 2016, 108, 71104. [Google Scholar] [CrossRef]
- Agrawal, R.; Espinosa, H.D. Giant Piezoelectric Size Effects in Zinc Oxide and Gallium Nitride Nanowires. A First Principles Investigation. Nano Lett. 2011, 11, 786–790. [Google Scholar] [CrossRef] [PubMed]
- Teng, C.H.; Zhang, L.; Deng, H.; Ku, P.C. Mechanisms of inhomogeneous broadening in InGaN dot-in-wire structures. J. Appl. Phys. 2019, 126, 083104. [Google Scholar] [CrossRef]
- Zhang, L.; Lee, L.K.; Teng, C.H.; Hill, T.A.; Ku, P.C.; Deng, H. How much better are InGaN/GaN nanodisks than quantum wells-Oscillator strength enhancement and changes in optical properties. Appl. Phys. Lett. 2014, 104, 51116. [Google Scholar] [CrossRef] [Green Version]
- Chung, K.; Sui, J.; Demory, B.; Teng, C.H.; Ku, P.C. Monolithic integration of individually addressable light-emitting diode color pixels. Appl. Phys. Lett. 2017, 110, 111103. [Google Scholar] [CrossRef]
- Chuang, S.L. Physics of Photonic Devices; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, J.; Ku, P.-C. An Empirical Model for GaN Light Emitters with Dot-in-Wire Polar Nanostructures. Micromachines 2020, 11, 82. https://doi.org/10.3390/mi11010082
Sui J, Ku P-C. An Empirical Model for GaN Light Emitters with Dot-in-Wire Polar Nanostructures. Micromachines. 2020; 11(1):82. https://doi.org/10.3390/mi11010082
Chicago/Turabian StyleSui, Jingyang, and Pei-Cheng Ku. 2020. "An Empirical Model for GaN Light Emitters with Dot-in-Wire Polar Nanostructures" Micromachines 11, no. 1: 82. https://doi.org/10.3390/mi11010082
APA StyleSui, J., & Ku, P.-C. (2020). An Empirical Model for GaN Light Emitters with Dot-in-Wire Polar Nanostructures. Micromachines, 11(1), 82. https://doi.org/10.3390/mi11010082





