Actuating Voltage Waveform Optimization of Piezoelectric Inkjet Printhead for Suppression of Residual Vibrations
Abstract
:1. Introduction
2. Equivalent Circuit Model
3. Results and Discussion
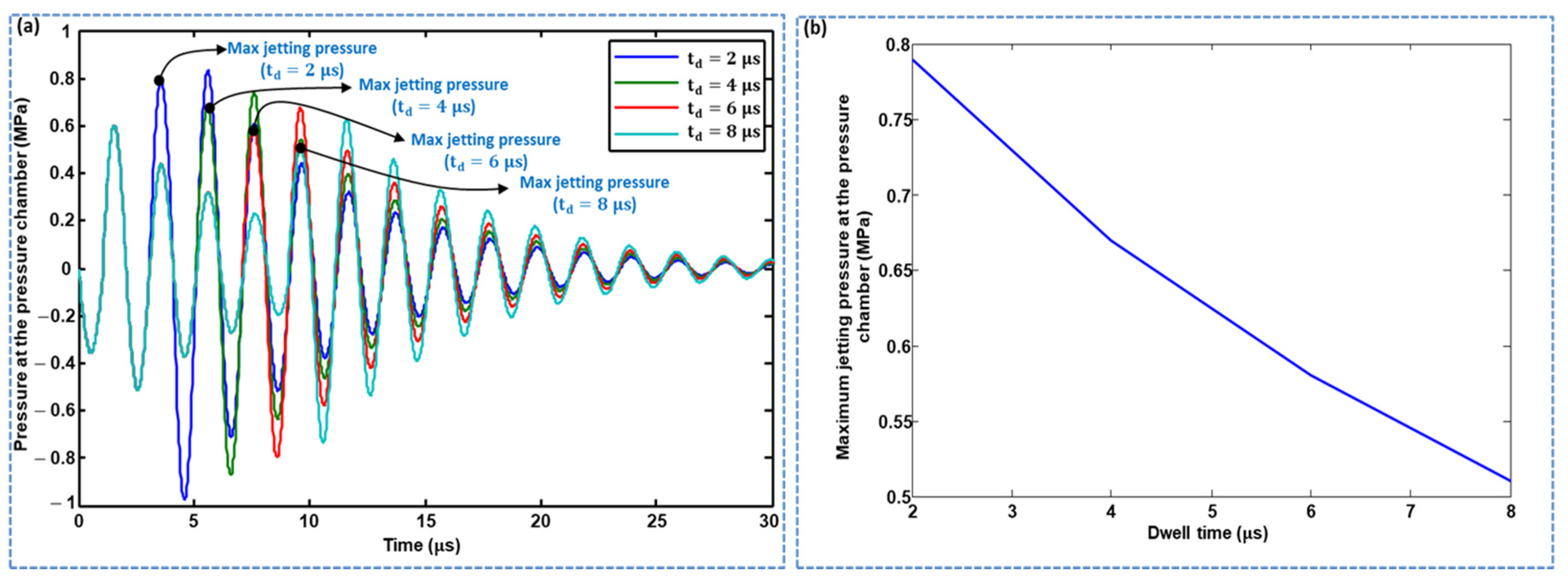
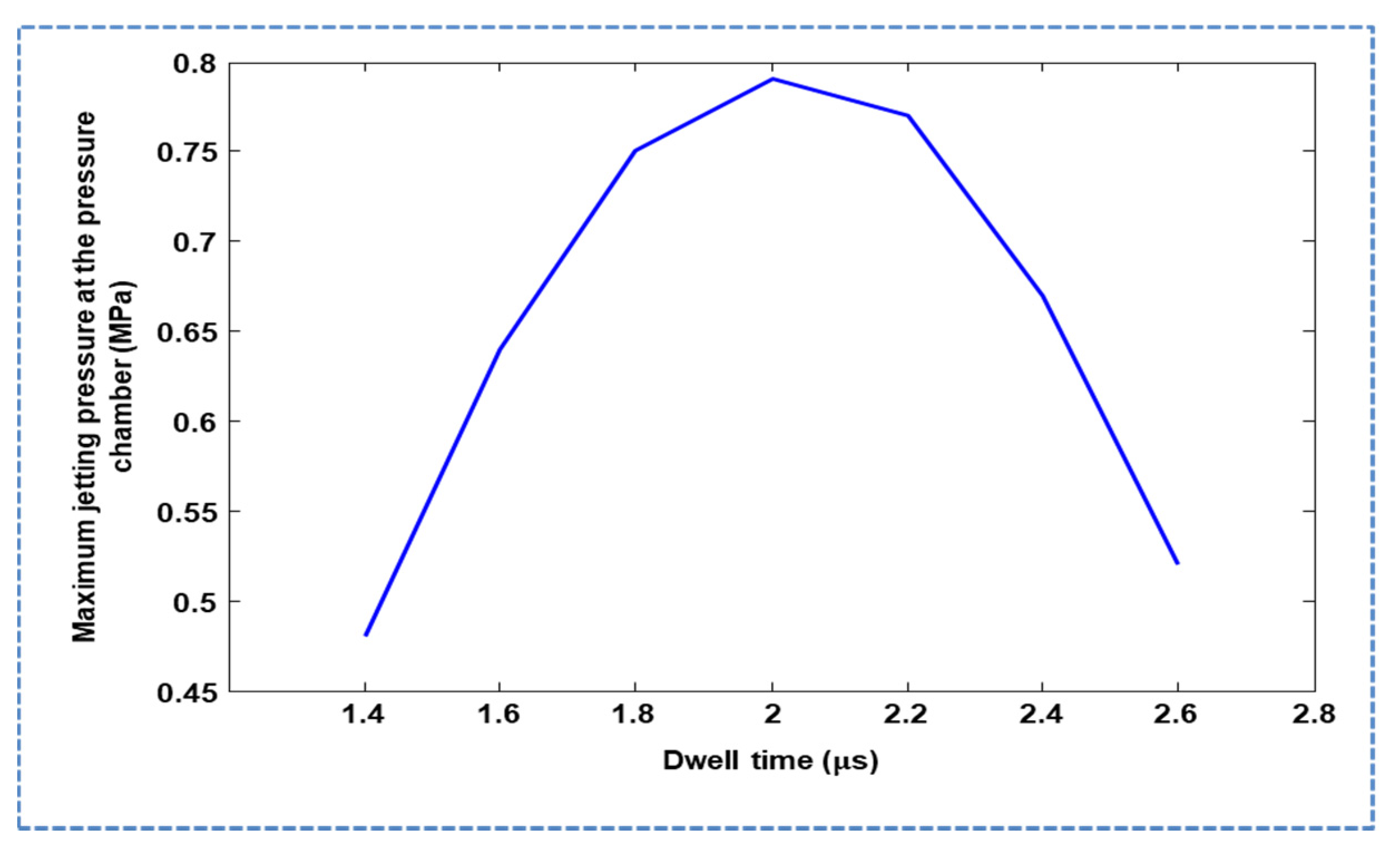
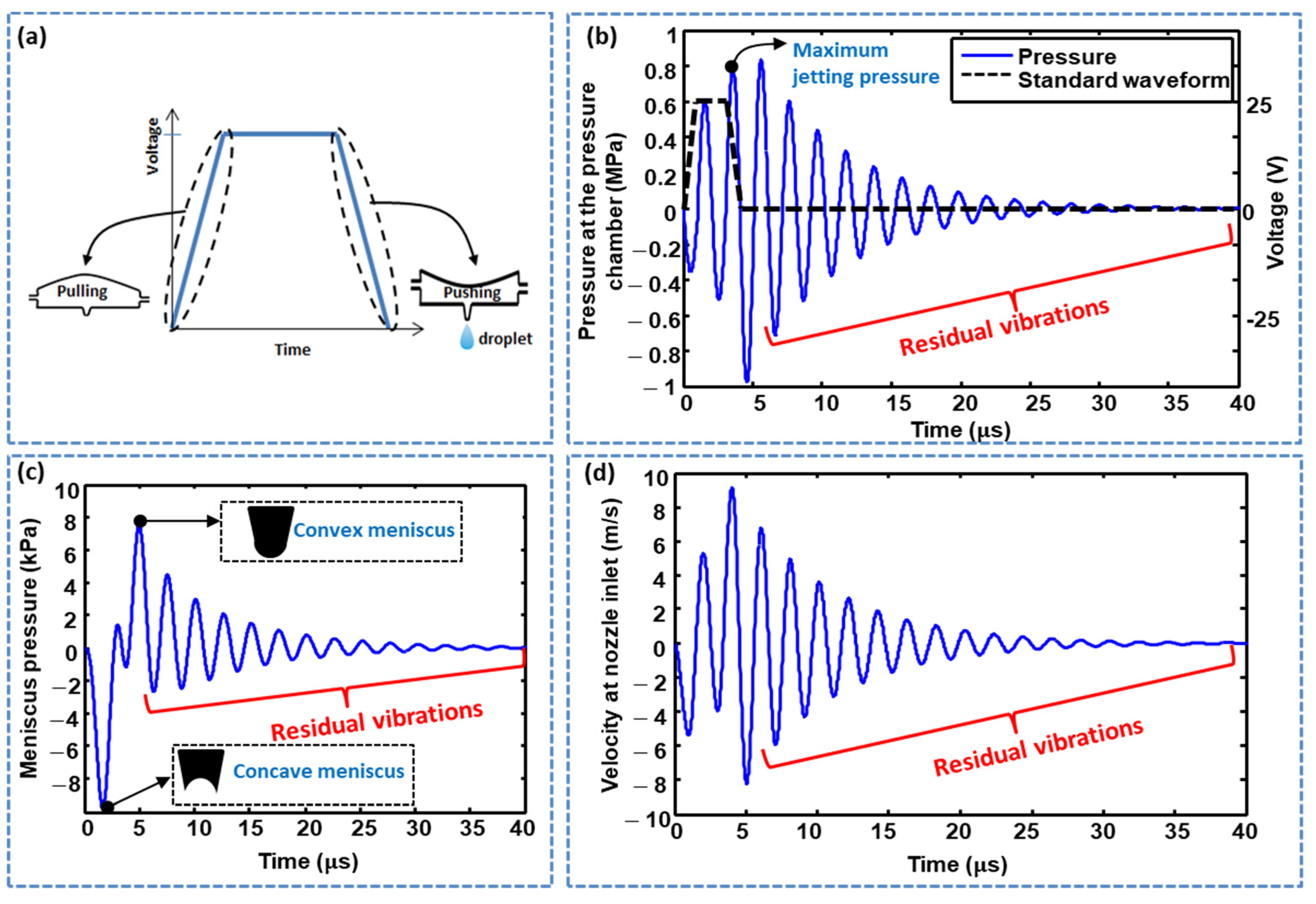
3.1. Standard Waveform Optimization
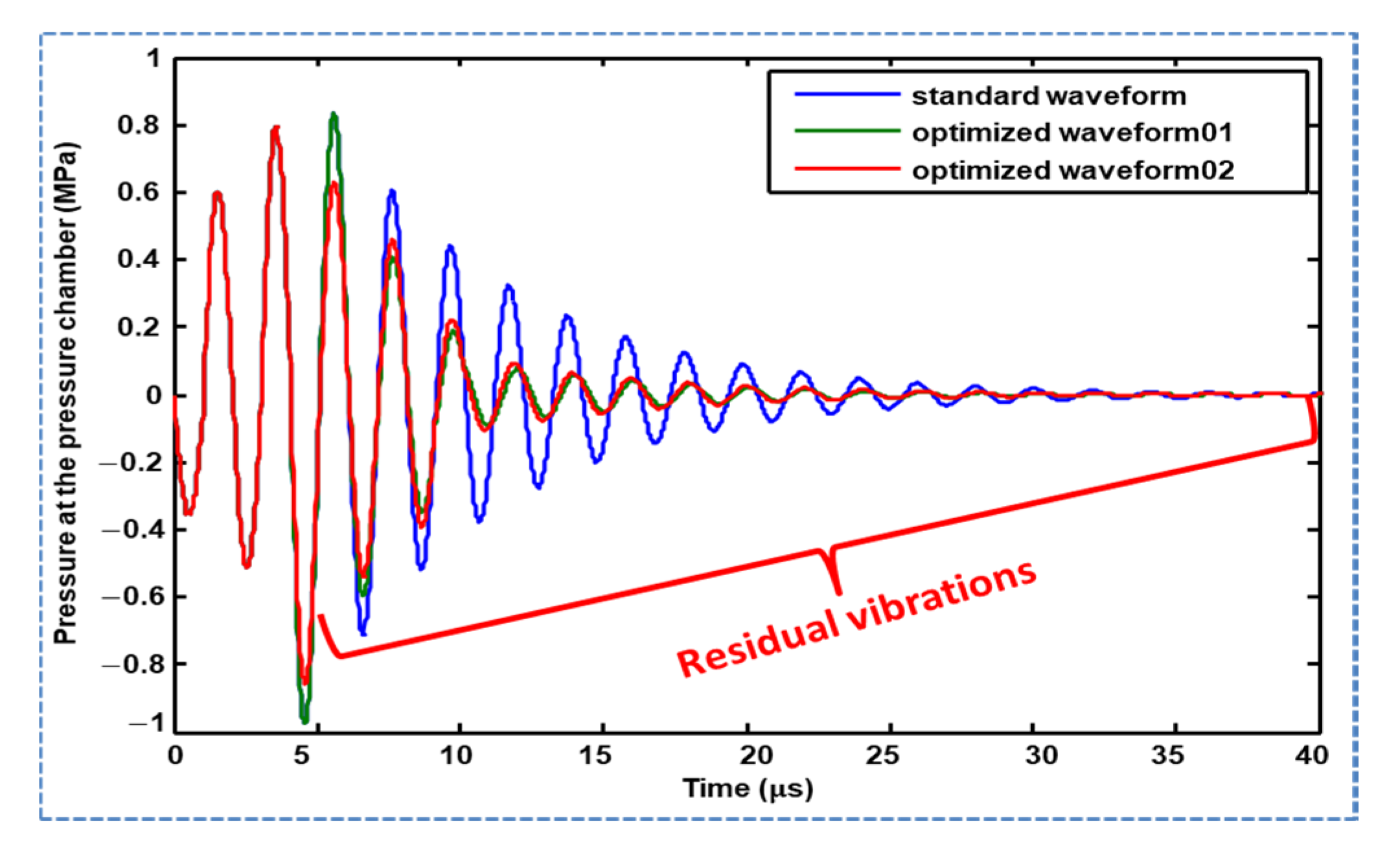
3.2. Optimization of Waveform 01 and Waveform 02
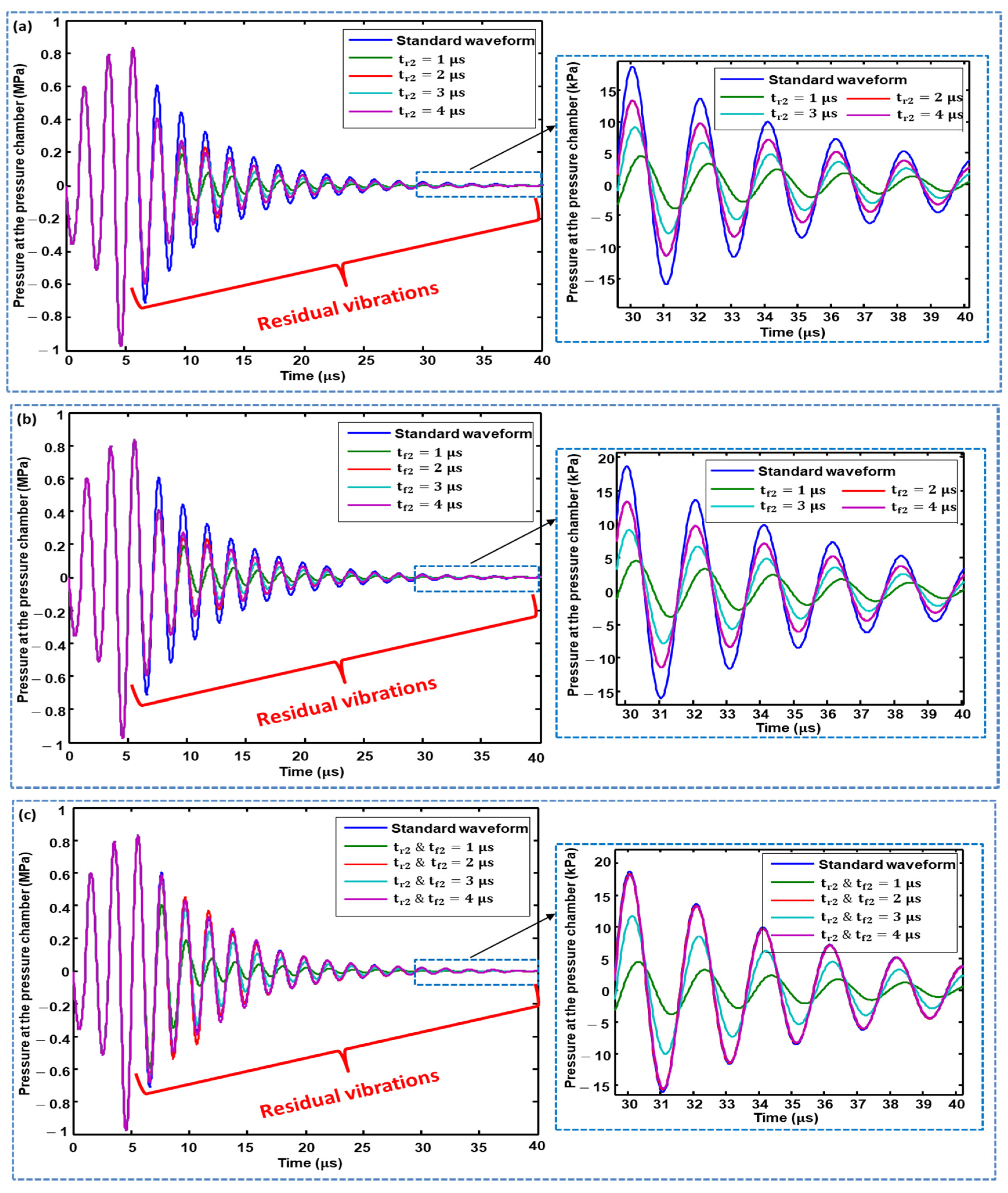
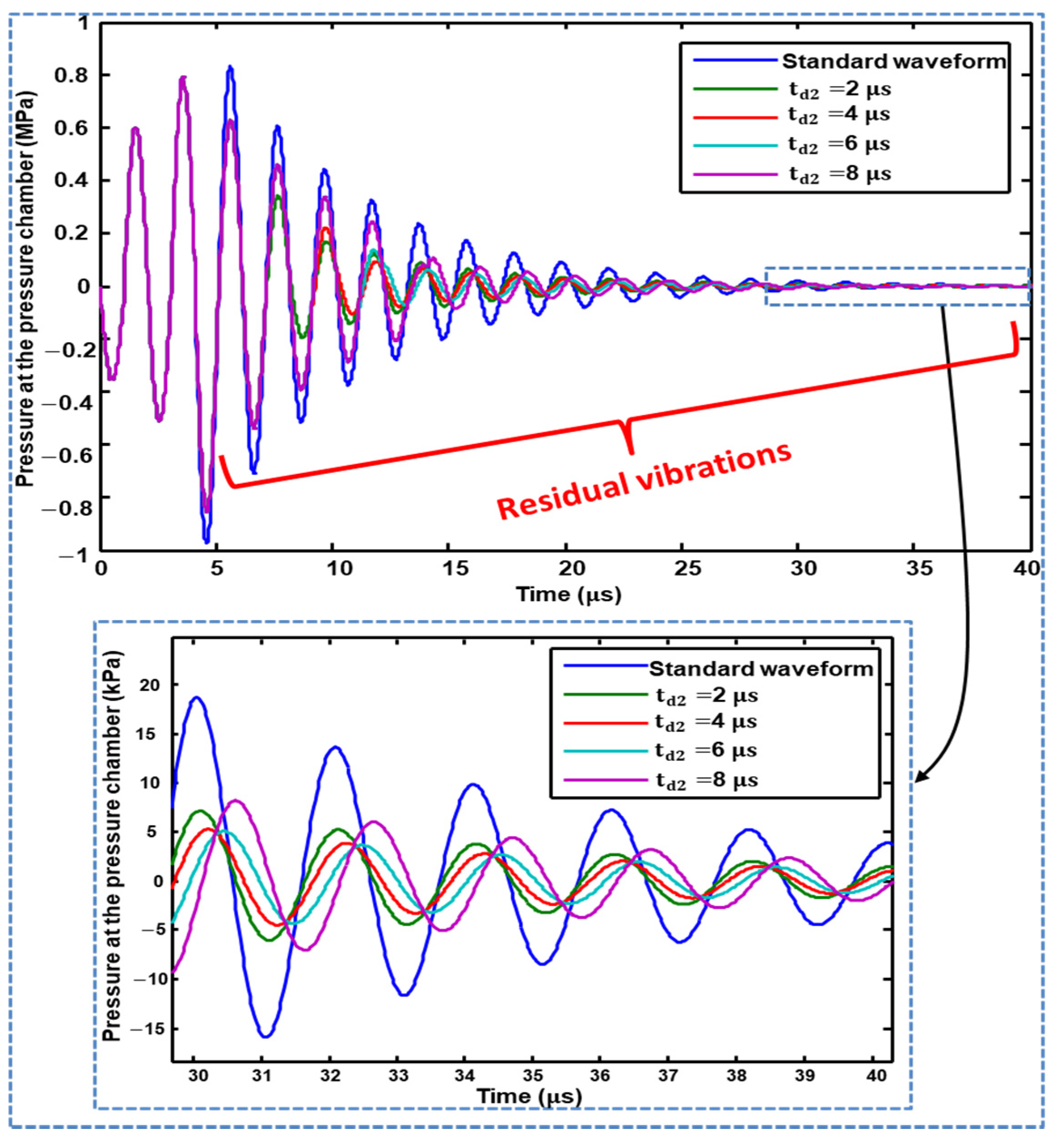
3.2.1. Waveform 01 Optimization
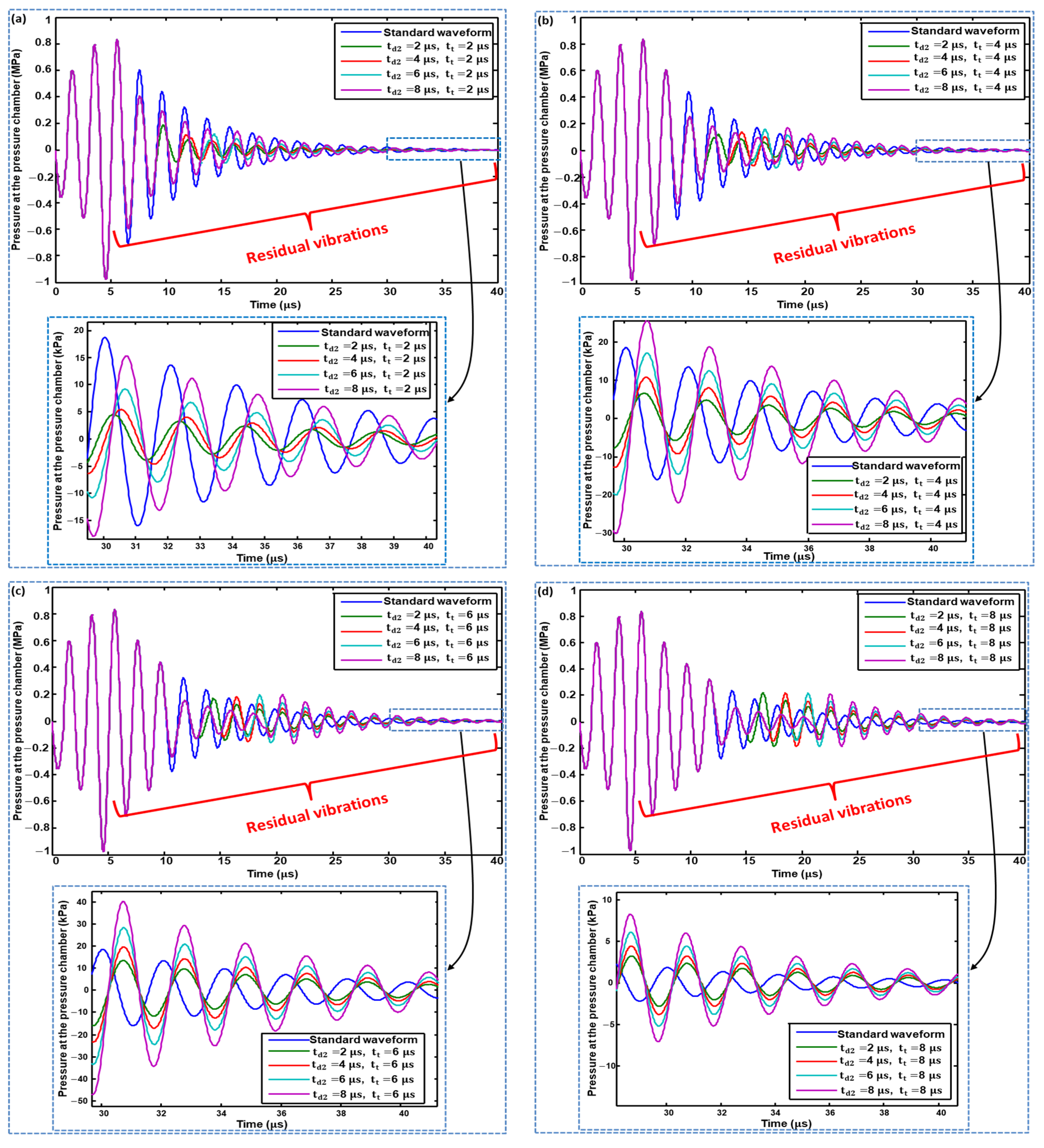
3.2.2. Waveform 02 Optimization
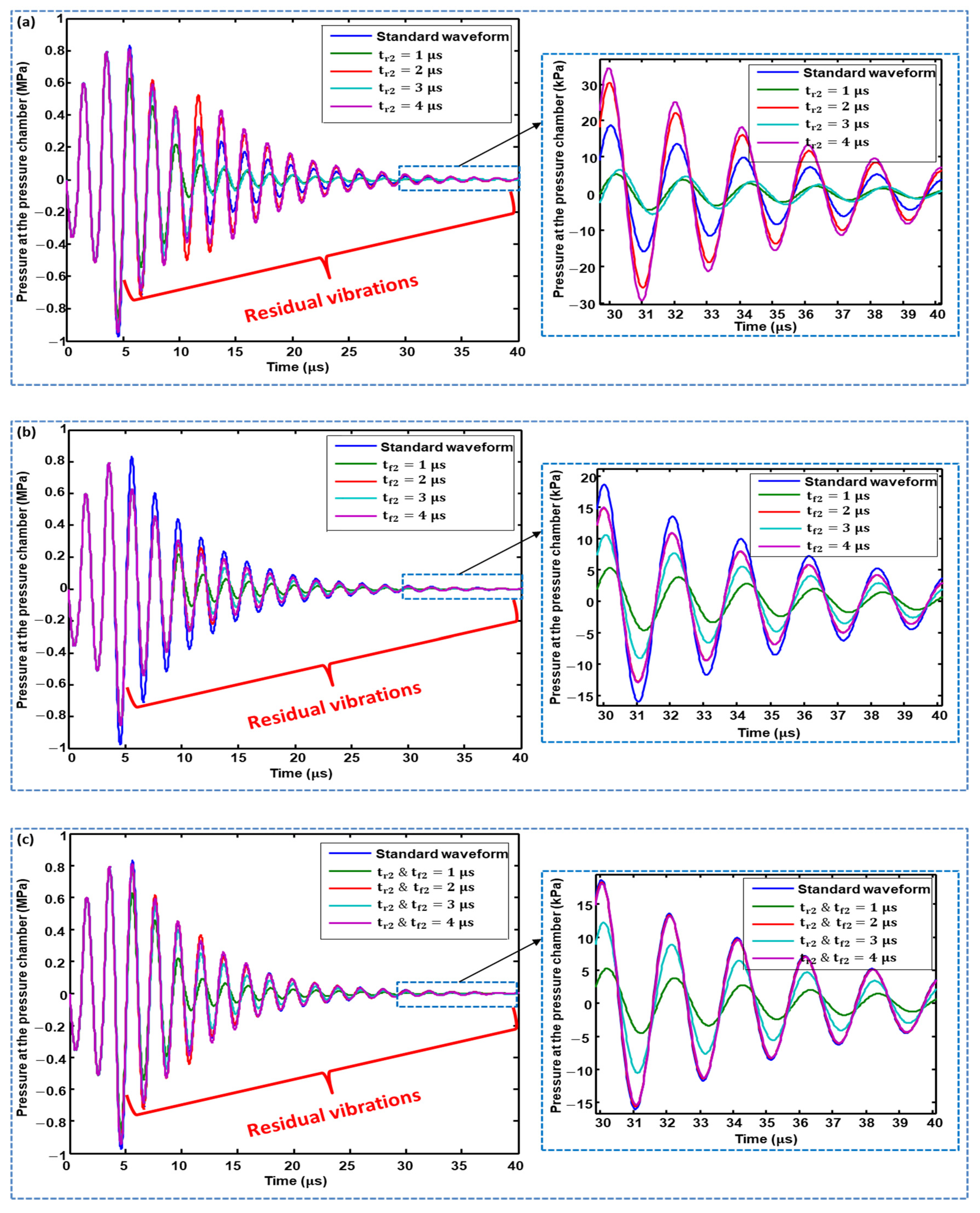
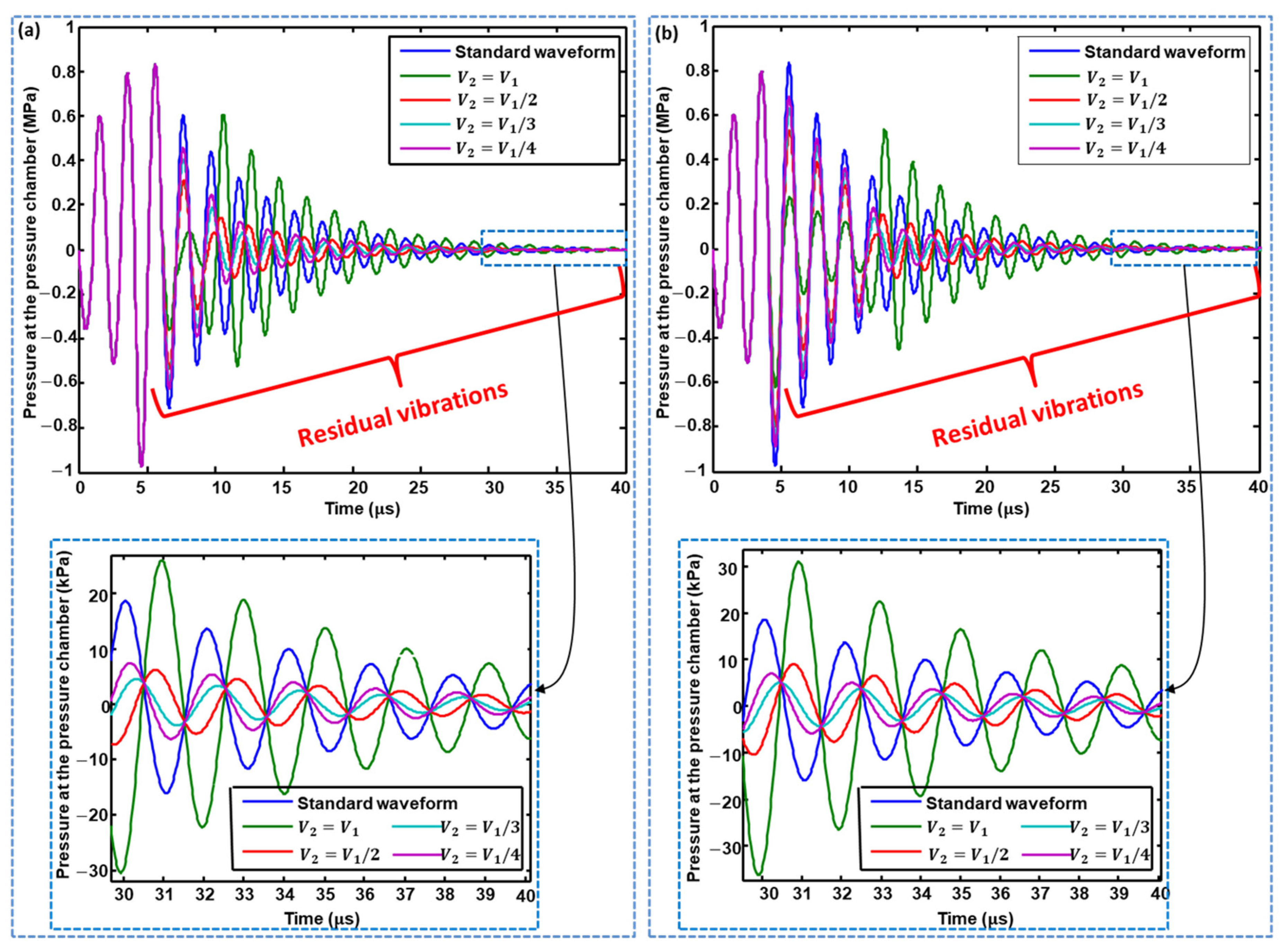
3.2.3. Voltage Amplitude Optimization of 2nd Pulse
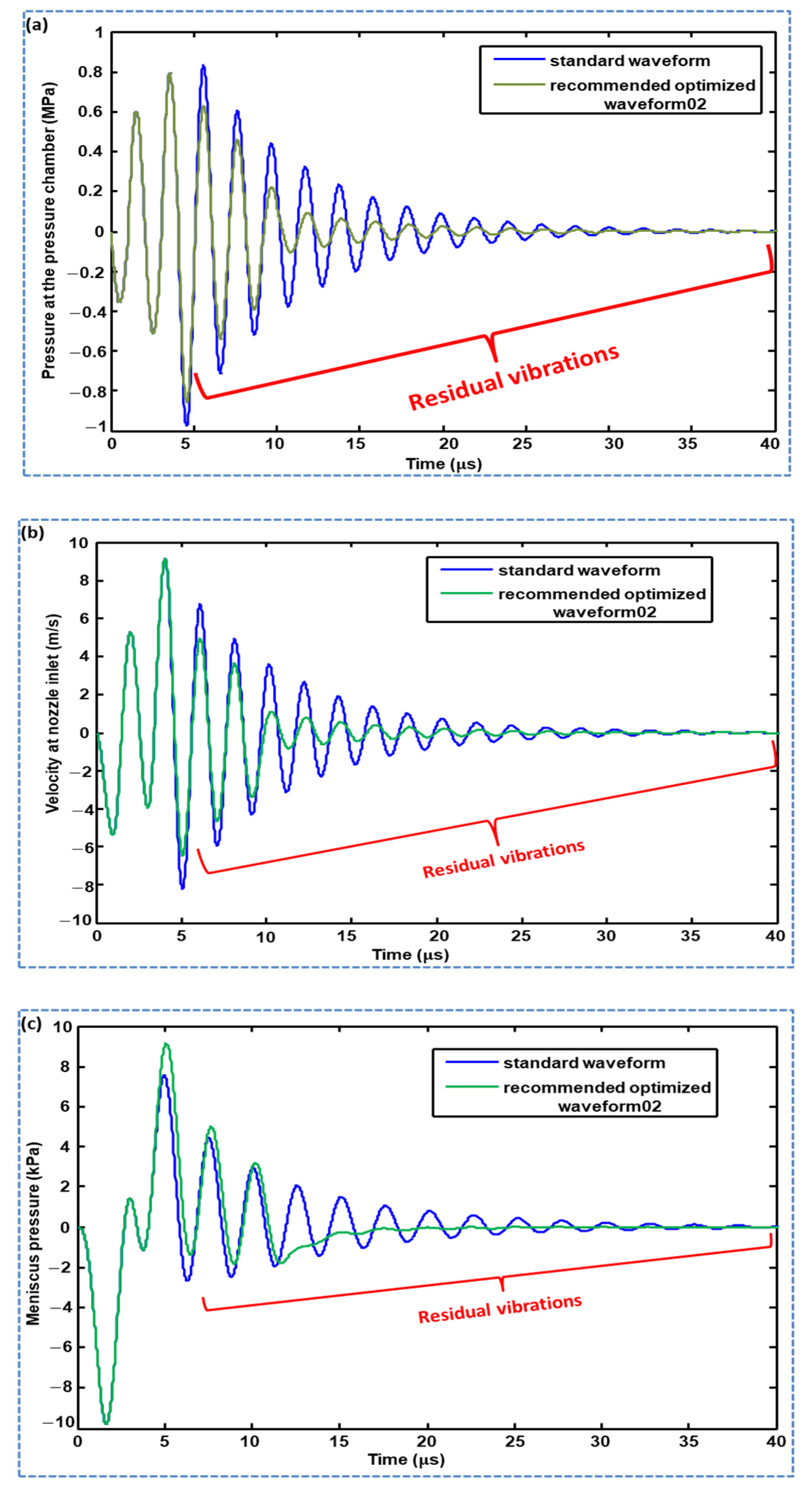
3.3. Comparison of Waveform 01 and Waveform 02
4. Conclusions and Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Trimizi, M.A.; Ham, Y.B.; An, B.C.; Choi, Y.M.; Park, J.H.; Yun, S.N. Development of a piezo-driven liquid jet dispenser with hinge-lever amplification mechanism. Micromachines 2020, 11, 117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foresti, D.; Kroll, K.T.; Amissah, R.; Sillani, F.; Homan, K.A.; Poulikakos, D.; Lewis, J.A. Acoustophoretic printing. Sci. Adv. 2018, 4, eaat1659. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Liu, J.; Li, K.; Liu, Y. Piezoelectric micro-jet devices: A review. Sens. Actuators A Phys. 2019, 297, 111552. [Google Scholar] [CrossRef]
- Lim, J.H.; Kuk, K.; Shin, S.J.; Baek, S.S.; Kim, Y.J.; Shin, J.W.; Oh, Y.S. Failure mechanisms in thermal inkjet printhead analyzed by experiments and numerical simulation. Microeletron. Reliab. 2005, 45, 473–478. [Google Scholar] [CrossRef]
- Gao, D.; Zhou, J.G. Designs and applications of electrohydrodynamic 3D printing. Int. J. Bioprinting 2019, 5, 172. [Google Scholar] [CrossRef] [PubMed]
- Gruene, M.; Unger, C.; Koch, L.; Deiwick, A.; Chichkov, B. Dispensing pico to nanolitre of a natural hydrogel by laser-assisted bioprinting. BioMed. Eng. 2011, 10, 19. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, M.K.; Friend, J.R.; Yeo, L.Y. Interfacial jetting phenomena induced by focused surface vibrations. Phys. Rev. Lett. 2009, 103, 024501. [Google Scholar] [CrossRef] [Green Version]
- Modak, C.D.; Kumar, A.; Tripathy, A.; Sen, P. Drop impact printing. Nat. Commun. 2020, 11, 4327. [Google Scholar] [CrossRef]
- Ezzeldin, M.; Van den Bosch, P.P.J.; Weiland, S. Improving the performance of an inkjet printhead using model predictive control. IFAC Proc. Vol. 2011, 44, 11544–11549. [Google Scholar] [CrossRef] [Green Version]
- Khalate, A.A.; Bombois, X.; Babuška, R.; Wijshoff, H.; Waarsing, R. Performance improvement of a drop-on-demand inkjet printhead using an optimization-based feedforward control method. Control Eng. Pract. 2011, 19, 771–781. [Google Scholar] [CrossRef]
- Oktavianty, O.; Haruyama, S.; Ishii, Y.; Darmawan, Z. Effect of front and back suppressing vibration on actuation waveform design of DoD inkjet printer to droplet speed and volume. Univers. J. Mech. Eng. 2019, 7, 12–18. [Google Scholar] [CrossRef]
- Kim, B.H.; Kim, S.I.; Lee, J.C.; Shin, S.J.; Kim, S.J. Dynamic characteristics of a piezoelectric driven inkjet printhead fabricated using MEMS technology. Sens. Actuators A Phys. 2012, 173, 244–253. [Google Scholar] [CrossRef]
- Kwon, K.S.; Kim, W. A waveform design method for high-speed inkjet printing based on self-sensing measurement. Sens. Actuators A Phys. 2010, 140, 75–83. [Google Scholar] [CrossRef]
- Kwon, K.S. Waveform design methods for piezo inkjet dispensers based on measured meniscus motion. J. Microelectromech. Syst. 2009, 18, 1118–1125. [Google Scholar] [CrossRef]
- Chung, J.; Ko, S.; Grigoropoulos, C.P.; Bieri, N.R.; Dockendorf, C.; Poulikakos, D. Damage-free low temperature pulsed laser printing of gold nanoinks on polymers. J. Heat Transf. 2005, 127, 724–732. [Google Scholar] [CrossRef]
- Bogy, D.B.; Talke, F.E. Experimental and theoretical study of wave propagation phenomena in drop-on-demand ink jet devices. IBM J. Res. Dev. 1984, 28, 314–321. [Google Scholar] [CrossRef]
- Wei, H.; Xiao, X.; Yin, Z.; Yi, M.; Zou, H. A waveform design method for high DPI piezoelectric inkjet print-head based on numerical simulation. Microsyst. Technol. 2017, 23, 5365–5373. [Google Scholar] [CrossRef]
- Shield, T.W.; Bogy, D.B.; Talke, F.E. Drop formation by dod ink-jet nozzles: A comparison of experiment and numerical simulation. IBM J. Res. Dev. 1987, 31, 96–110. [Google Scholar] [CrossRef]
- Wijshoff, H. The dynamics of the piezo inkjet printhead operation. Phys. Rep. 2010, 491, 77–177. [Google Scholar] [CrossRef]
- Kim, S.; Sung, J.; Lee, M.H. Pressure wave and fluid velocity in a bend-mode inkjet nozzle with double PZT actuators. J. Therm. Sci. 2013, 22, 29–35. [Google Scholar] [CrossRef]
- Kim, B.H.; Lee, H.S.; Kim, S.W.; Kang, P.; Park, Y.S. Hydrodynamic responses of a piezoelectric driven MEMS inkjet print-head. Sens. Actuators A Phys. 2014, 210, 131–140. [Google Scholar] [CrossRef]
- Shah, M.A.; Lee, D.G.; Hur, S. Design and characteristic analysis of a MEMS piezo-driven recirculating inkjet printhead using lumped element modeling. Micromachines 2019, 10, 757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Huang, J.; Peng, J. Hydrodynamic response model of a piezoelectric inkjet print-head. Sens. Actuators A Phys. 2019, 285, 50–58. [Google Scholar] [CrossRef]
- Hamano, H.; Shimizu, T.; Shibata, T.; Suetomi, Y.; Hiejima, K.; Kuramochi, Y. Shear-mode piezo inkjet head with two recirculating paths. NIP Digit. Fabr. Conf. 2019, 2019, 173–176. [Google Scholar] [CrossRef]
- Crankshaw, M.; Rulman, M.; Zarezadeh, H.; Douaire, M.; Condie, A. Ink recirculation-Xaar TF TechnologyTM: A study of the benefits. NIP Digit. Fabr. Conf. 2016, 2016, 207–211. [Google Scholar]
- Jackson, N.; Voit, W.; Trip, R.; Condie, A.; Plc, X. Jetting very high viscosities with piezo-electric drop-on-demand printheads for increased capability of photopolymer 3D printing. NIP Digit. Fabr. Conf. 2019, 2019, 89–93. [Google Scholar] [CrossRef]
- Prasad, S.A.N.; Gallas, Q.; Horowitz, S.; Homeijer, B.; Sankar, B.V.; Cattafesta, L.N.; Sheplak, M. Analytical electroacoustic model of a piezoelectric composite circular plate. AIAA J. 2006, 44, 2311–2318. [Google Scholar] [CrossRef]
- Szczech, J.B.; Megaridis, C.M.; Gamota, D.R.; Zhang, J. Fine-line conductor manufacturing using drop-on-demand PZT printing technology. IEEE Trans. Electron. Packag. Manuf. 2002, 25, 26–33. [Google Scholar] [CrossRef]
- Chang, J.B.; Liu, Y.; Huang, B. Effects of dwell time of excitation waveform on meniscus movements for a tubular piezoelectric print-head: Experiments and model. J. Micromech. Microeng. 2017, 27, 075023. [Google Scholar] [CrossRef]
- Chen, A.U.; Basaran, O.A. A new method for significantly reducing drop radius without reducing nozzle radius in drop-on-demand drop production. Phys. Fluids 2002, 14, L1–L4. [Google Scholar] [CrossRef]



| Waveform 01 | Waveform 02 (Recommended) | |||||
|---|---|---|---|---|---|---|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, M.A.; Lee, D.-G.; Lee, B.Y.; Kim, N.W.; An, H.; Hur, S. Actuating Voltage Waveform Optimization of Piezoelectric Inkjet Printhead for Suppression of Residual Vibrations. Micromachines 2020, 11, 900. https://doi.org/10.3390/mi11100900
Shah MA, Lee D-G, Lee BY, Kim NW, An H, Hur S. Actuating Voltage Waveform Optimization of Piezoelectric Inkjet Printhead for Suppression of Residual Vibrations. Micromachines. 2020; 11(10):900. https://doi.org/10.3390/mi11100900
Chicago/Turabian StyleShah, Muhammad Ali, Duck-Gyu Lee, Bo Yeon Lee, Nam Woon Kim, Hyojin An, and Shin Hur. 2020. "Actuating Voltage Waveform Optimization of Piezoelectric Inkjet Printhead for Suppression of Residual Vibrations" Micromachines 11, no. 10: 900. https://doi.org/10.3390/mi11100900
APA StyleShah, M. A., Lee, D.-G., Lee, B. Y., Kim, N. W., An, H., & Hur, S. (2020). Actuating Voltage Waveform Optimization of Piezoelectric Inkjet Printhead for Suppression of Residual Vibrations. Micromachines, 11(10), 900. https://doi.org/10.3390/mi11100900




