An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling
Abstract
:1. Introduction
2. Experiments and Method
2.1. Rolling Experiments
2.2. Measurement and Characterization of Surface
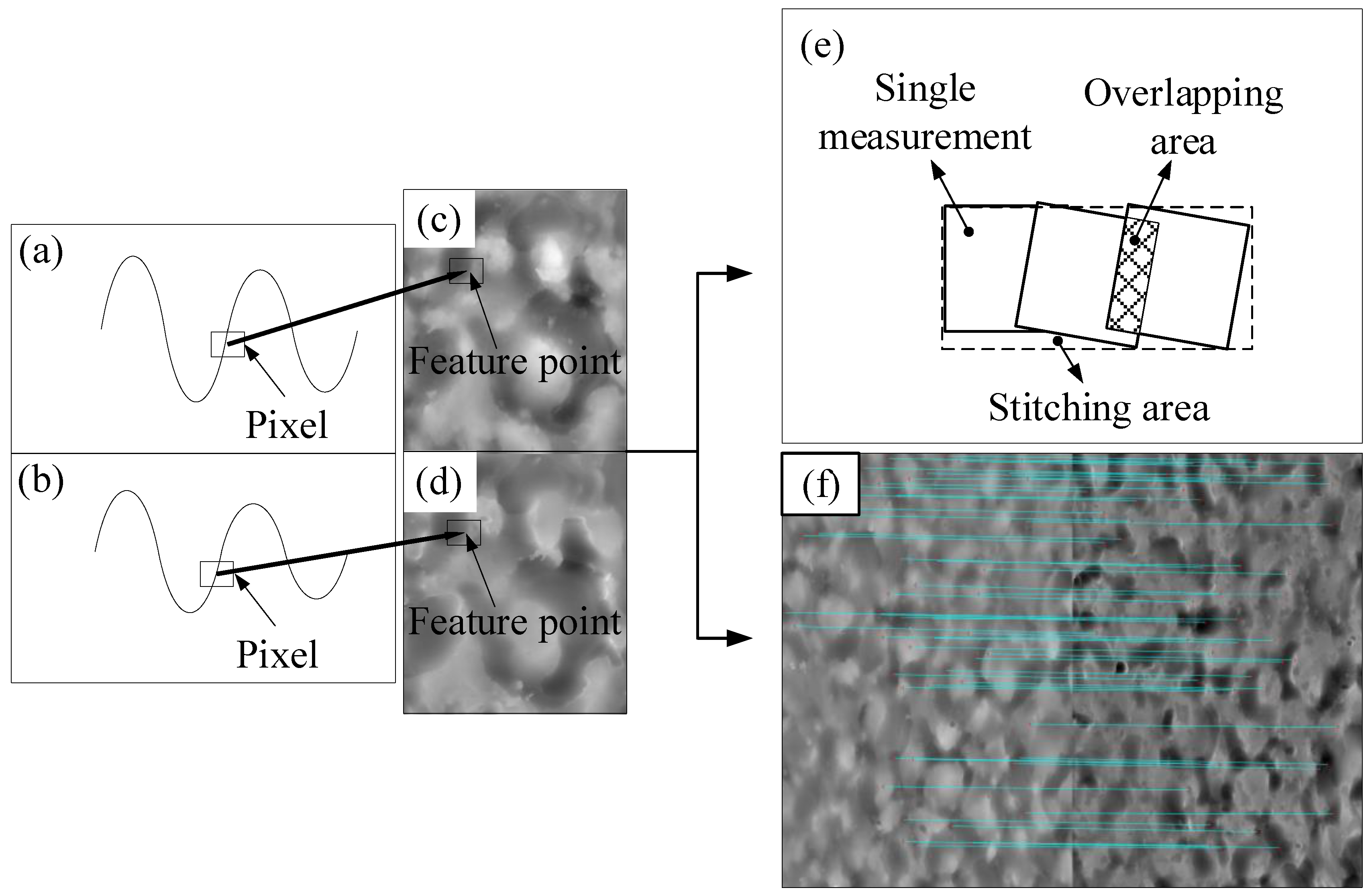
2.3. Surface Microtopography Stitching and Matching Based on Scale-invariant Feature Transform (SIFT) Algorithm
3. Results and Discussion
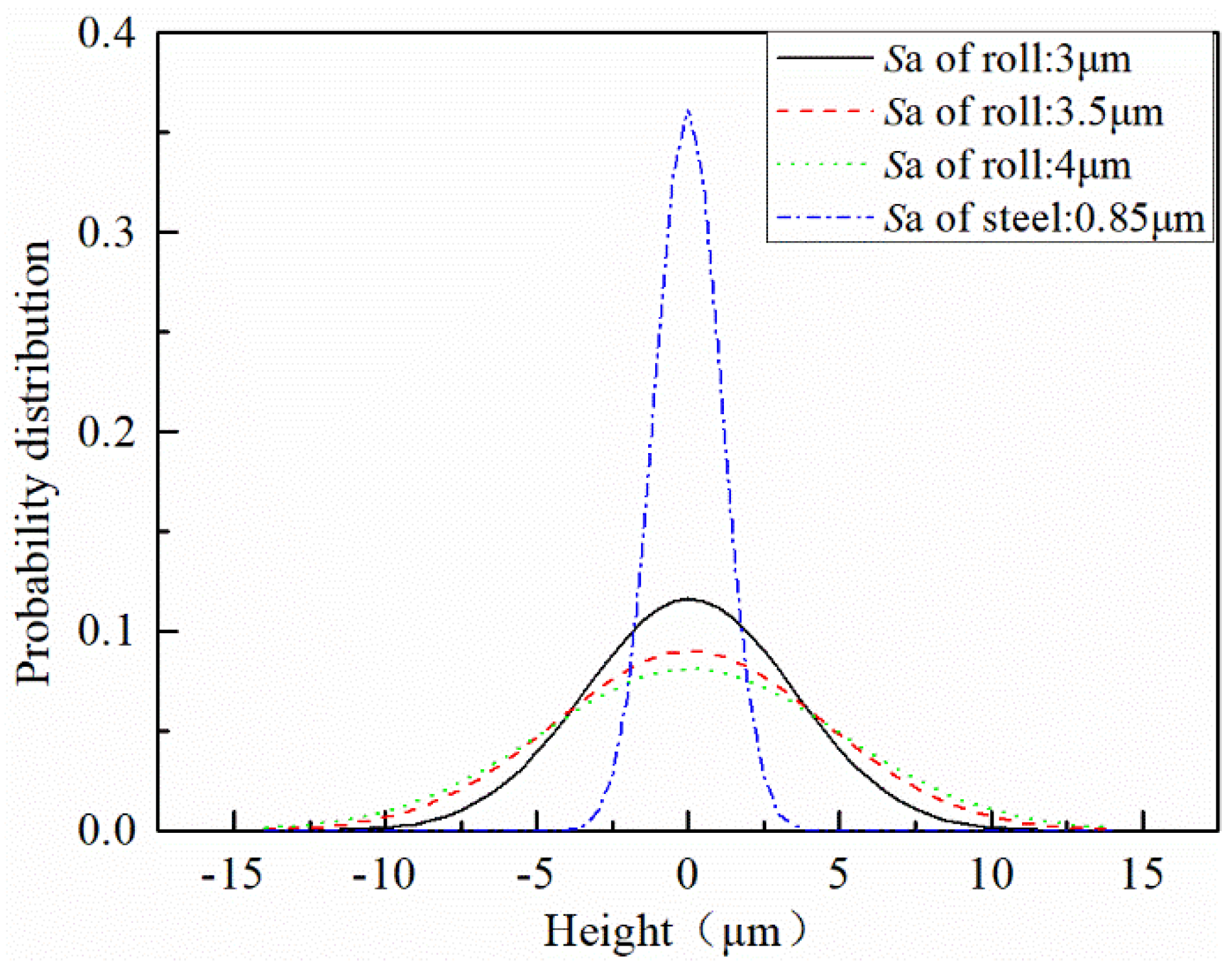
3.1. Roller and Strip Initial Surface Topography
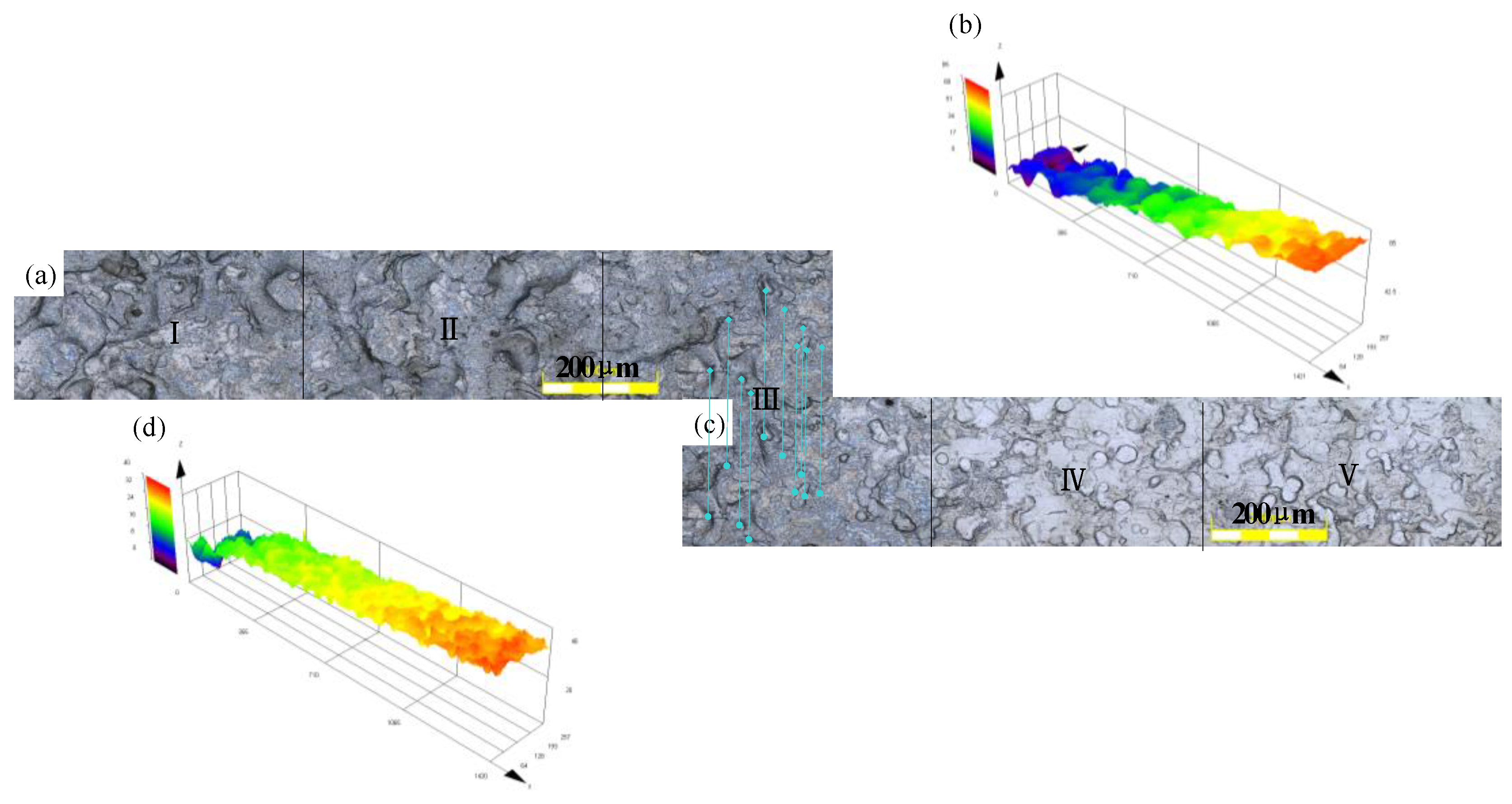
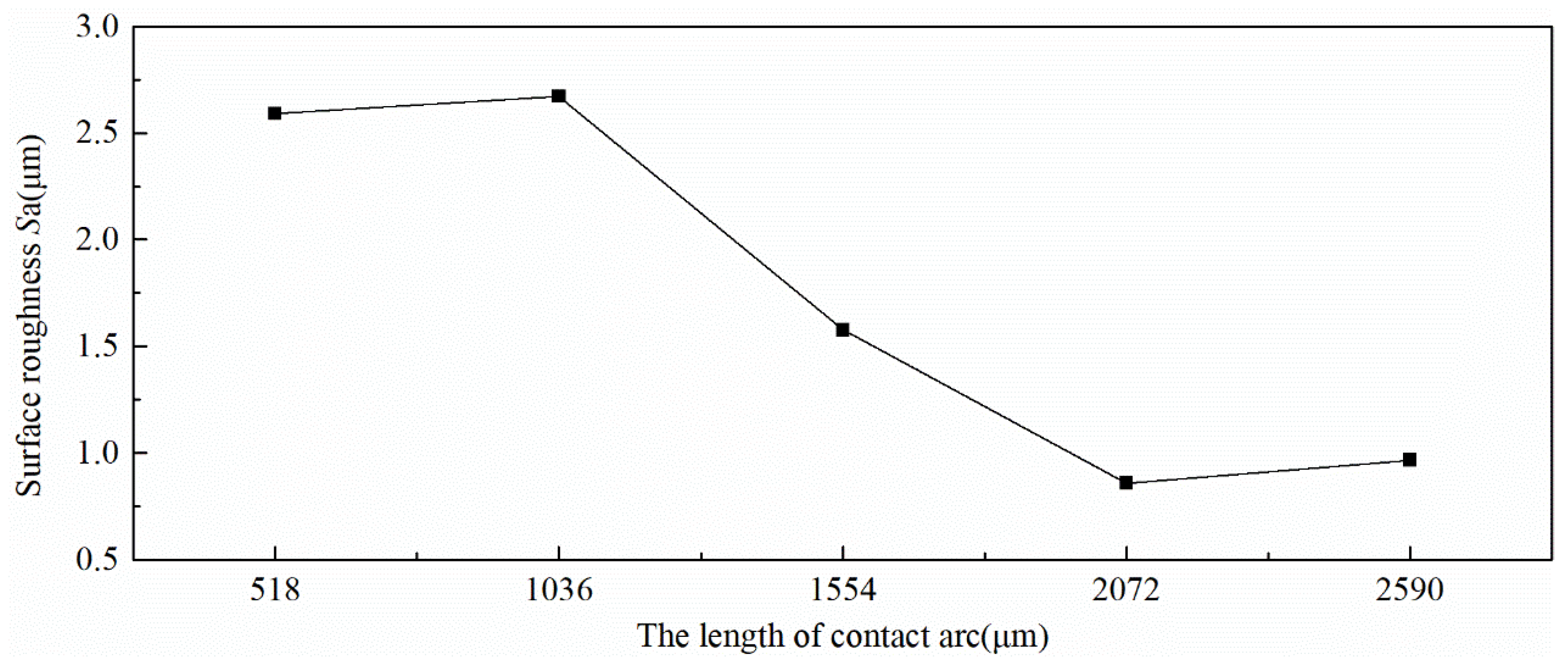
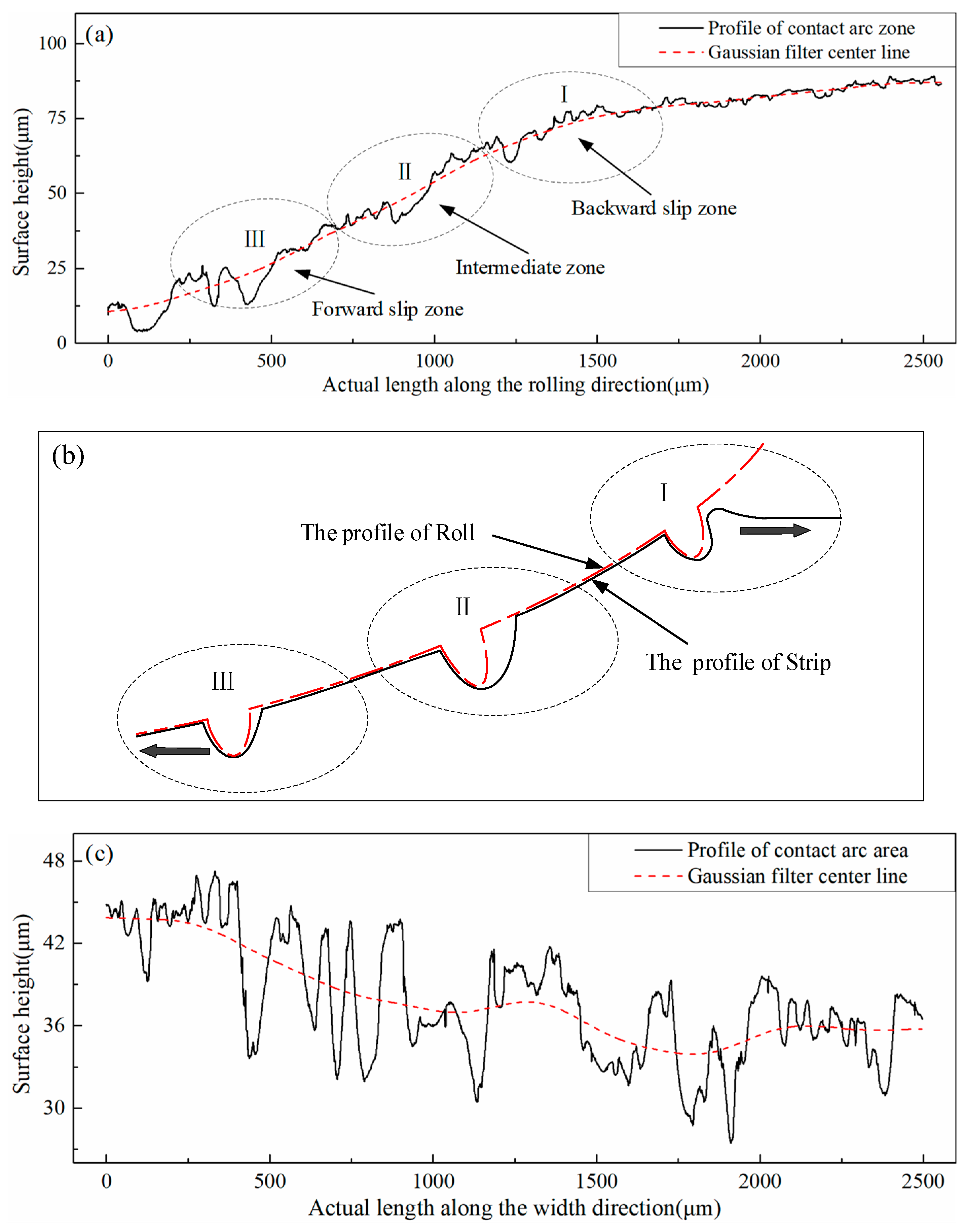
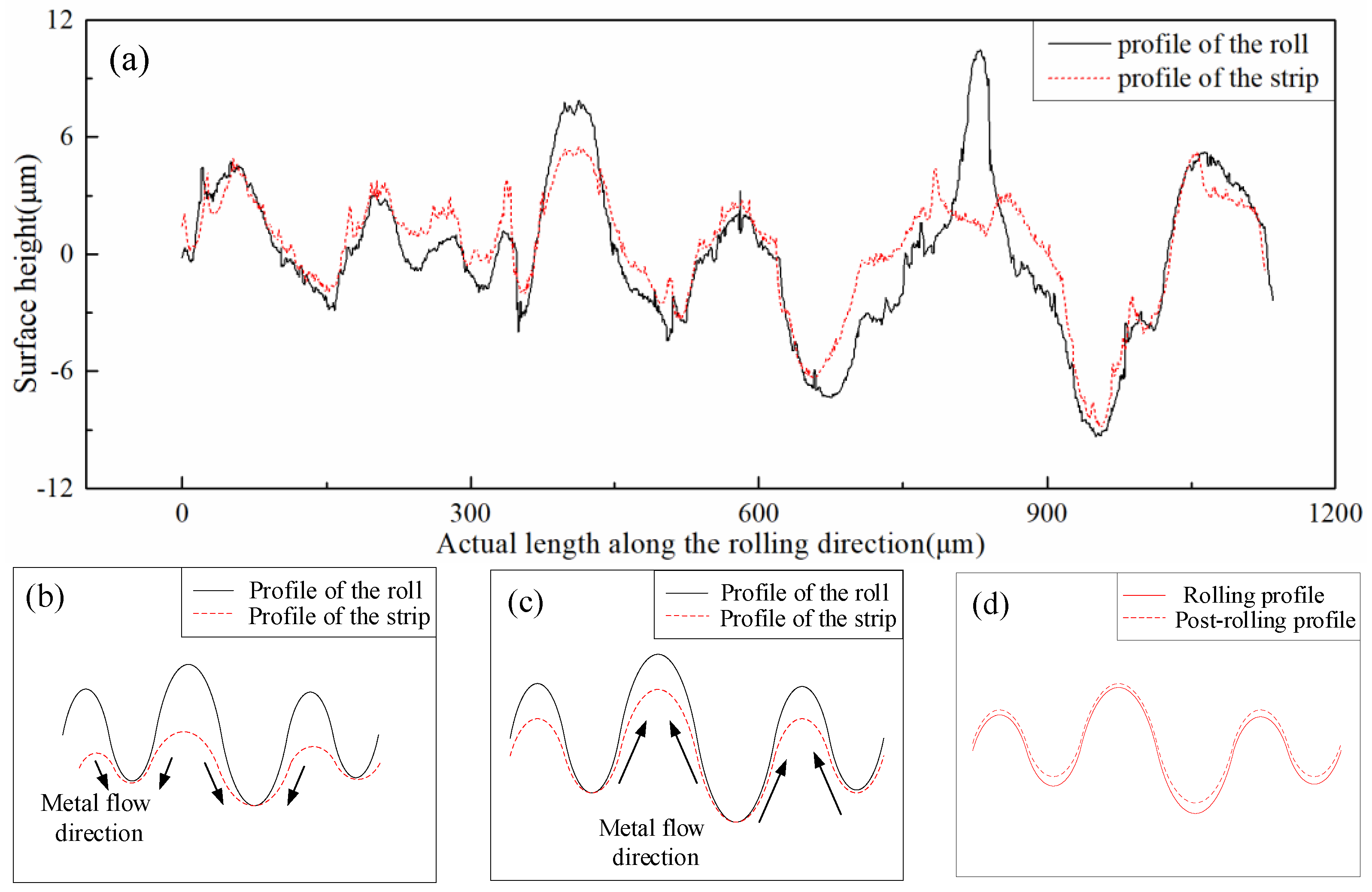
3.2. Surface Topography of Strip Arc Contact Zone
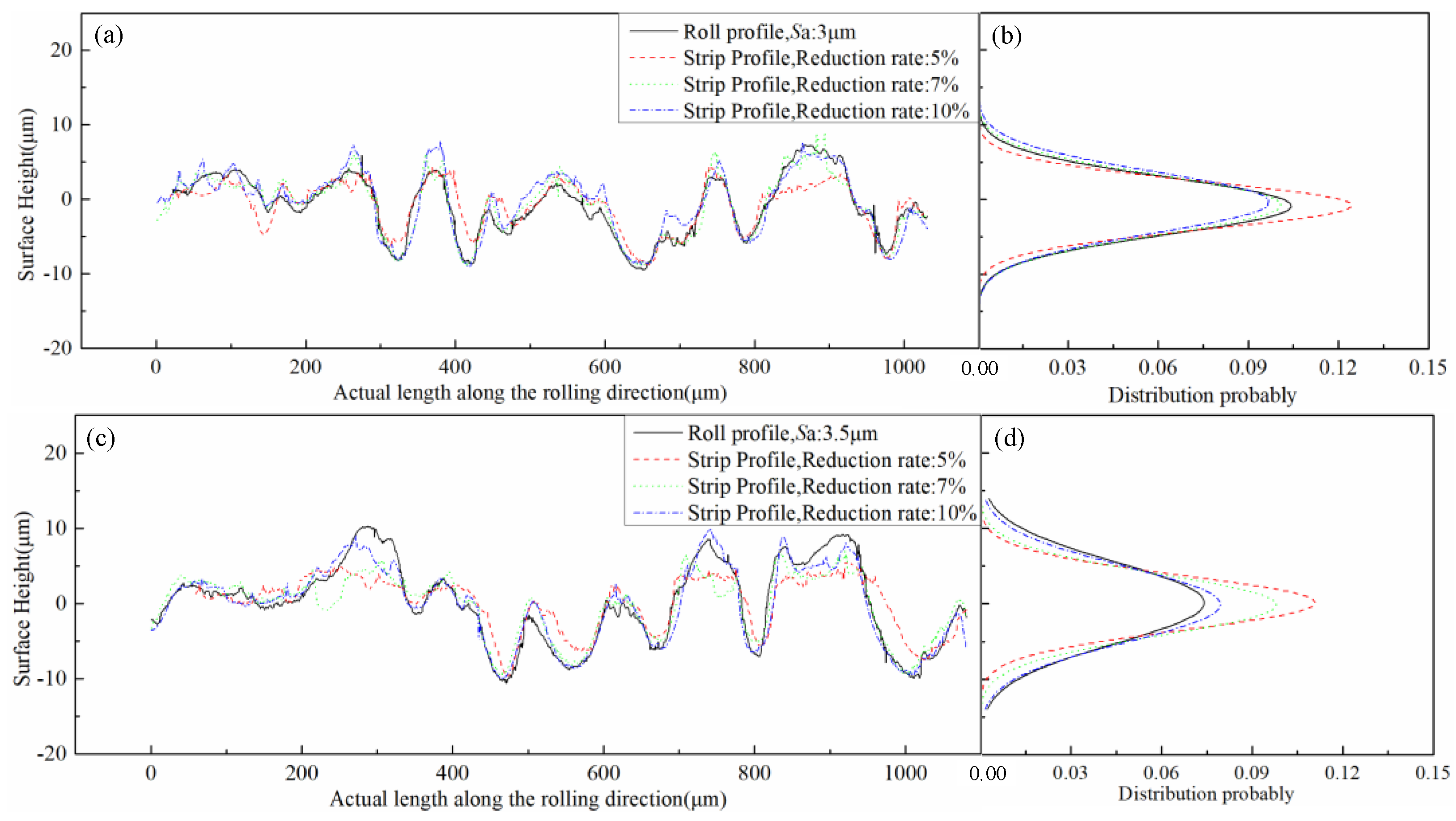
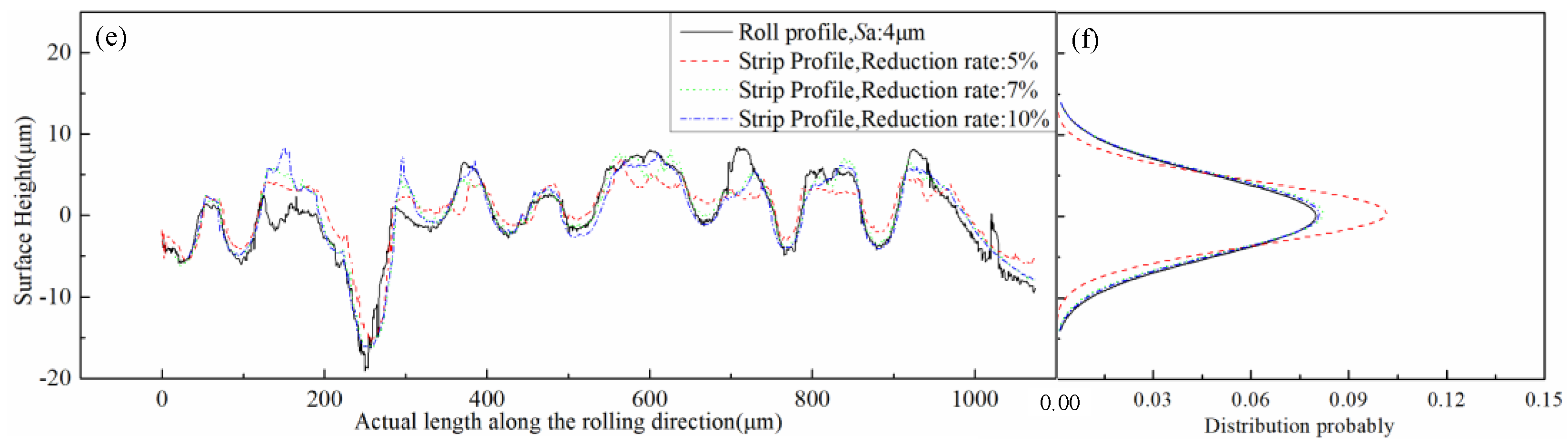
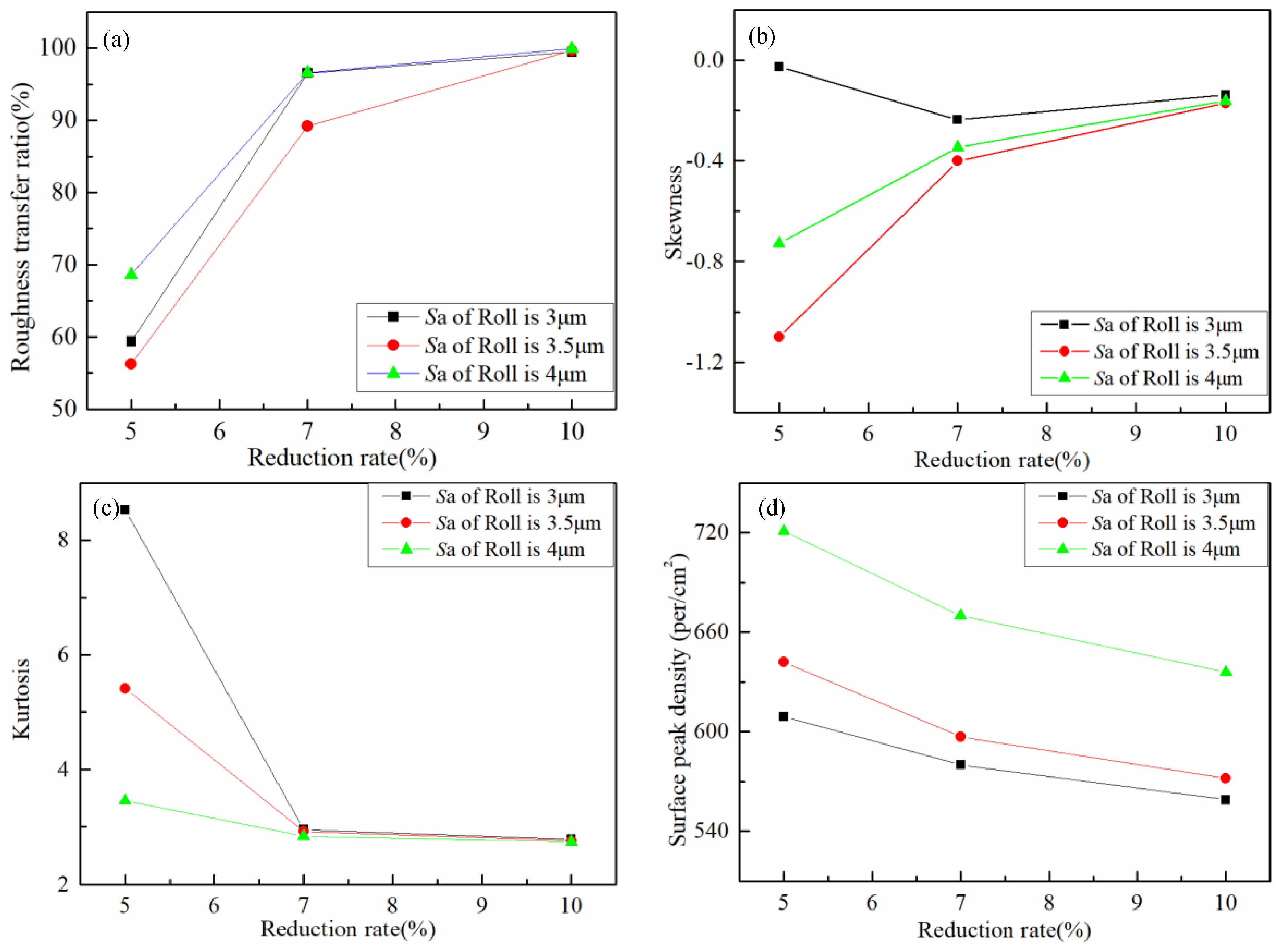
3.3. Surface Topography of the Strip after Cold Rolling
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Influence of surface preparation on roughness parameters, friction and wear. Wear 2009, 266, 482–487. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Li, Y. Modeling and optimization of surface roughness in incremental sheet forming using a multi-objective function. Mater. Manuf. Processes. 2014, 29, 808–818. [Google Scholar] [CrossRef]
- Sedlaček, M.; Podgornik, B.; Vižintin, J. Correlation between standard roughness parameters skewness and kurtosis and tribological behaviour of contact surfaces. Tribol. Int. 2010, 48, 102–112. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, J.; Li, H. Effect of surface spacing parameters on mixed lubrication condition. Proc. Inst. Mech. Eng. Part J. 2014, 228, 577–583. [Google Scholar] [CrossRef]
- Masjedi, M.; Khonsari, M. On the effect of surface roughness in point-contact EHL: Formulas for film thickness and asperity load. Tribol. Int. 2015, 82, 228–244. [Google Scholar] [CrossRef]
- Scheers, J.; Vermeulen, M.; De, M. Assessment of steel surface roughness and waviness in relation with paint appearance. Int. J. Mach. Tool. Manuf. 1998, 38, 647–656. [Google Scholar] [CrossRef]
- Mancini, E.; Sasso, M.; Amodio, D.; Ferretti, R.; Sanfilippo, F. Surface Defect Generation and Recovery in Cold Rolling of Stainless Steel Strips. J. Tribol. 2010, 133, 012202. [Google Scholar] [CrossRef]
- Mazur, V.L. Production of rolled steel with specified surface roughness. Steel Transl. 2015, 45, 371–377. [Google Scholar] [CrossRef]
- Gorbunov, A.V.; Belov, V.K.; Begletsov, D.O.; Sotnikov, A.S. Influence of roller treatment on the surface topography of cold-rolled sheet. Steel Transl. 2010, 40, 68–73. [Google Scholar] [CrossRef]
- Plouraboué, F.; Boehm, M. Multi-scale roughness transfer in cold metal rolling. Tribol. Int. 1999, 32, 45–57. [Google Scholar] [CrossRef] [Green Version]
- Lenard, J. The effect of roll roughness on the rolling parameters during cold rolling of an aluminum alloy. J. Mater. Process. Technol. 2004, 152, 144–153. [Google Scholar] [CrossRef]
- Ma, B.; Tieu, A.; Lu, C.; Jiang, Z. An experimental investigation of steel surface characteristic transfer by cold rolling. J. Mater. Process. Technol. 2002, 125, 657–663. [Google Scholar] [CrossRef]
- Kijima, H. Influence of lubrication on roughness crushing in skin-pass rolling of steel strip. J. Mater. Process. Technol. 2015, 216, 1–9. [Google Scholar] [CrossRef]
- Kijima, H. Influence of roll radius on roughness transfer in skin-pass rolling of steel strip. J. Mater. Process. Technol. 2014, 214, 1111–1119. [Google Scholar] [CrossRef]
- Kijima, H.; Niels, B. Skin-pass rolling I—Studies on roughness transfer and elongation under pure normal loading. Int. J. Mach. Tool. Manuf. 2008, 48, 1313–1317. [Google Scholar] [CrossRef]
- Kijima, H.; Bay, N. Skin-pass rolling II-Studies of roughness transfer under combined normal and tangential loading. Int. J. Mach. Tools Manuf. 2008, 48, 1308–1312. [Google Scholar] [CrossRef]
- Shi, J.; Mcelwain, D.; Domanti, S. Some surface profiles of a strip after plane-strain indentation by rigid bodies with serrated surfaces. J. Mater. Process. Technol. 2002, 124, 227–237. [Google Scholar] [CrossRef]
- Shi, J.; Mcelwain, D.; Domanti, S. Some plastic deformation modes for indentation of half space by a rigid body with serrated surface as a model of roughness transfer in metal forming. J. Eng. Mater. Technol. Trans. ASME 2002, 124, 146–151. [Google Scholar] [CrossRef]
- Ahmed, R.; Sutcliffe, M. Identification of surface features on cold-rolled stainless steel strip. Wear 2000, 244, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Çolak, B.; Kurgan, N. An experimental investigation into roughness transfer in skin-pass rolling of steel strips. Int. J. Adv. Manuf. Technol. 2018, 96, 3321–3330. [Google Scholar] [CrossRef]
- Qu, F.; Xie, H.; Jiang, Z. Finite element method analysis of surface roughness transfer in micro flexible rolling. MATEC Web Conf. 2016, 80, 04002. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; He, Z.; Lu, L. Correlation of surface features with corrosion behaviors of interstitial free steel processed by temper rolling. J. Mater. Technol. 2020, 36, 39–46. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, L.; Qu, P.; Li, S.; Jiang, Z. A simple approach for analysing the surface texture transfer in cold rolling of metal strips. Int. J. Adv. Manuf. Technol. 2018, 95, 597–608. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, X.; Zhang, J.; Li, H.; Jia, S. Evolution on Topography of Textured Work Rolls and Steel Strips during Cold Rolling and Temper Rolling. Steel Res. Int. 2017, 88, 1600469. [Google Scholar] [CrossRef]
- Cong, Y.; Chen, X.R.; Li, Y.T. Research on the SIFT Algorithm in Image Matching. Appl. Mech. Mater. 2011, 121, 4656–4660. [Google Scholar] [CrossRef]
- Ran, M.; Xiao, S.; Zhou, X.; Xiao, W. Asphalt Pavement Texture 3D Reconstruction Based on Binocular Vision System with SIFT Algorithm. In Proceedings of the 2017 International Conference on Smart Grid and Electrical Automation (ICSGEA), Changsha, China, 27–28 May 2017; pp. 213–218. [Google Scholar]
- Lin, K.; Wu, Q.; Kong, L.; Li, P.; Yang, H. A Facial Features Matching Method with Age Robustness Based on SIFT Algorithm. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017; pp. 20–23. [Google Scholar]
- Elkoca, O. A study on the characteristics of electrical discharge textured skin pass mill work roll. Surf. Coat. Technol. 2008, 202, 2765–2774. [Google Scholar] [CrossRef]
- Malcolm, A. Accuracy of replication for non-destructive surface finish measurement. In Proceedings of the Singapore International Ndt Conference & Exhibition, Singapore, 13–17 October 1996. [Google Scholar]
- Gadelmawla, E.S.; Koura, M.M.; Maksoud, T.M.A.; Elewa, I.M.; Soliman, H.H. Roughness parameters. J. Mater. Process. Technol. 2002, 123, 133–145. [Google Scholar] [CrossRef]
- Jamari, J. Matching and stitching for surface identification. ROTASI 2006, 8, 1–4. [Google Scholar]



| Sa of Work Roll (μm) | Reduction Rate |
|---|---|
| 3 μm | 5% |
| 3.5 μm | 7% |
| 4 μm | 10% |
| Specimen | Sa (μm) | Ssk | Sku | Sds (per/cm2) |
|---|---|---|---|---|
| A(Resin) | 2.99 | −0.004 | 2.821 | 556 |
| B(Resin) | 3.50 | −0.045 | 2.853 | 569 |
| C(Resin) | 4.07 | −0.036 | 2.958 | 636 |
| D(strip steel) | 0.85 | −0.036 | 3.591 | 606 |
| The Number of Part | Sa (μm) | Ssk | Sku | Sds (per/cm2) |
|---|---|---|---|---|
| 1 | 2.59 | −0.376 | 2.699 | 574 |
| 2 | 2.67 | −0.813 | 3.099 | 596 |
| 3 | 1.57 | −0.731 | 4.506 | 677 |
| 4 | 0.86 | −0.072 | 2.602 | 634 |
| 5 | 0.97 | −0.200 | 2.555 | 615 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Yang, Q.; Wang, X.; He, H.; Sun, Y.; Li, W. An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling. Micromachines 2020, 11, 916. https://doi.org/10.3390/mi11100916
Xu D, Yang Q, Wang X, He H, Sun Y, Li W. An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling. Micromachines. 2020; 11(10):916. https://doi.org/10.3390/mi11100916
Chicago/Turabian StyleXu, Dong, Quan Yang, Xiaochen Wang, Hainan He, Youzhao Sun, and Wenpei Li. 2020. "An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling" Micromachines 11, no. 10: 916. https://doi.org/10.3390/mi11100916
APA StyleXu, D., Yang, Q., Wang, X., He, H., Sun, Y., & Li, W. (2020). An Experimental Investigation of Steel Surface Topography Transfer by Cold Rolling. Micromachines, 11(10), 916. https://doi.org/10.3390/mi11100916





