Silicon 3D Microdetectors for Microdosimetry in Hadron Therapy
Abstract
:1. Introduction
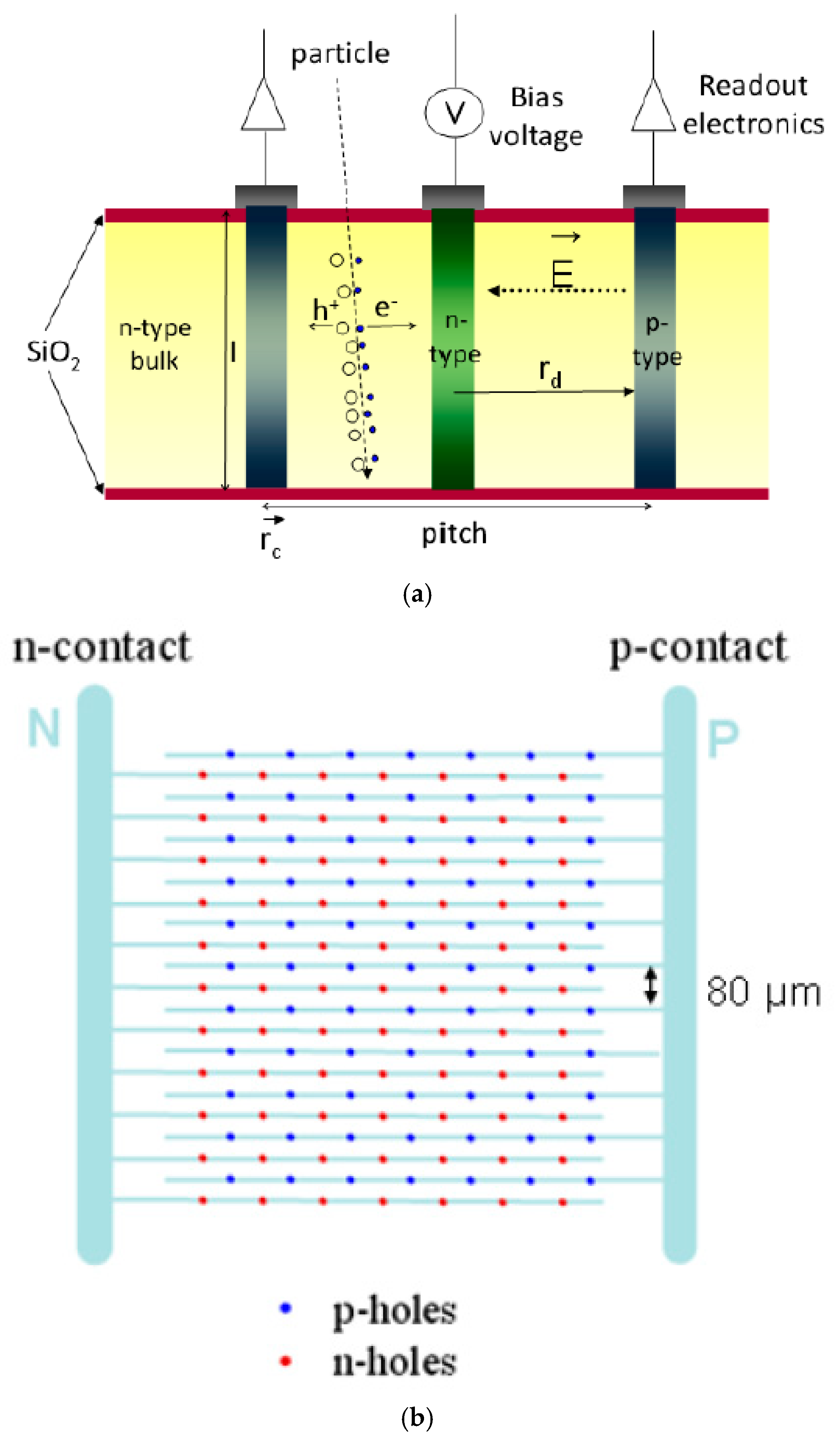
2. Silicon‒Based 3D Microdosimeters
2.1. Ultra-Thin 3D Silicon Detectors
2.1.1. Microfabrication Processes
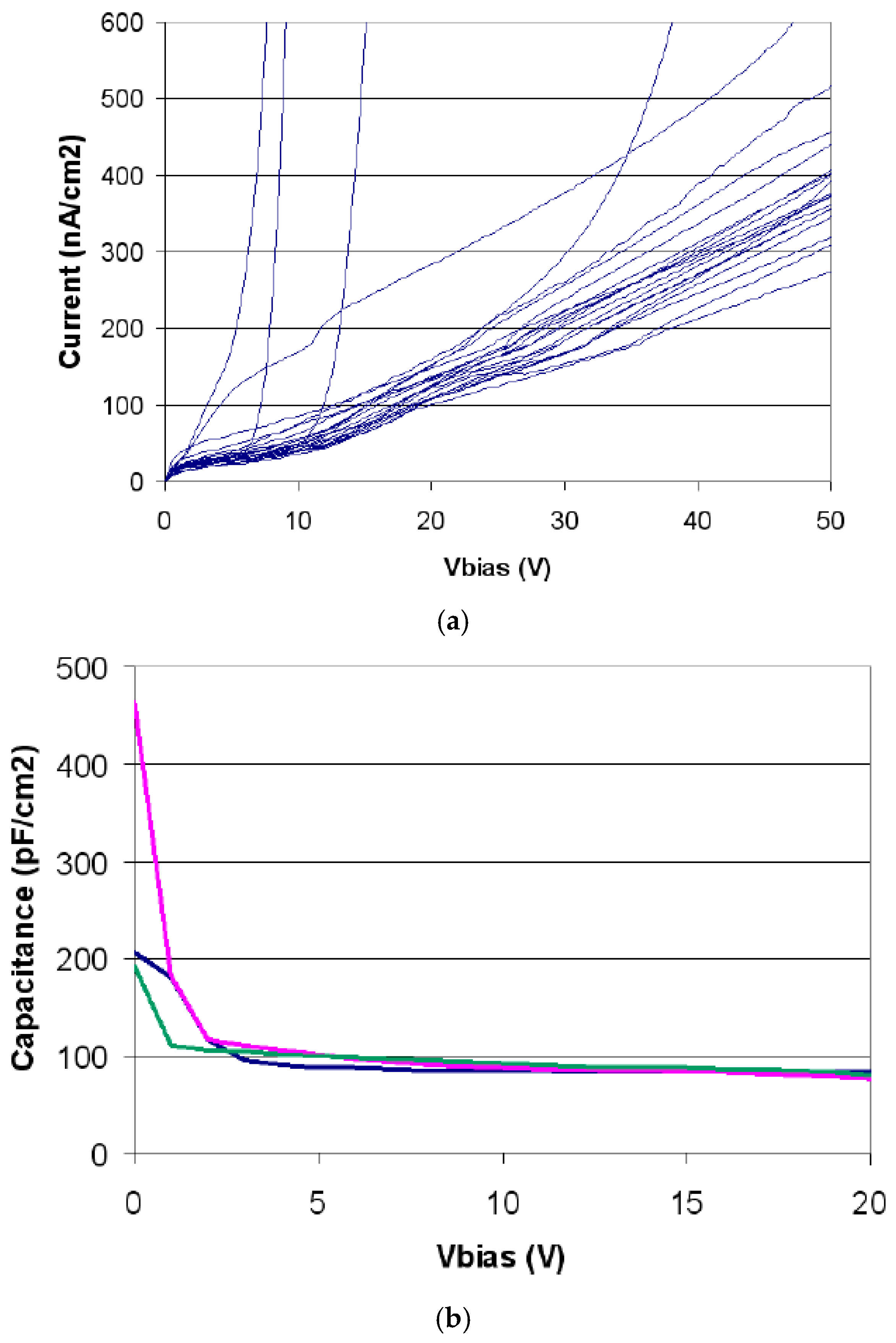
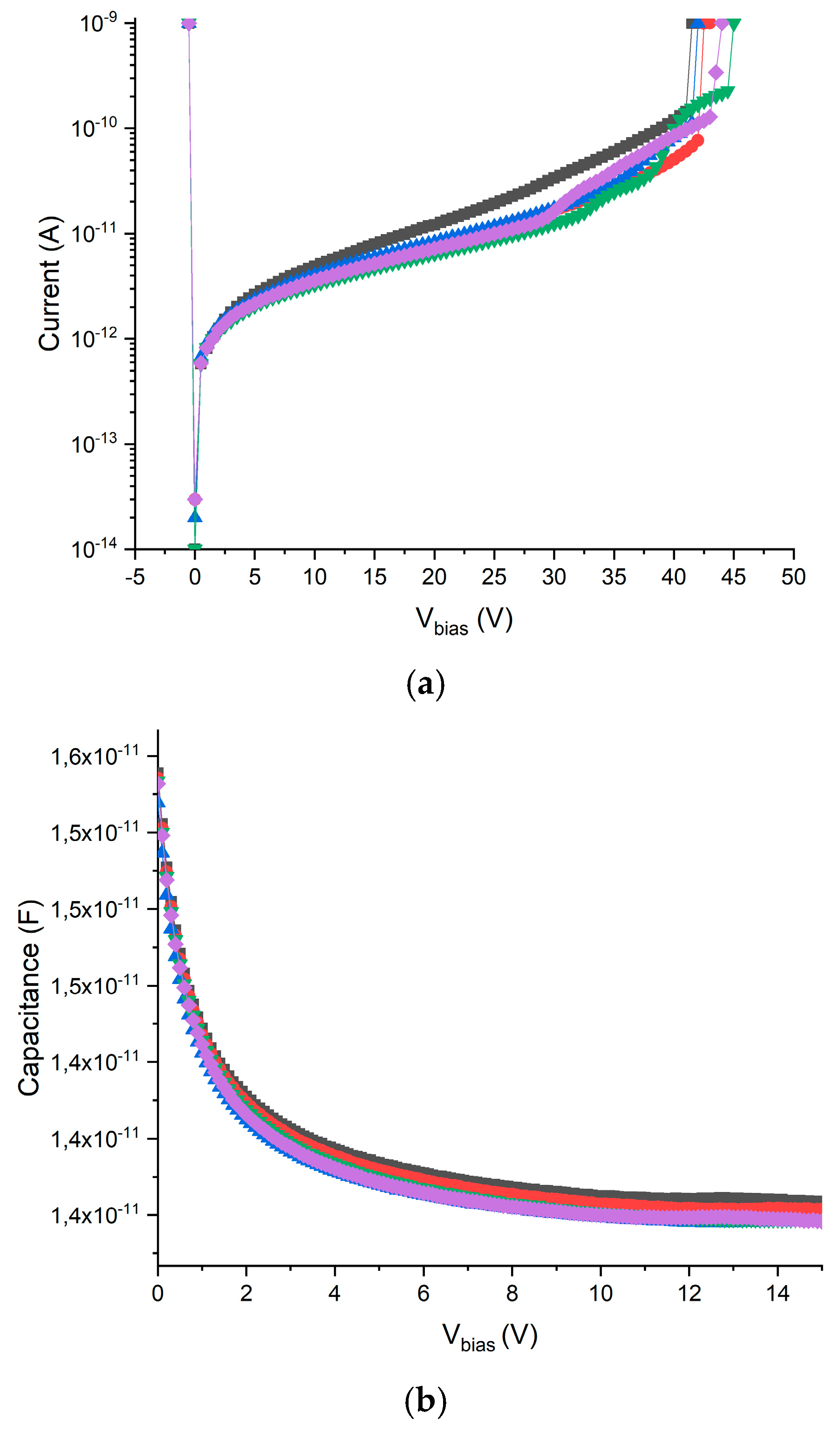
2.1.2. Electrical Characterization
2.1.3. Readout Electronics
2.2. 3D‒Cylindrical Microdetectors
2.2.1. Microfabrication Processes
2.2.2. Electrical Characterization
2.2.3. CCE Characterization
2.2.4. Readout Electronics
3. Microdosimetry Results
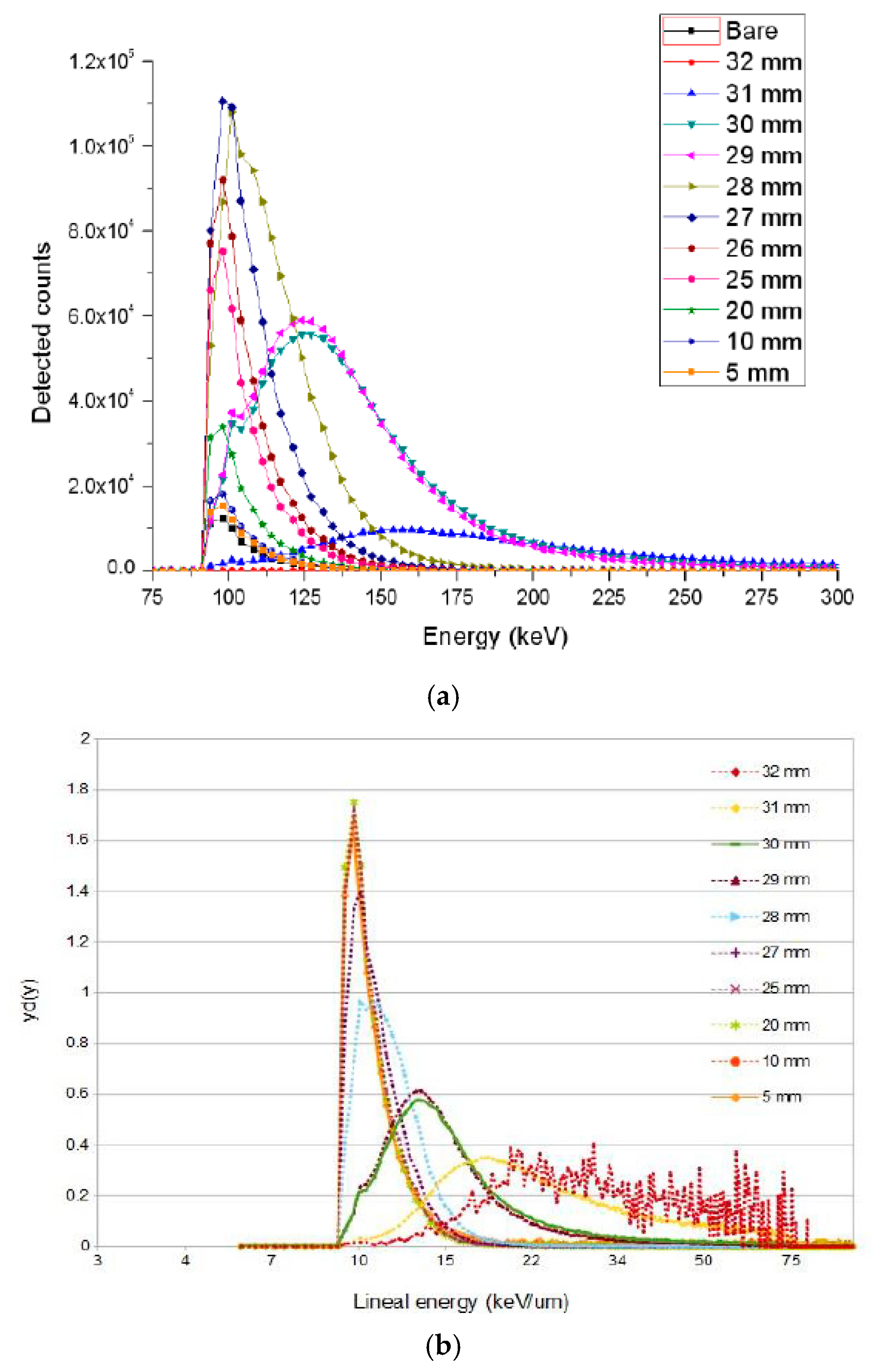
3.1. U3DTHINs
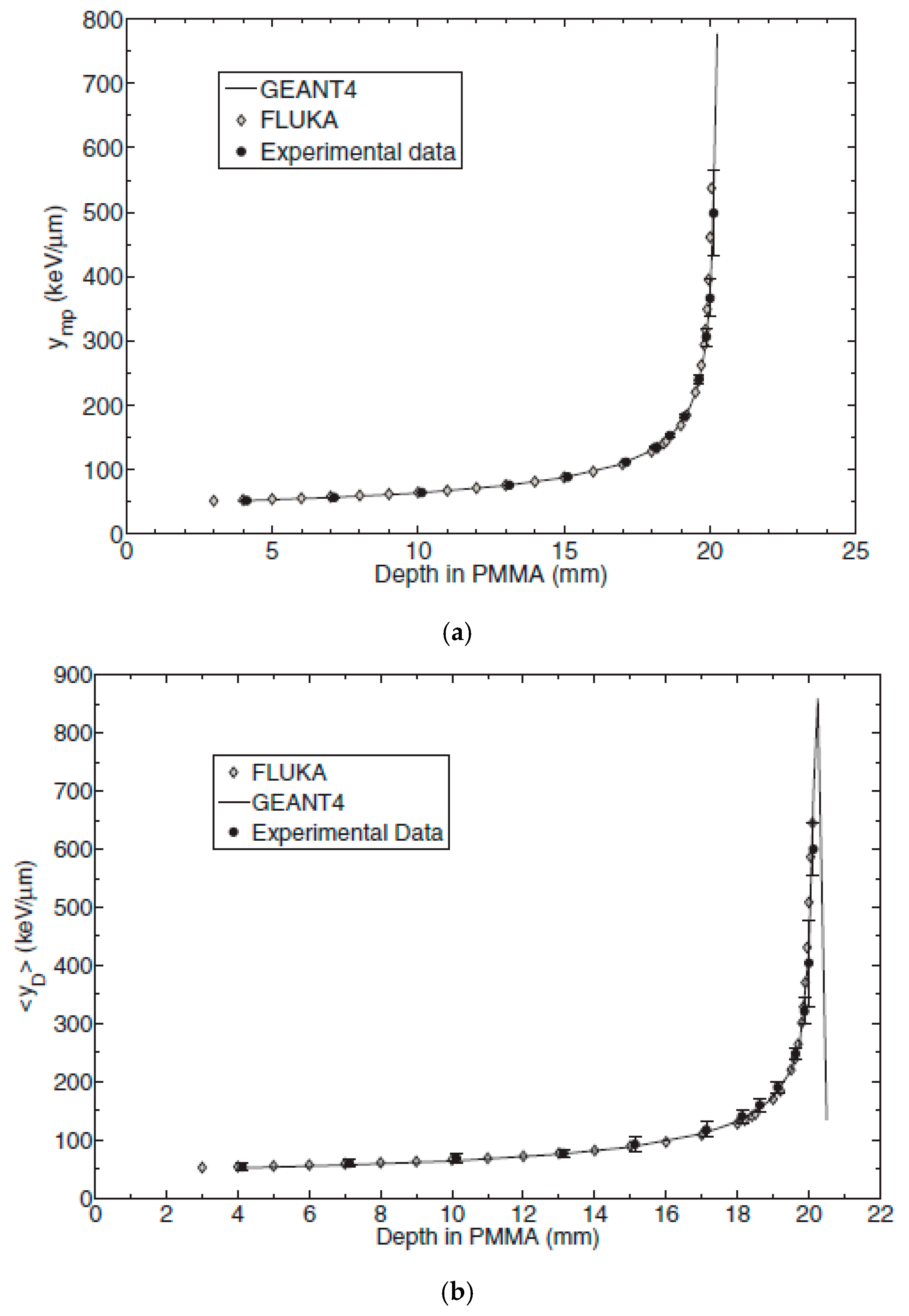
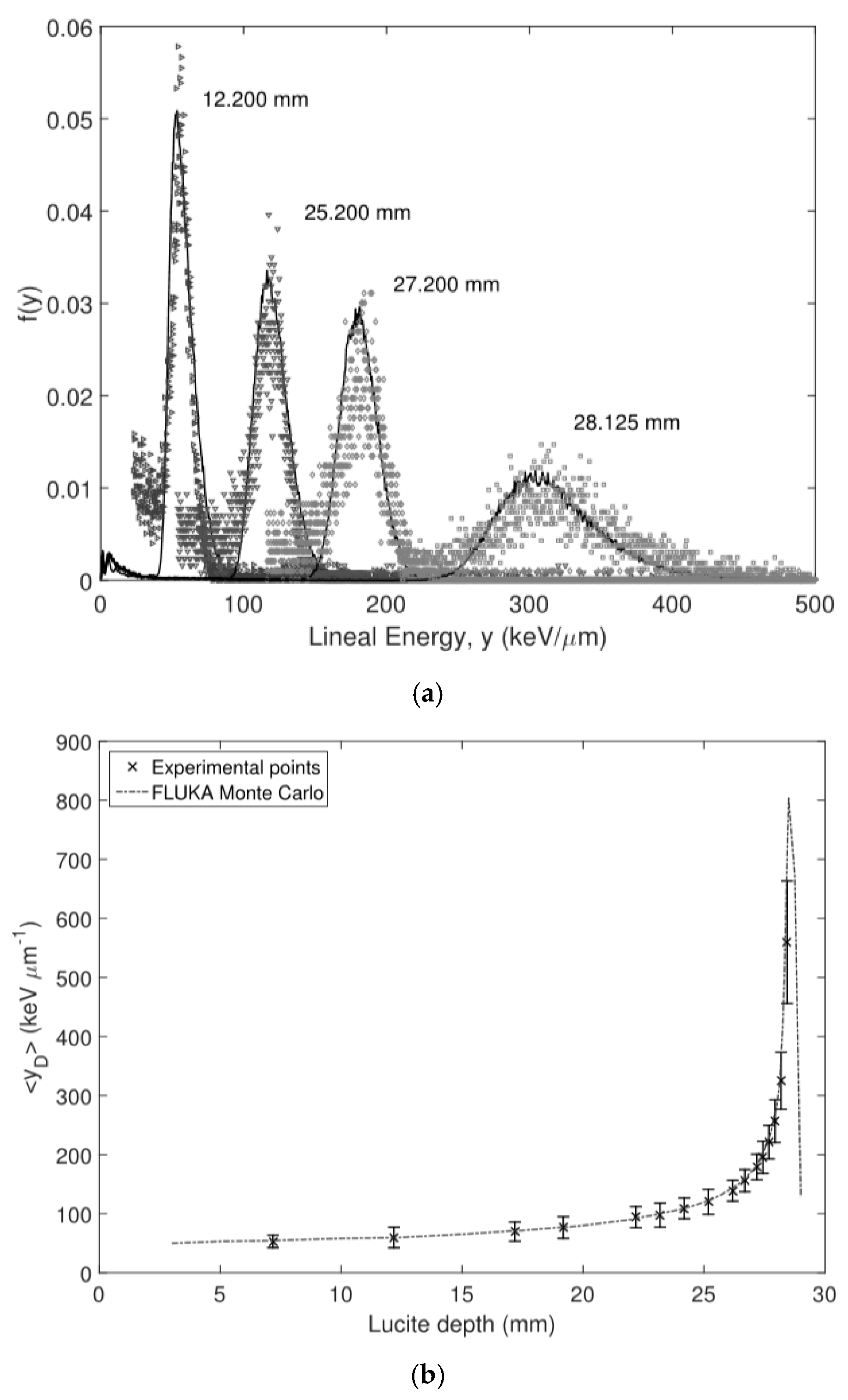
3.2. 3D‒Cylindrical Microdetectors
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Delaney, G.; Jacob, S.; Featherstone, C.; Barton, M. The role of radiotherapy in cancer treatment. Cancer 2005, 104, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Durante, M.; Loeffler, J.S. Charged particles in radiation oncology. Nat. Rev. Clin. Oncol. 2010, 7, 37–43. [Google Scholar] [CrossRef]
- Schardt, D.; Elsaesser, T.; Schulz-Ertner, D. Heavy-ion tumor therapy: Physical and radiobiological benefits. Rev. Mod. Phys. 2010, 82, 383–425. [Google Scholar] [CrossRef]
- Wilson, R.R. Radiological Use of Fast Protons. Radiology 1946, 47, 487–491. [Google Scholar] [CrossRef]
- Noda, K. Review of Hadron Therapy accelerators worldwide and future trends. In Proceedings of the IPAC2011, San Sebastián, Spain, 4–9 September 2011; pp. 3784–3788. [Google Scholar]
- PTCOG. Particle Therapy Facilities in Operation. Available online: https://www.ptcog.ch/ (accessed on 1 September 2020).
- Rossi, H.H.; Zaider, M. Microdosimetry and Its Applications; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- ICRU. Linear Energy Transfer ICRU Report 16; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1970. [Google Scholar]
- Kellerer, A.M.; Chmelevsky, D. Criteria for the applicability of LET. Radiat. Res. 1975, 63, 226. [Google Scholar] [CrossRef] [Green Version]
- Kellerer, A.M.; Rossi, H.H. The theory of dual radiation action. Curr. Top. Radiat. Res. Q. 1972, 8, 85–158. [Google Scholar]
- IAEA. Relative Biological Effectiveness in Ion Beam Therapy (TRS no 461); International Atomic Energy Agency: Vienna, Austria, 2008. [Google Scholar]
- ICRU. Prescribing, Recording, and Reporting Proton-Beam Therapy. ICRU Report 78; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 2007. [Google Scholar]
- Paganetti, H. Relative biological effectiveness (RBE) values. Phys. Med. Biol. 2014, 59, R419. [Google Scholar] [CrossRef]
- Grassberger, C.; Paganetti, H. Elevated LET components in clinical proton beams. Phys. Med. Biol. 2011, 56, 6677–6691. [Google Scholar] [CrossRef]
- Howard, M.E.; Beltran, C.; Anderson, S.; Tseung, W.C.; Sarkaria, J.N.; Herman, M.G. Investigating Dependencies of Relative Biological Effectiveness for Proton Therapy in Cancer Cells. Int. J. Part Ther. 2017, 4, 12–22. [Google Scholar] [CrossRef] [Green Version]
- Peeler, C.R.; Mirkovic, D.; Titt, U.; Blanchard, P.; Gunther, J.R.; Mahajan, A.; Mohan, R.; Grosshans, D.R. Clinical evidence of variable proton biological effectiveness in pediatric patients treated for ependymoma. Radiother. Oncol. 2016, 121, 395–401. [Google Scholar] [CrossRef] [Green Version]
- Ödén, J.; Eriksson, K.; Toma-Dasu, I. Incorporation of relative biological effectiveness uncertainties into proton plan robustness evaluation. Acta Oncol. 2017, 56, 769–778. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Horcicka, M.; Meyer, C.; Buschbacher, A.; Durante, M.; Kramer, M. Algorithms for the optimization of RBE-weighted dose in particle therapy. Phys. Med. Biol. 2012, 58, 275–286. [Google Scholar] [CrossRef] [PubMed]
- Jones, B. Why RBE must be a variable and not a constant in proton therapy. Br. J. Radiol. 2016, 89, 20160116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kase, Y.; Kanai, T.; Matsumoto, Y.; Furusawa, Y.; Okamoto, H.; Asaba, T.; Sakama, M.; Shinoda, H. Microdosimetric Measurements and Estimation of Human Cell Survival for Heavy-Ion Beams. Radiat. Res. 2006, 166, 629–638. [Google Scholar] [CrossRef] [PubMed]
- Rossi, H.H.; Rosenzweig, W. A Device for the Measurement of Dose as a Function of Specific Ionization. Radiology 1955, 64, 404–411. [Google Scholar] [CrossRef]
- ICRU. Microdosimetry ICRU Report 36; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1983. [Google Scholar]
- Colautti, P.; Conte, V.; Selva, A.; Chiriotti, S.; Pola, A.; Bortot, D.; Fazzi, A.; Agosteo, S.; Treccani, M.; De Nardo, L.; et al. Miniaturized microdosimeters as LET monitors: First comparison of calculated and experimental data performed at the 62 MeV/u 12C beam of INFN-LNS with four different detectors. Phys. Medica 2018, 52, 113–121. [Google Scholar] [CrossRef]
- Bianchi, A.; Selva, A.; Colautti, P.; Bortot, D.; Mazzucconi, D.; Pola, A.; Agosteo, S.; Petringa, G.; Cirrone, G.; Reniers, B.; et al. Microdosimetry with a sealed mini-TEPC and a silicon telescope at a clinical proton SOBP of CATANA. Radiat. Phys. Chem. 2020, 171, 108730. [Google Scholar] [CrossRef]
- Dicello, J.F.; Amols, H.I.; Zaider, M.; Tripard, G. A Comparison of Microdosimetric Measurements with Spherical Proportional Counters and Solid-State Detectors. Radiat. Res. 1980, 82, 441–453. [Google Scholar] [CrossRef]
- Orlic, M.; Lazarevic, V.; Boreli, F. Microdosimetric Counters Based on Semiconductor Detectors. Radiat. Prot. Dosim. 1989, 29, 21. [Google Scholar] [CrossRef]
- Kadachi, A.; Waheed, A.; Al-Eshaikh, M.; Obeid, M. Use of photodiode in microdosimetry and evaluation of effective quality factor. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1998, 404, 400–406. [Google Scholar] [CrossRef]
- McNulty, P.J.; Roth, D.R.; Beauvais, W.J.; Abdel-Kader, W.G.; Stassinopoulos, E.G. Microdosimetry in Space Using Microelectronic Circuits. In Biological Effects and Physics of Solar and Galactic Cosmic Radiation; Swenberg, C.E., Horneck, G., Stassinopoulos, E.G., Eds.; NATO ASI Series (Series A: Life Sciences); Springer: Boston, MA, USA, 1993; Volume 243B. [Google Scholar]
- Bradley, P.D.; Rosenfeld, A.B.; Zaider, M. Solid State Microdosimetry. Nucl. Instrum. Methods. B 2001, 184, 135–157. [Google Scholar] [CrossRef]
- Agosteo, S.; Borsato, E.; Corso, F.D.; Fazzi, A.; Gonella, F.; Introini, M.V.; Lorenzoli, M.; Pegoraro, M.; Pola, A.; Varoli, V.; et al. Study of the direct response of a monolithic silicon telescope to charged particles at different energies. Prog. Nucl. Sci. Technol. 2014, 4, 717–720. [Google Scholar] [CrossRef]
- Rosenfeld, A.B. Novel detectors for silicon based microdosimetry, their concepts and applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 809, 156–170. [Google Scholar] [CrossRef]
- Guardiola, C.; Pellegrini, G.; Lozano, M.; Fleta, C.; Quirion, D.; Gómez, F. Microdosimeter Based On 3D Semiconductor Structures, Method for Producing Said Microdosimeter, and Use of Said Microdosimeter. International Patent Application No. PCT/ES2015/070056; ES Patent Application No. WO/2015/114193, 6 August 2015. [Google Scholar]
- Guardiola, C.; Quirion, D.; Pellegrini, G.; Fleta, C.; Esteban, S.; Cortés-Giraldo, M.A.; Gómez, F.; Solberg, T.; Carabe, A.; Lozano, M. Silicon-based 3D-microstructures for radiation dosimetry in hadrontherapy. Appl. Phys. Lett. 2015, 107, 023505. [Google Scholar] [CrossRef]
- Fleta, C.; Esteban, S.; Baselga, M.; Quirion, D.; Pellegrini, G.; Guardiola, C.; Cortés-Giraldo, M.; López, J.G.; Ramos, M.J.; Gómez, F.; et al. 3D-cylindrical silicon microdosimeters: Fabrication, simulation and charge collection study. J. Instrum. 2015, 10, P10001. [Google Scholar] [CrossRef]
- Guardiola, C.; Fleta, C.; Rodríguez, J.; Lozano, M.; Gómez, F. Preliminary microdosimetric measurements with ultra-thin 3D silicon detectors of a 62 MeV proton beam. J. Instrum. 2015, 10, P01008. [Google Scholar] [CrossRef]
- Esteban, S. Development of Advanced Silicon Sensors for Neutron Detection and Microdosimetry. Ph.D. Thesis, Universitat Autònoma de Barcelona, Barcelona, Spain, 2016. [Google Scholar]
- Gómez, F.; Fleta, C.; Esteban, S.; Quirion, D.; Pellegrini, G.; Lozano, M.; Prezado, Y.; Dos Santos, M.; Guardiola, C.; Montarou, G.; et al. Measurement of carbon ion microdosimetric distributions with ultrathin 3D silicon diodes. Phys. Med. Biol. 2016, 61, 4036–4047. [Google Scholar] [CrossRef]
- Prieto-Pena, J.; Gomez, F.; Fleta, C.; Guardiola, C.; Pellegrini, G.; Donetti, M.; Giordanengo, S.; Gonzalez-Castano, D.M.; Pardo-Montero, J. Microdosimetric Spectra Measurements on a Clinical Carbon Beam at Nominal Therapeutic Fluence Rate with Silicon Cylindrical Microdosimeters. IEEE Trans. Nucl. Sci. 2019, 66, 1840–1847. [Google Scholar] [CrossRef]
- Prieto-Pena, J. Development of Silicon Sensors for Dosimetry and Microdosimetry. Ph.D. Thesis, Universidade de Santiago de Compostela, Santiago de Compostela, Spain, 2019. [Google Scholar]
- Prieto-Pena, J.; Gomez, F.; Guardiola, C.; Jiménez-Ramos, M.C.; Garcia-Lopez, J.; Baratto-Roldán, A.; Baselga, M.; Pardo-Montero, J.; Fleta, C. Impact of charge collection efficiency and electronic noise on the performance of solid-state 3D microdetectors. Phys. Med. Biol. 2020, 65, 175004. [Google Scholar] [CrossRef]
- Tran, L.T.; Prokopovich, D.A.; Petasecca, M.; Lerch, M.; Fleta, C.; Pellegrini, G.; Guardiola, C.; Reinhard, M.I.; Rosenfeld, A.B. Ultra-Thin 3-D Detector: Charge Collection Characterization and Application for Microdosimetry. IEEE Trans. Nucl. Sci. 2014, 61, 3472–3478. [Google Scholar] [CrossRef]
- Manfredotti, C.; Giudice, A.L.; Ricciardi, C.; Paolini, C.; Massa, E.F.; Fizzotti, F.; Vittone, E. CVD diamond microdosimeters. Nucl. Instrum. Methods Phys. Res. A 2001, 458, 360–364. [Google Scholar] [CrossRef]
- Rollet, S.; Angelone, M.; Magrin, G.; Marinelli, M.; Milani, E.; Pillon, M.; Prestopino, G.; Verona, C.; Verona-Rinati, G. A novel microdosimeter based upon artificial single crystal diamond. IEEE Trans. Nucl. Sci. 2012, 59. [Google Scholar] [CrossRef] [Green Version]
- Zahradnik, I.A.; Pomorski, M.; De Marzi, L.; Tromson, D.; Barberet, P.; Skukan, N.; Bergonzo, P.; Devès, G.; Herault, J.; Kada, W.; et al. scCVD Diamond Membrane based Microdosimeter for Hadron Therapy. Phys. Status Solidi 2018, 215, 1800383. [Google Scholar] [CrossRef]
- Verona, C.; Magrin, G.; Solevi, P.; Bandorf, M.; Marinelli, M.; Stock, M.; Verona Rinati, G. Toward the use of single crystal diamond based detector for ion-beam therapy microdosimetry. Radiat. Meas. 2018, 110, 25–31. [Google Scholar] [CrossRef]
- Parker, S.I.; Kenney, C.; Segal, J. 3D—A proposed new architecture for solid-state radiation detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1997, 395, 328–343. [Google Scholar] [CrossRef]
- Pellegrini, G.; Roy, P.; Bates, R.; Jones, D.; Mathieson, K.; Melone, J.; O’Shea, V.; Smith, K.M.; Thayne, I.; Thornton, P.; et al. Technology development of 3D detectors for high-energy physics and imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2002, 487, 19–26. [Google Scholar] [CrossRef]
- Pellegrini, G.; García, F.; Fernández-Martínez, P.; Cabruja, E.; Lozano, M.; Orava, R.; Ullan, M. Fabrication and simulation of novel ultra-thin 3D silicon detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 604, 115–118. [Google Scholar] [CrossRef]
- Pellegrini, G.; Fernández-Martínez, P.; Bassignana, D.; Cabruja, E.; Fleta, C.; Guardiola, C.; Lozano, M.; Quirion, D.; Ullán, M. 3D double sided detector fabrication at IMB-CNM. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2013, 699, 27–30. [Google Scholar] [CrossRef]
- Guardiola, C. Novel Silicon Sensors for Neutron Detection. Ph.D. Thesis, Universidad Autónoma de Barcelona, Barcelona, Spain, 2012. [Google Scholar]
- Montalbano, A.; Bassignana, D.; Li, Z.; Liu, S.; Lynn, D.; Pellegrini, G.; Tsybychev, D. A systematic study of BNL׳s 3D-Trench Electrode detectors. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 765, 23–28. [Google Scholar] [CrossRef]
- Lange, J.; Örn, C.; Areste, M.C.; Cavallaro, E.; Förster, F.; Grinstein, S.; Paz, I.L.; Manna, M.; Pellegrini, G.; Quirion, D.; et al. 3D silicon pixel detectors for the High-Luminosity LHC. J. Instrum. 2016, 11, C11024. [Google Scholar] [CrossRef] [Green Version]
- Terzo, S.; Grinstein, S.; Manna, M.; Pellegrini, G.; Quirion, D. A new generation of radiation hard 3D pixel sensors for the ATLAS upgrade. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, A982, 164587. [Google Scholar] [CrossRef]
- Mac Raighne, A.; Akiba, K.; Alianelli, L.; Bates, R.; Van Beuzekom, M.; Buytaert, J.; Campbell, M.; Collins, P.; Crossley, M.; Dumps, R.; et al. Precision scans of the Pixel cell response of double-sided 3D Pixel detectors to pion and X-ray beams. J. Instrum. 2011, 6, P05002. [Google Scholar] [CrossRef] [Green Version]
- Balbuena, J.P. Development of Innovative Silicon Radiation Detectors. Ph.D. Thesis, Universitat Autònoma de Barcelona, Barcelona, Spain, 2012. [Google Scholar]
- Manna, M.; Grieco, C.; Grinstein, S.; Hidalgo, S.; Pellegrini, G.; Quirion, D.; Terzo, S. First characterisation of 3D pixel detectors irradiated at extreme fluences. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 979, 164458. [Google Scholar] [CrossRef]
- García, F.; Pelligrini, G.; Fernández-Martínez, P.; Lozano, M.; Orava, R.; Ullan, M. A novel ultra-thin 3D detector—For plasma diagnostics at JET and ITER tokamaks. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2009, 607, 57–60. [Google Scholar] [CrossRef]
- Guardiola, C.; Fleta, C.; Quirion, D.; Rodríguez, J.; Lozano, M.; Teixidor, F.; Viñas, C.; Popescu, A.R.; Domingo, C.; Amgarou, K. Ultra–thin 3D silicon sensors for neutron detection. J. Instrum. 2012, 7, P03006. [Google Scholar] [CrossRef]
- Guardiola, C.; Gómez, F.; Fleta, C.; Rodríguez, J.; Quirion, D.; Pellegrini, G.; Lousa, A.; Martínez-de-Olcoz, L.; Pombar, M.; Lozano, M. Neutron measurements with ultra-thin 3D siliconsensors in a radiotherapy treatment room using a siemens PRIMUS linac. Phys. Med. Biol. 2013, 58, 3227–3242. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurements; John Willey and Sons: New York, NY, USA, 2010. [Google Scholar]
- Breese, M.; Vittone, E.; Vizkelethy, G.; Sellin, P. A review of ion beam induced charge microscopy. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 2007, 264, 345–360. [Google Scholar] [CrossRef]
- Samnøy, A.T.; Ytre-Hauge, K.S.; Malinen, E.; Tran, L.; Rosenfeld, A.; Povoli, M.; Kok, A.; Summanwar, A.; Röhrich, D. Microdosimetry with a 3D silicon on insulator (SOI) detector in a low energy proton beamline. Radiat. Phys. Chem. 2020, 176, 109078. [Google Scholar] [CrossRef]
- Pola, A.; Bortot, D.; Mazzucconi, D.; Fazzi, A.; Galer, S.; Kirkby, K.; Merchant, M.; Palmans, H.; Agosteo, S. Characterization of a pixelated silicon microdosimeter in micro-beams of light ions. Radiat. Meas. 2020, 133, 106296. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guardiola, C.; Fleta, C.; Quirion, D.; Pellegrini, G.; Gómez, F. Silicon 3D Microdetectors for Microdosimetry in Hadron Therapy. Micromachines 2020, 11, 1053. https://doi.org/10.3390/mi11121053
Guardiola C, Fleta C, Quirion D, Pellegrini G, Gómez F. Silicon 3D Microdetectors for Microdosimetry in Hadron Therapy. Micromachines. 2020; 11(12):1053. https://doi.org/10.3390/mi11121053
Chicago/Turabian StyleGuardiola, Consuelo, Celeste Fleta, David Quirion, Giulio Pellegrini, and Faustino Gómez. 2020. "Silicon 3D Microdetectors for Microdosimetry in Hadron Therapy" Micromachines 11, no. 12: 1053. https://doi.org/10.3390/mi11121053
APA StyleGuardiola, C., Fleta, C., Quirion, D., Pellegrini, G., & Gómez, F. (2020). Silicon 3D Microdetectors for Microdosimetry in Hadron Therapy. Micromachines, 11(12), 1053. https://doi.org/10.3390/mi11121053




