Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System
Abstract
:1. Introduction
2. Materials and Methods
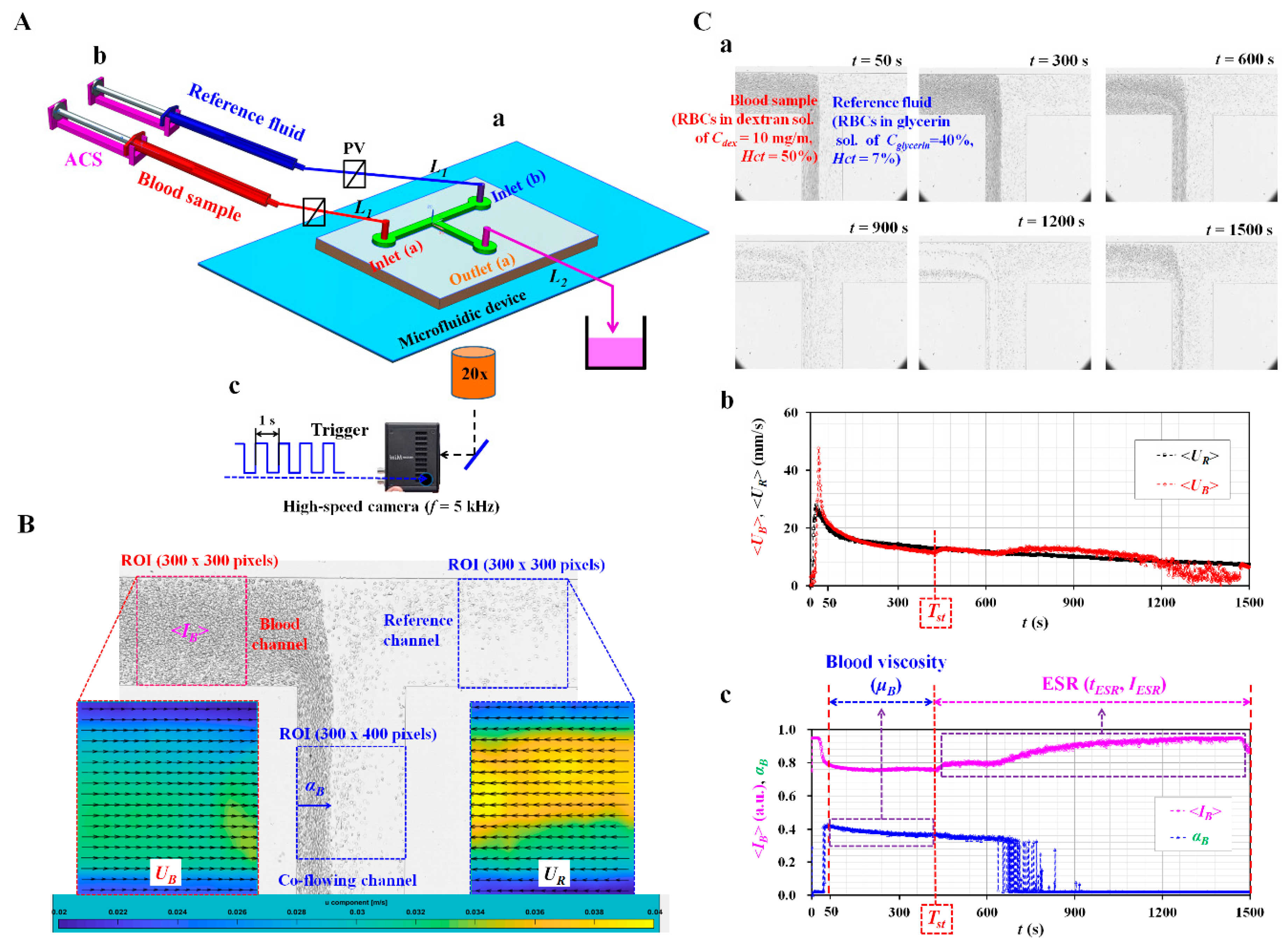
2.1. Fabrication of Microfluidic Device and Experimental Procedure
2.2. Quantification of Microscopic Image Intensity, Blood Velocity Fields, and Interfacial Location
2.3. Quantification of Blood Viscosity and ESR
2.4. Selection of Base Solution in Reference Fluid
2.5. Statistical Analysis
3. Results and Discussion
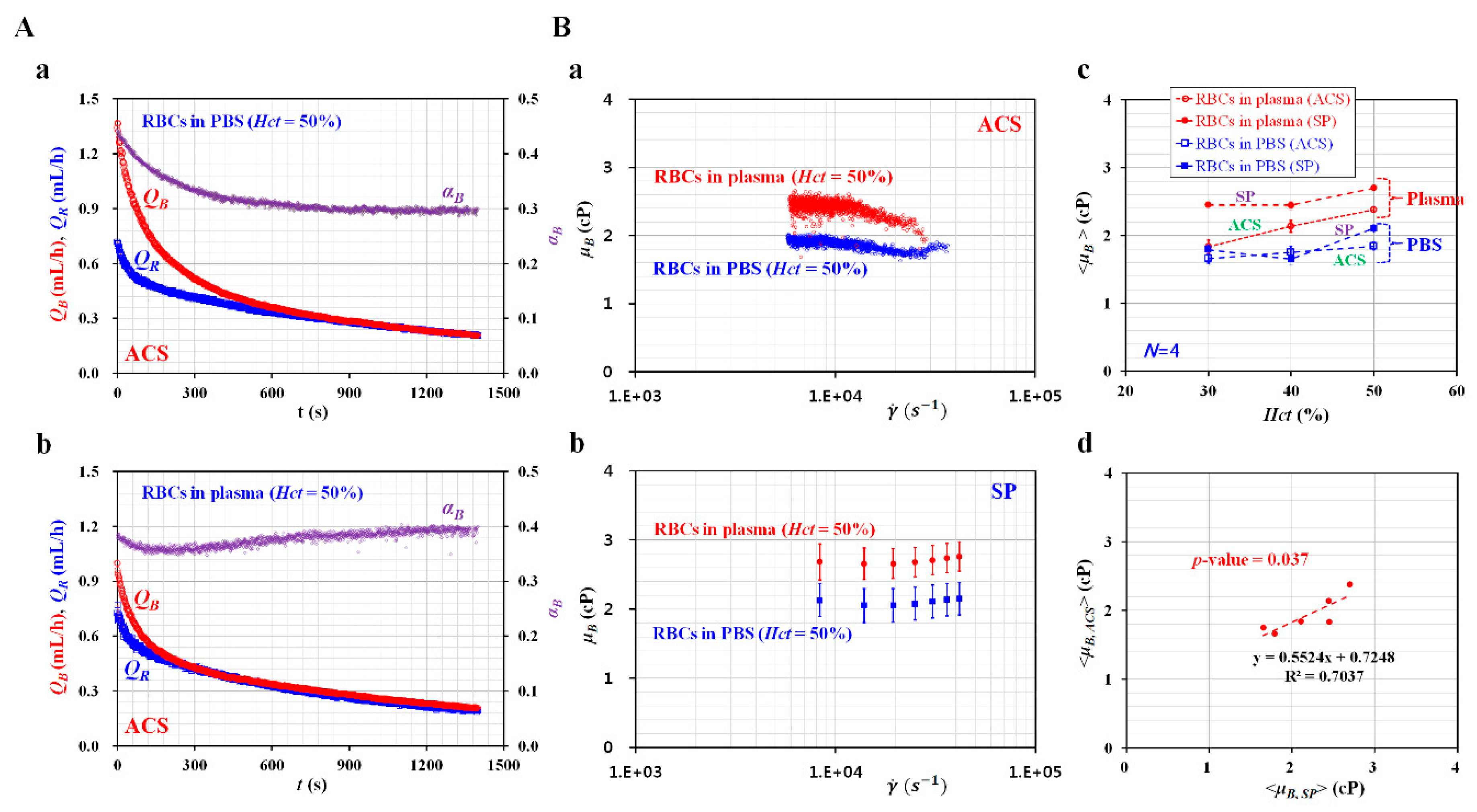
3.1. Contribution of RBCs Added into Reference Fluid to Viscosity and Velocity Fields
3.2. Relationship between Flow Rate of Syringe Pump and Averaged Velocity Obtained by μPIV
3.3. Quantitative Comparison of Blood Viscosity with Respect to Fluid Delivery System (ACS, SP)
3.4. Quantitative Measurement of ESR with Respect to base Solution and Hematocrit
3.5. Variations of Blood Viscosity and ESR for Blood Samples Composed of Specific Dextran Solutions
3.6. Variations of Blood Viscosity and ESR for Blood Samples Composed of Hardened RBCs
4. Conclusions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Figure A1

Appendix A.2. Figure A2

Appendix A.3. Figure A3

Appendix A.4. Blood Sample Preparation
Appendix A.5. Variation of Velocity, Interface, and Viscosity with Respect to Relocation of Object Plane

References
- Popel, A.S.; Johnson, P.C. Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 2005, 37, 43–69. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lipowsky, H.H. Microvascular Rheology and Hemodynamics. Microcirculation 2005, 12, 5–15. [Google Scholar] [CrossRef]
- Danesh, J.; Collins, R.; Peto, R.; Lowe, G.D.O. Haematocrit, viscosity, erythrocyte sedimentation rate: Meta-analyses of prospective studies of coronary heart disease. Eur. Heart J. 2000, 21, 515–520. [Google Scholar] [CrossRef] [PubMed]
- Jones, C.M.; Baker-Groberg, S.M.; Cianchetti, F.A.; Glynn, J.J.; Healy, L.D.; Lam, W.Y.; Nelson, J.W.; Parrish, D.C.; Phillips, K.G.; Scott-Drechsel, D.E.; et al. Measurement science in the circulatory system. Cell Mol. Bioeng. 2014, 7, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oore-ofe, O.; Soma, P.; Buys, A.V.; Debusho, L.K.; Pretorius, E. Characterizing pathology in erythrocytes using morphological and biophysical membrane properties: Relation to impaired hemorheology and cardiovascular function in rheumatoid arthritis. Biochim. Biophys. Acta-Biomembr. 2017, 1859, 2381–2391. [Google Scholar]
- Kang, Y.J.; Lee, S.-J. In vitro and ex vivo measurement of the biophysical properties of blood using microfluidic platforms and animal models. Analyst 2018, 143, 2723–2749. [Google Scholar] [CrossRef]
- Yeom, E.; Kim, H.M.; Park, J.H.; Choi, W.; Doh, J.; Lee, S.-J. Microfluidic system for monitoring temporal variations of hemorheological properties and platelet adhesion in LPS-injected rats. Sci. Rep. 2017, 7, 1801. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J.; Yeom, E.; Lee, S.-J. Microfluidic biosensor for monitoring tmporal variations of hemorheological and hemodynamic properties using an extracorporeal rat bypass loop. Anal. Chem. 2013, 85, 10503–10511. [Google Scholar] [CrossRef]
- Kang, Y.J.; Lee, S.-J. Blood viscoelasticity measurement using steady and transient flow controls of blood in a microfluidic analogue of Wheastone-bridge channel. Biomicrofluidics 2013, 7, 054122. [Google Scholar] [CrossRef] [Green Version]
- Schmid-Schonbein, H.; Gaehtgens, P.; Hirsch, H. On the shear rate dependence of red cell aggregation in vitro. J. Clin. Investig. 1968, 47, 1447–1454. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.J.; Lee, S.Y.; Jee, S.; Atajanov, A.; Yang, S. Micro-viscometer for measuring shear-varying blood viscosity over a wide-ranging shear rate. Sensors 2017, 17, 1442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, Y.J.; Yang, S. Integrated microfluidic viscometer equipped with fluid temperature controller for measurement of viscosity in complex fluids. Microfluid. Nanofluidics 2013, 14, 657–668. [Google Scholar] [CrossRef]
- Oh, S.; Kim, B.; Lee, J.K.; Choi, S. 3D-printed capillary circuits for rapid, low-cost, portable analysis ofblood viscosity. Sens. Actuator B Chem. 2018, 259, 106–113. [Google Scholar] [CrossRef]
- Kang, Y.J.; Ryu, J.; Lee, S.-J. Label-free viscosity measurement of complex fluids using reversal flow switching manipulation in a microfluidic channel. Biomicrofluidics 2013, 7, 044106. [Google Scholar] [CrossRef] [Green Version]
- Khnouf, R.; Karasneh, D.; Abdulhay, E.; Abdelhay, A.; Sheng, W.; Fan, Z.H. Microfluidics-based device for the measurement of blood viscosity and its modeling based on shear rate, temperature, and heparin concentration. Biomedical Microdevices 2019, 21, 80. [Google Scholar] [CrossRef]
- Isiksacan, Z.; Erel, O.; Elbuken, C. A portable microfluidic system for rapid measurement of the erythrocyte sedimentation rate. Lab Chip 2016, 16, 4682–4690. [Google Scholar] [CrossRef]
- Zeng, N.F.; Mancuso, J.E.; Zivkovic, A.M.; Smilowitz, J.T.; Ristenpart, W.D. Red blood cells from individuals with abdominal obesity or metabolic abnormalities exhibit less deformability upon entering a constriction. PLoS ONE 2016, 11, e0156070. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Duffy, S.P.; Matthews, K.; Deng, X.; Santoso, A.T.; Islamzada, E.; Ma, H. Deformability based sorting of red blood cells improves diagnostic sensitivity for malaria caused by Plasmodium falciparum. Lab Chip 2016, 16, 645–654. [Google Scholar] [CrossRef]
- Berry, S.B.; Fernandes, S.C.; Rajaratnam, A.; DeChiara, N.S.; Mace, C.R. Measurement of the hematocrit using paper-based microfluidic devices. Lab Chip 2016, 16, 3689–3694. [Google Scholar] [CrossRef]
- Kim, B.J.; Lee, Y.S.; Zhbanov, A.; Yang, S. A physiometer for simultaneous measurement of whole blood viscosity and its determinants: Hematocrit and red blood cell deformability. Analyst 2019, 144, 3144–3157. [Google Scholar] [CrossRef]
- Han, Z.; Tang, X.; Zheng, B. A PDMS viscometer for microliter Newtonian fluid. J. Micromech. Microeng. 2007, 17, 1828–1834. [Google Scholar] [CrossRef]
- Srivastava, N.; Davenport, R.D.; Burns, M.A. Nanoliter Viscometer for Analyzing Blood Plasma and Other Liquid Samples. Anal. Chem. 2005, 77, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Cho, Y.I.; Lee, D.-H.; Park, C.-M.; Moon, H.-W.; Hur, M.; Kim, J.Q.; Yun, Y.-M. Analycal performance evaluation of the scanning tube viscometer for measurement of whole blood viscosity. Clin. Biochem. 2013, 46, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Song, J.M.; Yeom, E. 3D printed microfluidic viscometer based on the co-flowing stream. Biomicrofluidics 2019, 13, 014104. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Jang, I.; Song, S.; Bae, S.-C. Development of a paper-based viscometer for blood plasma using colorimetric analysis. Anal. Chem. 2019, 91, 4868–4875. [Google Scholar] [CrossRef]
- Marinakis, G.N.; Barbenel, J.C.; Tsangaris, S.G. A new capillary viscometer for small samples of whole blood. Proc. Inst. Mech. Eng. 2002, 216, H1502. [Google Scholar] [CrossRef]
- Solomon, D.E.; Abdel-Raziq, A.; Vanapalli, S.A. A stress-controlled microfluidic shear viscometer based on smartphone imaging. Rheol. Acta 2016, 55, 727–738. [Google Scholar] [CrossRef]
- Kim, W.-J.; Kim, S.; Huh, C.; Kim, B.K.; Kim, Y.J. A novel hand-held viscometer applicable for point-of-care. Sens. Actuator B Chem. 2016, 234, 239–246. [Google Scholar] [CrossRef]
- Pop, G.A.M.; Sisschops, L.L.A.; Iliev, B.; Struijk, P.C.; van der Heven, J.G.; Hoedemaekers, C.W.E. On-line blood viscosity monitoring in vivo with a central venous catheter using electrical impedance technique. Biosens. Bioelectron. 2013, 41, 595–601. [Google Scholar] [CrossRef]
- Zeng, H.; Zhao, Y. Rheological analysis of non-Newtonian blood flow using a microfluidic device. Sens. Actuator A Phys. 2011, 166, 207–213. [Google Scholar] [CrossRef]
- Li, Y.; Ward, K.R.; Burns, M.A. Viscosity measurements using microfluidic droplet length. Anal. Chem. 2017, 89, 3996–4006. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J. Periodic and simultaneous quantification of blood viscosity and red blood cell aggregation using a microfluidic platform under in-vitro closed-loop circulation. Biomicrofluidics 2018, 12, 024116. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.J. Microfluidic-based technique for measuring RBC aggregation and blood viscosity in a continuous and simultaneous fashion. Micromachines 2018, 9, 467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kang, Y.J.; Kim, B.J. Multiple and periodic measurement of RBC aggregation and ESR in parallel microfluidic channels under on-off blood flow control. Micromachines 2018, 9, 318. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nam, J.-H.; Yang, Y.; Chung, S.; Shin, S. Comparison of light-transmission and -backscattering methods in the measurement of red blood cell aggregation. J. Biomed. Opt. 2010, 15, 027003. [Google Scholar] [CrossRef] [Green Version]
- Baskurt, O.K.; Uyuklu, M.; Meiselman, H.J. Time Course of Electrical Impedance During Red Blood Cell Aggregation in a Glass Tube: Comparison with Light Transmittance. IEEE Trans. Biomed. Eng. 2010, 57, 969–978. [Google Scholar] [CrossRef]
- Antonova, N.; Riha, P.; Ivanov, I. Time dependent variation of human blood conductivity as a method for an estimation of RBC aggregation. Clin. Hemorheolo. Microcir. 2008, 39, 69–78. [Google Scholar] [CrossRef]
- Brust, M.; Aouane, O.; Thie’baud, M.; Flormann, D.; Verdier, C.; Kaestner, L.; Laschke, M.W.; Selmi, H.; Benyoussef, A.; Podgorski, T.; et al. The plasma protein fibrinogen stabilizes clusters of red blood cells in microcapillary flows. Sci. Rep. 2014, 4, 4348. [Google Scholar] [CrossRef] [Green Version]
- Kaliviotis, E.; Sherwood, M.; Balabani, S. Partitioning of red blood cell aggregates in bifurcating microscale flows. Sci. Rep. 2017, 7, 44563. [Google Scholar] [CrossRef] [Green Version]
- Tomaiuolo, G.; Lanotte, L.; Ghigliotti, G.; Misbah, C.; Guido, S. Red blood cell clustering in Poiseuille microcapillary flow. Phys. Fluids 2012, 24, 051903. [Google Scholar] [CrossRef] [Green Version]
- Yeom, E.; Lee, S.-J. Microfluidic-based speckle analysis for sensitive measurement of erythrocyte aggregation: A comparison of four methods for detection of elevated erythrocyte aggregation in diabetic rat blood. Biomicrofluidics 2015, 9, 024110. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Kinnunen, M.; Khokhlova, M.D.; Lyubin, E.V.; Priezzhev, A.V.; Meglinski, I.; Fedyanin, A.A. Optical tweezers study of red blood cell aggregation and disaggregation in plasma and protein solutions. J. Biomed. Opt. 2016, 21, 035001. [Google Scholar] [CrossRef]
- Zhbanov, A.; Yang, S. Effects of aggregation on blood sedimentation and conductivity. PLoS ONE 2015, 10, e0129337. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J.; Ha, Y.-R.; Lee, S.-J. Microfluidic-based measurement of erythrocyte sedimentation rate for biophysical assessment of blood in an in vivo malaria-infected mouse. Biomicrofluidics 2014, 8, 044114. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Microfluidic-based biosensor for sequential measurement of blood pressure and RBC aggregation over continuously varying blood flows. Micromachines 2019, 10, 577. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Simultaneous measurement of blood pressure and RBC aggregation by monitoring on–off blood flows supplied from a disposable air-compressed pump. Analyst 2019, 144, 3556–3566. [Google Scholar] [CrossRef]
- Kang, Y.J. RBC deformability measurement based on variations of pressure in multiple micropillar channels during blood delivery using a disposable air-compressed pump. Anal. Methods 2018, 10, 4549–4561. [Google Scholar] [CrossRef]
- Gao, J.X.; Yeo, L.P.; Chan-Park, M.B.; Miao, J.M.; Yan, Y.H.; Sun, J.B.; Lam, Y.C.; Yue, C.Y. Antistick postpassivation of high-aspect ratio silicon molds fabricated by deep-reactive ion etching. J. Microelectromech. Syst. 2006, 15, 84–93. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man. Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Kang, Y.J. Continuous and simultaneous measurement of the biophysical properties of blood in a microfluidic environment. Analyst 2016, 141, 6583–6597. [Google Scholar] [CrossRef]
- Cheng, N.-S. Formula for the viscosity of a glycerol-water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Linderkamp, O.; Friederichs, E.; Boehler, T.; Ludwig, A. Age dependency of red blood cell deformability and density: Studies in transient erythroblastopenia of childhood. Br. J. Haematol. 1993, 83, 125–129. [Google Scholar] [CrossRef]
- Bourdon, C.J.; Olsen, M.G.; Gorby, A.D. The depth of corretion in miciro-PIV for high numerical aperature and immersion objectives. J. Fluid Eng. Trans. ASME 2006, 128, 883–886. [Google Scholar] [CrossRef]





© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.J. Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System. Micromachines 2020, 11, 215. https://doi.org/10.3390/mi11020215
Kang YJ. Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System. Micromachines. 2020; 11(2):215. https://doi.org/10.3390/mi11020215
Chicago/Turabian StyleKang, Yang Jun. 2020. "Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System" Micromachines 11, no. 2: 215. https://doi.org/10.3390/mi11020215
APA StyleKang, Y. J. (2020). Microfluidic-Based Biosensor for Blood Viscosity and Erythrocyte Sedimentation Rate Using Disposable Fluid Delivery System. Micromachines, 11(2), 215. https://doi.org/10.3390/mi11020215




