Microfluidic In-Situ Measurement of Poisson’s Ratio of Hydrogels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Channel and Particle Fabrication
2.2. Experimental Protocol
2.3. Analysis
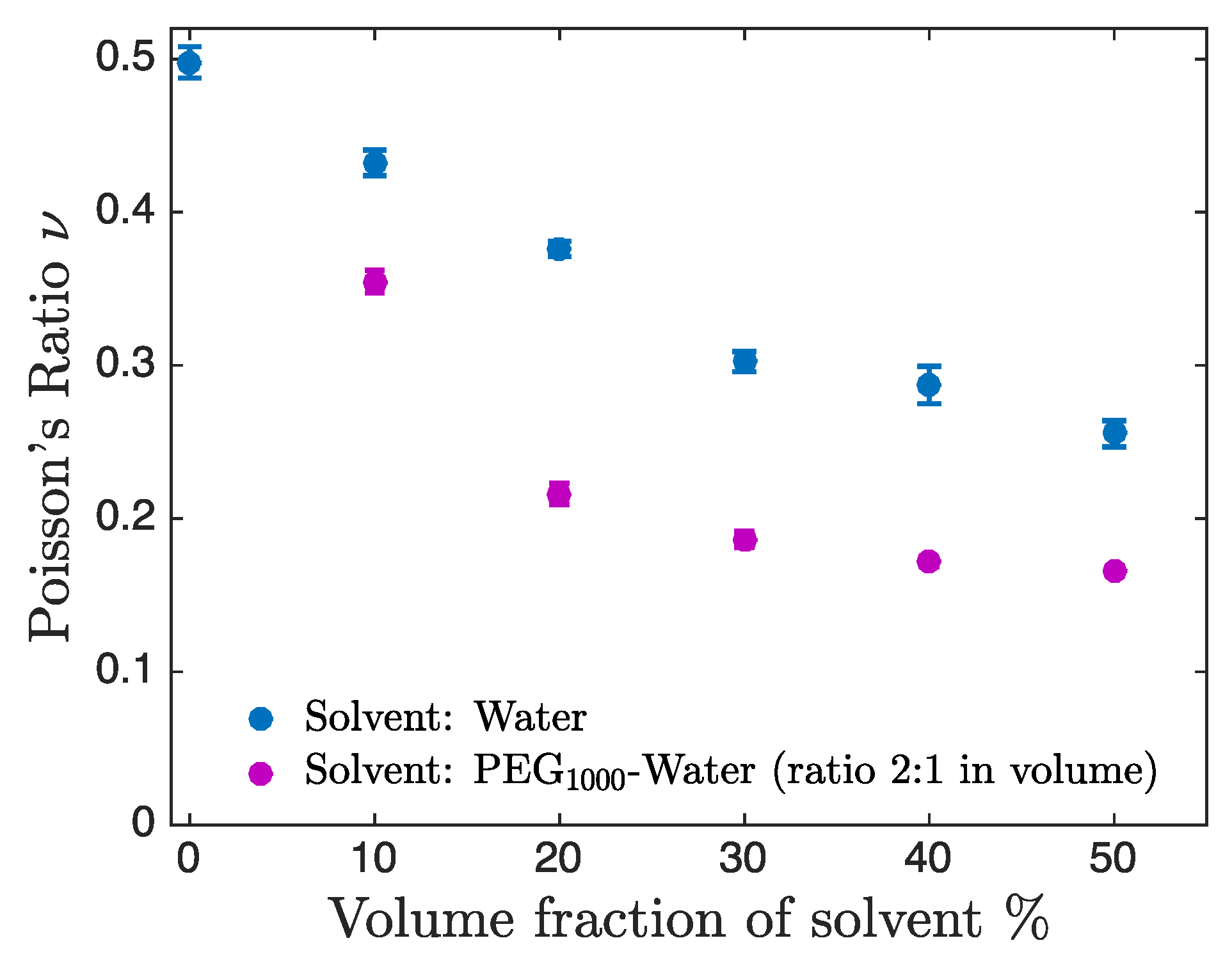
3. Results and Discussion
3.1. Validation of the Method
3.2. Limitations
3.3. Dependence of Poisson’s Ratio on the Solvent Composition
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nayak, S.; Lee, H.; Chmielewski, J.; Lyon, L.A. Folate-mediated cell targeting and cytotoxicity using thermoresponsive microgels. J. Am. Chem. Soc. 2004, 126, 10258–10259. [Google Scholar] [CrossRef]
- Soppimath, K.S.; Tan, D.W.; Yang, Y.Y. pH-triggered thermally responsive polymer core–shell nanoparticles for drug delivery. Adv. Mater. 2005, 17, 318–323. [Google Scholar] [CrossRef]
- Ambrosio, L.; De Santis, R.; Nicolais, L. Composite hydrogels for implants. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 1998, 212, 93–99. [Google Scholar] [CrossRef]
- Liu, Y.; Genzer, J.; Dickey, M.D. “2D or not 2D”: Shape-programming polymer sheets. Prog. Polym. Sci. 2016, 52, 79–106. [Google Scholar] [CrossRef]
- Crandall, S.H.; Lardner, T.J.; Archer, R.R.; Cook, N.H.; Dahl, N.C. An Introduction to the Mechanics of Solids; Mcgraw Hill Science Engineering Math: New York, NY, USA, 1978. [Google Scholar]
- Li, Y.; Hu, Z.; Li, C. New method for measuring Poisson’s ratio in polymer gels. J. Appl. Polym. Sci. 1993, 50, 1107–1111. [Google Scholar] [CrossRef]
- Wyss, H.M.; Franke, T.; Mele, E.; Weitz, D.A. Capillary micromechanics: Measuring the elasticity of microscopic soft objects. Soft Matter 2010, 6, 4550–4555. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Advances in Chemical Engineering: Characterization of Flow, Particles and Interfaces; Academic Press: Cambridge, MA, USA, 2009; Volume 37. [Google Scholar]
- Boudou, T.; Ohayon, J.; Picart, C.; Tracqui, P. An extended relationship for the characterization of Young’s modulus and Poisson’s ratio of tunable polyacrylamide gels. Biorheology 2006, 43, 721–728. [Google Scholar] [PubMed]
- Hurley, D.C.; Turner, J.A. Measurement of Poisson ’s ratio with contact-resonance atomic force microscopy. J. Appl. Phys. 2007, 102, 033509. [Google Scholar] [CrossRef] [Green Version]
- Evans, K. Measurement of Poisson ’s Ratio; Springer: Berlin, Germany, 1999; pp. 140–142. [Google Scholar]
- Moram, M.; Barber, Z.; Humphreys, C. Accurate experimental determination of the Poisson ’s ratio of GaN using high-resolution x-ray diffraction. J. Appl. Phys. 2007, 102, 023505. [Google Scholar] [CrossRef]
- Dendukuri, D.; Panda, P.; Haghgooie, R.; Kim, J.M.; Hatton, T.A.; Doyle, P.S. Modeling of oxygen-inhibited free radical photopolymerization in a PDMS microfluidic device. Macromolecules 2008, 41, 8547–8556. [Google Scholar] [CrossRef] [Green Version]
- Wexler, J.S.; Trinh, P.H.; Berthet, H.; Quennouz, N.; du Roure, O.; Huppert, H.E.; Linder, A.; Stone, H.A. Bending of elastic fibres in viscous flows: The influence of confinement. J. Fluid Mech. 2013, 720, 517–544. [Google Scholar] [CrossRef] [Green Version]
- Berthet, H.; du Roure, O.; Lindner, A. Microfluidic Fabrication Solutions for Tailor-Designed Fiber Suspensions. Appl. Sci. 2016, 6, 385. [Google Scholar] [CrossRef] [Green Version]
- Duprat, C.; Berthet, H.; Wexler, J.S.; du Roure, O.; Lindner, A. Microfluidic in situ mechanical testing of photopolymerized gels. Lab A Chip 2014, 15, 244–52. [Google Scholar] [CrossRef] [PubMed]
- Nagel, M.; Brun, P.T.; Berthet, H.; Lindner, A.; Gallaire, F.; Duprat, C. Oscillations of confined fibres transported in microchannels. J. Fluid Mech. 2018, 835, 444–470. [Google Scholar] [CrossRef] [Green Version]
- Cappello, J.; Bechert, M.; Duprat, C.; du Roure, O.; Gallaire, F.; Lindner, A. Transport of flexible fibers in confined microchannels. Phys. Rev. Fluids 2019, 4, 034202. [Google Scholar] [CrossRef] [Green Version]
- Bechert, M.; Cappello, J.; Daïeff, M.; Gallaire, F.; Lindner, A.; Duprat, C. Controlling transport dynamics of confined asymmetric fibers. arXiv 2019, arXiv:1903.00761. [Google Scholar] [CrossRef] [Green Version]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. HISTORICAL commentary NIH Image to ImageJ : 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef]
- Gervais, T.; El-Ali, J.; Günther, A.; Jensen, K.F. Flow-induced deformation of shallow microfluidic channels. Lab A Chip 2006, 6, 500–507. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.M. Buckling of Bars, Plates, and Shells; Bull Ridge Corporation: Blacksburg, VA, USA, 2006. [Google Scholar]
- Onyia, M.E.; Rowland-Lato, E.O. Determination of the Critical Buckling Load of Shear Deformable Unified Beam. Int. J. Eng. Technol. 2018, 10, 647–657. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.P. Friction and lubrication of hydrogels—its richness and complexity. Soft Matter 2006, 2, 544–552. [Google Scholar] [CrossRef]
- Gabler, S.; Stampfl, J.; Koch, T.; Seidler, S.; Schuller, G.; Redl, H.; Juras, V.; Trattnig, S.; Weidisch, R. Determination of the viscoelastic properties of hydrogels based on polyethylene glycol diacrylate (PEG-DA) and human articular cartilage. Int. J. Mater. Eng. Innov. 2009, 1, 3–20. [Google Scholar] [CrossRef]
- Lee, A.G.; Arena, C.P.; Beebe, D.J.; Palecek, S.P. Development of macroporous poly (ethylene glycol) hydrogel arrays within microfluidic channels. Biomacromolecules 2010, 11, 3316–3324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, S.; Hu, Y.; Zhao, X.; Suo, Z. Poroelasticity of a covalently crosslinked alginate hydrogel under compression. J. Appl. Phys. 2010, 108, 113514. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, X.; Vlassak, J.J.; Suo, Z. Using indentation to characterize the poroelasticity of gels. Appl. Phys. Lett. 2010, 96, 121904. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 023001. [Google Scholar] [CrossRef]
- Punter, M.T.; Vos, B.E.; Mulder, B.M.; Koenderink, G.H. Poroelasticity of (bio) polymer networks during compression: Theory and experiment. arXiv 2020, arXiv:1910.00490. [Google Scholar] [CrossRef] [Green Version]
- Duchêne, C.; Filipe, V.; Huille, S.; Lindner, A. Clogging of microfluidic constrictions by monoclonal antibody aggregates: Role of aggregate shape and deformability. Soft Matter 2020, 16, 921–928. [Google Scholar] [CrossRef]
- Bommireddy, Y.; Agarwal, A.; Yettella, V.; Tomar, V.; Gonzalez, M. Loading-unloading contact law for micro-crystalline cellulose particles under large deformations. Mech. Res. Commun. 2019, 99, 22–31. [Google Scholar] [CrossRef] [Green Version]





| PEGDA | PI | Water | PEG:water Ratio 2:1 in Volume | Name |
|---|---|---|---|---|
| 90% | 10% | 0% | 0% | pure PEGDA |
| 80% | 10% | 10% | 0% | PW |
| 70% | 10% | 20% | 0% | PW |
| 60% | 10% | 30% | 0% | PW |
| 50% | 10% | 40% | 0% | PW |
| 40% | 10% | 50% | 0% | PW |
| 80% | 10% | 0% | 10% | PP |
| 70% | 10% | 0% | 20% | PP |
| 60% | 10% | 0% | 30% | PP |
| 50% | 10% | 0% | 40% | PP |
| 40% | 10% | 0% | 50% | PP |
| 30% | 10% | 0% | 60% | PP |
| 20% | 10% | 0% | 70% | PP |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cappello, J.; d’Herbemont, V.; Lindner, A.; du Roure, O. Microfluidic In-Situ Measurement of Poisson’s Ratio of Hydrogels. Micromachines 2020, 11, 318. https://doi.org/10.3390/mi11030318
Cappello J, d’Herbemont V, Lindner A, du Roure O. Microfluidic In-Situ Measurement of Poisson’s Ratio of Hydrogels. Micromachines. 2020; 11(3):318. https://doi.org/10.3390/mi11030318
Chicago/Turabian StyleCappello, Jean, Vincent d’Herbemont, Anke Lindner, and Olivia du Roure. 2020. "Microfluidic In-Situ Measurement of Poisson’s Ratio of Hydrogels" Micromachines 11, no. 3: 318. https://doi.org/10.3390/mi11030318
APA StyleCappello, J., d’Herbemont, V., Lindner, A., & du Roure, O. (2020). Microfluidic In-Situ Measurement of Poisson’s Ratio of Hydrogels. Micromachines, 11(3), 318. https://doi.org/10.3390/mi11030318





