Silicon Multi-Pass Gas Cell for Chip-Scale Gas Analysis by Absorption Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
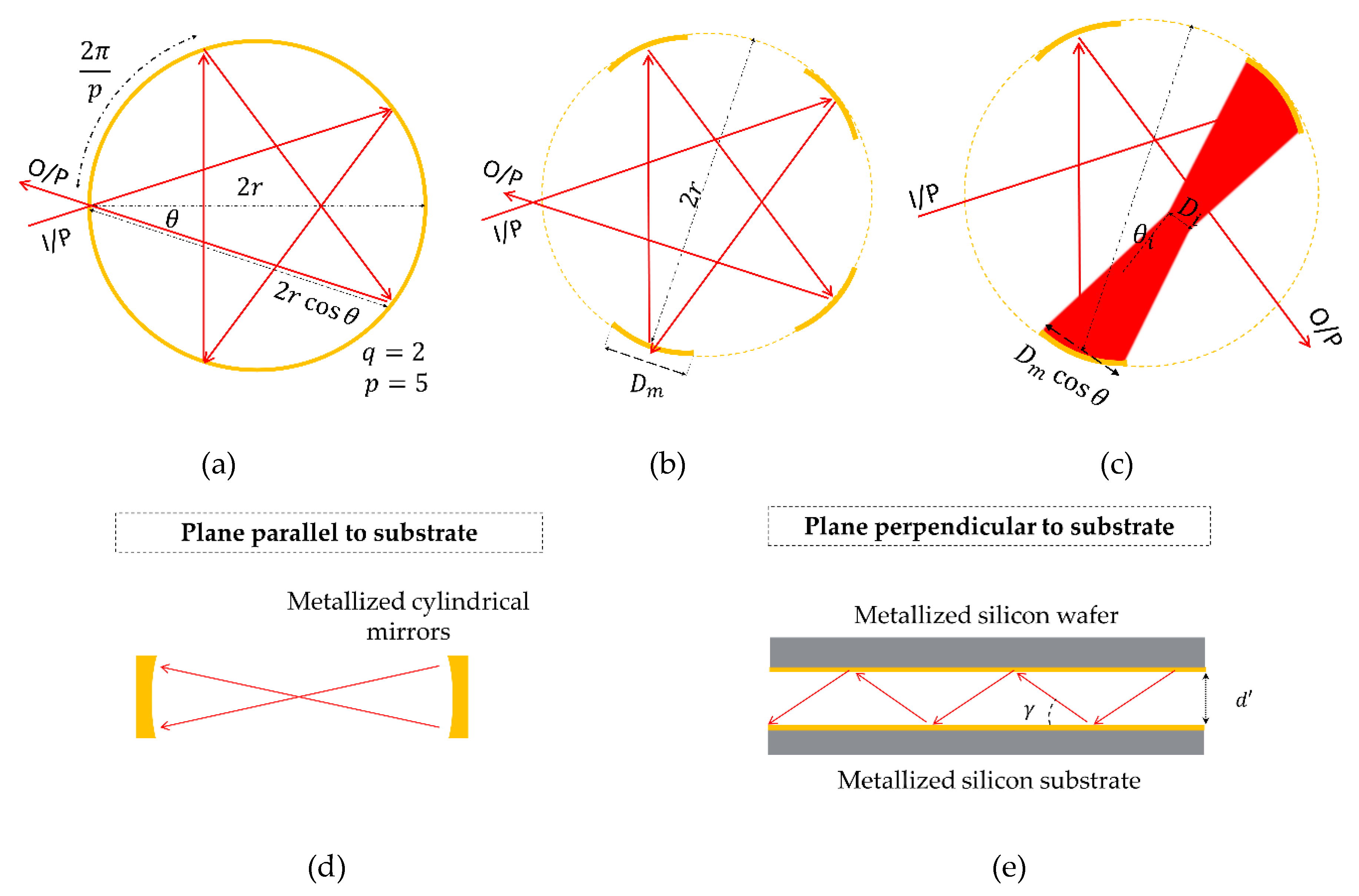
2.1. Design Considerations
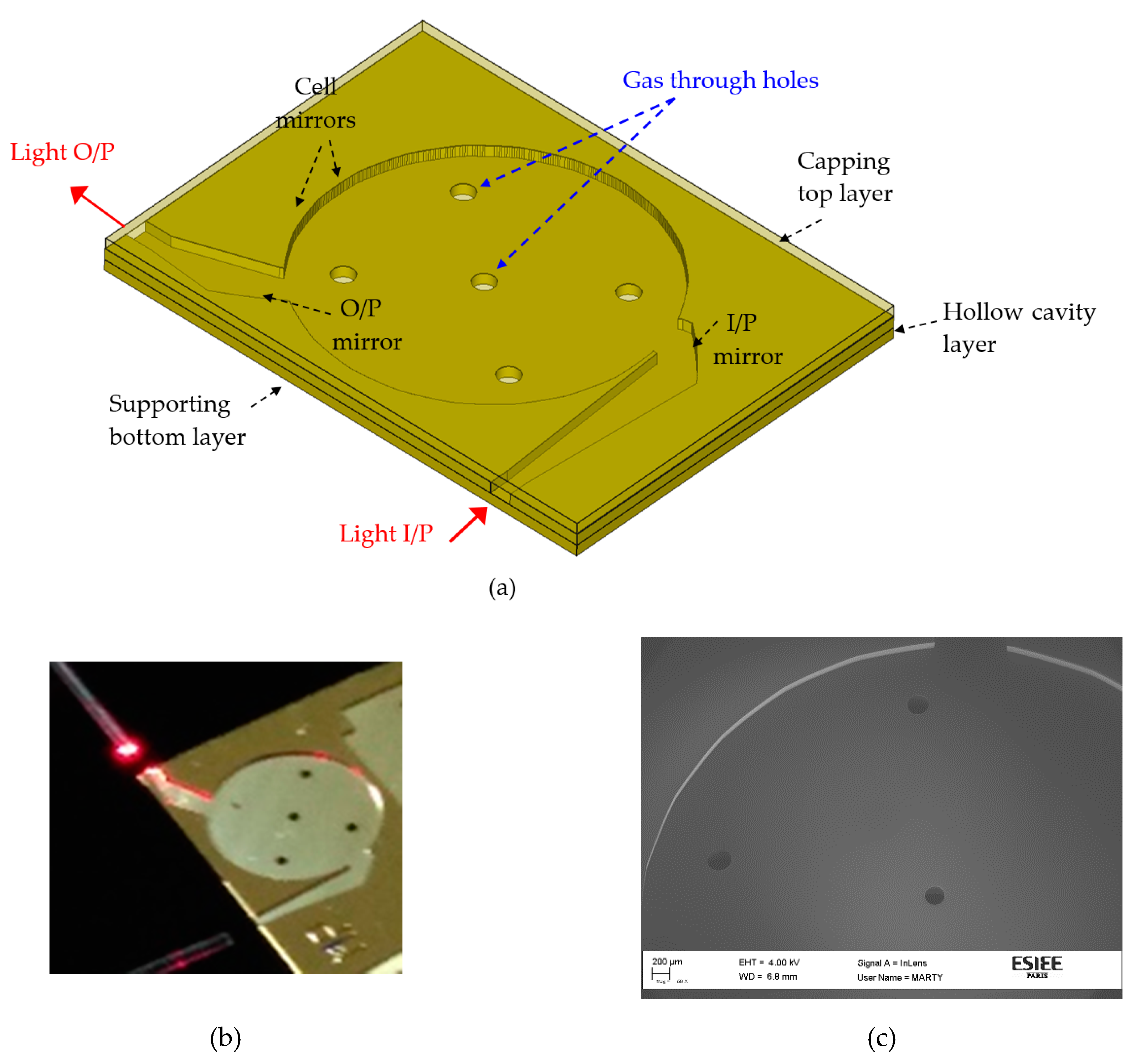
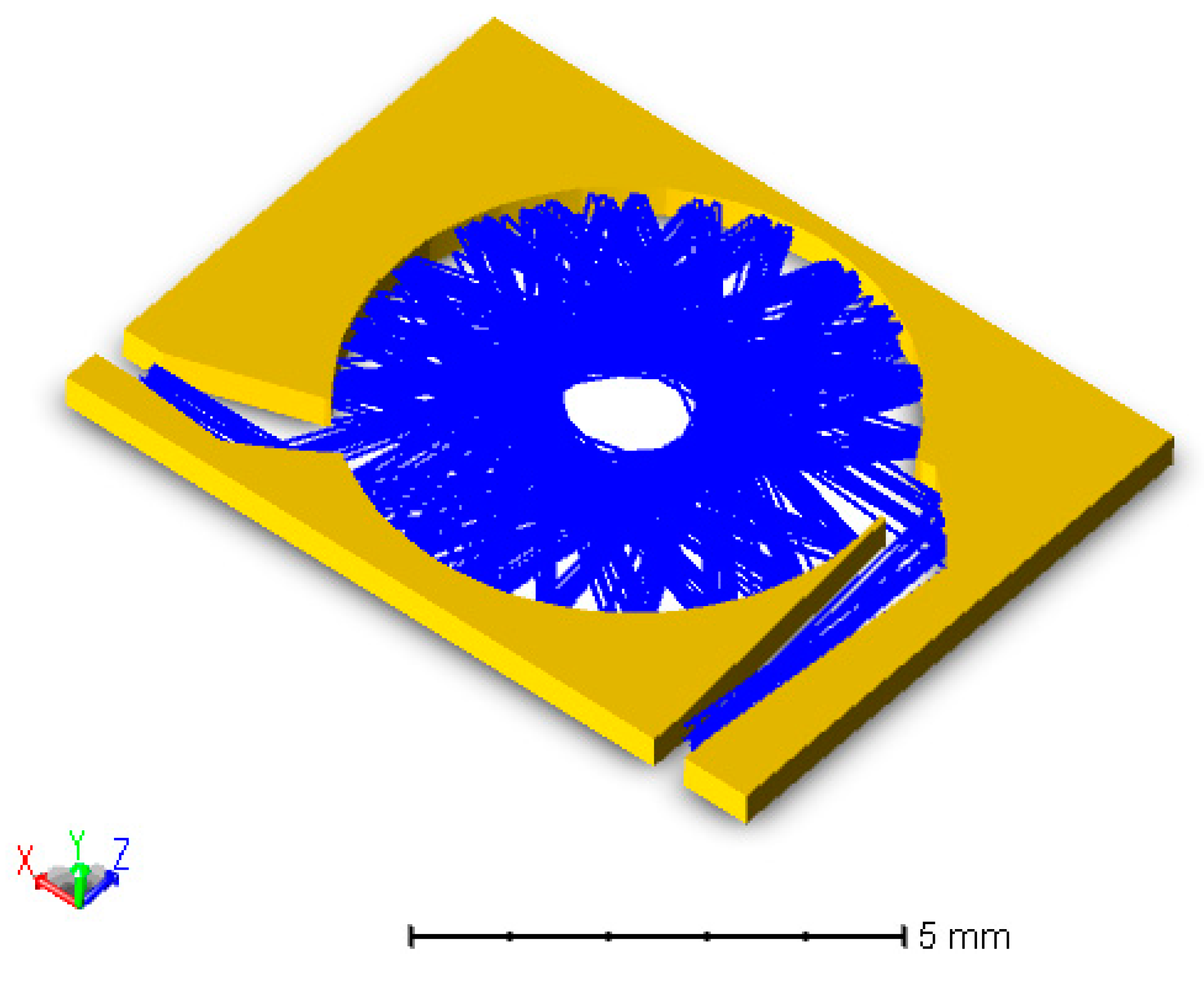
2.2. Proposed Micro-Fabricated Gas Cells
2.3. Fabrication Steps
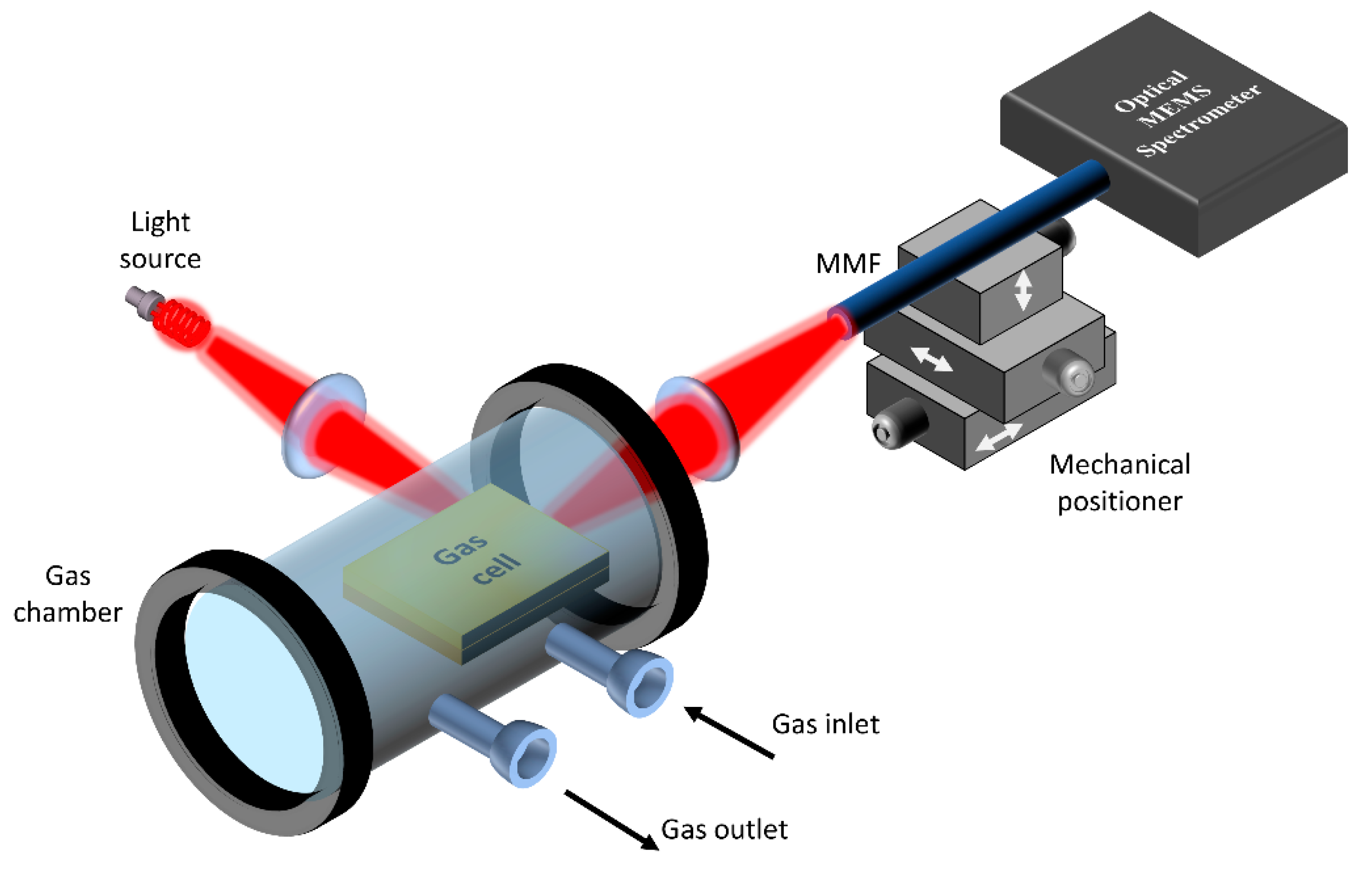
2.4. Experimental Setup
3. Results
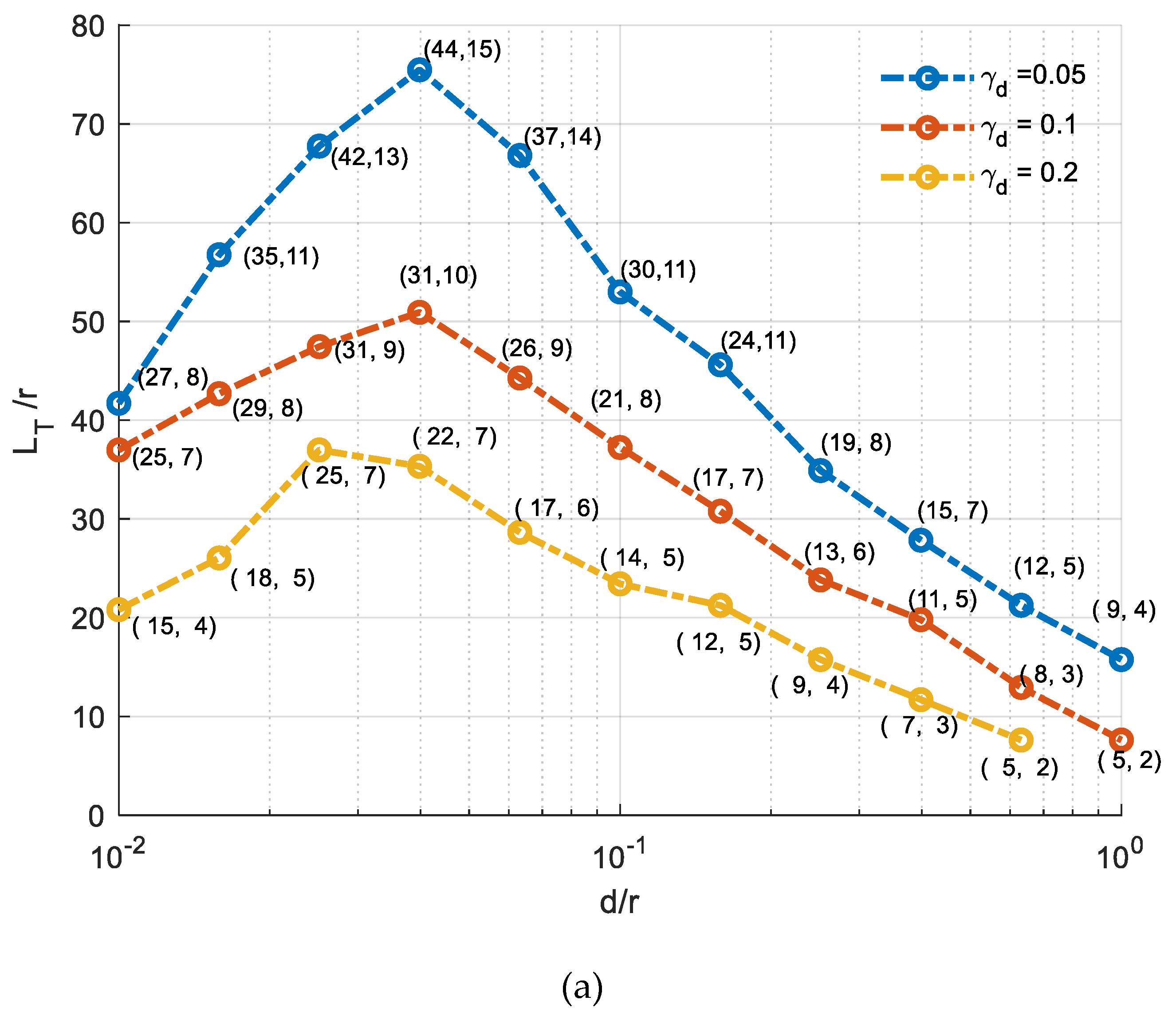
3.1. Modeling and Simulation
- and are integers.
- is relatively prime (co-prime).
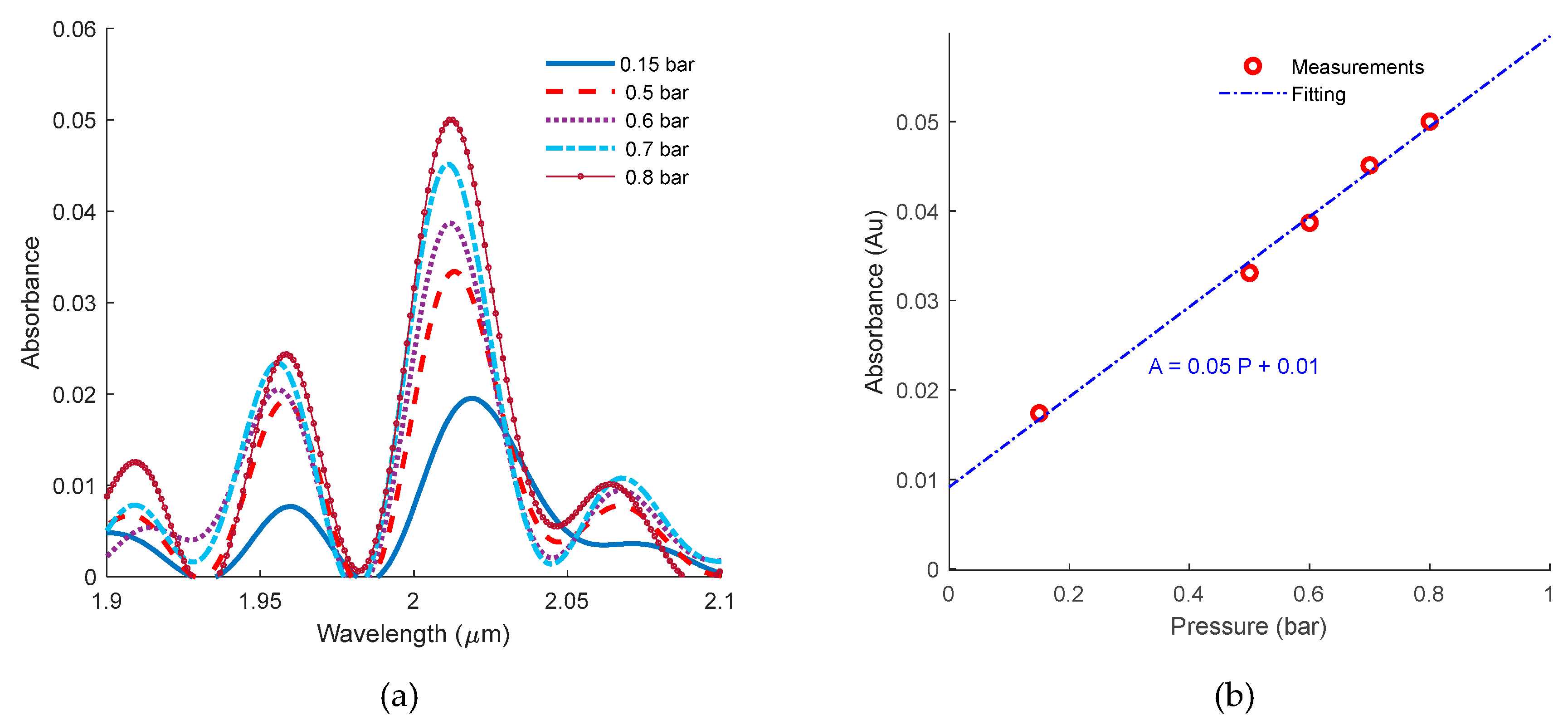
3.2. Experimental Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Meng, F.-L.; Guo, Z.; Huang, X.-J. Graphene-based hybrids for chemiresistive gas sensors. TrAC Trends Anal. Chem. 2015, 68, 37–47. [Google Scholar] [CrossRef]
- Biasioli, F.; Gasperi, F.; Yeretzian, C.; Märk, T.D. PTR-MS monitoring of VOCs and BVOCs in food science and technology. TrAC Trends Anal. Chem. 2011, 30, 968–977. [Google Scholar] [CrossRef]
- Yole Développment. Gas and Particle Sensors 2018—Market & Technology Report; Yole Développment: Lyon, France, 2018. [Google Scholar]
- Qin, Y.; Gianchandani, Y.B. A fully electronic microfabricated gas chromatograph with complementary capacitive detectors for indoor pollutants. Microsyst. Nanoeng. 2016, 2, 15049. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fathy, A.; Sabry, Y.M.; Nazeer, S.; Bourouina, T.; Khalil, D.A. On-chip parallel Fourier transform spectrometer for broadband selective infrared spectral sensing. Microsyst. Nanoeng. 2020, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Eltagoury, Y.M.; Sabry, Y.M.; Khalil, D.A. All-Silicon Double-Cavity Fourier-Transform Infrared Spectrometer On-Chip. Adv. Mater. Technol. 2019, 4, 1900441. [Google Scholar] [CrossRef]
- Othman, A.M.; Kotb, H.E.; Sabry, Y.M.; Khalil, D. Combining MEMS FTIR Spectrometer and Widened-Spectrum Mode-Locked Fiber Laser for Gas-Sensing. In Proceedings of the The European Conference on Lasers and Electro-Optics, Munich, Germany, 23–27 June 2019; p. ch_p_12. [Google Scholar]
- Gerguis, J.O.; Sabry, Y.M.; Omran, H.; Khalil, D. Spectroscopic Gas Sensing Based on a MEMS-SOA Swept Fiber Laser Source. J. Light. Technol. 2019, 37, 5354–5360. [Google Scholar] [CrossRef]
- Mu, Y.; Hu, T.; Gong, H.; Ni, R.; Li, S. A Trace C2H2 Sensor Based on an Absorption Spectrum Technique Using a Mid-Infrared Interband Cascade Laser. Micromachines 2018, 9, 530. [Google Scholar] [CrossRef] [Green Version]
- Herriott, D.R.; Schulte, H.J. Folded optical delay lines. Appl. Opt. 1965, 4, 883–889. [Google Scholar] [CrossRef]
- Daher, N.; Guichard, F.; Jolly, S.W.; Délen, X.; Quéré, F.; Hanna, M.; Georges, P. Multipass cells: 1D numerical model and investigation of spatio-spectral couplings at high nonlinearity. JOSA B 2020, 37, 993–999. [Google Scholar] [CrossRef]
- Kaumanns, M.; Pervak, V.; Kormin, D.; Leshchenko, V.; Kessel, A.; Ueffing, M.; Chen, Y.; Nubbemeyer, T. Multipass spectral broadening of 18 mJ pulses compressible from 1.3 ps to 41 fs. Opt. Lett. 2018, 43, 5877–5880. [Google Scholar] [CrossRef]
- Cai, B.; Hao, C.; Xie, Z.; Sheng, D. Applications of multipass cells in atomic magnetometers and co-magnetometers. Bull. Am. Phys. Soc. 2019, 64, 4. [Google Scholar]
- White, J.U. Long optical paths of large aperture. JOSA 1942, 32, 285–288. [Google Scholar] [CrossRef]
- McManus, J.B.; Kebabian, P.L.; Zahniser, M.S. Astigmatic mirror multipass absorption cells for long-path-length spectroscopy. Appl. Opt. 1995, 34, 3336–3348. [Google Scholar] [CrossRef] [PubMed]
- Chernin, S.M.; Barskaya, E.G. Optical multipass matrix systems. Appl. Opt. 1991, 30, 51–58. [Google Scholar] [CrossRef]
- Chernin, S.M. New generation of multipass systems in high resolution spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1996, 52, 1009–1022. [Google Scholar] [CrossRef]
- Hawe, E.; Fitzpatrick, C.; Chambers, P.; Lewis, E. An investigation into the use of an integrating sphere as a gas absorption cell. J. Opt. A Pure Appl. Opt. 2007, 9, S12. [Google Scholar] [CrossRef]
- Thoma, M.L.; Kaschow, R.; Hindelang, F.J. A multiple-reflection cell suited for absorption measurements in shock tubes. Shock Waves 1994, 4, 51–53. [Google Scholar] [CrossRef]
- Manninen, A.; Tuzson, B.; Looser, H.; Bonetti, Y.; Emmenegger, L. Versatile multipass cell for laser spectroscopic trace gas analysis. Appl. Phys. B 2012, 109, 461–466. [Google Scholar] [CrossRef] [Green Version]
- Tuzson, B.; Mangold, M.; Looser, H.; Manninen, A.; Emmenegger, L. Compact multipass optical cell for laser spectroscopy. Opt. Lett. 2013, 38, 257–259. [Google Scholar] [CrossRef]
- Yang, Z.; Zou, M.; Sun, L. Generalized optical design of the multiple-row circular multi-pass cell with dense spot pattern. Opt. Express 2019, 27, 32883–32891. [Google Scholar] [CrossRef]
- Mangold, M.; Tuzson, B.; Hundt, M.; Jágerská, J.; Looser, H.; Emmenegger, L. Circular paraboloid reflection cell for laser spectroscopic trace gas analysis. JOSA A 2016, 33, 913–919. [Google Scholar] [CrossRef] [PubMed]
- Sabry, Y.M.; Saadany, B.; Khalil, D.; Bourouina, T. Silicon micromirrors with three-dimensional curvature enabling lensless efficient coupling of free-space light. Light Sci. Appl. 2013, 2, e94. [Google Scholar] [CrossRef]
- Guo, Y.; Sun, L. Compact optical multipass matrix system design based on slicer mirrors. Appl. Opt. 2018, 57, 1174–1181. [Google Scholar] [CrossRef] [PubMed]

| 0.01 | 0.03 | 0.05 | 0.07 | 0.09 | ||
|---|---|---|---|---|---|---|
| 0.91 | (5, 11, 19.8) | (5, 11, 19.8) | (4, 9, 15.8) | (3, 7, 11.7) | (3, 7, 11.7) | |
| 0.93 | (6, 13, 23.8) | (5, 11, 19.8) | (4, 9, 15.8) | (3, 8, 12.9) | (3, 7, 11.7) | |
| 0.95 | (9, 19, 35.9) | (5, 12, 21.3) | (4, 9, 15.8) | (3, 8, 12.9) | (3, 7, 11.7) | |
| 0.97 | (10, 21, 39.9) | (5, 12, 21.3) | (4, 9, 15.8) | (3, 8, 12.9) | (3, 7, 11.7) | |
| 0.99 | (10, 21, 39.9) | (5, 12, 21.3) | (4, 9, 15.8) | (3, 8, 12.9) | (3, 7, 11.7) | |
| Parameter | Value |
|---|---|
| Metallization material | Gold |
| Cell radius | 3 |
| Cell () | 22, 9 |
| Depth | 0.19 |
| Input mirror (,) | 8.8, 1.2 |
| Output mirror () | 6.7, 1.4 |
| Cell mirrors () | 5.3, 0.9 |
| Cell area | 7 × 8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathy, A.; Sabry, Y.M.; Gnambodoe-Capochichi, M.; Marty, F.; Khalil, D.; Bourouina, T. Silicon Multi-Pass Gas Cell for Chip-Scale Gas Analysis by Absorption Spectroscopy. Micromachines 2020, 11, 463. https://doi.org/10.3390/mi11050463
Fathy A, Sabry YM, Gnambodoe-Capochichi M, Marty F, Khalil D, Bourouina T. Silicon Multi-Pass Gas Cell for Chip-Scale Gas Analysis by Absorption Spectroscopy. Micromachines. 2020; 11(5):463. https://doi.org/10.3390/mi11050463
Chicago/Turabian StyleFathy, Alaa, Yasser M. Sabry, Martine Gnambodoe-Capochichi, Frederic Marty, Diaa Khalil, and Tarik Bourouina. 2020. "Silicon Multi-Pass Gas Cell for Chip-Scale Gas Analysis by Absorption Spectroscopy" Micromachines 11, no. 5: 463. https://doi.org/10.3390/mi11050463
APA StyleFathy, A., Sabry, Y. M., Gnambodoe-Capochichi, M., Marty, F., Khalil, D., & Bourouina, T. (2020). Silicon Multi-Pass Gas Cell for Chip-Scale Gas Analysis by Absorption Spectroscopy. Micromachines, 11(5), 463. https://doi.org/10.3390/mi11050463






